Copula-Based Joint Probability Analysis of Compound Floods from Rainstorm and Typhoon Surge: A Case Study of Jiangsu Coastal Areas, China
Abstract
1. Introduction
2. Materials and Methods
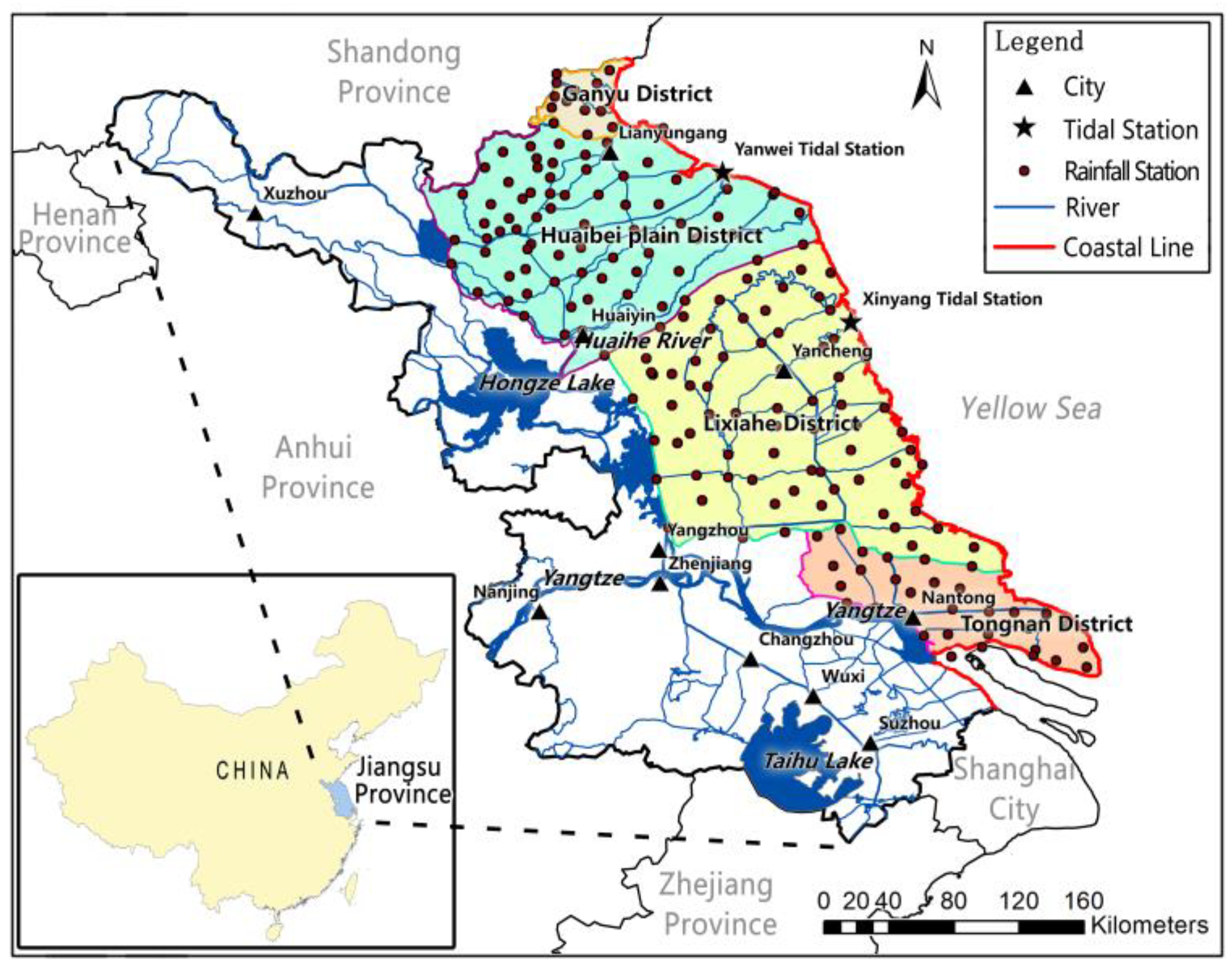
2.1. Study Area and Data
2.2. Marginal Distribution
2.3. Copula Functions
2.4. Parameter Estimations
3. Statistical Features of Historical Typical Hydrological Events in the Study Areas during the Period of 1960–2012
3.1. Rainstorms
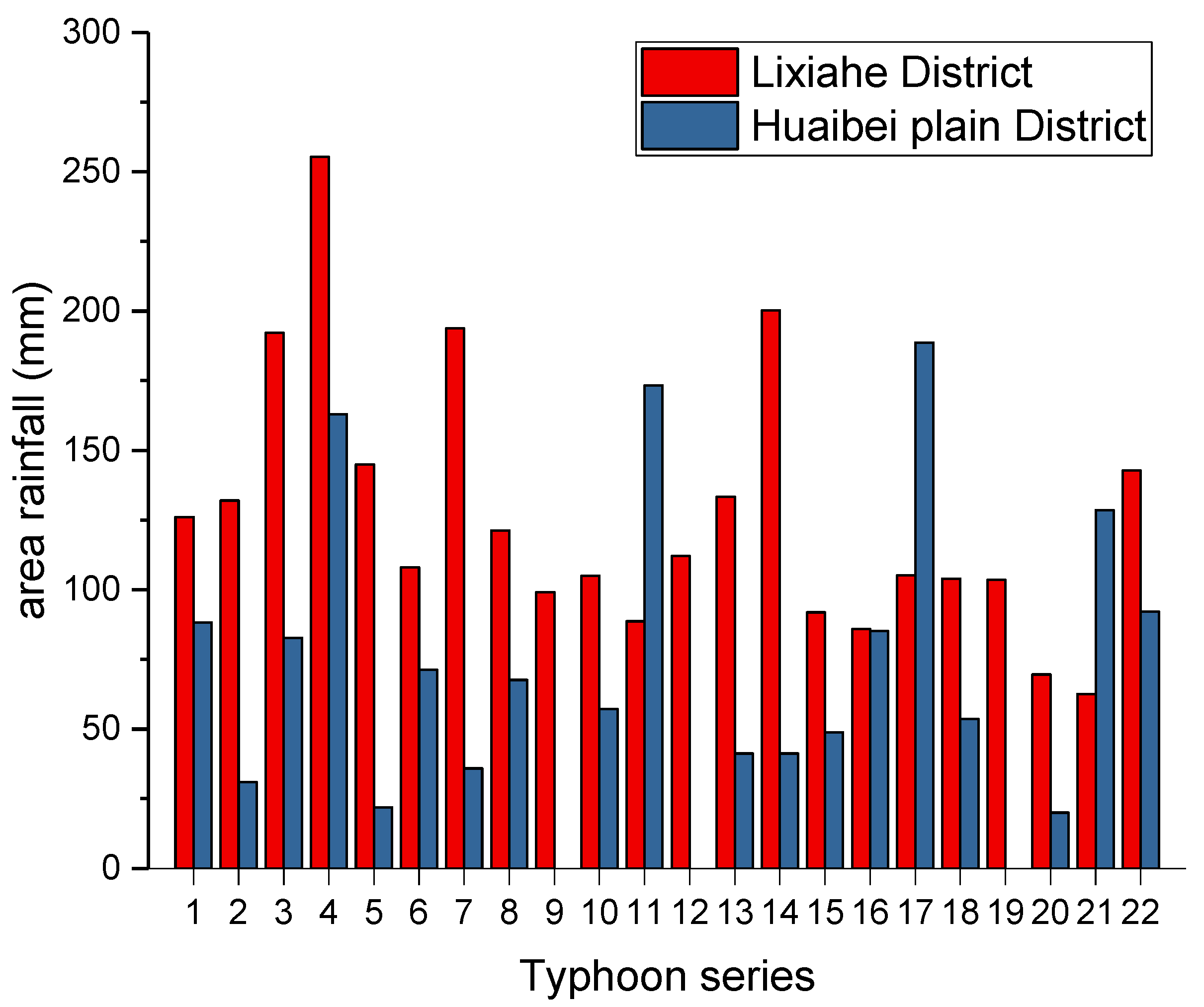
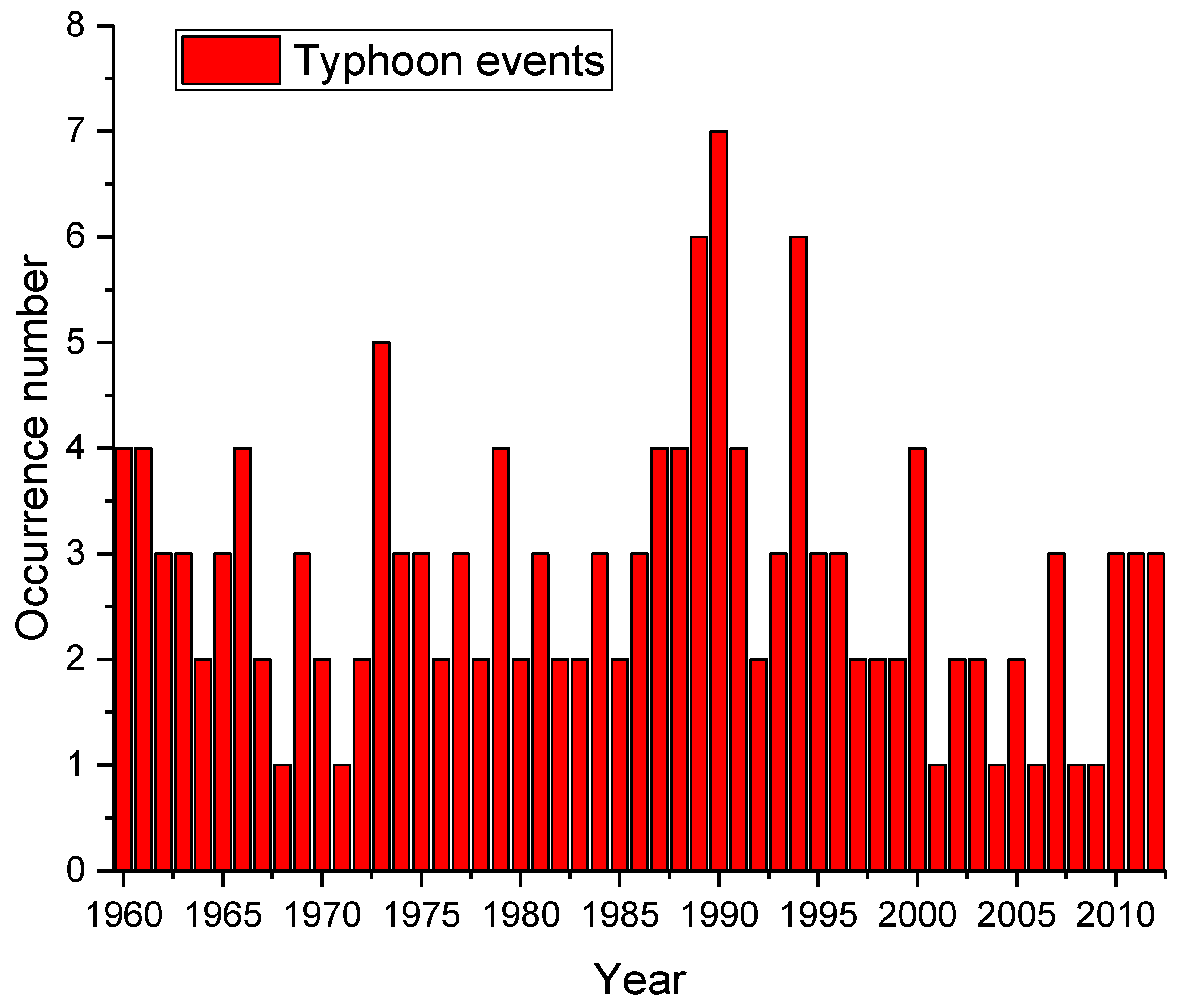
3.2. Typhoons and Typhoon Surges
4. Results and Discussion
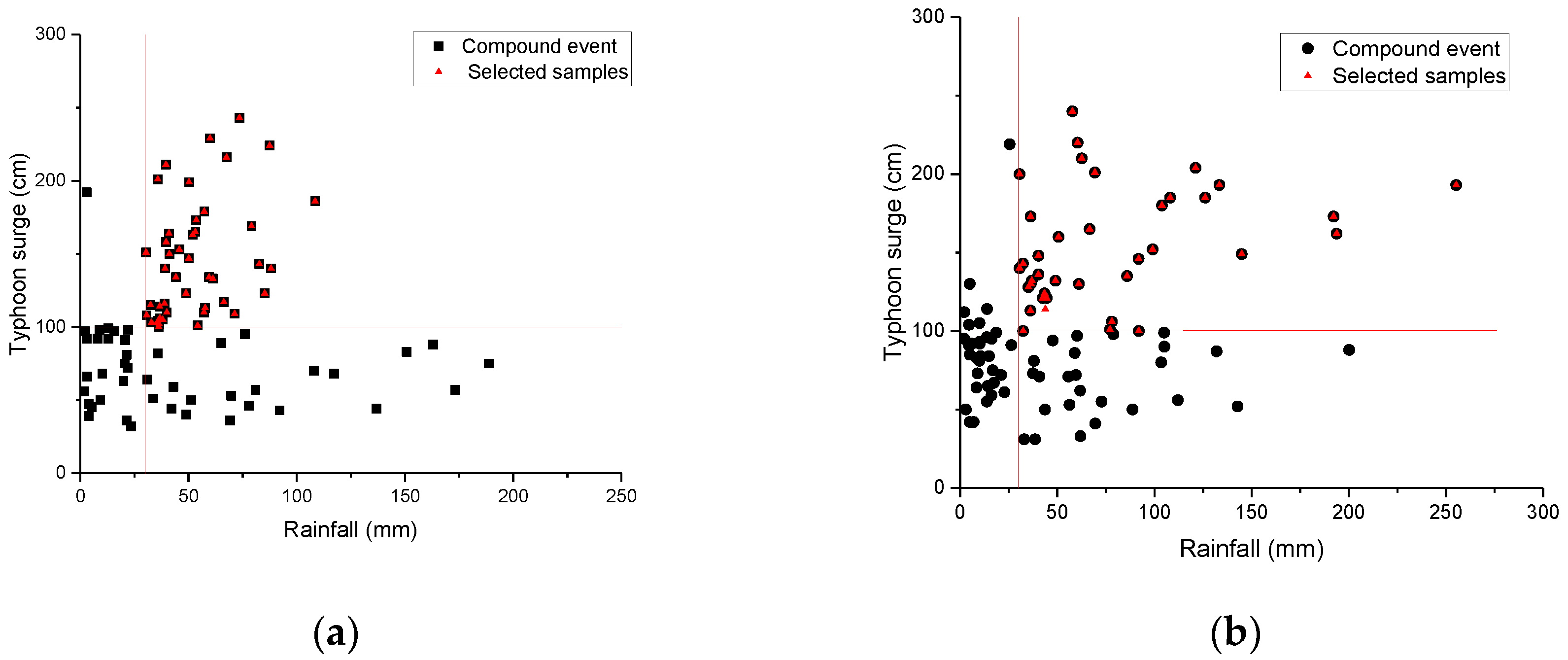
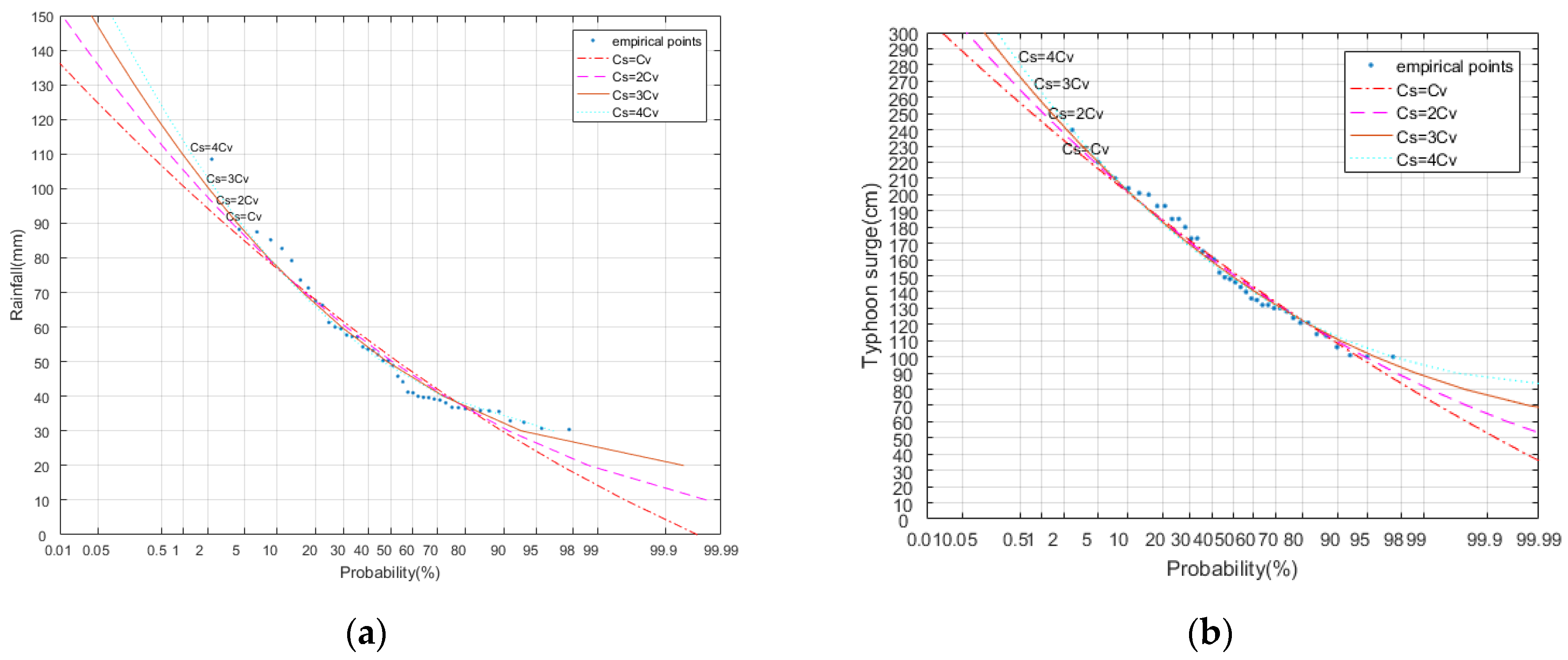
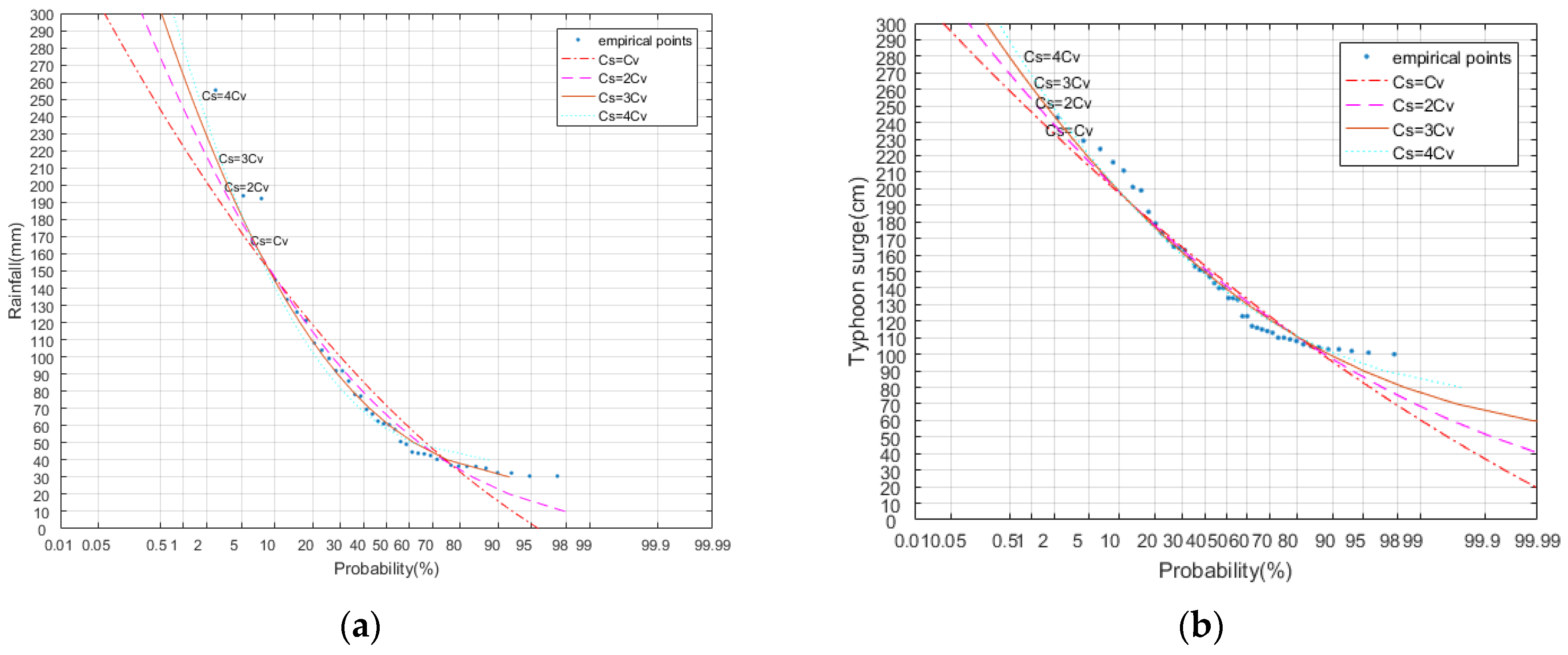
4.1. Marginal Distributions of Compound Events
4.2. Determination of the Disaster Risk Model
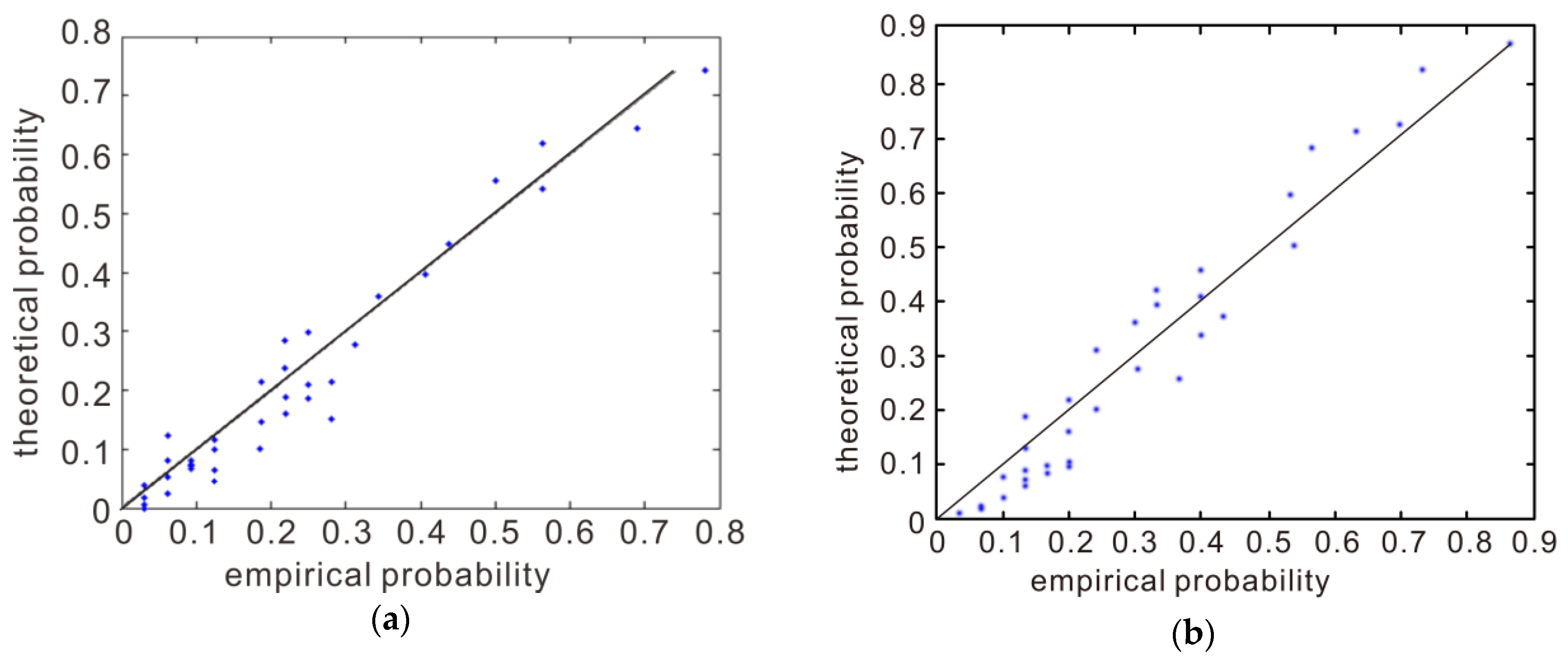
4.3. Selection of Copula Functions
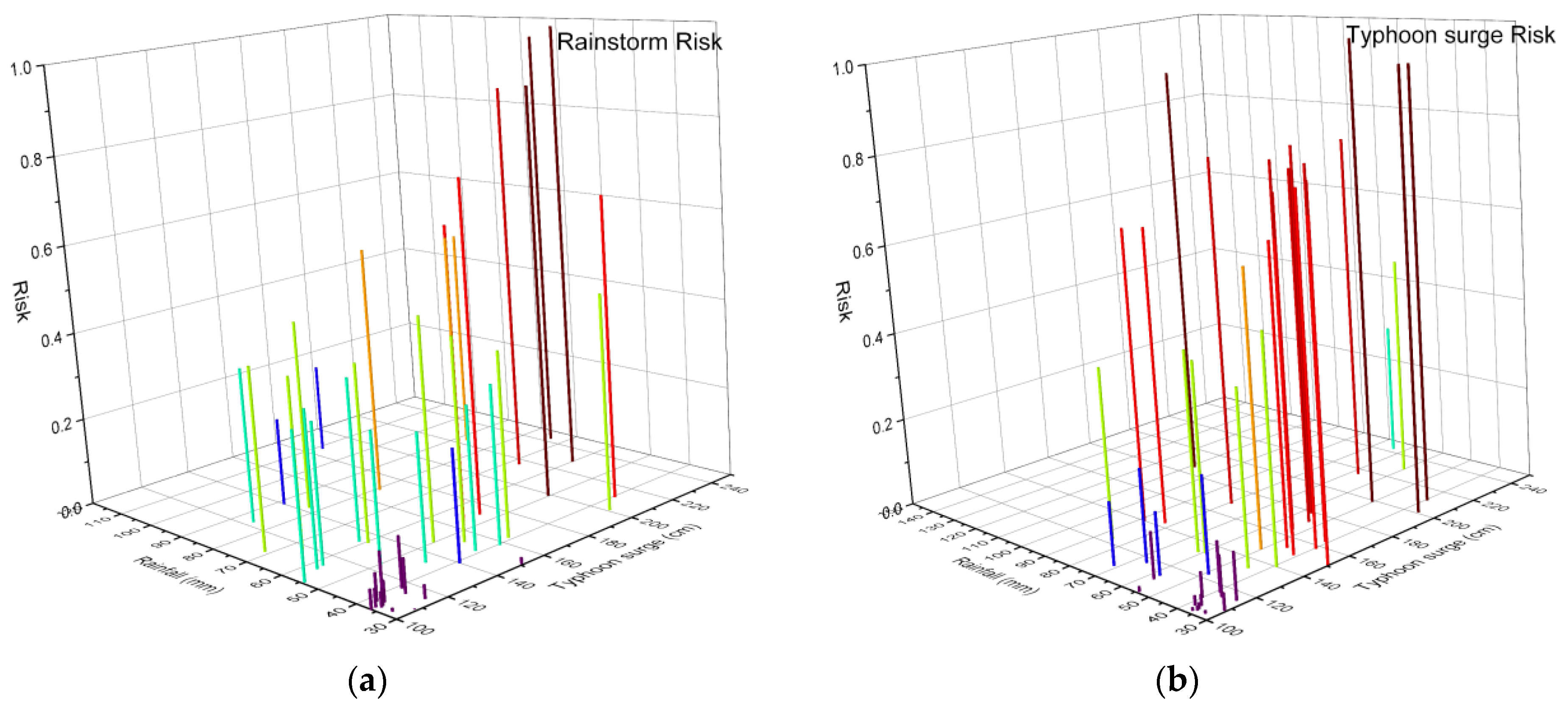
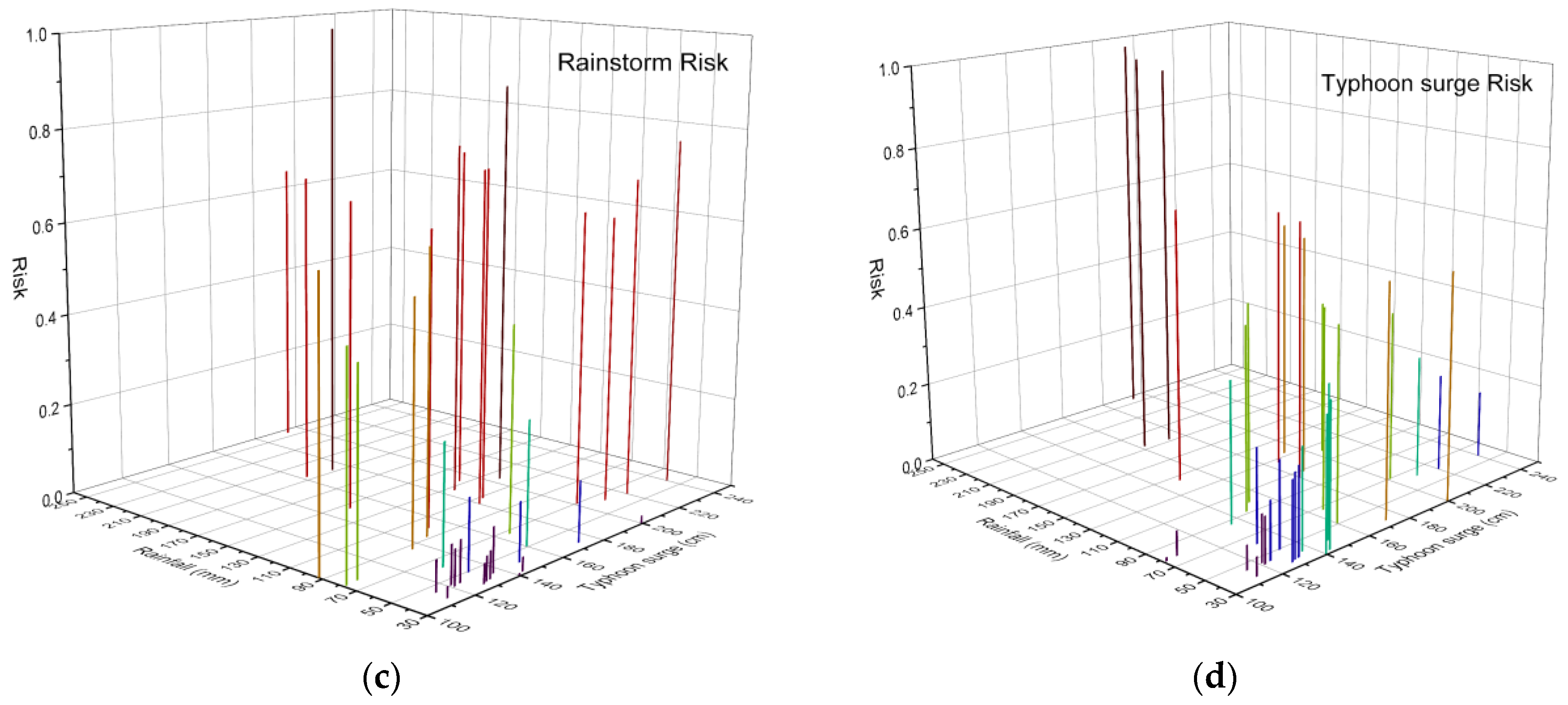
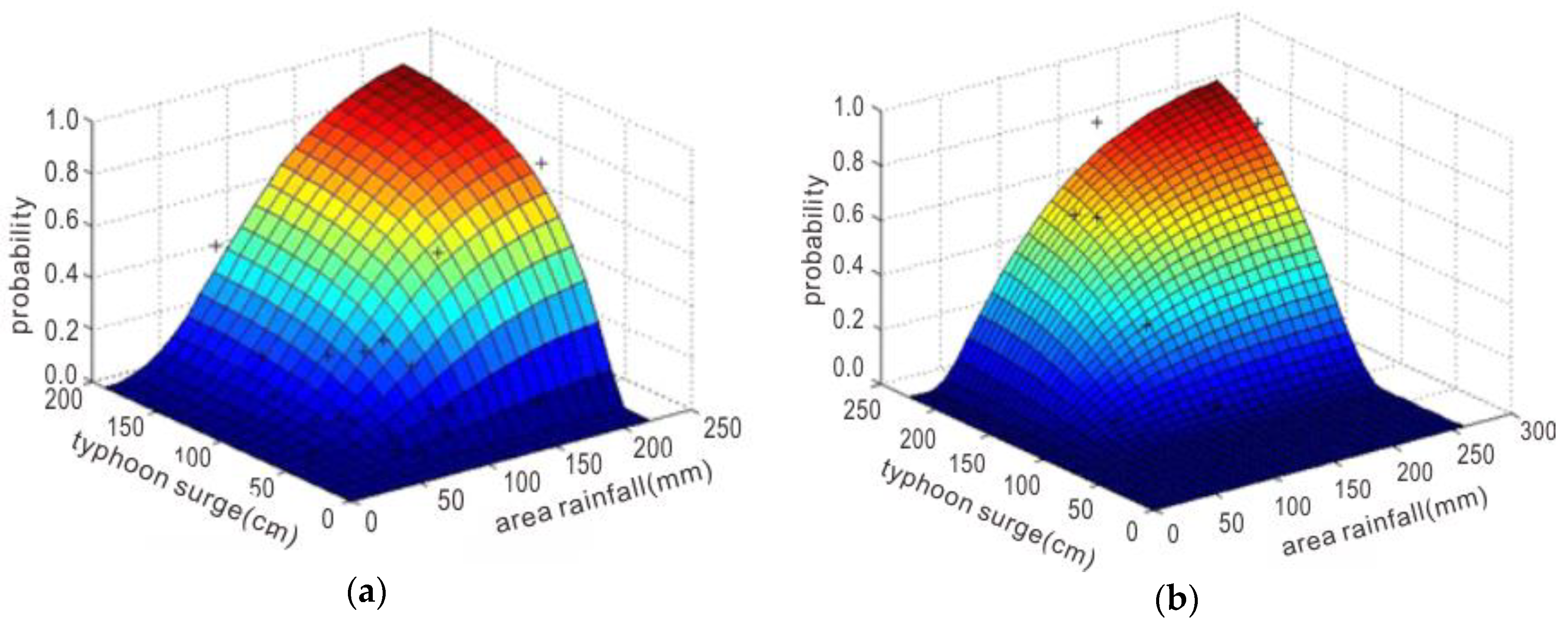
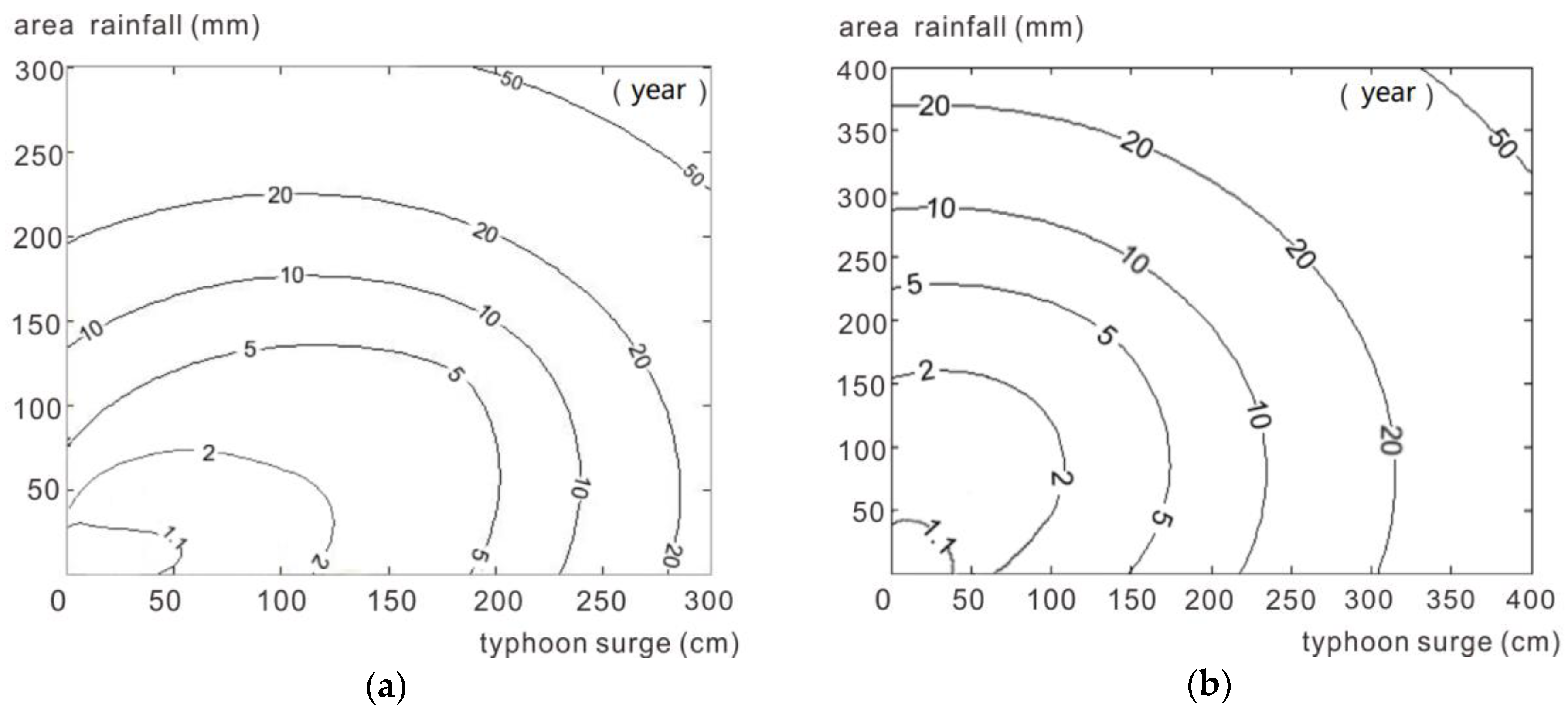
4.4. Joint Probability Distribution of Compound Events and Their Return Period
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tseng, C.M.; Jan, C.D.; Wang, J.S.; Wang, C.M. Application of artificial neural networks in typhoon surge forecasting. Ocean Eng. 2007, 34, 1757–1768. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfeemorlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Adger, W.N.; Hughes, T.P.; Folke, C.; Carpenter, S.R.; Rockström, J. Social-Ecological Resilience to Coastal Disasters. Science 2005, 309, 1036–1039. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zhong, P.A.; Zhang, Y.; Xu, B.; Ma, B.; Yan, K. Integrated flood risk assessment and zonation method: A case study in Huaihe River basin, China. Nat. Hazards 2015, 78, 635–651. [Google Scholar] [CrossRef]
- Wahl, T.; Mudersbach, C.; Jensen, J. Assessing the hydrodynamic boundary conditions for risk analyses in coastal areas: A stochastic storm surge model. Nat. Hazards Earth Syst. Sci. 2011, 11, 2925–2939. [Google Scholar] [CrossRef]
- Wang, J.; Gao, W.; Xu, S.; Yu, L. Evaluation of the combined risk of sea level rise, land subsidence, and storm surges on the coastal areas of Shanghai, China. Clim. Chang. 2012, 115, 537–558. [Google Scholar] [CrossRef]
- Qiang, Z.; Wu, L.G.; Liu, Q.F. Tropical cyclone damages in China 1983–2006. Am. Meteorol. Soc. 2009, 90, 489–495. [Google Scholar]
- Denny, J.L.; Yevjevich, V. Probability and Statistics in Hydrology. J. Am. Stat. Assoc. 1972, 68, 755. [Google Scholar] [CrossRef]
- Bras, R.L.; Rodríguez-Iturbe, I. Random Functions and Hydrology; Addison-Wesley: New York, NY, USA, 1984. [Google Scholar]
- Chebana, F.; Ouarda, T.B.M.J. Multivariate quantiles in hydrological frequency analysis. Environmetrics 2011, 22, 63–78. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; Tomasicchio, G.R.; D’Alessandro, F. Practical guidelines for the multivariate assessment of the structural risk in coastal and off-shore engineering. Coast. Eng. 2015, 95, 77–83. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de Répartition À N Dimensions Et Leurs Marges; Publications de Institute de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Sklar, A. Random Variables, Distribution Functions, and Copulas: A Personal Look Backward and Forward. Lect. Notes Monogr. Ser. 1996, 28, 1–14. [Google Scholar]
- Nelsen, B. An Introduction to Copulas; Springer: New York, NY, USA, 2006; p. 315. [Google Scholar]
- Zhao, P.; Lü, H.; Fu, G.; Zhu, Y.; Su, J.; Wang, J. Uncertainty of Hydrological Drought Characteristics with Copula Functions and Probability Distributions: A Case Study of Weihe River, China. Water 2017, 9, 334. [Google Scholar] [CrossRef]
- Hu, S.Y.; Wang, Z.Z.; Wang, Y.T.; Wu, H.Y.; Jin, J.L.; Feng, X.C.; Liang, C. Encounter probability analysis of typhoon and plum rain in the Taihu Lake Basin. Sci. China Technol. Sci. 2010, 53, 3331–3340. [Google Scholar] [CrossRef]
- Jenqtzong, S.; Wang, H.Y.; Changtai, T. Copula-based depth-duration-frequency analysis of typhoons in Taiwan. Hydrol. Res. 2010, 41, 414–423. [Google Scholar]
- Tao, S.; Dong, S.; Wang, N.; Soares, C.G. Estimating storm surge intensity with Poisson bivariate maximum entropy distributions based on copulas. Nat. Hazards 2013, 68, 791–807. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.; Luther, M. Increasing Risk of Compound Flooding from Storm Surge and Rainfall for Major US Coastal Cities. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Kwon, T.; Yoon, S. Analysis of extreme wind speed and precipitation using copula. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 23–28 April 2017. [Google Scholar]
- Dong, S.; Jiao, C.S.; Tao, S.S. Joint return probability analysis of wind speed and rainfall intensity in typhoon-affected sea area. Nat. Hazards 2017, 86, 1193–1205. [Google Scholar] [CrossRef]
- Woodruff, J.D.; Irish, J.L.; Camargo, S.J. Coastal flooding by tropical cyclones and sea-level rise. Nature 2013, 504, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, M.K.; Oppenheimer, M.; Kopp, R.E. Amplification of flood frequencies with local sea level rise and emerging flood regimes. Environ. Res. Lett. 2017, 12, 64009. [Google Scholar] [CrossRef]
- Wu, Y.; Zhong, P.A.; Xu, B.; Zhu, F.; Ma, B. Changing of flood risk due to climate and development in Huaihe River basin, China. Stoch. Environ. Res. Risk Assess. 2017, 31, 935–948. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Pugh, D.T. Tides, Surges and Mean Sea-Level; John Wiley & Sons, Inc.: New York, NY, USA, 1987; pp. 53–56. [Google Scholar]
- Srikanthan, R.; Mcmahon, T.A. Log Pearson III distribution—An empirically-derived plotting position. J. Hydrol. 1981, 52, 161–163. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Kluwer Academic: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Liu, D.; Guo, S.; Lian, Y.; Xiong, L.; Chen, X. Climate-informed low-flow frequency analysis using nonstationary modelling. Hydrol. Process. 2015, 29, 2112–2124. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Pan, S.; Pan, Y.; Fang, J.; Sowa, D.M.A. Estimation of mean and extreme waves in the East China Seas. Appl. Ocean Res. 2016, 56, 35–47. [Google Scholar] [CrossRef]
- Sadegh, M.; Ragno, E.; Aghakouchak, A. Multivariate Copula Analysis Toolbox (MvCAT): Describing dependence and underlying uncertainty using a Bayesian framework. Water Resour. Res. 2017. [Google Scholar] [CrossRef]
- Fasano, G.; Franceschini, A. A multidimensional version of the Kolmogorov–Smirnov test. Mon. Not. R. Astron. Soc. 1987, 225, 9–20. [Google Scholar] [CrossRef]
- Stephens, M.A. Anderson–Darling Test for Goodness of Fit; John Wiley & Sons, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Hafner, C.M.; Manner, H. Dynamic stochastic copula models: Estimation, inference and applications. J. Appl. Econom. 2012, 27, 269–295. [Google Scholar] [CrossRef]
- Genest, C.; Quessy, J.F.; Rémillard, B. Asymptotic Local Efficiency of Cramér-Von Mises Tests for Multivariate Independence. Ann. Stat. 2007, 35, 166–191. [Google Scholar] [CrossRef]
- Omelka, M.; Gijbels, I.; Veraverbeke, N. Improved Kernel Estimation of Copulas: Weak Convergence and Goodness-of-Fit Testing. Ann. Stat. 2009, 37, 3023–3058. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.-P. Statistical Inference Procedures for Bivariate Archimedean Copulas. Publ. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Fermanian, J.D. Goodness-of-Fit Tests for Copulas; Academic Press, Inc.: New York, NY, USA, 2005; pp. 119–152. [Google Scholar]
- Zheng, F.; Leonard, M.; Westra, S. Application of the design variable method to estimate coastal flood risk. J. Flood Risk Manag. 2017, 10, 522–534. [Google Scholar] [CrossRef]





| Family | Expression | Parameter Space | Relationship between and | |
|---|---|---|---|---|
| Clayton | ||||
| Frank | ||||
| Gumbel |
| Type | Plum Rain | Typhoon Rain | Convective Rain |
|---|---|---|---|
| Number of occurrences | 62 | 22 | 105 |
| Duration (days) | 20–30 | 1–4 | 1–2 |
| Average area rainfall (mm) | 231.4 | 104.1 | 54.8 |
| Areas | Event | Mean Value | Coefficient of Variation | Skew Factor |
|---|---|---|---|---|
| Huaibei plain District | Area rainfall | 52.6 mm | 0.41 | 3.0 |
| Typhoon surge | 145.2 cm | 0.28 | 2.0 | |
| Lixiahe District | Area rainfall | 77.5 mm | 0.67 | 3.0 |
| Typhoon surge | 153.8 cm | 0.24 | 4.0 |
| Areas | Copula | Parameter | K–S | RMSE | AIC |
|---|---|---|---|---|---|
| Huaibei plain District | Clayton | −0.362 | 0.1065 | 0.0365 | −322.65 |
| Frank | 2.263 | 0.1454 | 0.0309 | −369.14 | |
| Gumbel | 0.930 | 0.1597 | 0.0321 | −365.06 | |
| Lixiahe District | Clayton | 4.50 | 0.1935 | 0.0332 | −323.40 |
| Frank | 6.42 | 0.1791 | 0.0354 | −338.73 | |
| Gumbel | 3.31 | 0.1224 | 0.0323 | −336.69 |
| Surge | 50 cm | 100 cm | 150 cm | 200 cm | 250 cm | |
|---|---|---|---|---|---|---|
| Rainstorm | ||||||
| Huaibei Plain District | 50 mm | 70% | 60% | 30% | 20% | 9% |
| 100 mm | 35% | 25% | 25% | 20% | 8% | |
| 150 mm | 20% | 15% | 15% | 10% | 6% | |
| 200 mm | 10% | 7% | 7% | 5% | 3% | |
| Lixiahe District | 50 mm | 55% | 30% | 15% | 8% | |
| 100 mm | 50% | 30% | 15% | 8% | ||
| 150 mm | 40% | 30% | 15% | 8% | ||
| 200 mm | 30% | 15% | 10% | 6% | ||
| 250 mm | 12% | 10% | 6% | 5% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, P.; Yuan, D.; Xiong, C. Copula-Based Joint Probability Analysis of Compound Floods from Rainstorm and Typhoon Surge: A Case Study of Jiangsu Coastal Areas, China. Sustainability 2018, 10, 2232. https://doi.org/10.3390/su10072232
Ai P, Yuan D, Xiong C. Copula-Based Joint Probability Analysis of Compound Floods from Rainstorm and Typhoon Surge: A Case Study of Jiangsu Coastal Areas, China. Sustainability. 2018; 10(7):2232. https://doi.org/10.3390/su10072232
Chicago/Turabian StyleAi, Ping, Dingbo Yuan, and Chuansheng Xiong. 2018. "Copula-Based Joint Probability Analysis of Compound Floods from Rainstorm and Typhoon Surge: A Case Study of Jiangsu Coastal Areas, China" Sustainability 10, no. 7: 2232. https://doi.org/10.3390/su10072232
APA StyleAi, P., Yuan, D., & Xiong, C. (2018). Copula-Based Joint Probability Analysis of Compound Floods from Rainstorm and Typhoon Surge: A Case Study of Jiangsu Coastal Areas, China. Sustainability, 10(7), 2232. https://doi.org/10.3390/su10072232





