Implementation of Observed Sky-View Factor in a Mesoscale Model for Sensitivity Studies of the Urban Meteorology
Abstract
:1. Introduction
2. Methodology
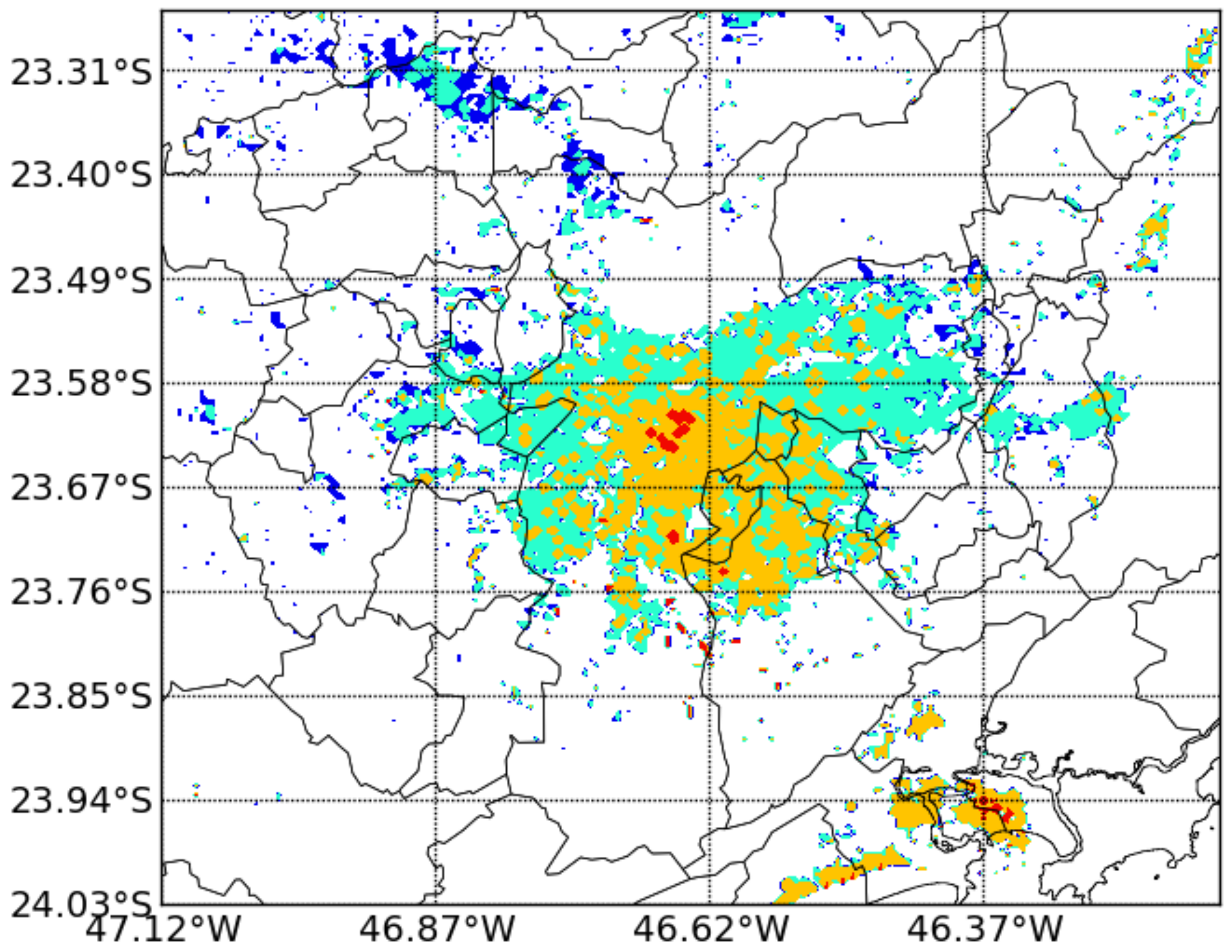
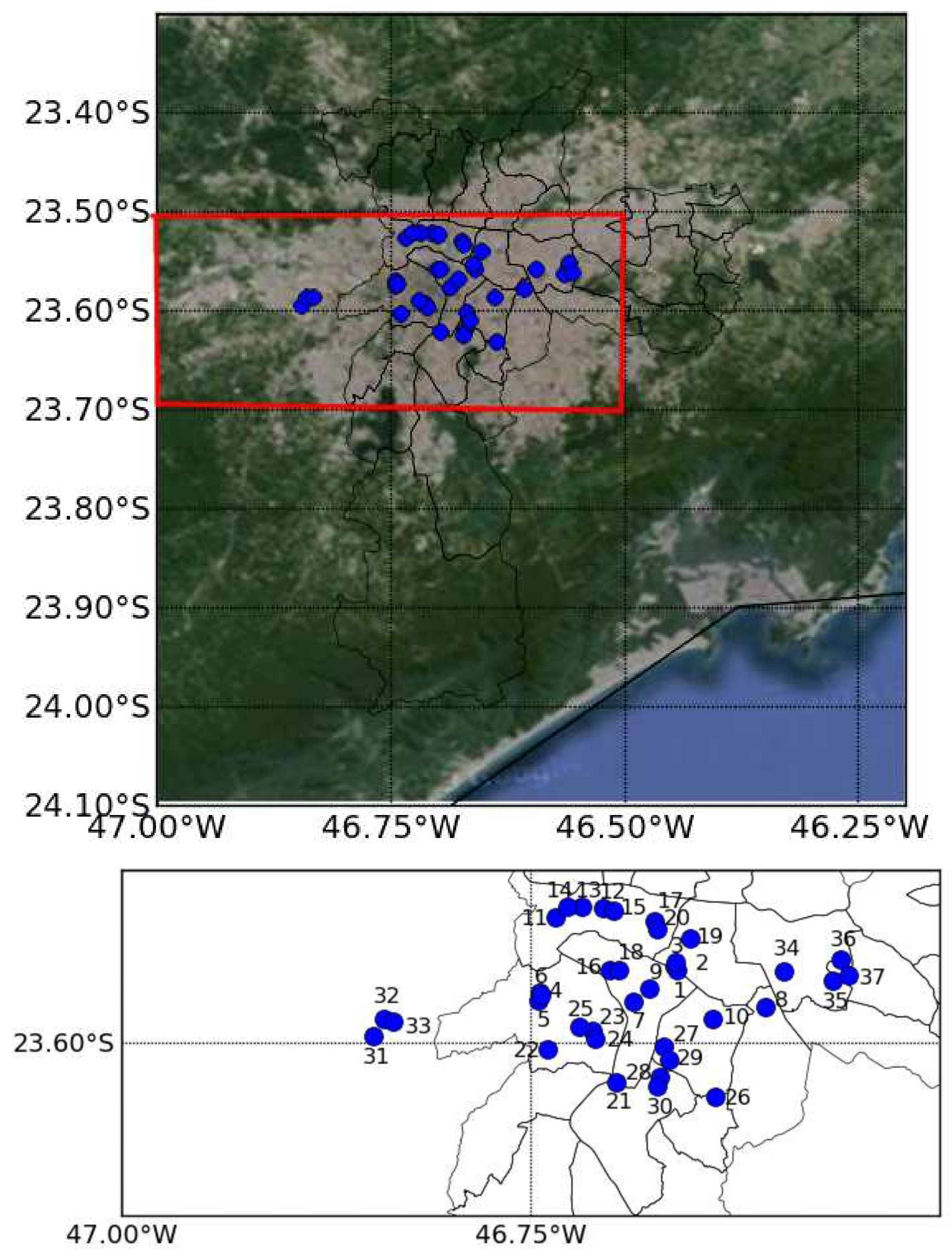
2.1. Sky-View Factor
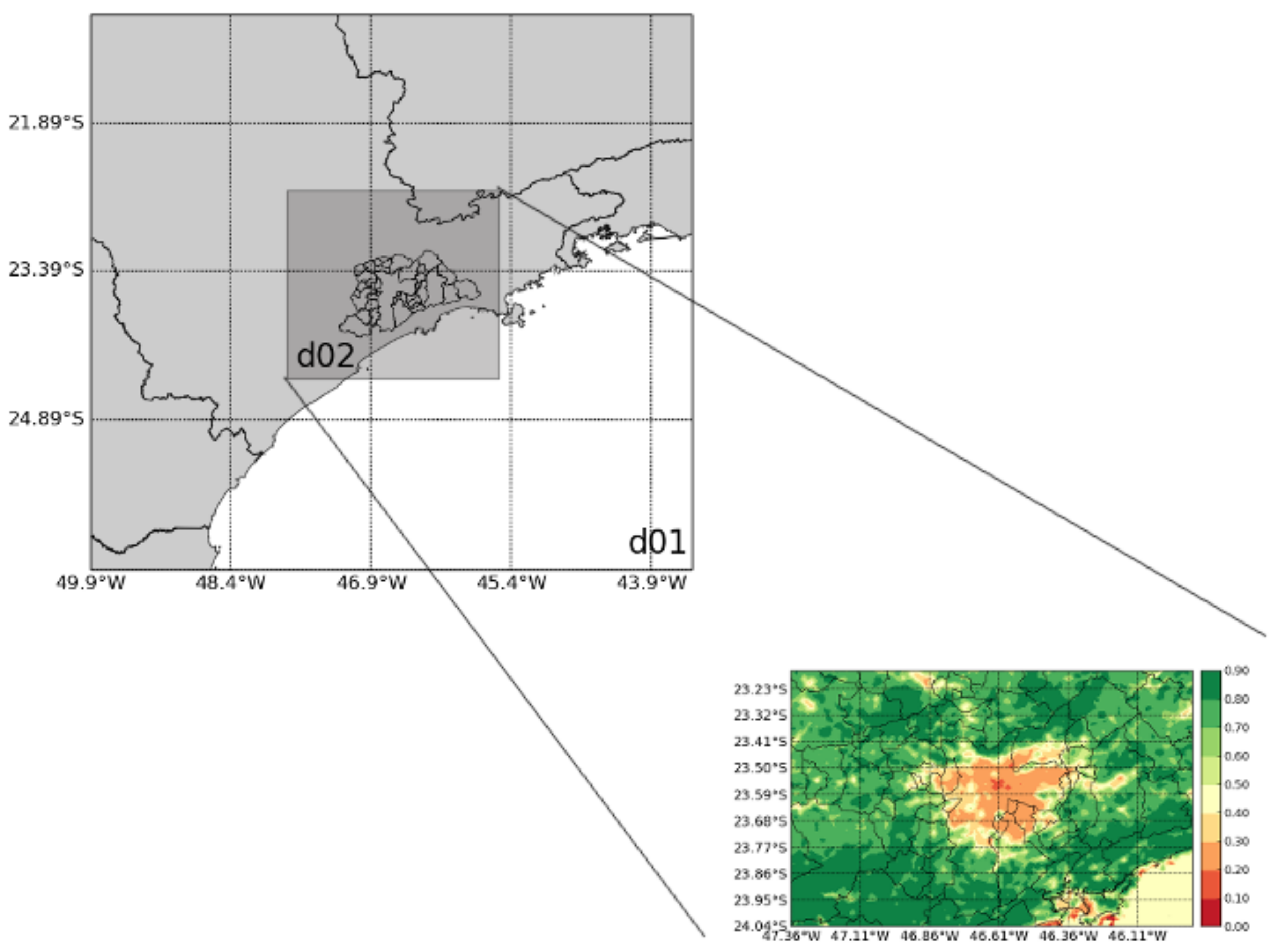
2.2. Modeling System
2.3. Simulations Description
- (i)
- Simulation A used the original formulation of the TEB scheme, in which the fundamental canopy geometric variable is the aspect-ratio, as given according to the urban-type classification (Table 2). From the aspect-ratio, the street and walls sky-view factors were computed using the mathematical formulation of the model (Masson’s TEB). In other words, Simulation A was the standard simulation.
- (ii)
- Simulation B used the observed street SVFs for each grid-point on the surface instead of computing them from the aspect-ratio. Wall SVF was obtained from Equation (1a). Thereby, the entire canopy radiation budget is now geometrically ruled by observed SVFs, but not by the aspect-ratios. The aspect-ratios, however, play their role in other aspects of the model dynamics such as scaling the roughness length and influencing the momentum sink.
- (iii)
- Simulation C used the street and wall SVFs as in Simulation A, but the aspect-ratios was computed as a function of the observed street SVF, according to
3. Results and Discussion
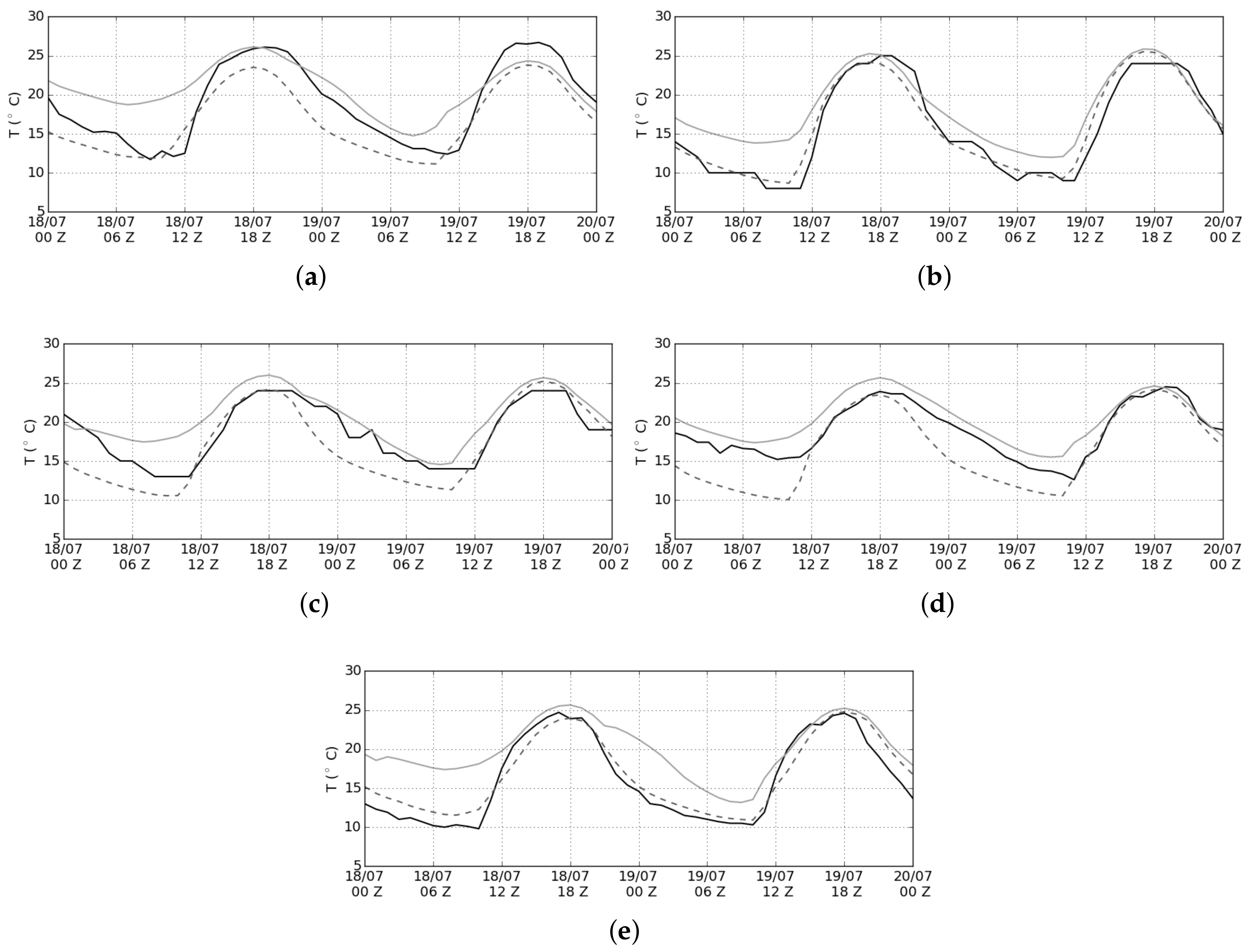
3.1. Evaluation
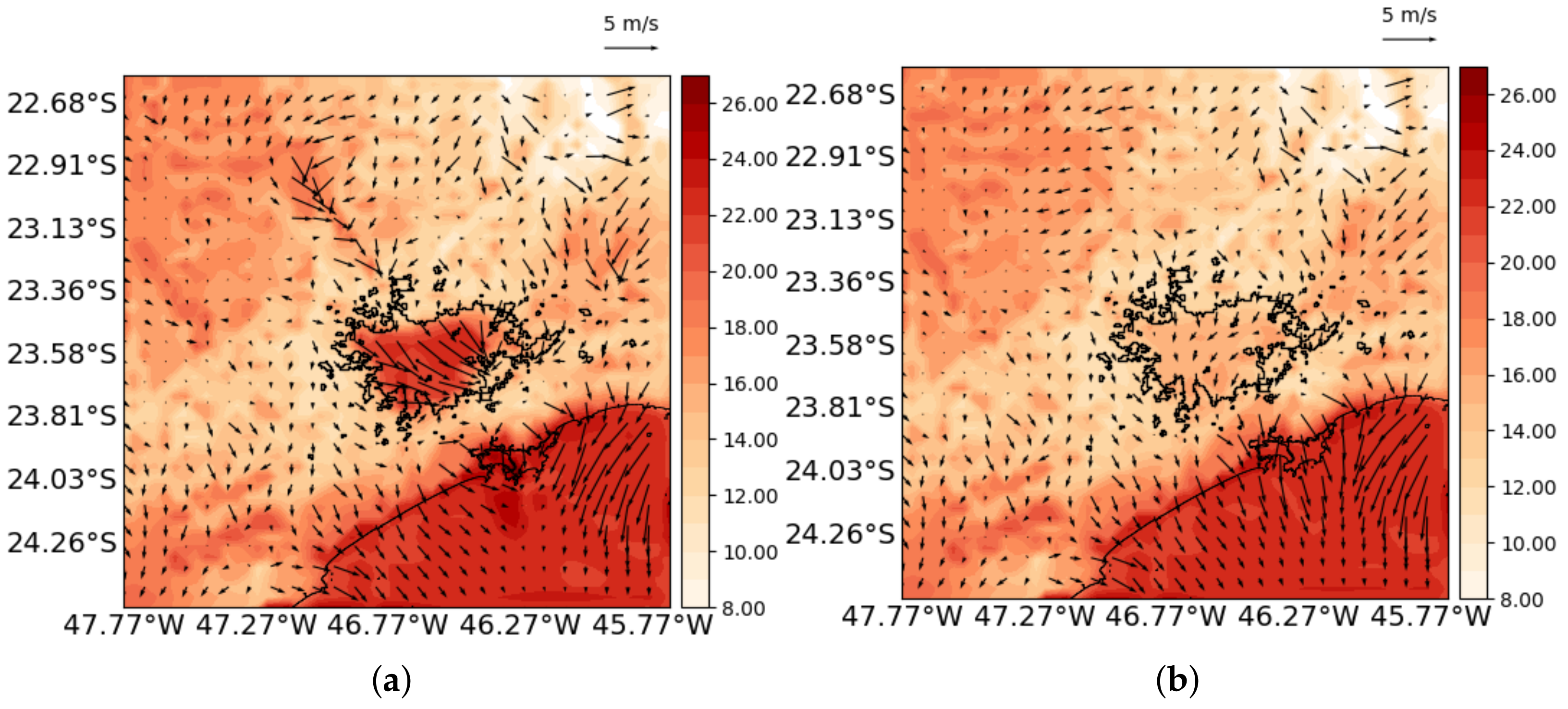
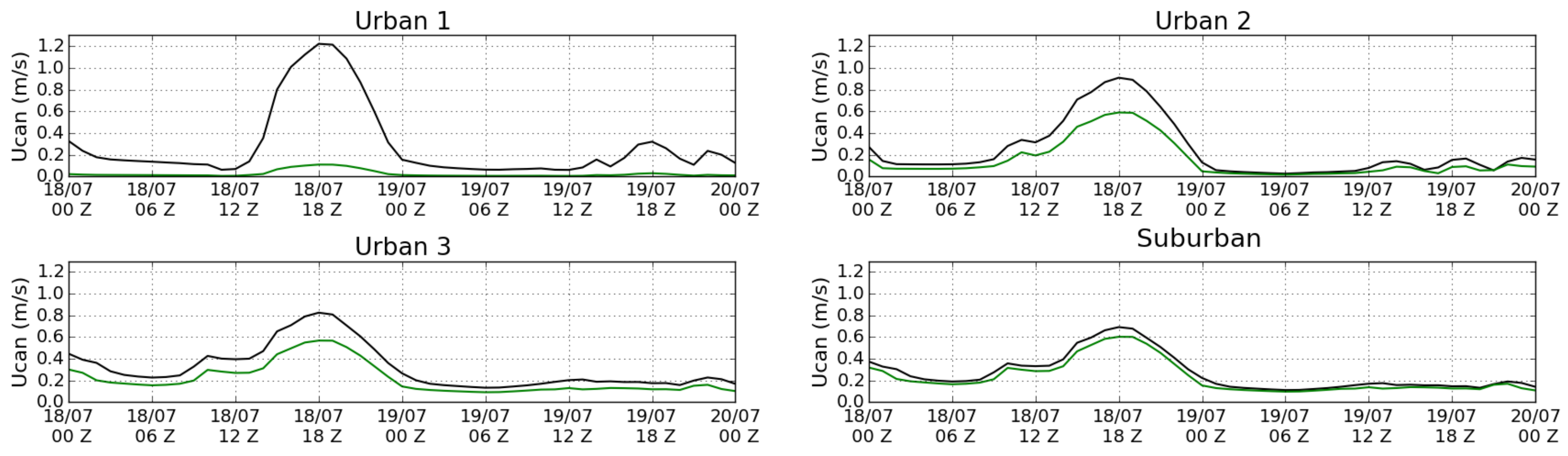
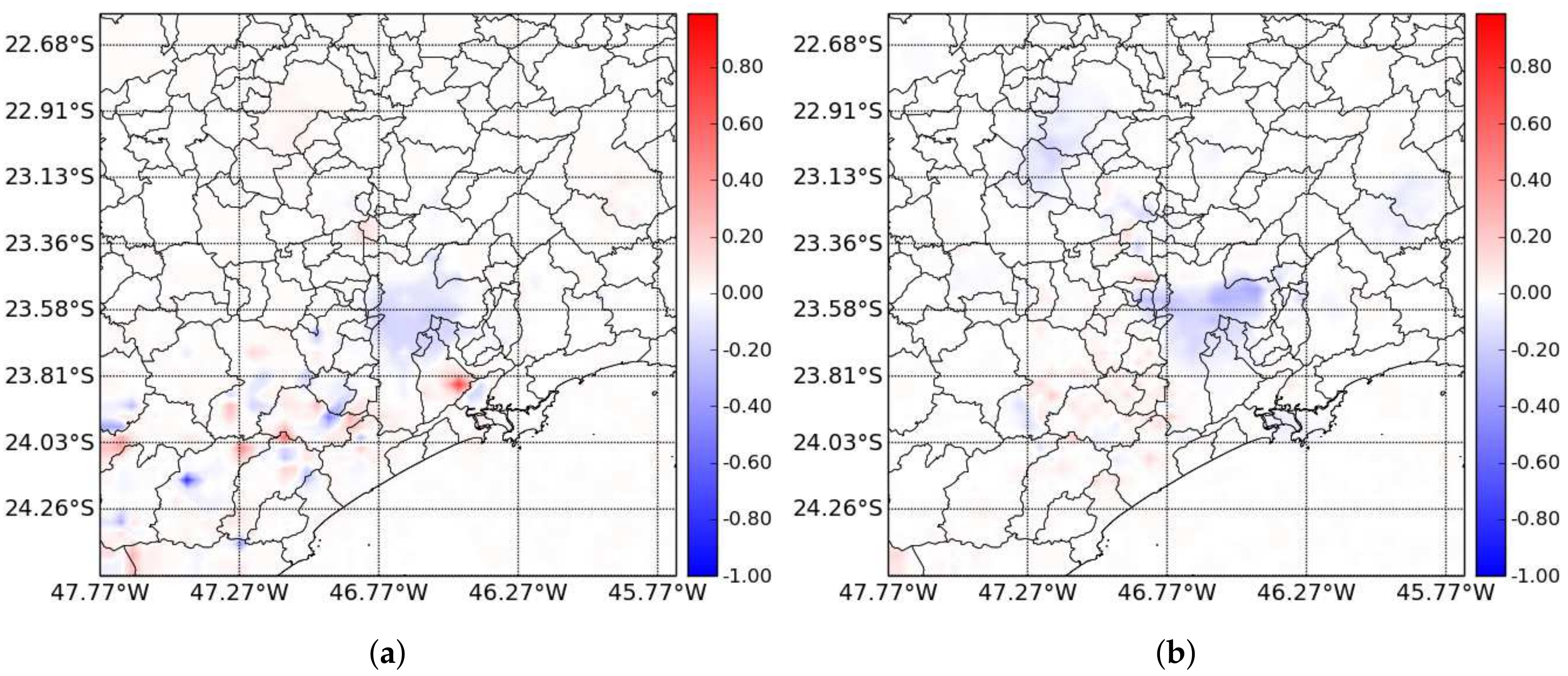
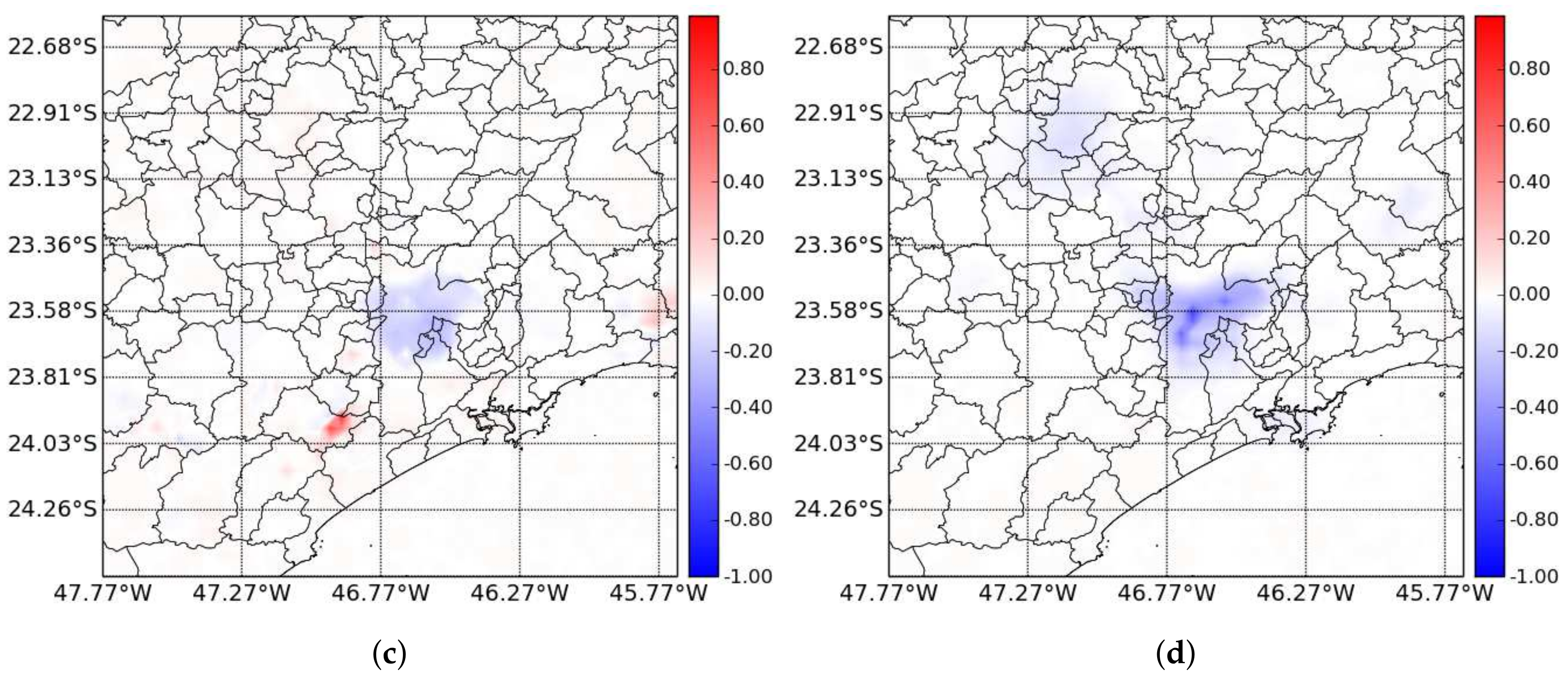
3.2. Sensitivity Tests
4. Conclusions and Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SVF | Sky View Factor |
| TEB | Town Energy Budget |
| MASP | Metropolitan Area of São Paulo |
| CAD | Computer-Aided Design |
| GIS | Geographic Information System |
| BRAMS | Brazilian Developments on the Regional Atmospheric Modeling System |
| LEAF | Land Ecosystem-Atmosphere Feedback |
| NDVI | Normalized Difference Vegetation Index |
| GFS | Global Forecasting System |
| NCEP | National Center for Environmental Prediction |
References
- The World Bank. Urban Population (% of Total) the United Nations Population Division’s World Urbanization Prospects. Available online: https://data.worldbank.org/indicator/SP.URB.TOTL.IN.ZS (accessed on 18 December 2017).
- Kusaka, H.; Kondo, H.; Kikegawa, Y.; Kimura, F. A simple single-layer urban canopy model for atmospheric models: Comparison with multi-layer and slab models. Bound.-Layer Meteorol. 2001, 101, 229–258. [Google Scholar] [CrossRef]
- Martilli, A.; Clappier, A.; Rotach, M.W. An urban surface Exchange parameterization for mesoscale models. Bound.-Layer Meteorol. 2002, 104, 261–304. [Google Scholar] [CrossRef]
- Masson, V. A physically-based scheme for the urban energy budget in atmospheric models. Bound.-Layer Meteorol. 2000, 94, 357–397. [Google Scholar] [CrossRef]
- Hamdi, R.; Schayes, G. Sensitivity study of the urban heat island intensity to urban characteristics. Int. J. Climatol. 2007, 28, 973–982. [Google Scholar] [CrossRef]
- Freitas, E.D.; Rozoff, C.; Cotton, W.R.; Silva Dias, P.L. Interactions of urban heat island and sea breeze circulations during winter over the Metropolitan Area of São Paulo—Brazil. Bound.-Layer Meteorol. 2007, 122, 43–65. [Google Scholar] [CrossRef]
- Salamanca, F.; Martilli, A.; Tewari, M.; Chen, F. A Study of the Urban Boundary Layer Using Different Urban Parameterizations and High-Resolution Urban Canopy Parameters with WRF. J. Appl. Meteorol. Climatol. 2011, 50, 1107–1128. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M.; Chen, F. Numerical simulations of boundary-layer processes and urban-induced alterations in an Alpine valley. Int. J. Climatol. 2014, 34, 1111–1131. [Google Scholar] [CrossRef]
- Svensson, M.K. Sky view factor analysis—Implications for urban air temperature differences. Meteorol. Appl. 2004, 11, 201–211. [Google Scholar] [CrossRef]
- Upmanis, H.; Chen, D. Influence of geographical factors and meteorological variables on nocturnal urban-park temperature differences A case study of summer 1995 in Goteborg, Sweden. Clim. Res. 1999, 13, 125–139. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: London, UK, 1987; p. 435. [Google Scholar]
- Watson, I.; Johnson, G. Graphical Estimation of sky-view factor in urban environments. J. Climatol. 1987, 7, 193–197. [Google Scholar] [CrossRef]
- Santamouris, M. Energy and Climate in the Urban Built Environment; James & James Science Publishers Ltd.: London, UK, 2001. [Google Scholar]
- Eliasson, I. Urban Nocturnal Temperatures, street geometry and land use. Atmos. Environ. 1996, 30, 379–392. [Google Scholar] [CrossRef]
- Marciotto, E.R.; Oliveira, A.P.; Hanna, S.R. Modeling study of the aspect ratio influence on urban canopy energy fluxes with a modified wall-canyon energy budget scheme. Build. Environ. 2010, 45, 2497–2505. [Google Scholar] [CrossRef]
- Hanna, S.; Marciotto, E.R.; Britter, R. Urban Energy Fluxes in Built-Up Downtown Areas and Variations across the Urban Area, for Use in Dispersion Models. J. Appl. Meteorol. Climatol. 2011, 50, 1341–1353. [Google Scholar] [CrossRef]
- Marciotto, E.R. Variability of energy fluxes in relation to the net-radiation of urban and suburban areas: A case study. Meteorol. Atmos. Phys. 2013, 121, 17–28. [Google Scholar] [CrossRef]
- Georgakis, C.; Santamouris, M. Experimental investigation of air flow and temperature distribution in deep urban canyons for natural ventilation purposes. Energy Build. 2006, 38, 367–376. [Google Scholar] [CrossRef]
- Marciotto, E.R.; Fisch, G. Wind tunnel study of turbulent flow past an urban canyon model. Environ. Fluid Mech. 2013, 13, 403–416. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M. Characterization of the Thermal Structure inside an Urban Canyon: Field Measurements and Validation of a Simple Model. J. Appl. Meteorol. Climatol. 2013, 52, 64–81. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Numerical study on the effects of aspect ratio and orientation of an urban street canyon on outdoor thermal comfort in hot and dry climate. Build. Environ. 2006, 41, 94–108. [Google Scholar] [CrossRef]
- Memon, R.A.; Leung, D.Y.C.; Liu, C.H. Effects of building aspect ratio and wind speed on air temperatures in urban-like street canyons. Build. Environ. 2010, 45, 176–188. [Google Scholar] [CrossRef]
- Chen, L.; Ng, E.; An, X.; Ren, C.; Lee, M.; Wang, U.; He, Z. Sky view factor analysis of street canyons and its implications for daytime intra-urban air temperature differentials in high-rise, high-density urban areas of Hong Kong: A GIS-based simulation approach. Int. J. Climatol. 2012, 32, 121–136. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Cess, R.D. Radiation Heat Transfer; Brooks/Cole Publishing Company: Belmont, CA, USA, 1978. [Google Scholar]
- Grimmond, C.S.B.; Potter, S.K.; Zutter, H.N.; Souch, C. Rapid Methods to estimate Sky-View Factors applied to Urban Areas. Int. J. Climatol. 2001, 21, 903–913. [Google Scholar] [CrossRef]
- Hammerle, M.; Gál, T.; Unger, J.; Matzarakis, A. Introducing a script for calculating the sky view factor used for urban climate investigations. Acta Climatol. Chorol. 2011, 45, 83–92. [Google Scholar]
- Hammerle, M.; Gál, T.; Unger, J.; Matzarakis, A. Comparison of models calculating the sky view factor used for urban climate investigations. Theor. Appl. Climatol. 2011, 105, 521–527. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Nduka, I.C.; Iguisi, E.O.; Ati, O.F. An Assessment of the impact of Sky View Factor (SVF) on the Micro-climate of Urban Kano. Aust. J. Basic Appl. Sci. 2011, 5, 81–85. [Google Scholar]
- Santos, I.G.; Lima, H.G.; Assis, E.S. A graphical method for the Sky View Factor calculation in the Urban Heat Island Studies. In Proceedings of the 20th Passive and Low Energy Architeture, Santiago, Chile, 9–12 November 2003. [Google Scholar]
- Andrade, M.F.; Ynoue, R.; Freitas, E.D.; Todesco, E.; Vela, A.G.; Ibarra, S.; Martins, L.D.; Martins, J.A.; Carvalho, V.S.B. Air Quality forecasting system of Southeastern Brazil. Front. Environ. Sci. 2015, 3, 9. [Google Scholar] [CrossRef]
- Gouvêa, M.L. Cenários de Impacto das Propriedades da Superfície Sobre o Conforto térmico Humano na Cidade de São Paulo. Master’s Thesis, University of São Paulo, São Paulo, Brazil, 2007. [Google Scholar]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Morais, M.V.B.; Freitas, E.D.; Urbina Guerrero, V.V.; Martins, L.D. A modeling analysis of urban canopy parameterization representing the vegetation effects in the Megacity of São Paulo. Urban Clim. 2016, 17, 102–115. [Google Scholar] [CrossRef]
- Morais, M.V.B.; Marciotto, E.R.; Urbina Guerrero, V.V.; Freitas, E.D. Effective albedo estimates for the Metropolitan Area of São Paulo using empirical sky-view factors. Urban Clim. 2017, 21, 183–194. [Google Scholar] [CrossRef]
- Freitas, S.R.; Longo, K.M.; Silva Dias, M.A.F.; Chatfield, R.; Silva Dias, P.; Artaxo, P.; Andreae, M.O.; Grell, G.; Rodrigues, L.F.; Fazenda, A.; et al. The Coupled Aerosol and Tracer Transport Model to the Brazilian developments on the Regional Atmospheric Modeling System (CATT-BRAMS)—Part 1: Model description and evaluation. Atmos. Chem. Phys. 2009, 9, 2843–2861. [Google Scholar] [CrossRef]
- Freitas, S.R.; Panetta, J.; Longo, K.M.; Rodrigues, L.F.; Moreira, D.S.; Rosário, N.E.; Silva Dias, P.L.; Silva Dias, M.A.F.; Souza, E.P.; Freitas, E.D.; et al. The Brazilian developments on the Regional Atmospheric Modeling System (BRAMS 5.2): An integrated environmental model tuned for tropical areas. Geosci. Model Dev. 2017, 10, 189–222. [Google Scholar] [CrossRef]
- Lee, T.J. The Impact of Vegetation on the Atmospheric Boundary Layer and Convective Storms. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1992. [Google Scholar]
- Walko, R.L.; Band, L.E.; Baron, J.; Kittel, T.G.F.; Lammers, R.; Lee, T.J.; Ojima, D.; Pielke, R.A.; Taylor, C.; Tague, C.; et al. Coupled atmosphere-biophysics-hydrology models for environmental modeling. J. Appl. Meteorol. 2000, 39, 931–944. [Google Scholar] [CrossRef]
- SVMA (Secretaria do Verde e Meio Ambiente). Atlas ambiental de São Paulo. Available online: http://atlasambiental.prefeitura.sp.gov.br/conteudo/coberturavegetal/vegapres02.pdf (accessed on 13 November 2017).
- Klemp, J.B.; Wilhelmson, R.B. The simulation of three-dimensional convective storm dynamics. J. Atmos. Sci. 1978, 35, 1070–1096. [Google Scholar] [CrossRef]
- Chen, C.; Cotton, W.R. The physics of the marine stratocumulus-capped mixed layer. Bound.-Layer Meteorol. 1987, 25, 289–321. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: 1. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Hill, G.E. Factors controlling the size and spacing of cumulus clouds as revealed by numerical experiments. J. Atmos. Sci. 1974, 31, 646–673. [Google Scholar] [CrossRef]
- Lilly, D.K. On the numerical simulation of buoyant convection. Tellus 1962, 2, 148–172. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 2nd ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Hallak, R.; Pereira Filho, A.J. Metodologia para análise de desempenho de simulaćões de sistemas convectivos na região metropolitana de São Paulo com o modelo ARPS: Sensibilidade a variaćões com os esquemas de advecćão e assimilaćão de dados. Rev. Bras. Meteorol. 2011, 26, 591–608. [Google Scholar] [CrossRef]
- Pielke, R.A., Sr. Mesoscale Meteorological Modeling, 3rd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Daley, R. Atmospheric Data Analysis, 1st ed.; Cambridge Press: New York, NY, USA, 1991; p. 457. [Google Scholar]

| Nudging points in lateral boundary region | 5 |
| Nudging time scale at lateral boundary | 3600 s |
| Nudging time scale at top boundary | 1800 s |
| Lateral Boundary Condition | Klemp [40] |
| Short and long wave Parameterization | Chen and Cotton [41] |
| Frequency of radiation tendency update | 1800 s |
| Number of soil layers | 4 (−2.0, −1.5, −0.25 and −0.05 m) |
| Soil saturation degree | 0.49, 0.44, 0.42, 0.35 |
| Turbulence Parameterization | Anisotropic deformation Smagorinski [42] with formulations by Hill [43] and Lilly [44] |
| Parameters | Urban 1 | Urban 2 | Urban 3 | Suburban |
|---|---|---|---|---|
| Roof Albedo | 0.18 | 0.18 | 0.18 | 0.18 |
| Street Albedo | 0.08 | 0.08 | 0.08 | 0.08 |
| Wall Albedo | 0.14 | 0.14 | 0.14 | 0.14 |
| Roof Emissivity | 0.9 | 0.9 | 0.9 | 0.9 |
| Street Emissivity | 0.95 | 0.95 | 0.95 | 0.95 |
| Wall Emissivity | 0.9 | 0.9 | 0.9 | 0.9 |
| Aspect-Ratio | 10 | 2 | 1.25 | 0.6 |
| Building Heights (m) | 50 | 20 | 10 | 5 |
| Roughness Length (m) | 3 | 2 | 1 | 0.5 |
| Traffic Sensible Heat Flux () | 90 | 60 | 60 | 10 |
| Traffic Latent Heat Flux () | 10 | 10 | 5 | 5 |
| Industrial Sensible Heat Flux () | 14 | 14 | 10 | 10 |
| Industrial Latent Heat Flux () | 50 | 50 | 30 | 30 |
| Urban Fraction | 0.7 | 0.6 | 0.5 | 0.5 |
| Vegetation Type | Short Grass | Mixed Forest | Evergreen broadleaf tree | Short Grass |
| Surface Station | Latitude | Longitude | Altitude |
|---|---|---|---|
| São Caetano | 233610 S | 463429 W | 740 m |
| Guarulhos Airport (METAR) | 232600 S | 462800 W | 751 m |
| Congonhas Airport (METAR) | 233803 S | 463859 W | 802 m |
| Mirante do Santana (INMET) | 232947 S | 463712 W | 792 m |
| IAG | 233904 S | 463721 W | 799 m |
| Site | SVF | Site | SVF | Site | SVF |
|---|---|---|---|---|---|
| 1 | 0.6161 | 14 | 0.8612 | 27 | 0.6539 |
| 2 | 0.4286 | 15 | 0.6889 | 28 | 0.8218 |
| 3 | 0.6687 | 16 | 0.1816 | 29 | 0.8077 |
| 4 | 0.7309 | 17 | 0.6618 | 30 | 0.5846 |
| 5 | 0.6939 | 18 | 0.8327 | 31 | 0.7707 |
| 6 | 0.9204 | 19 | 0.5482 | 32 | 0.8394 |
| 7 | 0.5732 | 20 | 0.5391 | 33 | 0.8508 |
| 8 | 0.5613 | 21 | 0.8052 | 34 | 0.7994 |
| 9 | 0.9098 | 22 | 0.8270 | 35 | 0.7506 |
| 10 | 0.8071 | 23 | 0.7886 | 36 | 0.6179 |
| 11 | 0.7355 | 24 | 0.5771 | 37 | 0.8176 |
| 12 | 0.7980 | 25 | 0.7036 | ||
| 13 | 0.9126 | 26 | 0.6201 |
| Urban Type | Observed SVF | Standard Deviation | N | Numerical SVF | |
|---|---|---|---|---|---|
| Urban 1 | 0.62 | 0.10 | 5 | 0.05 | 0.50 |
| Urban 2 | 0.68 | 0.17 | 19 | 0.24 | 0.40 |
| Urban 3 | 0.79 | 0.07 | 10 | 0.35 | 0.24 |
| Suburban | 0.83 | 0.09 | 3 | 0.57 | 0.19 |
| Simulation A | Simulation B | |||||
|---|---|---|---|---|---|---|
| Station | BIAS | RMSE | BIAS | RMSE | ||
| São Caetano | 1.85 | 3.44 | 1.65 | −1.24 | 2.78 | 1.02 |
| Guarulhos | 2.44 | 3.28 | 1.16 | 0.21 | 1.43 | 0.52 |
| Congonhas | 1.93 | 2.50 | 1.19 | −1.69 | 2.38 | 1.17 |
| Mirante | 1.55 | 1.89 | 0.99 | −2.40 | 3.20 | 1.95 |
| IAG | 3.85 | 4.67 | 1.71 | 0.65 | 1.59 | 0.69 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morais, M.V.B.d.; Freitas, E.D.d.; Marciotto, E.R.; Urbina Guerrero, V.V.; Martins, L.D.; Martins, J.A. Implementation of Observed Sky-View Factor in a Mesoscale Model for Sensitivity Studies of the Urban Meteorology. Sustainability 2018, 10, 2183. https://doi.org/10.3390/su10072183
Morais MVBd, Freitas EDd, Marciotto ER, Urbina Guerrero VV, Martins LD, Martins JA. Implementation of Observed Sky-View Factor in a Mesoscale Model for Sensitivity Studies of the Urban Meteorology. Sustainability. 2018; 10(7):2183. https://doi.org/10.3390/su10072183
Chicago/Turabian StyleMorais, Marcos Vinicius Bueno de, Edmilson Dias de Freitas, Edson R. Marciotto, Viviana Vanesa Urbina Guerrero, Leila Droprinchinski Martins, and Jorge Alberto Martins. 2018. "Implementation of Observed Sky-View Factor in a Mesoscale Model for Sensitivity Studies of the Urban Meteorology" Sustainability 10, no. 7: 2183. https://doi.org/10.3390/su10072183
APA StyleMorais, M. V. B. d., Freitas, E. D. d., Marciotto, E. R., Urbina Guerrero, V. V., Martins, L. D., & Martins, J. A. (2018). Implementation of Observed Sky-View Factor in a Mesoscale Model for Sensitivity Studies of the Urban Meteorology. Sustainability, 10(7), 2183. https://doi.org/10.3390/su10072183







