An Occupant-Oriented Calculation Method of Building Interior Cooling Load Design
Abstract
1. Introduction
2. Methodology
2.1. Concept of Load Disturbances
2.2. Definition of “Representative Interior Load”
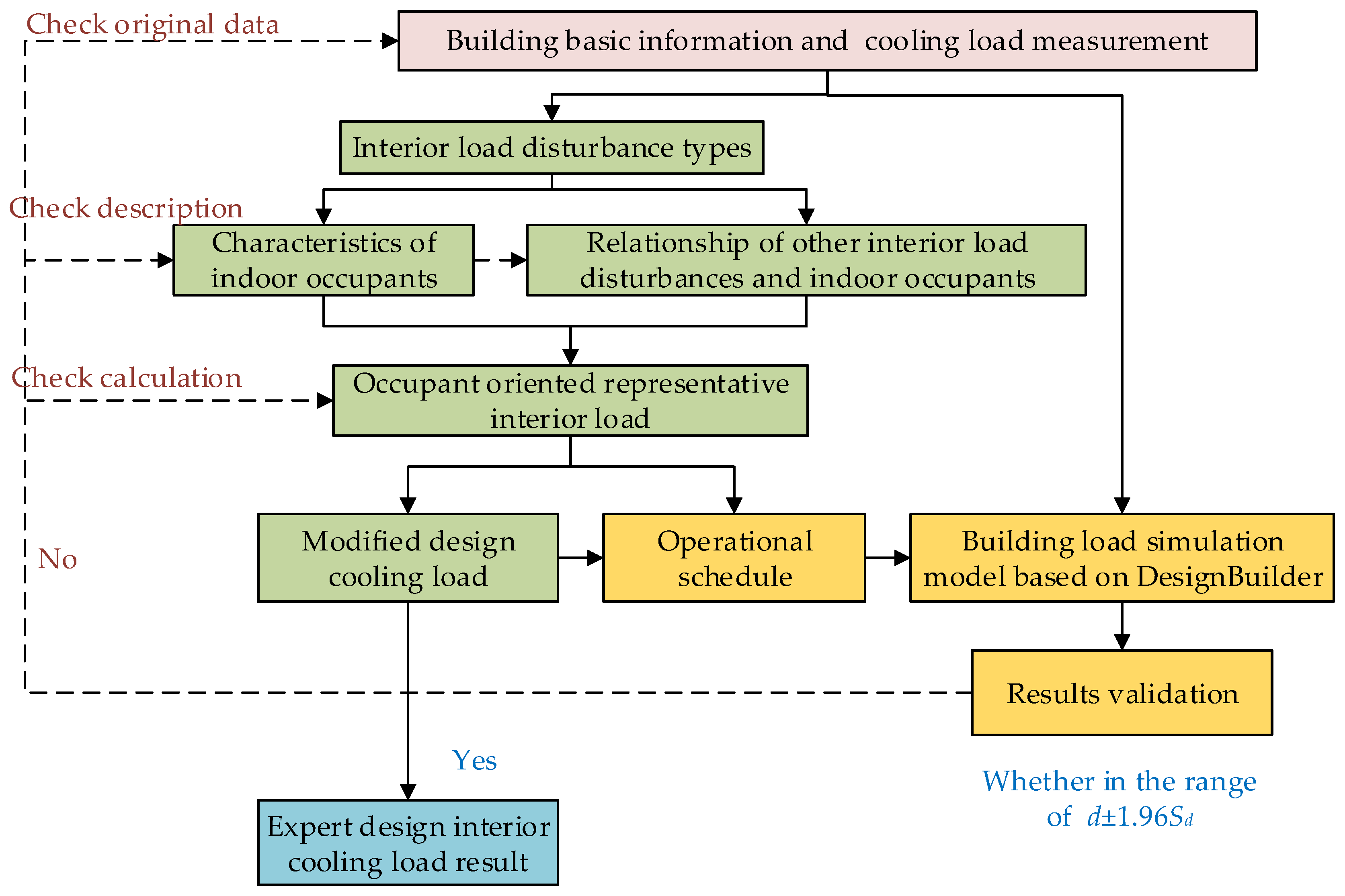
2.3. Modeling and Uncertainty Estimation of Building Cooling Load
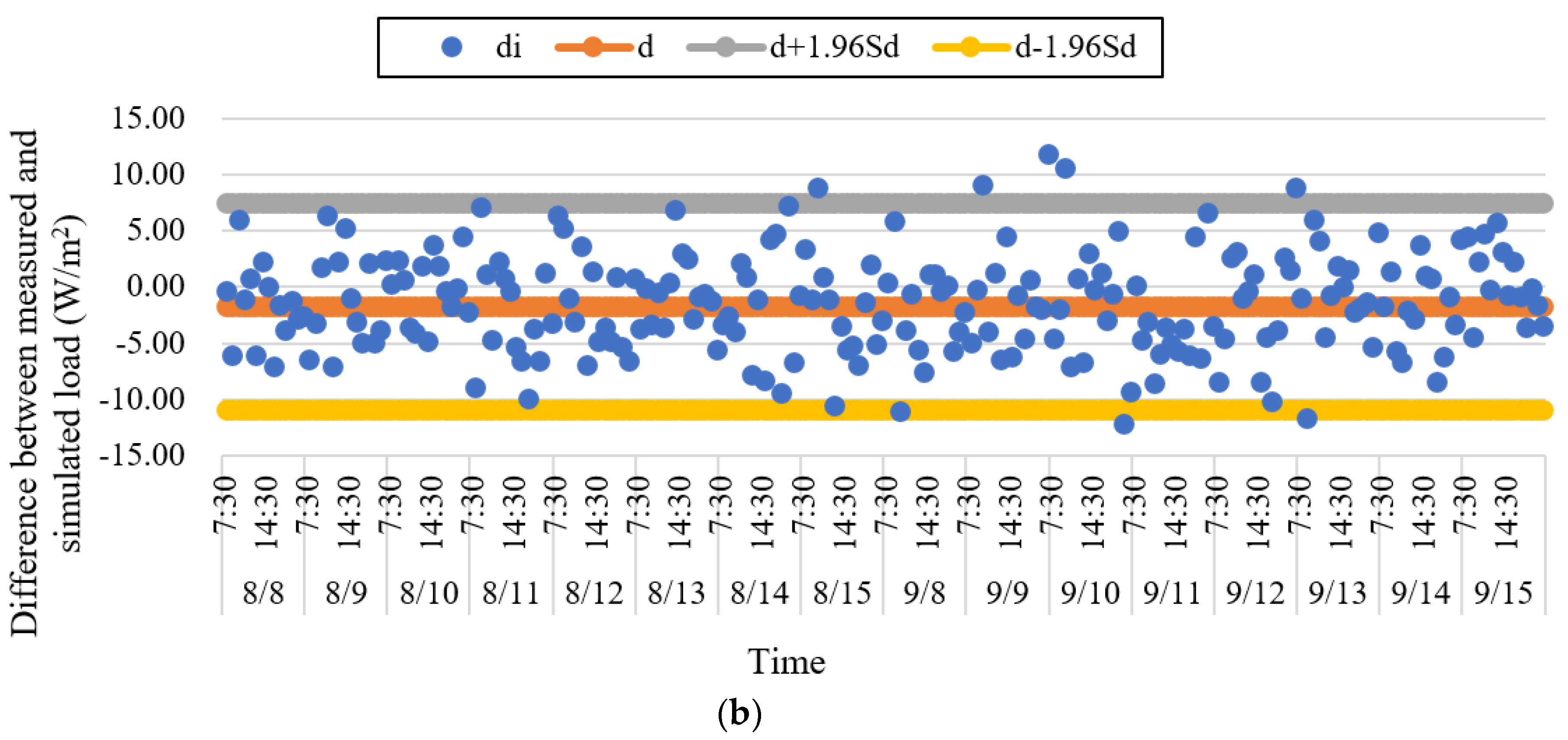
- (a)
- First one and the core is the interior cooling load calculation. Three relationships described in Equations (6)–(8) are the emphases. The relationships are formulated in the following sections based on the case study of three typical university buildings.
- (b)
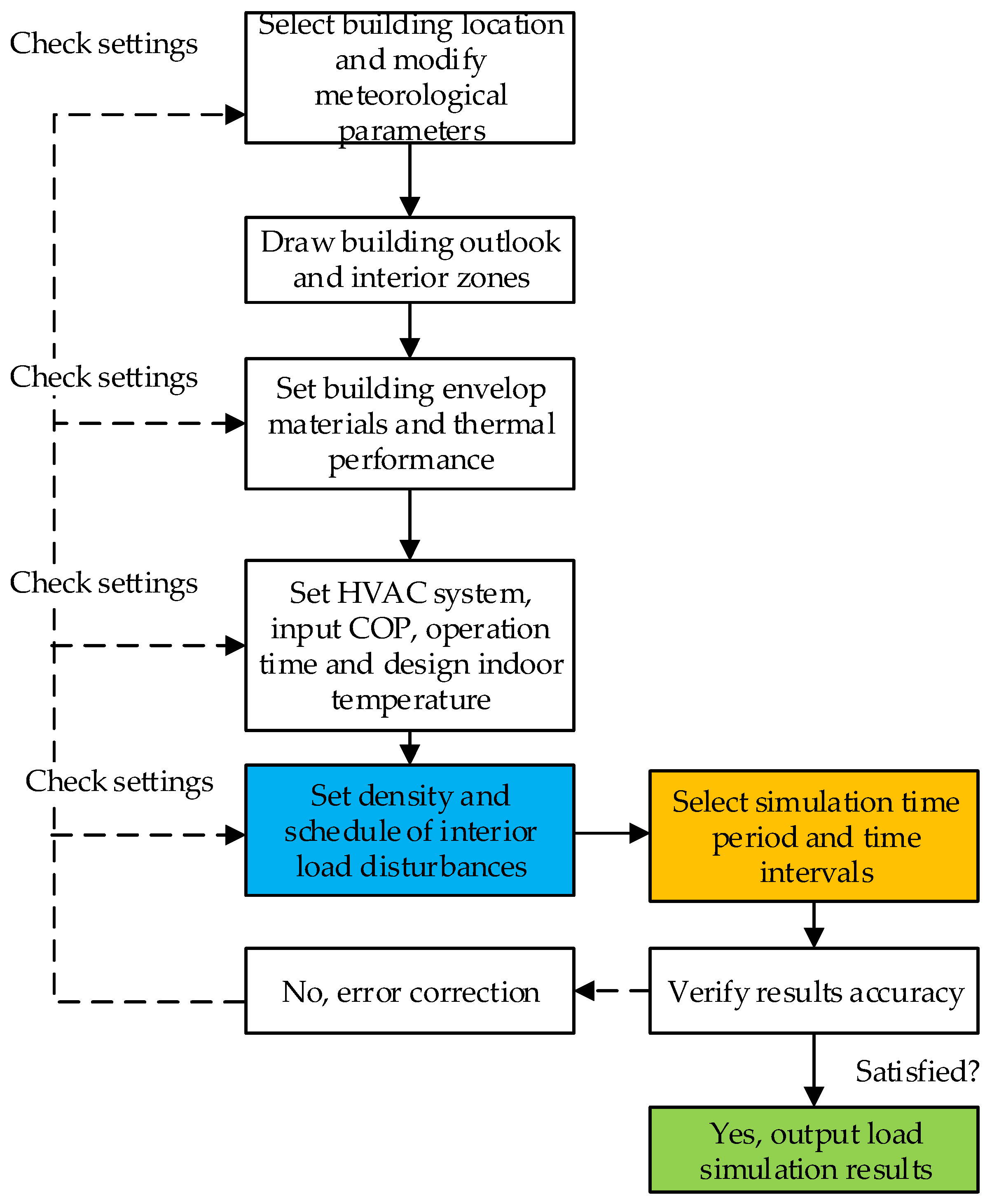
- The second part is the basic building cooling load simulation model based on the basic building information, such as building shape, envelope, etc., and indoor and outdoor meteorological parameters. In this paper, the building cooling load simulation models are established with DesignBuilder tool. DesignBuilder is dynamic simulation software that has a comprehensive builder graphical interface and uses EnergyPlus as core calculator [25,26]. The procedure of establishing a building load simulation model based on DesignBuilder is shown in Figure 2.
- (c)
- The third part is the checking and verifying procedure. To verify the accuracy of simulated building cooling loads based on the representative interior load, the Bland-Altman plot method is applied to compare simulated building cooling loads with the measured actual loads. The verification parameter is [27]
2.4. Case Study
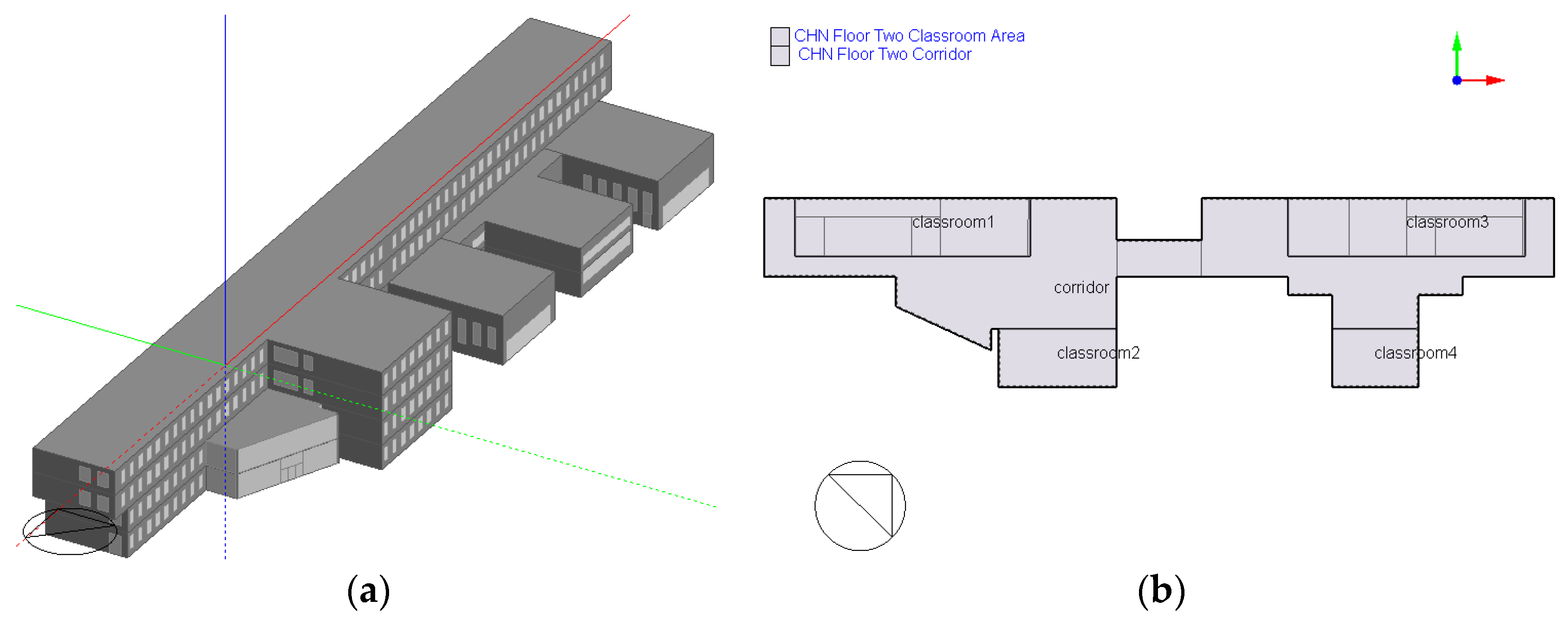
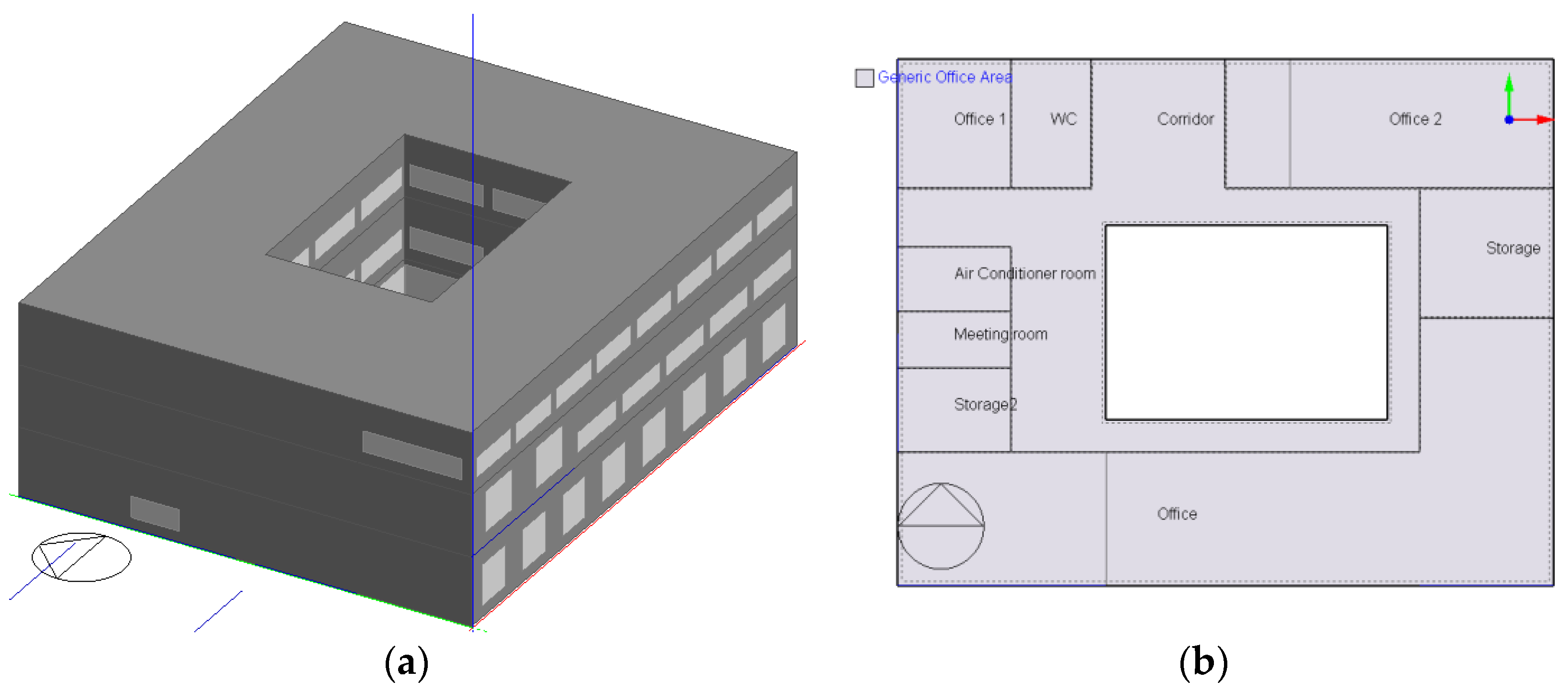
2.4.1. Basic Information
2.4.2. Building Usage Data Collection
3. Characteristics Analysis of Interior Load Disturbances
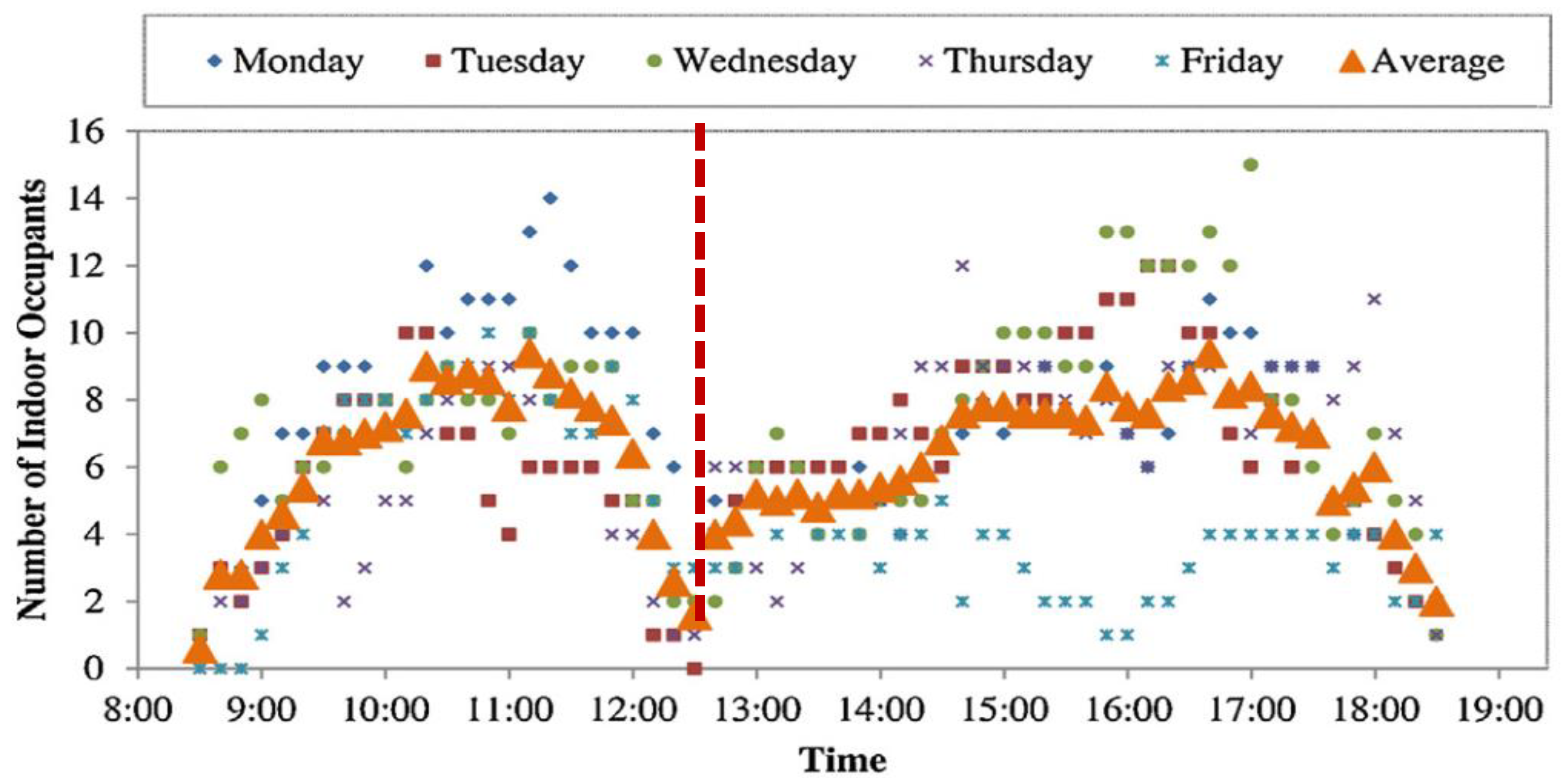
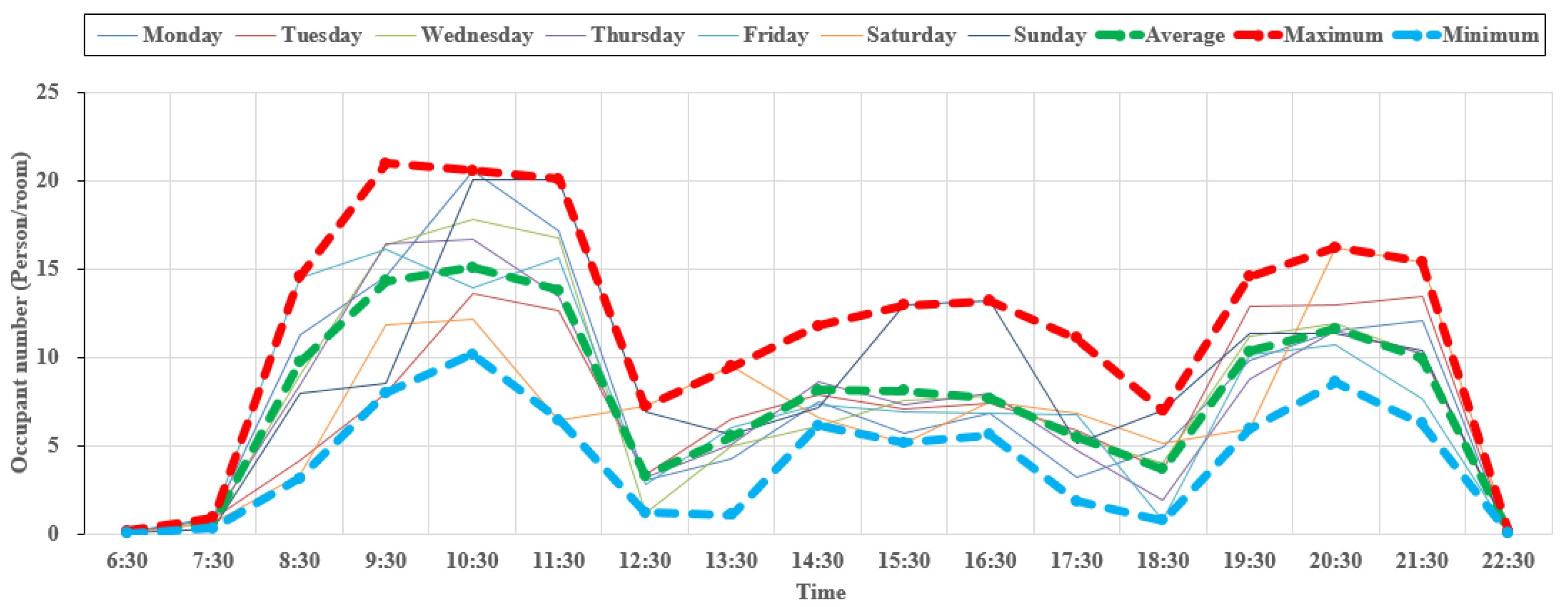
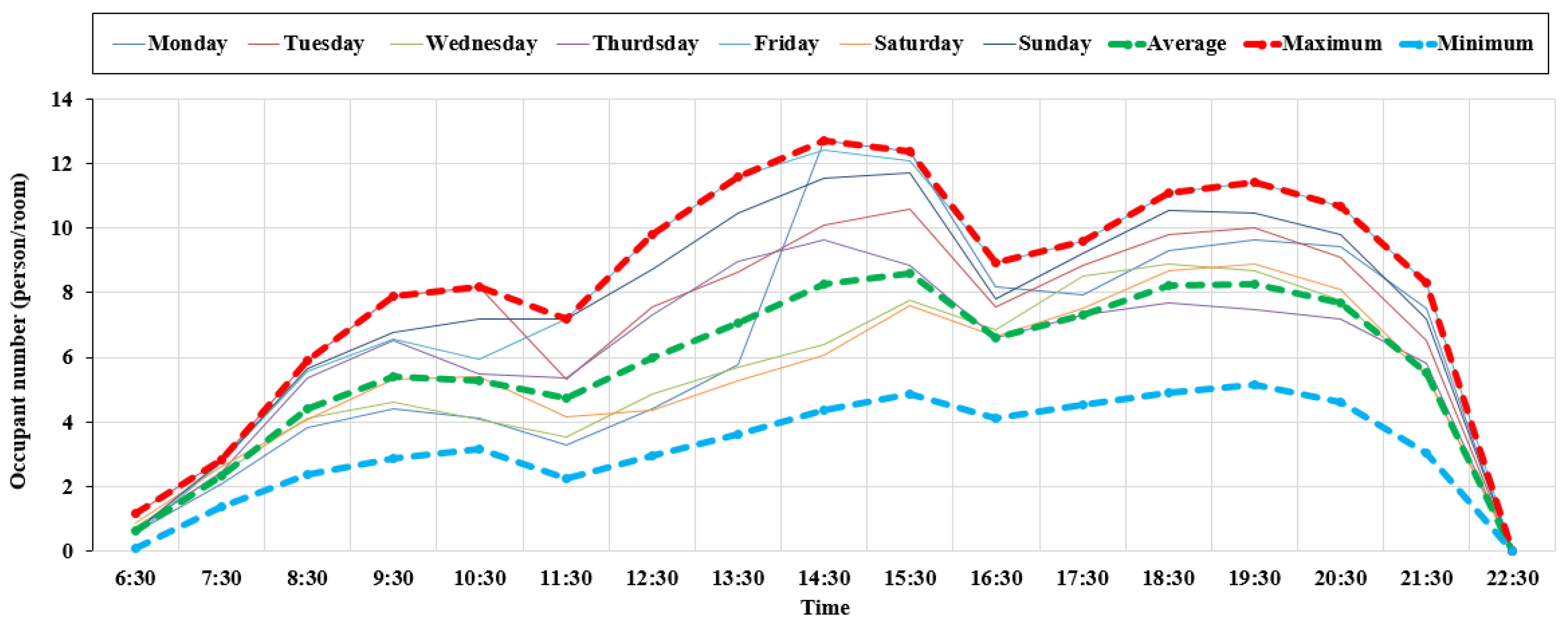
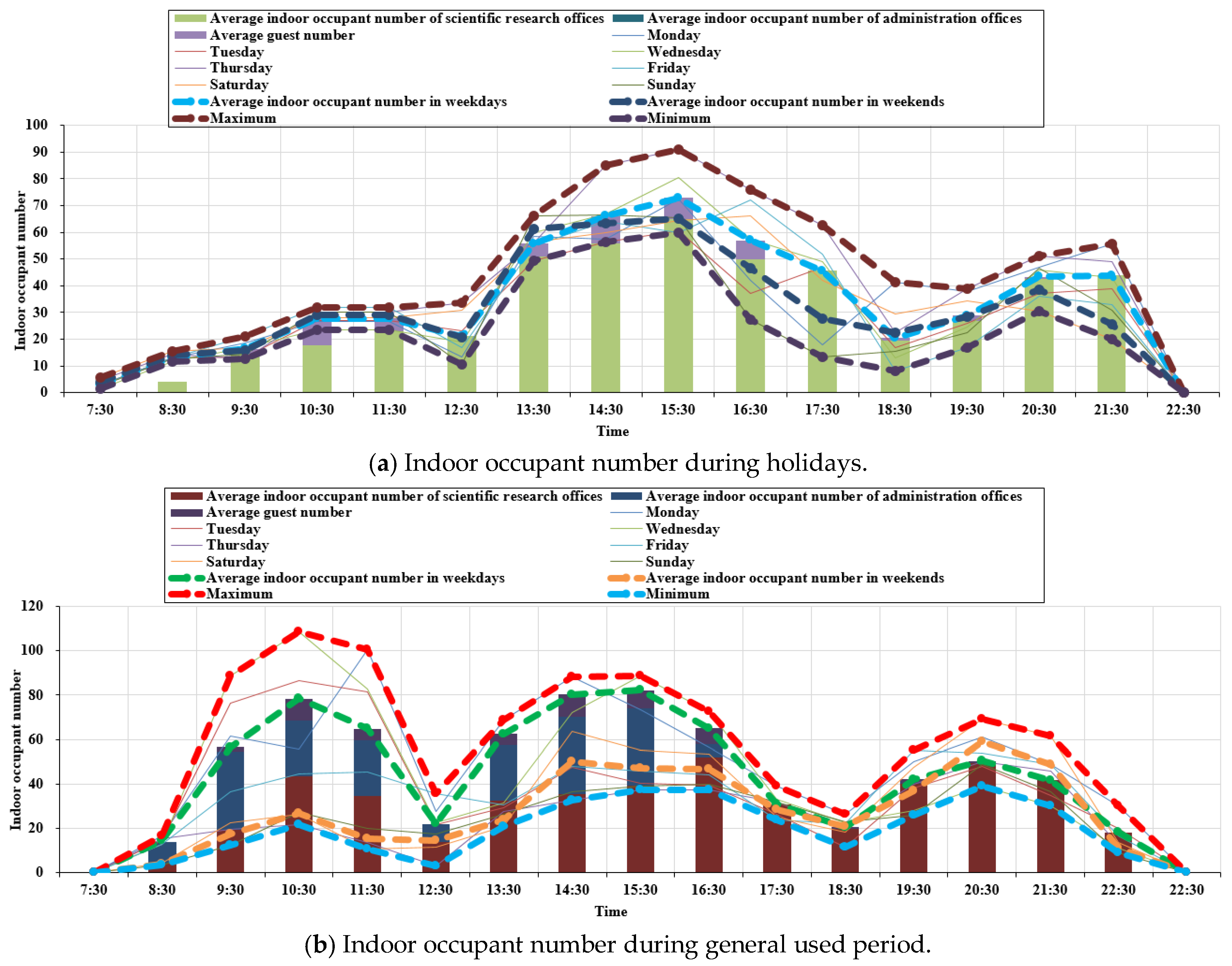
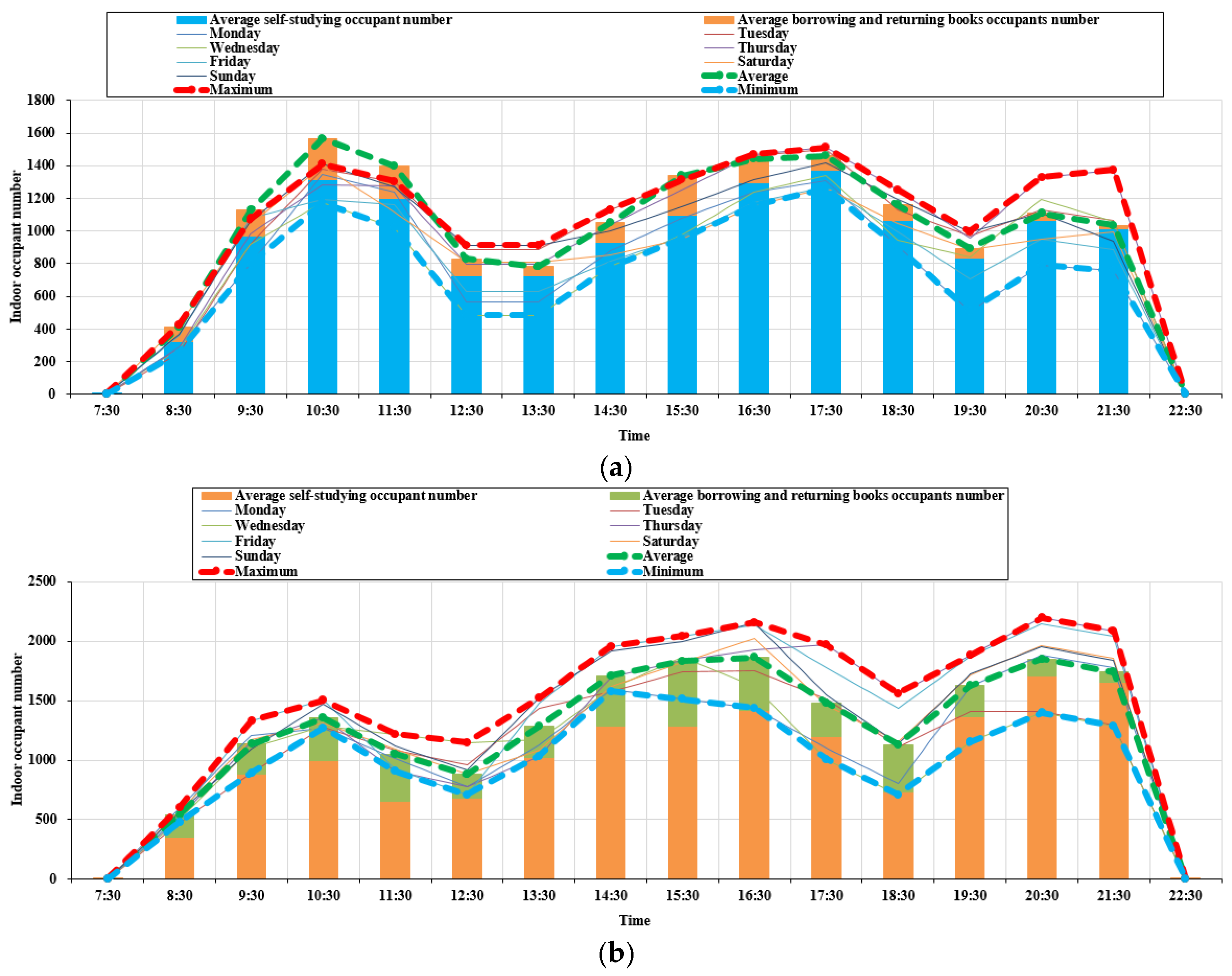
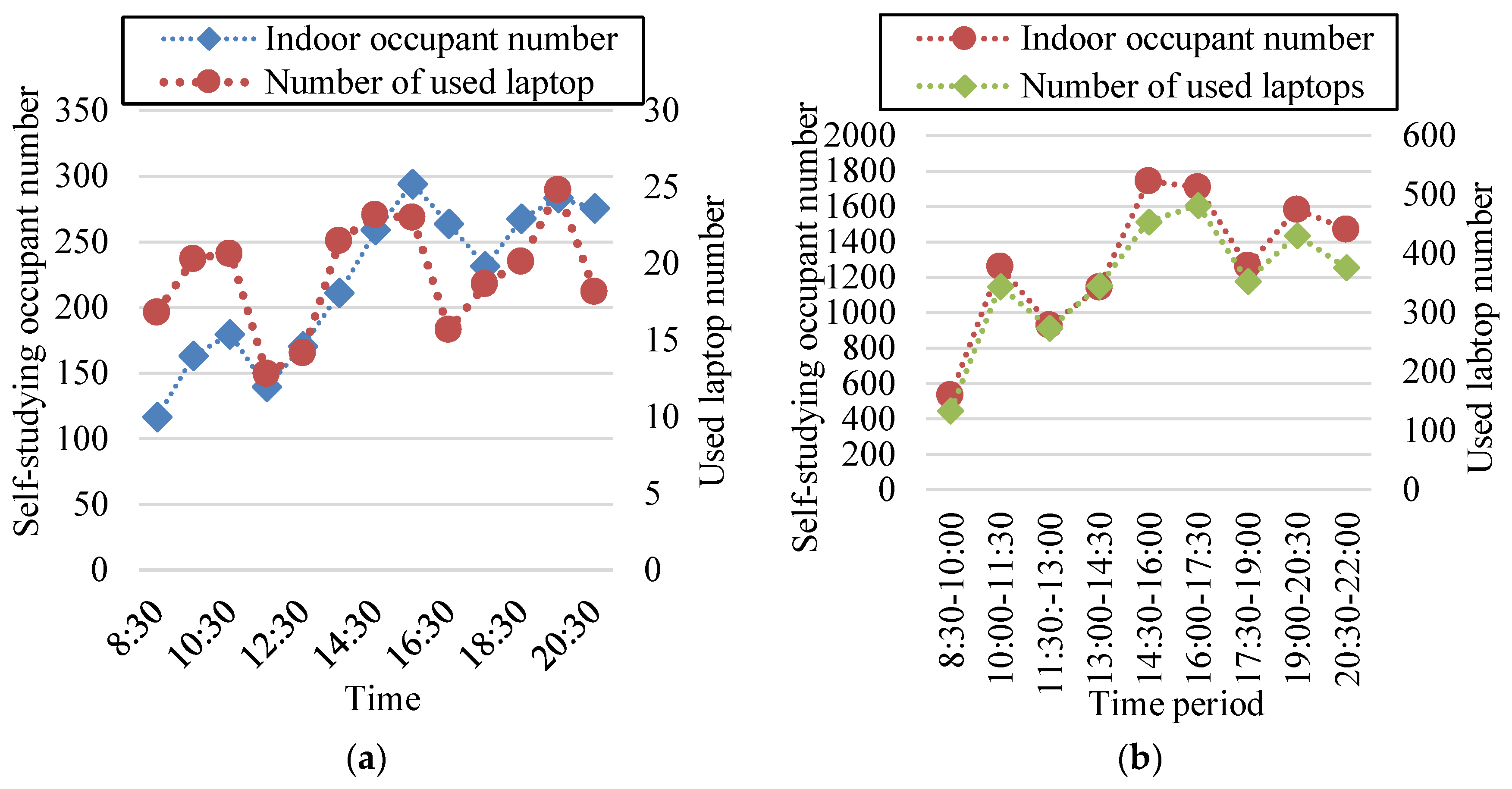
3.1. Indoor Occupants Analysis
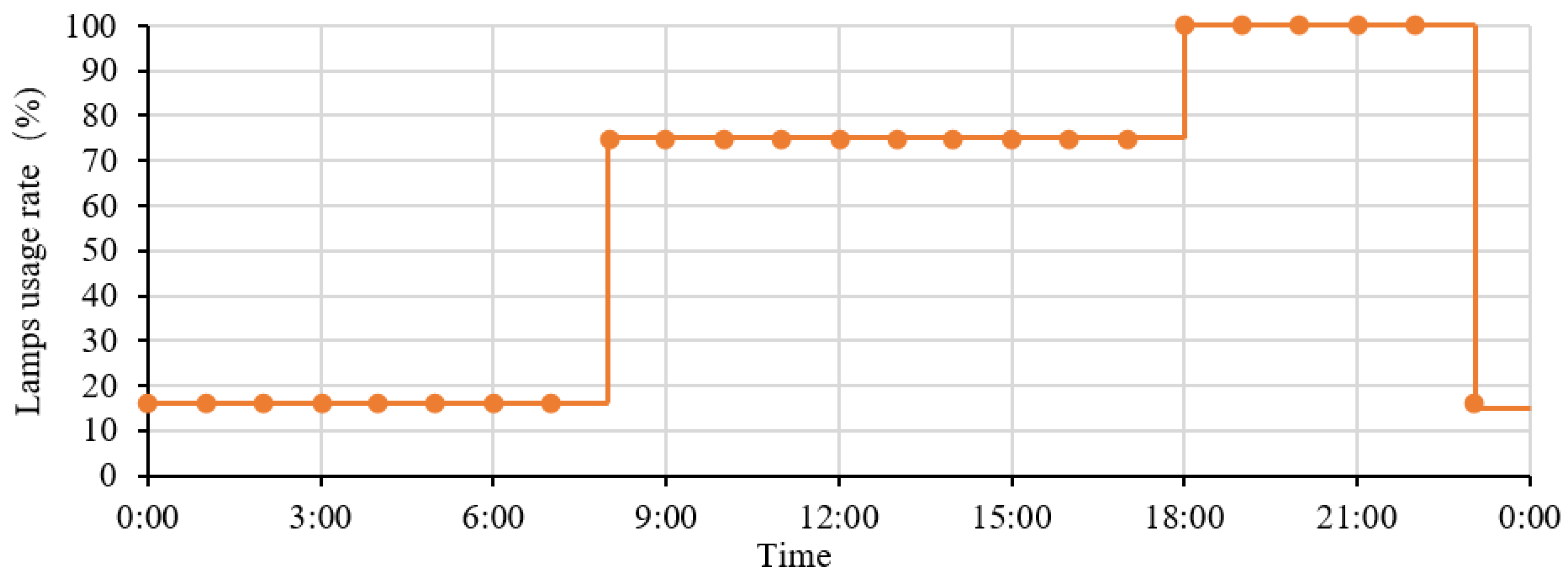
3.2. Lamps Usage Analysis
3.3. Equipment Usage Analysis
- (1)
- Electrical boilers are installed in hot water rooms in the teaching building. Because the machine rooms are not air-conditioned, the heat release will not be accounted into interior loads.
- (2)
- The booking borrowing and returning machines are computers in essence and are used in the operational time of the library. There are 6 managers working in the library. Everyone uses a computer when working. The TVs in the library are always on and printers are generally on standby.
- (3)
- Guests generally do not use equipment in the office building. Computers are installed for both administration and scientific research occupants. However, laptops might also be used by scientific research workers. The probability was tested as 5%.
4. Results and Discussion
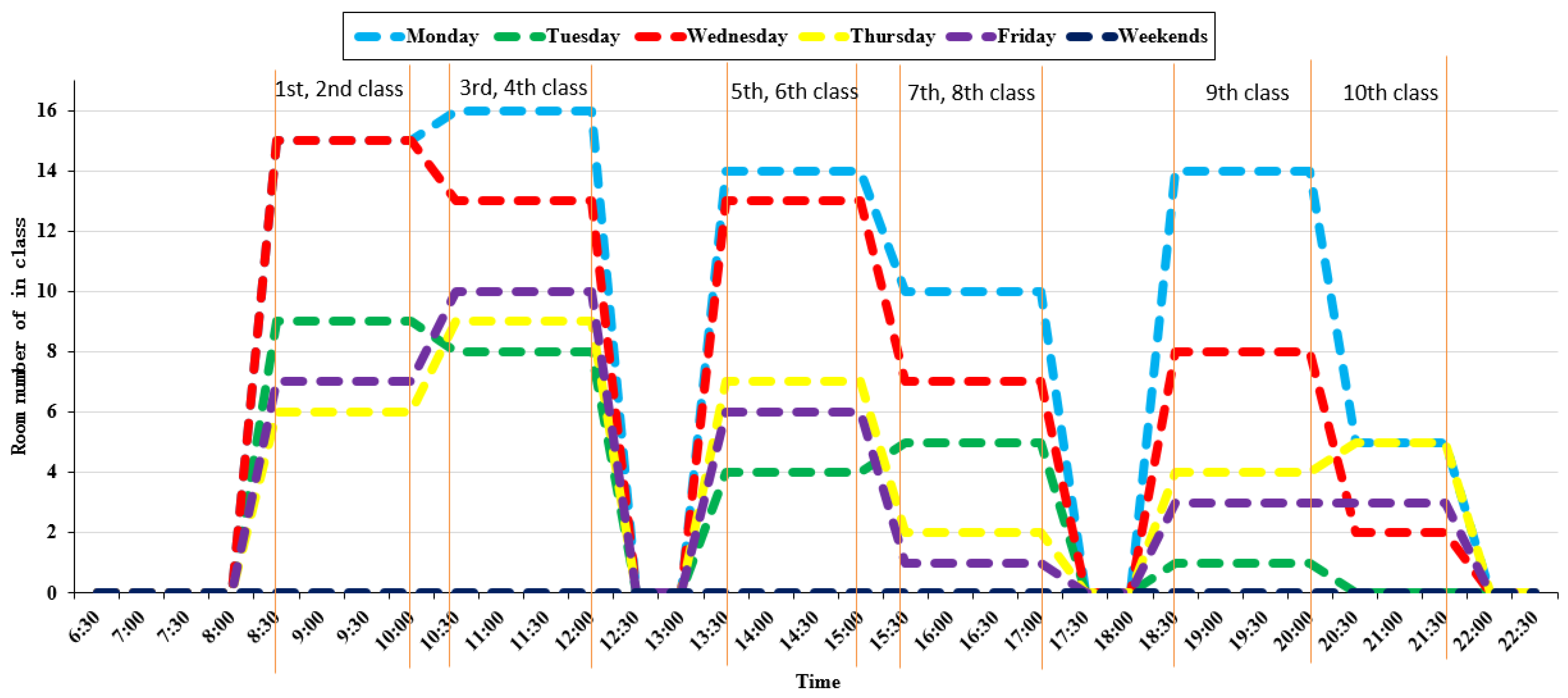
4.1. Indoor Occupant Number Modelling
4.1.1. Classification of Indoor Occupants
- (1)
- For the teaching building, students taking class only use lamps and teaching projection equipment, such as computers and projectors. About 50% of lamps and a computer and projector are generally used in an in-class room, while for self-studying students, the teaching projection equipment is not allowed to be turned on. Laptops can be used.
- (2)
- For the office building, three types of occupants were classified, namely, the occupants working in the scientific research offices, occupants working in the administration offices, and guests. The on-duty time of occupants working in administration offices is fixed, while it is flexible for occupants working in the scientific research offices. Guests only come to the office building during on-duty time (8:30–16:30).
- (3)
- For the library, three types of occupants were classified. The book managers in the library are responsible for books borrowing and returning. Students that come to the library to borrow and return books are the second type. The third type of occupants is the self-studying students. Personal mobile computers, namely, laptops, can be used.
4.1.2. Time-Varying Indoor Occupant Number
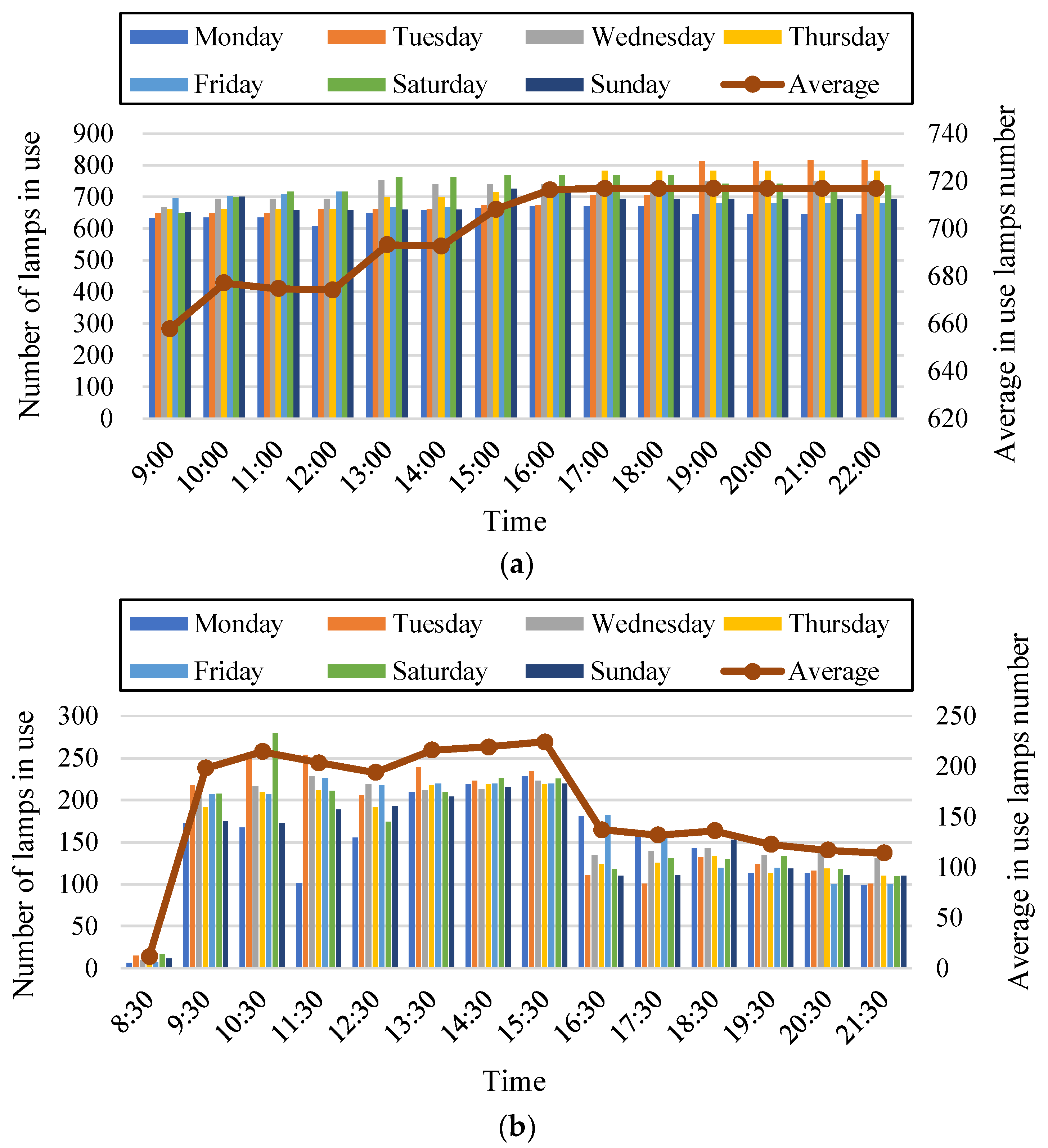
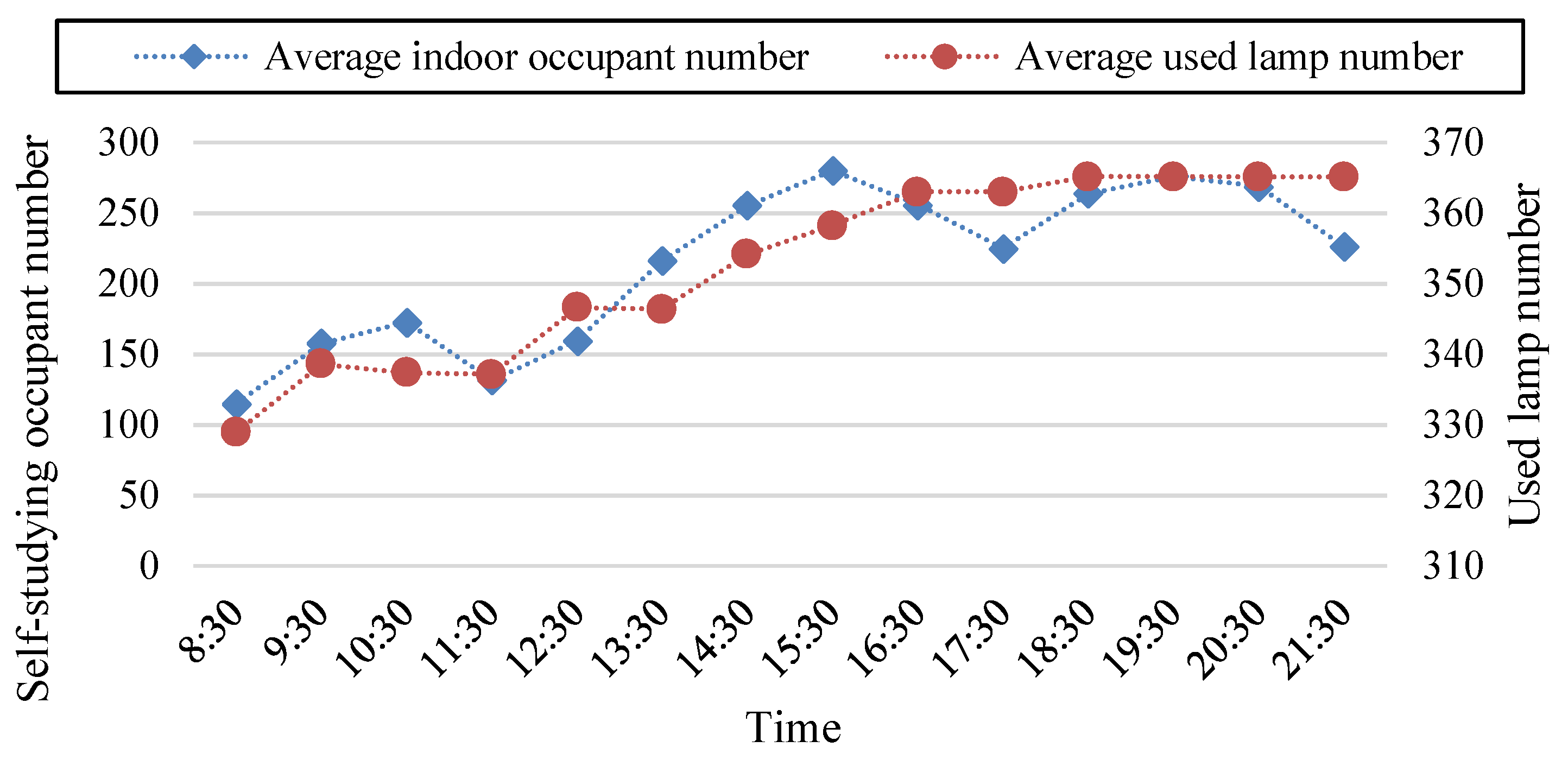
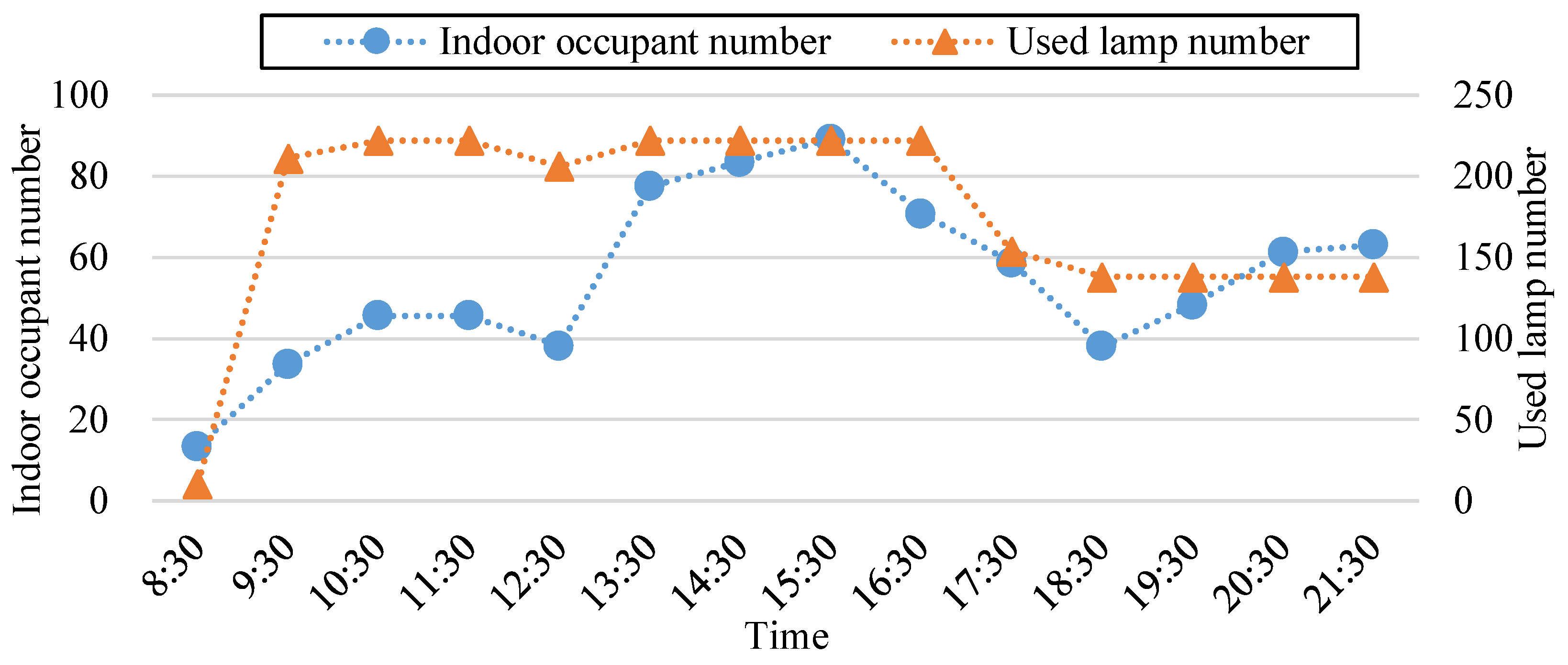
4.2. Relationship of Lamps and Equipment in Use with Indoor Occupants
4.2.1. Relationship of Lamps in Use with Indoor Occupants
4.2.2. Relationship of Equipment in Use with Indoor Occupants
4.3. Quantification of Representative Interior Load
4.3.1. Maximum Interior Load Density
4.3.2. Time-Varying Occupant Oriented Representative Interior Load
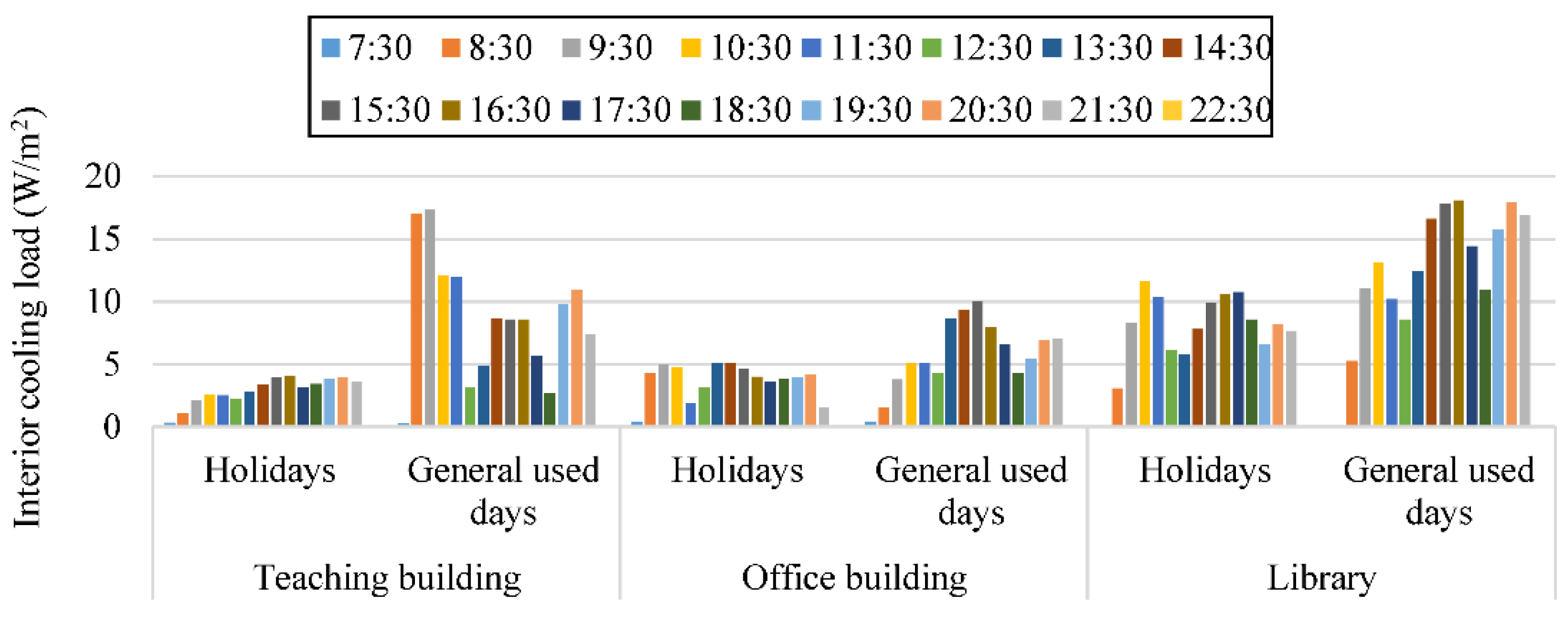
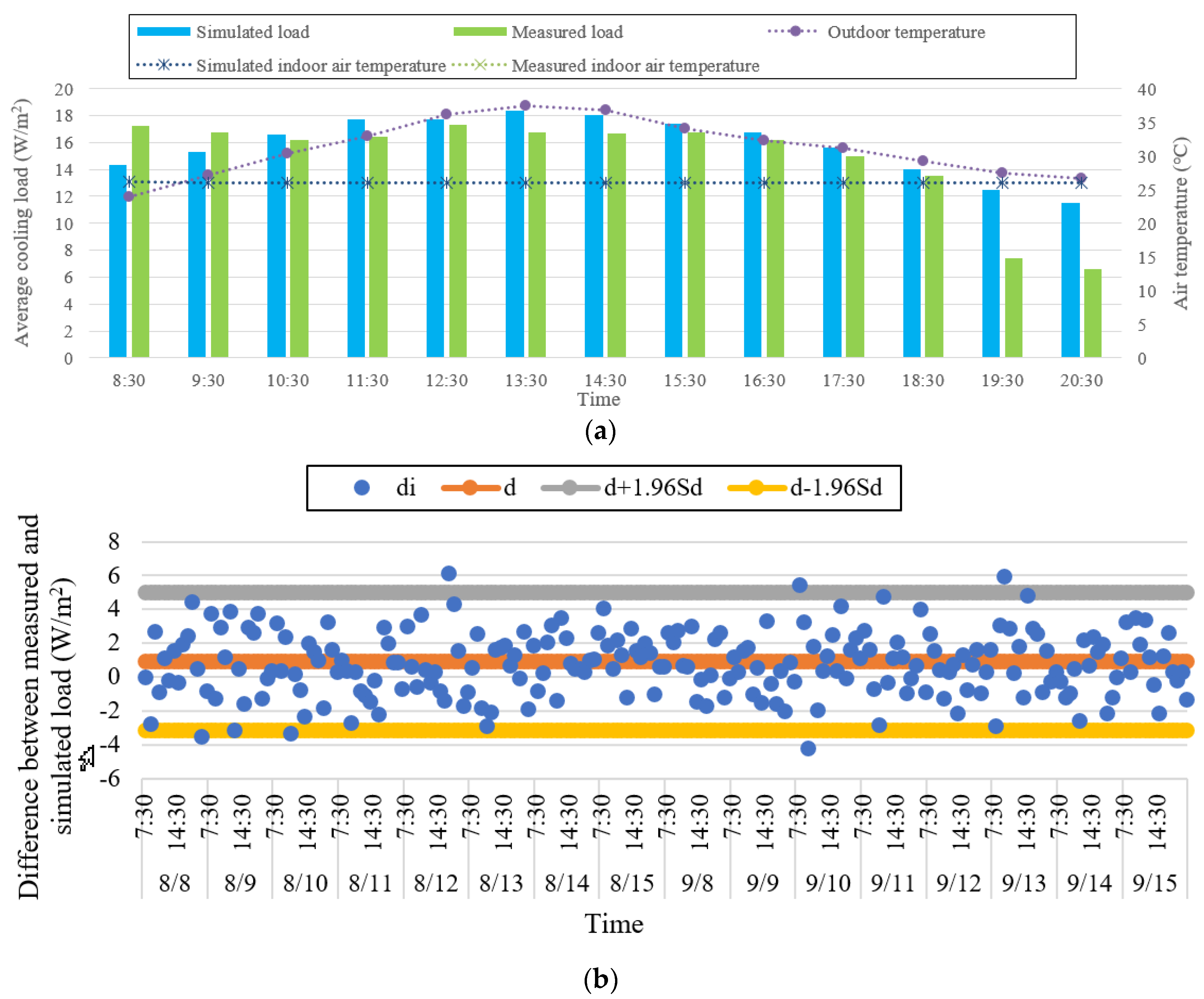
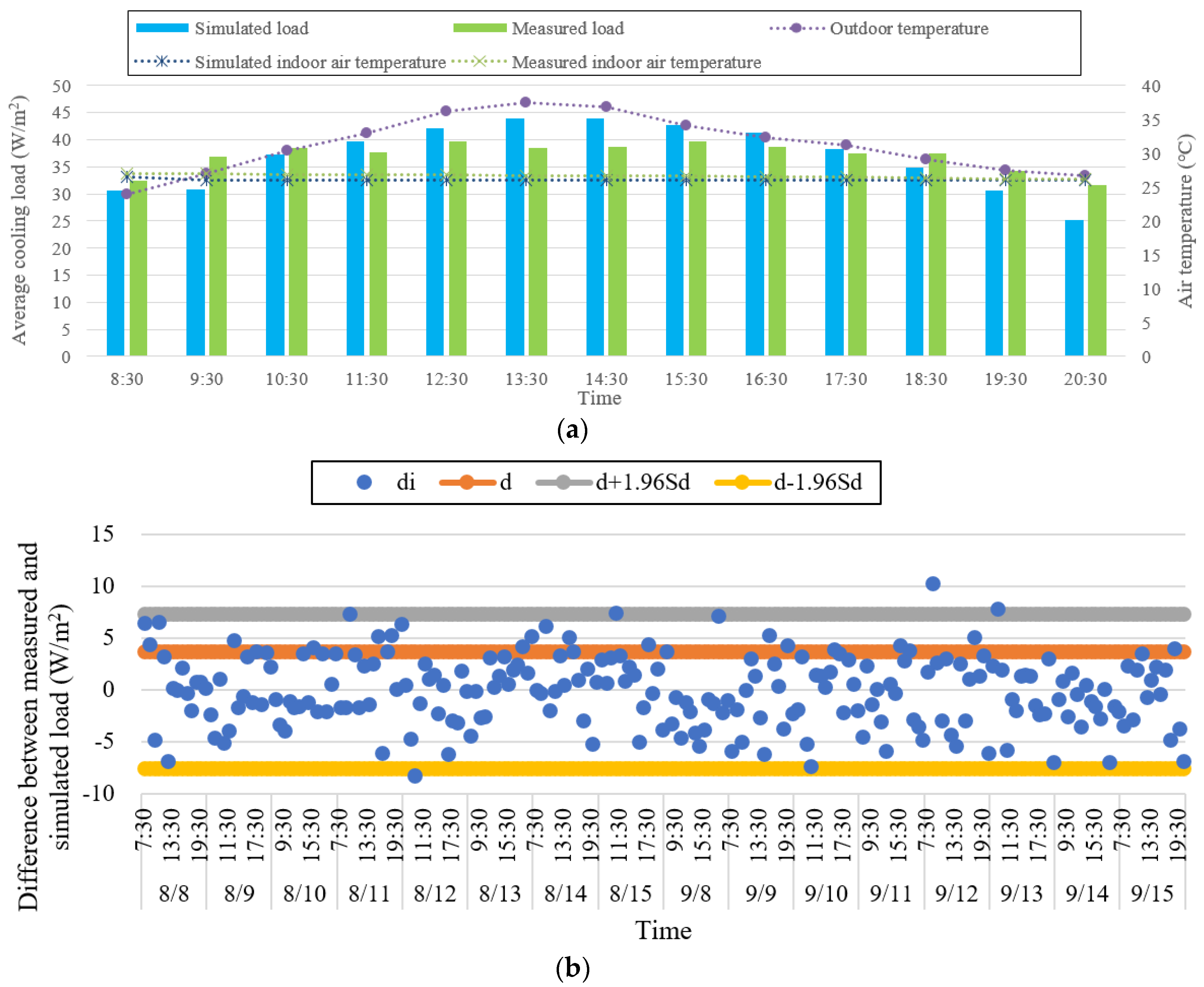
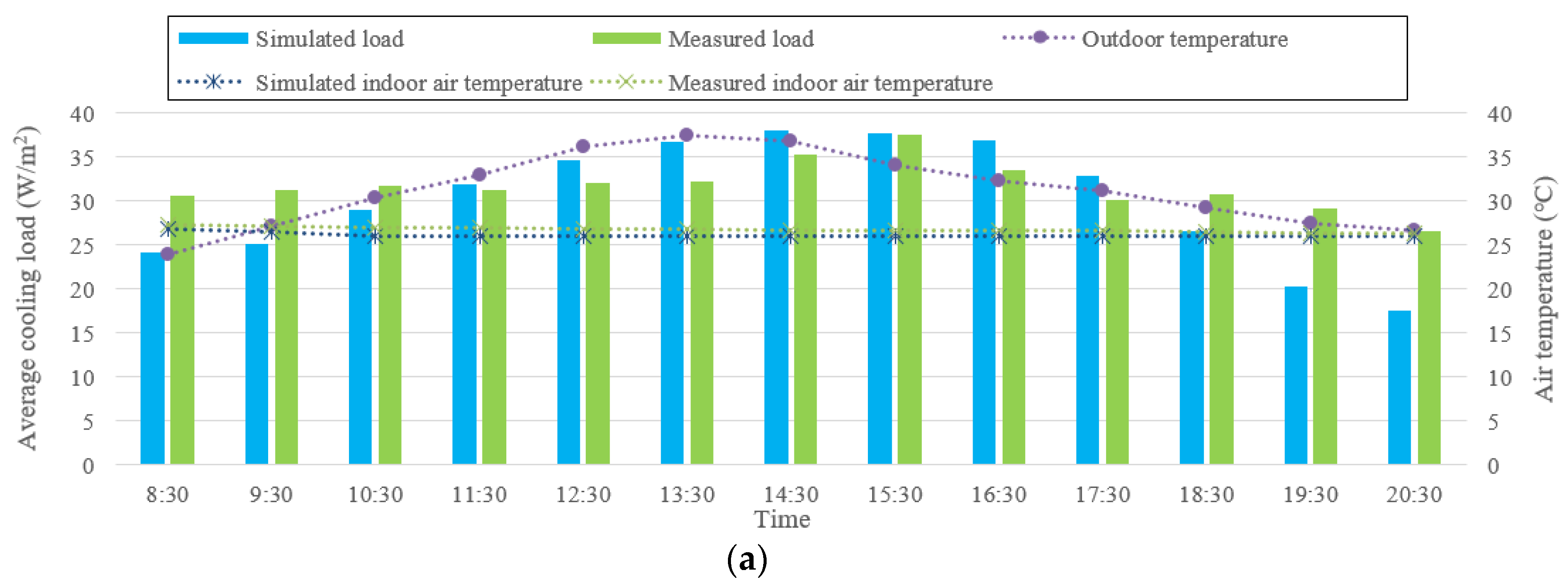
4.4. Modified Cooling Load Results Validation and Discussion
5. Conclusions
- (1)
- The proposed occupant-oriented representative interior load is a combination of all interior disturbances. Occupants are the core of interior cooling loads. Occupants should be categorized based on their equipment usage. Through quantitative analysis, it was observed that the maximum representative interior loads were 196.43, 329.94, and 402.58 W/person, respectively, for the case buildings, indicating the different natures of occupants in various building types.
- (2)
- The time-varying indoor occupant number followed a trimodal distribution of university buildings, which could be described by quadratic polynomials with the time interval of 1 h. The used lamps and equipment were in exponential and linear relationships with the indoor occupants, respectively. Considering the maximum indoor occupant number, the design interior cooling load of the case buildings was modified as 17.36, 9.96, and 18.12 W/m2, respectively, counting for 50.80%, 17.12%, and 30.14% of the total cooling loads. The over-estimating rate of the interior cooling loads resulted in the oversized chillers, which were proved to be more than 50%.
- (3)
- The proposed representative interior load calculation method can easily be applied in the building load simulation by inputting the time-varying schedules. A consistency rate of more than 90% has been achieved in the case buildings. The feasibility and accuracy can be proved to be meaningful with regard to the proposed occupant-oriented interior cooling load design method.
6. Patents
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Cooling load (W) | |
| Heat release (W) | |
| Input power (W) | |
| number | |
| Cooling load coefficient | |
| Building floor area (m2) | |
| Function | |
| Mean value of the difference between two groups of data | |
| Undetermined coefficients of quadratic polynomials | |
| Undetermined coefficients of exponential relationships | |
| Greek letters | |
| Usage rate (%) | |
| Clustering coefficient to adjust heat gain based on normal percentage of men, women, and children | |
| Subscripts | |
| Interior load disturbance types | |
| Exterior cooling load | |
| Fresh air cooling load | |
| Interior cooling load | |
| Representative interior load | |
| Occupant | |
| Lighting | |
| Equipment | |
| Equipment type i | |
| Laptops | |
| Computers | |
| Printers | |
| Water dispensers | |
| Shredders | |
| Number of data sets | |
| Data set j | |
| Time | |
| Morning period, 7:30–12:30 | |
| Afternoon period, 13:30–17:30 | |
| Night period, 18:30–22:30 | |
| Classrooms in the teaching building | |
| Self-studying | |
| In-class | |
| Offices in the office building | |
| Administration workers | |
| Scientific research workers | |
| Guests | |
| The library | |
| Borrowing and returning books occupants | |
| Management workers | |
| Limit point of occupant number | |
| Others | |
References
- Wang, Z.; Zhu, H.; Ding, Y.; Zhu, T.; Zhu, N.; Tian, Z. Energy efficiency evaluation of key energy consumption sectors in China based on a macro-evaluating system. Energy 2018, 153, 65–79. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, H. Urban Sustainability through Public Architecture. Sustainability 2018, 10, 1249. [Google Scholar] [CrossRef]
- Labanca, N.; Bertoldi, B. Beyond energy efficiency and individual behaviors: Policy insights from social practice theories. Energy Policy 2018, 115, 494–502. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.; Xia, J. Energy Performance Analysis of an Integrated Distributed Variable-Frequency Pump and Water Storage System for District Cooling Systems. Appl. Sci. 2017, 7, 1139. [Google Scholar] [CrossRef]
- Hong, T.; Yang, L.; Hill, D.; Feng, W. Data and analytics to inform energy retrofit of high performance buildings. Appl. Energy 2014, 126, 90–106. [Google Scholar] [CrossRef]
- Masini, A.; Menichetti, E. The impact of behavioural factors in the renewable energy investment decision making process: Conceptual framework and empirical findings. Energy Policy 2012, 40, 28–38. [Google Scholar] [CrossRef]
- Escrivá-Escrivá, G. Basic actions to improve energy efficiency in commercial buildings in operation. Energy Build. 2011, 43, 3106–3111. [Google Scholar] [CrossRef]
- Jia, M.; Srinivasan, R.S.; Raheem, A.A. From occupancy to occupant behavior: An analytical survey of data acquisition technologies, modeling methodologies and simuation coupling mechanisms for building energy efficiency. Renew. Sustain. Energy Rev. 2017, 68, 525–540. [Google Scholar] [CrossRef]
- Yan, D.; O’Brien, W.; Hong, T.; Mahdavi, A. Occupant behavior modeling for building performance simulation: Current state and future challenges. Energy Build. 2015, 107, 264–278. [Google Scholar] [CrossRef]
- Kwok, S.S.K.; Lee, E.W.M. A study of the importance of occupancy to building cooling load in prediction by intelligent approach. Energy Convers. Manag. 2011, 52, 2555–2564. [Google Scholar] [CrossRef]
- Escrivá, G.E.; Álvarez-Bel, C.; Valencia-Salazar, I. Method for modeling space conditioning aggregated daily load curves: Application to a university building. Energy Build. 2010, 42, 1275–1282. [Google Scholar] [CrossRef]
- López-Rodríguez, M.A.; Santiago, I.; Trillo-Montero, D.; Torriti, J.; Moreno-Munoz, A. Analysis and modeling of active occupancy of the residential sector in Spain: An indicator of residential electricity consumption. Energy Policy 2013, 62, 742–751. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Aiello, M. Energy intelligent buildings based on user activity: A survey. Energy Build. 2013, 56, 244–257. [Google Scholar] [CrossRef]
- Gunay, H.B.; O’Brien, W.; Beausoleil-Morrison, I. A critical review of observation studies, modeling, and simulation of adaptive occupant behaviors in offices. Build. Environ. 2013, 70, 31–47. [Google Scholar] [CrossRef]
- Gul, M.S.; Patidar, S. Understanding the energy consumption and occupancy of a multi-purpose academic building. Energy Build. 2015, 87, 155–165. [Google Scholar] [CrossRef]
- Lee, M.Y. Design and Cooling Performances of an Air Conditioning System with Two Parallel efrigeration Cycles for a Special Purpose Vehicle. Appl. Sci. 2017, 7, 190. [Google Scholar]
- Zhao, H.; Magoules, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Virote, J.; Neves-Silva, R. Stochastic models for building energy prediction based on occupant behavior assessment. Energy Build. 2012, 53, 183–193. [Google Scholar] [CrossRef]
- Parson, R. ASHRAE Handbook-Fundamentals; ASHRAE Inc.: Atlanta, GA, USA, 2009; pp. 17–19. [Google Scholar]
- Lu, Y. Design Manual for Practical Heating and Air Conditioning, 2nd ed.; China Architecture & Building Press: Beijing, China, 2008; pp. 1479–1481, 1547–1558. ISBN 978-7-112-09749-4. [Google Scholar]
- Ding, Y.; Wang, Z.; Feng, W.; Marnay, C.; Zhou, N. Influence of occupancy-oriented interior cooling load on building cooling load design. Appl. Therm. Eng. 2016, 96, 411–420. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Wang, Z.; Liu, M.; He, Q. A simplified model of dynamic interior cooling load evaluation for office buildings. Appl. Therm. Eng. 2016, 108, 1190–1199. [Google Scholar] [CrossRef]
- Castillo, L.; Enríquez, R.; Jiménez, M.J.; Heras, M.R. Dynamic integrated method based on regression and averages, applied to estimate the thermal parameters of a room in an occupied office building in Madrid. Energy Build. 2014, 81, 337–362. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T. Research on short-term and ultra-short-term cooling load prediction models for office buildings. Energy Build. 2017, 154, 254–267. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J. Optimization of Passive Envelop Energy Efficient Measures for Office Buildings in Different Climate Regions of China Based on Modified Sensitivity Analysis. Sustainability 2018, 10, 907. [Google Scholar] [CrossRef]
- Rey-Hernández, J.M.; Velasco-Gómez, E.; José-Alonso, J.F.S.; Tejero-González, A.; Rey-Martínez, F.J. Energy Analysis at a Near Zero Energy Building. A Case-Study in Spain. Energies 2018, 11, 857. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T.; Yang, F. Effect of input variables on cooling load prediction accuracy of an office building. Appl. Therm. Eng. 2018, 128, 225–234. [Google Scholar] [CrossRef]
- Kofler, M.J.; Renisch, C.; Kastner, W. A semantic representation of energy-related information in future smart homes. Energy Build. 2012, 47, 169–179. [Google Scholar] [CrossRef]
- Brown, N.; Bull, R.; Faruk, F.; Ekwevugbe, T. Novel instrumentation for monitoring after-hours electricity consumption of electrical equipment, and some potential savings from a switch-off campaign. Energy Build. 2012, 47, 74–83. [Google Scholar] [CrossRef]
- Ekwevugbe, T.; Brown, N.; Pakka, V.; Fan, D. Improved occupancy monitoring in non-domestic buildings. Sustain. Cities Soc. 2017, 30, 97–107. [Google Scholar] [CrossRef]
- Painter, B.; Brown, N.; Cook, M.J. Practical application of a sensor overlay system for building monitoring and commissioning. Energy Build. 2012, 48, 29–39. [Google Scholar] [CrossRef]
- Widen’, J.; Nilsson, A.M.; Wackelgard, E. A combined Markov-chain and bottom-up approach to modeling of domestic lighting demand. Energy Build. 2009, 41, 1001–1012. [Google Scholar] [CrossRef]
- Andersen, P.D.; Iversen, A.; Madsen, H.; Rode, C. Dynamic modeling of presence of occupants using inhomogeneous Markov chains. Energy Build. 2014, 69, 213–223. [Google Scholar] [CrossRef]
- Page, J.; Robinson, D.; Morel, N.; Scartezzini, J.-L. A generalised stochastic model for the simulation of occupant presence. Energy Build. 2008, 40, 83–98. [Google Scholar] [CrossRef]
- Kim, Y.S.; Heidarinejad, M.; Dahlhausen, M.; Srebric, J. Building energy model calibration with schedules derived from electricity use data. Appl. Energy 2017, 190, 997–1007. [Google Scholar] [CrossRef]
- Yang, J.; Santamouris, M.; Lee, S.E. Review of occupancy sensing systems and occupancy modeling methodologies for the application in institutional buildings. Energy Build. 2016, 121, 344–349. [Google Scholar] [CrossRef]
- Yang, Z.; Becerik-Gerber, B. A model calibration framework for simultaneous multi-level building energy simulation. Appl. Energy 2015, 149, 415–431. [Google Scholar] [CrossRef]
- Torriti, J. A review of time use models of residential electricity demand. Renew. Sustain. Energy Rev. 2014, 37, 265–272. [Google Scholar] [CrossRef]
- Ding, Y.; Fu, Q.; Tian, Z.; Li, M.; Zhu, N. Influence of indoor design air parameters on energy consumption of heating and air conditioning. Energy Build. 2013, 56, 78–84. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, Y. An occupant-based energy consumption prediction model for office equipment. Energy Build. 2015, 109, 12–22. [Google Scholar] [CrossRef]

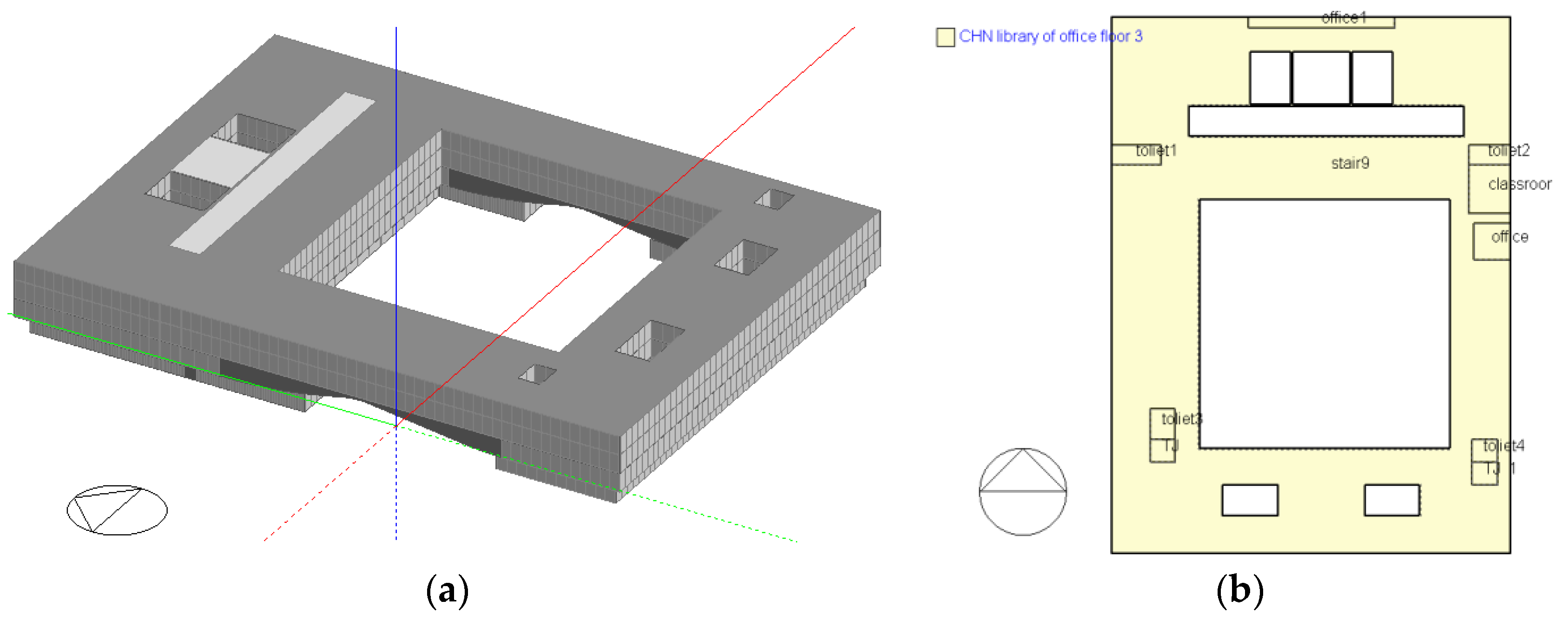
| Building Type | Building Function | Building Area | Floor | Story Height | Orientation | Operation Time | Usage Rate |
|---|---|---|---|---|---|---|---|
| Office building | Administration offices in the 1st and 2nd floor, scientific research rooms in 3rd floor | 3690 m2 | 3 | 3.0 m | South | 6:30–22:30; working time: 8:30–16:30 | Office rooms occupy 80% building areas, others are meeting rooms, machine rooms, and corridor |
| Teaching building | Taking class and self-studying | 6340 m2 | 4 | 4.5 m | South | 6:30–22:30 | Classrooms occupy 80% building areas, others are machine rooms and corridor 80% |
| Library | Reading, borrowing and returning books, self-studying | 41,410 m2 | 4 | 4.5 m | South | 8:00–22:00 | Book reading area occupy 80%, others are special used rooms, hot water rooms, and machine rooms |
| Exterior views |  The office building |  Teaching building |  Library | ||||
| Case Building | Heat Transfer Coefficient (W/(m2·K)) | Glass | Sun-Shading Type | Window to Wall Ratio | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exterior Wall | Roof | Exterior Window | Solar Heat Gain Coefficient | Visible Transmittance | S | W | E | N | Inner Side | ||
| Teaching building | 0.580 | 0.480 | 2.590 | 0.592 | 0.428 | Curtains | 0.80 | 0.30 | 0.30 | 0.80 | / |
| Office building | 0.550 | 0.480 | 2.260 | 0.505 | 0.720 | Horizontal shutters | 0.60 | 0.05 | 0.55 | 0.65 | 0.90 |
| Library | 0.550 | 0.480 | 2.200 | 0.505 | 0.720 | Horizontal shutters | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 |
| Item | Content | Item | Content |
|---|---|---|---|
| Room type | Class room | Number | 30 |
| Average area (m2) | 209 | Full-check occupant number | 200 |
| Installed lamps | |||
| Average lamps per room | 32 | Rated power (W) | 28 |
| Equipment information | |||
| Equipment1 | Computers | Number per room | 1 |
| Equipment2 | Projectors | Number per room | 1 |
| Item | Content | Item | Content |
|---|---|---|---|
| Small office rooms | |||
| Room type | Administration offices | Full-check occupants (number per room) | 1–2 |
| Average area (m2) | 23 | Number | 5 |
| Electrical appliances | |||
| Lamps (number per room) | 4 | Rated power (W) | 24 |
| Computers (number per room) | 1–2 | Rated power (W) | 300 |
| Printers (number per room) | 1 | Rated power (W) | 250 |
| Water dispenser (number per room) | 1 | Rated power (W) | 500 |
| Median office rooms | |||
| Room type | Administration offices | Full-check occupants (number per room) | 5 |
| Average area (m2) | 54 | Number | 6 |
| Electrical appliances | |||
| Lamps (number per room) | 8 | Rated power (W) | 24 |
| Computers (number per room) | 5 | Rated power (W) | 300 |
| Printers (number per room) | 1 | Rated power (W) | 250 |
| Water dispenser (number per room) | 1 | Rated power (W) | 500 |
| Shredders (number per room) | 1 | Rated power (W) | 135 |
| Large office rooms | |||
| Room type | Research rooms | Full-check occupants (number per room) | 16 |
| Average area (m2) | 115 | Number | 6 |
| Electrical appliances | |||
| Lamps (number per room) | 26 | Rated power (W) | 24 |
| Computers (number per room) | 16 | Rated power (W) | 300 |
| Printers (number per room) | 1 | Rated power (W) | 250 |
| Water dispenser (number per room) | 1 | Rated power (W) | 500 |
| Shredders (number per room) | 1 | Rated power (W) | 135 |
| Projectors (number per room) | 1 | Rated power (W) | 350 |
| Appliances | Number | Rated Power | |
|---|---|---|---|
| Lamps | Type1 | 2743 | 11 |
| Type2 | 328 | 36 | |
| Computers | 50 | 300 | |
| Multiple function printers | 8 | 2000 | |
| Printers | 4 | 250 | |
| TVs | 30 | 73 | |
| R2 | 8:30–12:30 | 12:30–18:30 | 13:30–18:30 | 12:30–17:30 |
|---|---|---|---|---|
| 5 min | 0.9355 | 0.7615 | 0.8867 | 0.8415 |
| 10 min | 0.9355 | 0.7542 | 0.8869 | 0.8652 |
| 30 min | 0.9601 | 0.8275 | 0.9085 | 0.8892 |
| 1 h | 0.9609 | 0.9258 | 0.9258 | 0.9720 |
| Building | Equipment Type | Description |
|---|---|---|
| Teaching building | Computers | |
| Laptops | ||
| Others | ||
| Office building | Computers | |
| Laptops | ||
| Others | ||
| Library | Computers | |
| Laptops | ||
| Others |
| Case Building | Maximum Indoor Occupant Density (People/m2) | |||
|---|---|---|---|---|
| Measured Data | Present Time | Original Design Data | Correction Factor of Holidays | |
| Teaching building | 0.1 | 11:30 | 0.5 | 0.61 |
| Office building | 0.04 | 10:30 | 0.25 | 0.84 |
| Library | 0.05 | 16:30, 20:30 | 0.5 | 0.76 |
| Computer Types | Average Rated Power (W) | Steady Input Power (W) | Sate Probability (%) | |||
|---|---|---|---|---|---|---|
| Standby | Low | Medium | High | |||
| Administration offices | ||||||
| Computer | 300 | 105.94 | 0.09 | 4.85 | 84.77 | 10.29 |
| Scientific research offices | ||||||
| Computer | 300 | 96.13 | 16.67 | 34.85 | 24.24 | 24.24 |
| Laptops | 120 | 40.35 | 19.89 | 22.17 | 32.82 | 25.12 |
| Thin & light laptops | 60 | 15.73 | 15.36 | 54.37 | 17.96 | 12.31 |
| Teaching building /Library | ||||||
| Laptops | 120 | 34.79 | 15.25 | 35.32 | 42.46 | 6.97 |
| Thin & light laptops | 60 | 13.79 | 25.19 | 42.51 | 30.77 | 1.53 |
| Ratio of state input power to rated power | 0.05 | 0.20 | 0.40 | 0.60 | ||
| Case Building | Occupants Type | Time Period | R2 | |||
|---|---|---|---|---|---|---|
| Teaching building | Self-studying occupants during holidays | −10.70 | 100.78 | −76.61 | 7:30–12:30 | 0.9847 |
| −10.24 | 86.75 | 56.38 | 13:30–17:30 | 0.9115 | ||
| −17.08 | 111.12 | 83.89 | 18:30–22:30 | 0.9358 | ||
| Self-studying occupants during general used period | −43.79 | 324.65 | −261.71 | 7:30–12:30 | 0.9871 | |
| −13.21 | 107.92 | −9.35 | 13:30–17:30 | 0.9434 | ||
| −71.20 | 410.30 | −255.36 | 18:30–22:30 | 0.9788 | ||
| Office building | Scientific research workers during holidays | −10.94 | 69.29 | −72.87 | 7:30–12:30 | 0.9246 |
| −2.83 | 24.99 | −1.90 | 13:30–17:30 | 0.9035 | ||
| −3.57 | 17.83 | 22.06 | 18:30–22:30 | 0.9276 | ||
| Administration workers during general used period | −3.75 | 20.00 | 8.75 | 7:30–12:30 | / | |
| −4.00 | 26.00 | −10.00 | 13:30–17:30 | / | ||
| Scientific research workers during general used period | −3.01 | 29.14 | −26.31 | 7:30–12:30 | 0.9523 | |
| −5.21 | 39.90 | 9.82 | 13:30–17:30 | 0.9146 | ||
| −6.94 | 41.93 | −0.73 | 18:30–22:30 | 0.9552 | ||
| Library | Self-studying occupants during holidays | −125.30 | 1065.50 | −1072.90 | 7:30–12:30 | 0.9215 |
| −51.94 | 559.49 | −233.54 | 13:30–17:30 | 0.8994 | ||
| −164.86 | 804.66 | 161.61 | 18:30–22:30 | 0.9503 | ||
| Self-studying occupants during general used period | −127.41 | 1067.10 | −974.63 | 7:30–12:30 | 0.9637 | |
| −95.19 | 808.18 | 125.47 | 13:30–17:30 | 0.9778 | ||
| −342.88 | 1843.00 | 487.31 | 18:30–22:30 | 0.9107 |
| Exterior | Fresh Air | Interior | Total | |
|---|---|---|---|---|
| Case building | Teaching building | |||
| Modified cooling load (W/m2) | 13.49 | 3.32 | 17.36 | 34.17 |
| Percentage (%) | 39.48 | 9.72 | 50.80 | 100 |
| Recommended cooling load (W/m2) | 63.17–94.75 | 15.55–23.33 | 81.28–121.92 | 160–240 |
| Over-estimating rate (times) | 4.68–7.03 | |||
| Case building | Office building | |||
| Modified cooling load (W/m2) | 32.61 | 15.61 | 9.96 | 58.18 |
| Percentage (%) | 56.05 | 26.83 | 17.12 | 100 |
| Recommended cooling load (W/m2) | 50.45–67.26 | 24.15–32.20 | 15.41–20.55 | 90–120 |
| Over-estimating rate (times) | 1.55–2.06 | |||
| Case building | Library | |||
| Modified cooling load (W/m2) | 37.50 | 4.50 | 18.12 | 60.12 |
| Percentage (%) | 62.37 | 7.49 | 30.14 | 100 |
| Recommended cooling load (W/m2) | 62.37–99.79 | 7.49–11.98 | 30.14–48.22 | 100–160 |
| Over-estimating rate (times) | 1.66–2.66 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ding, Y.; Deng, H.; Yang, F.; Zhu, N. An Occupant-Oriented Calculation Method of Building Interior Cooling Load Design. Sustainability 2018, 10, 1821. https://doi.org/10.3390/su10061821
Wang Z, Ding Y, Deng H, Yang F, Zhu N. An Occupant-Oriented Calculation Method of Building Interior Cooling Load Design. Sustainability. 2018; 10(6):1821. https://doi.org/10.3390/su10061821
Chicago/Turabian StyleWang, Zhaoxia, Yan Ding, Huiyan Deng, Fan Yang, and Neng Zhu. 2018. "An Occupant-Oriented Calculation Method of Building Interior Cooling Load Design" Sustainability 10, no. 6: 1821. https://doi.org/10.3390/su10061821
APA StyleWang, Z., Ding, Y., Deng, H., Yang, F., & Zhu, N. (2018). An Occupant-Oriented Calculation Method of Building Interior Cooling Load Design. Sustainability, 10(6), 1821. https://doi.org/10.3390/su10061821






