Simplicity and Sustainability: Pointers from Ethics and Science
Abstract
1. Introduction
2. Systems, Energy, and Entropy
- “The system is a nonsummative whole, that is, it cannot be reduced to its parts without altering their pattern. Aggregates, like a brick wall or a library or the content of a shopping cart, where components can be added or subtracted without affecting the relations between other components, do not qualify.
- The system is homeostatic. It stabilizes itself through negative feedback; that is, the system adjusts its output to produce and sustain a match between the input it will receive and its internally coded requirements.
- The system is self-organizing. Where a mismatch between input and code persists, the system searches for and encodes a new pattern by which it can function. Incorporating positive feedback, differentiation and complexification of structure emerge.
- The system is not only a whole, but part within a larger whole. Whether a cell or organ, atom or animal, it comprises subsystems. It also is, itself, a subsystem within a wider system of whose character and in whose functioning it is an integral and codeterminative component. Open systems in interaction form more inclusive structures or patterns as a function of their mutual adaptations”.
“A part, as I said—whether mechanical or organic—is intrinsically related to the whole, but this is not so for a fragment. As the Latin root of the word indicates, and as the related English word ‘fragile’ shows, to fragment is to break up or smash. To hit a watch with a hammer would not produce parts, but fragments that are separated in ways that are not significantly related to the structure of the watch”.
- An isolated system: No exchange of energy or matter with the outside environment.
- A closed system: Only energy is exchanged with the outside environment. Earth is an example of such a system. Interestingly, as mentioned in Moran and Shapiro [12] (p. 2), in a closed system, the boundaries of the system do not play a key role; instead, it is the quantity of matter which is being studied.
- An open system: Both matter and energy can be exchanged with the outside environment.
“Any system is an entity which can be investigated in its own right must have boundaries, either spatial or dynamic. Strictly speaking, spatial boundaries exist only in naïve observations, and all boundaries are ultimately dynamic. One cannot exactly draw the boundaries of an atom (with valences sticking out, as it were, to attract other atoms), of a stone (an aggregate of molecules and atoms which mostly consist of empty space, with particles in planetary distances), or of an organism (continually exchanging matter with the environment)”.
“No process is possible whose sole result is the complete conversion of heat into work”.[Kelvin]
“No process is possible whose sole result is the transfer of heat from a colder to a hotter body”.[Clausius]
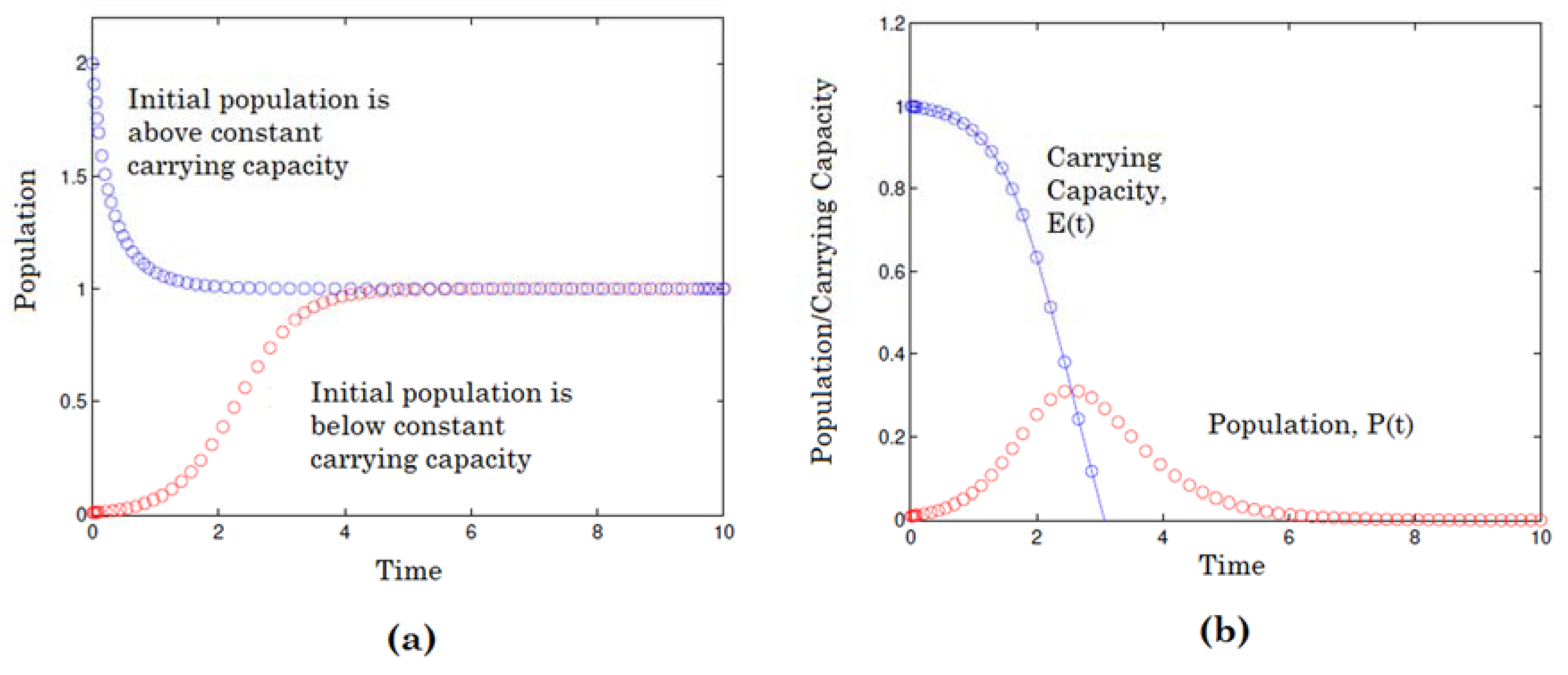
3. Mathematical Modeling
“When a society becomes unstable, when social control breaks down and discontinuities grow even bigger, then it is but a question of time before it eventually collapses. It is towards such a collapse that our educational system, together with the rest of the institutions of our industrial society, are leading us. To avoid it, education must, among other things, be designed to promote stability rather than change—but this cannot be done in an industrial society in which the promotion of instability, implicit as it is in our notion of progress, is the avowed object of public policy”.
“It is scarcely necessary to remark that a stationary condition of capital and population implies no stationary state of human improvement. There would be as much scope as ever for all kinds of mental culture, and moral and social progress; as much room for improving the Art of Living and much more likelihood of its being improved, when minds cease to be engrossed by the art of getting on”.
4. Simplicity
4.1. Functional Simplicity
- FS1.
- Predictability, reliability
- FS2.
- Cheap in terms of economic cost and material content of the product
- FS3.
- Having value or functionality
- FS4.
- Stackable: Can be used to create newer, more complex objects with different functions
4.2. Aesthetics and the Occam’s Razor
“A theory is the simpler, the more easily it could be falsified. The degree of falsifiability depends on the number of parameters that have to be fixed in order to make it logically possible for the theory to be falsified. The simpler theory is richer, more powerful, it says more”.
- SS1:
- Given two or more choices, the one involving the least number of assumptions or hypothesis is the simpler one.
- SS2:
- Given two or more choices, the one with the greatest aesthetic value can be considered the simplest choice.
4.3. Personal Simplicity
- PS1.
- Reliability and stability
- PS2.
- Ability to live meagerly
- PS3.
- Ability to live creatively and finding value in work and life
- PS4.
- Living ethically
“Poverty is involuntary whereas simplicity is consciously chosen. Poverty is repressive; simplicity is liberating. Poverty generates a sense of helplessness, passivity, and despair; simplicity fosters personal empowerment, creativity, and a sense of ever present opportunity. Poverty is mean and degrading to the human spirit; simplicity has both beauty and a functional integrity that elevate our lives. Poverty is debilitating; simplicity is enabling”.
“By ‘technology’ let us denote a package of feasible recipes containing at least one such recipe for every commodity necessary for the maintenance of the funds involved. That is, a technology consists of a general system by which environmental matter-energy is used for various purposes. To be sure, no technology can produce its own environmental source of support”.
“In matters of development there is a problem of choosing the right ‘level of technology’ to fit the given circumstances; in other words, there is a choice of technology and it cannot be assumed that the level of technology used by affluent societies is the only possible level, let alone that it is necessarily the best for poor societies ... The technologies most likely to be appropriate for development in conditions of poverty would be in a sense ‘intermediate’ between—to speak symbolically—the hoe and the tractor, or the panga and the combine harvester”.
“That ‘creativity’ is beyond analysis is a romantic illusion we must now outgrow. It cannot be learned perhaps, but it can certainly be encouraged and abetted. We can put ourselves in the way of having ideas, by reading and discussion and by acquiring the habit of reflection, guided by the familiar principle that we are not likely to find answers to questions not yet formulated in the mind”.
4.4. Environmental Simplicity
- (1)
- “An environmental ethic must hold that there are nonhuman beings which have moral standing”.
- (2)
- “An environmental ethic must hold that the class of those beings which have moral standing includes but is larger than the class of conscious beings—that is, all conscious beings and some nonconscious beings must be held to have moral standing”.
- (1)
- “According to the principle of moral consideration, wild living things are deserving of the concern and consideration of all moral agents simply in virtue of their being members of the Earth’s community of life”.
- (2)
- “The principle of intrinsic value states that, regardless of what kind of entity it is in other respects, if it is a member of the Earth’s community of life, realization of its good is something intrinsically valuable”.
“(P1) X is irreplaceable.(C) Therefore, X ought to be preserved”.
“To the man who is truly ethical all life is sacred, including that which from the human point of view seems lower in the scale. He makes distinctions only as each case comes before him and under pressure of necessity, as, for example, when it falls to him to decide which of two lives he must sacrifice in order to preserve the other. But all through this series of decisions he is conscious of acting on subjective grounds and arbitrarily, and knows that he bears the responsibility for the life which is sacrificed”.
4.5. Attitudes towards Simplicity
- (1)
- Attitude of respect and reverence for life as a whole. In this idealistic view, we recognize that we are part of nature and that there are many other species striving to live and realize their potentiality. The nature of existence is such that we need material food to survive, and therefore, in some ways we have to take something away from nature. However, we do that in an attitude of reverence and conservation; conservation in the sense that if we really do not need it, we would not take it. We leave it for other beings and for the future generations. This may be called the attitude of custodian-ship or guardian-ship.
- (2)
- Attitude of respect along with the notion of reusing whatever can be reused. It is difficult to clearly separate this category from the first one, but this might seem to be a more pragmatic attitude with acceptance of consumption behavior. This attitude is also accompanied by a respect for conservation principles whereby we do not callously discard items after using them; instead we try to reuse whatever is possible. The concept of conservation or “not using” is not as important or vital as in the first category and the concept of utility begins to enter into our system of ethics. This attitude may be called the attitude of partnership, with some responsibility as a custodian.
- (3)
- Attitude of recycling or extreme pragmatism. At this point we have generally put the burden of un-ease on others. We no longer have to think: (i) whether we really need to use this thing; and (ii) whether we can reuse. Instead, we use it and not even think about the consequences (at least not that deeply), yet we are aware that we need to recycle. However, recycling is not free; it requires energy and other raw materials. This attitude may be called the attitude of partial ownership, with a bit of responsibility as a partner.
- (4)
- Attitude of not-caring (or not-thinking). This has been the predominant attitude in the last few hundred years, and especially more during the last few decades. Here, Nature is basically for man’s use. There is no inherent or intrinsic value in nature as a whole, or in any other life form. The concept of utility is perhaps at its peak here. This attitude may be called the attitude of full ownership with all the rights associated with it.
“I conceive a strip-miner to be a model exploiter, and as a model nurturer I take the old-fashioned idea or ideal of a farmer. The exploiter is a specialist, an expert; the nurturer is not. The standard of the exploiter is efficiency; the standard of the nurturer is care. The exploiter’s goal is money, profit; the nurturer’s goal is health—his land’s health, his own, his family’s, his community’s, his country’s. Whereas the exploiter asks of a piece of land only how much and how quickly it can be made to produce, the nurturer asks the question that is much more complex and difficult: What is its carrying capacity? (That is: How much can be taken from it without diminishing it? What can it produce dependably for an infinite time?) The exploiter wishes to earn as much as possible by as little work as possible; the nurturer expects, certainly, to have a decent living from his work, but his characteristic wish is to work as well as possible. The competence of the exploiter is in organization; that of the nurturer is in order—a human order, that is, that accommodates itself both to other order and to mystery. The exploiter typically serves an institution or organization; the nurturer serves land, household, community, place. The exploiter thinks in terms of numbers, quantities, ‘hard facts’; the nurturer in terms of character, condition, quality, kind”.
5. Relating Simplicity to Sustainability
“…they are unconvincing but never tedious. In any case it may be argued that mathematicians should have a turn at examining the beautiful and the good; philosophers, theologians, writers on aesthetics and other experts have been probing these matters for more than 2000 years without making any notable advance”.
6. Conclusions
- EN1:
- When we take anything which is more than what we really need (more than our share), we are depriving other beings, somewhere and at some time, of having the same or at least equal access to those resources.
- EN2:
- Simplicity, in the modern age, and as a collective idea must include the suspension of growth as an economic idea but as an improvement in quality for all. From a social standpoint simplicity is therefore the most essential factor in sustainability.
“It is perfectly clear that [automation] will produce an unemployment situation, in comparison with which … the depression of the [nineteen] thirties will seem a pleasant joke. This depression will ruin many industries—possibly even the industries which have taken advantage of the new potentialities …”.
Author Contributions
Conflicts of Interest
References
- Daly, H.; Cobb, J. For the Common Good; Beacon Press: Boston, MA, USA, 1989. [Google Scholar]
- Abdallah, S.; Thompson, S.; Michaelson, J.; Marks, N.; Steuer, N. The Happy Planet Index 2.0: Why Good Lives Don’t Have to Cost the Earth; The New Economics Foundation (NEF): London, UK, 2009. [Google Scholar]
- Helliwell, J.; Layard, R.; Sachs, J. World Happiness Report; the Earth Institute, Columbia University: New York, NY, USA, 2012. [Google Scholar]
- United Nations Website. Available online: http://www.un.org/sustainabledevelopment/sustainable-development-goals/ (accessed on 29 November 2017).
- Mainzer, K. Thinking in Complexity, 4th ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Meadows, D.H. Thinking in Systems; Chelsea Green Publishing: Hartford, VT, USA, 2008. [Google Scholar]
- Laszlo, E. The Systems View of the World, 2nd ed.; Hampton Pr: New York, NY, USA, 1972. [Google Scholar]
- Macy, J. Mutual Causality in Buddhism and General Systems Theory: The Dharma of Natural Systems; SUNY Press: Buffalo, NY, USA, 1991. [Google Scholar]
- Bohm, D. Unfolding Meaning; Routledge: London, UK, 1985. [Google Scholar]
- Adkins, C.J. Equilibrium Thermodynamics, 3rd ed.; Cambridge University Press: New York, NY, USA, 1984. [Google Scholar]
- Massoudi, M. A System Theory approach to Interfaith Dialogue. Intercult. Educ. 2006, 17, 421–437. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Kirwan, A.D., Jr. Mother Nature’s Two Laws: Ringmaster for Circus Earth; World Scientific Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Von Bertalanffy, L. General System Theory: Foundations, Developments, Applications, revised ed.; George Braziller Inc.: New York, NY, USA, 1968. [Google Scholar]
- Kestin, J. A Course in Thermodynamics; Revised Printing; Hemisphere Publishing Company: Washington, DC, USA, 1979. [Google Scholar]
- Kestin, J.; Dorfman, J.R. A Course in Statistical Thermodynamics; Academic Press Inc.: New York, NY, USA, 1971. [Google Scholar]
- Georgescu-Roegen, N. The Entropy Law and the Economic Process; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Lindsay, R.B. Entropy consumption and values in physical science. Am. Sci. 1959, 47, 678–696. [Google Scholar]
- Rifkin, J. Entropy, Into the Greenhouse World, revised ed.; Bentam Books: New York, NY, USA, 1989. [Google Scholar]
- Massoudi, M. A Possible Ethical Imperative Based on the Entropy Law. Entropy 2016, 18, 389. [Google Scholar] [CrossRef]
- Aris, R. Mathematical Modeling Techniques; Dover Publications, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Truesdell, C. An Idiot’s Fugitive Essays on Science; Springer: New York, NY, USA, 1984. [Google Scholar]
- Mazumdar, J. An Introduction to Mathematical Physiology and Biology; Cambridge University Press: New York, NY, USA, 1999; Volume 15. [Google Scholar]
- Daly, H. Beyond Growth: The Economics of Sustainable Development; Beacon Press: Boston, MA, USA, 1996. [Google Scholar]
- Pimentel, D.; Houser, J.; Preiss, E.; White, O.; Fang, H.; Mesnick, L.; Alpert, S. Water resources: Agriculture, the environment, and society. BioScience 1997, 47, 97–106. [Google Scholar] [CrossRef]
- Lomberg, B. The Skeptical Environmentalist; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Simon, J. The Ultimate Resource 2, revised ed.; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Meadows, D.H.; Meadows, D.L.; Randers, J.; Behrens, W.W. The Limits to Growth. 1972. Available online: https://books.google.com.hk/books?hl=zh-N&lr=&id=38tVDgAAQBAJ&oi=fnd&pg=PT25&dq=+Meadows,+D.H.%3B+Meadows,+D.L.%3B+Randers,+J.%3B+Behrens,+W.W.+The+limits+to+growth&ots=kotO9bZXcE&sig=ZAaNF0npFB-xKKe-3xS5QDobBd8&redir_esc=y#v=onepage&q&f=false (accessed on 4 April 2018).
- Meadows, D.; Jorgen, R.; Dennis, M. Limits to Growth: The 30-Year Update; Chelsea Green Publishing: Hartford, VT, USA, 2004. [Google Scholar]
- Foster, J.B. Ecology against Capitalism; NYU Press: New York, NY, USA, 2002. [Google Scholar]
- Wigner, E.P. The unreasonable effectiveness of mathematics in the natural sciences. Richard courant lecture in mathematical sciences delivered at New York University, May 11, 1959. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Goldsmith, E. The Great U-Turn; Green Books: Devon, UK, 1988. [Google Scholar]
- Chung, B.J.; McDermid, K.; Vaidya, A. On the affordances of the MaxEP principle. Eur. Phys. J. B 2014, 87, 20. [Google Scholar] [CrossRef]
- Mill, J.S. Of the Stationary State. Principles of Political Economy Book IV: Influence of the Progress of Society; Longman Green and Co.: London, UK, 1848. [Google Scholar]
- Muller, R.A. Now: The Physics of Time; W. W. Norton & Company: New York, NY, USA, 2016. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Leoplod, A. A Sand County Almanac; Oxford University Press: New York, NY, USA, 1949. [Google Scholar]
- Whitesides, G. George Whitesides: Toward a Science of Simplicity; TED: New York, NY, USA, 2010. [Google Scholar]
- Baker, A. Simplicity; The Stanford Encyclopedia of Philosophy: Stanford, CA, USA, 2016. [Google Scholar]
- Newton, I. The Mathematical Principles of Natural Philosophy (Principia Mathematica); Citadel Press: New York, NY, USA, 1964. [Google Scholar]
- Post, H.R. Simplicity in Scientific Theories. Br. J. Philos. Sci. 1960, 11, 32–41. [Google Scholar] [CrossRef]
- Plato, L.; Meskin, A. Aesthetic value. In Encyclopedia of Quality of Life and Well-Being Research; Springer: Dordrecht, The Netherlands, 2014; pp. 76–78. [Google Scholar]
- Hoffman, P. The Man Who Loved Only Numbers; Hyperioncop: New York, NY, USA, 1998; p. 26. [Google Scholar]
- Koestler, A. The Act of Creation; Penguin Books: New York, NY, USA, 1964. [Google Scholar]
- Orrell, D. Truth or Beauty: Science and the Quest for Order; Yale University Press: New Haven, CT, USA, 2012. [Google Scholar]
- Elgin, D. Voluntary Simplicity; Harper Collins: New York, NY, USA, 1981. [Google Scholar]
- Johnson, L.E. A Morally Deep World; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Georgescu-Roegen, N. Technology Assessments: The Case of the Direct Use of Solar Energy. Atl. Econ. J. 1978, 4, 15–21. [Google Scholar] [CrossRef]
- Schumacher, E.F. Small Is Beautiful; Harper & Row: New York, NY, USA, 1973. [Google Scholar]
- Schumacher, E.F. Good Works; Harper & Row: New York, NY, USA, 1977. [Google Scholar]
- Sternberg Robert, J. (Ed.) Handbook of Creativity; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Getzels, J.W.; Taylor, I.A. (Eds.) Perspectives in Creativity; Aldine: Chicago, IL, USA, 1975. [Google Scholar]
- Sternberg, R.J. What is the common thread of creativity? Its dialectical relation to intelligence and wisdom. Am. Psychol. 2001, 56, 360–362. [Google Scholar] [CrossRef] [PubMed]
- Neumann, C.J. Fostering creativity: A model for developing a culture of collective creativity in science. EMBO Rep. 2007, 8, 202–206. [Google Scholar] [CrossRef] [PubMed]
- Spendlove, D. Creativity in Education: A review. Des. Technol. Educ. Int. J. 2005, 10, 9–18. [Google Scholar]
- Getzels, J.W.; Csikszentmihalyi, M. The Creative Vision: A Longitudinal Study of Problem Solving in Art; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Simonton, D. Origins of Genius; Cambridge Press: New York, NY, USA, 1999. [Google Scholar]
- Simonton, D.K. Genius, Creativity and Leadership: Historiometric Enquiries; Harvard University Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Simonton, D.K. Creativity. Cognitive, personal, developmental, and social aspects. Am. Psychol. 2000, 55, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Massoudi, M. Can scientific writing be creative? J. Sci. Educ. Technol. 2003, 12, 115–128. [Google Scholar] [CrossRef]
- Munakata, M.; Vaidya, A. Fostering Creativity through Personalized Education. Primus 2013, 23, 764–775. [Google Scholar] [CrossRef]
- Munakata, M.; Vaidya, A. Encouraging creativity in mathematics and science through photography. Teach. Math. Appl. Int. J. IMA 2012, 31, 121–132. [Google Scholar] [CrossRef][Green Version]
- Robinson, K.; Aronica, L. The Element: How Finding Your Passion Changes Everything; Viking: New York, NY, USA, 2009. [Google Scholar]
- Medawar, P.B. Induction and Intuition in Scientific Thought; American Philosophical Society: Philadelphia, PA, USA, 1969. [Google Scholar]
- Schwartz, B. Why We Work; Simon and Schuster: New York, NY, USA, 2015. [Google Scholar]
- Regan, T. The nature and possibility of an environmental ethic. Environ. Ethics 1981, 3, 19–34. [Google Scholar] [CrossRef]
- Rolston, H., III. Environmental Ethics; Temple University Press: Philadelphia, PA, USA, 1988. [Google Scholar]
- Singer, P. How Are We to Live; Prometheus Books: Amherst, NY, USA, 1995. [Google Scholar]
- Gunn, A.S. Why should we care about rare species? Environ. Ethics 1980, 2, 17–37. [Google Scholar] [CrossRef]
- Taylor, P.W. The ethics of respect for nature. Environ. Ethics 1981, 3, 197–218. [Google Scholar] [CrossRef]
- Martin, J.N. The concept of irreplaceable. Environ. Ethics 1979, 1, 31–48. [Google Scholar] [CrossRef]
- Marshall George, N.; David, P. Schweitzer: A Biography; JHU Press: Baltimore, MD, USA, 2000; p. 190. [Google Scholar]
- Berry, W. The Unsettling of America; Sierra Club: San Francisco, CA, USA, 1977. [Google Scholar]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics; Springer: New York, NY, USA, 1992. [Google Scholar]
- Newman, J.R. The World of Mathematics; Dover Publications: Mineola, NY, USA, 2000; Volumes 1–4. [Google Scholar]
- Birkhoff, G.D. A mathematical theory of aesthetics. Rice Inst. Pam. 1932, 19, 189–342. [Google Scholar]
- Birkhoff, G.D. A mathematical approach to ethics. Rice Inst. Pam.-Rice Univ. Stud. 1941, 28, 23. [Google Scholar]
- Popper, K. Conjectures and Refutations, 5th ed.; Routledge: London, UK, 1989. [Google Scholar]
- Naess, A. Ecology, Community, and Lifestyle; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Bar-Yam, Y. Dynamics of Complex Systems; Addison-Wesley: Reading, MA, USA, 1997; Volume 213. [Google Scholar]
- Berry. Available online: http://billmoyers.com/segment/wendell-berry-on-his-hopes-for-humanity/ (accessed on 4 April 2018).
- Alexander, S. Sufficiency Economy: Enough, For Everyone, Forever. Available online: http://simplicitycollective.com/enough-for-everyone-forever (accessed on 4 April 2018).
- Wiener, N. The Human Use of Human Beings: Cybernetics and Society (No. 320); Perseus Books Group: New York, NY, USA, 1988. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massoudi, M.; Vaidya, A. Simplicity and Sustainability: Pointers from Ethics and Science. Sustainability 2018, 10, 1303. https://doi.org/10.3390/su10041303
Massoudi M, Vaidya A. Simplicity and Sustainability: Pointers from Ethics and Science. Sustainability. 2018; 10(4):1303. https://doi.org/10.3390/su10041303
Chicago/Turabian StyleMassoudi, Mehrdad, and Ashwin Vaidya. 2018. "Simplicity and Sustainability: Pointers from Ethics and Science" Sustainability 10, no. 4: 1303. https://doi.org/10.3390/su10041303
APA StyleMassoudi, M., & Vaidya, A. (2018). Simplicity and Sustainability: Pointers from Ethics and Science. Sustainability, 10(4), 1303. https://doi.org/10.3390/su10041303





