Multi-Criterion Two-Sided Matching of Public–Private Partnership Infrastructure Projects: Criteria and Methods
Abstract
1. Introduction
2. Literature Review
2.1. PPP Infrastructure Projects
2.2. TSM Satisfaction Evaluative Criteria of PPP Infrastructure Projects
- Financial strength: Many scholars have reported various kinds of financial strength for TSM of PPP infrastructure projects, such as capital strength [22,23,24,28], financing capacity [17,24,28,29], and financial guarantee [30]. This criterion is used to measure financial credibility of private sectors to deal with capital crises [31].
- Technical ability: This criterion category is the ability to establish project parameters and in-house expertise [32]. The private sectors have to show their technical ability including advanced technology [23,24,25,29], project implementation plans [22], personnel reserve [15,23,30] and critical equipment [15,22], to carry out all construction activities required for a specific PPP infrastructure project.
- Management ability: One of the most critical factors for the successful completion of PPP infrastructure projects is top management ability [28]. The private sectors have to show their management capacity to carry out all construction activities required for a specific PPP infrastructure project, including management formalization [1,17], project management capacity [22], ability of communication and cooperation [23], concession duration [15,30], risk management ability [22,29], and maintenance ability [24].
- Governmental insurance: Currently there are no special laws and regulations for PPP infrastructure projects to define the responsibility division between participants, project assessment, contract performance and change, and conflict-solving styles [15,17,27]. However, appropriate laws and regulations are the foundation for the private sector to participate in PPP infrastructure projects and the premise of TSM [7] because of a longer construction cycle and increasing risk of operating project construction.
- Governmental guarantee: The recoverable rate of investment is key for the private sector involved in PPP infrastructure projects, thus the public sector should offer the recoverable rate of investment to businesses via offering a government-backed rate [6,22,28], price [17,29], purchase, and compensation in the scope of given benefit level [1,6].
- Governmental credibility: The private sector involved in PPP infrastructure projects must be built on project understanding but the key information about the PPP project is disclosed by the public sector [1,15]. Many previous cases have demonstrated that unclear project information leads to a lack of trust in the public sector [6,27]. Moreover, the private sector is in a weak position when playing games with the public sector; and thus, the legitimate rights and interests of the private sector are hard to guarantee [22].
- Governmental risk-sharing: There are a series of unpredictable risks due to PPP infrastructure projects characteristically lasting a long time, and it would expose the private sector to serious damage if these risks occurred [1,9,33]. Therefore, risk-sharing of the government affects the quantity and quality of the private sector involved in PPP infrastructure projects [1,5,6,24,25,29]
2.3. TSM Selection Approaches
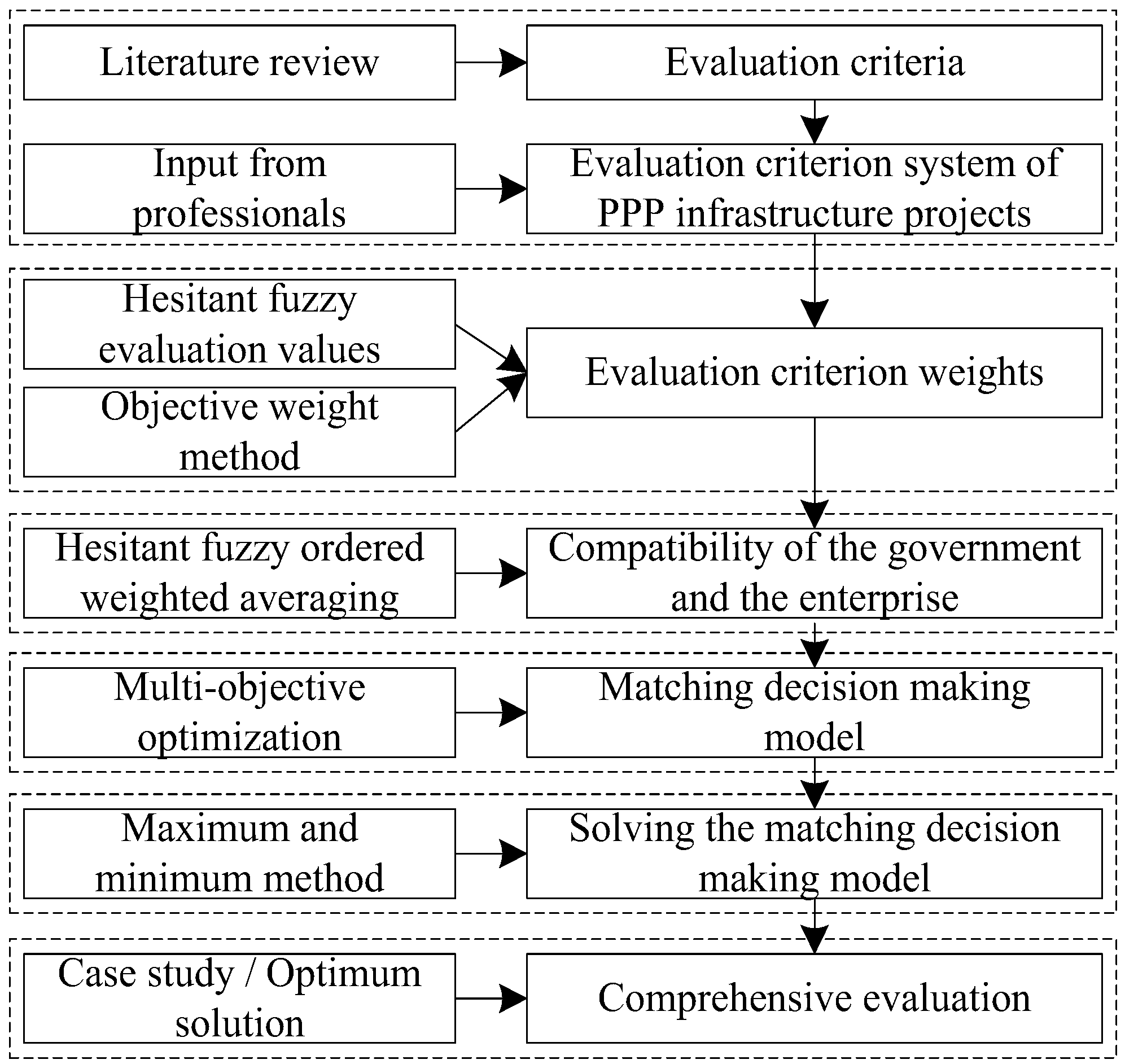
3. TSM Decision Making Model of PPP Infrastructure Projects Based on HFS
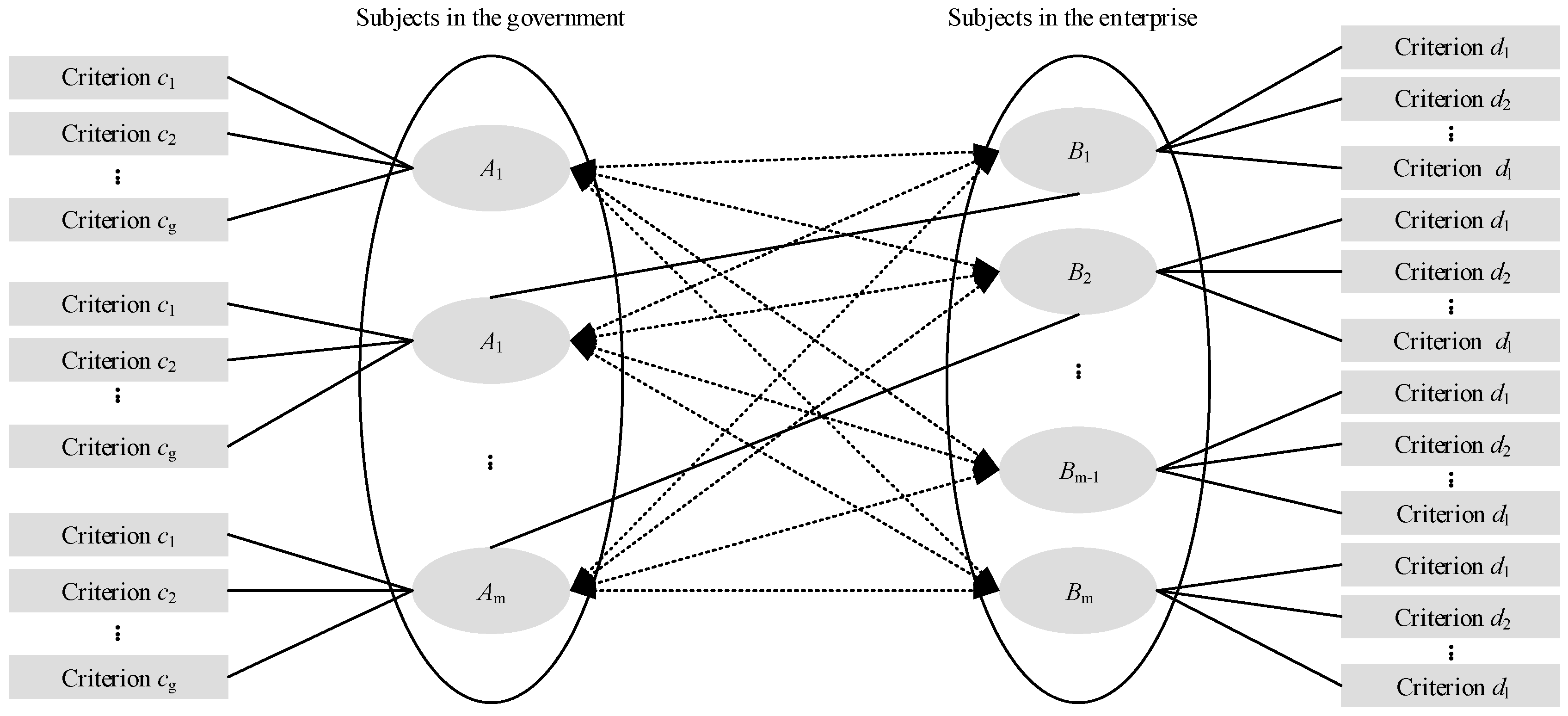
3.1. Description and Assumption
3.2. TSM Decision Making Model Development
4. Application of Proposed Model: Calculation Example
4.1. Data Sources
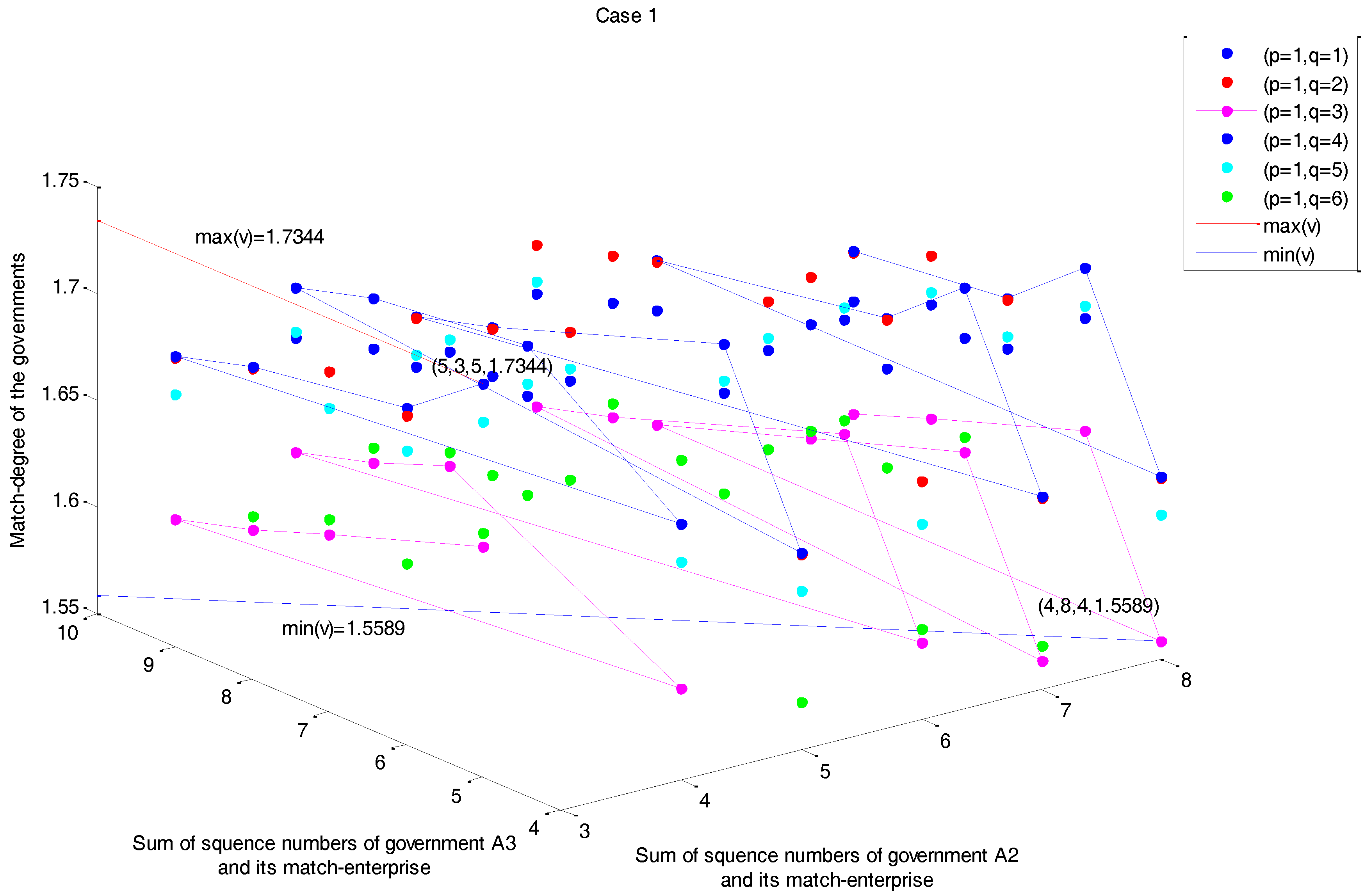
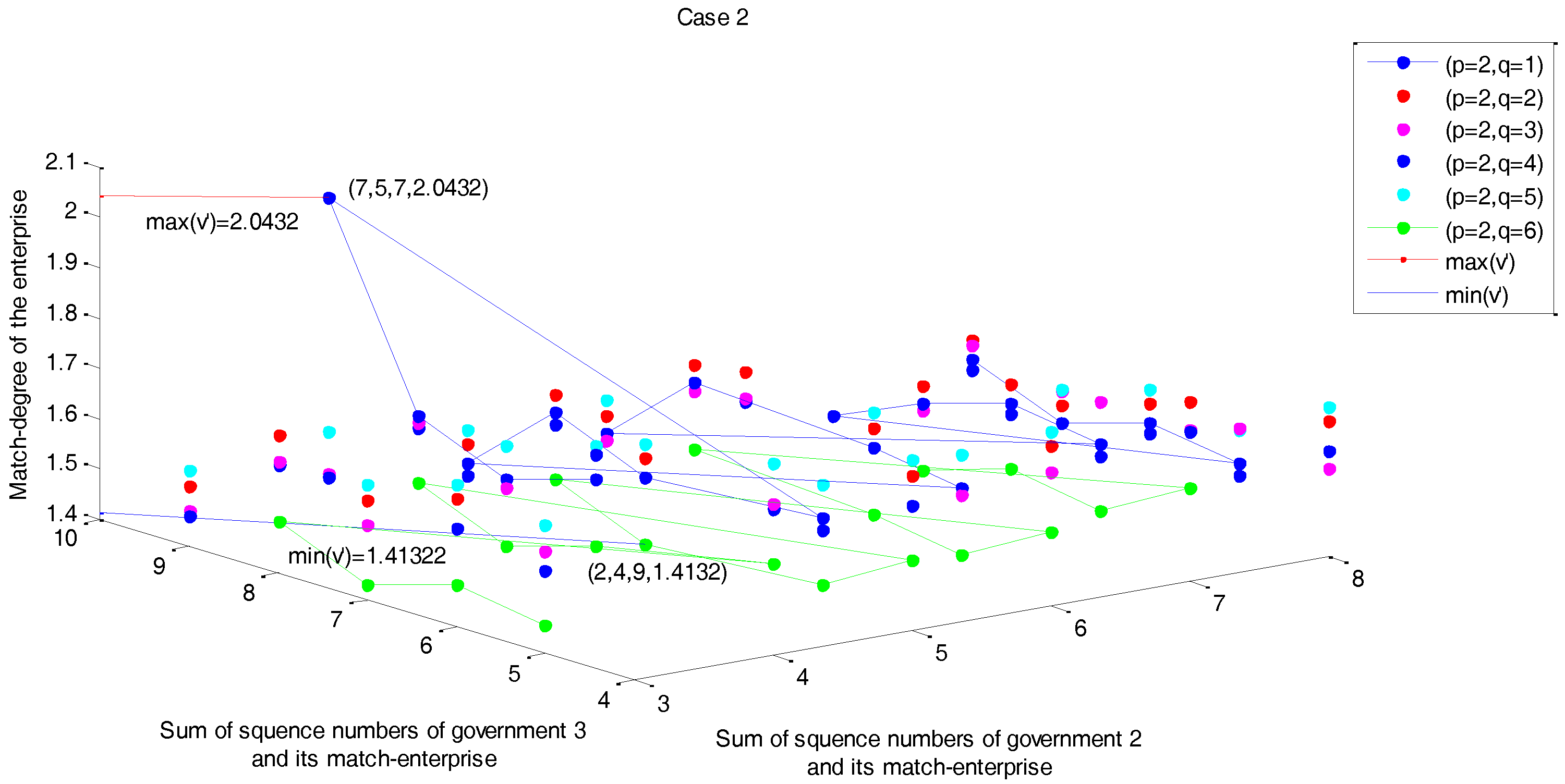
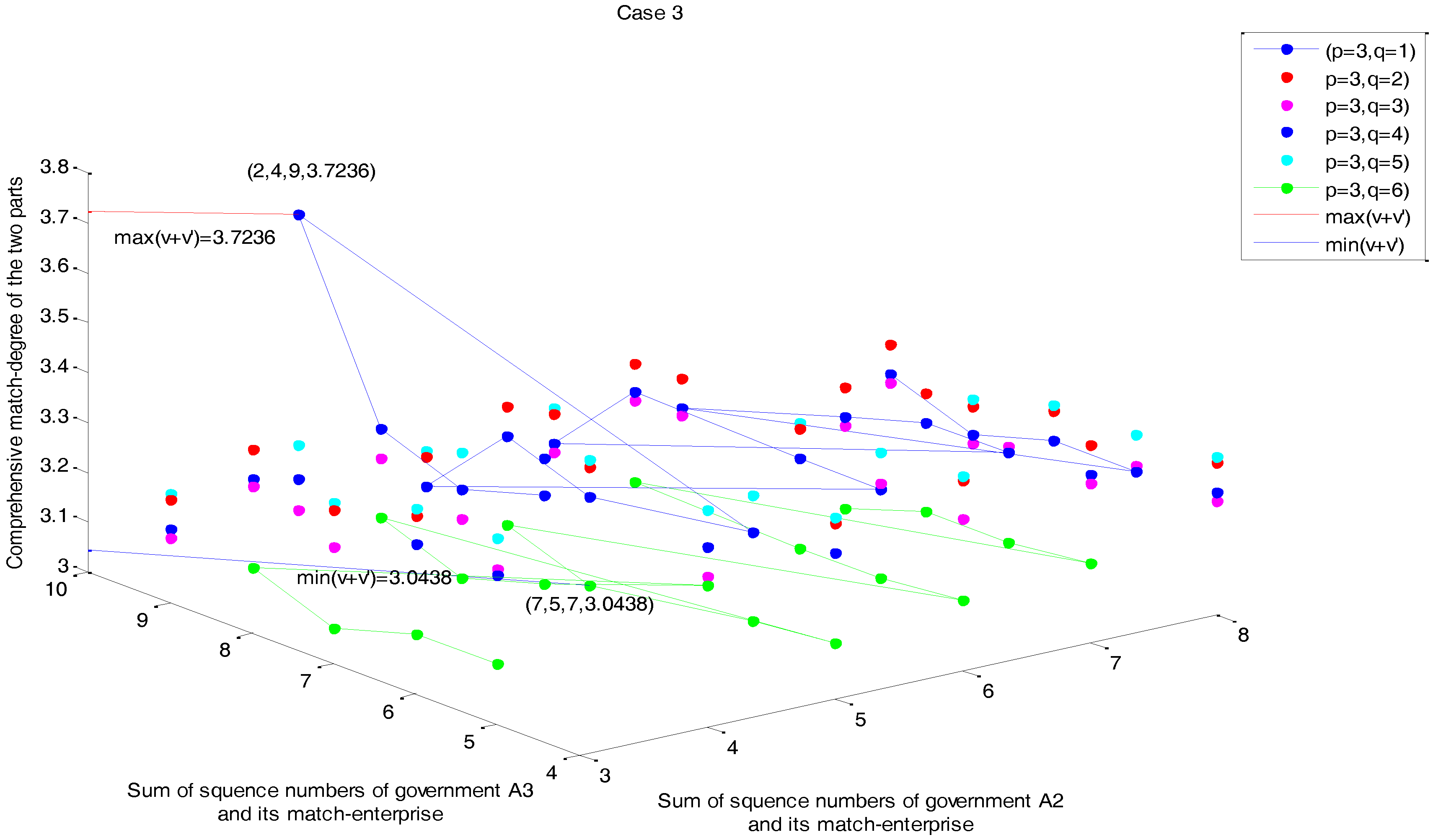
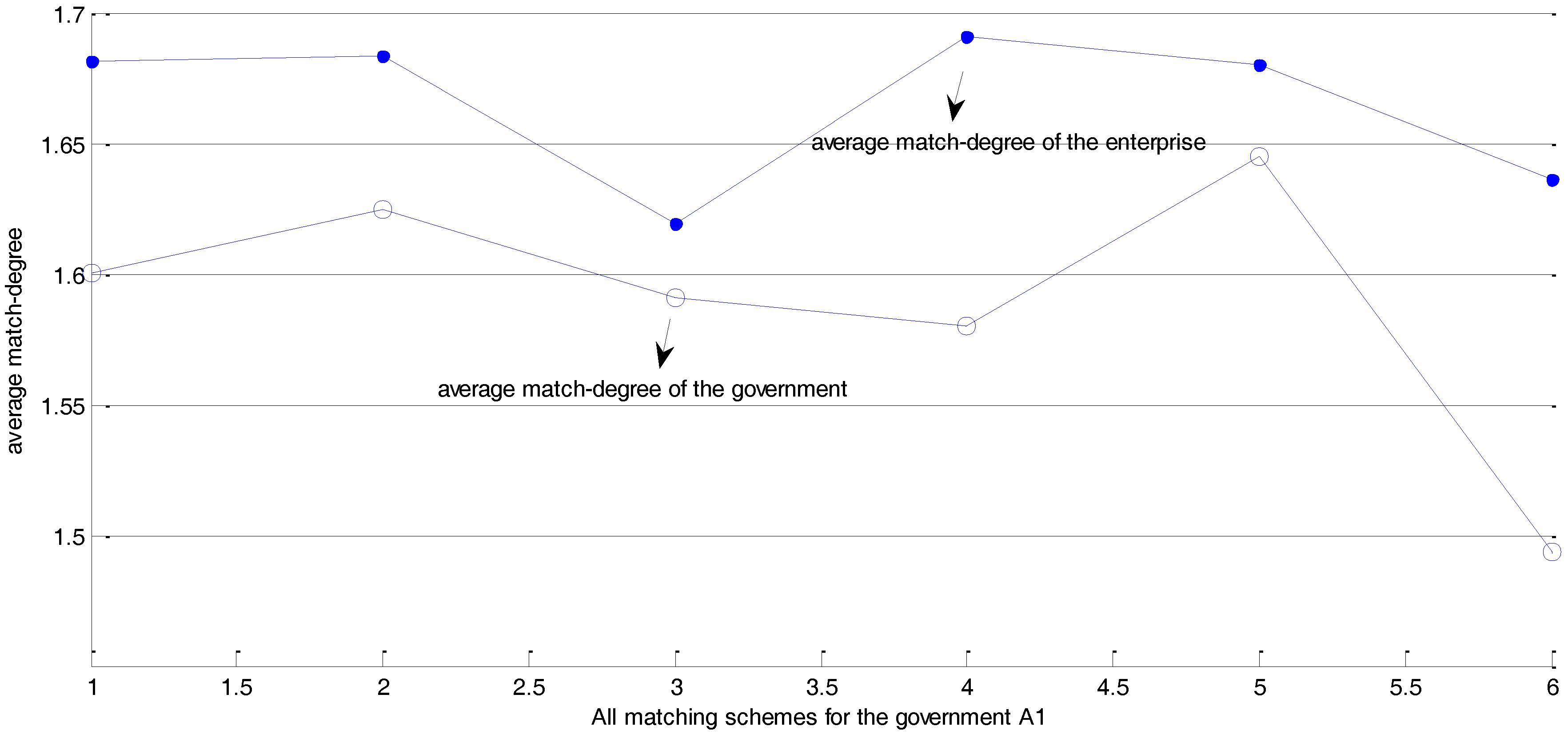
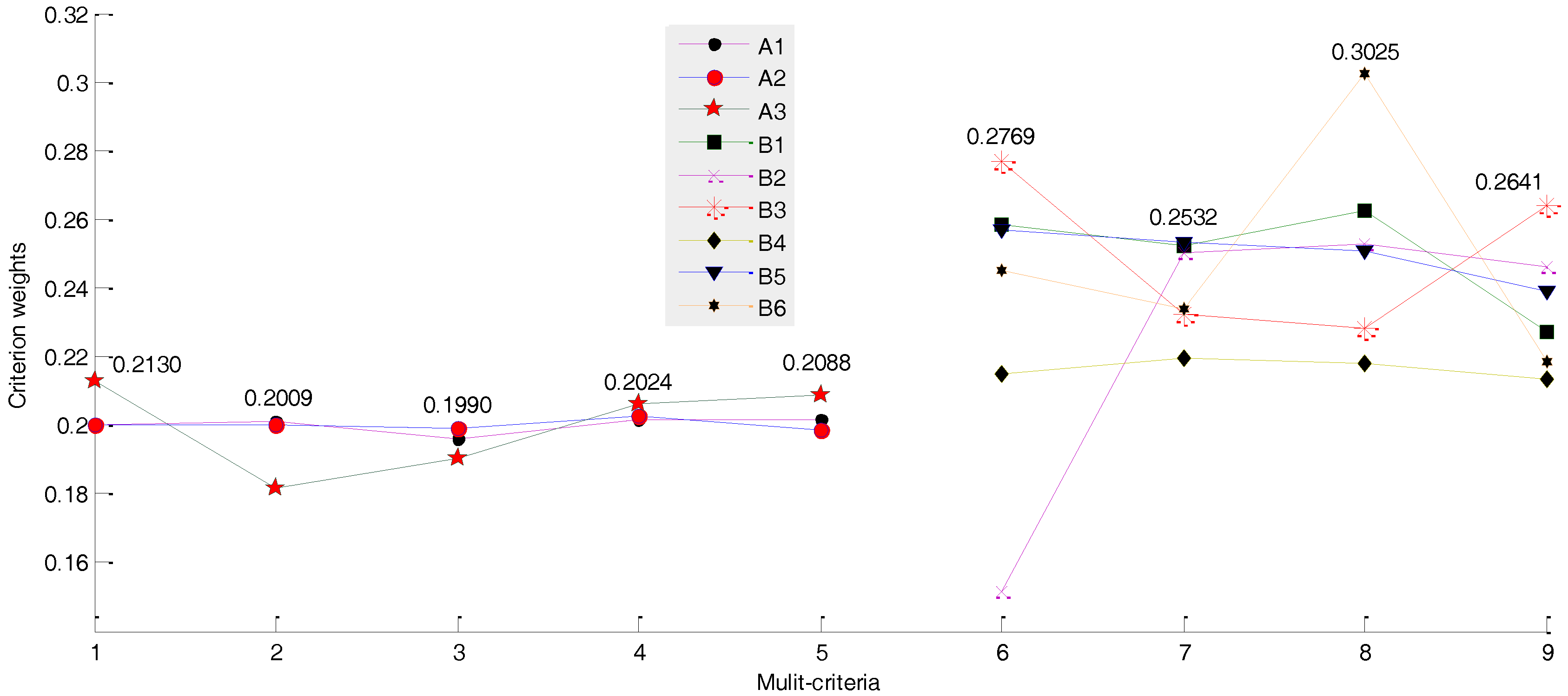
4.2. Model Results
4.3. Discussion and Findings
4.4. Practical Case
5. Implications
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. The Calculation Process of the Proposed Method
| Subjects in the Government | Criterion Weights | Subjects in the Enterprise | Criterion Weights | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | c5 | d1 | d2 | d3 | d4 | ||
| A1 | 0.1999 | 0.2009 | 0.1960 | 0.2016 | 0.2016 | B1 | 0.2582 | 0.2523 | 0.2624 | 0.2271 |
| A2 | 0.2001 | 0.2001 | 0.1990 | 0.2024 | 0.1984 | B2 | 0.1514 | 0.2500 | 0.2528 | 0.2461 |
| A3 | 0.2130 | 0.1818 | 0.1904 | 0.2060 | 0.2088 | B3 | 0.2769 | 0.2325 | 0.2282 | 0.2641 |
| B4 | 0.2150 | 0.2194 | 0.2180 | 0.2136 | ||||||
| B5 | 0.2567 | 0.2532 | 0.2509 | 0.2392 | ||||||
| B6 | 0.2450 | 0.2338 | 0.3025 | 0.2187 | ||||||
References
- Liu, T.T.; Wang, Y.; Wilkinson, S. Identifying critical factors affecting the effectiveness and efficiency of tendering processes in Public–Private Partnerships (PPPs): A comparative analysis of Australia and China. Int. J. Proj. Manag. 2016, 34, 701–716. [Google Scholar] [CrossRef]
- Ameyaw, E.E.; Chan, A.P.C. A fuzzy approach for the allocation of risks in Public–Private Partnership water-infrastructure projects in developing countries. J. Infrastruct. Syst. 2016, 22. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Wright, G.; Thatcher, D.; Wu, P.; Felix, P. Traffic volume prediction with segment-based regression kriging and its implementation in assessing the impact of heavy vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 1–12. [Google Scholar] [CrossRef]
- Tao, S.; Wu, C.; Sheng, Z.; Wang, X. Space-time repetitive project scheduling considering location and congestion. J. Comput. Civ. Eng. 2018, 32. [Google Scholar] [CrossRef]
- Carbonara, N.; Costantino, N.; Pellegrino, R. Concession period for PPPs: A win-win model for a fair risk sharing. Int. J. Proj. Manag. 2014, 32, 1223–1232. [Google Scholar] [CrossRef]
- Wibowo, A.; Alfen, H.W. Government-led critical success factors in PPP infrastructure development. Built Environ. Proj. Asset Manag. 2015, 5, 121–134. [Google Scholar] [CrossRef]
- Zou, W.W.; Kumaraswamy, M.; Chung, J.; Wong, J. Identifying the critical success factors for relationship management in PPP projects. Int. J. Proj. Manag. 2014, 32, 265–274. [Google Scholar] [CrossRef]
- Chou, J.S.; Leatemia, G.T. Critical process and factors for ex-post evaluation of Public–Private Partnership infrastructure projects in Indonesia. J. Manag. Eng. 2016, 32. [Google Scholar] [CrossRef]
- Ng, S.T.; Wong, Y.M.W.; Wong, J.M.W. Factors influencing the success of PPP at feasibility stage—A tripartite comparison study in Hong Kong. Habitat Int. 2012, 36, 423–432. [Google Scholar] [CrossRef]
- Wang, P.; Shen, J.; Zhang, B. A new method for two-sided matching decision making of PPP projects based on intuitionistic fuzzy choquet integral. J. Intell. Fuzzy Syst. 2016, 31, 2221–2230. [Google Scholar] [CrossRef]
- Ai, S.Z.; Du, R.; Brugha, C.M.; Wang, H.P. Pointing to priorities for multiple criteria decision making—The case of a MIS-based project in China. Int. J. Inf. Technol. Decis. 2016, 15, 683–702. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Zhang, S.; Chan, A.P.C.; Feng, Y.B.; Duan, H.X.; Ke, Y.J. Critical review on PPP Research—A search from the Chinese and International Journals. Int. J. Proj. Manag. 2016, 34, 597–612. [Google Scholar] [CrossRef]
- Carpintero, S.; Petersen, O.H. Bundling and unbundling in Public–Private Partnerships: Implications for risk sharing in urban transport projects. Proj. Manag. J. 2015, 46, 35–46. [Google Scholar] [CrossRef]
- Chan, A.P.C.; Yeung, J.F.Y.; Yu, C.C.P.; Wang, S.Q.; Ke, Y.J. Empirical study of risk assessment and allocation of Public–Private Partnership projects in China. J. Manag. Eng. 2010, 27, 136–148. [Google Scholar] [CrossRef]
- Heravi, G.; Hajihosseini, Z. Risk allocation in Public–Private Partnership infrastructure projects in developing countries: Case study of the Tehran-Chalus Toll Road. J. Infrastruct. Syst. 2012, 18, 210–217. [Google Scholar] [CrossRef]
- Chan, A.P.C.; Lam, P.T.I.; Chan, D.W.M.; Cheung, E.; Ke, Y.J. Critical success factors for PPPs in infrastructure developments: Chinese perspective. J. Constr. Eng. Manag. 2010, 136, 484–494. [Google Scholar] [CrossRef]
- Mirzadeh, I.; Birgisson, B. Evaluation of highway projects under government support mechanisms based on an option-pricing framework. J. Constr. Eng. Manag. 2015, 142. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Wu, P.; Wang, J.; He, Q.; Wang, X. Estimating the environmental costs and benefits of demolition waste using life cycle assessment and willingness-to-pay: A case study in Shenzhen. J. Clean. Prod. 2018, 172, 14–26. [Google Scholar] [CrossRef]
- Xu, Y.L.; Sun, C.S.; Skibniewski, M.J.; Chan, A.P.C.; Yeung, J.F.Y.; Cheng, H. System Dynamics (SD) -based concession pricing model for PPP highway projects. Int. J. Proj. Manag. 2012, 30, 240–251. [Google Scholar] [CrossRef]
- Brandao, L.E.T.; Saraiva, E. The option value of government guarantees in infrastructure projects. Constr. Manag. Econ. 2008, 26, 1171–1180. [Google Scholar] [CrossRef]
- Chou, J.S.; Tserng, H.P.; Lin, C.; Yeh, C.P. Critical factors and risk allocation for PPP policy: Comparison between HSR and general infrastructure projects. Transp. Policy 2012, 22, 36–48. [Google Scholar] [CrossRef]
- Ismail, S. Critical success factors of public private partnership (PPP) implementation in Malaysia. Asia-Pacific J. Bus. Adm. 2013, 5, 6–19. [Google Scholar] [CrossRef]
- Kwak, Y.H.; Chih, Y.Y.; Ibbs, C.W. Towards a comprehensive understanding of public private partnerships for infrastructure development. Calif. Manag. Rev. 2009, 51, 51–78. [Google Scholar] [CrossRef]
- Zhang, X.Q. Criteria for selecting the private-sector partner in public private partnerships. J. Constr. Eng. Manag. 2005, 131, 631–644. [Google Scholar] [CrossRef]
- Chai, J.; Wu, C.; Zhao, C.; Chi, H.L.; Wang, X.; Ling, B.W.K.; Teo, K.L. Reference tag supported RFID tracking using robust support vector regression and Kalman filter. Adv. Eng. Inform. 2017, 32, 1–10. [Google Scholar] [CrossRef]
- Zhang, S.B.; Gao, Y.; Feng, Z.; Sun, W.Z. PPP application in infrastructure development in China: Institutional analysis and implications. Int. J. Proj. Manag. 2015, 33, 497–509. [Google Scholar] [CrossRef]
- Belassi, W.; Tukel, O.I. A new framework for determining critical success/failure factors in projects. Int. J. Proj. Manag. 1996, 14, 141–151. [Google Scholar] [CrossRef]
- Wang, W.X.; Li, Q.M.; Deng, X.P.; Li, J.H. Critical success factors of infrastructure projects under PPP model in China. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, 2007. WiCOM 2007, Shanghai, China, 21–25 September 2007; pp. 4970–4974. [Google Scholar]
- Aziz, A.M.A. Successful delivery of Public–Private Partnerships for infrastructure development. J. Constr. Eng. Manag. 2007, 133, 918–931. [Google Scholar] [CrossRef]
- Hwang, B.G.; Zhao, X.; Yu, G.S. Risk identification and allocation in underground rail construction joint ventures: Contractors’ perspective. J. Civ. Eng. Manag. 2016, 22, 758–767. [Google Scholar] [CrossRef]
- Ahadzi, M.; Bowles, G. Public–Private Partnerships and contract negotiations: An empirical study. Constr. Manag. Econ. 2004, 22, 967–978. [Google Scholar] [CrossRef]
- Shen, L.Y.; Platten, A.; Deng, X.P. Role of public private partnerships to manage risks in public sector projects in Hong Kong. Int. J. Proj. Manag. 2006, 24, 587–594. [Google Scholar] [CrossRef]
- Xie, J.Z.; Ng, S.T. Multiobjective Bayesian network model for Public–Private Partnership decision support. J. Constr. Eng. Manag. 2013, 139, 1069–1081. [Google Scholar] [CrossRef]
- Kasperski, A.; Zieliński, P. On combinatorial optimization problems on matroids with uncertain weights. Eur. J. Oper. Res. 2007, 177, 851–864. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Hou, L.; Zhao, C.; Wu, C.; Moon, S.; Wang, X. Discrete Firefly Algorithm for Scaffolding Construction Scheduling. J. Comput. Civ. Eng. 2016, 31. [Google Scholar] [CrossRef]
- Zhao, C.; Wu, C.; Chai, J.; Wang, X.; Yang, X.; Lee, J.; Kim, M. Decomposition-based multi-objective firefly algorithm for RFID network planning with uncertainty. Appl. Soft Comput. 2017, 55, 549–564. [Google Scholar] [CrossRef]
- Li, D.F.; Wan, S.P. Fuzzy linear programming approach to multiattribute decision making with multiple types of attribute values and incomplete weight information. Appl. Soft Comput. 2013, 13, 4333–4348. [Google Scholar] [CrossRef]
- Oliveira, C.; Antunes, C.H. Multiple objective linear programming models with interval coefficients—An illustrated overview. Eur. J. Oper. Res. 2007, 181, 1434–1463. [Google Scholar] [CrossRef]
- Zhao, Z. Advancing Public Interest in Public–Private Partnership of State Highway Development; Humphrey Institute of Public Affairs Report No. MN/RC 2011–09; Minnesota Department of Transportation: Minneapolis, MN, USA, 2011.
- Koch, C.; Buser, M. Emerging metagovernance as an institutional framework for public private partnership networks in Denmark. Int. J. Proj. Manag. 2006, 24, 548–556. [Google Scholar] [CrossRef]
- Garvin, M.J.; Bosso, D. Assessing the effectiveness of infrastructure public–private partnership programs and projects. Public Works Manag. Policy 2008, 13, 162–178. [Google Scholar] [CrossRef]
- Scandizzo, P.L.; Ventura, M. Sharing risk through concession contracts. Eur. J. Oper. Res. 2010, 207, 363–370. [Google Scholar] [CrossRef]
| Criteria | Sub-Criteria | Belassi and Tukel [28] | Zhang [25] | Wang et al. [29] | Aziz [30] | Kwak et al. [24] | Chan et al. [15] | Chan et al. [17] | Chou et al. [22] | Ismail [23] | Zhang et al. [27] | Wibowo and Alfen [6] | Liu et al. [1] | Total Number of Hits of a Certain Criterion |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Financial strength | Capital strength | √ | √ | √ | √ | √ | 5 | |||||||
| Financing capacity | √ | √ | √ | √ | √ | √ | √ | 7 | ||||||
| Financial guarantee | √ | 1 | ||||||||||||
| Technical ability | Advanced technology | √ | √ | √ | √ | √ | √ | 6 | ||||||
| Project implementation plans | √ | √ | √ | √ | √ | 5 | ||||||||
| Personnel reserve | √ | √ | √ | 3 | ||||||||||
| Critical equipment | √ | √ | 2 | |||||||||||
| Management ability | Management formalization | √ | √ | √ | √ | 4 | ||||||||
| Project management capacity | √ | √ | √ | √ | √ | √ | 6 | |||||||
| Ability of communication and cooperation | √ | √ | √ | √ | √ | √ | √ | 7 | ||||||
| Concession duration | √ | √ | √ | √ | 4 | |||||||||
| Risk management ability | √ | √ | √ | √ | 4 | |||||||||
| Maintenance ability | √ | √ | √ | 3 | ||||||||||
| Relevant experience | Financing experience | √ | √ | 2 | ||||||||||
| Constructing experience | √ | √ | √ | 3 | ||||||||||
| Operating experience | √ | √ | 2 | |||||||||||
| Credit level | Enterprise qualification | √ | 1 | |||||||||||
| Honor on projects | √ | 2 | ||||||||||||
| Social reputation | √ | √ | √ | √ | 4 | |||||||||
| Government guarantee | Legal guarantee | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | 11 | |
| Approval guarantee | √ | √ | √ | √ | √ | 5 | ||||||||
| Government support | Political support | √ | √ | √ | √ | √ | √ | √ | √ | √ | 9 | |||
| Interest rate guarantee | √ | √ | √ | √ | √ | √ | √ | √ | 8 | |||||
| Price guarantee | √ | √ | √ | √ | √ | 5 | ||||||||
| Government credibility | ---------- | √ | √ | √ | 3 | |||||||||
| Government risk-sharing | Restriction of competition | √ | √ | √ | √ | √ | √ | √ | 7 | |||||
| Information transparency | √ | √ | √ | √ | 4 | |||||||||
| Contract spirits | √ | √ | √ | √ | √ | √ | √ | 7 | ||||||
| Risk-taking | √ | √ | √ | √ | √ | √ | √ | 7 | ||||||
| 11 | 13 | 18 | 12 | 11 | 13 | 10 | 14 | 8 | 2 | 10 | 14 | -- |
| Sub-Criterion | Description |
|---|---|
| 1. Capital strength | Total funds, quantity and scale invested for completed construction projects |
| 2. Financing capacity | The scale of financing possible |
| 3. Financial guarantee ability | Ability of obtaining financing guarantee from financial institutions for the construction project |
| 4. Advanced technology | The leading technology in the world |
| 5. Project implementation plans | Plan formulation of activities or process of hard work from start to finish |
| 6. Personnel reserve | Human resources to meet the demand of long-term development goal for the enterprise |
| 7. Critical equipment | Key equipment to ensure continuous, stable, efficient and economic operation of the entire machinery |
| 8. Management formalization | Degree of standardization on enterprise strategic management, marketing management, human resource management, financial and tax management, material management, etc. |
| 9. Project management capacity | Ability of plan, organization, coordination, implementation and control of project managers |
| 10. Ability of communication and cooperation | Skills of coordination and communication with the government |
| 11. Concession duration | Specified period of recycling project costs on investment, operation and maintenance, and obtaining a reasonable return |
| 12. Risk management ability | Ability of minimizing the risk in a certain risky environment |
| 13. Maintenance Ability | Ability of operation and maintenance for infrastructure projects |
| 14. Financing experience | Experiences of financing the similar infrastructure projects |
| 15. Constructing experience | Experiences of constructing the similar infrastructure projects |
| 16. Operating experience | Experiences of operating the similar infrastructure projects |
| 17. Enterprise qualifications | The qualification and level of quality standard adapted to the qualification |
| 18. Honor on projects | National or provincial honor gained by the enterprises for their completed projects |
| 19. Social reputation | Credit evaluation given by partners cooperating in the enterprise |
| Sub-Criterion | Description |
|---|---|
| 1. Legal guarantee | Laws define the responsibility division between the parties, project assessment, contract performance and change, and the way conflicts, etc. |
| 2. Approval guarantee | The government need to provide the provision of legal guarantee to businesses involved in infrastructure projects |
| 3. Police guarantee | The government needs to set up corresponding approval for security and incentives to encourage more businesses to participate in PPP infrastructure projects |
| 4. Interest rate guarantee | The government should offer the recoverable rate of investment to businesses via offering government-backed rate in the scope of given benefit level |
| 5. Price guarantee | The government should offer the recoverable rate of investment to businesses via offering government-backed price in the scope of given benefit level |
| 6. Purchase guarantee | The government should offer the recoverable rate of investment to businesses via offering government-backed purchase in the scope of given benefit level |
| 7. Restriction of competition | Similar projects will not build at any given time |
| 8. Information transparency | Key information about the PPP Project disclosed by the government |
| 9. Contract spirits | The government’s contract spirits to guarantee the legitimate rights and interests of businesses |
| 10. Contract spirits | The government ought to initially bear the risks of land policy changes, legal policy changes and exchange rate changes |
| Subjects in the Government | Criteria | Initial Evaluative Values | |||||
|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | B6 | ||
| A1 | c1 | (0.78,0.75,0.83) | (0.91,0.87,0.90) | (0.55,0.64,0.56) | (0.65,0.72,0.50) | (0.48,0.55,0.65) | (0.47,0.57,0.49) |
| c2 | (0.75,0.87,0.67) | (0.85,0.73,0.83) | (0.53,0.49,0.41) | (0.86,0.83,0.78) | (0.68,0.72,0.56) | (0.39,0.47,0.56) | |
| c3 | (0.85,0.70,0.69) | (0.67,0.53,0.49) | (0.85,0.63,0.71) | (0.48,0.53,0.62) | (0.74,0.55,0.60) | (0.74,0.79,0.83) | |
| c4 | (0.53,0.49,0.41) | (0.68,0.70,0.83) | (0.57,0.47,0.49) | (0.89,0.92,0.80) | (0.72,0.68,0.48) | (0.55,0.56,0.64) | |
| c5 | (0.58,0.40,0.59) | (0.63,0.56,0.58) | (0.71,0.47,0.63) | (0.73,0.82,0.69) | (0.78,0.84,0.80) | (0.56,0.58,0.63) | |
| A2 | c1 | (0.69,0.71,0.82,0.75) | (0.83,0.80,0.86,0.71) | (0.47,0.82,0.63,0.55) | (0.63,0.72,0.48,0.52) | (0.58,0.68,0.55,0.62) | (0.53,0.49,0.50,0.49) |
| c2 | (0.92,0.71,0.68,0.73) | (0.79,0.87,0.63,0.85) | (0.51,0.81,0.38,0.71) | (0.78,0.84,0.80,0.91) | (0.42,0.38,0.60,0.48) | (0.55,0.72,0.65,0.61) | |
| c3 | (0.74,0.65,0.72,0.80) | (0.66,0.72,0.83,0.76) | (0.74,0.79,0.68,0.83) | (0.48,0.38,0.50,0.62) | (0.66,0.58,0.42,0.55) | (0.77,0.69,0.82,0.86) | |
| c4 | (0.65,0.42,0.56,0.50) | (0.84,0.86,0.91,0.85) | (0.65,0.56,0.58,0.49) | (0.84,0.86,0.91,0.89) | (0.72,0.68,0.58,0.72) | (0.52,0.63,0.47,0.55) | |
| c5 | (0.55,0.48,0.35,0.42) | (0.72,0.56,0.64,0.72) | (0.55,0.48,0.63,0.38) | (0.78,0.60,0.58,0.74) | (0.78,0.69,0.78,0.84) | (0.35,0.55,0.48,0.65) | |
| A3 | c1 | (0.49,0.52,0.64) | (0.74,0.83,0.79) | (0.47,0.49,0.56) | (0.62,0.58,0.72) | (0.42,0.63,0.58) | (0.56,0.75,0.55) |
| c2 | (0.55,0.40,0.39) | (0.82,0.79,0.85) | (0.55,0.71,0.60) | (0.84,0.79,0.87) | (0.59,0.72,0.55) | (0.60,0.48,0.49) | |
| c3 | (0.65,0.73,0.92) | (0.74,0.48,0.79) | (0.83,0.91,0.79) | (0.48,0.32,0.48) | (0.64,0.56,0.55) | (0.79,0.87,0.85) | |
| c4 | (0.39,0.40,0.41) | (0.68,0.84,0.79) | (0.62,0.71,0.59) | (0.76,0.84,0.80) | (0.63,0.58,0.56) | (0.56,0.65,0.41) | |
| c5 | (0.50,0.48,0.72) | (0.56,0.55,0.75) | (0.72,0.58,0.63) | (0.56,0.48,0.60) | (0.86,0.83,0.80) | (0.49,0.62,0.47) | |
| Subjects in the Enterprise | Criteria | Initial Evaluative Values | ||
|---|---|---|---|---|
| A1 | A2 | A3 | ||
| B1 | d1 | (0.58,0.55,0.36) | (0.68,0.72,0.73) | (0.63,0.58,0.60) |
| d2 | (0.59,0.40,0.60) | (0.71,0.78,0.82) | (0.74,0.68,0.50) | |
| d3 | (0.50,0.58,0.38) | (0.65,0.79,0.68) | (0.54,0.60,0.46) | |
| d4 | (0.92,0.90,0.82) | (0.64,0.49,0.53) | (0.69,0.58,0.38) | |
| B2 | d1 | (0.50,0.69,0.63,0.48) | (0.79,0.81,0.83,0.69) | (0.59,0.60,0.58,0.40) |
| d2 | (0.52,0.40,0.49,0.60) | (0.71,0.86,0.75,0.63) | (0.49,0.60,0.38,0.55) | |
| d3 | (0.56,0.48,0.65,0.71) | (0.63,0.74,0.87,0.72) | (0.53,0.62,0.48,0.39) | |
| d4 | (0.89,0.84,0.78,0.80) | (0.54,0.63,0.48,0.67) | (0.54,0.57,0.48,0.62) | |
| B3 | d1 | (0.49,0.63,0.58) | (0.68,0.46,0.71) | (0.57,0.85,0.77) |
| d2 | (0.62,0.38,0.58) | (0.56,0.67,0.87) | (0.64,0.50,0.55) | |
| d3 | (0.39,0.42,0.62) | (0.68,0.73,0.86) | (0.63,0.46,0.50) | |
| d4 | (0.78,0.86,0.82) | (0.57,0.69,0.48) | (0.63,0.58,0.58) | |
| B4 | d1 | (0.55,0.72,0.62) | (0.72,0.68,0.63) | (0.79,0.81,0.63) |
| d2 | (0.42,0.58,0.62) | (0.86,0.87,0.65) | (0.55,0.36,0.63) | |
| d3 | (0.55,0.48,0.71) | (0.86,0.78,0.78) | (0.55,0.66,0.50) | |
| d4 | (0.79,0.86,0.78) | (0.64,0.49,0.56) | (0.64,0.44,0.56) | |
| B5 | d1 | (0.62,0.73,0.58,0.60) | (0.72,0.46,0.68,0.75) | (0.69,0.58,0.59,0.68) |
| d2 | (0.51,0.63,0.60,0.42) | (0.92,0.73,0.82,0.80) | (0.56,0.65,0.48,0.53) | |
| d3 | (0.36,0.42,0.48,0.56) | (0.86,0.73,0.77,0.75) | (0.58,0.49,0.50,0.62) | |
| d4 | (0.89,0.80,0.79,0.88) | (0.57,0.63,0.46,0.39) | (0.63,0.57,0.48,0.39) | |
| B6 | d1 | (0.34,0.55) | (0.81,0.78) | (0.59,0.58) |
| d2 | (0.58,0.55) | (0.82,0.86) | (0.50,0.68) | |
| d3 | (0.43,0.69) | (0.68,0.73) | (0.59,0.63) | |
| d4 | (0.89,0.76) | (0.63,0.49) | (0.78,0.57) | |
| Criteria | Initial Evaluative Values | ||||
|---|---|---|---|---|---|
| STTG | MTR | BFG | CRCC | BMTRO | |
| c1 | (0.63,0.68,0.52) | (0.83,0.75,0.58) | (0.57,0.74,0.71) | (0.72,0.49,0.54) | (0.79,0.55,0.49) |
| c2 | (0.72,0.55,0.48) | (0.68,0.59,0.47) | (0.63,0.48,0.79) | (0.65,0.39,0.77) | (0.92,0.68,0.78) |
| c3 | (0.56,0.64,0.39) | (0.74,0.48,0.79) | (0.68,0.63,0.91) | (0.49,0.58,0.87) | (0.44,0.57,0.63) |
| c4 | (0.58,0.65,0.63) | (0.82,0.41,0.69) | (0.55,0.63,0.75) | (0.57,0.49,0.75) | (0.55,0.58,0.73) |
| c5 | (0.67,0.69,0.55) | (0.49,0.38,0.54) | (0.62,0.81,0.56) | (0.44,0.36,0.39) | (0.53,0.60,0.75) |
| Subjects in the Enterprise | Criteria | Initial Evaluative Values | Subjects in the Enterprise | Criteria | Initial Evaluative Values |
|---|---|---|---|---|---|
| STTG | d1 | (0.78,0.89,0.62) | CRCC | d1 | (0.53,0.82,0.78) |
| d2 | (0.69,0.64,0.61) | d2 | (0.80,0.72,0.91) | ||
| d3 | (0.55,0.68,0.69) | d3 | (0.64,0.64,0.57) | ||
| d4 | (0.40,0.39,0.36) | d4 | (0.53,0.49,0.73) | ||
| MTR | d1 | (0.49,0.50,0.47,0.63) | BMTRO | d1 | (0.36,0.48,0.36) |
| d2 | (0.63,0.69,0.55,0.78) | d2 | (0.64,0.52,0.30) | ||
| d3 | (0.77,0.80,0.85,0.83) | d3 | (0.76,0.69,0.63) | ||
| d4 | (0.49,0.50,0.50,0.64) | d4 | (0.81,0.59,0.86) | ||
| BFG | d1 | (0.71,0.82,0.60,0.53) | |||
| d2 | (0.42,0.39,0.47,0.34) | ||||
| d3 | (0.58,0.63,0.54,0.55) | ||||
| d4 | (0.76,0.69,0.61,0.70) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.; Wu, C.; Sheng, Z.; Wang, X. Multi-Criterion Two-Sided Matching of Public–Private Partnership Infrastructure Projects: Criteria and Methods. Sustainability 2018, 10, 1178. https://doi.org/10.3390/su10041178
Liang R, Wu C, Sheng Z, Wang X. Multi-Criterion Two-Sided Matching of Public–Private Partnership Infrastructure Projects: Criteria and Methods. Sustainability. 2018; 10(4):1178. https://doi.org/10.3390/su10041178
Chicago/Turabian StyleLiang, Ru, Changzhi Wu, Zhaohan Sheng, and Xiangyu Wang. 2018. "Multi-Criterion Two-Sided Matching of Public–Private Partnership Infrastructure Projects: Criteria and Methods" Sustainability 10, no. 4: 1178. https://doi.org/10.3390/su10041178
APA StyleLiang, R., Wu, C., Sheng, Z., & Wang, X. (2018). Multi-Criterion Two-Sided Matching of Public–Private Partnership Infrastructure Projects: Criteria and Methods. Sustainability, 10(4), 1178. https://doi.org/10.3390/su10041178




