First and Second Law Analyses of Trans-critical N2O Refrigeration Cycle Using an Ejector
Abstract
:1. Introduction
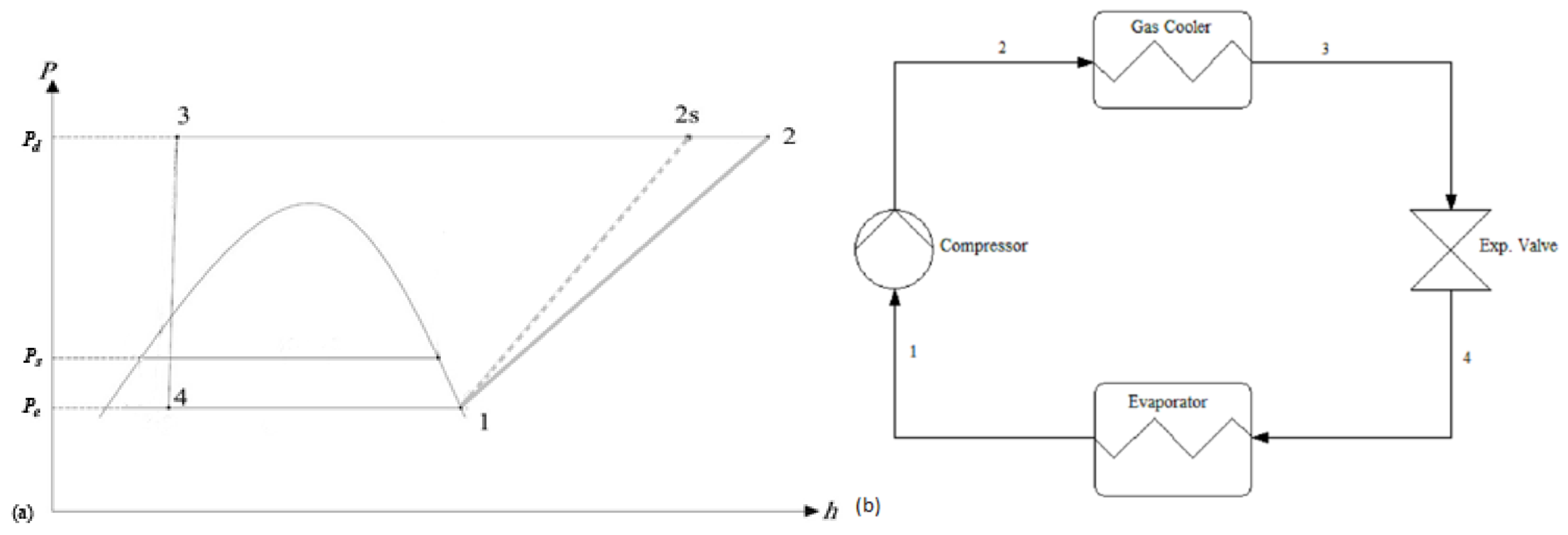
2. System Description
2.1. Ejector–Expansion Refrigeration Cycle
2.2. Vapor-Compression Refrigeration Cycle (VCRC), Internal Heat Exchanger Cycle (IHEC)
2.3. Assumptions
- All processes are at steady state and there are no flow losses within the system.
- There is no heat loss from the compressor.
- The fluid undergoes a constant enthalpy process in the expansion valve.
- The N2O at the inlet of the compressor and the outlet of the evaporator is a saturated vapor.
- The mixing process in the mixing chamber occurs at a constant evaporation pressure.
- Changes in the potential and kinetic energies at the outlet and inlet of components are negligible.
- The dead state temperature for the analysis is 35 °C.
- The heat sink temperature is 5 °C higher than the evaporation temperature.
3. System Modelling
3.1. Energy Analysis
3.2. Exergy Analysis
4. Results and Discussion
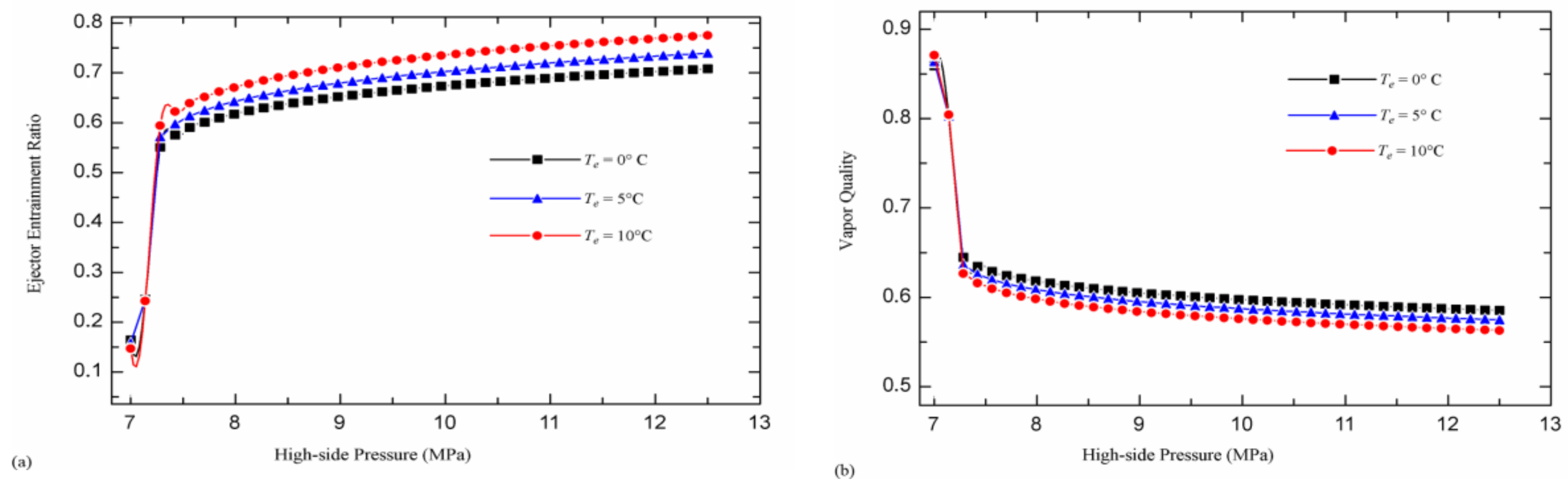
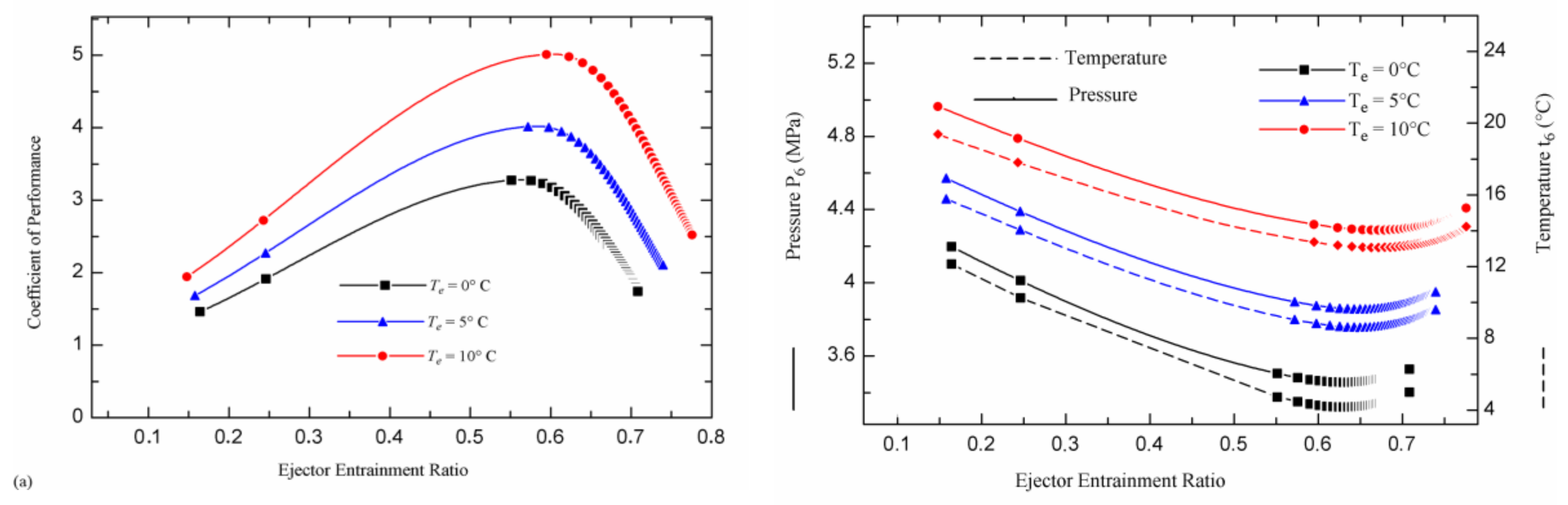
4.1. Ejector Entrainment Ratio Analysis
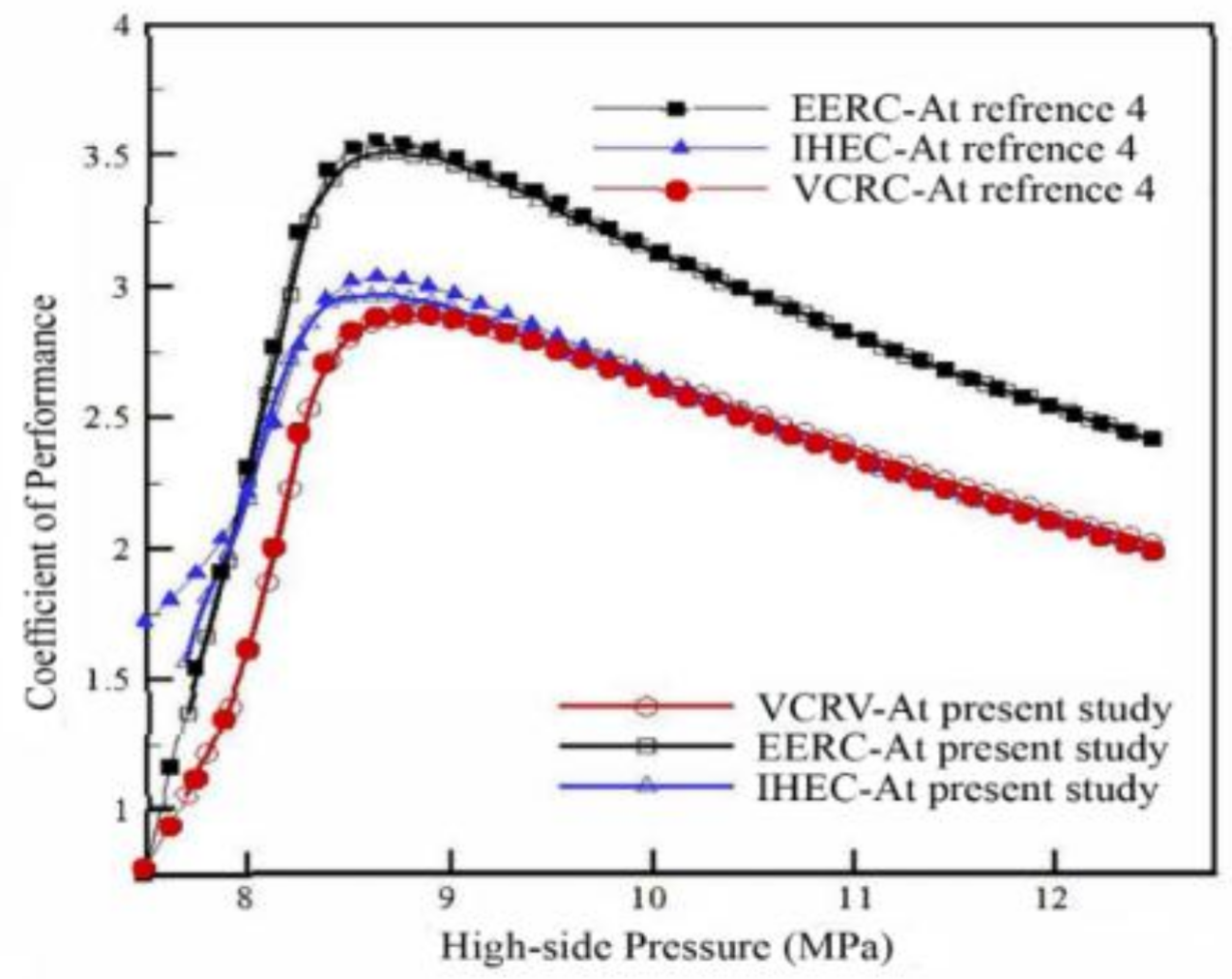
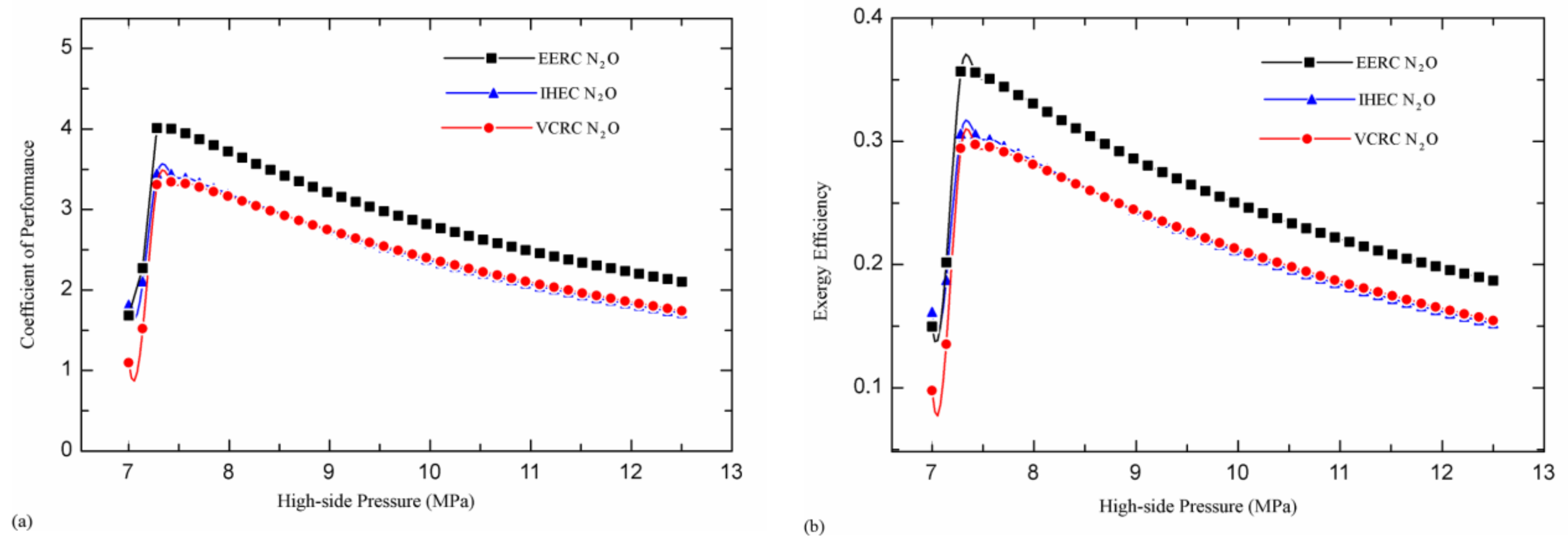
4.2. Comparison of Three Trans-critical N2O Refrigeration Cycles
4.3. Comparison of Three Cycle Types Using Trans-critical N2O and CO2 Working Fluids
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Ψ | Specific stream exergy (kJ/kg) |
| η | Efficiency |
| ε | Heat exchanger effectiveness (%) |
| COP | Coefficient of performance |
| ex | exergy (kJ) |
| h | Specific enthalpy (kJ/kg) |
| Exergy destruction rate (kW) | |
| Mass flow rate (kg/s) | |
| P | Pressure (MPa) |
| Heat transfer rate (kW) | |
| s | Specific entropy (kJ/kg K) |
| Entropy generation rate (kW/K) | |
| T | Temperature (°C) |
| U | Entrainment ratio of ejector |
| v | Velocity (m/s) |
| Work rate (kW) | |
| x | Quality (kg/kg) |
| Subscripts | |
| amb | Ambient |
| c | Compressor |
| d | Discharge pressure of ejector; Diffuser |
| eva /e | Evaporator |
| exp | Expansion valve |
| gc | Gas cooler |
| gen | Generation |
| Hex | Heat Exchanger |
| n | Ejector nozzle |
| r | Heat sink temperature |
| s | Vapor–liquid separator |
| 0 | Dead state of system |
References
- Calm, J.M. The next generation of refrigerants–historical review, considerations and outlook. Int. J. Refrig. 2008, 31, 1123–1133. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Garai, A.; Sarkar, J. Thermodynamic analysis and optimization of a novel N2O-CO2 cascade system for refrigeration and heating. Int. J. Refrig. 2009, 32, 1077–1084. [Google Scholar] [CrossRef]
- Kruse, H.; Rüssmann, H. The natural fluid nitrous oxide—an option as substitute for low temperature synthetic refrigerants. Int. J. Refrig. 2006, 29, 799–806. [Google Scholar] [CrossRef]
- Deng, J.; Jiang, P.; Lu, T.; Lu, W. Particular characteristics of transcritical CO2 refrigeration cycle with an ejector. Appl. Therm. Eng. 2007, 27, 381–388. [Google Scholar] [CrossRef]
- Sadeghi, M.; Yari, M.; Mahmoudi, S.M.S.; Jafari, M. Thermodynamic analysis and optimization of a novel combined power and ejector refrigeration cycle – Desalination system. Appl. Energy. 2017, 208, 239–251. [Google Scholar] [CrossRef]
- Ünal, S.; Erdinç, M.T.; Kutlu, C. Optimal thermodynamic parameters of two-phase ejector refrigeration system for buses. Appl. Therm. Eng. 2017, 124, 1354–1367. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. Thermodynamic analyses and optimization of a transcritical N2O refrigeration cycle. Int. J. Refrig. 2010, 33, 33–40. [Google Scholar] [CrossRef]
- Aghazadeh Dokandari, D.; Setayesh Hagh, A.; Mahmoudi, S.M.S. Thermodynamic investigation and optimization of novel ejector-expansion CO2/NH3 cascade refrigeration cycles (novel CO2/NH3 cycle). Int. J. Refrig. 2014, 46, 26–36. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Galanis, N. Comparison of ejector predicted performance by thermodynamic and CFD models. Int. J. Refrig. 2016, 68, 28–36. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. Optimization of a transcritical N2O refrigeration/heat pump cycle (NIK-06-T1-14). In Proceedings of the 8th IIR G Lorentzen Conference on Natural Working fluids, Copenhagen, Denmark, 7–10 September 2008. [Google Scholar]
- Sarkar, J.; Bhattacharyya, S.; Ramgopal, M. Optimization of a transcritical CO2 heat pump cycle for simultaneous cooling and heating applications. Int. J. Refrig. 2004, 27, 830–838. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S.; Ramgopal, M. Natural refrigerant-based subcritical and transcritical cycles for high temperature heating. Int. J. Refrig. 2007, 30, 3–10. [Google Scholar] [CrossRef]
- Seckin, C. Thermodynamic analysis of a combined power/refrigeration cycle: Combination of Kalina cycle and ejector refrigeration cycle. Energy Convers. Manag. 2018, 157, 631–643. [Google Scholar] [CrossRef]
- Lee, T.S.; Liu, C.H.; Chen, T.W. Thermodynamic analysis of optimal condensing temperature of cascade-condenser in CO2/NH3 cascade refrigeration systems. Int. J. Refrig. 2006, 29, 1100–1108. [Google Scholar] [CrossRef]
- Carrillo, J.A.E.; Sanchez de la flor, F.J.; Salmeron Lissen, J.M. Thermodynamic comparison of ejector cooling cycles. Ejector characterisation by means of entrainment ratio and compression efficiencys. Int. J. Refrig. 2017, 74, 371–384. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Aghagoli, A.; Raoofi, R. Thermodynamic analysis of the ejector refrigeration cycle using the artificial neural network. Int. J. Energy 2017, 129, 201–215. [Google Scholar] [CrossRef]
- Yari, M.; Mahmoudi, S.M.S. Thermodynamic analysis and optimization of novel ejector-expansion TRCC (transcritical CO2) cascade refrigeration cycles (Novel transcritical CO2 cycle). Int. J. Energy. 2011, 36, 6839–6850. [Google Scholar] [CrossRef]
- Yari, M. Performance analysis and optimization of a new two-stage ejector-expansion transcritical CO2 refrigeration cycle. Int. J. Therm. Sci. 2009, 48, 1997–2005. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Thermodynamic and thermoeconomic analysis and optimization of a novel combined cooling and power (CCP) cycle by integrating of ejector refrigeration and Kalina cycles. Int. J. Energy. 2017, 139, 262–276. [Google Scholar] [CrossRef]
- Jeon, Y.; Dongwoo, J.; Sunjaekim, K.; Kim, Y. Effects of ejector geometries on performance of ejector-expansion R410A air conditioner considering cooling seasonal performance factor. Appl. Energy 2017, 205, 761–768. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Theoretical model of transcritical CO2 ejector with non-equilibrium phase change correlation. Int. J. Refrig. 2018, 86, 218–227. [Google Scholar] [CrossRef]
- Fang, Y.; Croquer, S.; Poncet, S.; Bartosiewicz, Y. Drop-in replacement in a R134 ejector refrigeration cycle by HFO refrigerantsRemplacement. Int. J. Refrig. 2017, 17, 87–98. [Google Scholar] [CrossRef]
- Ma, Z.; Bao, H.; Roskilly, A.H. Thermodynamic modelling and parameter determination of ejector for ejection refrigeration systems. Int. J. Refrig. 2017, 75, 117–128. [Google Scholar] [CrossRef]
- Choudhary, K.; Dasgupta, M.S.; Sunder, S. Energetic and exergetic investigation of a N2O ejector expansion transcritical refrigeration cycle. Int. J. Energy Procedia 2017, 109, 122–129. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Exergy: Energy, Environment and Sustainable Development, 2nd ed.; Elsevier: New York, NY, USA, 2013. [Google Scholar]



| Unit | Energy Equations | Exergy Destruction Equations |
|---|---|---|
| Compressor | , | |
| Gas cooler | ||
| Ejector | , , , , , | |
| Expansion valve | ||
| Evaporator |
| Unit | Energy Equations | Exergy Destruction Equations |
|---|---|---|
| Compressor | , | |
| Gas cooler | ||
| Expansion valve | ||
| Evaporator |
| Unit | Energy Equations | Exergy Destruction Equations |
|---|---|---|
| Compressor | , | |
| Gas cooler | ||
| Internal Hex | − | |
| Expansion valve | ||
| Evaporator |
| State | T (°C) | P (MPa) | h (kJ/kg) | s (kJ/kg. K) | X | (kg/s) |
|---|---|---|---|---|---|---|
| 1 | 5 | 3.53 | 396.3 | 1.54 | 1 | 1 |
| 2 | 80.25 | 8.5 | 444.6 | 1.58 | - | 1 |
| 3 | 36 | 8.5 | 254 | 0.99 | - | 1 |
| 4 | 5 | 3.53 | 254 | 1.03 | 0.35 | 1 |
| State | T (°C) | P (MPa) | h (kJ/kg) | s (kJ/kg. K) | X | (kg/s) |
|---|---|---|---|---|---|---|
| 1 | 34.4 | 3.53 | 439.9 | 1.69 | - | 1 |
| 2 | 119.6 | 8.5 | 502.8 | 1.74 | - | 1 |
| 3 | 36 | 8.5 | 254 | 0.99 | - | 1 |
| 4 | 21.5 | 8.5 | 210.4 | 0.85 | - | 1 |
| 5 | 5 | 3.53 | 210.4 | 0.87 | 0.15 | 1 |
| 6 | 5 | 3.53 | 396.3 | 1.54 | 1 | 1 |
| State | T (°C) | P (MPa) | h (kJ/kg) | s (kJ/kg. K) | X | (kg/s) |
|---|---|---|---|---|---|---|
| 1 | 8.5 | 3.86 | 394.4 | 1.52 | 1 | 0.6 |
| 2 | 75 | 8.5 | 435.1 | 1.55 | - | 0.6 |
| 3 | 36 | 8.5 | 254 | 0.99 | - | 0.6 |
| 4 | 5 | 3.53 | 246.9 | 1.01 | 0.32 | 0.6 |
| 5 | 5 | 3.53 | 308.3 | 1.22 | 0.59 | 1 |
| 6 | 8.5 | 3.86 | 310.8 | 1.23 | 0.60 | 1 |
| 7 | 8.5 | 3.86 | 185 | 0.781 | 0 | 0.4 |
| 8 | 5 | 3.53 | 185 | 0.783 | 0.04 | 0.4 |
| 9 | 5 | 3.53 | 396.3 | 1.54 | 1 | 0.4 |
| Device | EERC | IHEC | VCRC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Loss (kJ) | (%) | Loss/exeva | Loss (kJ) | (%) | Loss/exeva | Loss (kJ) | (%) | Loss/exeva | |
| Compressor | 4.02 | 32.46 | 0.58 | 10.08 | 29.77 | 0.67 | 8.74 | 32.69 | 0.77 |
| Gas cooler | 1.98 | 15.96 | 0.29 | 11.30 | 33.38 | 0.75 | 4.25 | 15.92 | 0.35 |
| Ejector | 4.68 | 37.79 | 0.68 | - | - | - | - | - | - |
| Exp. valve | 0.19 | 1.55 | 0.03 | 7.09 | 20.94 | 0.48 | 11.25 | 42.05 | 1.03 |
| Evaporator | 1.51 | 12.22 | 0.22 | 3.29 | 9.74 | 0.22 | 2.49 | 9.33 | 0.22 |
| Internal HX | - | - | - | 2.08 | 6.15 | 0.14 | - | - | - |
| Overall (N2O cycle) | 12.40 | 100 | 1.80 | 33.85 | 100 | 2.26 | 26.75 | 100 | 2.37 |
| Overall (CO2 cycle) * | 13.65 | 100 | 2.20 | 38.05 | 100 | 2.74 | 30.92 | 100 | 2.94 |
| Tgc (°C) | Teva (°C) | POPT,High-side (MPa) | COPmax | (%) |
|---|---|---|---|---|
| 36 | 0 | 8.678 | 2.89 | 31.4 |
| 5 | 8.637 | 3.51 | 31.2 | |
| 10 | 8.658 | 4.33 | 30.3 | |
| 38 | 0 | 9.128 | 2.61 | 28.3 |
| 5 | 9.128 | 3.14 | 28.0 | |
| 10 | 9.120 | 3.82 | 26.7 | |
| 40 | 0 | 9.573 | 2.37 | 25.7 |
| 5 | 9.585 | 2.83 | 25.2 | |
| 10 | 9.584 | 3.40 | 23.8 |
| Tgc (°C) | Teva (°C) | POPT,High-side (MPa) | COPmax | (%) |
|---|---|---|---|---|
| 36 | 0 | 7.335 | 3.28 | 35.6 |
| 5 | 7.327 | 4.02 | 35.7 | |
| 10 | 7.314 | 5.01 | 35.1 | |
| 38 | 0 | 7.786 | 2.91 | 31.6 |
| 5 | 7.779 | 3.53 | 31.4 | |
| 10 | 7.766 | 4.34 | 30.4 | |
| 40 | 0 | 8.222 | 2.61 | 28.3 |
| 5 | 8.219 | 3.15 | 28.0 | |
| 10 | 8.206 | 3.82 | 26.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghazadeh Dokandari, D.; S. Mahmoudi, S.M.; Bidi, M.; Haghighi Khoshkhoo, R.; Rosen, M.A. First and Second Law Analyses of Trans-critical N2O Refrigeration Cycle Using an Ejector. Sustainability 2018, 10, 1177. https://doi.org/10.3390/su10041177
Aghazadeh Dokandari D, S. Mahmoudi SM, Bidi M, Haghighi Khoshkhoo R, Rosen MA. First and Second Law Analyses of Trans-critical N2O Refrigeration Cycle Using an Ejector. Sustainability. 2018; 10(4):1177. https://doi.org/10.3390/su10041177
Chicago/Turabian StyleAghazadeh Dokandari, Damoon, S. M. S. Mahmoudi, M. Bidi, Ramin Haghighi Khoshkhoo, and Marc A. Rosen. 2018. "First and Second Law Analyses of Trans-critical N2O Refrigeration Cycle Using an Ejector" Sustainability 10, no. 4: 1177. https://doi.org/10.3390/su10041177
APA StyleAghazadeh Dokandari, D., S. Mahmoudi, S. M., Bidi, M., Haghighi Khoshkhoo, R., & Rosen, M. A. (2018). First and Second Law Analyses of Trans-critical N2O Refrigeration Cycle Using an Ejector. Sustainability, 10(4), 1177. https://doi.org/10.3390/su10041177






