Life Cycle Cost Assessment of Preventive Strategies Applied to Prestressed Concrete Bridges Exposed to Chlorides

Abstract

This paper applies Life Cycle Assessment methodology to aid in the decision making to select the preventive measure against chloride corrosion in concrete structures that works best for the socio-economic context of the structure. The assumed model combines the concepts of Life Cycle Cost Analysis and Social Life Cycle Analysis to assess the impacts on users derived from the maintenance activities associated with each alternative analyzed in terms of economic costs. The model has been applied to a prestressed concrete bridge to obtain a preventive measure that can reduce the total costs incurred over the period of analysis by up to 58.5% compared to the cost of the current solution.

1. Introduction

Corrosion of reinforcing steel in concrete structures is one of the most important durability problems associated with this material. Currently, construction companies of different countries state that the refurbishment and maintenance of buildings represents up to 30% of the activity of the construction sector [1]. The poor durability of many concrete structures, which results in short structural service lives, is not sustainable [2] neither in social nor in economic terms. In recent times, it has been common practice to deal with concrete deterioration mechanisms once the problem is detected and not before it arises. Such kinds of strategies result in greater socio-economic impacts, since they require more material in the long term than a design based on prevention. Although there are several mechanisms that may degrade concrete in severe environments, experience demonstrates that the most critical threat to concrete structures exposed to marine environments is chloride-induced corrosion of the reinforcing steel bars [3,4,5]. Research has been carried out on this specific mechanism for many years [6,7,8,9], leading to the development of different preventive measures to increase resistance to corrosion from the beginning of the structure life cycle, thus resulting in less maintenance-demanding solutions.

Some of the measures developed to prevent chloride corrosion focus on the reinforcement itself and others seek to prevent corrosion by reducing the porosity of the concrete cover. Corrosion can also be prevented by isolating the structure from the environment by means of surface protection treatments or by altering the kinetics of the reactions or electrochemical potential of the affected metals. Although the degree of knowledge associated with some of these measures is still precarious, the use of preventive measures such as those mentioned above is common when a concrete structure is exposed to chlorides. It is the task of the designer to find the solution that entails the lowest cost and consumption of resources [10,11,12,13]. Regarding durability, decision support techniques, such as Life Cycle Cost Assessment (LCCA) can be used to find a durable solution with the minimum associated costs [14].

Cost comparison is the usual procedure for selecting the best design alternative. However, when only considering the costs derived from implementing a particular solution, it may happen that the costs associated to the maintenance operations of the structure can exceed the initial investment, thus tilting the balance in favor of other alternatives with higher initial investment costs [15] but lesser maintenance. This leads to the consideration of LCCA techniques in order to evaluate the costs generated throughout every stage of the life cycle of a structure. In addition, the economic costs deferred over time have associated social costs that can also be evaluated by means of Social Life Cycle Assessment (SLCA) techniques. When applied to the choice of the most appropriate prevention measure, it is common practice to overlook the social impacts generated. In urban environments, this impact may lead to adopting preventive measures that are more expensive in economic terms, but that require fewer interventions and, consequently, generate less social costs. Thus, the integration of social criteria in decision making is presented as an effective step towards a sustainable structural design [16,17].

It is possible to integrate both methodologies when choosing between different prevention measures. The present paper proposes an LCCA based methodology for decision-making regarding the most appropriate preventive measure for concrete structures exposed to chlorides, taking into account economic and social criteria. The economic and social costs considered in the proposed methodology are described below.

2. Materials and Methods

2.1. Bridge Description

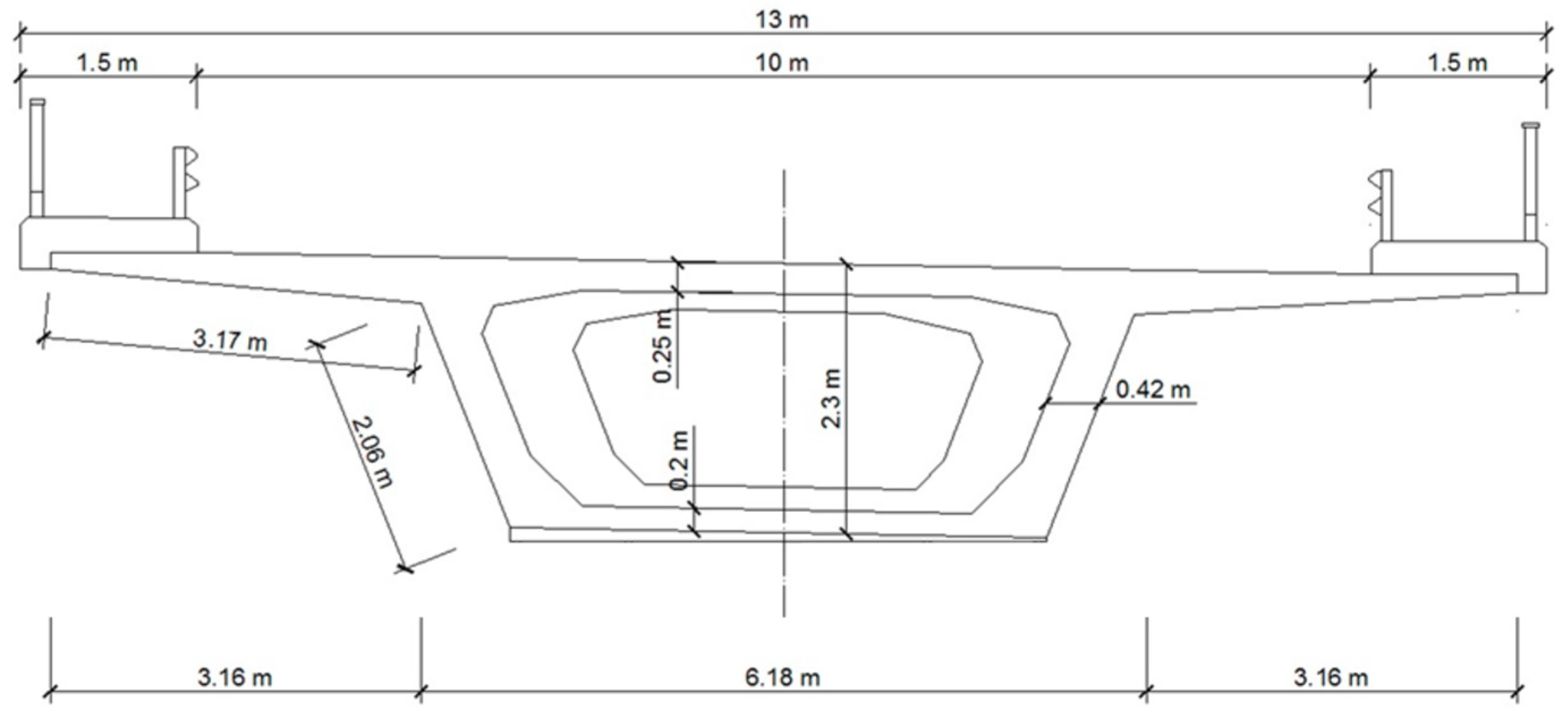
In the present paper, some of the most usual preventive strategies against chloride corrosion are applied to a particular bridge deck. The subject in this study is the bridge of Illa de Arosa, in Galicia, Spain. A cross-section of the bridge deck is shown in Figure 1. The input data regarding the durability and geometry characterization of this structure has been obtained from the literature [18]. The concrete mix of the bridge deck has a cement content of 485 kg/m³, and a water/cement ratio w/c = 0.45. The concrete cover of the deck is 30 mm. A steel amount of 100 kg/m³ of concrete has been assumed, as is usual for these types of prestressed structures. This quantity does not include the steel of the prestressing tendons. The deck has a width of 13 m and a section depth of 2.3 m. The deck, with a span of 50 m, is located 9.6 m over the high tide sea water level. It is worth noting that according to the Spanish regulations for marine environments, the deck is designed for no cracking of concrete, i.e., concrete remains uncracked.

The particular preventive measures evaluated in the present study are as follows. Firstly, an increase in the reinforcement concrete cover to 35 mm, 45 mm, and to 50 mm (measures R35, R40, and R50, respectively, henceforth) are considered, taking into account that as more concrete cover is considered, the steel amount needed to guarantee the proper structural behavior of the bridge deck is greater. The steel amounts considered are 112 kg/m for R35, 136 kg/m for R45, and 147 kg/m for R50. A second group of measures consists of the addition to the existing concrete mixture of fly ash, silica fume, or polymers. The resulting concrete mixes have been assumed to be applied to the whole deck, although only the properties of the cover will affect the durability performance of the design alternative. Additions of 10% and 20% of fly ash (measures CV10 and CV20), additions of 5% and 10% of silica fume (measures HS5 and HS10), and additions of 10% and 20% of styrene-butadiene rubber (SBR) latex (measures HMP10 and HMP20) have been assumed in the analysis. The mentioned percentages are expressed in relation to the cement content of the reference concrete mix design. In the cases where fly ash or silica fume are added, the amount of cement is partially substituted by those components, as they contribute to the resistance development of the resulting concrete. The cement amount considered in the mix proportions of those alternatives is reduced according to the efficiency factor associated to the specific addition. In the present study, efficiency factors of K = 0.3 and K = 2 have been assumed for fly ash and silica fume additions, respectively. It is worth noting that the addition of silica fume may reduce the critical chloride threshold [19]. This effect, which is a consequence of the decrease in the chloride binding capacity of the resulting concrete when such additions are considered, has been taken into account in the present study. Thirdly, a decrement in the water/cement ratio to w/c = 0.40 and to w/c = 0.35 (measures AC40 and AC35) is considered. When the water/cement ratio is reduced, it is common practice to add special additives in order to increase concrete workability. As these products may increase the economic impacts of the measure, the addition of superplasticisers has been considered in the definition of measures AC40 and AC35. The concrete mixes corresponding to the design alternatives presented above are shown in

Table 1. Concrete mix design for the different alternatives.

	Cement	Water	w/b	Fly Ash	Silica Fume	Polymer (SBR)	Plasticiser	Gravel	Sand
	(kg/m3)	(L/m3)	(%)	(kg/m3)	(kg/m3)	(kg/m3)	(kg/m3)	(kg/m3)	(kg/m3)
REF 1	485.6	218.5	0.45	-	-	-	-	926.7	827.9
AC40	500	200	0.40	-	-	-	7.5	948.0	844.1
AC35	500	175	0.35	-	-	-	10	976.7	882.8
CV10	471	218.5	0.45	48.6	-	-	-	926.7	798.3
CV20	456.4	218.5	0.45	97.1	-	-	-	926.7	768.7
HS5	437	218.5	0.45	-	24.3	-	-	926.7	849.1
HS10	388.4	218.5	0.45	-	48.6	-	-	926.7	870.2
HMP10	485.6	218.5	0.45	-	-	48.6	-	926.7	827.9
HMP20	485.6	218.5	0.45	-	-	97.1	-	926.7	827.9

¹ This mix is also considered in alternatives R35, R45, R50, INOX, GALV, HIDRO and SEAL.

. It shall be noted that, in order to make alternatives comparable, the alternative designs shall not only guarantee the same service life under an appropriate maintenance, but the resulting design should also have the same mechanical strength as the reference design. According to the mix proportions reported by León et al. [18], the reference design has a mean compressive strength f_cm equal to 40 MPa, with a modulus of elasticity E_c equal to 29 GPa. The alternative concrete mixes have been designed in order to reach the reference compressive strength and elastic modulus.

Next, the replacement of the existing ordinary steel with galvanized steel (measure GALV) and with stainless steel (measure INOX) are considered. Finally, treatment the exposed deck surface with a generic silane-based hydrophobic impregnation (measure HIDRO) and with a silicate-based sealant product (measure SEAL) is considered. Fifteen preventive measures are considered. It shall be said that there are other ways to deal with corrosion in severe environments, such as cathodic protection. These other relevant measures have been excluded from the present analysis, as their performance is hard to assess in the same terms as the presented strategies.

2.2. Durability Performance of the Preventive Measures

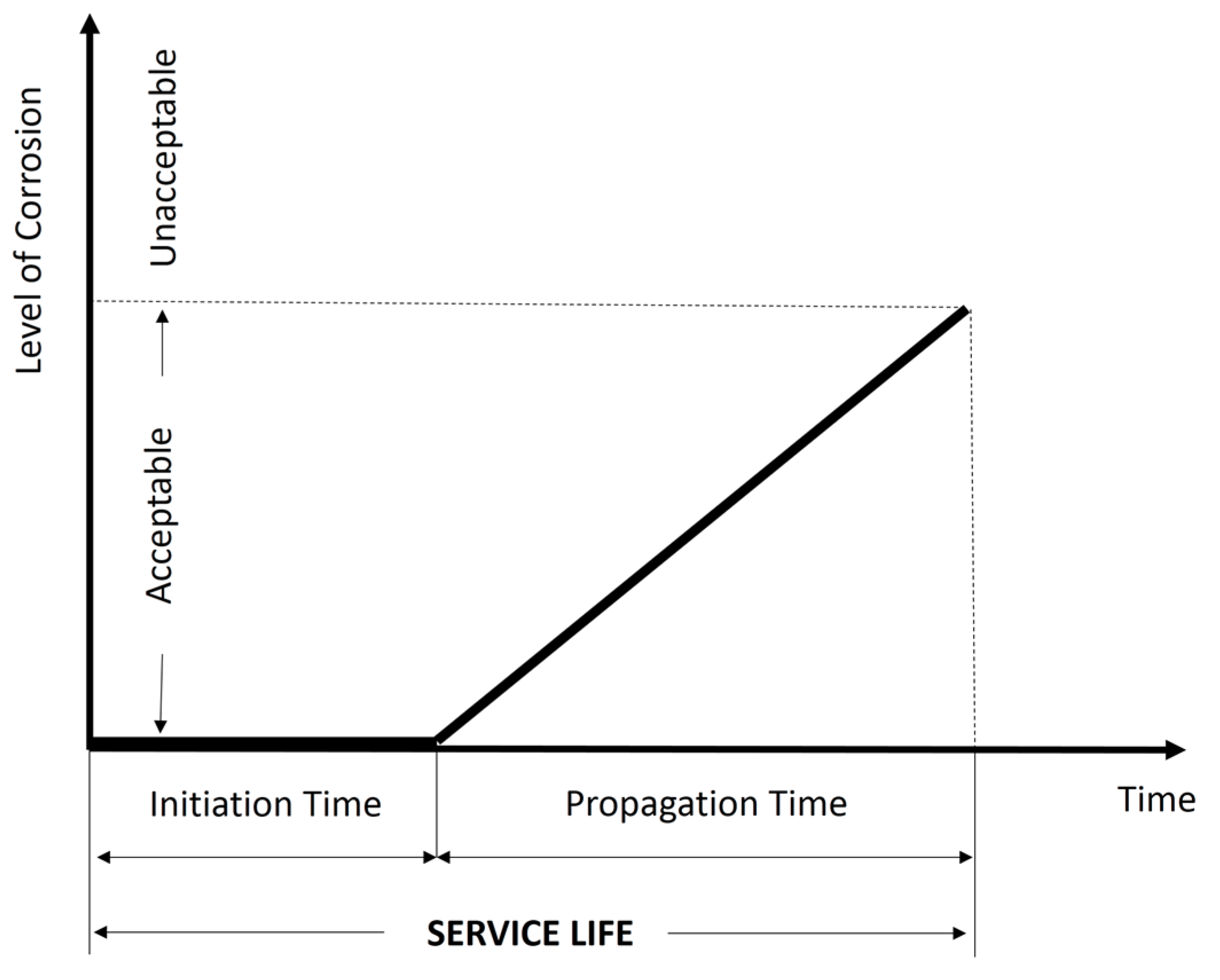
The assessment of the durability of a structure requires a criterion indicating the time at which it becomes necessary to perform a maintenance operation. In the case of prestressed concrete bridges, it is usual to consider the time to corrosion initiation (Figure 2) as proposed by Tuutti [20] as the time where maintenance activities shall be held. The time to corrosion initiation is the time where chlorides reach a concentration high enough to start the corrosive process of the reinforcement. Consequently, this maintenance criterion guarantees that, when maintenance operations are performed, the reinforcing steel is still not damaged by corrosion, and it is not necessary to replace it.

The calculation of the initiation time requires a physical model that describes how chloride ions move through the concrete cover. Existing models for the prediction of the required time to initiate corrosion are based on Fick’s second law of diffusion, and they assume that the porous concrete cover is a homogeneous material in which ions migrate through a diffusion process. A deterministic solution of the Fick’s equation for the diffusion of chlorides in the concrete cover is used in this analysis, namely, the one proposed in Fib Bulletin 34 [21] that assumes a constant, time independent surface chloride concentration. So, the chloride concentration to be expected in the concrete cover at a specific depth x and in a particular time t is expressed as:

$$C\left(x,t\right)=C_0+\left(C_{s,\Delta x}-C_0\right)\times \left(1-erf\frac{x-\Delta x}{2\sqrt{D_{app,C}\times t}}\right)$$

(1)

where C(x,t) is the chloride concentration (wt.%/binder) at concrete depth x (mm) and time t (years); C_s,Δx is the chloride concentration at depth Δx (wt.%/binder); Δx is the depth of the convection zone (mm), which is the surface layer depth for which the process of chloride penetration differs from Fick’s second law of diffusion; erf(.) is the Gauss error function; and D_app,C is the apparent coefficient of chloride diffusion through concrete (mm²/years). Note that if Δx is considered to be zero, the term C_s,Δx = C_s is the chloride concentration at the concrete surface. The model proposed by Fib Bulletin 34 [21] assumes that the chloride front advances in only one direction. However, this hypothesis is not true when specific bars are exposed to two simultaneously advancing fronts, as is the case of reinforcing bars located at the edges of the studied section. In such cases, the use of one-dimensional models results in inaccurate, overestimated service lives. In the present study, the Fib model has been slightly modified in order to consider the two-dimensional advance of chlorides, the so called corner effect:

$$C\left(x,y,t\right)=C_0+\left(C_s-C_0\right)\times \left(1-erf\frac{x-\Delta x}{2\sqrt{D_{app,C,x}\times t}}\times erf\frac{y-\Delta y}{2\sqrt{D_{app,C,y}\times t}}\right)$$

(2)

The concrete cover in the y-direction (r_y) is assumed to be constant and equal to 50 mm for every alternative analyzed, while the cover in the x-direction (r_x) is assumed to vary between 30 mm and 50 mm depending on the prevention alternative studied. The apparent diffusion coefficient is obtained from the experimental non-steady state migration coefficient using the equation proposed by Fib [21]:

$$D_{app,C}=exp\left(b_e\times \left(\frac{1}{T_{ref}}-\frac{1}{T_{real}}\right)\right)\times D_{RCM,0}\times k_t\times {\left(\frac{t_0}{t}\right)}^{\alpha }$$

(3)

where b_e is a regression variable (constant); T_ref is the standard test temperature (°C); T_real is the temperature of the structural element (°C); D_RCM,0 is the non-steady state chloride migration coefficient (mm²/years); k_t is a transfer parameter (constant); t₀ is a reference point of time (years); and α is an age factor, which is assumed to be equal to 0.5 according to the Spanish concrete code EHE-08 [22]. In the present study, T_ref and T_real are assumed to be the same, and the transfer variable is considered to be k_t = 1 as suggested by Fib [21]. The age factor α determines the way the diffusion coefficient varies with the time. As reference time, t₀ = 0.0767 years (namely 28 days) has been considered.

Table 2. Durability characterization of the analyzed preventive strategies.

Design Alternative	Description	DRCM,0 (×10−12 m2/s)	Ccrít (%)	rx (mm)	Service Life (Years)	Reference
REF	Current bridge design	10	0.6	30	7.1	[22]
R35		10	0.6	35	11.2
R45		10	0.6	45	21.1
R50		10	0.6	50	26.5
AC40	w/c = 0.40	6.15	0.6	30	18.8	[23,24]
AC35	w/c = 0.35	4.32	0.6	30	43.1
INOX	Stainless steel reinforcement bars	10	5	30	>100	[25]
GALV	Galvanized steel reinforcement bars	10	1.2	30	23.4	[26]
HMP10	Polymer modified concrete (10%)	7.32	0.6	30	13.2	[27,28]
HMP20	Polymer modified concrete (20%)	3.04	0.6	30	75.6
HS5	5% Silica fume	3.31	0.38	30	36.2	[19,29]
HS10	10% Silica fume	1.38	0.22	30	>100
CV10	10% Fly ash	6.16	0.6	30	18.6	[30]
CV20	20% Fly ash	5.23	0.6	30	26.1
HIDRO	Hydrophobic surface treatment	7.73	0.6	30	5 1	[31,32]
SEAL	Sealant surface treatment	4.87	0.6	30	5 1	[33]

¹ In the present study, the service life of surface treatments (HIDRO and SEAL) is limited to five years according to manufacturer specifications.

shows the value of the parameters that allow for the characterization of the analyzed measures in terms of durability.

It is assumed that the surface concentration of chlorides and the age coefficient is the same for all the alternatives evaluated. Back to the Tuutti model presented above, the time to corrosion initiation can be obtained by equalizing the chloride concentration at the rebar depth C(r_x, r_y, t) to the critical chloride concentration for each specific measure. In the calculations, and on the basis of the distance between the bridge deck bottom surface and the mean sea water level, a surface chloride content of C_s = 3.34% is assumed for the evaluation of the bridge deck. Table 2 shows the resulting expected service lives for the analyzed prevention alternatives considering the durability parameters assumed in the present study. It shall be noted that the effectiveness of the surface treatments depends greatly on the porosity of the substrate [34]. Consequently, the diffusion coefficients presented in Table 2 for HIDRO and SEAL have been obtained considering the w/c ratio of the REF alternative (current bridge design), namely w/c = 0.45. However, the durability performance of these treatments is very sensitive to ageing and weathering as derived from the existing literature [33,35,36,37]. In particular, conventional treatments are very affected by microcracking of the concrete cover, for when those cracks are deeper than the treatment thickness, barrier properties are lost and the impregnation becomes ineffective [38,39]. Periodic reapplication of surface treatments is, therefore, desirable in order to reestablish the protective effect of these measures. For these reasons, the present study limits the service life of surface treatments to five years according to manufacturer specifications.

2.3. Life Cycle Cost Analysis (LCCA)

In general, the economic costs associated with a structure can be divided into initial investment and maintenance costs. The investment costs correspond to the costs incurred at the moment of the initial economic analysis. Four main categories are usually distinguished chronologically: planning costs, land acquisition costs, construction costs, and interruption costs. The present study only considers the costs derived from the construction activities. It shall be noted that many of the investment costs are very similar between the different alternatives to be evaluated, for example, the costs associated to excavation or piles construction. Only those costs that are different between alternatives are considered in the present paper, as they are the ones that will have an influence on the final decision.

The maintenance costs, which are generated throughout the service life of the structure, are necessary for the infrastructures to be in operating condition throughout the required service life of the project, and they directly depend on the durability performance of the structure against the dominating degradation mechanism. Maintenance operations include the activities of hydrodemolition of the concrete cover, cleaning of the outermost reinforcement, and shotcreting with the corresponding concrete mixture to restore the original cover. In the case of surface treatment, maintenance operations consist only of the reapplication of the treatment.

The unitary costs assumed in the present study for the basic materials considered in the evaluation of both initial investment and maintenance costs are shown in

Table 3. Parameters considered in Life Cycle Cost Analysis (LCCA).

Parameter	Cost	Unit
Ordinary Portland Cement	87.77	€/t
Sand	13.98	€/t
Gravel	16.36	€/t
Fly Ash	38	€/t
Silica Fume	1.14	€/kg
SBR Latex	4.7	€/l
Superplastiziser	1.38	€/kg
Reinforcing Steel—B 500 S	0.8	€/kg
Reinforcing Steel—Stainless	4.5	€/kg
Hydrophobic Surface Treatment	19.01	€/m2
Sealant Surface Treatment	29.04	€/m2

. These costs are usual for the Spanish construction sector.

2.4. Social Life Cycle Assessment (SLCA)

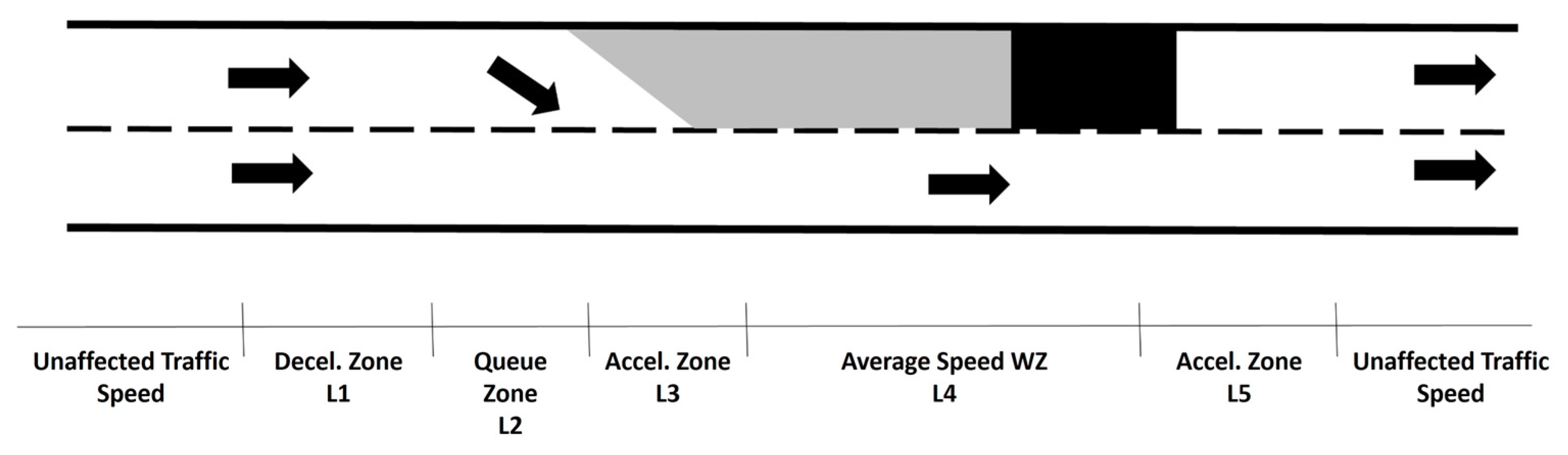
The social costs of a construction over its lifetime are difficult to quantify in monetary terms. These costs affect both users of the infrastructure and third parties who do not make use of it. For the road bridge studied, the main social costs affecting users [40,41] of the infrastructure are quantified. The user related costs considered in the present study are the Vehicle Operating Costs (VOC) and the Vehicle Delay Costs (VDC). The Vehicle Operating Costs are those costs arising from the normal use of the vehicles that must be borne by its users, such as fuel consumption, tire wear, and maintenance. These costs can be quantified as the cost increase derived from the circulation in zones affected by the construction or maintenance of the bridge with regard to the costs associated to the circulation in normal, unaffected travelling conditions. According to Seshadri and Harrison [42], the traffic behavior along a zone affected by maintenance or construction works allows us to identify five different sections, as shown in Figure 3.

The value of the vehicle’s operating costs can be defined by the following equation [43]:

$$VOC={\displaystyle \sum }_{j=1}^{24}\left({\displaystyle \sum }_{k=1}^5\left(L_k-\frac{S_{ak}}{S_n}·L_k\right)·HT·{\displaystyle \sum }_{i=1}^4\left(VO{C}_i·p_i\right)\right)$$

(4)

where L_k is the length of the affected zone k depending on the behavior of the traffic involved, as shown in Figure 3, S_ak is the traffic speed in the zone k affected by maintenance works, S_an stands for the traffic speed under normal, unaffected conditions, HT is the average hourly traffic, p_i is the percentage of class i vehicles with respect to the total vehicle flow, and VOC_i represents the operating costs associated to class i vehicles, defined as the sum of the costs derived from fuel consumption, tire consumption, and maintenance costs. In the present paper, the assumed parameter values regarding the characterization of the traffic behavior along the Working Zone are shown in

Table 4. Characterization of the Working Zone traffic behavior.

Section	Section Length (m)	Traffic Speed (km/h)
L1—Deceleration Zone	100	60
L2—Queue Zone	75	20
L3—Acceleration Zone	50	30
L4—Average Speed	250	40
L5—Acceleration Zone	50	50

. In the analysis, a traffic speed under normal conditions of S_an = 80 km/h has been considered. The vehicle classes assumed in the present methodology are described in

Table 5. Cost per hour of a person travelling, with regard to their objective, according to De Rus [44].

Vehicle Class	Class Description	Cost of Driver’s Working Time (€ /h)	Cost of Passenger’s Leisure Time (€ /h)	Occupation Rate
Class 1	Motorcycles and vehicles with vertical height from the first axle of 1.10 m	22.34	7.15	2
Class 2	Vehicles with two axles and a vertical height greater than 1.10 m	22.34	-	1
Class 3	Vehicles with three axles and a vertical height greater than 1.10 m	17.93	5.13	24
Class 4	Vehicles with more than three axles and a vertical height greater than 1.10 m	17.93	-	1

Note: For every vehicle class, it is assumed that 1 passenger is working. For vehicle classes 1 and 3, an additional 1 and 23 passengers are assumed to be “not working” respectively, according to Gervásio [45].

.

On the other hand, the economic quantification of the delays generated by maintenance operations on road users (VDC) is calculated by assessing the difference between the costs derived from the time spent by the driver on crossing the section affected by the works and those resulting from the time spent under normal operating conditions. In addition, the reason for the driver’s travel is also assessed and different estimates are made if the journey is for work or for other reasons. The value of the vehicle’s delay costs (VDC) can be defined by the following equation:

$$VDC={\displaystyle \sum }_{j=1}^{24}\left({\displaystyle \sum }_{k=1}^5\left(\frac{L_k}{S_{ak}}-\frac{L_k}{S_n}\right)\times HT\times {\displaystyle \sum }_{i=1}^{4}DT{C}_i\times p_i\right)$$

(5)

where the meaning of the different variables is the same as that presented in the definition of VOC. In Equation (5), DTC_i is the hourly cost associated to a class i vehicle user, and it depends on the user’s reason for travelling. This concept can be evaluated as:

$$DT{C}_i={\displaystyle \sum }_m\left(T{C}_m\times O{R}_{i,m}\right)$$

(6)

where OR_i,m is the occupation rate of passengers inside a class i vehicle that are travelling with a particular objective m, and TC_m is the hourly cost of a person travelling with a particular objective m as shown in Table 5. Two travel objectives are assumed, namely m = 1 for working reasons and m = 2 for non-working reasons. The relation between both costs, when no data is available, can be estimated as:

$$T{C}_{m=2}=0.25\times T{C}_{m=1}$$

(7)

Equations presented to evaluate VOC and VDC are based on the model developed by Gervásio [43]. For both the quantification of VOC and VDC, it is assumed that the maintenance operations only affect a 300 m long road section, and that the repair activities last six weeks. The average daily traffic is assumed to be 6000 vehicles per day, with an average traffic speed of 80 km/h. The costs derived from the use of vehicles are shown in

Table 6. Costs associated to the assumed vehicle classes.

Vehicle Class	Class 1		Class 2	Class 3	Class 4
Traffic composition	11%		78%	3%	8%
Fuel type	Gasoline	Diesel	Diesel	Diesel	Diesel
Fuel consumption (l/100 km)	5.9	4.8	4.5	44	44
Fuel cost (€/l)	1.33	1.13	1.13	1.13	1.13
Average service life for vehicles (years) 1	10		8	12	12
Service life of tires (km) 1	40,000		40,000	75,000	200,000
Tire cost (€) 1	73		62	333	463.6
Mean travel distance km/year 1	20,000		30,000	70,000	85,000
Yearly vehicle maintenance cost (€) 1	1575		1860	16,316	28,027
Vehicle depreciation (€) 1	17,177		11,563	21,653	84,451

¹ This data has been obtained from Gervásio [45].

.

Both the economic and the social costs, all transformed into monetary terms, will occur in different time instants, depending on the initiation time resulting for each of the treatment alternatives considered. In the resolution of the proposed model, the temporality of the maintenance actions is taken into account through the following concepts: selection of an appropriate period of analysis, consideration of a residual benefit, and cost discounting to present values.

The analysis period is the time frame in which the different alternatives are compared. The choice of the analysis period greatly influences the results of the socio-economic evaluation; choosing a period equal to the shorter service life of the alternatives may not capture the differences in the behavior of the alternatives in the long term, penalizing those that have longer service lives. This period should be long enough to adequately reflect the existing performance differences between the alternatives being compared. The current LCCA includes the impacts derived for an analysis period of the first 100 years of bridge life. This is the required service life for bridge structures according to European Committee for Standardization [46]. The consideration of the durability performance shown in Table 2 results in the number of maintenance operations to be held during the analysis period.

The residual benefit represents the monetary value of the alternative at the end of the analysis period. This value should be taken into account in the evaluation of projects where the solution has a longer service life than the analysis period considered in the economic evaluation [47]. In a simplified way, the economic value of the structure in its optimum state corresponds to the value of the initial investment. From this point onwards, the structure loses value as the end of its useful life approaches, when its state becomes inadmissible from the point of view of durability and its residual value becomes zero. In cost accounting, this residual value of a solution when the end of the analysis period is reached is considered as a benefit, thus reducing the life cycle costs.

The criterion assumed to determine the residual value of an alternative is to take into account the advance of the critical chloride content. By calculating the depth reached by the critical chloride content at the end of the analysis period, it is possible to estimate the residual value of the alternative in question; if the critical chloride content has reached the reinforcement depth, the residual value of the structure is zero. If not, it is assumed that the residual value of the structure is a fraction of the installation costs of the alternative. In particular, this fraction is proportional to the penetration depth of the chlorides in relation to the concrete cover of the design.

Finally, the temporary aspect of costs and benefits remains to be addressed. Over time, the value of money varies depending on financial concepts such as the interest rates of the investment or the inflation rates. In order to properly compare two alternatives, it is necessary to convert the costs generated over time into comparable monetary values. As a criterion, the comparison is made in terms of present monetary value, using the discount rate. The equation for calculating costs in terms of present costs is as follows:

$$LCC={\displaystyle \sum }_{t=t_0}^{t_{SL}}{C}_i\times \frac{1}{{\left(1+d\right)}^{t-t_0}}$$

(8)

where LCC is the Life Cycle Cost of the structure, C_i represents the economic costs associated to time t, t₀ is the time associated to the beginning of the analysis period, t_SL is the number of years considered in the analysis, and d is the discount rate. In Europe, the European Commission proposes a discount rate of between 3.5% and 5.5% for project evaluation. In the present paper, a discount rate of 5% is considered.

3. Results and Discussion

According to the methodology proposed, the resulting installation and maintenance costs per meter of bridge deck are presented in Figure 4 for the preventive strategies analyzed in this study. As explained above, since the assumed maintenance criterion is to repair the bridge when the initiation time is reached, the reinforcement will not have been affected by corrosion, and consequently, the maintenance operation will consist on removing the chloride contaminated concrete cover and executing it again. Regarding the surface treatments (HIDRO and SEAL), the maintenance activities consist in the reapplication of the treatment, without demolishing the existing concrete cover.

It is observed that there are several alternatives with initial costs very similar to the installation costs of the reference alternative. Those are the alternatives where the cost of the materials is very close to the reference case, namely the ones based on surface treatments (hydrophobic and sealant treatments), the addition of fly ash, the reduction of the water/cement ratio, and the increase of the concrete cover up to 35 mm.

The addition of silica fume in the concrete mix results in solutions with initial costs significantly greater than the those of the reference alternative, namely 28% to 33% greater for HS5 and HS10, respectively. It is observed that an excessive concrete cover (R45 and R50) leads to great initial costs as well, due to the associated increase in the reinforcing steel demand. On the other hand, those solutions where the reinforcement material is modified, namely by using galvanized or stainless steel reinforcements, result in almost the highest initial costs, due to the high costs of materials [48]. At last, it is observed that the most expensive solutions in terms of initial costs are those where the reference concrete is modified with polymers. This conclusion is in good accordance with Fowler [49], and is derived from the high costs of the polymer materials. Consequently, the economic limitation of polymer modified concretes or stainless steel used as reinforcement is only assumable in cases where good durability is required. As can be observed, the service life of both HMP10 and HMP20 solutions is considerable, and this results in lower or almost no maintenance costs. In the case of INOX, no maintenance is required.

Focusing on the costs generated during the service stage of the bridge, the results show that the alternatives with the least number of interventions are, in general, the ones with the lowest maintenance costs, as expected. An exception to the previous statement is made by alternatives involving surface treatments; as explained above, such alternatives require frequent maintenance. The costs associated with each of these maintenance operations are, however, small if compared to the cost of repair for any of the other alternatives. This means that, despite demanding a high number of repairs, they are preferable in terms of economic costs if compared to the other alternatives. It is also interesting to highlight the significant maintenance costs associated with the reference solution, which almost doubles the maintenance costs of the next more expensive alternative. However, it is worth noting that an increase of only 5 mm in the concrete cover may reduce the maintenance costs of the reference alternative by up to 40%.

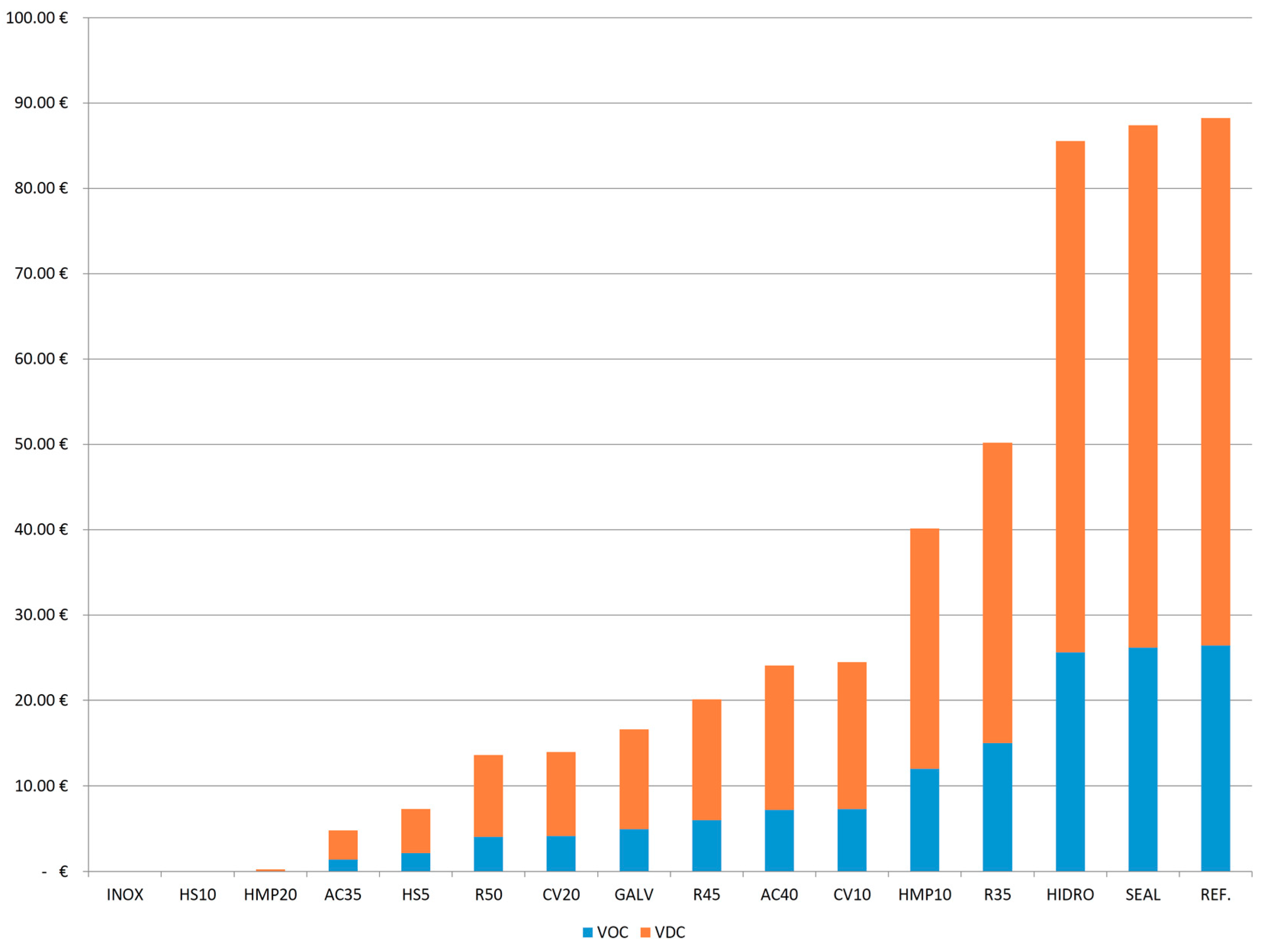
By analyzing the social impact of the different alternatives in terms of user costs (Figure 5), it can be observed that those measures that require a greater number of interventions are the ones that generate the greatest social impact. Thus, alternatives HIDRO and SEAL, despite requiring faster maintenance operations, generate the greatest social costs, exceeding those resulting from the reference alternative. The reference alternative, which also requires intensive maintenance throughout its service life, results in high social costs as well. The rest of the analyzed measures show a significantly lower social impact.

Table 7. Total socio-economic costs of the analyzed alternatives, in €/m of deck. VOC = vehicle operating costs; VDC = vehicle delay costs.

Alternative	Investment Costs	Maintenance Costs	VOC	VDC	Residual Value	Total
AC35	1481.67 €	143.84 €	1.44 €	3.37 €	−7.66 €	1622.65 €
HIDRO	1406.91 €	230.92 €	25.61 €	59.93 €	−10.70 €	1712.68 €
HS10	1832.96 €	-	-	-	−2.24 €	1830.72 €
CV20	1511.39 €	409.19 €	4.19 €	9.80 €	−1.94 €	1932.63 €
HS5	1768.90 €	219.50 €	2.18 €	5.11 €	−3.20 €	1992.50 €
AC40	1475.82 €	707.39 €	7.22 €	16.88 €	−7.64 €	2199.66 €
R45	1579.74 €	654.04 €	6.02 €	14.09 €	−3.13 €	2250.76 €
CV10	1514.56 €	720.65 €	7.34 €	17.16 €	−7.18 €	2252.53 €
R50	1778.83 €	507.79 €	4.08 €	9.54 €	−3.06 €	2297.17 €
SEAL	1471.19 €	795.83 €	26.17 €	61.22 €	−11.19 €	2343.22 €
R35	1480.19 €	1506.24 €	15.02 €	35.14 €	−0.80 €	3035.79 €
GALV	2903.18 €	494.98 €	4.98 €	11.64 €	−16.04 €	3398.74 €
INOX	3941.28 €	-	-	-	−29.97 €	3911.31 €
REF.	1380.64 €	2555.78 €	26.43 €	61.83 €	−9.61 €	4015.07 €
HMP10	3033.84 €	1296.54 €	12.02 €	28.12 €	−9.79 €	4360.72 €
HMP20	4560.74 €	32.59 €	0.08 €	0.19 €	−23.49 €	4570.11 €

shows the discounted total costs incurred by each of the different designs. It is observed that the user costs are significantly lower than the costs derived from maintenance. These costs depend on the socio-economic context of the infrastructure and on the traffic intensity registered. When considering both installation, maintenance ,and user costs, it is concluded that using polymer modified concrete is the most expensive prevention alternative, with a resulting cost that is even greater than the costs derived from the reference design. The difference between the cost of both strategies is, however, less than 15%. The use of stainless steel shows similar economic impact to the reference alternative. In this case, the same as in the case of HMP20, the total costs are mainly those associated with the installation phase of the structure, i.e., neither of them incurs maintenance costs (INOX) or maintenance costs are generated far into the future (HMP20).

On the other hand, it shall be noted the high cost of maintenance derived from the reference design. For this alternative, the costs that are generated over the service life almost double the initial investment. Something similar happens for those alternatives in which the modification of the solution does not significantly affect the durability of the solution, as is the case with alternative R35. While this slight increase in the concrete cover significantly reduces maintenance costs, they still carry a significant weight on the final cost of the solution. Obviously, the more a solution contributes to improving the durability performance of the structure against corrosion, the lower the maintenance costs will be.

The prevention strategies that generate less costs throughout the life cycle of the structure, considering both economic and social costs on users, are those based on reducing the water to cement ratio of the original concrete mix (AC35), applying hydrophobic surface treatments on the deck surface (HIDRO), and adding of silica fume and fly ash on the concrete mix design (HS10, HS5, and CV20). As can be observed, the durability performance of both AC35 and HIDRO is far below the performance of other, more expensive solutions such as HMP20 or INOX. However, the resulting life cycle costs are the lowest, namely between 41.5% and 42.6% of the costs associated to the reference design. This is due to the fact that material costs in both cases are very competitive. Consequently, the combined effect of the inexpensive maintenance activities together with the more than acceptable durability performance in the case of AC35, and the low costs of maintenance in the case of HIDRO design, make them the most desirable strategies. It shall be highlighted that the life cycle costs of these alternatives only differ between 11% and 15% with the costs derived from alternatives HS10 and CV20, making them also very cost-efficient solutions in chloride laden environments. It has to be noted that the design HS10 does not incur any costs related to maintenance, as the service life associated to this alternative is greater than the required service life.

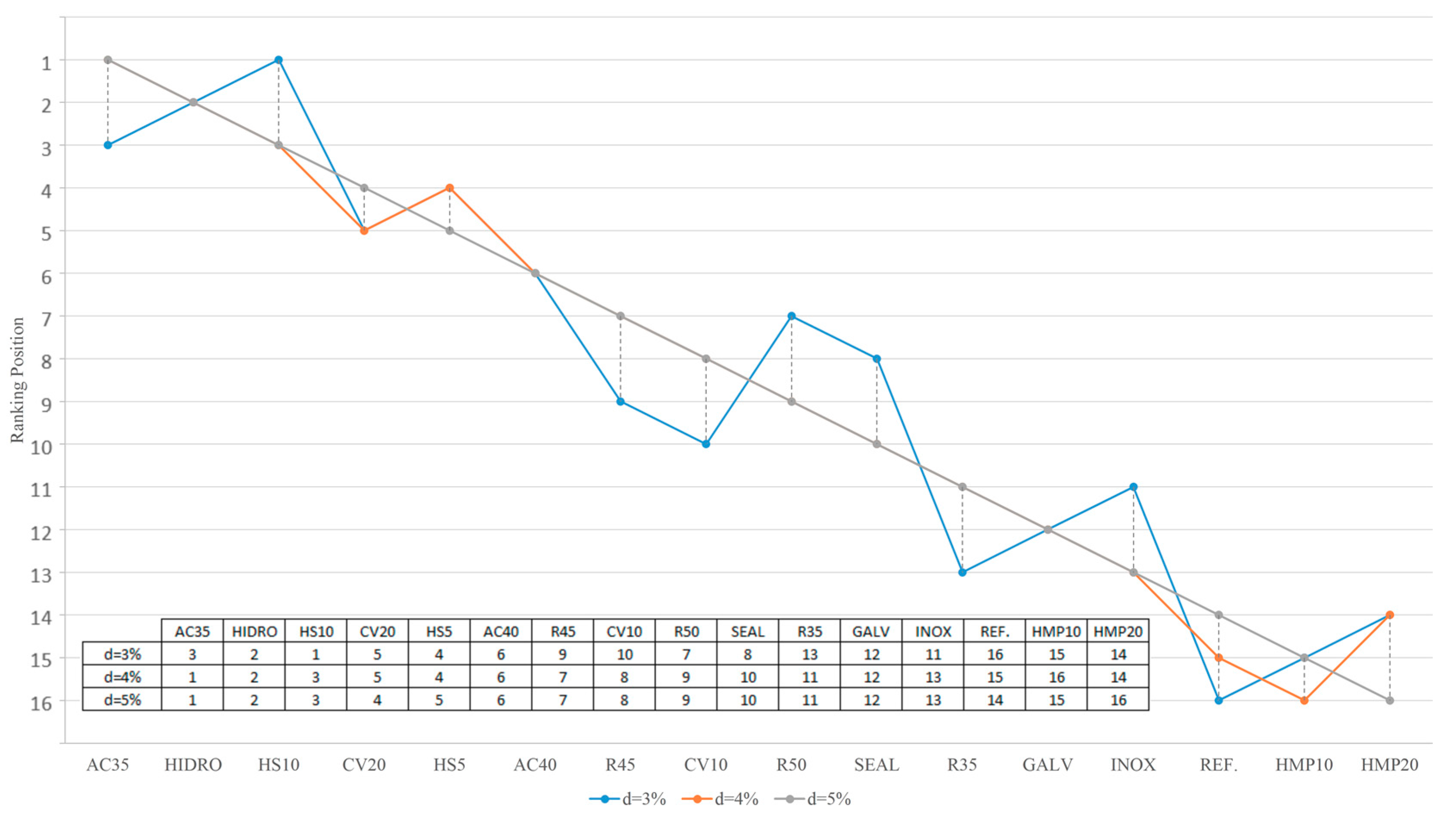
The results presented above are based on the assumption of a discount rate d = 5%. However, the assumed discount rate is highly uncertain when considering a period of analysis of 100 years. Taking into account that uncertainties about discount rate tends to be a key contributor on LCCA results when considered [50,51], a sensitivity analysis on this parameter is performed, taking into account three discount rates within the usual range for infrastructures in Europe, namely d = 3%, d = 4%, and d = 5%. For these three scenarios, the different preventive strategies have been ranked, based on the resulting life cycle total costs, including both economic and user impacts. Results are presented in Figure 6, where a rank value of 1 means that the alternative results in the lowest life cycle discounted costs.

It can be observed that the main conclusions derived above are robust, as they do not significantly depend on the chosen discount rate. There are, however, slight differences in the rankings. In Figure 6, a dashed line marks the ranking changes resulting from the analysis scenarios. It is observed that the worst alternatives, regardless of the discount rate assumed in the evaluation, are the reference alternative and the strategies based on polymer modified concrete. On the other hand, the best alternatives vary between measures HS10, AC35, and HIDRO. It is observed that, in general, the lower the chosen discount rate, the more preferable are those solutions with either less maintenance demand, such as HS10, or those with lower maintenance costs, such as hydrophobic surface treatments. However, it shall be highlighted that the differences between the best and worst of the alternatives HS10, AC35, and HIDRO in terms of total life cycle costs are found to be less than 10%. In consequence, it can be concluded that results presented in this paper are robust.

4. Conclusions and Future Lines of Research

LCCA methodology has been used to assess the different preventive measures against chloride corrosion of concrete reinforcement. These measures have been evaluated taking into account both their durability performance against corrosion and the economic and social costs derived during the life cycle of the structure. The exposed methodology has been applied to a prestressed concrete bridge in the Arosa Isle.

It has been shown that those alternatives with better performance in terms of durability against chloride corrosion, namely the use of stainless steel or polymer-modified concrete, are the ones that incur greater life cycle costs. Those alternatives that perform the worst, namely the reference alternative or the increase of the concrete cover up to 35 mm, show similar resulting life cycle costs. In these cases, in contrast to the previously described alternatives, the major part of the resulting costs is derived from maintenance, which can be up to three times greater than the installation costs, as the case of the reference design. From the results presented above, it seems reasonable to state that the optimum in economic terms is derived from a compromise solution between durability performance and material costs. For the bridge studied, the alternatives that perform best economically consist in reducing the water/cement ratio of the reference alternative up to w/c = 0.35 and treating the concrete surface by means of hydrophobic products. The addition of high amounts of silica fume and fly ash also provide very cost efficient solutions throughout the structure’s life cycle. In particular, the addition of 10% silica fume results in a very cost-efficient, maintenance free solution.

It shall be highlighted that, although the LCCA methodology presented here is applicable in general terms to concrete bridge decks exposed to severe environments, the conclusions drawn are based on a particular bridge. The transferability of the obtained results is, therefore, dependent to the specific context of the structure to be evaluated. Further research is suggested to evaluate the combined effect of some of the presented preventive measures, and to bring to light both their compatibilities and their cost competitiveness.