1. Introduction
A typical bridge supports vertical loads and lateral displacements on the super-structure using bearing and expansion joints. Mechanical devices in these joints are subject to damage caused by the thermal expansion and contraction of the bridge structure, and abutment backfill settlement. This means that consistent maintenance and repairs are required during its service life, as otherwise, the bridge superstructure may be damaged.
In Europe and the US, the integral abutment bridge (IAB) was developed and has been widely used to eliminate the use of bearings and expansion joints from the joint bridge. In the IAB, instead of the general reverse T-shaped abutment (T-abutment), the stub abutment is mainly employed because it exhibits integrated behavior through the use of a rigid link with a super-structure and a pile foundation [
1]. As the super-structure and the sub-structure of the IAB always exhibit rigid-link integration, the super-structural behavior is closely related to the sub-structure of the bridge, including the pile foundation and the pressure. In particular, the lateral displacement of the super-structure (by thermal expansion, drying shrinkage, creep, and other causes) largely influences bridge behavior [
2]. The IAB bridge is advantageous because it integrates super-structure and sub-structure so that it does not fall down during earthquakes. In recent years, research into the application of seismic isolation bearings on the semi-IAB bridge has begun. These seismic isolation bearings have previously been applied to building structures rather than bridges but have also recently been applied to bridges [
3,
4].
The lateral displacement of the IAB super-structure leads to a passive earth pressure on the stub abutment. In this regard, Civjan, et al. [
5], Nam and Park [
6], and Park and Nam [
7] defined the passive soil-pressure changes by conducting long-term field measurements on IABs. Ahn, et al. [
8] analytically defined the passive earth pressure using long-term thermal expansion of the pre-stressed concrete (PSC) girder in the IAB. In addition, the lateral displacement of the super-structure is resisted by the pile foundation on the stub abutment, for which theoretical, numerical, analytic, and experimental studies have been conducted by some researchers [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29]. According to these studies, the IAB is governed by the maximum bending moment that acts on the pile-head and is generated by the lateral displacement of the girder. Such a lateral displacement is affected by the thermal expansion of the girder, which is further influenced by creep (CR) and shrinkage (SH) [
30,
31,
32]. Therefore, the span of an IAB is limited so as not to exceed the maximum pile-head bending moment capacity when resisting bending that is caused by excessive lateral displacement of the girder [
9,
10,
33,
34]. To reduce this limitation, studies involving the hinge bar and elastic pad installed in the IAB abutment for the purpose of reducing the maximum pile-head bending moment are ongoing [
9,
35,
36,
37].
The various advantages of the IAB, as well as its weaknesses, result from its integration-type condition. The IAB abutment uses lateral earth pressure on the front fill to resist the lateral displacement. However, this fill reduces the under-bridge space thereby requiring a longer bridge span to compensate for the reduction. Also, although the non-compacted backfill has been dumped to reduce the earth pressure of the IAB [
7,
33,
38], local deformation and approach slab settlement cause bumps at the bridge ends [
2].
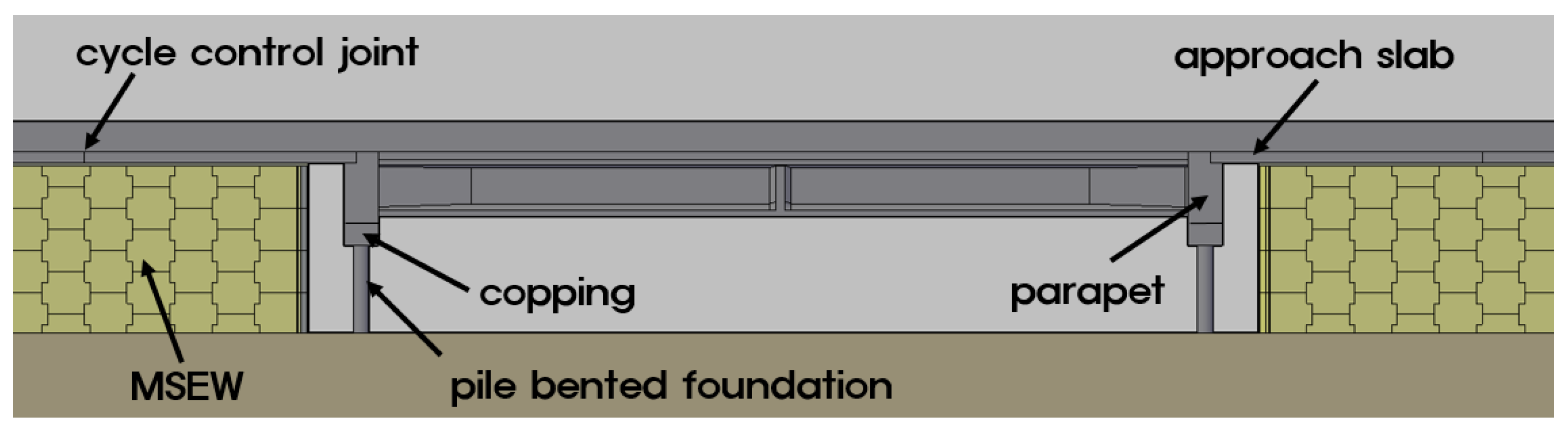
To overcome these IAB-associated problems, Nam, et al. [
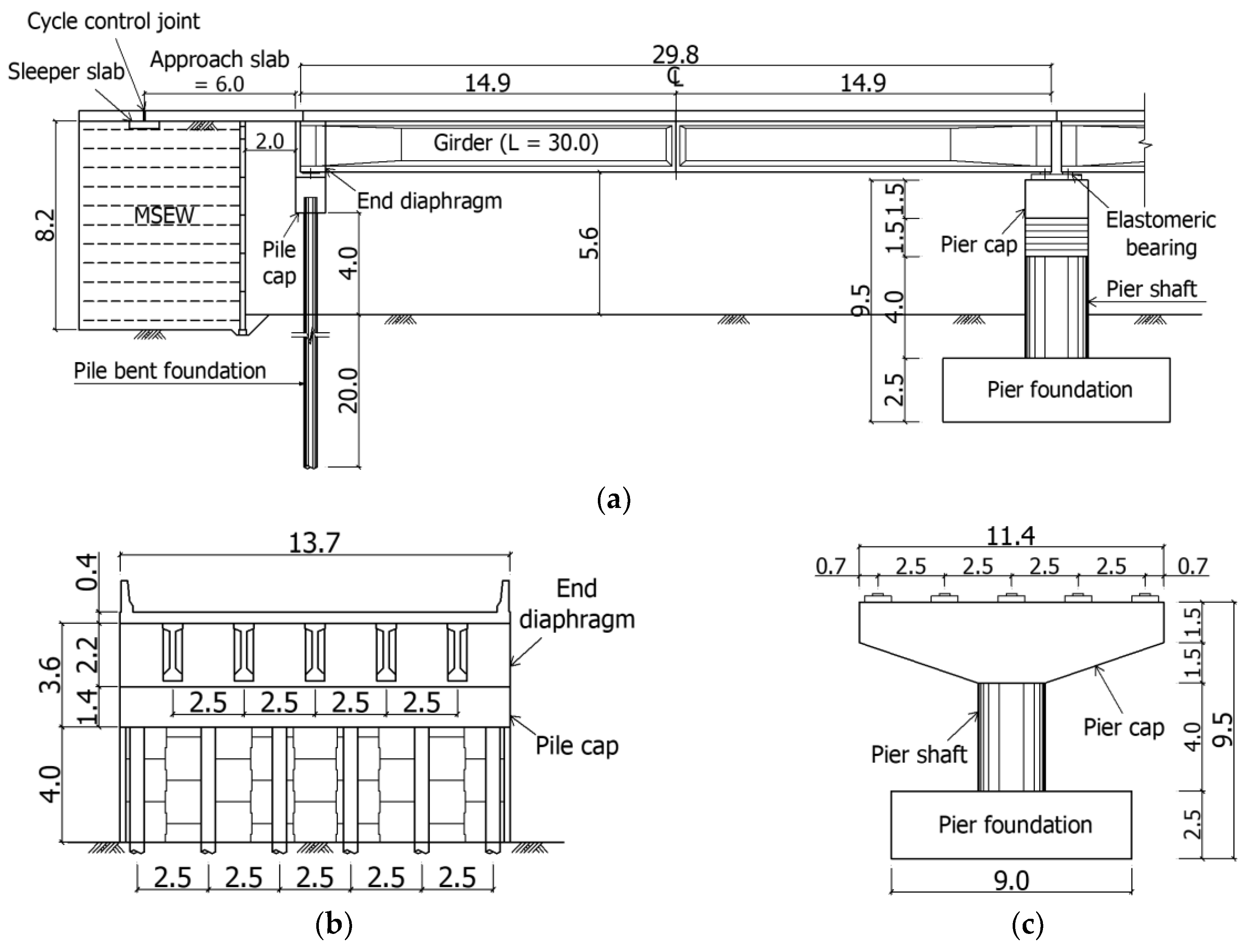
39] developed an integrated and pile-bent abutment with a mechanically stabilized earth-wall (IPM) bridge by combining the advantages of the IAB and the mechanically stabilized earth-abutment bridge, as shown in
Figure 1 [
2]. The super-structure of the IPM bridge is integrated with the abutment, and the vertical load of the super-structure and its lateral displacement are supported by the pile foundation, as is the case for a typical integral abutment. However, in the IPM bridge, the horizontal earth pressure is resisted by the mechanically stabilized earth wall (MSEW). By separating the earth pressure from the abutment, neither the fill-in front of the abutment, nor the non-compacted backfill, is needed. Furthermore, the piles in the IPM bridge form a pile-bent, and the protruded piles from the ground surface allow for decreased interaction with the member force of the pile-heads, in contrast to IABs [
2,
40].
Based on the previous study of the IPM bridge (Park and Nam [
2]), the PSC girder was used for the super-structure and the steel-pipe pile was used for the sub-structure for the IPM bridge; the length and the skew angle of the bridge, the height of the pile-bent extrusion, and the ground stiffness were selected as parameters, as listed in
Table 1. The purpose of their analysis was to define the bridge behavior differences between the IPM and IAB, as well as to review their effects on bridge formation, pile protrusion height, and ground stiffness. The individual load effects were also reviewed. The results of the study by Park and Nam [
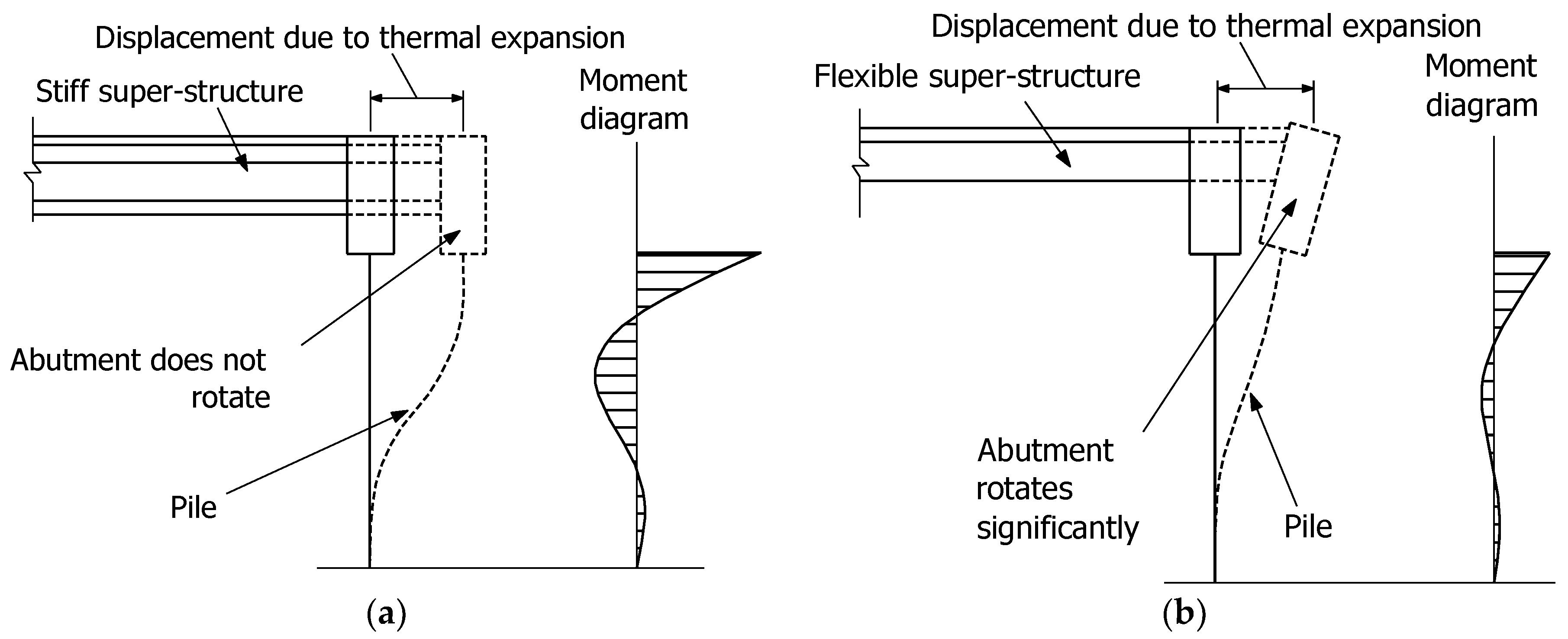
2] show that lateral displacement caused by thermal expansion, drying shrinkage, and CR on the PSC girder are predominant in the IPM bridge, especially in regard to the behavior of the pile-bent. For the pile-bent, member forces decreased and lateral displacement increased when the pile protrusion height was increased. Moreover, most of the analysis focused on the bridge behavior involving the PSC girder and the steel-pipe pile, whereas the super- and sub-structural characteristics were not examined. The effect of thermal expansion (Δ Thermal) which occurs in the stiff super-structure of the IPM bridge is described in
Figure 2a, whereas
Figure 2b shows that the effect of abutment rotation occurring with a flexible superstructure is similar to that of the IPM bridge [
31]. Consequently, the pile is governed by super-structural characteristics, whereas the bending moment on the pile is controlled by bending rigidity. Thus, the IPM pile-bent behavior could vary depending on the super- and sub-structural characteristics.
Accordingly, this study defined the IPM bridge behavior according to the super- and sub-structural characteristics. The parameters for the structural analysis include the super- and sub-structural types and the bending rigidity, as listed in
Table 1. The analysis regarding the effect of shrinkage was conducted on the two types of super-structure—the influence of drying shrinkage on the PSC girder and the non-drying shrinkage influence on the steel girder. These shrinkage effects are also present in the steel-pipe pile and the cast-in-place (CIP) concrete piles, which are types of sub-structure. This served to review the effects of the super- and sub-structural characteristics, individually, in combination, and in response to thermal loads. In addition, the member forces and displacement that were imposed on the pile-head as well as the overall displacement were reviewed according to the super- and sub-structural characteristics, considering that the super- and sub-structures of the IPM bridge produce maximum member force on the pile-head.
2. Materials and Methods
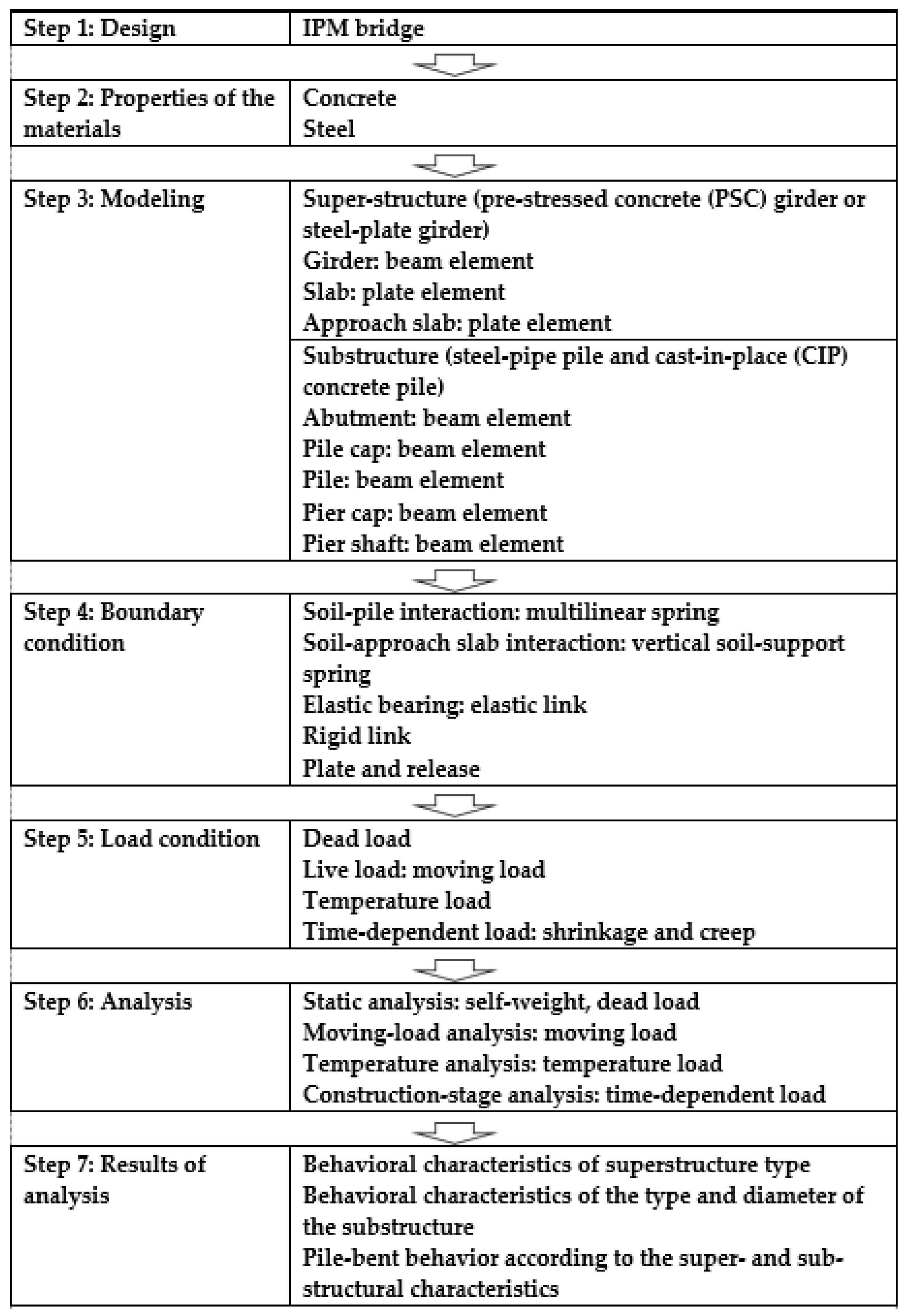
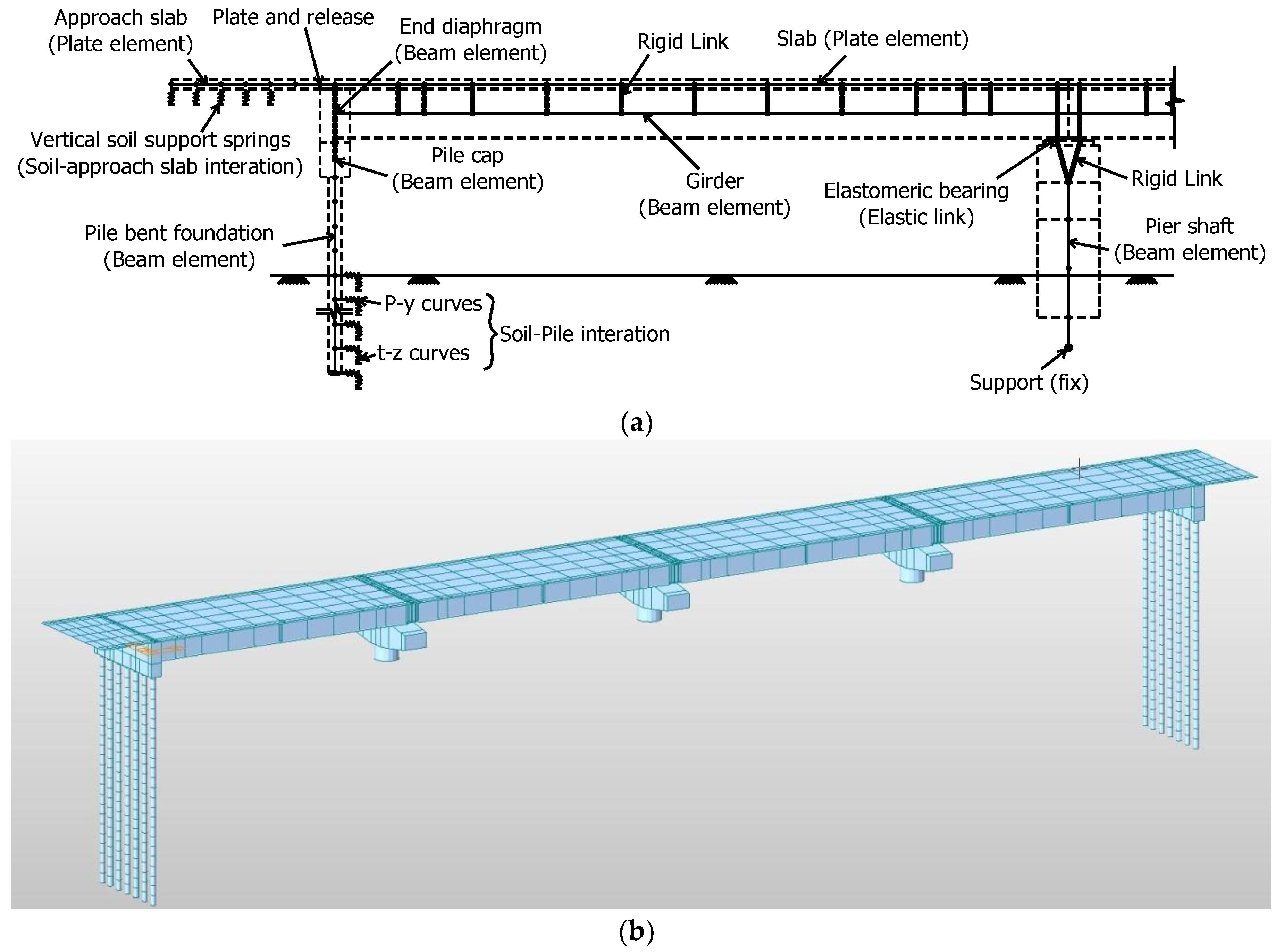
This study conducted a three-dimensional (3D) structural analysis in seven steps to define the IPM bridge behavior according to super- and sub-structural characteristics, as shown in
Figure 3. In Step 1, the IPM bridge was designed. In Step 2, the material characteristics were input. In Step 3, the IPM bridge was modeled based on the design drawings. The IPM bridge model super-structure consisted of the PSC and steel-plate girders, whereas the sub-structure was comprised of steel-pipe piles and CIP concrete piles. The parametric analysis conditions for these materials are described in
Figure 4. In Step 4, the boundary conditions were created. The soil-structure interaction needed to be identified to define the IPM bridge behavior in detail. In particular, the soil-pile interaction controls the pile-bent behavior that supports the super-structural lateral load. In Step 5, the loading conditions that were proposed in the design standards were set. In the IAB, like those of the IPM bridge, the thermal and time-dependent loads, including dry shrinkage and CR, needed to be specified; these are loading conditions common to both IAB and IPM bridges. In Step 6, a structural analysis was conducted on the IPM bridge model under loading conditions. In Step 7, the results were analyzed. For this study, the behavioral characteristics were reviewed according to the super-structure type, as well as the type and the diameter of the sub-structure. Moreover, the pile-bent behavior was reviewed according to the super- and sub-structural characteristics.
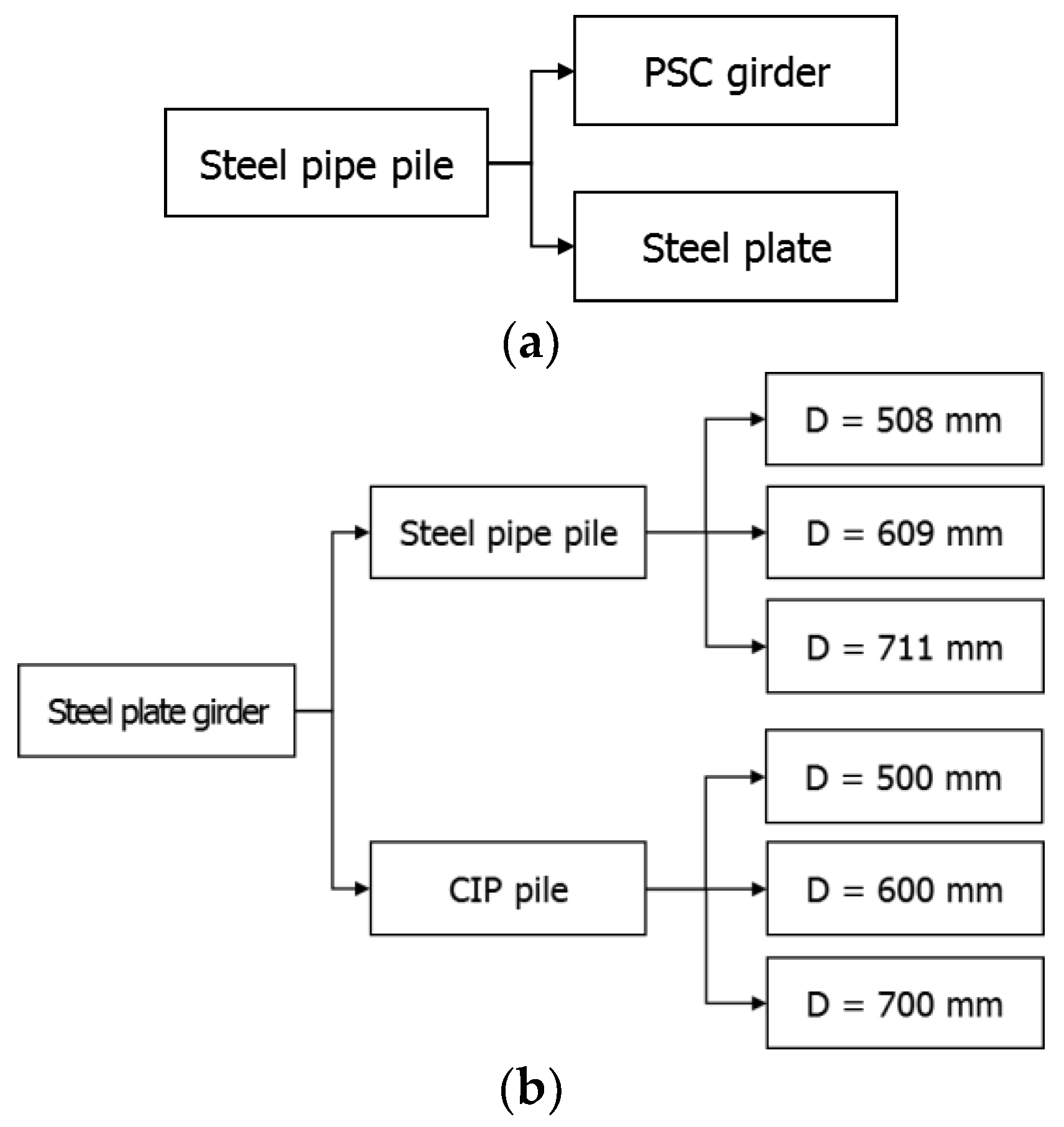
The parametric analysis conditions of this study are shown in
Figure 4. The parametric analysis conditions for the examination of the IPM bridge behavior according to super-structure type are provided in
Figure 4a. The structural analysis of the effect of the super-structural form was conducted by modeling the sub-structure as a 508-mm diameter steel-pipe pile, and the super-structure as PSC and steel-plate girders, respectively. The parametric analysis conditions for the examination of the IPM bridge behavior according to the sub-structure type and diameter are provided in
Figure 4b. The IPM bridge behavior according to the sub-structural characteristics was analyzed by modeling the super-structure using a PSC girder and the sub-structures using steel-pipe piles and CIP concrete piles, respectively. At this point, the diameters of the steel-pipe and CIP concrete piles were increased from 508 mm to 711 mm, and 500 mm to 700 mm, respectively. In the structural analysis involving the PSC girder and the 508 mm diameter steel-pipe piles, the results reported by Park and Nam [
2] were cited.
2.1. Bridge Analyses
The main subject of this study, the IPM bridge, is an integral form of the super-structure, abutment, and pile. The pile foundation is partially exposed as the abutment is separated from the backfill, and the earth pressure on the abutment is entirely supported by the MSEW. The design complies with the IPM Bridge Design Guidelines [
41] that are based on ASSHTO (2002), ASSHTO (2012), VTrans [
42], KECRI [
33], MLTMA (2008), and MLTMA [
43].
The span of the IPM bridge considered in this study is continuous and consists of four girders each having a span of 30 m to give a total bridge length of 120 m, as shown in
Figure 5. It has no skew angle, and its sub-structure consists of two IPM abutments and three reverse T-type piers. The reverse T-type pier is a typical reinforced-concrete pier with a 4 m shaft height. A total of 10 elastomeric bearings, as movable bearings, were installed in the pier. The pile-bent foundation has a 4 m protrusion height and 20 m of penetration depth into the ground. The pile-head fixed in a pile-cap is 1.4 m to resist the bearing stress on the pile-head due to the weight of the super-structure. The width at the end diaphragm was integrated with the super-structure and was designed to be 2.2 m in consideration of the lateral girder displacement. The IAB end diaphragm was designed by taking into account passive earth pressure and is an important research item in the present study [
6,
7,
8,
9]. However, in the IPM bridge, the MSEW supports earth pressure and is therefore not a consideration in abutment design. The MSEW consists of panels and metal strips, each with a height and width of 8.2 m and 13.7 m, respectively. The super-structures of the IPM bridge are integrated into the end diaphragm, and the approach slab is connected by the dowel bar. A cycle control joint (CCJ) is installed at between the approach slab and the road pavement [
40]. The CCJ replaces the expansion joints of general joint bridges and accommodates the temperature expansion of the super-structure. A sleeper slab is installed beneath the CCJ to prevent settlements of the approach slab.
Table 2 lists the bridge information and the ground conditions of the IPM bridge, as used in the structural analysis. As mentioned earlier, the bridge length is 120 m, the skew angle is 0°, and the pile protrusion length is 4 m. In the Standard Penetration Test (SPT), sandy soil ground conditions and an
N-value of 20 were assumed. As for the structural analysis of the PSC girder and the steel-pipe pile under the conditions of the IPM bridge information listed in
Table 1, the results of Park and Nam [
2] are cited. Park and Nam [
2] considered the effect of protruded heights of the pile-bent to be 4~10 m. However, only protruded heights of the pile-bent of 4 m were considered in this paper. According to Park and Nam [
2], the lower the protrusion height that the pile-bent develops, the larger the bending moment. Hence, only the lowest protrusion height of 4 m was considered in this paper to investigate the behavior of the pile-bent according to the super-structure and the sub-structure.
2.2. Super-Structure Properties
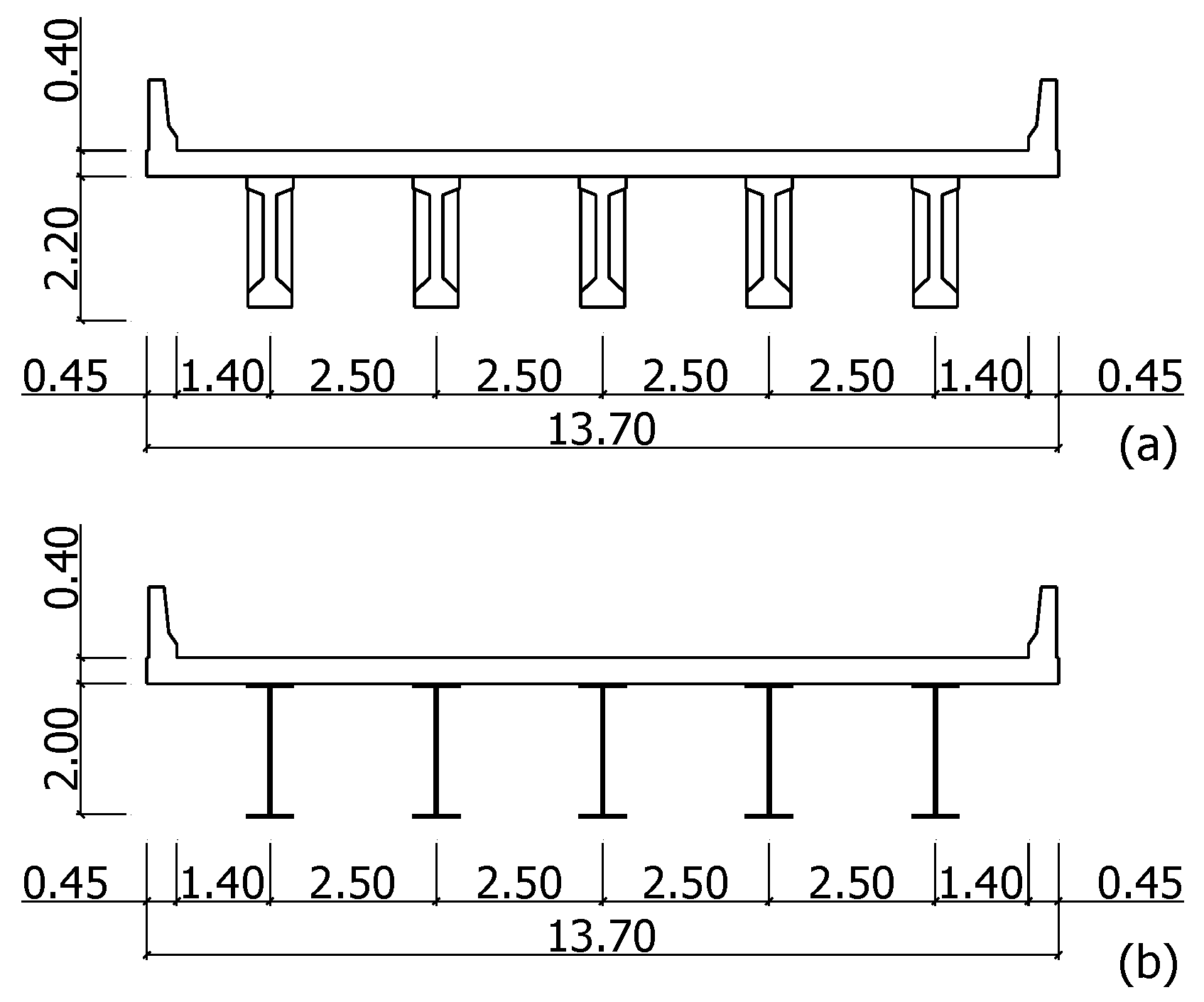
For this investigation, the PSC and steel-plate girders properties were used to define the IPM bridge behavior according to the super-structural characteristics. The cross-section specifications of the girder in the structural analysis are provided in
Figure 6 and
Table 3. According to Olson, Holloway, Buenker, Long and LaFave [
31], the super-structure rotation governs the member forces on the pile-head. In turn, the super-structure rotation is controlled by material properties, the girder height, and the end-diaphragm formation. Among the several influencing factors that were suggested by Olson, Holloway, Buenker, Long and LaFave [
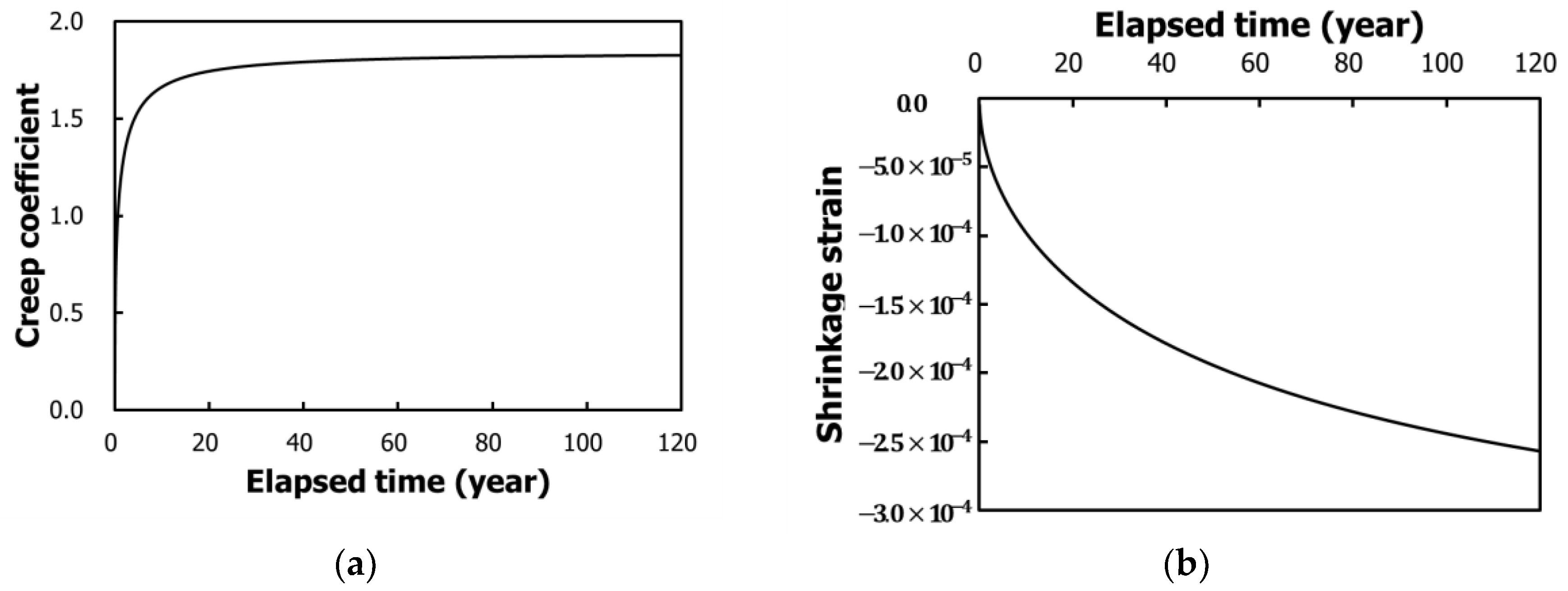
31], only the influence of material properties is considered in this study. The determination of the cross-sectional specifications was not made to produce major differences in the girder height, axial stiffness, and bending rigidity. Consequently, the behavioral characteristics were defined according to the material properties of concrete and steel that either create or do not create shrinkage (SH) and CR.
The PSC girder used in this study has a standard cross-section of 30 m and was developed by the Korea Expressway Corporation (KEC). As for the designed steel-plate girder, its height, axial stiffness, and bending rigidity are similar to those of the KEC PSC girder. The PSC and steel-plate girder heights are 2.2 m and 2.0 m, respectively. A slight girder height gap is present, whereas the modeled end-diaphragm formations are identical. The girders were placed in five equally spaced points at intervals of 2.5 m.
2.3. Sub-Structure Properties
Typically, for the IAB, the H-section pile is oriented at its weak axis to ensure flexibility in the lateral displacement of the super-structure [
9,
10,
11,
12,
13,
15,
16,
33]. However, in a skew bridge, it is difficult to precisely orient the pile at its weak axis as torsion is generated on the pile-head [
2]. Therefore, the IPM Bridge Design Guidelines [
41] recommend the use of steel-pipe pile as the pile-bent.
To define the IPM bridge characteristics according to the sub-structural characteristics, this study used a CIP concrete pile along with the other concrete materials, in addition to the steel-pipe pile, as recommended by the Bridge Design Guidelines [
41]. The CIP concrete pile is widely used in single pile-bents of large-scale marine bridges. Hence, as a pile-bent, its behavior, according to its sub-structural characteristics, was defined via structural analysis. The thermal expansion, drying SH, and CR of the CIP concrete pile were not considered, while the IMP bridge behavior was defined only according to the bending rigidity of the sub-structure.
Table 4 lists the cross-sectional specifications of the pile-bents that were used in the structural analysis. The diameter of the steel pipe pile is from 508–711 mm with a thickness of 12.0 mm, whereas the diameter of the CIP concrete pile is from 500–600 mm.
4. Analysis Results
Under fixed conditions, the design of the IPM bridge is the same as that of a typical IAB, where the pile supports the vertical and horizontal loads, moments, and vertical and horizontal displacements, whereas the pile-bent is integrated into the abutment as the fixed condition. Under such a fixed pile connection condition, the largest bending moment occurred in the pile-head. Therefore, the pile-head stress should not exceed its acceptable stress level [
31,
33,
41].
The results of the structural analysis that was conducted in this study show that the applied bending moment and displacement on the pile-head are the same as those described by Park and Nam [
2]. In the parametric analysis, the effects of the individual and combined loads in terms of the super-structure type were first identified. Then, the effects of pile type and diameter were identified according to the super-structural characteristics. The IPM bridge is an IAB type that integrates the super-structure and sub-structure. Therefore, the super-structure has expansion and contraction movements according to the seasonal temperature changes. Therefore, the structural analysis results of the IPM bridge were classified into expansion (summer) and contraction (winter).
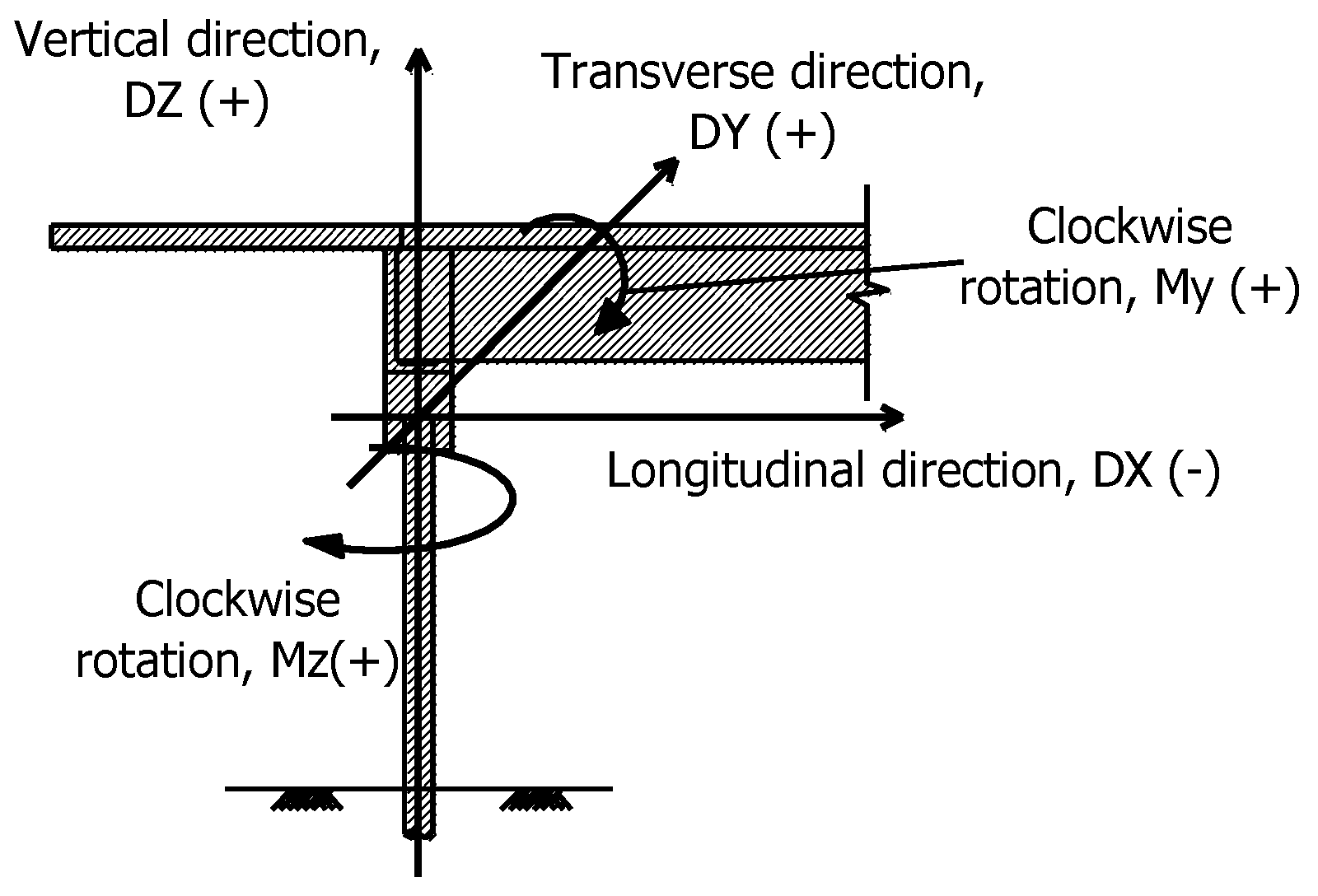
The sign convention suggested by Park and Nam [
2] and complied with in the present study, is provided in
Figure 10. The displacement value in the longitudinal direction was negative (−) when the value was shrunk along the
x-axis, and its value was positive (+) when it was expanded toward the back face of the abutment. The displacement value in the transverse direction is positive (+) when it occurred on the left side and negative (−) when it occurred on the right side. The bending moments that acted on the pile-bents in the direction of the rotation of the super-structure girder, subsequently defined as My in this present study, are positive (+) when their direction is clockwise and negative (−) when rotation is counter-clockwise. As for the moment that causes torsion on the pile-bent foundation, subsequently defined as Mz in the present study, the moment is positive (+) when it occurs in the clockwise direction and negative (−) when it is in the counter-clockwise direction.
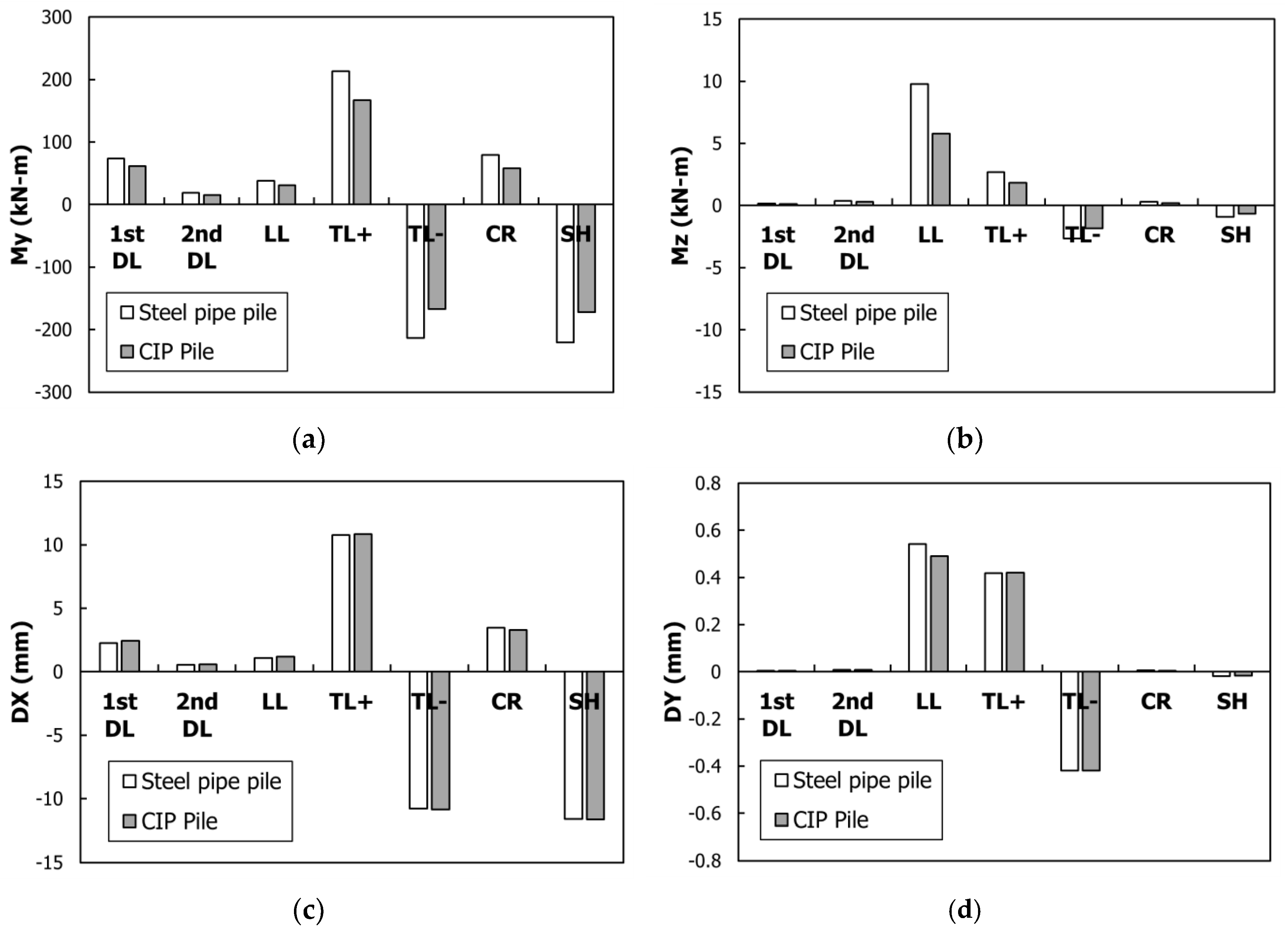
4.1. Pile-Head Behavior According Super-Structure Types
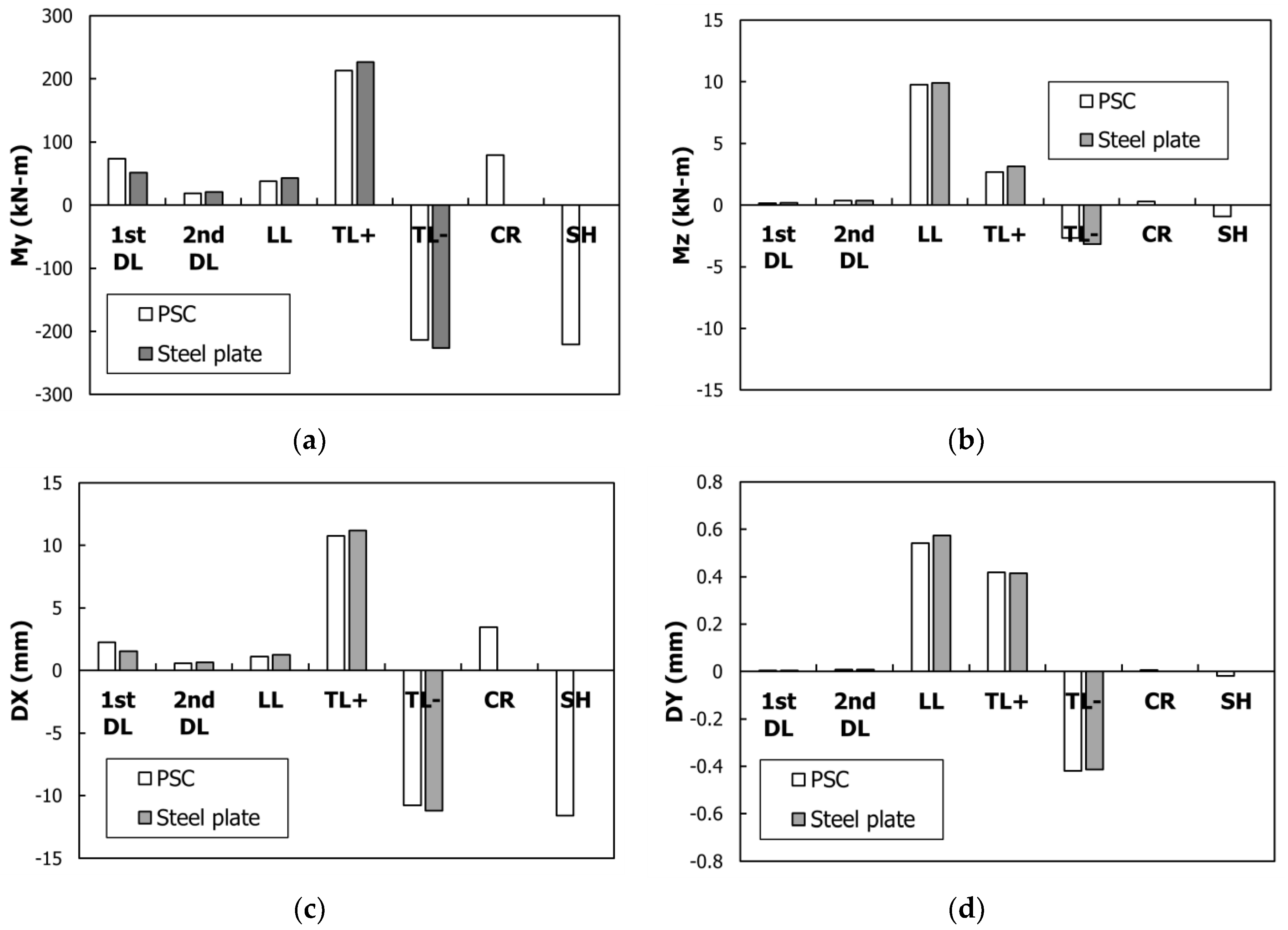
The behavior that occurs in the pile-head under individual conditions, per super-structure type, is shown in
Figure 11. The structural analysis was conducted by modeling the sub-structure with a 508 mm diameter steel-pipe pile, and the super-structure with the PSC and steel-plate girders, respectively. The My bending moment acting on the pile-head is shown in
Figure 11a. Comparing the PSC and steel-plate girders, the first DLs are bigger in the PSC girder than those in the steel-plate girder. This is because the cross-sectional area of the PSC girder is larger compared with that of the steel-plate girder. The temperature load (TL) is bigger in the steel-plate girder with a relatively higher
. Moreover, the time-dependent loads, SH, and CR occurred in the PSC girder only. The individual loads that exerted the greatest effect on the My bending moment of the PSC girder, enumerated in the same sequential order as that of Park and Nam [
2], are temperature increase (TL+), temperature decrease (TL−), SH, and CR. In the steel-plate girder, the greatest effects were from the TL+ and the TL−.
The Mz bending moment that acted on the pile-head as torsion is shown in
Figure 11b. In both the PSC girder and steel-plate girder, the loads LL, TL+, and TL− were respectively applied. The longitudinal displacement of the pile-head (DX) is shown in
Figure 11c. In the same way that the My bending moment is shown in
Figure 11a, the TL+, TL−, SH, and CR were respectively applied in the PSC girder. In the steel-plate girder, the TL+ and the TL− showed the greatest effects. The pile-head transverse displacement (DY) is shown in
Figure 11d. In the same way that the My bending moment is shown in
Figure 11b, the LL, TL+, and TL− were respectively applied.
Consequently, the time-dependent loads, SH, and CR were applied in the PSC girder. The My bending moment and the DX of the pile-head, and the Mz bending moment and the DY that were applied as torsion, produced equal individual-load effects.
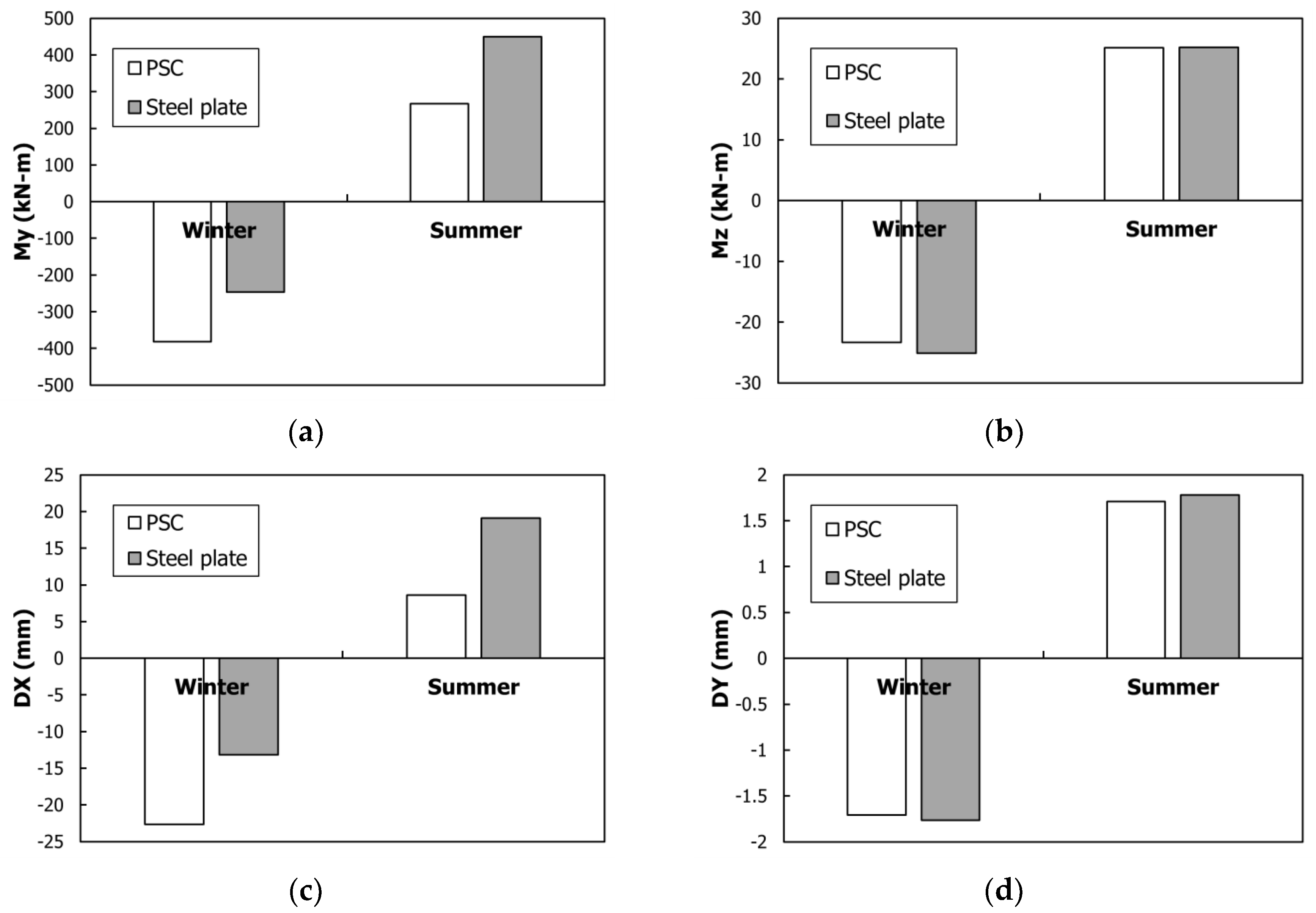
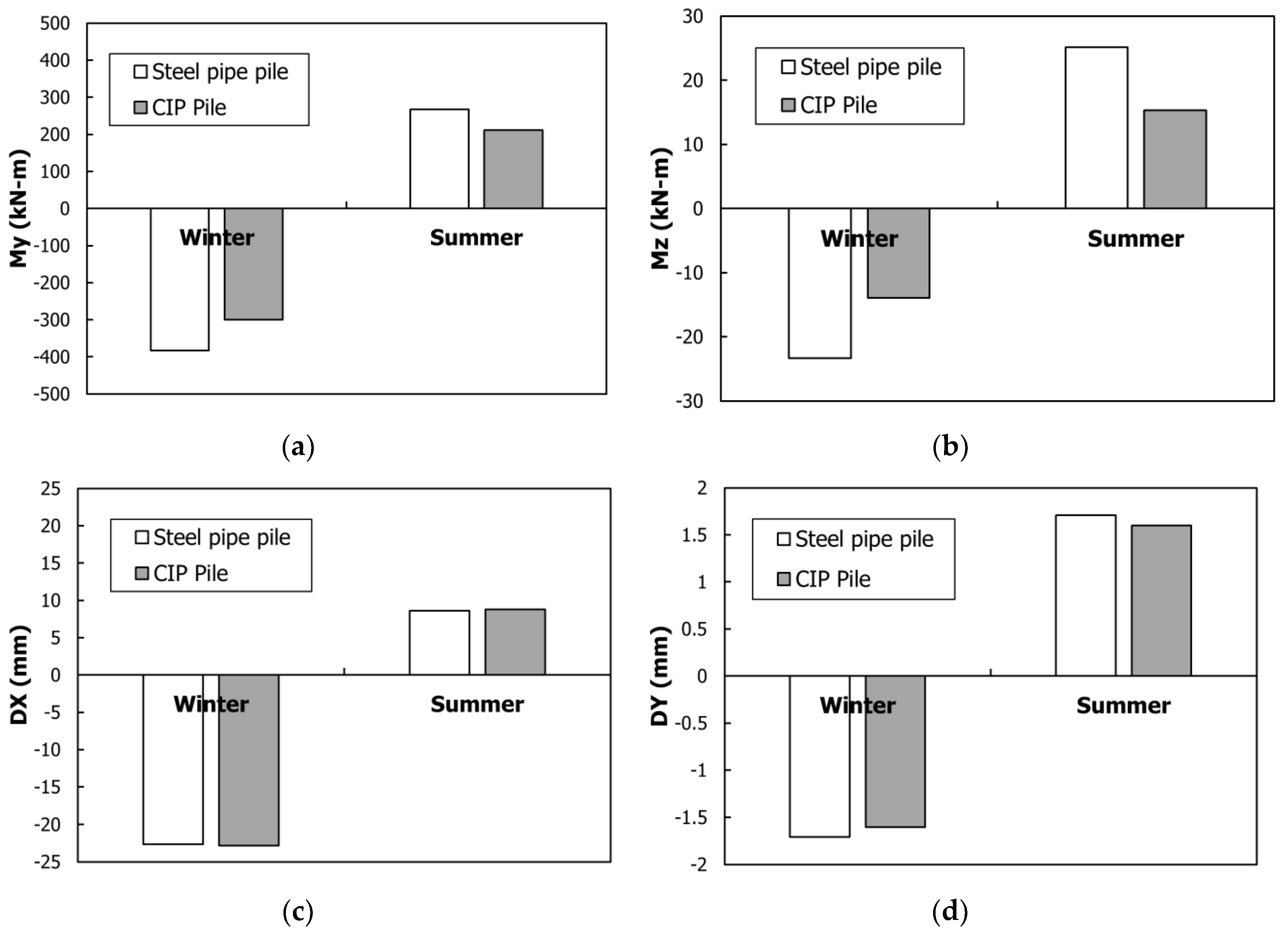
The effect of the combined load per super-structure type on the pile-head is shown in
Figure 12. As suggested by AASHTO [
50], the individual loads in
Figure 11 make up the combined load of 1.3 DL + 2.15 LL + 1.3 TL + 1.3 SH + 1.3 CR. At this point, TL was classified either as TL+ or TL−. Therefore, the summer case involved a TL+ combination, whereas the winter case involved a TL− combination. The purpose of the consideration of the seasonal behavior of the IPM bridge is that contraction and expansion occur according to individual loads, as described in
Figure 11, and when the individual loads are combined, the combination actually acts on the IPM bridge.
Figure 12a shows the My bending load that was applied to the pile-head. A major application of the PSC girder was in the winter case, whereas a major application of the steel-plate girder was in the summer case. The reason for the major application of the PSC girder in the winter case is described in
Figure 11a, wherein the effects on the SH and the TL− are evident. In contrast, the expansion that decreased in the PSC girder in the summer case is due to a combination of the TL+ and SH. Accordingly, for the steel-plate girder in the summer case, a smaller My occurred. The effect of the individual loads shown in
Figure 11 is the same as the behavior of DX and is almost the same as that of My.
The Mz that acted on the pile-head as torsion is shown in
Figure 12b. The Mz of the steel-plate girder is greater than that of the PSC girder in the winter case, whereas both are almost the same in the summer case. As described in
Figure 11a, the My of the PSC girder is greatly influenced by the time-dependent loads, whereas Mz is hardly influenced by the time-dependent loads. Accordingly, the application of Mz as torsion in the winter case is significantly advantageous for the steel-plate girder with a relatively large
. The effect of the individual loads, shown in
Figure 11, is the same as the DY behavior and almost the same as that of the My behavior.
According to Park and Nam [
2], TL+ and TL− as well as the time-dependent loads, SH, and CR, increase as the bridge length increases. Therefore, an applicable bridge-length limit applies not only for the IPM bridge but also for the IAB, as listed in
Table 8. Based on the maximum span limits listed, the length limit of the concrete-bridge with a thermal expansion is longer than the limit of the steel-girder bridge. However, in view of the review of the combined load effects of the IPM bridge based on the super-structure type, the contraction-based deformation in the PSC bridge, which is influenced by the time-dependent loads, drying shrinkage, and CR, compared with that in the steel-plate girder, is greater, resulting in a greater pile-head My bending moment. In particular, owing to the major TL and SH effects, the magnitude of the My bending moment on the pile-head that was imposed by the super-structural contraction of the PSC girder is greater than that in the steel-plate girder. Therefore, the IAB and IPM bridge extensions need to be rechecked in the review of the drying shrinkage and CR effects, based on
Table 8.
4.2. Effect of the Pile-Head by the Pile Type and Diameter
4.2.1. Effect of the Pile Type
In this section, the bending moment and the displacement of the pile-head according to the pile type is reviewed, where the PSC girder representing the time-dependent behavior is set as the super-structure.
The individual load effect by pile type is shown in
Figure 13. The moments, My in
Figure 12a and Mz, applied as torsion in
Figure 13b, are large in the steel-pipe pile. However, the DX in
Figure 13c and the DY in
Figure 13d are nearly the same in the steel-pipe pile and the CIP concrete pile. Thus, a difference in the individual load effect by pile type is nonexistent, in contrast with the effect of the type of super-structure. This is because the IPM bridge sub-structure is controlled by the super-structural characteristics, as described in
Figure 2 [
31].
The combined load effects according to the super-structure type were reviewed as described in
Figure 14. As suggested by AASHTO [
50], the combined load of 1.3 DL + 2.15 LL + 1.3 TL + 1.3 SH + 1.3 CR was obtained using the individual loads, as shown in
Figure 13. Under this combined load, the bending moment was large in the steel-pipe pile, whereas the displacements were almost the same in the steel-pipe and CIP concrete piles. The bending-stiffness (EI) values listed in
Table 3 are
for the 508 mm diameter steel-pipe pile and
for the 500 mm diameter CIP concrete pile. Therefore, the bending moment of the steel-pipe pile with the relatively greater EI was calculated to be large.
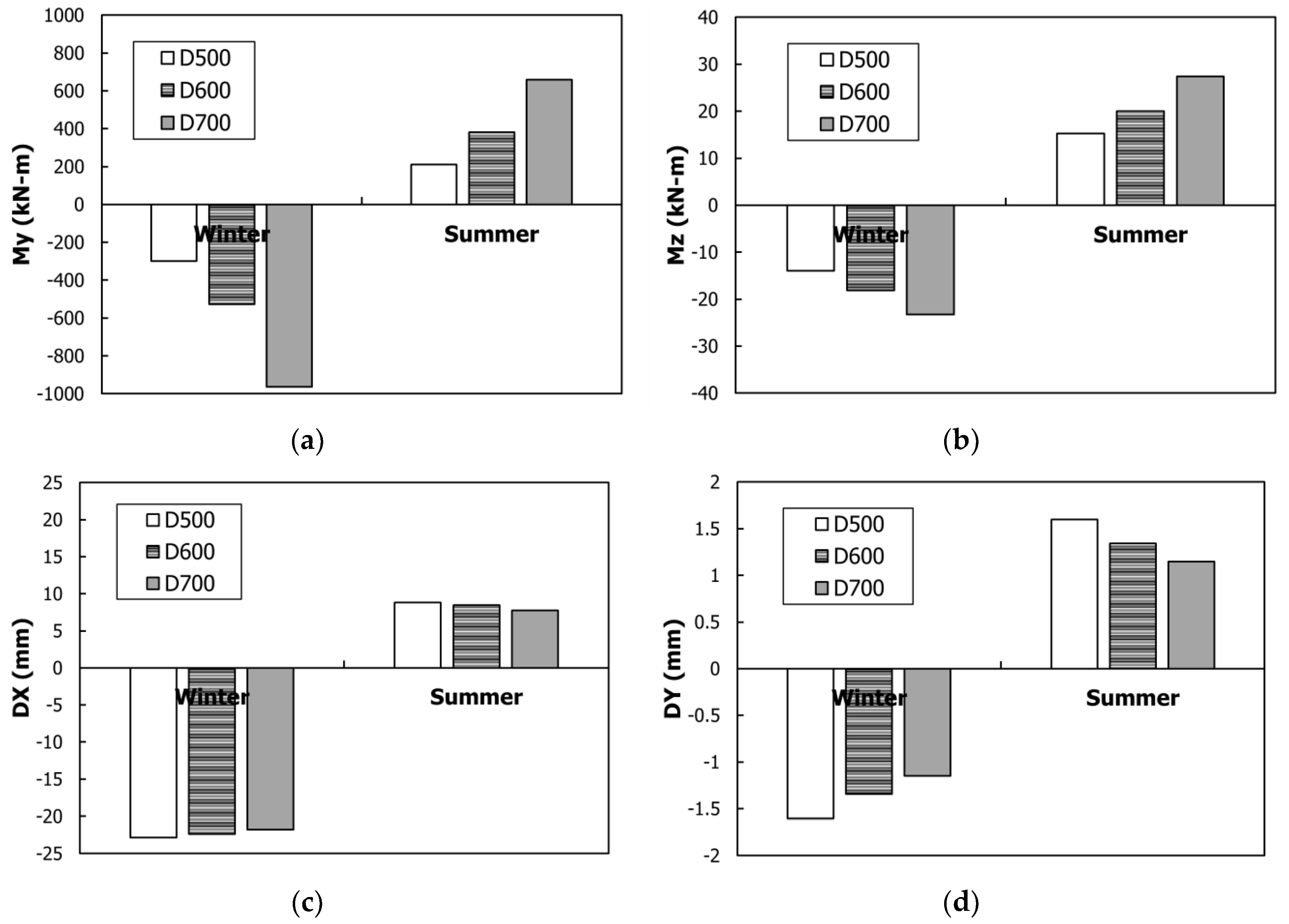
4.2.2. Effect According to the Pile Diameter
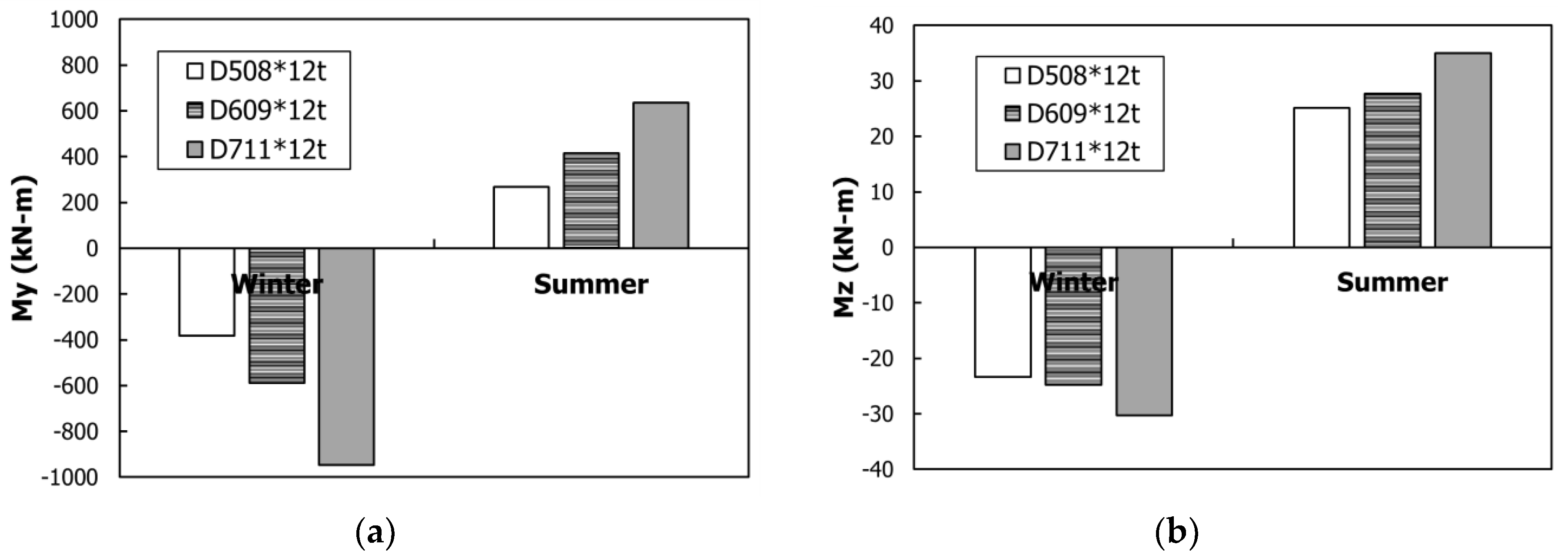
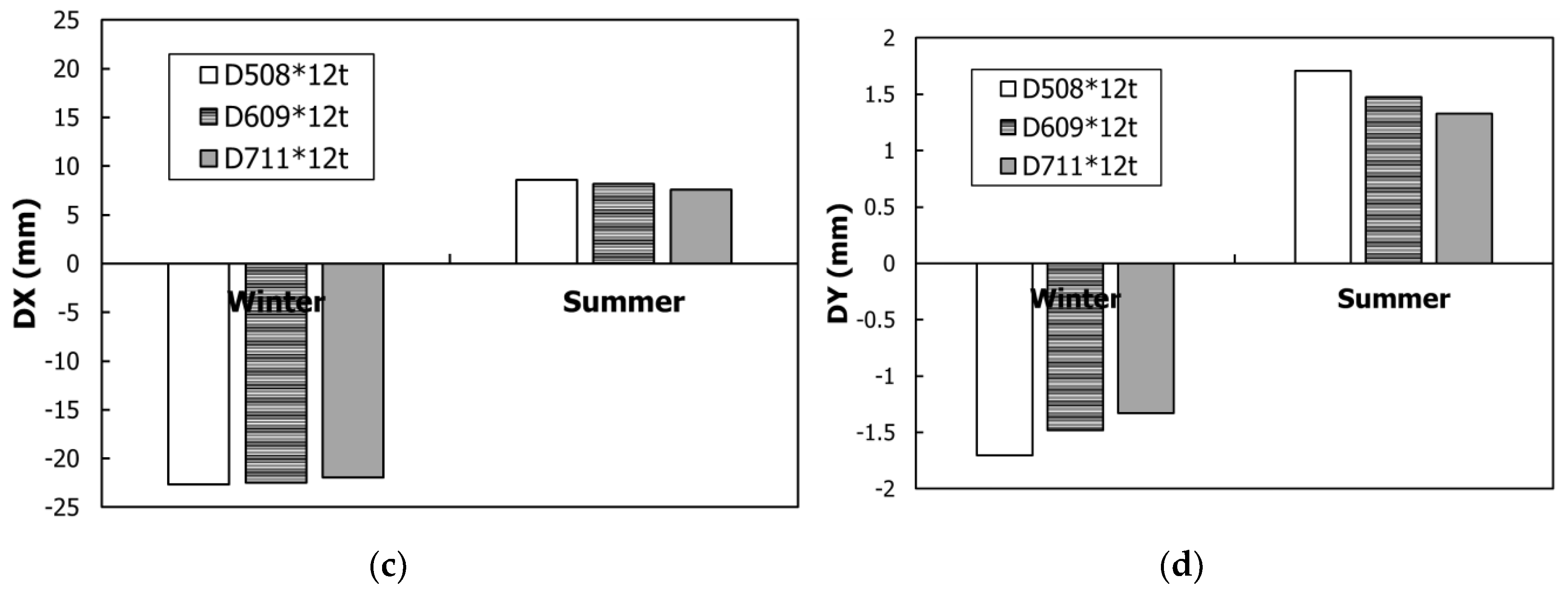
In this section, a review of the combined load effect according to the diameter of the steel-pipe and CIP concrete piles is presented. The analysis was conducted in three steps with a 100 mm increase in the pile diameter per step, starting at 508 mm for the steel-pipe pile and 500 mm for the CIP pile. The bridge super-structure was the PSC girder. The combined load effects according to the diameter of the steel-pipe pile and CIP concrete pile are shown in
Figure 15 and
Figure 16, respectively. For both pile types, as the diameter of the pile-head was increased, its EI increased, whereas the displacement decreased. This phenomenon occurred because the super-structural lateral displacement was resisted by the EI of the pile-head.
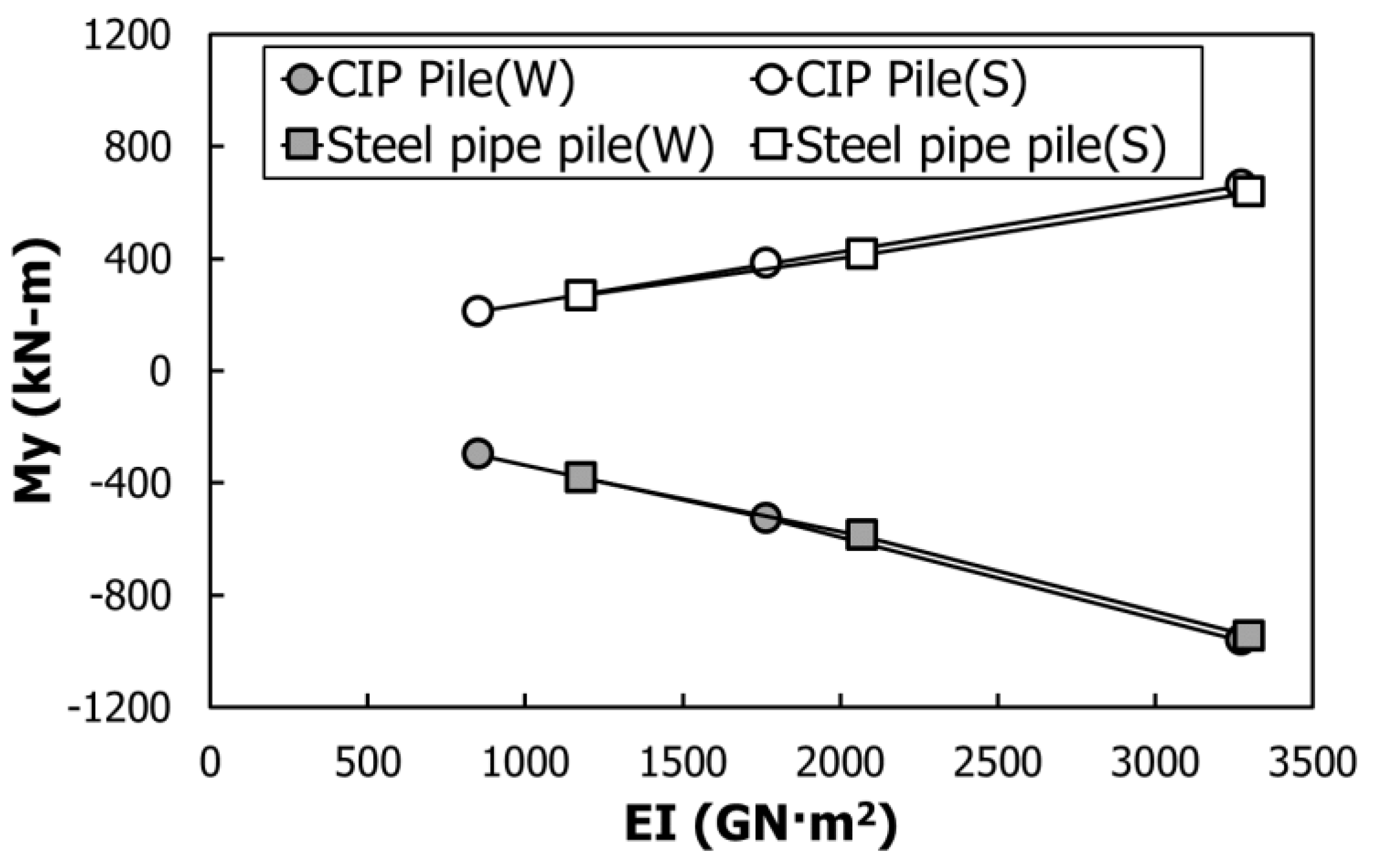
The change in the pile-head bending moment according to the bending rigidity of the steel pile and CIP pile is shown in
Figure 17. In this figure, W and S refer to the winter case and the summer case, respectively. Flexural stiffness and allowable bending moments of piles are the main design factors when designing the pile of IPM bridge. The bending moment increased linearly as the bending rigidity increased, regardless of the pile material. Owing to the design of the IPM bridge, the structural analysis yielded a linear increase in the bending moment. Consequently, the bending moment occurred in the pile according to the bending rigidity, regardless of the material type, which is different from that in the super-structure. The IPM Bridge Design Guidelines [
41] recommend using steel pipe piles because of their flexibility. Since steel pipes increase the flexural stiffness based on the diameter, the optimum pile should be selected through the p-y analysis, as shown in the IPM Bridge Design Guidelines [
41].
4.3. Pile-Bent Behavior According to the Characteristics of the Super- and Sub-Structures
This section reviews the pile-bent behavior according to the super- and sub-structural characteristics. In the IPM bridge, the super-structure is integrated with the sub-structure, and expansion and contraction can occur in the super-structure due to seasonal temperature variations. If the individual loads are combined, the IPM bridge appears to show different summer and winter behaviors [
2]. To identify the pile-bent behavior versus the seasonal behavior of the IPM bridge, the contraction and expansion behavior of the pile-bent was calculated according to the summer TL+ and the winter TL−. As suggested by AASHTO (2002), 1.3 DL + 2.15 LL + 1.3 TU + 1.3 SH + 1.3 CR was used as the load combination.
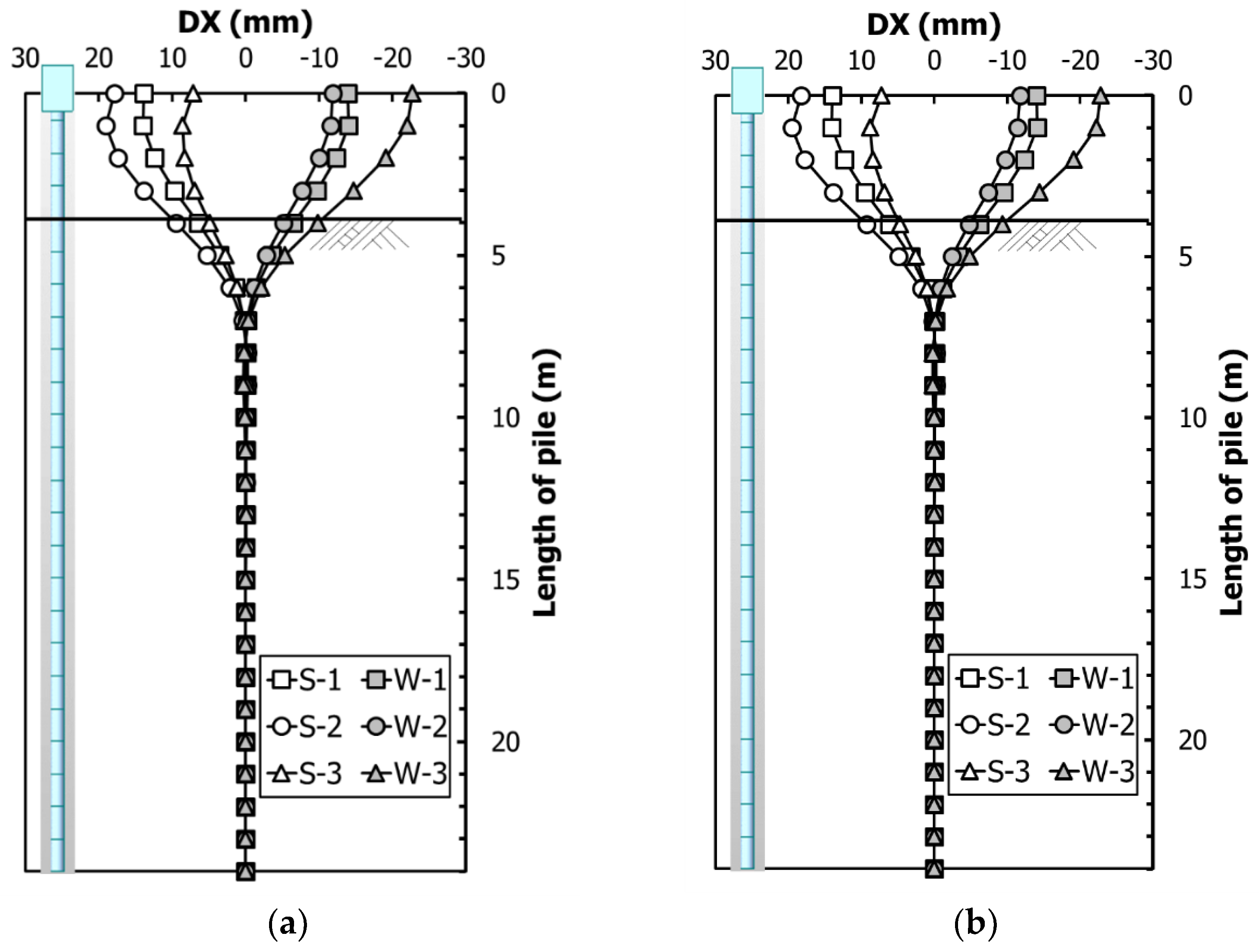
The longitudinal-displacement behavior versus the seasonal thermal load according to the pile type that supports the PSC girder is shown in
Figure 18. In
Figure 14, S−1 and W−1 indicate the TL+ and the TL−, respectively; S−2 and W−2 are combinations of the TL, DL, and LL, and S−3 and W−3 add the time-dependent loads, such as the drying SH and the CR. The temperature was set as −15 °C for winter and +35 °C for summer, with a temperature change that is based on an installation temperature of 10 °C so that it remains within ±25 °C.
The seasonal behavior of the steel pile in the PSC girder is shown in
Figure 18a. The figure also cites the results that were suggested by Park and Nam [
2]. According to Park and Nam [
2], the DX of the pile-bent in the cases of S−1 and W−1 is ±13.92 mm, and showed symmetry in the drying SH and expansion behaviors. When the DL and the LL were applied, girder deflection and abutment rotation occurred, and DX showed an increase toward the back of the abutment. In S−2, the summer TL+ showed a displacement of +17.93 mm, whereas in W−2, the winter TL− showed a displacement of −11.89 mm. The DX value that is shown in
Figure 18b is almost the same as the value that was identified from the seasonal behavior comparison between the CIP pile and the steel pile, shown in
Figure 14c.
The DX behavior versus the seasonal thermal load according to the pile type that supports the steel-plate girder is shown in
Figure 19. Comparing the results between the PSC girder shown in
Figure 18a, and the steel-plate girder shown in
Figure 19a, where both girders are being supported by the same steel pile, it is seen that expansion is greater than contraction in the steel-plate girder without the time-dependent loads (S−3 and W−3). This result is the same as that of the super-structure-type effect shown in
Figure 12. In the comparison between the seasonal behaviors of the steel pile in
Figure 19a and the CIP pile in
Figure 19b, where both piles supporting the steel-plate bridge, a behavioral difference is not evident. This is the same as the PSC girder results shown in
Figure 18.
6. Conclusions
The IPM bridge was developed to overcome problems of general integral abutment bridges by separating earth pressure from the abutment. Also, the IPM bridge removes expansion joints and bearings by integrating the super-structure and the abutment and does not need many piles because it separates the earth pressure from backfills. Therefore, it is superior in cost, durability and maintainability to traditional bridges and is sustainable due to using less material.
As for the pile diameter effect on the IPM bridge, the bending moment increased whereas the displacement decreased as the pile diameter was increased. This is because the super-structural lateral displacement was resisted by the bending rigidity of the pile-bent, which increased due to the increase in pile diameter. Moreover, the bending moment increased linearly as the bending rigidity increased, regardless of the pile material. The linear increase in the bending moment is due to the design of the IPM bridge to behave as such within the elastic region.
In the IPM bridge, the bending moments (My) of the PSC girder and the steel-plate girder were governed by the occurrence of the time-dependent loads. In particular, seasonal behavior occurred according to thermal load combinations in addition to the large effect of the time-dependent loads.
The contraction behavior in the PSC girder is large owing to the time-dependent loads, whereas the expansion behavior in the steel-plate girder is large owing to the greater thermal expansion coefficient and temperature range, as compared with those of the PSC girder. In general, the suggested bridge length limits using PSC girders in both the IAB and the IPM bridge are larger than that for the steel bridge, which needs to be reviewed again with consideration of the long-term and seasonal behaviors.
In the IPM bridge, the sub-structural behavior was controlled by the super-structural characteristics. Moreover, the bending moment occurred according to the bending rigidity, regardless of the pile type. As the sub-structure behavior is controlled by the super-structure and the IPM bridge abutment rotation, a more detailed study on this relationship needs to be conducted in the future.