Abstract
Exposed to aggressive environments, the rebar in reinforced concrete (RC) bridges will be corroded gradually. Durability of RC material mostly depends on the rebar corrosion behavior. In this research, influences of crack on rebar corrosion were investigated. Firstly, RC specimens with different crack number, width and spacing were prepared and the rebar corrosion was conducted through an accelerated chloride penetration method. Then, corrosion current densities of rebar were calculated from electrochemical test methods including liner polarization (LP), Tafel potentiodynamic polarization (TPP) and electrochemical impedance spectroscopy (EIS) measurements. Finally, the discussion was presented about a more reasonable electrochemical testing method for rebar corrosion in RC material. Besides, the significant influence factor among crack width, number and spacing was evaluated based on both One-way analysis of variance (One-way ANOVA) and Turkey’s honest significant difference (Turkey’s HSD) test. The results revealed that a more reasonable way to obtain corrosion current densities of rebar is combining EIS measurement with TPP measurement. Crack number shows the most significant effect on corrosion behavior of rebar, while crack spacing possesses the least one.
1. Introduction
Reinforced concrete (RC) is one of the most widely used materials for bridge structures. The deteriorated durability of RC structures causes structural safety problems and expensive maintenance costs. Besides, in the process of bridge reinforcement, environmental problems including noise pollution, dust pollution and consumption of natural resources will occur. Meanwhile, the corrosion of rebar in concrete is crucial to the durability of RC structures, especially in chloride aggressive environments [1,2]. Rebar in concrete are not prone to corrosion within a short time in sound concrete due to the high and stable alkalinity of concrete pore solution. However, cracks will be formed due to material shrinkage, thermal gradients and repeated mechanical loading causing a higher osmotic pressure, which often leads to a higher chloride diffusion coefficient in concrete [3,4]. Besides, cracks provide a convenient channel for water ingression, harmful ions and oxygen towards the internal concrete and the surface of rebar, which could result in accelerating corrosion of rebar. Therefore, it is necessary to investigate corrosion behavior of rebar under the effect of crack in chloride aggressive environment [5,6,7,8].
A large number of laboratorial studies have been conducted focusing on durability of concrete and rebar corrosion under the actions of chloride penetration and crack. Wang et al. [9] introduced feedback controlled splitting tests to generate crack width-controlled concrete specimens and studied the relationship between crack characteristics and concrete permeability. Ye et al. [10] established a model of chloride penetration into cracked concrete subject to drying-wetting cycles based on Fick’s second law. Marsavina et al. [11] made artificial cracks on concrete specimens by a thin copper to perform a concrete chloride penetration test. They demonstrated that the chloride diffusivity in cracked concrete is much stronger than sound concrete. Du et al. [12] and Liu et al. [13] simulated chloride diffusivity in cracked concrete using multi-component ionic transport models and found that the geometry of crack affects chloride transport. Papakonstantinou and Shinozuka [14] established a probabilistic model for rebar corrosion in reinforced concrete structures of large dimensions considering crack effects to simulate the complex phenomena involved in a detailed and simple way, appropriate for implementation on large-scale, real structures. Cao et al. [15] found that oxygen is a crucial factor influencing rebar corrosion propagation process during the full RC structures’ service life. Zhu et al. [16] investigated the influence of load-induced cracking behavior on the process of chloride penetration into concrete. Pacheco et al. [17] analyzed bending cracks in RC samples by measuring the electrical resistance across the crack and illustrated that cracks in concrete represent fast routes for chloride penetration, which can result in rebar corrosion. Besides, Šavija and Schlangen [18] claimed that chloride induced corrosion of rebar is one of the most important mechanisms causing deterioration of RC structures and the requirements for their premature repair or replacement. Pedrosa and Andrade [19] indicated that rebar corrosion causes several damage types that influence the structure service life. They analyzed the effect of a range of distinct corrosion rates on the crack growth rate, and they established an empirical model to describe the relation between crack width and the corrosion rate applied for the first stage of cracking. Based on the existed researches, there are different types of cracks caused by temperature, loading and rebar corrosion deteriorating the durability of RC structures, and each crack type has its own distribution inside concrete cover. Thus, performing a laboratorial study on comprehensive effects of crack parameters (such as crack number, width and spacing) on corrosion behavior of rebar could better illustrate the effect of crack on the durability of RC structures.
Nowadays, electrochemical measurements are popular to analyze the corrosion behavior of rebar. The reason is that rebar corrosion is an electrochemical process. An oxidation reaction occurs (Fe → Fe2+ + 2e−) at the anodic area of rebar. The electrons given by anodic area are consumed at the cathodic area (O2 + 2H2O + 4e− → 4OH−). Pore solution as a conducting medium for the transportation of electrons and ions ensure the corrosion process to proceed [20]. The electrochemical nature of corrosion means that electrochemical techniques can be used to monitor the corrosion behavior such as corrosion rate or corrosion current density of rebar in concrete. The commonly used electrochemical techniques include liner polarization (LP), Tafel potentiodynamic polarization (TPP) and electrochemical impedance spectroscopy (EIS) measurements [21]. These techniques are widely used in the studies of carbon steel and alloy steel corrosion [22]. There are a large volume of published researches describing the corrosion behavior of rebar by immersing them into chloride solution [23] or cement extract solution [24,25]. Meanwhile, some researches focus on the corrosion behavior of rebar in real concrete material. Andrade et al. [26] analyzed influence of environmental factors and cement chemistry on corrosion behavior of rebars in concrete by using EIS measurement, and they indicated that redox activity caused by harmful ions in the rebar’s oxides layer greatly influences the electrochemical behavior of rebars in the passivity potential domain. In addition, Andrade et al. [27] indicated that different geometrical dispositions of the electrodes used in EIS measurement may affect the test results much. Wang et al. [21] analyzed corrosion rate of rebar in concrete under cyclic freeze-thaw and chloride salt action using LP and TPP measurements. They illustrated that TPP measurement is rapid and easy to operate, read corrosion current directly and provides sufficiently accurate results. Gerengi et al. [28] used EIS measurements to investigate corrosion behavior of rebar in reinforced concrete exposed to sulphuric acid, and they claimed that EIS measurement is one of the most widely used techniques in recent years. Andrade and Alonso [29] applied a non-destructive electrochemical test method for the estimation in large size concrete structures of the instantaneous corrosion current density and discussed the accuracy and applicability of this measurement used in real RC material. In summary, most of the literatures applied one of the electrochemical measurements. However, combining multiple electrochemical measurements may show a more accurate way to undertake the study on rebar corrosion.
In this paper, corrosion current density (icorr) of rebar was treated as the index for estimating the effect of crack on durability of RC material. Firstly, icorr values of rebar were tested by TPP, LP and EIS measurements. Subsequently, a more reasonable electrochemical testing method was recommended for rebar in RC material. Finally, the effect of crack width, number and spacing on durability of RC material was analyzed by statistical analysis methods.
2. Materials and Methods
2.1. Materials and Mixture
Q235 rebars (equivalent to SS400 and A36, i.e., yield strength is 235 MPa) with diameter 7 mm were cut into 110 mm long. Rebars were polished with 340# to 2000# grit silicon carbide emery paper in order to remove the passivation layers and guarantee no pit corrosion on their surfaces. Subsequently, according to a national standard [30], ethanol and acetone treatments were used to degrease surfaces of rebar, so the electrochemical properties of each rebar were sensitive to the effect of chloride ions. One end of each rebar was welded to a copper wire.
PO 42.5 type ordinary Portland cement was used in this study conforming to the requirements of the national standard [31]. Crushed stones with diameters ranging from 2.36 mm to 20.00 mm and natural sands with fineness modulus of 2.7 were adopted as coarse and fine aggregates, respectively. The mixture proportions of concrete used in this study are listed in Table 1. Slump of the mixture was tested to be 40 mm, which means the concrete mixture has favorable cohesiveness and meets well with the requirement of the national standard [32].

Table 1.
Mixture proportions of concrete.
2.2. Specimen Preparation
RC samples used in this study were composed of concrete (cracked or sound) and rebar. Samples were made with artificial cracks by means of positing and removal of required thin copper sheets with different number, width and spacing inside samples. Figure 1 shows the dimensions of the specimen and relative position among concrete, crack and rebar. The length of each crack is 60 mm and the depth is 19 mm. The length direction of each crack is perpendicular to the length direction of rebar. The combinations of crack width, number and spacing in samples are given in Table 2.
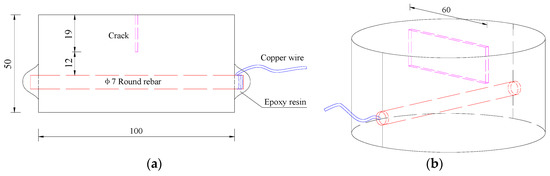
Figure 1.
Specimen dimension and rebar arrangement: (a) Front view of the sample; (b) Stereoscopic view of the sample.

Table 2.
Design of specimens.
Cylinders of φ100 mm × 50 mm were casted in plastic modules and compacted by vibrating table. They were allowed to cure at the condition of 20 °C and 95% relative humidity. Copper sheets were removed from specimens after a 4-h curing period. Specimens were removed from moulds after a 24-h curing period. Besides, the weld and exposed parts of rebar must be covered with a layer of epoxy resin to protect rebar from corrosion during the curing time. After that, all specimens were cured under the normal curing condition (20 °C and 95% relative humidity) for 28 days before further experiments.
2.3. Experimental Methods
2.3.1. Scheme Design
After curing, in order to investigate the influence of crack on corrosion behavior of rebar in concrete, an experimental procedure was determined and shown in Figure 2. Firstly, RC samples must be vacuum-saturated by vacuum water saturation instrument to guarantee they were well conductive. Secondly, electrochemical properties of rebar in concrete were tested by LP, TPP and EIS measurements. Subsequently, the accelerated chloride penetration experiment was conducted for 96 h so that chloride ions can rapidly penetrate into concrete along with the depth direction of crack and corrode the rebar. Then, the vacuum-saturated treatment will be conducted in a second time before testing electrochemical properties of rebar again. Finally, electrochemical test measurements were performed again to obtain electrochemical properties of rebar after the accelerated chloride penetration experiment. The rationality of electrochemical test procedure and test times will be discussed in the Section 2.3.4.
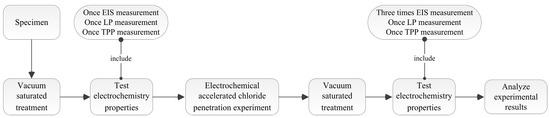
Figure 2.
Experimental procedure.
2.3.2. Vacuum-Saturated Treatment
According to a national standard [30], the vacuum-saturated treatment must be performed before the accelerated chloride penetration experiment in order to ensure chloride ions could penetrate into concrete steadily. Also, it is necessary before testing electrochemical properties of rebar to guarantee RC samples were conductive. The vacuum-saturated procedure consisted of conditioning RC samples into a vacuum desiccator and applying a vacuum pressure of 5 kPa for 3 h. Subsequently, the desiccator was filled with deionized water until all samples were immersed, and the pressure was maintained for another one hour. Finally, samples were continuously immersed for 18 h without vacuum pressure.
2.3.3. Accelerated Chloride Penetration Experiment
In general, it will take a long time to observe the corrosion of rebar due to the slow corrosion process of chloride ions by immersing RC samples into chloride solution. However, the accelerated chloride penetration experiment used in this study showed a more effective way to accelerate the corrosion process of rebar affected by chloride ions, which could simulate the natural aggressive environment well. The experimental setup is displayed in Figure 3. Each specimen was placed between two acrylic cells defined as cathode cell and anode cell. The volume of each cell is 270 cm3. Cathode cell was filled with 3.5 wt % NaCl solution, and anode cell was filled with 0.3 mol/L NaOH solution. Two stainless steel-based plates as cathode electrode and anode electrode were placed into these two cells. The cracked surface of specimen was placed into the cathode cell, and the other side was placed into the anode cell. Then, these two cells were connected to a DC regulated power supply, and the applied voltage was 20.0 V. This designed accelerated chloride penetration system was electrified for 96 h.

Figure 3.
Experimental setup for accelerated chloride penetration.
2.3.4. Corrosion Density Test for Bar Based on Electrochemical Measurements
Nowadays, electrochemical measurements including TPP, LP and EIS measurements are popularly used in the studies of steel corrosion under different conditions. These three measurements were employed in this study to evaluate the electrochemical properties of rebar under an accelerated chloride penetration. Corrosion current density (icorr) is used as the index to evaluate the corrosion behavior of rebar.
The electrochemical measurements were carried out by CS350H electrochemical workstation in this study based on the three-electrode system shown in Figure 4. In this system, the rebar embedded in concrete was treated as the working electrode (WE) with a polarization area of 21.98 cm2, a saturated calomel electrode (SCE) with potassium chloride salt bridge placed in a Luggin capillary was used as the referenced electrode (RE) and a stainless steel-based plate with 2 mm × 100 mm × 150 mm was used as the counter electrode (CE).

Figure 4.
Experimental setup for electrochemical measurements (a three-electrode system).
Corrosion density is used to evaluate the corrosion behavior of rebar, and it can be obtained from TPP measurement directly or calculated by Stern-Geary equation
where icorr is the corrosion density (μA/cm2); B is the Stern-Geary coefficient (mV/Decade); Rp is polarization resistance (Ω·cm2). The value of B can be calculated from TPP measurement or estimated to fall within the range from 25 mV to 52 mV. Song [33] demonstrated the estimated range value of B is applicable only in a uniform corrosion system at its corrosion potential, whereas the RC structure may be subjected to a non-uniform corrosion. The typical value (25 mV~52 mV) of B is not acceptable in a RC corrosion system. Therefore, the value of B should be calculated from TPP curves more accurately. Meanwhile, Rp can be obtained from LP and EIS measurements. The details of these three measurements are as follows.
TPP measurement is an electrochemical test method to characterize corrosion properties of metal materials based on the three-electrode system. TPP curves can be obtained by monitoring the potential used steady fixed levels of current at specific potential. In TPP curves, the current density I (A/cm2) and polarization potential E (V) under potentiodynamic polarization of rebar always conform to the Butler–Volmer equation:
where Ecorr is the corrosion potential (V vs. SCE), respectively. ba and bc are the anodic Tafel slope and cathodic Tafel slope, respectively (mV/Decade). Values of these electrochemical parameters can be obtained by a curve-fitting approach named Tafel extrapolation method. Schematic illustration parameters in TPP curve are shown in Figure 5.
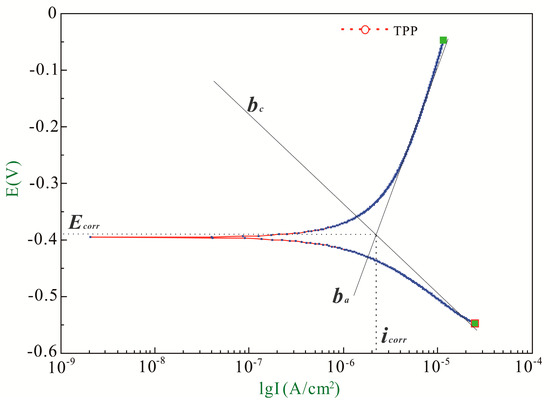
Figure 5.
Schematic illustration of the Tafel potentiodynamic polarization (TPP) curve with Tafel electrode slopes.
The Stern–Geary coefficient B related to ba and bc can be calculated by
After obtaining a stable open circuit potential (OCP), TPP measurement could be carried out from −250 mV to 250 mV vs. OCP, the scanning rate of which is 1 mV/s.
Besides, LP measurement is another electrochemical method to obtain resistances of metal materials accurately. Polarization curves in LP measurement can be obtained as the same method in TPP measurement. As shown in Figure 6, the value of Rp is defined as the slope of potential to current density, can be obtained as follows:
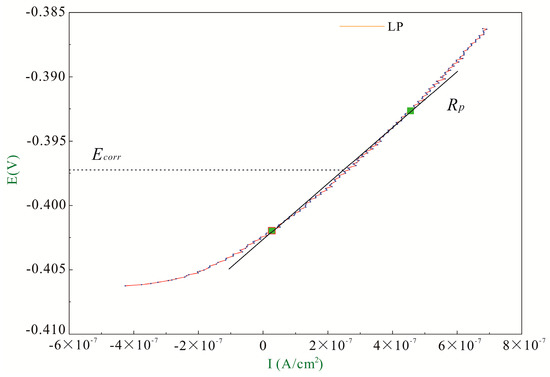
Figure 6.
Schematic illustration of polarization resistance.
In this study, LP measurements were carried out from −10 mV to 10 mV vs. OCP with the scanning rate of 0.167 mV/s.
In addition, EIS measurement based on alternating currents (AC) used to analyze corrosion mechanisms of steel has been well documented for many years [34]. Applied AC amplitude signal was equal to 10 mV over the frequency range from 0.01 Hz to 100,000 Hz. To better understand the electrochemical phenomena, an equivalent circuit was used to simulate the electrochemical behavior of rebar. The equivalent circuit is illustrated in Figure 7, which shows the solution resistance (Rp1), concrete resistance (Rp2), polarization resistance of rebar (Rp3), external concrete capacitance (CPE1) and double layer capacitance on the surface of rebar (CPE2).
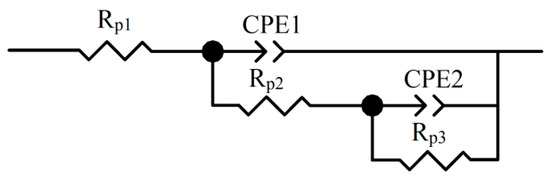
Figure 7.
Equivalent circuit for reinforced concrete (RC) samples.
The immittance Z (Ω·cm2) of this equivalent circuit is given by
in which,
where Tn and pn are parameters of CPE (μF·cm2); ω is the frequency of applied AC (Hz); j = . The obtained impedance data could be analyzed by Z view program to fit with the immittance equation of this equivalent circuit.
The voltage applied in EIS measurements is much smaller than those of LP and TPP measurements, which means EIS measurements display a smaller disturbance and better reproducibility of electrochemical systems than the others [35]. Therefore, EIS measurements can be performed continuously, while the others cannot because the error in a continuous test procedure can be very large. The disturbances of these three measurements are ranked from small to large: EIS measurements, LP measurements, TPP measurements. Therefore, the test sequence should be the same as the disturbance. Besides, EIS, LP and TPP measurements should be conducted only once on each specimen before an accelerated chloride penetration experiment. Because the electrochemical property of each rebar in concrete is very stable after 28-day curing, and the test results are treated as unique initial values to evaluate the differences of corrosion behavior of rebar. Furthermore, EIS, LP and TPP measurements should be conducted three times, one time and one time, respectively, after accelerated chloride penetration experiments in order to obtain more statistical random sampling test results and quantitatively analyze the effects of crack on electrochemical properties of rebar.
2.4. Statistical Analysis Methods
After obtaining icorr of rebar, One-way analysis of variance (ANOVA) combined with Turkey’s honest significant difference (Turkey’s HSD) test was performed to analyze the effect of crack on rebar corrosion and determine the most significant factor that influences durability of RC material. One-way ANOVA was used in this study to determine whether crack width, number or spacing is the most significant factor, and Turkey’s HSD test was performed for further judging the accuracy of the One-way ANOVA results. The details of these two methods are as follows:
2.4.1. One-Way ANOVA
The most commonly used statistical method to analyze the contribution of each level in one factor of experimental results is One-way ANOVA and F-tests method, which can take advantage of sums of squares to separate the overall variance in the response into variances caused by measurement error and processing parameters [36].
In One-way ANOVA, the sum of square SST can be calculated by
where m, n are the number of levels in each factor and the number of experimental results in each level, respectively. yij is the jth experimental result of level i. N is the number of all experimental results, which is equal to m × n.
The level square of deviance SSi can be calculated by
The error square of deviance SSe can be obtained by
The estimate of variance is given by
where MSi and MSe are the estimate of variance for level i and error, respectively. and are corresponding degrees of freedom, which can be obtained by
F-value is given by
In this method, whether the influence factor is significant or not depends on F-value. The larger F-value is, the higher the influence factor is.
2.4.2. Turkey’s HSD Test
Meanwhile, Turkey’s HSD is a statistical test procedure. It is a post-hoc and single-step multiple comparison procedure, which can be performed combining with analysis of variance method to determine means that are significantly different from each other or not [37,38].
In Turkey’s HSD test, HSD value is the critical value to judge whether the influence of factor is significant or not. HSD critical value can be calculated by
where is studentized range; is significant level; is number of levels in each factor; , and are number of degrees of freedom, estimate of variance of error, number of test results in each level, respectively. In this study, the range values of means between each two levels in specific factor will be calculated and compared with HSDα. If the range value of means is larger than HSDα, the two levels are said to have significant effects on rebar corrosion.
3. Results and Discussion
3.1. Recommendation of Reasonable Electrochemical Test Method
As an example, icorr values of sample B2 calculated from 3 measurements are analyzed to illustrate the reasonable electrochemical test method for rebar in the RC corrosion system.
In TPP measurements, anodic and cathodic potentiodynamic polarization curves for rebar in sample B2 are shown in Figure 8. The curve tested before the chloride penetration is defined as initial curve, while the curve tested after the chloride penetration is defined as final curve.
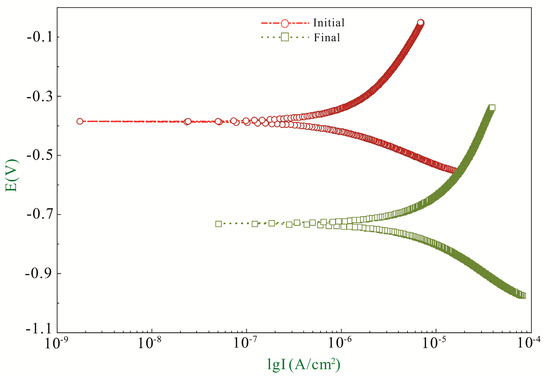
Figure 8.
TPP curves of rebar in sample B2.
The anodic and cathodic curves are extrapolated up to their intersection at a point where corrosion current density and corrosion potential can be obtained, as shown in Figure 5. The anodic Tafel slopes (ba), cathodic Tafel slopes (bc), Stern-Geary coefficient (B), corrosion current density (icorr) and corrosion potential (Ecorr vs. SCE) obtained from TPP curves are listed in Table 3.

Table 3.
Electrochemical parameters from TPP curves of rebar in sample B2.
It can be concluded icorr increases and Ecorr (vs. SCE) decreases under the action of chloride penetration. Meanwhile, both ba and bc increase, which illustrates the anodic and cathodic reactions are all accelerated and affected by the environmental loading.
In LP measurements, the current density can be also calculated by Equation (1). In Equation (1), B is obtained from TPP curves and Rp is calculated from line polarization curves by Equation (4). The calculated Rp and icorr from LP measurements are listed in Table 4.

Table 4.
Electrochemical parameters from liner polarization (LP) curves of rebar in sample B2.
It can be seen that Rp is reduced while icorr increases under the action of chloride penetration, which infers that rebar is continuously corroded.
In addition, the corrosion current density can be also obtained by EIS measurements. Figure 9 depicts the impedance spectra of rebar in sample B2. The curves before and after the chloride penetration experiment are defined as one initial curve and three final curves, respectively. From Figure 9, it can be seen that the radius of the capacitive loop shrinks after the chloride penetration experiment decreases, which indicates the corrosion resistance of rebar is declined. The equivalent circuit is fitted with impedance spectra by Equation (5), and the results are shown in Table 5.
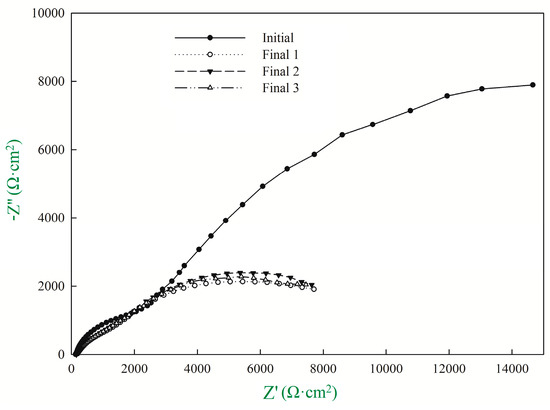
Figure 9.
Impedance spectra of rebar in sample B2.

Table 5.
Fitting parameters from electrochemical impedance spectroscopy (EIS) of rebar in sample B2.
In Table 5, icorr is calculated by Equation (1), where B is obtained from TPP curves, and Rp is equal to Rp3. From Table 5, it can be concluded that the impedance spectra of rebar in sample B2 obtained from three continuous tests is reproducible. Besides, both Rp2 and Rp3 decrease after the chloride penetration, which indicates that material properties of concrete were degraded and the rebar was corroded gradually under the process of chloride penetration.
The corrosion current densities obtained from 3 measurements are compared and shown in Figure 10. It can be seen the corrosion current densities from EIS measurements are larger than those of TPP and LP measurements. The reason is that Rp in TPP and LP measurements contain not only the resistance of rebar but also the resistance of concrete in the test conductive circuit, while Rp from EIS measurements is exactly the resistance of rebar. Thus, Rp from EIS measurements is smaller than those from TPP and LP measurements. According to Equation (1), icorr calculated from EIS measurements is greater than the others. Inductively, the reasonable way to calculate icorr of rebar is EIS measurement combined with TPP measurement, namely, Rp and B should be calculated by EIS measurement and TPP measurement. After that, icorr can be calculated by Stern-Geary equation. In this way, the corrosion behavior of rebar can be judged more accurately compared with only a single measurement.
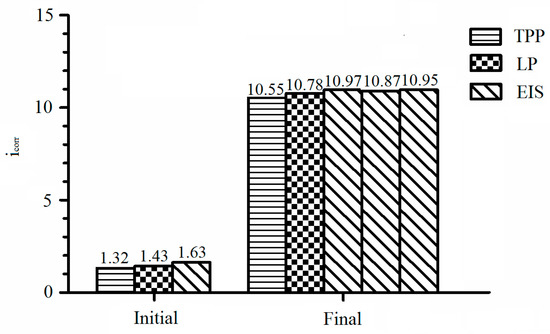
Figure 10.
Comparison of corrosion current densities obtained from 3 measurements.
3.2. The Effect of Crack on Corrosion Behavior of Rebar
icorr of rebar in each specimen could be obtained by the same test method of B2 discussed above. The variation of corrosion current densities is calculated by
where , and are the nth variation of icorr, the nth corrosion current density and initial corrosion current density, respectively. The results are listed in Table 6. The average value for 3 variations of icorr and corresponding standard deviations are also calculated. The results can be used to analyze effects of crack width, number and spacing on corrosion behavior of rebar under the aggressive environment. Comparative evaluations were conducted based on One-way ANOVA and Turkey’s HSD test.

Table 6.
Variation of corrosion current density in each sample.
In One-way ANOVA, corrosion current densities of rebar in sample N, A1, A2 and A3 are used to analyze the effect of crack width on rebar corrosion. One-way ANOVA results for crack width are listed in Table 7.

Table 7.
One-way ANOVA for crack width.
Besides, corrosion current densities of rebar in sample N, A2, B1 and C1 are used to analyze the effect of crack number on rebar corrosion. Results of One-way ANOVA for crack number are listed in Table 8.

Table 8.
One-way ANOVA for crack number.
In addition, corrosion current densities of rebar in sample B1 and B2 are used to analyze the effect of crack spacing on rebar corrosion. Results of One-way ANOVA for crack spacing are listed in Table 9.

Table 9.
One-way ANOVA for crack spacing.
From Table 7, Table 8 and Table 9, it can be concluded that F-values of crack width and crack number are larger than F0.01 (3,8), which means the probability is 99% that crack width and crack number present a significant influence of rebar corrosion. Meanwhile, F-value of crack number is larger than that of crack width, which means the influence of crack number is larger than crack width. Besides, F-value of crack spacing is between F0.1 (1,4) and F0.05 (1,4), which means that the probability is 90% that crack spacing is the significant effect on rebar corrosion.
According to the conclusions discussed above, it is more likely that crack width and crack number are the statistically significant effects of rebar corrosion. However, it doesn’t mean that there is a larger magnitude between these two factors [39]. Therefore, Turkey’s HSD test as a post-hoc multiple comparisons method should be conducted to determine the significant effects of three influence factors on rebar corrosion.
Similar to One-way ANOVA, means of corrosion current densities of rebar in sample N, A1, A2 and A3 are performed Turkey’s HSD test to determine if crack width is the significant effect on rebar corrosion. Results of Turkey’s HSD test are listed in Table 10.

Table 10.
Turkey’s honest significant difference (HSD) test results for crack width.
In Table 10, most range values between each two levels (K0.05–K0 etc.) in crack width factor is larger than HSD0.01, which means the influence between each two levels is significant at 0.01 level. It is also proved that crack width has a statistically significant influence on rebar corrosion.
Besides, means of corrosion current densities of rebar in sample N, A2, B1 and C1 are adopted to perform Turkey’s HSD test to determine if crack number is the significant effect on rebar corrosion. Results are listed in Table 11.

Table 11.
Turkey’s HSD test results for crack number.
In Table 11, all range values between each two levels (K1–K0 etc.) in crack number factor is larger than HSD0.01, which means the influence between each two levels is significant at 0.01 level. It is also proved that crack number has a statistically significant influence on rebar corrosion.
In addition, means of corrosion current densities of rebar in sample B1 and B2 are adopted to perform Turkey’s HSD test to determine if crack spacing is the significant effect on rebar corrosion. Results are listed in Table 12.

Table 12.
Turkey’s HSD test results for crack spacing.
In Table 12, the range value of means between 15 mm spacing level and 25 mm spacing level in crack spacing factor is not significantly different, which can be concluded that crack spacing is not a significant effect on rebar corrosion. Moreover, the results of Turkey’s HSD test reveal that crack width and crack number possess a greater effect on rebar corrosion. In summary, the influence degrees of three factors including crack width, number and spacing on rebar corrosion can be ranked as crack number, crack width and crack spacing from the greatest to the least.
Crack leads to the greater capillarity and osmotic pressure, resulting in a serious corrosion of rebar in the vicinity of cracks. Meanwhile, the larger crack width causes a more oxygen and adverse ion aqueous solution to diffuse into concrete. It is said that rebar corrosion rate maybe depend on total crack width. To some extent, the total crack width would increase with increasing of crack number. Therefore, crack number presents the most significant effect on corrosion of rebar.
4. Conclusions
Electrochemical tests were carried out for evaluating the corrosion behavior of rebar (reflecting the durability of RC material) under the effect of crack. The major work of this study includes the recommendation of the reasonable electrochemical test method for rebar in RC material and quantitative analysis of the effect of crack number, width and spacing on rebar corrosion. The following conclusions were drawn:
- (1)
- Due to the EIS excluding the polarization resistance (Rp) error caused by concrete and Stern-Geary coefficient (B) from TPP reflecting the non-uniform corrosion of rebar in RC material, a more accurate electrochemical test method combining EIS with TPP measurements was recommended for rebar corrosion behavior in RC material.
- (2)
- The influences of crack parameters (i.e., crack width, number and spacing) on durability of RC material were analyzed based on One-way ANOVA and Turkey’s HSD test. Results revealed that crack number presents the most significant effect, while crack spacing possesses the least one. As for wondering that if the influence on rebar corrosion caused by total crack width of multiple cracks is equal to that caused by an individual crack width, this also has become the topic which the authors further deliberated from now on.
Acknowledgments
The authors express their appreciation for the financial supports of National Natural Science Foundation of China (Nos. 51478203, 51408258).
Author Contributions
Yongchun Cheng and Yuwei Zhang designed the experiments and wrote the paper; Yuwei Zhang and Guojin Tan performed the experiments and analyzed the experimental results; Yubo Jiao wrote a part of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kwon, S.J. Current Trends of Durability Design and Government Support in South Korea: Chloride Attack. Sustainability 2017, 9, 417. [Google Scholar] [CrossRef]
- Yang, K.H.; Singh, J.; Lee, B.Y.; Kwon, S.J. Simple technique for tracking chloride penetration in concrete based on the crack shape and width under steady-state conditions. Sustainability 2017, 9, 282. [Google Scholar] [CrossRef]
- Wang, H.L.; Dai, J.G.; Sun, X.Y.; Zhang, X.L. Characteristics of concrete cracks and their influence on chloride penetration. Constr. Build. Mater. 2016, 107, 216–225. [Google Scholar] [CrossRef]
- Ji, Y.; Hu, Y.; Zhang, L. Laboratory studies on influence of transverse cracking on chloride-induced corrosion rate in concrete. Cem. Concr. Compos. 2016, 69, 28–37. [Google Scholar] [CrossRef]
- Zhu, X.; Zi, G.; Cao, Z.; Cheng, X. Combined effect of carbonation and chloride ingress in concrete. Constr. Build. Mater. 2016, 110, 369–380. [Google Scholar] [CrossRef]
- Lambert, P.; Page, C.L.; Vassie, P.R.W. Investigations of reinforcement corrosion. 2. Electrochemical monitoring of steel in chloride-contaminated concrete. Mater. Struct. 1991, 24, 351–358. [Google Scholar] [CrossRef]
- Shaheen, F.; Pradhan, B. Effect of chloride and conjoint chloride–sulfate ions on corrosion of reinforcing steel in electrolytic concrete powder solution (ECPS). Constr. Build. Mater. 2015, 101, 99–112. [Google Scholar] [CrossRef]
- Tennakoon, C.; Shayan, A.; Sanjayan, J.G.; Xu, A. Chloride ingress and steel corrosion in geopolymer concrete based on long term tests. Mater. Des. 2017, 116, 287–299. [Google Scholar] [CrossRef]
- Wang, K.; Jansen, D.C.; Shah, S.P.; Karr, A.F. Permeability study of cracked concrete. Cem. Concr. Res. 1997, 27, 381–393. [Google Scholar] [CrossRef]
- Ye, H.; Jin, N.; Jin, X.; Fu, C. Model of chloride penetration into cracked concrete subject to drying–wetting cycles. Constr. Build. Mater. 2012, 36, 259–269. [Google Scholar] [CrossRef]
- Marsavina, L.; Audenaert, K.; Schutter, G.D.; Faur, N.; Marsavina, D. Experimental and numerical determination of the chloride penetration in cracked concrete. Constr. Build. Mater. 2009, 23, 264–274. [Google Scholar] [CrossRef]
- Du, X.; Jin, L.; Ma, G. A meso-scale numerical method for the simulation of chloride diffusivity in concrete. Finite Elem. Anal. Des. 2014, 85, 87–100. [Google Scholar] [CrossRef]
- Liu, Q.F.; Yang, J.; Xia, J.; Easterbrook, D.; Li, L.Y. A numerical study on chloride migration in cracked concrete using multi-component ionic transport models. Comput. Mater. Sci. 2015, 99, 396–416. [Google Scholar] [CrossRef]
- Papakonstantinou, K.G.; Shinozuka, M. Probabilistic model for steel corrosion in reinforced concrete structures of large dimensions considering crack effects. Eng. Struct. 2013, 57, 306–326. [Google Scholar] [CrossRef]
- Cao, C.; Cheung, M.M.S.; Chan, B.Y.B. Modelling of interaction between corrosion-induced concrete cover crack and steel corrosion rate. Corros. Sci. 2013, 69, 97–109. [Google Scholar] [CrossRef]
- Zhu, W.; François, R.; Fang, Q.; Zhang, D. Influence of long-term chloride diffusion in concrete and the resulting corrosion of reinforcement on the serviceability of RC beams. Cem. Concr. Compos. 2016, 71, 144–152. [Google Scholar] [CrossRef]
- Pacheco, J.; Šavija, B.; Schlangen, E.; Polder, R.B. Assessment of cracks in reinforced concrete by means of electrical resistance and image analysis. Constr. Build. Mater. 2014, 65, 417–426. [Google Scholar] [CrossRef]
- Šavija, B.; Schlangen, E. Chloride ingress in cracked concrete—A literature review. In Proceedings of the International PhD Conference on Concrete Durability, Madrid, Spain, 19 November 2010; Andrade, C., Gulikers, J., Eds.; RILEM Publications: Madrid, Spain, 2012; pp. 133–142. [Google Scholar]
- Pedrosa, F.; Andrade, C. Corrosion induced cracking: Effect of different corrosion rates on crack width evolution. Constr. Build. Mater. 2016, 133, 525–533. [Google Scholar] [CrossRef]
- Zhou, Y.; Gencturk, B.; Willam, K.; Attar, A. Carbonation-Induced and Chloride-Induced Corrosion in Reinforced Concrete Structures. J. Mater. Civ. Eng. 2014, 27, 46–70. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q.; Wang, L.; Yao, Y.; Li, K. Corrosion of rebar in concrete under cyclic freeze–thaw and Chloride salt action. Constr. Build. Mater. 2014, 53, 40–47. [Google Scholar] [CrossRef]
- Andrade, C.; Garcés, P.; Martínez, I. Galvanic currents and corrosion rates of reinforcements measured in cells simulating different pitting areas caused by chloride attack in sodium hydroxide. Corros. Sci. 2008, 50, 2959–2964. [Google Scholar] [CrossRef]
- Qi, X.; Mao, H.; Yang, Y. Corrosion behavior of nitrogen alloyed martensitic stainless steel in chloride containing solutions. Corros. Sci. 2017, 120, 90–98. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, Y.; Ni, Z.; Huang, R. Corrosion behavior of steel submitted to chloride and sulphate ions in simulated concrete pore solution. Constr. Build. Mater. 2016, 115, 1–5. [Google Scholar] [CrossRef]
- Liu, M.; Cheng, X.; Li, X.; Zhou, C.; Tan, H. Effect of carbonation on the electrochemical behavior of corrosion resistance low alloy steel rebars in cement extract solution. Constr. Build. Mater. 2016, 130, 193–201. [Google Scholar] [CrossRef]
- Andrade, C.; Keddam, M.; Nóvoa, X.R.; Pérez, M.C.; Rangel, C.M.; Takenouti, H. Electrochemical behaviour of steel rebars in concrete: Influence of environmental factors and cement chemistry. Electrochim. Acta 2001, 46, 3905–3912. [Google Scholar] [CrossRef]
- Andrade, C.; Soler, L.; Alonso, C.; Nóvoa, X.R.; Keddam, M. The importance of geometrical considerations in the measurement of steel corrosion in concrete by means of AC impedance. Corros. Sci. 1995, 37, 2013–2023. [Google Scholar] [CrossRef]
- Gerengi, H.; Kocak, Y.; Jazdzewska, A.; Kurtay, M.; Durgun, H. Electrochemical investigations on the corrosion behaviour of reinforcing steel in diatomite- and zeolite-containing concrete exposed to sulphuric acid. Constr. Build. Mater. 2013, 49, 471–477. [Google Scholar] [CrossRef]
- Andrade, C.; Alonso, C. Test methods for on-site corrosion rate measurement of steel reinforcement in concrete by means of the polarization resistance method. Mater. Struct. 2004, 37, 623–643. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Methods of Long-Temper Formance and Durability of Ordinary Concrete; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2009; (In Chinese).
- General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Common Portland Cement; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2007; (In Chinese).
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Quality Control of Concrete; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2011; (In Chinese).
- Song, G. Theoretical analysis of the measurement of polarisation resistance in reinforced concrete. Cem. Concr. Compos. 2000, 22, 407–415. [Google Scholar] [CrossRef]
- Song, H.W.; Saraswathy, V. Corrosion Monitoring of Reinforced Concrete Structures-A Review. Int. J. Electrochem. Sci. 2007, 2, 1–28. [Google Scholar]
- Martínez, I.; Andrade, C. Polarization resistance measurements of bars embedded in concrete with different chloride concentrations: EIS and DC comparison. Mater. Corros. 2015, 62, 932–942. [Google Scholar] [CrossRef]
- Keleştemur, O.; Yildiz, S.; Gökçer, B.; Arici, E. Statistical analysis for freeze–thaw resistance of cement mortars containing marble dust and glass fiber. Mater. Des. 2014, 60, 548–555. [Google Scholar] [CrossRef]
- Brown, A. A new software for carrying out one-way ANOVA post hoc tests. Comput. Methods Program Biomed. 2005, 79, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Stoline, M.R. The Status of Multiple Comparisons: Simultaneous Estimation of all Pairwise Comparisons in One-Way ANOVA Designs. Am. Stat. 1981, 35, 134–141. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).







