Identification of Vehicle-Pedestrian Collision Hotspots at the Micro-Level Using Network Kernel Density Estimation and Random Forests: A Case Study in Shanghai, China
Abstract
1. Introduction
2. Method
2.1. Generation of Vehicle-Pedestrian Collision Density Surface
2.2. Calculation of Potential of Vehicle-Pedestrian Collision Reduction
2.3. Identification of Vehicle-Pedestrian Collision Hot Spots
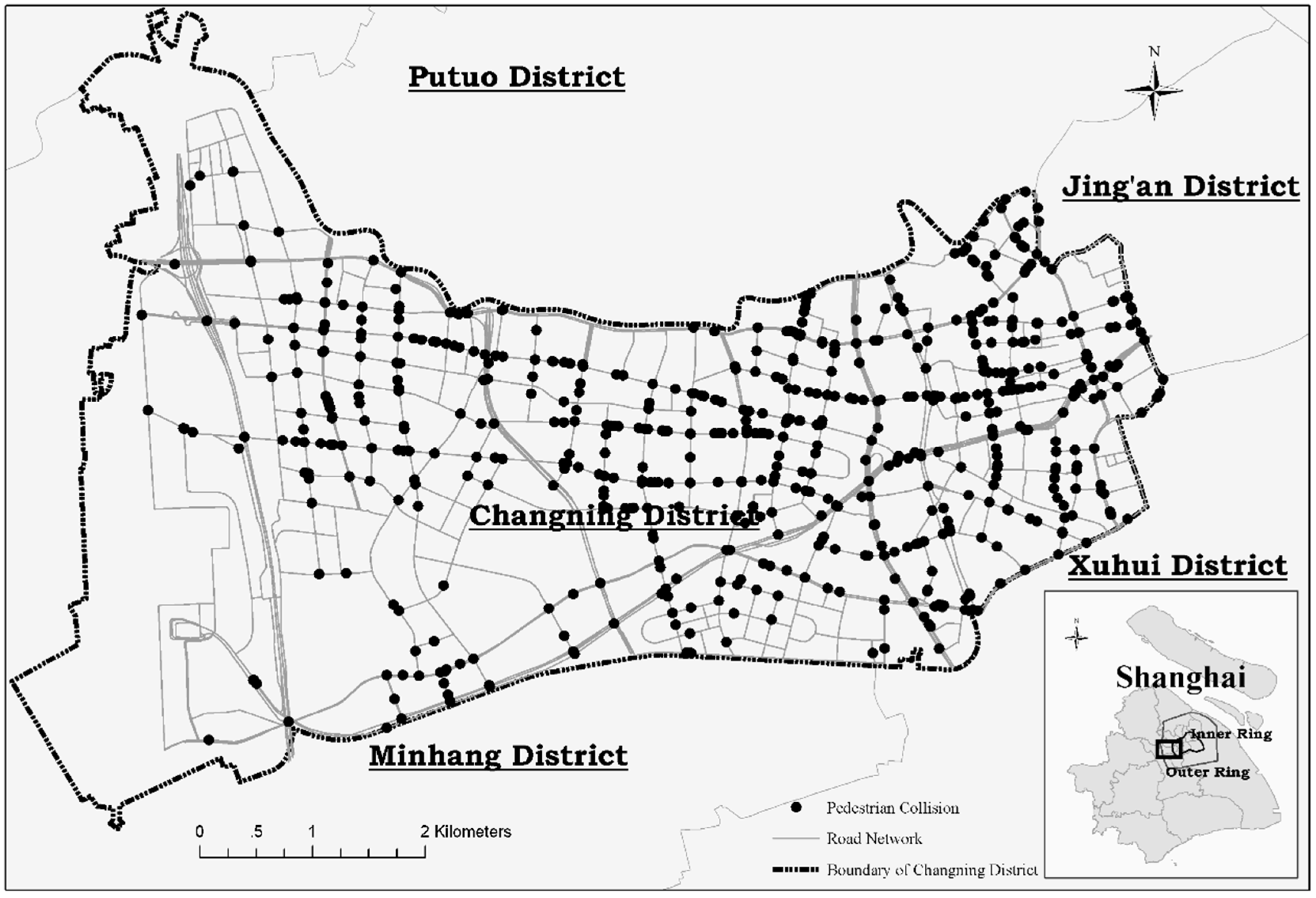
3. Study Area and Data
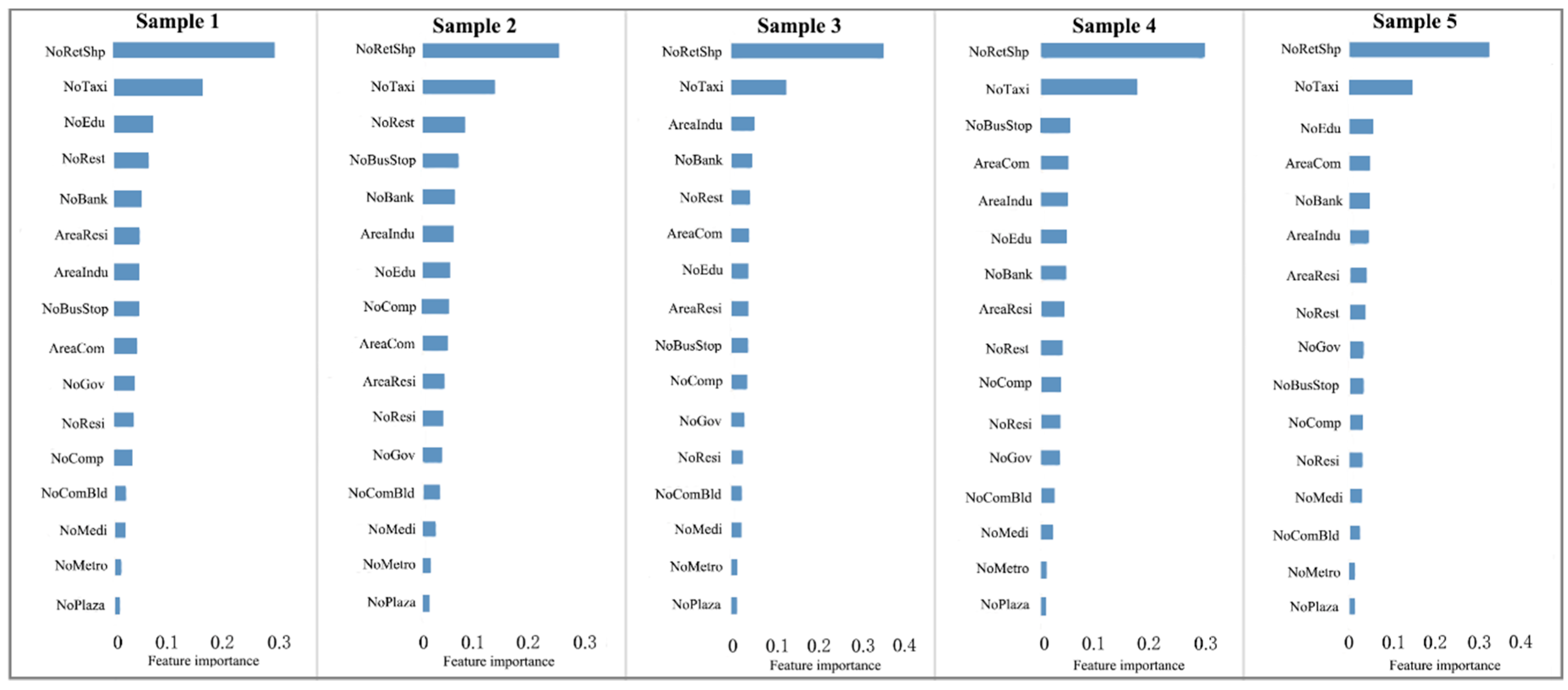
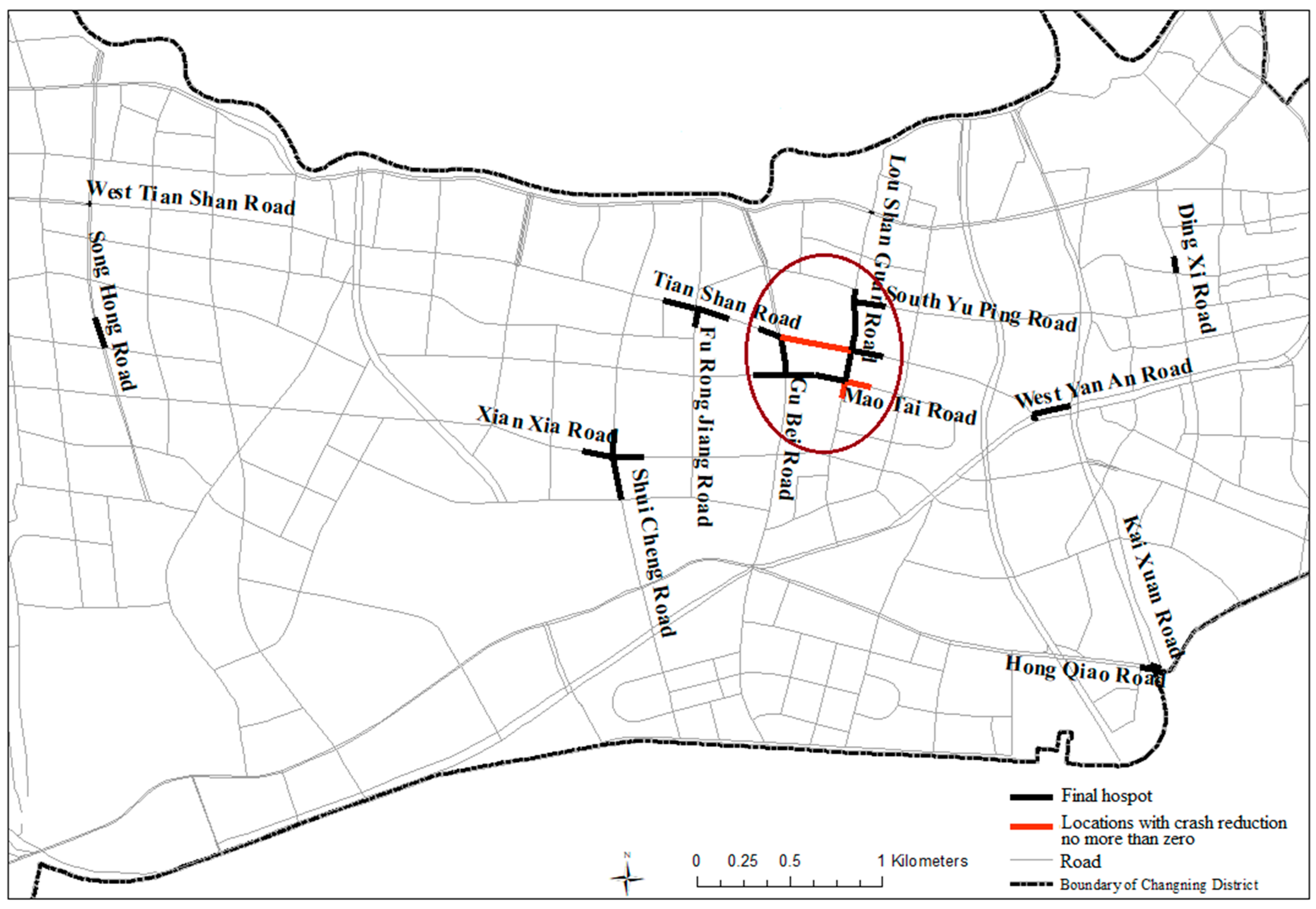
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- WHO. Global Status Report on Road Safety 2015; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- Loo, B.P.Y.; Yao, S. The Identification of Traffic Crash Hot Zones under the Link-Attribute and Event-Based Approaches in a Network-Constrained Environment. Comput. Environ. Urban Syst. 2013, 41, 249–261. [Google Scholar] [CrossRef]
- Yamada, I.; Thill, J.C. Local Indicators of Network-Constrained Clusters in Spatial Patterns Represented by a Link Attribute. Ann. Assoc. Am. Geogr. 2010, 100, 269–285. [Google Scholar] [CrossRef]
- Harirforoush, H.; Bellalite, L. A New Integrated GIS-Based Analysis to Detect Hotspots: A Case Study of the City of Sherbrooke. Accid. Anal. Prev. 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Yan, J. Kernel Density Estimation of Traffic Accidents in a Network Space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef]
- Xie, Z.; Yan, J. Detecting Traffic Accident Clusters with Network Kernel Density Estimation and Local Spatial Statistics: An Integrated Approach. J. Transp. Geogr. 2013, 31, 64–71. [Google Scholar] [CrossRef]
- Cheng, W.; Washington, S.P. Experimental Evaluation of Hotspot Identification Methods. Accid. Anal. Prev. 2005, 37, 870–881. [Google Scholar] [CrossRef] [PubMed]
- Long, T.T.; Somenahalli, S.V.C. Using GIS to Identify Pedestrian-Vehicle Crash Hot Spots and Unsafe Bus Stops. J. Public Trans. 2011, 14, 99–114. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, P.; Chen, J.; Wang, H. Comparative Analysis of the Spatial Analysis Methods for Hotspot Identification. Accid. Anal. Prev. 2014, 66, 80–88. [Google Scholar] [CrossRef]
- Nie, K.; Wang, Z.; Du, Q.; Ren, F.; Tian, Q. A Network-Constrained Integrated Method for Detecting Spatial Cluster and Risk Location of Traffic Crash: A Case Study from Wuhan, China. Sustainability 2015, 7, 2662–2677. [Google Scholar] [CrossRef]
- Naji, H.A.H.; Xue, Q.; Lyu, N.; Wu, C.; Zheng, K. Evaluating the Driving Risk of near-Crash Events Using a Mixed-Ordered Logit Model. Sustainability 2018, 10, 2868. [Google Scholar] [CrossRef]
- Loo, B.P.; Yao, S.; Wu, J. Spatial Point Analysis of Road Crashes in Shanghai: A GIS-Based Network Kernel Density Method. In Proceedings of the 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011. [Google Scholar]
- Yamada, I.; Thill, J.C. Local Indicators of Network-Constrained Clusters in Spatial Point Patterns. Geogr. Anal. 2007, 39, 268–292. [Google Scholar] [CrossRef]
- Yao, S.; Loo, B.P.; Yang, B.Z. Traffic Collisions in Space: Four Decades of Advancement in Applied GIS. Ann. GIS 2016, 22, 1–14. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
- Flahaut, B.; Mouchart, M.; Martin, E.S.; Thomas, I. The Local Spatial Autocorrelation and the Kernel Method for Identifying Black Zones: A Comparative Approach. Accid. Anal. Prev. 2003, 35, 991–1004. [Google Scholar] [CrossRef]
- Erdogan, S.; Yilmaz, I.; Baybura, T.; Gullu, M. Geographical Information Systems Aided Traffic Accident Analysis System Case Study: City of Afyonkarahisar. Accid. Anal. Prev. 2008, 40, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Krisp, J.M.; Durot, S. Segmentation of Lines Based on Point Densities—An Optimisation of Wildlife Warning Sign Placement in Southern Finland. Accid. Anal. Prev. 2007, 39, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Deacon, J.A.; Charles, V.Z.; Deen, R.C. Identification of Hazardous Rural Highway Locations. Transp. Res. Rec. 1974, 410. [Google Scholar] [CrossRef]
- Norden, M.; Orlansky, J.; Jacobs, H. Application of Statistical Quality-Control Techniques to Analysis of Highway-Accident Data. Highw. Res. Board Bull. 1956, 117, 17–31. [Google Scholar]
- Morin, D.A. Application of Statistical Concepts to Accident Data. Highw. Res. Rec. 1967, 188, 72–79. [Google Scholar]
- Stokes, R.; Mutabazi, M. Rate-Quality Control Method of Identifying Hazardous Road Locations. Transp. Res. Rec. 1996, 1542, 44–48. [Google Scholar] [CrossRef]
- McGuigan, D.R.D. The Use of Relationships between Road Accidents and Traffic Flow in “Black-Spot” Identification. Traffic Eng. Control 1981, 22, 448–453. [Google Scholar]
- McGuigan, D.R.D. Non-Junction Accident Rates and Their Use In ‘black-Spot’ Identification. Traffic Eng. Control 1982, 23, 60–65. [Google Scholar]
- Mahalel, D.; Hakkert, A.S.; Prashker, J.N. A System for the Allocation of Safety Resources on a Road Network. Accid. Anal. Prev. 1982, 14, 45–56. [Google Scholar] [CrossRef]
- Cheng, W.; Washington, S. New Criteria for Evaluating Methods of Identifying Hot Spots. Transp. Res. Rec. 2008, 2083, 76–85. [Google Scholar] [CrossRef]
- Waller, L.A.; Gotway, C.A. Applied Spatial Statistics for Public Health Data; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Huang, H.; Hong, C.C. Modeling Road Traffic Crashes with Zero-Inflation and Site-Specific Random Effects. Stat. Methods Appl. 2010, 19, 445–462. [Google Scholar] [CrossRef]
- Anastasopoulos, P.C.; Mannering, F.L. A Note on Modeling Vehicle Accident Frequencies with Random-Parameters Count Models. Accid. Anal. Prev. 2009, 41, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Loo, B.P.Y.; Lam, W.W.Y. Measures of Activity-Based Pedestrian Exposure to the Risk of Vehicle-Pedestrian Collisions: Space-Time Path Vs. Potential Path Tree Methods. Accid. Anal. Prev. 2015, 75, 320–332. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.Y. Analysis of Freeway Accident Frequencies: Negative Binomial Regression Versus Artificial Neural Network. Saf. Sci. 2005, 43, 541–557. [Google Scholar] [CrossRef]
- Xie, Y.; Lord, D.; Zhang, Y. Predicting Motor Vehicle Collisions Using Bayesian Neural Network Models: An Empirical Analysis. Accid. Anal. Prev. 2007, 39, 922–933. [Google Scholar] [CrossRef]
- Zeng, Q.; Huang, H.; Xin, P.; Wong, S.C.; Gao, M. Rule Extraction from an Optimized Neural Network for Traffic Crash Frequency Modeling. Accid. Anal. Prev. 2016, 97, 87–95. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by Randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gromping, U. Variable Importance Assessment in Regression: Linear Regression Versus Random Forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Haas, J.; Ban, Y. Urban Growth and Environmental Impacts in Jing-Jin-Ji, the Yangtze, River Delta and the Pearl River Delta. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 42–55. [Google Scholar] [CrossRef]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M.C. Modeling Spatial Patterns of Fire Occurrence in Mediterranean Europe Using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Topouzelis, K.; Psyllos, A. Oil Spill Feature Selection and Classification Using Decision Tree Forest on Sar Image Data. ISPRS J. Photogramm. Remote Sens. 2012, 68, 135–143. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Chica-Rivas, M. Predictive Modelling of Gold Potential with the Integration of Multisource Information Based on Random Forest: A Case Study on the Rodalquilar Area, Southern Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 1336–1354. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Pu, R.; Zhang, Z. Mapping Robinia Pseudoacacia Forest Health Conditions by Using Combined Spectral, Spatial, and Textural Information Extracted from Ikonos Imagery and Random Forest Classifier. Remote Sens. 2015, 7, 9020–9044. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable Selection Using Random Forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Scikit-learn. Available online: https://scikit-learn.org/stable/ (accessed on 18 November 2018).
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, T.; Yu, Y. Using Cloud Computing to Process Intensive Floating Car Data for Urban Traffic Surveillance. Int. J. Geogr. Inf. Sci. 2011, 25, 1303–1322. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing Travel Patterns and City Structure with Taxi Trip Data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y.; Gao, Y.; Liu, Y. Understanding Urban Traffic-Flow Characteristics: A Rethinking of Betweenness Centrality. Environ. Plan. B Plan. Des. 2013, 40, 135–153. [Google Scholar] [CrossRef]
- Wang, X.; Fan, T.; Chen, M.; Deng, B.; Wu, B.; Tremont, P. Safety Modeling of Urban Arterials in Shanghai, China. Accid. Anal. Prev. 2015, 83, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.Y.; Yuan, H.; Li, Q.; Lam, W.H.K.; Shaw, S.L.; Yan, K. Map-Matching Algorithm for Large-Scale Low-Frequency Floating Car Data. Int. J. Geogr. Inf. Sci. 2014, 28, 22–38. [Google Scholar] [CrossRef]
- Yang, B.Z.; Loo, B.P.Y. Land Use and Traffic Collisions: A Link-Attribute Analysis Using Empirical Bayes Method. Accid. Anal. Prev. 2016, 95, 236–249. [Google Scholar] [CrossRef]
- Ozbil, A.; Peponis, J.; Stone, B. Understanding the Link between Street Connectivity, Land Use and Pedestrian Flows. Urban Des. Int. 2011, 16, 125–141. [Google Scholar] [CrossRef]
- Lamíquiz, P.J.; López-Domínguez, J. Effects of Built Environment on Walking at the Neighbourhood Scale. A New Role for Street Networks by Modelling Their Configurational Accessibility? Transp. Res. A Policy Pract. 2015, 74, 148–163. [Google Scholar] [CrossRef]
- Castro, P.S.; Zhang, D.; Li, S. Urban Traffic Modelling and Prediction Using Large Scale Taxi Gps Traces. In Proceedings of the 10th International Conference, Pervasive 2012, Newcastle, UK, 18–22 June 2012. [Google Scholar]
| Variable Name | Data Source | Description |
|---|---|---|
| NoMetro | Point of Interest | No. of metro stations within 500 m of a Reference Point |
| NoBusStop | POI | No. of bus stops within 500 m of a RP |
| NoGov | POI | No. of government institutions within 500 m of a RP |
| NoBank | POI | No. of banking service facilities within 500 m of a RP |
| NoComBld | POI | No. of commercial buildings within 500 m of a RP |
| NoRetShp | POI | No. of retail shops within 500 m of a RP |
| NoMedi | POI | No. of medical service facilities within 500 m of a RP |
| NoEdu | POI | No. of educational institutions within 500 m of a RP |
| NoComp | POI | No. of companies within 500 m of a RP |
| NoPlaza | POI | No. of pedestrian plazas within 500 m of a RP |
| NoResi | POI | No. of residence places within 500 m of a RP |
| NoRest | POI | No. of restaurants within 500 m of a RP |
| AreaResi | Land use | Residential area (sq. m) within 500 m of a RP |
| AreaIndu | Land use | Industrial area (sq. m) within 500 m of a RP |
| AreaCom | Land use | Commercial area (sq. m) within 500 m of a RP |
| NoTaxi | Global Positioning System tracking point | No. of taxies that pass a RP |
| Mean Cross-Validation Score | Mean Squared Error | Median Absolute Error | R2 | |
|---|---|---|---|---|
| Sample 1 | 0.61 (±0.12) | 0.0040 | 0.0247 | 0.6191 |
| Sample 2 | 0.59 (±0.09) | 0.0037 | 0.0260 | 0.6868 |
| Sample 3 | 0.59 (±0.12) | 0.0039 | 0.0260 | 0.6351 |
| Sample 4 | 0.56 (±0.20) | 0.0048 | 0.0278 | 0.6457 |
| Sample 5 | 0.58 (±0.07) | 0.0032 | 0.0292 | 0.6624 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Wang, J.; Fang, L.; Wu, J. Identification of Vehicle-Pedestrian Collision Hotspots at the Micro-Level Using Network Kernel Density Estimation and Random Forests: A Case Study in Shanghai, China. Sustainability 2018, 10, 4762. https://doi.org/10.3390/su10124762
Yao S, Wang J, Fang L, Wu J. Identification of Vehicle-Pedestrian Collision Hotspots at the Micro-Level Using Network Kernel Density Estimation and Random Forests: A Case Study in Shanghai, China. Sustainability. 2018; 10(12):4762. https://doi.org/10.3390/su10124762
Chicago/Turabian StyleYao, Shenjun, Jinzi Wang, Lei Fang, and Jianping Wu. 2018. "Identification of Vehicle-Pedestrian Collision Hotspots at the Micro-Level Using Network Kernel Density Estimation and Random Forests: A Case Study in Shanghai, China" Sustainability 10, no. 12: 4762. https://doi.org/10.3390/su10124762
APA StyleYao, S., Wang, J., Fang, L., & Wu, J. (2018). Identification of Vehicle-Pedestrian Collision Hotspots at the Micro-Level Using Network Kernel Density Estimation and Random Forests: A Case Study in Shanghai, China. Sustainability, 10(12), 4762. https://doi.org/10.3390/su10124762





