Is Big Good or Bad?: Testing the Performance of Urban Growth Cellular Automata Simulation at Different Spatial Extents
Abstract
1. Introduction
2. Materials and Methods
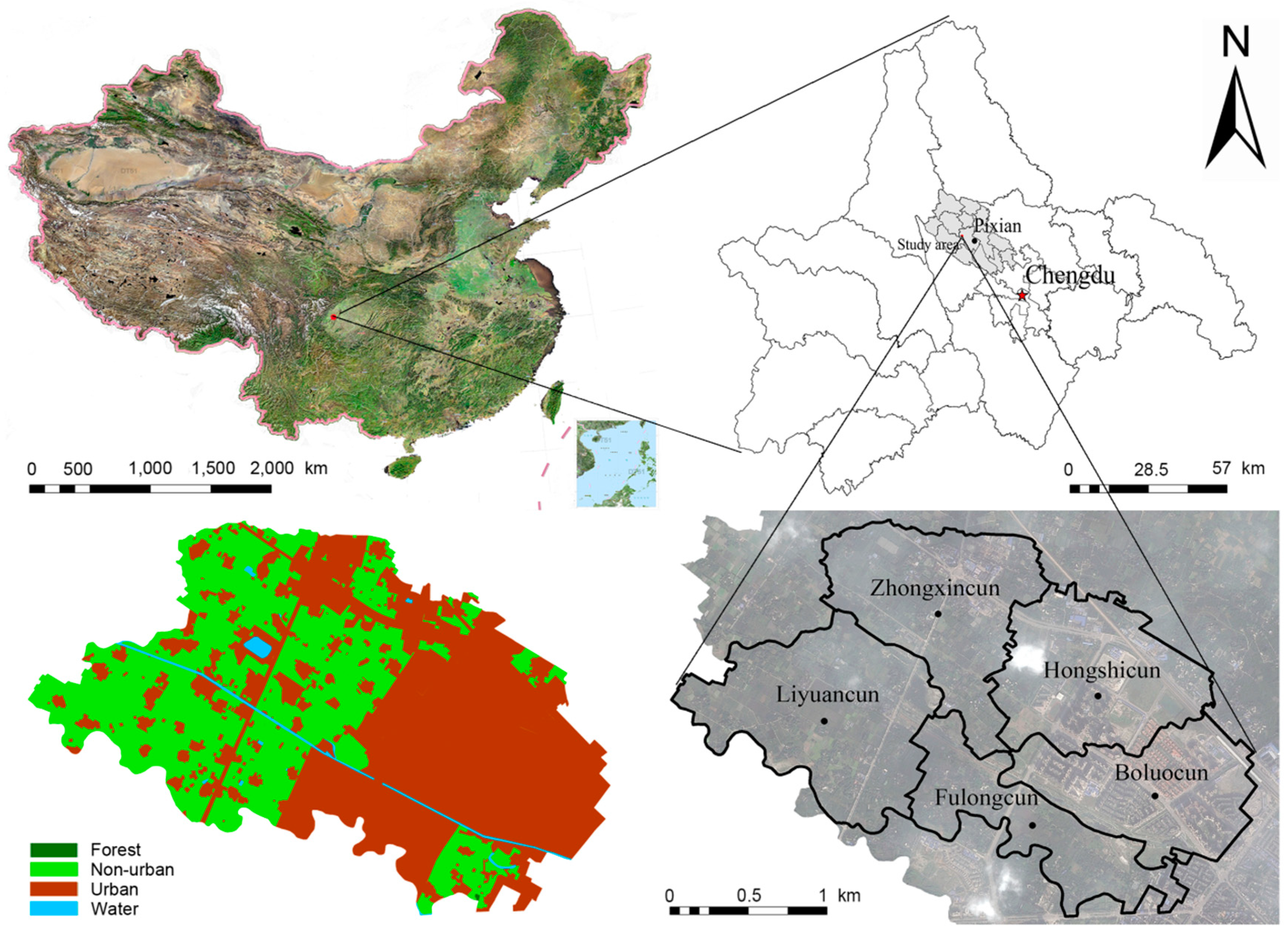
2.1. Study Area
2.2. Data and Methodology
2.2.1. Data
2.2.2. Model Framework
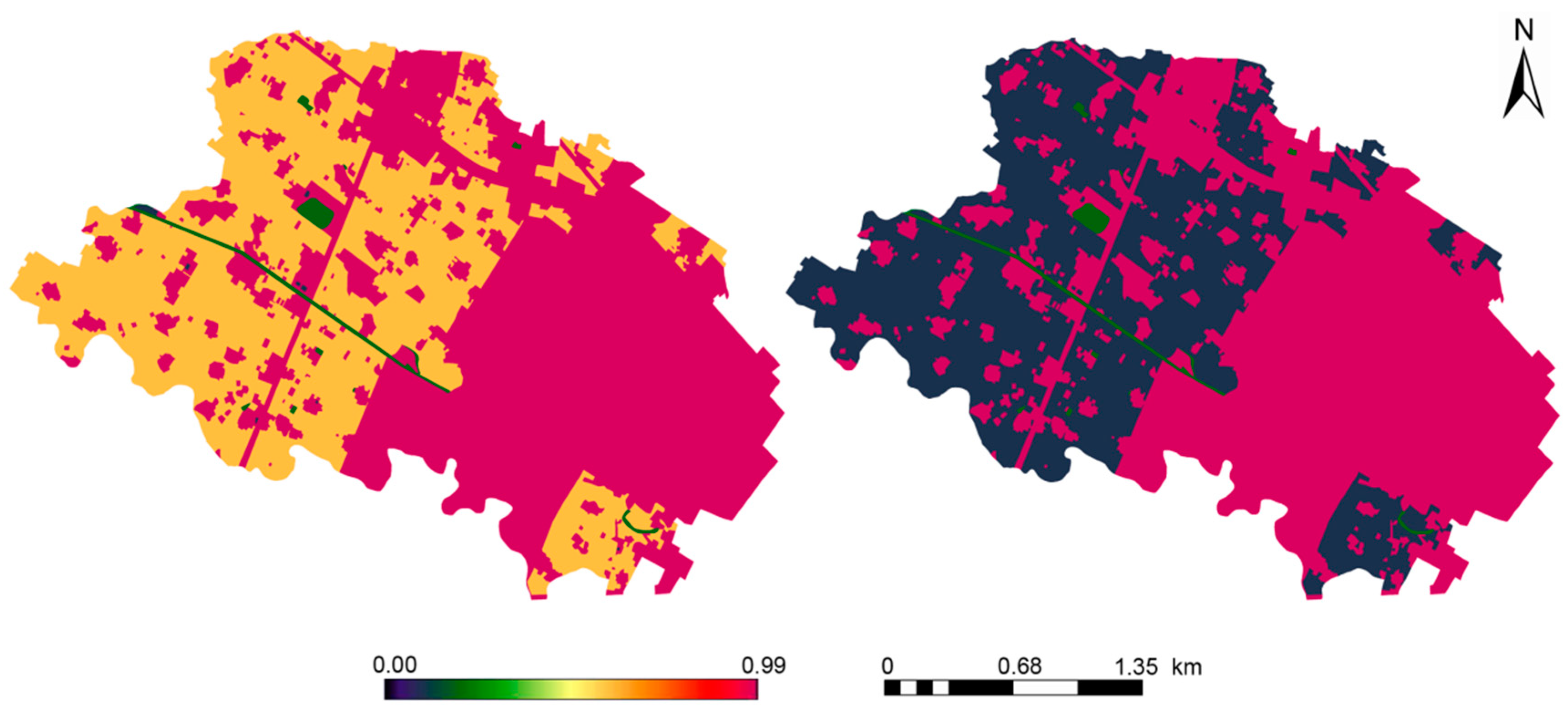
2.2.3. Model Calibration
3. Results
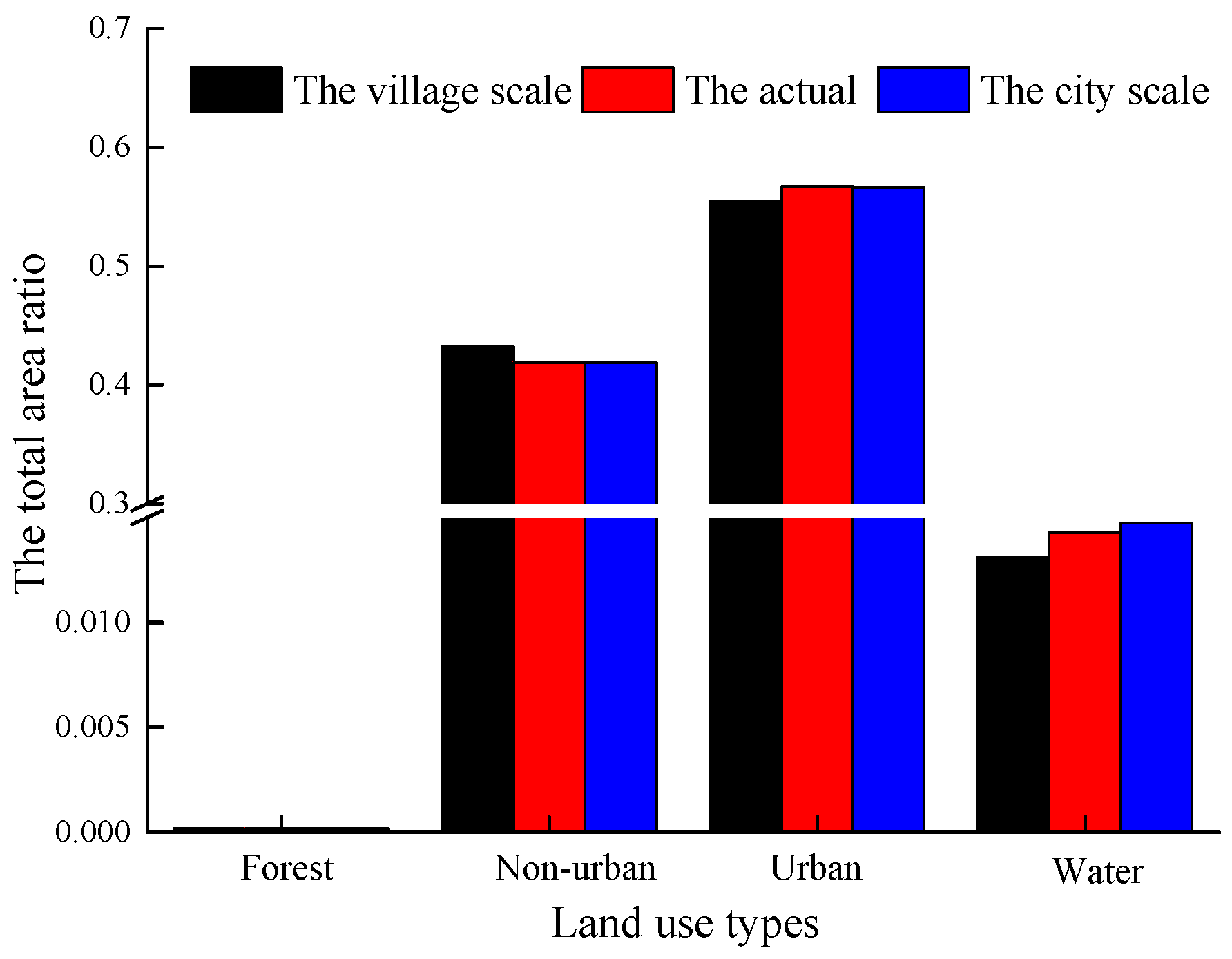
3.1. Amount of Land Use Change according to the Markov Model
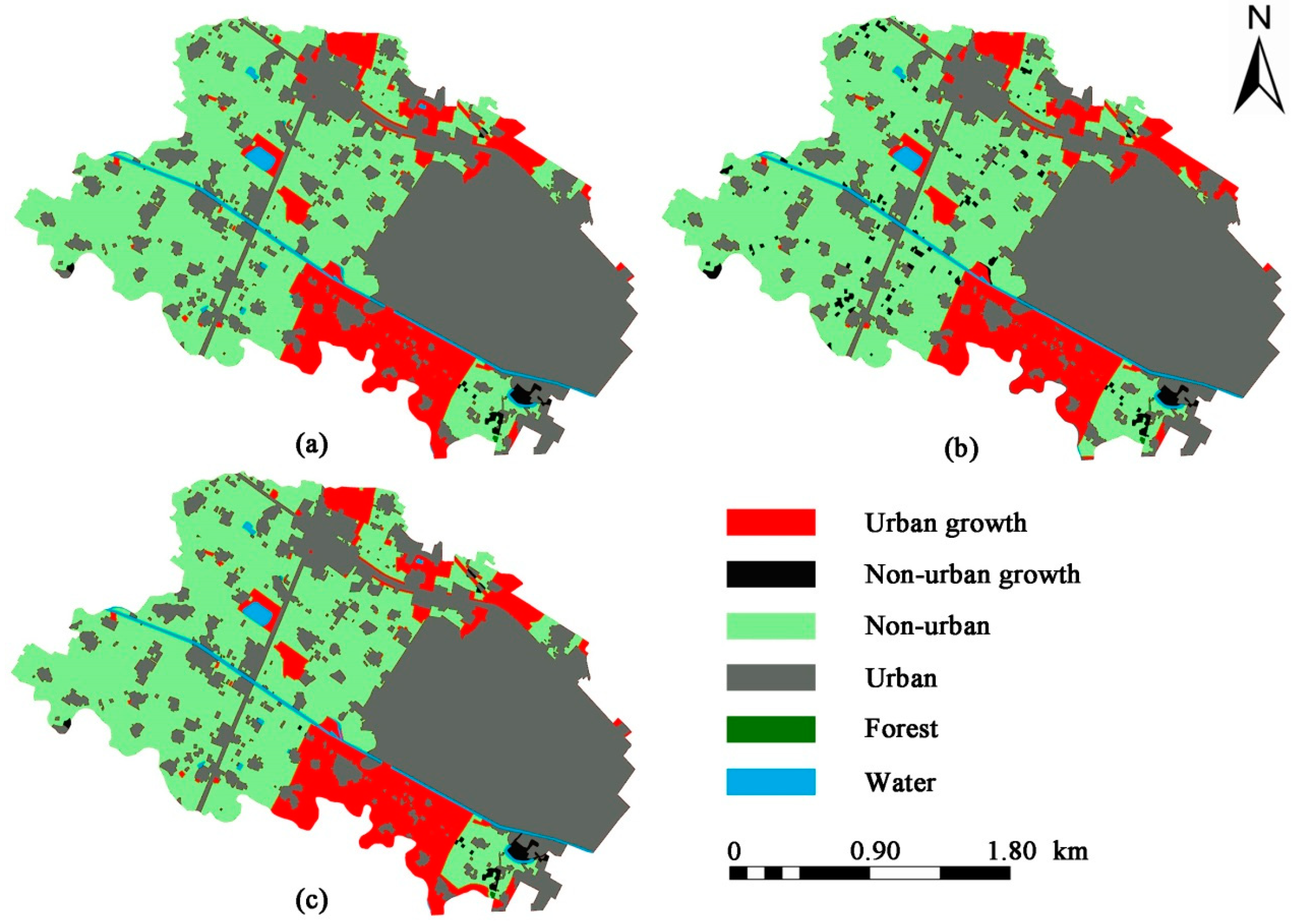
3.2. Simulated Spatial Distribution according to the CA Model
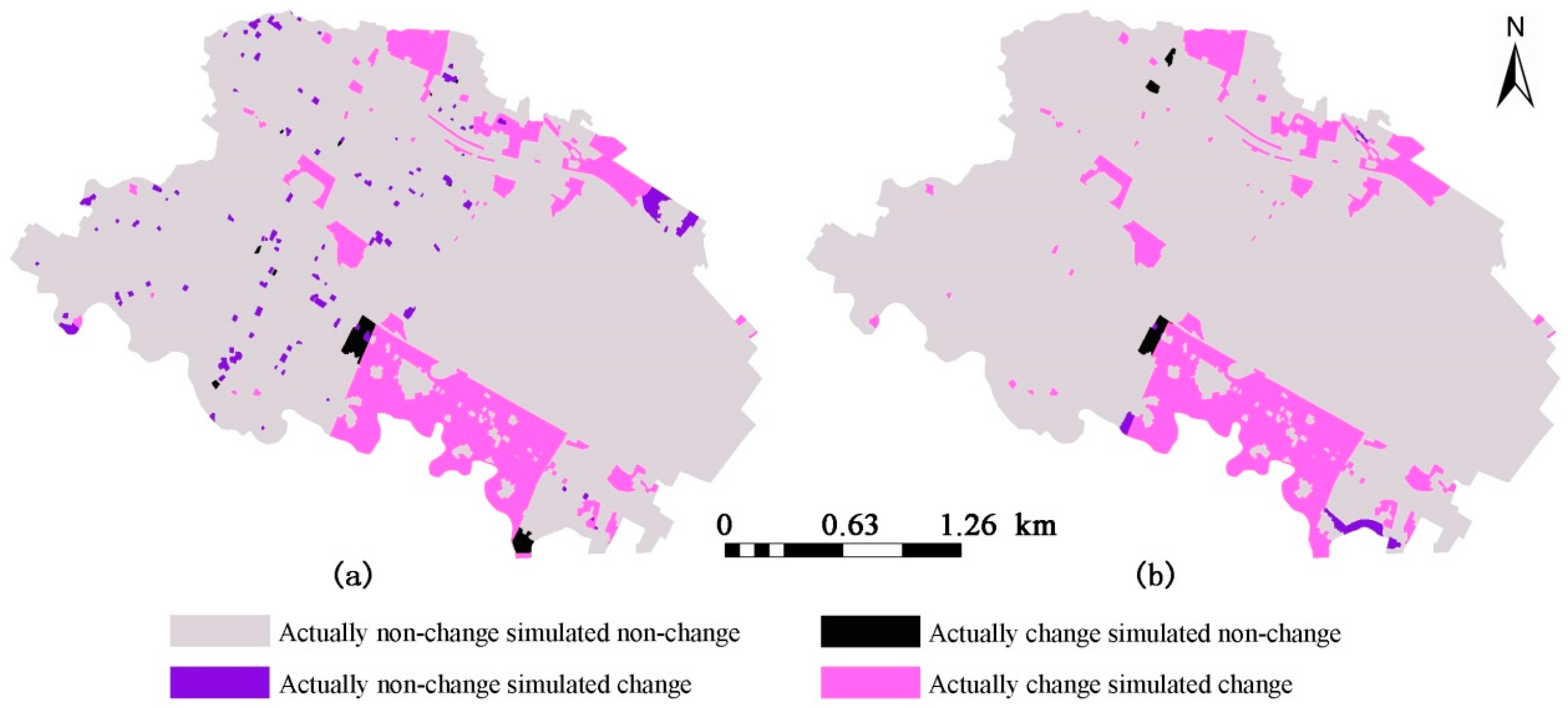
3.3. Comparing the Model Performance at the Two Spatial Extents
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crossman, N.D.; Bryan, B.A.; Ostendorf, B.; Collins, S. Systematic landscape restoration in the rural-urban fringe: Meeting conservation planning and policy goals. Biodivers. Conserv. 2007, 16, 3781–3802. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Wu, K.; Yu, X. Classification of Complex Rural-urban fringe Land Cover Using Evidential Reasoning Based on Fuzzy Rough Set: A Case Study of Wuhan City. Remote Sens. 2016, 8, 304. [Google Scholar] [CrossRef]
- Kong, C.; Lan, H.; Yang, G.; Xu, K. Geo-environmental suitability assessment for agricultural land in the rural-urban fringe using BPNN and GIS: A case study of Hangzhou. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Liu, Z.; Robinson, G.M. Residential development in the peri-rural-urban fringe: The example of Adelaide, South Australia. Land Use Policy 2016, 57, 179–192. [Google Scholar] [CrossRef]
- Dietzel, C.; Clarke, K. The effect of disaggregating land use categories in cellular automata during model calibration and forecasting. Comput. Environ. Urban Syst. 2006, 30, 78–101. [Google Scholar] [CrossRef]
- He, C.; Okada, N.; Zhang, Q.; Shi, P.; Li, J. Modelling dynamic urban expansion processes incorporating a potential model with cellular automata. Landsc. Urban Plan. 2008, 86, 79–91. [Google Scholar] [CrossRef]
- Syphard, A.D.; Clarke, K.C.; Franklin, J. Using a cellular automaton model to forecast the effects of urban growth on habitat pattern in southern California. Ecol. Complex. 2005, 2, 185–203. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.O. Data mining of cellular automata’s transition rules. Int. J. Geogr. Inf. Sci. 2004, 18, 723–744. [Google Scholar] [CrossRef]
- Gallent, N.; Shaw, D. Spatial planning, area action plans and the rural-urban fringe. J. Environ. Plan. Manag. 2008, 50, 617–638. [Google Scholar] [CrossRef]
- Jafari, M.; Majedi, H.; Monavari, S.; Alesheikh, A.; Zarkesh, K.M. Dynamic Simulation of Urban Expansion Based on Cellular Automata and Logistic Regression Model: Case Study of the Hyrcanian Region of Iran. Sustainability 2016, 8, 810. [Google Scholar] [CrossRef]
- Tian, G.; Ma, B.; Xu, X.; Liu, X.; Xu, L.; Liu, X.; Xiao, L.; Kong, L. Simulation of urban expansion and encroachment using cellular automata and multi-agent system model-A case study of Tianjin metropolitan region, China. Ecol. Indicators 2016, 70, 439–450. [Google Scholar] [CrossRef]
- Yang, X.; Chen, R.; Zheng, X.Q. Simulating land use change by integrating ANN-CA model and landscape pattern indices. Geom. Natl. Hazards Risk 2016, 7, 915–918. [Google Scholar] [CrossRef]
- White, R.W.; Engelen, G. Cellular automaton as the basis of integrated dynamic regional modeling. Environ. Plan. B Plan. Des. 1997, 24, 235–246. [Google Scholar] [CrossRef]
- Wu, F.; Webster, C.J. Simulation of land development through the integration of cellular automata and multi-criteria evaluation. Environ. Plan. B Plan. Des. 1998, 25, 103–126. [Google Scholar] [CrossRef]
- Clark, K.C.; Gaydos, L.J. Loose-coupling a cellular automation model and GIS: Long-term urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci. 1998, 12, 699–714. [Google Scholar] [CrossRef] [PubMed]
- Yeh, A.G.O.; Li, X. A cellular automata model to simulate development density for urban planning. Environ. Plan. B Plan. Des. 2002, 29, 431–450. [Google Scholar] [CrossRef]
- Zhao, Y.; Murayama, Y. A constrained CA model to simulate urban growth of the Tokyo Metropolitan Area. In Proceedings of the 9th International Conference on Geocomputation, National University of Ireland, Maynooth, Ireland, 3–5 September 2007. [Google Scholar]
- Campagnaro, T.; Frate, L.; Carranza, M.L.; Sitzia, T. Multi-scale analysis of alpine landscapes with different intensities of abandonment reveals similar spatial pattern changes: Implications for habitat conservation. Ecol. Indicators 2017, 74, 147–159. [Google Scholar] [CrossRef]
- Brown, D.G.; Page, S.; Riolo, R.; Zellner, M.; Rand, W. Path dependence and the validation of agent-based spatial models of land use. Int. J. Geogr. Inf. Sci. 2005, 19, 153–174. [Google Scholar] [CrossRef]
- Sang, L.; Zhang, C.; Yang, J.; Zhu, D.; Yun, W. Simulation of land use spatial pattern of towns and villages based on CA-Markov model. Math. Comput. Model. 2011, 54, 938–943. [Google Scholar] [CrossRef]
- Huang, Y.; Nian, P.; Zhang, W. The prediction of interregional land use differences in Beijing: A Markov model. Environ. Earth Sci. 2015, 73, 4077–4090. [Google Scholar] [CrossRef]
- Chengdu Bureau of Statistics; Chengdu Statistical Society. Chengdu Statistical Yearbook; China Statistics Press: Beijing, China, 2016.
- Gao, X.; Xu, A.; Liu, L.; Deng, O.; Zeng, M.; Ling, J.; Wei, Y. Understanding rural housing abandonment in China’s rapid urbanization. Habitat Int. 2017, 67, 13–21. [Google Scholar] [CrossRef]
- Kamusoko, C.; Aniya, M.; Adi, B.; Manjoro, M. Rural sustainability under threat in Zimbabwe-Simulation of future land use/cover changes in the Bindura district based on the Markov-cellular automata model. Appl. Geogr. 2009, 29, 435–447. [Google Scholar] [CrossRef]
- Guan, D.; Li, H.; Inohae, T.; Su, W.; Nagaie, T.; Hokao, K. Modeling urban land use change by the integration of cellular automaton and Markov model. Ecol. Model. 2011, 222, 3761–3772. [Google Scholar] [CrossRef]
- Yagoub, M.M.; Al Bizreh, A.A. Prediction of Land Cover Change Using Markov and Cellular Automata Models: Case of Al-Ain, UAE, 1992–2030. J. Indian Soc. Remote Sens. 2014, 42, 665–671. [Google Scholar] [CrossRef]
- Ku, C. Incorporating spatial regression model into cellular automata for simulating land use change. Appl. Geogr. 2016, 69, 1–9. [Google Scholar] [CrossRef]
- Li, X.; Lin, J.; Chen, Y.; Liu, X.; Ai, B. Calibrating cellular automata based on landscape metrics by using genetic algorithms. Int. J. Geogr. Inf. Sci. 2013, 27, 594–613. [Google Scholar] [CrossRef]
- Gant, R.L.; Robinson, G.M.; Fazal, S. Land-use change in the ‘edgelands’: Policies and pressures in London’s rural-urban fringe. Land Use Policy 2011, 28, 266–279. [Google Scholar] [CrossRef]
- Porta, J.; Parapar, J.; Doallo, R.; Barbosa, V.; Santé, I.; Crecente, R.; Díaz, C. A population-based iterated greedy algorithm for the delimitation and zoning of rural settlements. Comput. Environ. Urban Syst. 2013, 39, 12–26. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Chen, Y.; Long, H. The process and driving forces of rural hollowing in China under rapid urbanization. J. Geogr. Sci. 2010, 20, 876–888. [Google Scholar] [CrossRef]
- Long, H.; Li, Y.; Liu, Y.; Woods, M.; Zou, J. Accelerated restructuring in rural China fueled by ‘increasing vs. decreasing balance’ land-use policy for dealing with hollowed villages. Land Use Policy 2012, 29, 11–22. [Google Scholar] [CrossRef]
- Sun, H.; Liu, Y.; Xu, K. Hollow villages and rural restructuring in major rural regions of China: A case study of Yucheng City, Shandong Province. Chin. Geogr. Sci. 2011, 21, 354–363. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, F.; Zhang, Y. Appraisal of typical rural development models during rapid urbanization in the eastern coastal region of China. J. Geogr. Sci. 2009, 19, 557–567. [Google Scholar] [CrossRef]
- Xing, C.; Zhang, J. The preference for larger cities in China: Evidence from rural-urban migrants. China Econ. Rev. 2017, 43, 72–90. [Google Scholar] [CrossRef]
- Chen, R.; Ye, C.; Cai, Y.; Xing, X.; Chen, Q. The impact of rural out-migration on land use transition in China: Past, present and trend. Land Use Policy 2014, 40, 101–110. [Google Scholar] [CrossRef]
| 0.229 | 0.168 | 0.194 | 0.285 | −0.117 | −0.094 | 0.186 | 0.151 |
| Land Use | Transition Matrix at the City Level | Transition Matrix at the Village Level | ||||||
|---|---|---|---|---|---|---|---|---|
| Forest | Non-Urban | Urban | Water | Forest | Non-Urban | Urban | Water | |
| Forest | 0.747 | 0.209 | 0.037 | 0.007 | 1.000 | 0.000 | 0.000 | 0.000 |
| Non-urban | 0.148 | 0.461 | 0.351 | 0.040 | 0.000 | 0.901 | 0.099 | 0.000 |
| Urban | 0.036 | 0.364 | 0.580 | 0.020 | 0.000 | 0.005 | 0.995 | 0.000 |
| Water | 0.024 | 0.193 | 0.109 | 0.674 | 0.000 | 0.000 | 0.030 | 0.971 |
| The Kappa Value | The Neighborhood Configurations | |||||||
|---|---|---|---|---|---|---|---|---|
| 3 × 3 | 4 × 4 | 5 × 5 | 6 × 6 | 7 × 7 | 8 × 8 | 9 × 9 | 10 × 10 | |
| Village model | 0.835 | 0.896 | 0.925 | 0.954 | 0.921 | 0.870 | 0.854 | 0.783 |
| City model | 0.603 | 0.685 | 0.700 | 0.741 | 0.753 | 0.733 | 0.710 | 0.752 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Liu, Y.; Liu, L.; Li, Q.; Deng, O.; Wei, Y.; Ling, J.; Zeng, M. Is Big Good or Bad?: Testing the Performance of Urban Growth Cellular Automata Simulation at Different Spatial Extents. Sustainability 2018, 10, 4758. https://doi.org/10.3390/su10124758
Gao X, Liu Y, Liu L, Li Q, Deng O, Wei Y, Ling J, Zeng M. Is Big Good or Bad?: Testing the Performance of Urban Growth Cellular Automata Simulation at Different Spatial Extents. Sustainability. 2018; 10(12):4758. https://doi.org/10.3390/su10124758
Chicago/Turabian StyleGao, Xuesong, Yu Liu, Lun Liu, Qiquan Li, Ouping Deng, Yali Wei, Jing Ling, and Min Zeng. 2018. "Is Big Good or Bad?: Testing the Performance of Urban Growth Cellular Automata Simulation at Different Spatial Extents" Sustainability 10, no. 12: 4758. https://doi.org/10.3390/su10124758
APA StyleGao, X., Liu, Y., Liu, L., Li, Q., Deng, O., Wei, Y., Ling, J., & Zeng, M. (2018). Is Big Good or Bad?: Testing the Performance of Urban Growth Cellular Automata Simulation at Different Spatial Extents. Sustainability, 10(12), 4758. https://doi.org/10.3390/su10124758




