Dynamics of Cooperation in Minority Games in Alliance Networks
Abstract
1. Introduction
2. Theory and Motivation
3. Model
4. Simulation and Results
4.1. Simulation
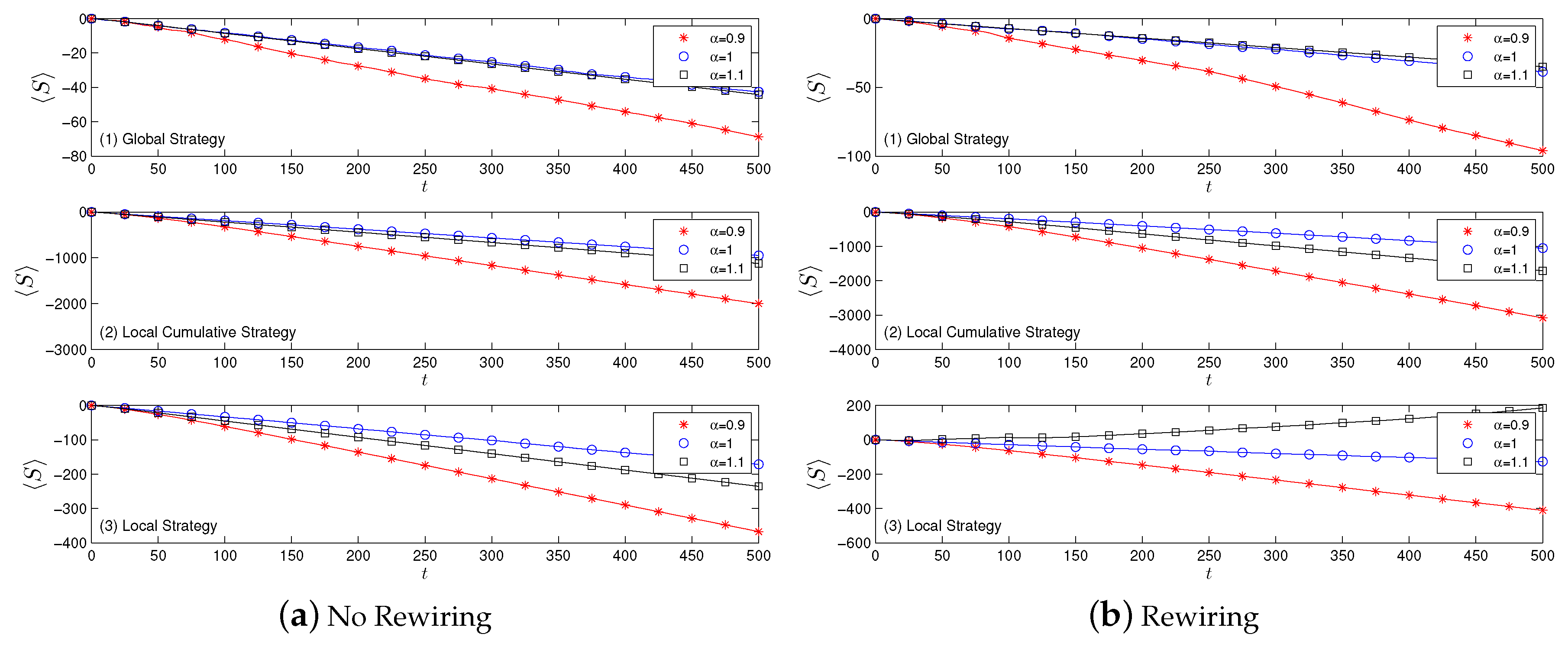
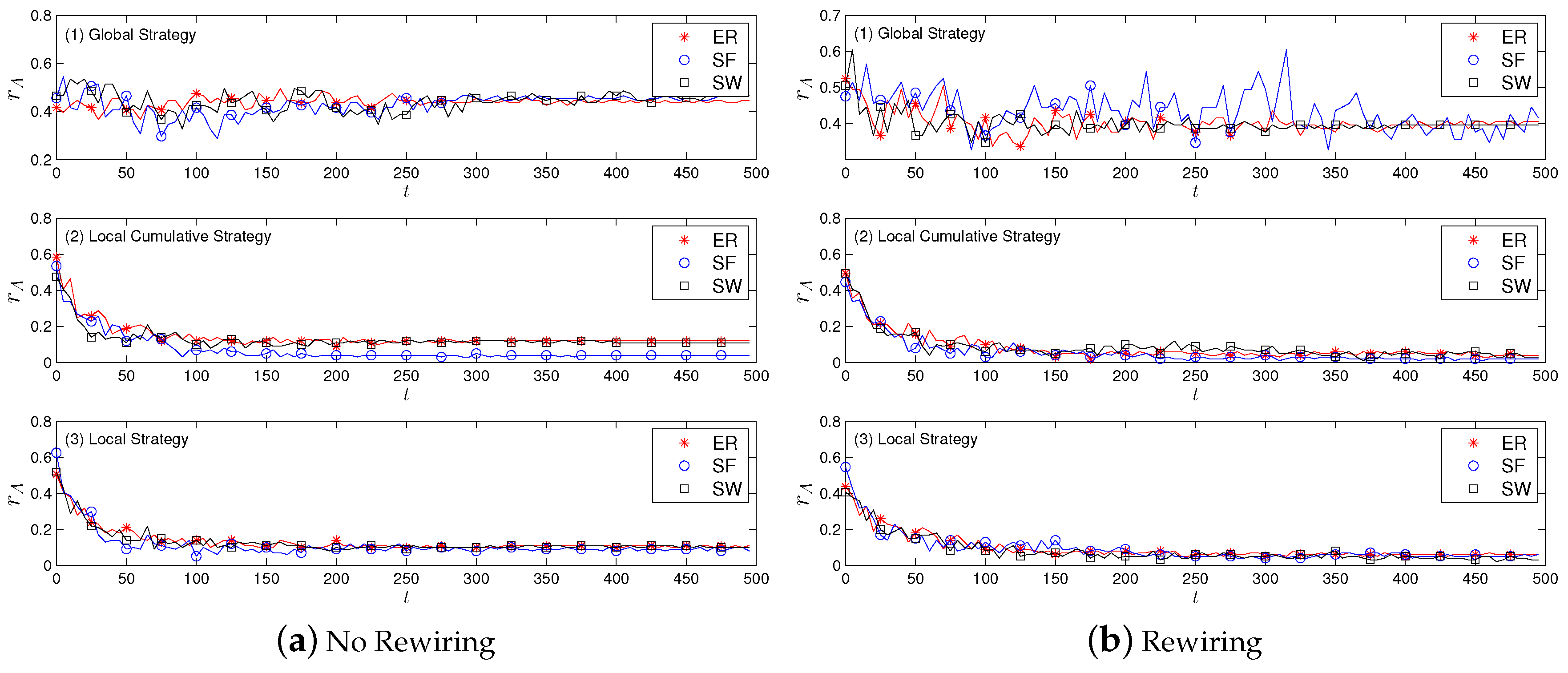
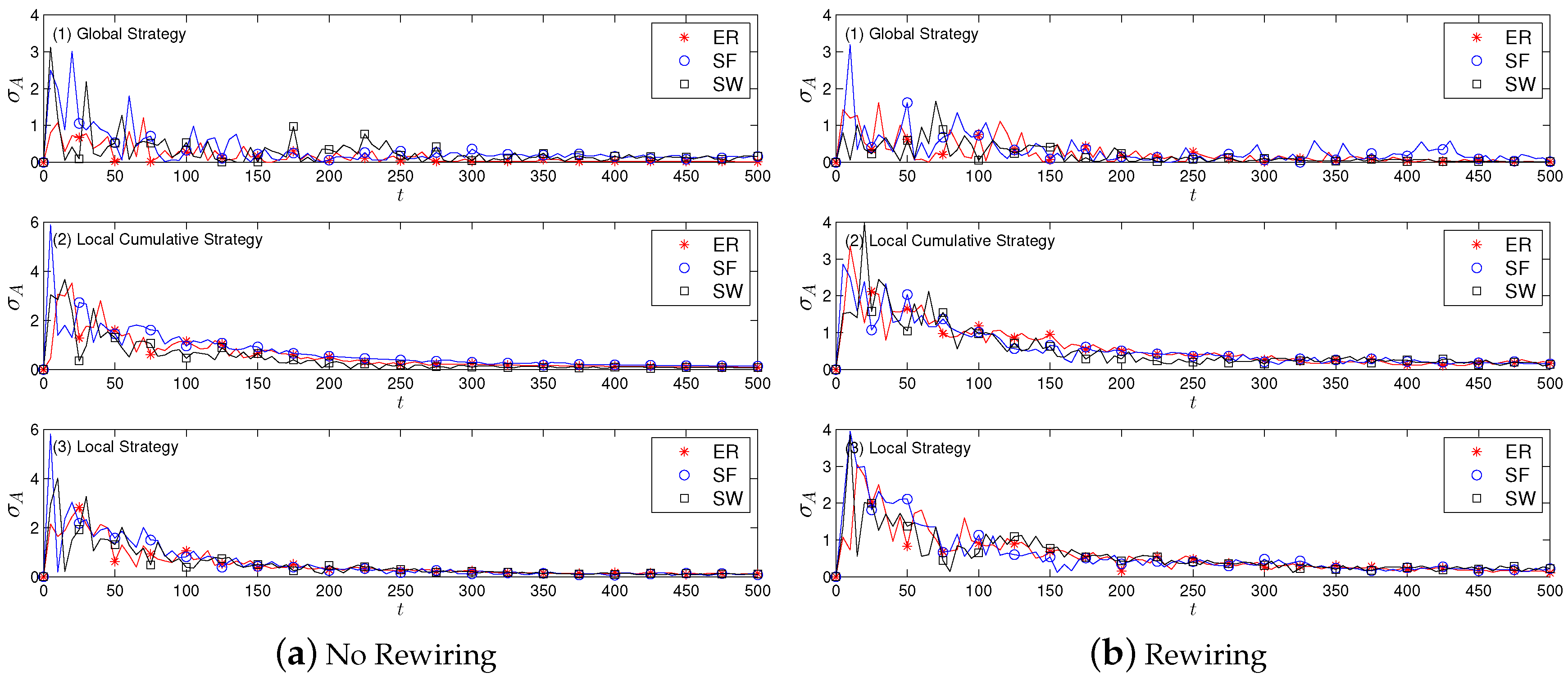
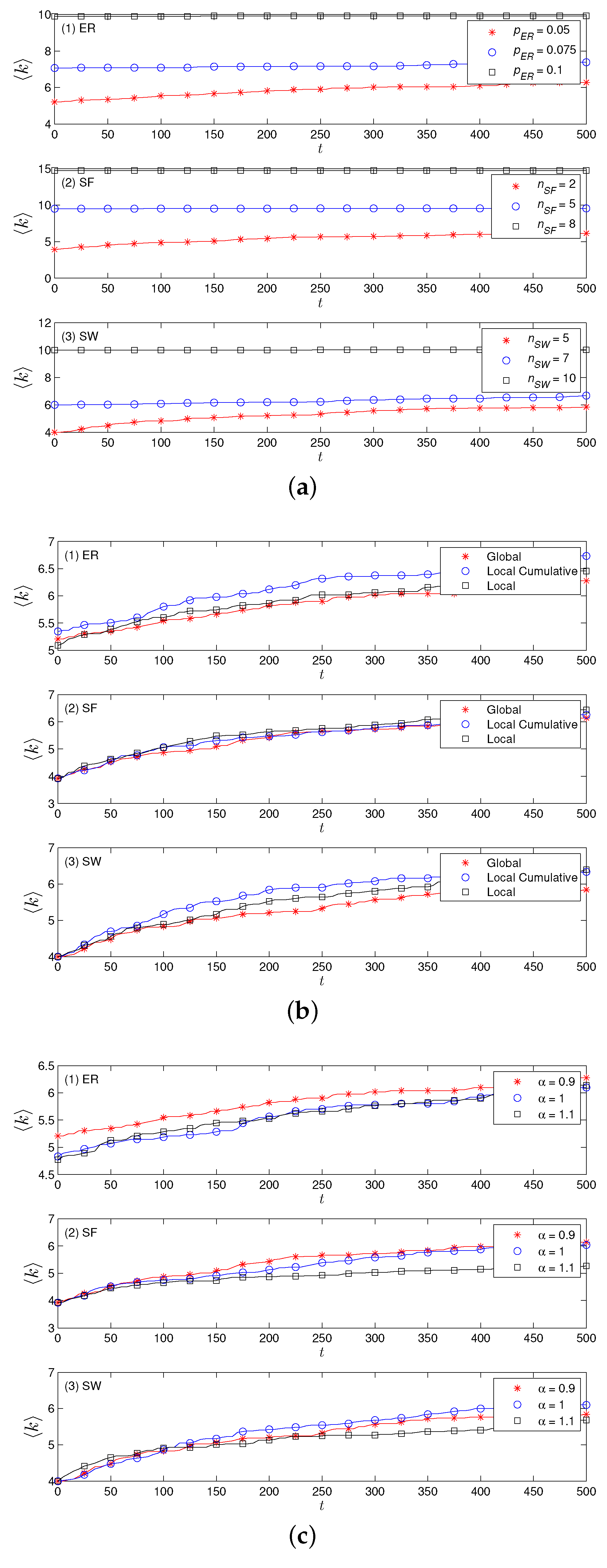
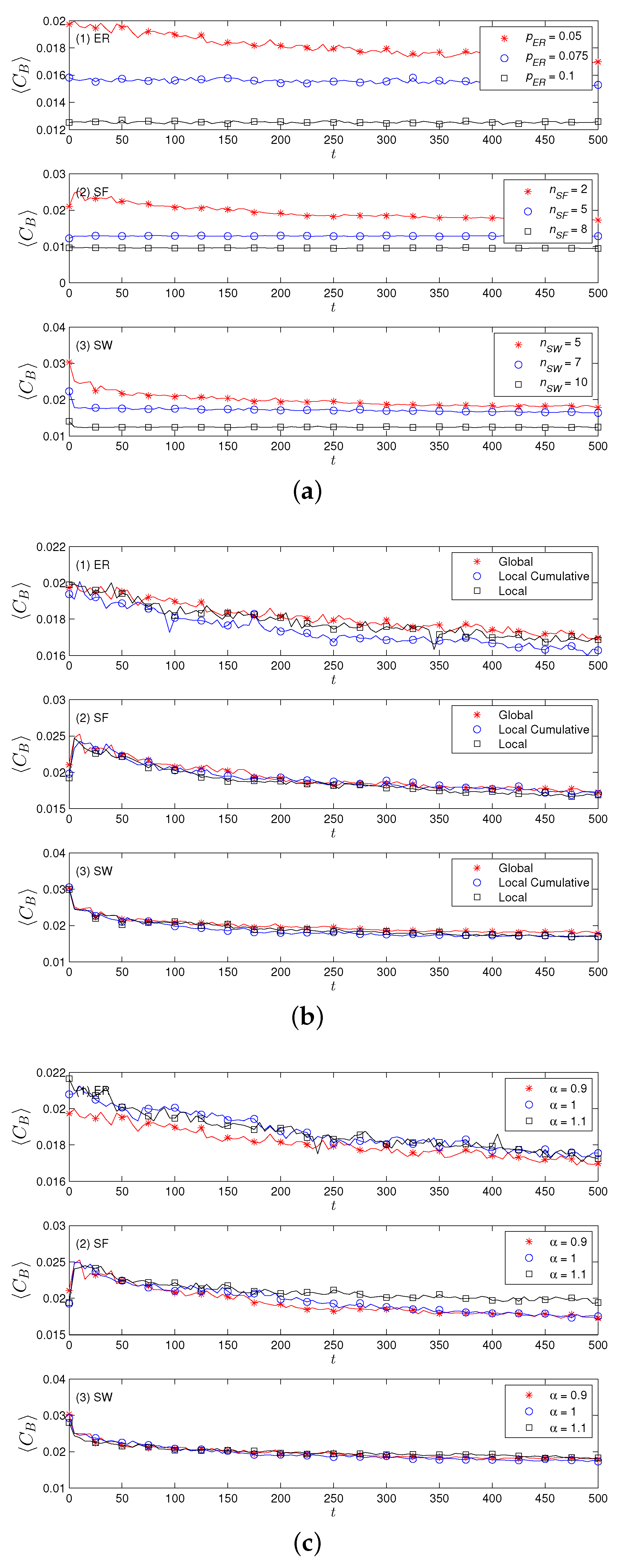
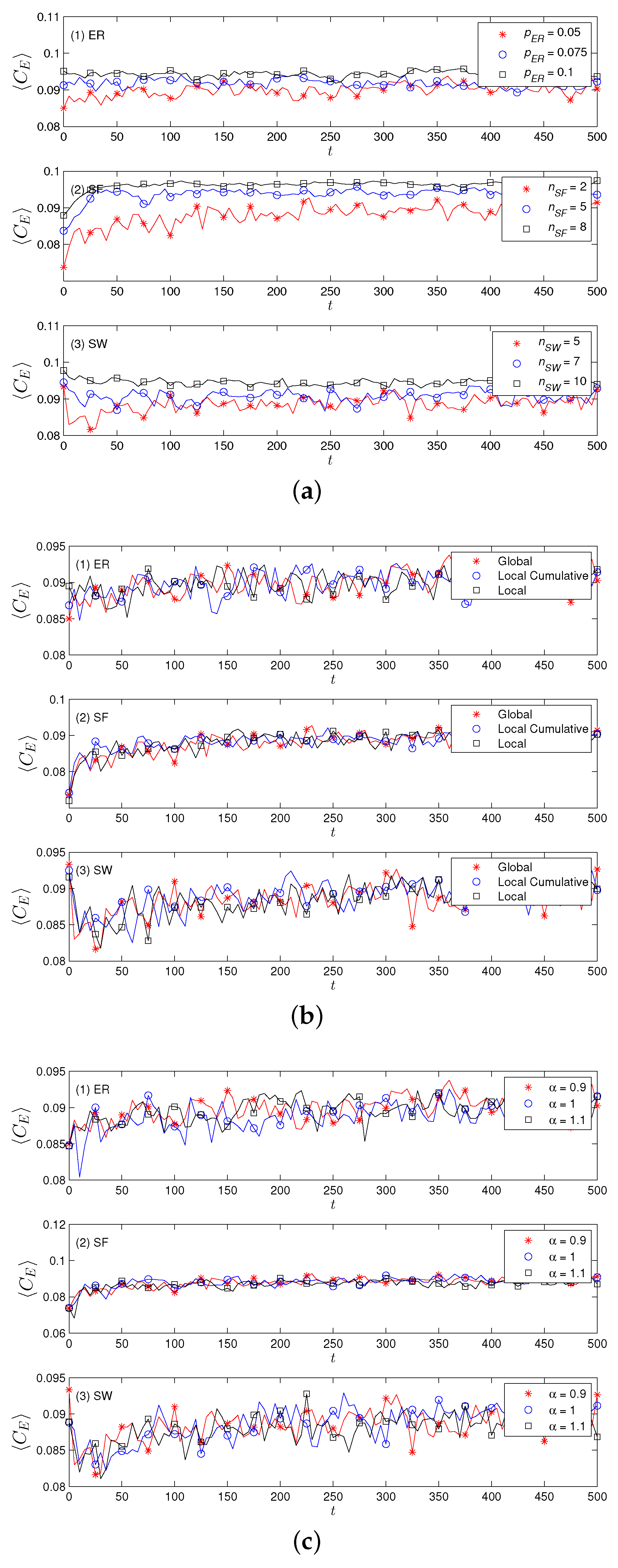
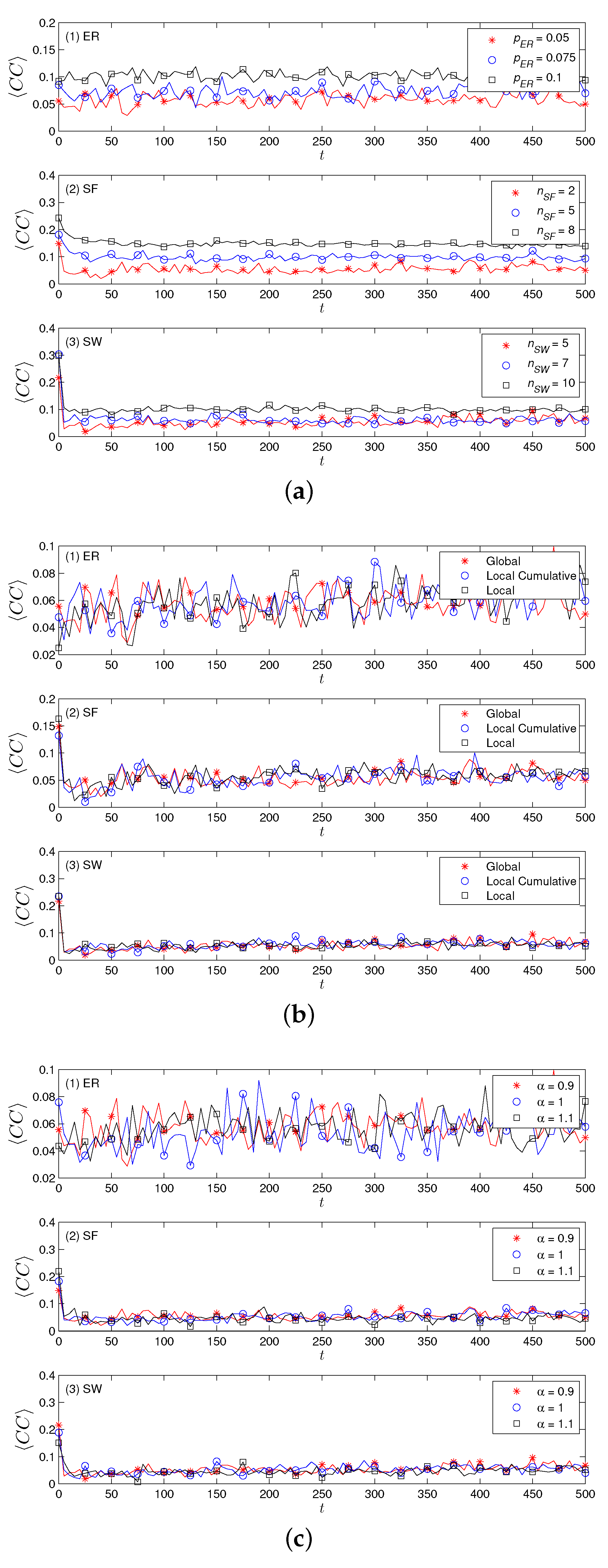
4.2. Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eguíluz, V.M.; Zimmermann, M.G.; Conde, C.J.C.; Miguel, M.S. Cooperation and the Emergence of Role Differentiation in the Dynamics of Social Networks. Am. J. Sociol. 2005, 110, 977–1008. [Google Scholar] [CrossRef]
- Gnyawali, D.R.; Charleton, T.R. Nuances in the Interplay of Competition and Cooperation: Towards a Theory of Coopetition. J. Manag. 2018, 44, 2511–2534. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Hauge, K.E.; Brekke, K.A.; Nyborg, K.; Lind, J.T. Sustaining cooperation through self-sorting: The good, the bad, and the conditional. Proc. Natl. Acad. Sci. USA 2018. [Google Scholar] [CrossRef] [PubMed]
- Phelps, C.C. A Longitudinal Study of the Influence of Alliance Network Structure and Composition on Firm Exploratory Innovation. Acad. Manag. J. 2010, 53, 890–913. [Google Scholar] [CrossRef]
- Gulati, R. Network location and learning: The influence of network resources and firm capabilities on alliance formation. Strateg. Manag. J. 1999, 20, 397–420. [Google Scholar] [CrossRef]
- Wassmer, U. Alliance Portfolios: A Review and Research Agenda. J. Manag. 2010, 36, 141–171. [Google Scholar] [CrossRef]
- Helen, L.; Kerry, B.; Lisa, B.; Caroline, B.; Keith, T. Improving Employees’ Work-Life Balance in the Construction Industry: Project Alliance Case Study. J. Constr. Eng. Manag. 2007, 133, 807–815. [Google Scholar]
- Dovev, L. Alliance portfolios and firm performance: A study of value creation and appropriation in the U.S. software industry. Strateg. Manag. J. 2007, 28, 1187–1212. [Google Scholar]
- Anthony, G.; Beamish, P.W. The effect of alliance network diversity on multinational enterprise performance. Strateg. Manag. J. 2005, 26, 333–354. [Google Scholar]
- Cattani, G.; Ferriani, S. A Core/Periphery Perspective on Individual Creative Performance: Social Networks and Cinematic Achievements in the Hollywood Film Industry. Organ. Sci. 2008, 19, 824–844. [Google Scholar] [CrossRef]
- Gracia-Lázaro, C.; Ferrer, A.; Ruiz, G.; Tarancón, A.; Cuesta, J.A.; Sánchez, A.; Moreno, Y. Heterogeneous networks do not promote cooperation when humans play a Prisoner’s Dilemma. Proc. Natl. Acad. Sci. USA 2012, 109, 12922–12926. [Google Scholar] [CrossRef] [PubMed]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Weisbuch, G.; Deffuant, G.; Amblard, F.; Nadal, J.P. Meet, discuss, and segregate! Complexity 2002, 7, 55–63. [Google Scholar] [CrossRef]
- Shang, Y. Deffuant model with general opinion distributions: First impression and critical confidence bound. Complexity 2013, 19, 38–49. [Google Scholar] [CrossRef]
- Shang, Y. Deffuant model of opinion formation in one-dimensional multiplex networks. J. Phys. A Math. Theor. 2015, 48, 395101. [Google Scholar] [CrossRef]
- Hanaki, N.; Peterhansl, A.; Dodds, P.S.; Watts, D.J. Cooperation in evolving social networks. Manag. Sci. 2007, 53, 1036–1050. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef]
- Shirado, H.; Christakis, N.A. Locally noisy autonomous agents improve global human coordination in network experiments. Nature 2017, 545, 370–374. [Google Scholar] [CrossRef]
- Rand, D.G.; Arbesman, S.; Christakis, N.A. Dynamic social networks promote cooperation in experiments with humans. Proc. Natl. Acad. Sci. USA 2011, 108, 19193–19198. [Google Scholar] [CrossRef]
- Stewart, A.J.; Parsons, T.L.; Plotkin, J.B. Evolutionary consequences of behavioral diversity. Proc. Natl. Acad. Sci. USA 2016, 113, E7003–E7009. [Google Scholar] [CrossRef] [PubMed]
- Sekara, V.; Stopczynski, A.; Lehmann, S. Fundamental structures of dynamic social networks. Proc. Natl. Acad. Sci. USA 2016, 113, 9977–9982. [Google Scholar] [CrossRef] [PubMed]
- Challet, D.; Zhang, Y.C. Emergence of cooperation and organization in an evolutionary game. Phys. A Stat. Mech. Its Appl. 1997, 246, 407–418. [Google Scholar] [CrossRef]
- Challet, D.; Marsili, M.; Zhang, Y.C. Minority Games: Interacting Agents in Financial Markets; Number 9780199686698 in OUP Catalogue; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Shang, Y. Consensus on averager-copier-voter networks of moving dynamical agents. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 023116. [Google Scholar] [CrossRef]
- Shang, Y. Hybrid consensus for averager–copier–voter networks with non-rational agents. Chaossolitons Fract. 2018, 110, 244–251. [Google Scholar] [CrossRef]
- Chesbrough, H.; Vanhaverbeke, W.; West, J. Open Innovation: Researching a New Paradigm; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Li, W.; Xu, J.; Zheng, M. Green Governance: New Perspective from Open Innovation. Sustainability 2018, 10, 3845. [Google Scholar] [CrossRef]
- Yun, J.J.; Won, D.; Park, K. Dynamics from open innovation to evolutionary change. J. Open Innov. Technol. Mark. Complex. 2016, 2, 7. [Google Scholar] [CrossRef]
- Yun, J.J.; Jung, K.; Yigitcanlar, T. Open Innovation of James Watt and Steve Jobs: Insights for Sustainability of Economic Growth. Sustainability 2018, 10, 1553. [Google Scholar] [CrossRef]
- Yun, J.J.; Won, D.; Jeong, E.; Park, K.; Lee, D.; Yigitcanlar, T. Dismantling of the Inverted U-Curve of Open Innovation. Sustainability 2017, 9, 1423. [Google Scholar] [CrossRef]
- Yun, J.J. How do we conquer the growth limits of capitalism? Schumpeterian Dynamics of Open Innovation. J. Open Innov. Technol. Mark. Complex. 2015, 1, 17. [Google Scholar] [CrossRef]
- Arthur, W.B. Inductive Reasoning and Bounded Rationality. Am. Econ. Rev. 1994, 84, 406–411. [Google Scholar]
- Challet, D.; Marsili, M.; Zecchina, R. Statistical Mechanics of Systems with Heterogeneous Agents: Minority Games. Phys. Rev. Lett. 2000, 84, 1824–1827. [Google Scholar] [CrossRef] [PubMed]
- Kristoufek, L.; Vosvrda, M. Herding, minority game, market clearing and efficient markets in a simple spin model framework. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 148–155. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Huang, Z.G.; Wu, Z.X.; Su, R.; Lai, Y.C. Controlling herding in minority game systems. Sci. Rep. 2016, 6, 20925. [Google Scholar] [CrossRef]
- Kutsuna, H.; Tagashira, S.; Fujita, S. A Fair and Efficient Congestion Control Scheme Based on Minority Game. In Proceedings of the 2006 14th IEEE International Conference on Networks, Singapore, 13–15 September 2006; Volume 1, pp. 1–6. [Google Scholar]
- Shafique, M.; Bauer, L.; Ahmed, W.; Henkel, J. Minority-Game-based resource allocation for run-time reconfigurable multi-core processors. In Proceedings of the 2011 Design, Automation Test in Europe, Grenoble, France, 14–18 March 2011; pp. 1–6. [Google Scholar]
- Elmachkour, M.; Sabir, E.; Kobbane, A.; Ben-Othman, J.; Koutbi, M.E. The greening of spectrum sensing: A minority game-based mechanism design. IEEE Commun. Mag. 2014, 52, 150–156. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Pósfai, M. Network Science, 1st ed.; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar]
- Roca, C.P.; Sánchez, A.; Cuesta, J.A. Individual Strategy Update and Emergence of Cooperation in Social Networks. J. Math. Sociol. 2012, 36, 1–21. [Google Scholar] [CrossRef]
- Caridi, I.; Ceva, H. The Minority Game with interactions. Phys. A Stat. Mech. Its Appl. 2004, 339, 574–582. [Google Scholar] [CrossRef]
- Slanina, F. Social organization in the Minority Game model. Phys. A Stat. Mech. Its Appl. 2000, 286, 367–376. [Google Scholar] [CrossRef]
- Kalinowski, T.; Schulz, H.J.; Briese, M. Cooperation in the Minority Game with local information. Phys. A Stat. Mech. Its Appl. 2000, 277, 502–508. [Google Scholar] [CrossRef]
- Quan, H.J.; Wang, B.H.; Hui, P.; Luo, X.S. Self-segregation and enhanced cooperation in an evolving population through local information transmission. Phys. A Stat. Mech. Its Appl. 2003, 321, 300–308. [Google Scholar] [CrossRef]
- Lavička, H.; Slanina, F. Evolution of imitation networks in Minority Game model. Eur. Phys. J. B 2007, 56, 53–63. [Google Scholar] [CrossRef]
- Shang, L.; Wang, X.F. Evolutionary minority game on complex networks. Phys. A Stat. Mech. Its Appl. 2007, 377, 616–624. [Google Scholar] [CrossRef]
- Burgos, E.; Ceva, H.; Perazzo, R. The evolutionary minority game with local coordination. Phys. A Stat. Mech. Its Appl. 2004, 337, 635–644. [Google Scholar] [CrossRef]
- Paczuski, M.; Bassler, K.E.; Corral, A. Self-Organized Networks of Competing Boolean Agents. Phys. Rev. Lett. 2000, 84, 3185–3188. [Google Scholar] [CrossRef] [PubMed]
- Shang, L.; Wang, X.F. A modified evolutionary minority game with local imitation. Phys. A Stat. Mech. Its Appl. 2006, 361, 643–650. [Google Scholar] [CrossRef]
- Fagiolo, G.; Valente, M. Minority Games, Local Interactions, and Endogenous Networks. Comput. Econ. 2005, 25, 41–57. [Google Scholar] [CrossRef]
- Chen, S.H.; Gostoli, U. On the complexity of the El Farol Bar game: A sensitivity analysis. Evol. Intell. 2016, 9, 113–123. [Google Scholar] [CrossRef]
- Chen, S.H.; Gostoli, U. Coordination in the El Farol Bar problem: The role of social preferences and social networks. J. Econ. Interact. Coord. 2017, 12, 59–93. [Google Scholar] [CrossRef]
- Anghel, M.; Toroczkai, Z.; Bassler, K.E.; Korniss, G. Competition-Driven Network Dynamics: Emergence of a Scale-Free Leadership Structure and Collective Efficiency. Phys. Rev. Lett. 2004, 92, 058701. [Google Scholar] [CrossRef] [PubMed]
- Kirley, M. Evolutionary minority games with small-world interactions. Phys. A Stat. Mech. Its Appl. 2006, 365, 52–528. [Google Scholar] [CrossRef]
- Cajueiro, D.O.; Camargo, R.S.D. Minority game with local interactions due to the presence of herding behavior. Phys. Lett. A 2006, 355, 280–284. [Google Scholar] [CrossRef]
- Quan, H.J.; Zhu, C.Y. Behaviors of imitated agents in an evolutionary minority game on NW small world networks. Phys. Procedia 2010, 3, 1741–1745. [Google Scholar] [CrossRef]
- Mello, B.A.; Souza, V.M.; Cajueiro, D.O.; Andrade, R.F. Network evolution based on minority game with herding behavior. Eur. Phys. J. B 2010, 76, 147–156. [Google Scholar] [CrossRef]
- Nishimoto, K.; Tanev, I.; Shimohara, K. Proposal of a Network-Based Minority Game Model with Observation and Modification Processes. Int. J. Comput. Theory Eng. 2013, 5, 690. [Google Scholar] [CrossRef]
- Chen, J.; Quan, H. Effect of imitation in evolutionary minority game on small-world networks. Phys. A Stat. Mech. Its Appl. 2009, 388, 945–952. [Google Scholar] [CrossRef]
- Moelbert, S.; Rios, P.D.L. The local minority game. Phys. A Stat. Mech. Its Appl. 2002, 303, 217–225. [Google Scholar] [CrossRef]
- Gulati, R.; Nohria, N.; Zaheer, A. Strategic Networks. Strateg. Manag. J. 2000, 21, 203–215. [Google Scholar] [CrossRef]
- Ahuja, G. Collaboration Networks, Structural Holes, and Innovation: A Longitudinal Study. Adm. Sci. Q. 2000, 45, 425–455. [Google Scholar] [CrossRef]
- Baum, J.A.C.; Calabrese, T.; Silverman, B.S. Do not go it alone: Alliance network composition and startups’ performance in Canadian biotechnology. Strateg. Manag. J. 2000, 21, 267–294. [Google Scholar] [CrossRef]
- Bae, J.; Insead, M.G. Partner Substitutability, Alliance Network Structure, and Firm Profitability in the Telecommunications Industry. Acad. Manag. J. 2004, 47, 843–859. [Google Scholar] [CrossRef]
- Walker, G.; Kogut, B.; Shan, W. Social Capital, Structural Holes and the Formation of an Industry Network. Organ. Sci. 1997, 8, 109–125. [Google Scholar] [CrossRef]
- Castro, I.; Casanueva, C.; Galán, J.L. Dynamic evolution of alliance portfolios. Eur. Manag. J. 2014, 32, 423–433. [Google Scholar] [CrossRef]
- Shang, Y. Distinct Clusterings and Characteristic Path Lengths in Dynamic Small-World Networks with Identical Limit Degree Distribution. J. Stat. Phys. 2012, 149, 505–518. [Google Scholar] [CrossRef]
- Hart, M.; Jefferies, P.; Johnson, N.; Hui, P. Crowd–anticrowd theory of the minority game. Phys. A Stat. Mech. Its Appl. 2001, 298, 537–544. [Google Scholar] [CrossRef]
- Sasidevan, V. Effect of detailed information in the minority game: Optimality of 2-day memory and enhanced efficiency due to random exogenous data. J. Stat. Mech. Theory Exp. 2016, 2016, 073405. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.-J.; Tang, Y.; Xiong, J.; Wang, W.-J.; Zhang, Y.-C. Dynamics of Cooperation in Minority Games in Alliance Networks. Sustainability 2018, 10, 4746. https://doi.org/10.3390/su10124746
Zhang X-J, Tang Y, Xiong J, Wang W-J, Zhang Y-C. Dynamics of Cooperation in Minority Games in Alliance Networks. Sustainability. 2018; 10(12):4746. https://doi.org/10.3390/su10124746
Chicago/Turabian StyleZhang, Xin-Jie, Yong Tang, Jason Xiong, Wei-Jia Wang, and Yi-Cheng Zhang. 2018. "Dynamics of Cooperation in Minority Games in Alliance Networks" Sustainability 10, no. 12: 4746. https://doi.org/10.3390/su10124746
APA StyleZhang, X.-J., Tang, Y., Xiong, J., Wang, W.-J., & Zhang, Y.-C. (2018). Dynamics of Cooperation in Minority Games in Alliance Networks. Sustainability, 10(12), 4746. https://doi.org/10.3390/su10124746





