1. Introduction
Sustainable urbanization has been raising living standards and enhancing household income tremendously. China’s government makes efforts to invest abundant funds to ensure healthcare insurance, and require health cost reductions to 30% by the end of 2018 [
1]. On the basis of rural revitalization policy in China, the demand for rational and available healthcare facility planning has attracted widespread attention. One of the most crucial issues is to achieve high healthcare service quality in developing cities or rural areas, which contributes to a comprehensive understanding of the development process overall within the whole healthcare system. With the worldwide trend of tremendous population growth, diseases increasing and environmental degradation, healthcare facility location problems (HCFLPs) have become increasingly noticeable in human society [
2,
3]. Unreasonable and unconsidered healthcare facility (HCF) location will impede economic growth, as well as increase morbidity and mortality. In some developing cities, the treatment technology and medical equipment of most hospitals may not satisfy the rigid demand due to the lagging economy. Therefore, completing the basic healthcare services in rural and remote regions should be prioritized. As a vital element in strategic management, optimizing HCF location plays a significant role in decision making for private and public organizations such as schools, warehouses and retail stores [
2]. Selecting appropriate positions is not only able to improve the service accessibility for patients, but also simultaneously enhance the service quality [
4].
Furthermore, most scholars have been focusing on location assignment for health system but ignoring the significance of improving capacity. It is obvious that different stakeholders (i.e., suppliers and customers) have their preferential objectives in facility location problems (FLPs) [
5]. Local governments generally expect to expand the scope of services to acquire higher social benefits, while the patients pursue greater capacity of each facility to obtain a better treatment environment. Thus, keeping the capacity in balance becomes a novel tendency in FLPs, which promotes availability gradually. Moreover, when generating healthcare planning strategy, decision-makers (DMs) will take numerous factors into account, such as travel distance, construction and management cost, transportation convenience, and capacity constraints [
6,
7,
8,
9]. Since these objectives often conflict with each other, a multiple objective decision making (MODM) approach is introduced to solve such a complex planning problem.
As the strategy horizon moves forward constantly, an uncertain environment needs to be taken into account for long-range planning [
8]. In a realistic world, the decision making process in a medical system involves a degree of uncertainty [
10]. For instance, there is probability between medical demand and cost, which leads to distinct optimal solutions. Combined with the aforementioned objectives, the computational procedure of this Non-deterministic Polynomial-Hard (NP-hard) problem becomes extraordinary sophisticated and diverse. To solve this problem, particle swarm optimization (PSO) algorithm is introduced to find optimal solutions due to its fast convergence and effective search ability [
11]. The PSO algorithm has been proved to successfully find optimal solutions under complex continuous search spaces. Although it does not guarantee optimality, it is appropriate for the current application [
12].
In general, this study aims to find applicable location-allocation solutions in uncertain environment, which plays a critical role to ensure access to public facilities and personal demands. Bi-level multiple objective programming is introduced to determine location and capacity distribution concurrently. In addition, a modified PSO algorithm is utilized to equilibrate the trade-off between complicated and multidimensional objectives. The eventual optimal results are reflected as two aspects: introduce new facilities and upgrade existing capacities.
The remainder of this paper is organized as follows:
Section 2 analyzes the current researches and
Section 3 describes the main problems in healthcare system. In
Section 4, the modeling process and algorithm application are introduced in detail. Following this,
Section 5 provides a numerical example to validate the availability and applicability of our approach. Finally,
Section 6 gives the conclusions and future research directions.
5. Case Study
In order to verify the effectiveness of the proposed optimal model, we use computational experiments based on the depressed region of Mao County, which is located in the northwest of Sichuan province. The test aims to illustrate how the proposed model can be applied to support healthcare planners in location and allocation decisions in an uncertain environment.
5.1. Study Area
Mao County has a per capita GDP of 30046 CNY in 2017, and is a remote region with poor economic development accessibility. The detailed location of study area is shown in
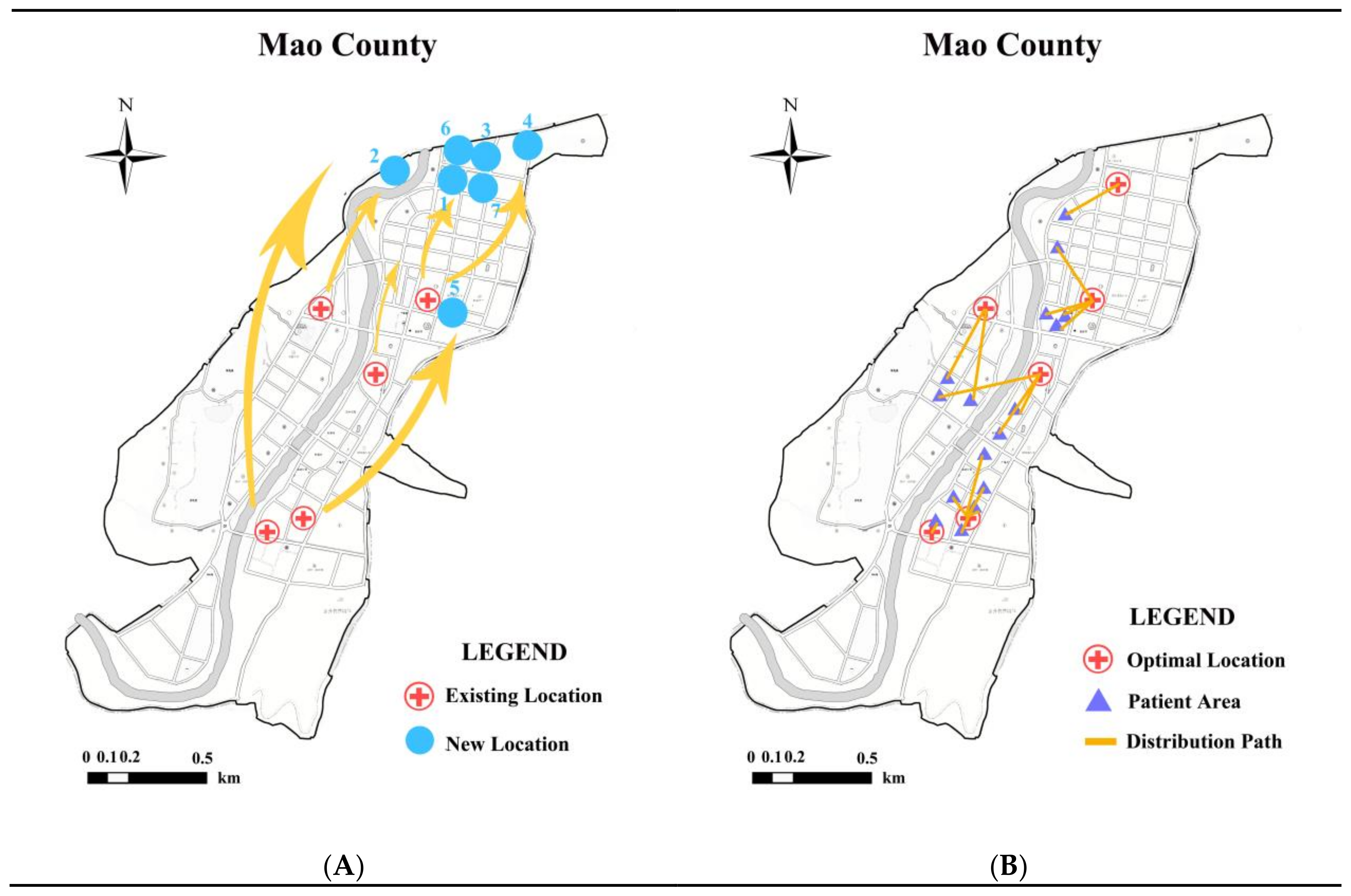
Figure 5. In our investigations, this developing region needs to provide sufficient healthcare facilities to the large scattered residents. What is more, there are 5 middle healthcare units and sixteen patient areas located in the township, which are presented in
Figure 6A. The total sickbed number of existing hospitals is 527, which does not satisfy the total requirements for nearly 800 (i.e.,
). Furthermore, the transportation advantage areas and environmentally tranquil areas around the existing hospitals are marked in
Figure 6B.
5.2. Date Acquisition and Processing
The numerical data about population, medical demand, healthcare information, etc., are obtained from two types of organization, i.e., governmental agencies and academic institutions. According to our field investigation in local governments, the map data referring to residential distribution and healthcare network are retrieved from Statistical Bureau, Health and Family Planning Bureau and Land Source Bureau. In order to obtain the weights for environmental elements, the authors have contacted five experienced experts from the Center for Rural Construction Integrated Management (CRCIM) in Sichuan Agriculture University. The experts selected four essential areas respectively from each environmental type (
Figure 6B), and gave the comprehensive weights (
Table 4) based on the method of the analytic hierarchy process (AHP) [
61]. Moreover, they proposed the morbidity of patient is generated by a uniform distribution
, and the uncertain sickbed price using a triangular fuzzy number
with a confidence level of 90%.
5.3. Case Solution
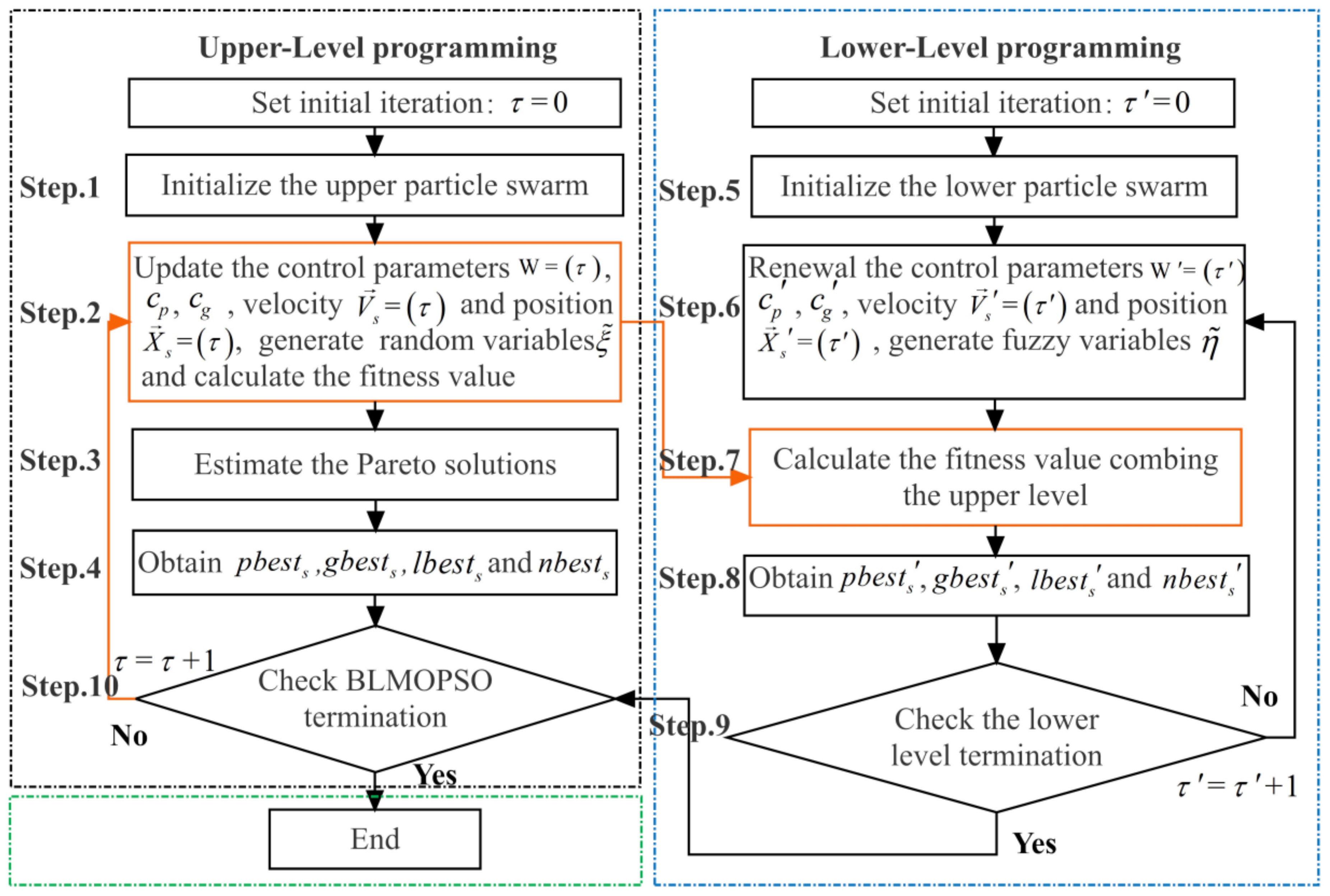
The BLMOPSO algorithm was conducted on a Windows 10 personal computer with 8 GB of RAM running at 2.8 GHz on an Intel Core i7 processor. The control parameters on each level were set as follows: iteration , swarm size s = 20, inertia weight in [0.1,0.9], personal and global acceleration coefficient in, local and near neighbor best acceleration constant .
Since operating one iteration on the upper-level needs 30 iterations on the lower-level, the performance period grows exponentially. After 900 iterations in total, the pareto solutions were generated within average 7 minutes. The seven solutions on the upper level are demonstrated in
Table 5, indicating the position and patient allocation scheme when constructing a new HCF. Notably, each location solution has a group of capacity scenarios on the lower level. Due to the space limitation, this research picked one of the capacity optimal solutions corresponding to an allocation scheme, which is shown in
Table 6.
5.4. Analytic Results
With respect to alternative decision making,
Figure 7A provides all of optimal solutions for governments to choose their preferences. That is to say, looking for to high service quality may situate the location far away from arterial road or quiet districts and, vice versa, pursuing a suitable medical environment could aggravate the travel burden. Furthermore, on the basis of primary results summarized in the tables as above, the location distributions of HCFs are illustrated in
Figure 7B.
Figure 8 displays the capacity allocation for one of the options selected in
Table 6. Obviously, availability and accessibility can be promoted by adding more sickbeds, but also cause the construction costs to rise. On the contrary, controlling the facility capacity can ease the financial pressure, but it may delay the best treatment for patients as well. Within this context, DMs should find a tradeoff among such conflicting objectives under different situations.
5.5. Comparative Analysis
This research compares the BLMPPSO with basic PSO in HCFLPs to validate its efficiency. Due to the complexity of multiple objective optimization compared to single objective programming, we studied four metrics of performance proposed in Gan et al. [
40] to further illustrate the exploration and exploitation ability of the algorithm.
Table 7 describes the iterative process of the pareto solutions, which discloses the diversity of the results.
Table 8 collects different types of indicator value, and shows that the proposed algorithm performs better in all directions.
5.6. Stability Analysis
The eventual optimal solutions are acquired based on 30 tests in order to avoid accidental events. Although the experience is likely to generate other potential situations, the authors select one of the results that occurred most frequently. The test statistics are recorded in
Table 9. In addition, the performance metric of “the extent” can test the stability of the results as well. Thus, the authors compared and calculated the error rates amongst the pareto solutions which with the same solution amount.
Table 10 shows that most of error rates are no more than 5%. According to these two tables, the solutions obtained in this study are credible and reasonable.
6. Conclusions and Future Research
This study presents a location-allocation optimal model for China’s healthcare system to enhance availability and accessibility by using bi-level multiple objective programming in an uncertain environment. The upper level considers the conflicts of social and environmental factors on location decision, while the lower level adjusts the facility capacity, including service quality and financial costs simultaneously. Since-facility spatial distribution is a complex and time-consuming problem, and an ameliorated BLMOPSO algorithm is designed to improve the accuracy of the results. In order to verify the applicability and versatility of the proposed model, an extensive computational experiment has been carried out by using the data obtained from a field investigation. It balances the tradeoffs among the four conflicting optimal targets, analyzes the efficiency of location decisions, and estimates the requirement for capacity increase. Moreover, the optimal pareto solutions illustrate that the DMs’ preference has a significant bearing on the spatial and capacity assignment of patient areas to healthcare units.
The characteristic contributions of this paper are: (1) the hierarchical programming carries out the location and capacity assignment to maintain a balance between supply and demand; (2) the proposed model considers uncertainty associated with medical demand and costs to simulate possible realization; (3) BLMOPSO is designed to efficiently tackle such a NP-hard problem by means of improving the global search and reducing the probability of falling into premature convergence; (4) the optimal results pave the way for the practical application in healthcare network design, and also can be popularized in other types of public facilities such as schools, warehouses and police stations.
The current research is original, and will be needed for future work in at least two aspects. On one hand, choosing an appropriate location depends on not only the external environment but also internal factors such as competition among hospitals, classes of patients and diagnostic cost. On the other hand, the optimal objectives of urban and rural areas may differ and should be adjusted according to regional conditions.