Abstract
Implementing cleaner production (CP) is effective to resolve the contradiction between economic growth and environmental crisis. To avoid destroying the ecological environment in the exploitation process of mineral resources, CP has been developed in many gold mines to achieve the goal of sustainable development. Thus, this paper aims to propose a favorable approach to assess CP for gold mines. First, according to the specific characteristics of gold mines, an evaluation criteria system of CP is established. Meanwhile, considering the diversity of evaluation information, crisp numbers and probabilistic linguistic term sets (PLTSs) are adopted to indicate the quantitative and qualitative information, respectively. Subsequently, a modified experts grading method based on PLTSs is proposed to calculate the sub-criteria weights’ values. Following this, an extended Tomada de Decisão Interativa Multicritério (TODIM) method with hybrid evaluation values is presented to obtain the ranking order. Finally, the hybrid multi-criteria decision making (MCDM) approach is applied to a case of assessing CP for gold mines to demonstrate its feasibility. Furthermore, the robustness and advantages of this approach are justified by sensitivity and comparison analyses. The results show that the proposed approach is feasible to solve such kinds of evaluation problems with hybrid decision making information and can provide some managerial suggestions for government and enterprises.
1. Introduction
Gold, as an important strategic mineral, is not only a special currency for reserves and investment, but also an essential material for jewelry, electronics, communications, and other industries [1]. However, considerable environmental problems occur as a result of the large-scale mining of gold ore [2,3]. Because of the particularity of gold ore, the component of gold is very low. In general, one ton of ore only contains a few grams of gold. Thus, in comparison with other types of ores, more waste residue may be produced during the gold mine’s lifetime [4,5,6]. As the gold ore is mined by the drilling and blasting method, quantities of waste gas [7,8], such as dust and blasting fumes, are emitted into the sky. Besides, most of the gold is extracted using fluoride, which leads to the discharge of a huge amount of waste water [9,10,11]. Numerous toxic and harmful substances are contained in this waste, which do great harm to the surrounding environment. In addition, as the traditional linear production model is still employed in many gold mines, the resource utilization efficiency in these mines is quite low [12].
Unlike the traditional production mode that achieves economic growth at the expense of environmental disruption, cleaner production (CP) is an innovative production approach. It applies an integrated preventative environmental strategy to processes, products, and services, so as to increase resource efficiency and reduce environmental pollution [13,14,15]. On account of the great issues of resources scarcity and environmental crisis, CP is essential for mines. Hilson and Nayee [16] defined CP in the mining sector as a superior level of environmental performance, which can only be achieved through improved strategy and housekeeping, sound process control, optimized plant layout, and the implementation of efficient management techniques. Song and Zhou [17] put forward a mining CP system, which is composed of a training system, lifecycle CP system, and monitoring and auditing system. Hilson [18] suggested that CP practices in the mining industry can be classified into three kinds, that is, managerial changes, policy changes, and physical changes. Rajaram et al. [19] deemed that sustainable mining is conducted in a manner that balances economic, environmental, and social considerations. The application of CP can help enterprises improve economic efficiency under the prerequisite of environmental protection [20,21,22]. Owing to the huge advantages of industrial pollution prevention, more and more mine enterprises prefer to adopt the novel CP pattern instead of the traditional one.
In order to assess the specific performance of CP for different enterprises, it is significant to develop appropriate and efficient evaluation methods [23]. Considering the variety of criteria, many researchers think that the evaluation of CP is a multi-criteria decision making (MCDM) problem. Tseng et al. [24] adopted the fuzzy analytic hierarchy process (AHP) method to discuss the different criteria for CP implementation in printed wire board manufacturing companies. Peng and Li [25] presented a fuzzy-soft comprehensive evaluation model to evaluate CP for aviation enterprises. Basappaji and Nagesha [26] proposed a fuzzy logic approach to assess the CP level for agro-based industries. Gong et al. [27] employed the evidential reasoning (ER) and data envelopment analysis (DEA) cross-efficiency approach to evaluate CP for iron and steel firms. Dong et al. [28] combined the AHP method and uncertainty measurement model to evaluate the CP for phosphorus chemical enterprises. Liang et al. [29] integrated the evaluation based on distance from average solution (EDAS) method with elimination and choice translating reality (ELECTRE) approach to evaluate the CP for gold mines.
Although the above methods can be well used to solve the CP evaluation problems to a certain extent, there are still some limitations:
(1) The formats of criteria values only include crisp numbers or fuzzy numbers, which cannot describe evaluation information thoroughly. In general, both quantitative and qualitative information is contained in the evaluation process of CP. Hence, they should be expressed respectively using different types of data.
(2) Likewise, these above-mentioned evaluation methods cannot handle the MCDM issues with multiple types of assessment values. As more than one type of evaluation value, like crisp numbers, triangular fuzzy numbers, or linguistic variables, may exist in the evaluation process, hybrid MCDM methods need to be proposed.
On account of the aforementioned deficiencies of existing approaches, a novel evaluation method of CP for gold mines can be proposed. In order to conquer limitation (1), hybrid types of data can be adopted to describe evaluation information. In the real world, quantitative evaluation information can be indicated by crisp numbers, and qualitative information is often described by linguistic phrases from experts, such as bad, good, and very good [30,31,32]. So far, numerous linguistic extensions have been developed, such as hesitant fuzzy linguistic term sets [33], linguistic intuitionistic fuzzy sets [34], and linguistic neutrosophic sets [35]. Recently, Pang et al. [36] put forward the novel concept of PLTSs (probabilistic linguistic term sets), based on extended hesitant fuzzy linguistic term sets with probability information. Evaluation information in the form of PLTSs simultaneously contains linguistic terms and probabilistic values. By using PLTSs, the original linguistic information can be comprehensively described.
For the sake of overcoming limitation (2), a MCDM method extended by crisp numbers and PLTSs can be proposed to deal with hybrid decision making problems. Up to now, numerous extended decision-making methods based on PLTSs have been proposed one after another, like the extended technique for order preference by similarity to an ideal solution (TOPSIS) [37], vlsekriterijumska optimizacija i kompromisno resenje (VIKOR) [38], the cloud model [39] and the linear programming method [40]. Nevertheless, the Tomada de Decisão Interativa Multicritério (TODIM) method has not been combined with PLTSs. As a classical decision making method, the TODIM method presented by Gomes and Lima [41] has been successfully employed to handle a variety of evaluation issues [42,43,44]. On the other hand, the types of data in these methods are only PLTSs, as opposed to hybrid decision making information. Accordingly, considering the diversity of criteria, an extended TODIM method based on crisp numbers and PLTSs can be proposed to assess the CP for gold mines.
Because the influence factors and conditions of different industries are various, these existing methods are not appropriate to assess CP for gold mines. To the best of our knowledge, the research on CP evaluation for gold mines is very scarce, the evaluation system of CP should be established after considering the specific features of gold mines.
Based on the motivations mentioned above, the objective of this paper is to propose a hybrid MCDM approach for assessing CP for gold mines. The main contributions of this paper are listed as follows:
(1) The evaluation criteria of CP for gold mines are identified, and the evaluation information is processed into two types of data. The precise values for quantitative criteria are expressed by crisp numbers, and the linguistic values for qualitative criteria are indicated by PLTSs, so that the evaluation information can be described more adequately.
(2) The modified experts grading method with PLTSs is proposed to obtain the criteria weights. The linguistic evaluation terms given by experts are expressed with PLTSs as opposed to scores or specific values, which can demonstrate the original linguistic information more fully and reasonably.
(3) A hybrid MCDM approach on the basis of an extended TODIM method is proposed to assess CP for gold mines, which can obtain stable and reliable evaluation results. Besides, these evaluation results can provide some managerial implications for government and enterprises.
For clarity, the rest of this paper is organized as follows. Section 2 introduces the evaluation criteria of CP for gold mines and some basic knowledge about PLTSs. In Section 3, three phases of the proposed hybrid MCDM approach are presented. In Section 4, the proposed approach is applied in assessing CP for gold mines. The sensitivity analysis, comparison analysis, and managerial implications are discussed in Section 5. Finally, some main conclusions are presented.
2. Materials and Methods
In this section, the evaluation criteria system of CP for gold mines is first established. Then, some basic concepts of PLTSs are introduced. These mentioned materials and methods will be useful in the remainder of this research.
2.1. Evaluation Criteria of Cleaner Production for Gold Mines
In this subsection, the evaluation criteria of CP for gold mines are recognized. However, there has not been an international standard for the evaluation of CP in gold mines so far. In order to select the appropriate criteria, some principles should be followed, which include the hierarchy principle, independence principle, combination of qualitative and quantitative criteria principle, and data with easy accessibility principle [45]. According to the specific characteristics of CP for gold mines and some existing literature [28,46,47], the evaluation criteria system is established with seven criteria and sixteen sub-criteria. The evaluation criteria system of CP for gold mines is shown in Figure 1, and the detailed descriptions of these criteria are indicated as follows.
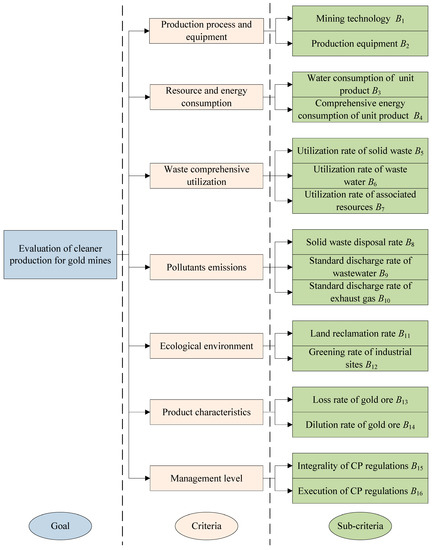
Figure 1.
Evaluation criteria system of cleaner production (CP) for gold mines.
(1) Production process and equipment
Selecting the appropriate production process and equipment is a key problem for CP in gold mines. In general, the more advanced the production process and equipment, the better the performance of CP [46]. Therefore, the sub-criteria of production process and equipment contain the mining technology and production equipment .
(2) Resource and energy consumption
Resource and energy are essential for the production of gold mines. During the production process, achieving the same production goals with less resources and energy is vital and encouraging. This way, the resource and energy can be utilized with higher efficiency. Besides, water, power, and fuel are main consumables in the mining process [28]. Hence, the sub-criteria of resource and energy consumption contain the water consumption of unit product and comprehensive energy consumption of unit product .
(3) Waste utilization
The waste produced in gold mines is also a valuable resource, which is worth developing and utilizing. In particular, the solid waste, waste water, and associated resources are of great value, and can be utilized and recycled [48]. Accordingly, the sub-criteria of waste utilization contain the utilization rate of solid waste , utilization rate of waste water , and utilization rate of associated resources .
(4) Pollutants emissions
Although the waste can be utilized in the whole production cycle to some extent, there is still some waste released into the environment. Among them, solid waste, waste water, and exhaust gas play important roles, which lead to environmental pollution [28]. Consequently, the sub-criteria of pollutants emissions contain the solid waste disposal rate , standard discharge rate of wastewater , and standard discharge rate of exhaust gas .
(5) Ecological environment
The development of gold mines may inevitably have some adverse effects on the environment [49]. On the one hand, large tracts of land are occupied by quantities of tailings and waste stone, and the surrounding ecological environment is seriously destructed. On the other hand, the surface environment of mining area is greatly damaged because of the strata subsidence and mining disturbance. Thus, the sub-criteria of ecological environments contain the land reclamation rate and greening rate of industrial sites .
(6) Product characteristics
Improving product characteristics is essential for CP. The product of gold mines is mainly gold ore, and the characteristics of gold ore have great influences on the downstream productions [46]. The loss rate and dilution rate are the two important characteristics of gold ore. As a result, the sub-criteria of product characteristics contain the loss rate of gold ore and dilution rate of gold ore .
(7) Management level
The management level makes a dramatic impact on the performance of CP for gold mines. The establishment and implementation of corresponding regulations are important for improving CP level [16]. Thus, the sub-criteria of management level contain the integrality of CP regulations and execution of CP regulations .
2.2. Probabilistic Linguistic Term Sets
In this subsection, some relevant concepts of PLTSs are described as follows.
(1) The definition of linguistic term set (LTS)
Suppose there is a completely ordered and discrete LTS, denoted as , then any element in this set is a linguistic variable. For any two linguistic terms , , if , then . Besides, the negation operator is defined as [50].
For example, if there are the following five linguistic variables: “”, “”, “”, “” and “”, then they can consist of a LTS as , their preference relation is . Furthermore, , , , , and .
(2) The definition of linguistic scale function
The linguistic scale function is defined as a mapping from a linguistic variable to a corresponding crisp number [51]. Besides, the characteristic of monotonically increasing should be met. Then, the linguistic scale function can be obtained with the following equation [51]:
Furthermore, the inverse function can be acquired as
Take as an example, because it is in the LTS , then . Based on Equation (1), it can map to a crisp number . Similarly, if we know , a corresponding linguistic variable can be obtained using Equation (2).
(3) The definition of probabilistic linguistic term set (PLTS)
Given a LTS , the probabilistic linguistic term set (PLTS) can be denoted as [36]
where is the linguistic value related to the probabilistic information , and is the number of elements in .
For instance, given an LTS , a PLTS represents that, for an objective, the probability of getting an evaluation with “poor” is 20%, that with “fair” is 30%, that with “good” is 20%, and that with “very good” is 10%.
(4) Normalization of PLTS
Given a PLTS with , the normalized PLTS can be calculated by [36]
Take as an example, because using Equation (4), it can be normalized as
(5) The operational rules between two PLTSs
Let and be two PLTSs, and let be a positive real number, then the operational rules are defined as [52]
where
where .
For example, suppose , , , and , then , , , , , and .
(6) The distance between two PLTSs
Considering two arbitrary normalized PLTSs and , if , the distance between them is defined by [36]
where and are the subscripts of the linguistic terms and , respectively.
However, if , linguistic terms are added to , so that the numbers of linguistic terms in and are equal. The added linguistic terms are the smallest ones in , and the probabilities of all the linguistic terms are zero. Then, the distance between and can be calculated using Equation (11).
For instance, assume and , then .
(7) The comparison method between two PLTSs
Given a PLTS , the score function and deviation degree of can be obtained, respectively, as [41]
Then, the comparison method between two PLTSs and can be obtained by [36]
, when or (, );
, when or (, ); and
, when and .
For example, given two PLTSs and , then , , , and . Because , then .
3. Hybrid Multi-Criteria Decision Making Approach
A hybrid MCDM approach is proposed to evaluate the performance of CP in this section. The structure of this method is shown in Figure 2. It can be seen that this approach includes three phases: collect evaluation information, calculate the sub-criteria weights, and determine the ranking order. The specific steps are presented in the rest of this section.
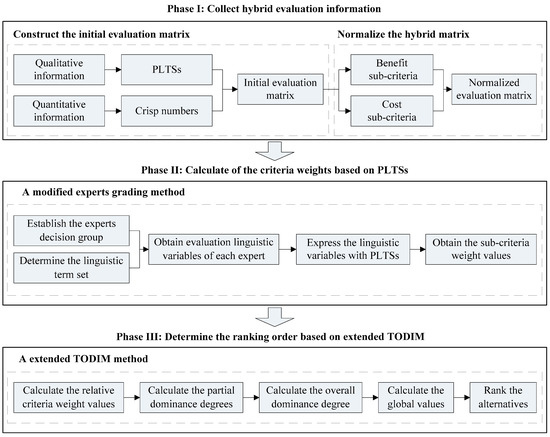
Figure 2.
Structure of the proposed hybrid multi-criteria decision making (MCDM) approach. PLTS—probabilistic linguistic term set; TODIM—Tomada de Decisão Interativa Multicritério.
3.1. Phase I: Collect Hybrid Evaluation Information
In Phase I, the evaluation information is collected, and the normalized hybrid decision matrix is obtained. In this research, crisp numbers and PLTSs are adopted to indicate certain and uncertain evaluation information, respectively. Thus, the initial evaluation information can be expressed by crisp numbers and PLTSs, respectively. The calculation steps are displayed as follows.
Step 1: Construct the initial evaluation matrix
Generally, the evaluation information is composed of quantitative information expressed by crisp numbers and qualitative information denoted by linguistic variables. Considering that PLTSs can indicate the original linguistic information intuitively and comprehensively, they are employed to describe the qualitative information.
Considering that experts are accustomed to making qualitative evaluations with linguistic phrases, such as “poor”, “fair”, “good”, and “very good” [37], the LTS can be expressed as . For group decision making methods, this qualitative evaluation information from experts can be combined by PLTSs. For example, ten experts are invited to make evaluations. If two experts consider that the value of criterion for alternative is slightly poor, three experts consider that it is fair, two experts consider that it is slightly good, one expert considers that it is good, and the remainder refuses to make a choice, then the comprehensive evaluation value of these ten experts can be expressed with a PLTS .
Consequently, in order to express quantitative and qualitative information simultaneously, crisp numbers and PLTSs are contained in the initial evaluation matrix, which is shown as
where is a crisp number, which represents the objective evaluation value of alternative for criterion ; and is a PLTS, which demonstrates the fuzzy evaluation value of alternative for criterion .
Step 2: Normalize the hybrid matrix
In general, both benefit and cost sub-criteria are included in the evaluation criteria system. In order to make the calculation convenient, the initial decision matrix should be normalized to make the type of all sub-criteria uniform.
For crisp numbers, the normalization values can be calculated by [48]
For PLTSs, the normalization values can be calculated by Equation (4). Besides, for PLTSs under cost sub-criteria, the evaluation values need to be changed according to Equation (8). Afterwards, the normalized evaluation matrix can be obtained as
3.2. Phase II: Calculate the Criteria Weights based on PLTSs
The aim of Phase II is to calculate the weight value of each criterion based on a modified experts grading method. In reality, experts are inclined to express the importance degrees of sub-criteria using linguistic phrases, such as “low”, “high”, and “very high”. However, these linguistic phrases are all expressed by scores in the traditional experts grading method, which cannot easily describe the initial evaluation information substantially. To improve the reasonability of decision making results, a modified experts grading method with PLTSs is proposed as follows.
Step 1: Determine the LTS
Generally, the linguistic terms used by experts to express the importance of sub-criteria are very low, low, slightly low, medium, slightly high, high, and very high, respectively [42]. Then, the LTS can be expressed as .
Step 2: Express the linguistic variables with PLTSs
After the LTS is determined, experts can provide their assessments on the importance of the sub-criteria individually and anonymously. Then, the linguistic variables provided by all experts can be processed and converted to PLTSs. For example, the PLTS means that 30% of experts think the importance of this criterion is slightly high, 20% of experts believe that it is high, and 50% of experts hold that it is very high.
Step 3: Obtain the sub-criteria weight values
The score function of PLTSs for each criterion can be calculated by Equation (12). Then, the weight values can be obtained by
where is the subscript of linguistic term .
3.3. Phase III: Determine the Ranking Order Based on Extended TODIM
In this phase, an extended TODIM method with hybrid evaluation values is proposed to determine the rank order of alternatives. The calculation steps are as follows.
Step 1: Calculate the relative sub-criteria weight values
First, the criterion with the highest weight value could be chosen as a reference criterion, denoted as . Then, the relative sub-criteria weight value of criterion to the reference criterion is
Step 2: Calculate the partial dominance degrees under sub-criteria
The partial dominance matrix indicates the degree of alternative () superior to alternative () under criterion . As the evaluation matrix is composed of crisp numbers and PLTSs, the partial dominance matrix can be calculated.
For crisp numbers, the partial dominance degree is calculated by
where means the attenuation factor of the losses; and indicates the distance between and , that is, .
For PLTSs, the partial dominance degree is obtained with
where indicates the distance between and , which can be obtained by Equation (11).
Step 3: Calculate the overall dominance degree for each alternative
The dominance matrix of alternative over is calculated by summing up the partial dominance matrices of all sub-criteria, which can be calculated as follows:
Step 4: Calculate the global values of alternatives
The global value of a certain alternative is determined by normalizing the dominance matrix, and the normalization equation is
Step 5: Rank the alternatives
After the value of is determined, the rank of each alternative can be obtained by ordering the values of . The higher the value, the better the alternative.
4. Case Study
Recently, a gold production corporation in China had a plan for evaluating the performance of CP for its gold mines. After a preliminary analysis and screening, four gold mines (denoted as , , , and ) were selected to be evaluated beforehand. If the evaluation results were acceptable, then the proposed method could be adopted and expanded to assess all gold mines. The development patterns of these four gold mines have a great difference, focuses on the comprehensive utilization of waste, focuses on the land reclamation, focuses on reducing the resource and energy consumption and diminishing the pollutants emission rate, and focuses on the green of industrial sites. Among them, can better enhance the utilization efficiency of gold resources and reduce environmental pollution, representing a favorable performance of CP. The specific calculation steps for assessing CP for these four gold mines are demonstrated as follows.
In Phase I, the initial sub-criteria values are obtained on the basis of on-site measurement and investigations. Particularly, as for the qualitative indicators, such as sub-criteria , , , and , a decision making team, contained by ten relevant decision makers (DMs), is invited to make evaluations under LTS . These DMs need to satisfy two conditions before being selected. One is that they should have abundant work experience in the gold mining industry. Another is that they should have rich knowledge through involvement in the management of CP construction projects in mines. The concrete characteristics of the selected experts are illustrated in Table 1. Each decision maker provides their linguistic evaluations under each qualitative criterion. Thereafter, the voting results of DMs are transformed into PLTSs, as shown in Table 2.

Table 1.
Characteristics of decision makers (DMs).

Table 2.
Initial hybrid evaluation matrix.
Considering that the dimensions, types, and units of sub-criteria are various, the initial evaluation matrix must be normalized. According to Equations (8) and (15), the normalized decision making matrix is determined, as shown in Table 3.

Table 3.
Normalized hybrid evaluation matrix.
In Phase II, the weight vector of sub-criteria is obtained based on the modified experts grading method. First, the linguistic evaluation information of sub-criteria is given by five DMs under LTS , as shown in Table 4. Then, the score function value of PLTSs for each sub-criterion is calculated based on Equation (12) (see the eighth column in Table 4). Finally, the weight vector is obtained by Equation (17), and the calculation result is demonstrated in the last column of Table 4.

Table 4.
Linguistic evaluation information of sub-criteria.
In Phase III, the evaluation results of CP for gold mines are obtained with the extended TODIM method. At first, because is the largest weight value, is selected as a reference criterion. Then, based on Equation (18), the relative sub-criteria weight values are calculated as follows: , , , , , , , , , , , , , , , and . Afterward, suppose , the partial dominance degrees under sub-criteria are computed based on Equations (19) and (20), and the overall dominance degree for each alternative is calculated according to Equation (21) (see Table 5).

Table 5.
Dominance of each alternative over other alternatives.
Finally, based on Equation (22), the global values of alternatives are calculated as follows: , , , and . Becauae , the ranking order is . Therefore, the optimal alternative is , and the worst alternative is .
5. Discussions
5.1. Sensitivity Analysis
In this subsection, the influence of parameter in Equations (19) and (20) on the evaluation results is discussed. In this study, is suggested. However, in some references [53,54], other values have been also employed. For the sake of confirming the stability of the decision making results, some other values are selected as contrasts. Generally, if , the influence of losses is weakened; and if , the influence of losses is exacerbated. Accordingly, the values are divided into two categories: and .
The global values of alternatives under different values are indicated in Figure 3. It is clear that the maximum and minimum global values are always 1 and 0, respectively, whereas other global values decreased with the increasing of values. Besides, the ranking results with different values are listed in Table 6. It can be seen that the ranking orders of alternatives are always consistent (namely, ). That is to say, the evaluation results are less sensitive to the values when the proposed method is employed. As a result, the sensitivity analysis verifies the robustness of the presented decision making framework to a certain extent.
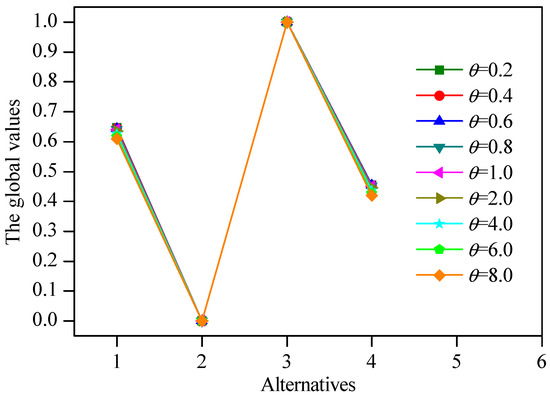
Figure 3.
Global values of alternatives with different values.

Table 6.
Ranking results with different values.
5.2. Comparison Analysis
In this subsection, a comparison analysis with other approaches is introduced to validate the feasibility and strengths of the proposed approach.
(1) Comparison of evaluation information processing approaches
As far as we know, evaluation information in most existing studies is mainly processed to a single type of data. For example, the type of evaluation information in literature [28,55] is crisp numbers, and the information format in literature [36,38,40] is PLTSs. So far, no hybrid type of evaluation information that contains both crisp numbers and PLTSs has been put forward. In the real world, the evaluation information is usually composed of quantitative and qualitative values simultaneously. Thus, the single type of evaluation values cannot easily express evaluation information comprehensively. Although multiple types of data were adopted in some literature [56,57,58], this hybrid evaluation information was transformed into the same type (such as real numbers or linguistic values) in the first step of their approaches, which may lead to information loss. Considering the diversity and complexity of information in the CP evaluation for gold mines, the hybrid type of data is more suitable to indicate evaluation information. Therefore, PLTSs are employed to describe qualitative information and crisp numbers are adopted to express quantitative information. As a result, original evaluation information can be indicated more effectively.
(2) Comparison of weight determination methods
With regard to the determination methods of sub-criteria weights, the experts grading method is a typical subjective weighting approach. However, the linguistic evaluation terms given by experts are all expressed by scores or specific values in the traditional experts grading method [59]. An obvious weakness of this method is that it is difficult to indicate the original evaluation information sufficiently. In contrast, the linguistic evaluation information can be well described using PLTSs. Consequently, the traditional experts grading method is modified by introducing the idea of PLTSs in this research, so that the decision making results can be more reasonable.
(3) Comparison of ranking methods
Compared with other ranking methods, the TODIM method based on prospect theory is an available tool to deal with MCDM problems. However, the classical TODIM method is adopted to handle the MCDM issues in which sub-criteria values are in the format of crisp numbers, and cannot deal with the hybrid MCDM problems with multiple types of sub-criteria values. On account of this deficiency, Liang et al. [42] extended the TODIM method based on crisp values and triangular fuzzy numbers; Fan et al. [58] extended the TODIM method based on crisp numbers, interval numbers, and triangular fuzzy numbers; Wang and Li [60] extended the TODIM method based on crisp numbers, interval numbers, triangular fuzzy numbers, and trapezoidal fuzzy numbers. Nevertheless, the TODIM method has not been extended based on crisp numbers and PLTSs. In comparison with the existing extended TODIM method, the extended TODIM method with crisp numbers and PLTSs is more favorable for solving those kinds of MCDM problems, which include both quantitative and qualitative evaluation information. Compared with other fuzzy extensions mentioned above, PLTSs containing hesitations and probabilities can depict the qualitative information more comprehensively. As a result, the TODIM method is extended based on crisp numbers and PLTSs to assess CP for gold mines in this research.
On the basis of the above analyses, the advantages of the proposed method are summarized as follows:
(1) Two formats of data are introduced to indicate the initial evaluation information. The crisp numbers are adopted to express precise information for quantitative sub-criteria, and the PLTSs are employed to describe linguistic information for qualitative sub-criteria.
(2) The classical experts grading method is modified with PLTSs. The PLTSs, as opposed to scores or specific values, are used to express linguistic evaluation information provided by experts, so that the initial linguistic information can be described more adequately.
(3) The traditional TODIM method is extended with crisp numbers and PLTSs, which can efficiently deal with practical hybrid MCDM problems, including quantitative and qualitative evaluation information.
5.3. Managerial Implication
To evaluate CP for gold mines, this paper developed a hybrid MCDM approach. The proposed method provides suggestions for assessing CP for gold mines. In order to improve the level of CP for gold mines, some specific managerial implications are suggested as follows.
(1) For government: The government can establish an institution for regularly evaluating the performance of CP for gold mines. For the enterprises with better performance of CP, government can provide some financial subsidies or rewards, such as preferential tax and loans. However, for the enterprises with worse performance of CP, government can adopt some punitive measures, such as increasing the pollution discharge fees. Meanwhile, government can find out the weaknesses of CP in the evaluation process, so that pertinent measures can be taken. For example, if some CP technologies in most enterprises are poor, government can increase investment to research and develop these technologies.
(2) For enterprises: Enterprises can know their own problems and recognize the gap between themselves and other companies in the evaluation process. For improving the performance of CP, on the one hand, enterprises can develop a CP technology system. The key points of CP technology systems include the following: advanced mining technology, energy cascade utilization technology, resource-saving technology, waste utilization technology, ‘zero emission’ technology, and land greening technology. Through adopting CP technologies, the economic and environmental benefits will be greatly enhanced. On the other hand, enterprises can optimize the CP management system. First, the comprehensive CP regulations should be established and improved. Then, the CP regulations should be effectively executed. Moreover, the implementation process should be specially supervised and evaluated.
6. Conclusions
As the traditional production pattern has caused plenty of resource loss and serious environmental pollution in the development of mineral resources, implementing CP has become an effective guarantee to achieve sustainable development for mining enterprises. This paper focused on proposing a hybrid MCDM approach to evaluate CP for gold mines. Considering the specific features of gold mines, the evaluation criteria system of CP was established with twelve quantitative sub-criteria and four qualitative sub-criteria. In order to describe evaluation information more adequately, the quantitative sub-criteria were expressed by crisp numbers, and the qualitative sub-criteria were indicated by PLTSs. Considering that the experts are inclined to describe the importance degrees of sub-criteria using linguistic variables, the traditional experts grading method was modified with PLTSs to obtain the sub-criteria weights. Besides, an extended TODIM method with two types of evaluation information (crisp numbers and PLTSs) was presented to get the ranking result. Finally, the proposed hybrid MCDM approach was applied to evaluate CP for gold mines. The sensitivity analysis and comparison analysis indicated that the raised approach had strong robustness and had large advantages in solving such hybrid MCDM problems. At the same time, the evaluation results can provide some managerial implications for government and enterprises.
In the future, the proposed approach can be employed to solve hybrid MCDM issues in other fields, or more decision making methods can be developed to evaluate CP for gold mines.
Author Contributions
W.L., G.Z., and S.L. conceived and worked together to achieve this work; W.L. wrote the paper; and G.Z. made contribution to the case study. Conceptualization, G.Z.; Funding acquisition, G.Z.; Methodology, W.L.; Writing—original draft, W.L.; Writing—review & editing, G.Z. and S.L.
Funding
This research was funded by National Key Research and Development Program of China (2018YFC0604606) and National Natural Science Foundation of China (51774321).
Acknowledgement
We sincerely thank the anonymous reviewers for their helpful and constructive suggestions and the editors for their careful and patient work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Harris, R.D.F.; Shen, J. The intrinsic value of gold: An exchange rate-free price index. J. Int. Money Financ. 2017, 79, 203–217. [Google Scholar] [CrossRef]
- Kumah, A. Sustainability and gold mining in the developing world. J. Clean. Prod. 2006, 14, 315–323. [Google Scholar] [CrossRef]
- Gorman, M.R.; Dzombak, D.A. A review of sustainable mining and resource management: Transitioning from the life cycle of the mine to the life cycle of the mineral. Resour. Conserv. Recycl. 2018, 137, 281–291. [Google Scholar] [CrossRef]
- Assawincharoenkij, T.; Hauzenberger, C.; Ettinger, K.; Sutthirat, C. Mineralogical and geochemical characterization of waste rocks from a gold mine in northeastern Thailand: Application for environmental impact protection. Environ. Sci. Pollut. Res. 2018, 25, 3488–3500. [Google Scholar] [CrossRef] [PubMed]
- Kiventerä, J.; Lancellotti, I.; Catauro, M.; Dal Poggetto, F.; Leonelli, C.; Illikainen, M. Alkali activation as new option for gold mine tailings inertization. J. Clean. Prod. 2018, 187, 76–84. [Google Scholar] [CrossRef]
- Xiao, R.; Wang, S.; Li, R.H.; Wang, J.J.; Zhang, Z.Q. Soil heavy metal contamination and health risks associated with artisanal gold mining in Tongguan, Shaanxi, China. Ecotoxicol. Environ. Saf. 2017, 141, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Mayala, L.P.; Veiga, M.M.; Khorzoughi, M.B. Assessment of mine ventilation systems and air pollution impacts on artisanal tanzanite miners at Merelani, Tanzania. J. Clean. Prod. 2016, 116, 118–124. [Google Scholar] [CrossRef]
- Euler, D.S. Application of ventilation management programs for improved mine safety. Int. J. Min. Sci. Technol. 2017, 27, 647–650. [Google Scholar]
- Jordaan, M.A.; Mimba, M.E.; NguemheFils, S.C.; Edith-Etakah, B.T.; Shapi, M.; Penaye, J.; Davies, T.C. Occurrence and levels of potentially harmful elements (PHEs) in natural waters of the gold mining areas of the Kette-Batouri region of Eastern Cameroon. Environ. Monit. Assess. 2018, 190, 416. [Google Scholar] [CrossRef] [PubMed]
- Tomiyasu, T.; Kodamatani, H.; Hamada, Y.K.; Matsuyama, A.; Imura, R.; Taniguchi, Y.; Hidayati, N.; Rahajoe, J.S. Distribution of total mercury and methylmercury around the small-scale gold mining area along the Cikaniki River, Bogor, Indonesia. Environ. Sci. Pollut. Res. 2017, 24, 2643–2652. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, P.C.S.; Neiva, A.M.R.; Silva, M.M.V.G.; Santos, A.C.T. Human health risks in an old gold mining area with circum-neutral drainage, central Portugal. Environ. Geochem. Health 2017, 39, 43–62. [Google Scholar] [CrossRef] [PubMed]
- Drace, K.; Kiefer, A.M.; Veiga, M.M.; Williams, M.K.; Ascari, B.; Knapper, K.A.; Logan, K.M.; Breslin, V.M.; Skidmore, A.; Bolt, D.A.; et al. Mercury-free, small-scale artisanal gold mining in Mozambique: Utilization of magnets to isolate gold at clean tech mine. J. Clean. Prod. 2012, 32, 88–95. [Google Scholar] [CrossRef]
- Gutiérrez Aguilar, C.M.; Panameño, R.; Perez Velazquez, A.; Angel Álvarez, B.E.; Kiperstok, A.; César, S.F. Cleaner production applied in a small furniture industry in Brazil: Addressing focused changes in design to reduce waste. Sustainability 2017, 9, 1867. [Google Scholar] [CrossRef]
- Matos, L.M.; Anholon, R.; da Silva, D.; Ordoñez, R.E.C.; Quelhas, O.L.G.; Leal Filho, W.; de Santa-Eulalia, L.A. Implementation of cleaner production: A ten-year retrospective on benefits and difficulties found. J. Clean. Prod. 2018, 187, 409–420. [Google Scholar] [CrossRef]
- Malinauskienė, M.; Kliopova, I.; Slavickaitė, M.; Staniškis, J.K. Integrating resource criticality assessment into evaluation of cleaner production possibilities for increasing resource efficiency. Clean Technol. Environ. 2016, 18, 1333–1344. [Google Scholar] [CrossRef]
- Hilson, G.; Nayee, V. Environmental management system implementation in the mining industry: A key to achieving cleaner production. Int. J. Miner. Process. 2002, 64, 19–41. [Google Scholar] [CrossRef]
- Song, S.Q.; Zhou, Y.Z. Demonstration research on cleaner production of mines. China Popul. Resour. Environ. 2003, 13, 106–110. [Google Scholar]
- Hilson, G. Defining “cleaner production” and “pollution prevention” in the mining context. Miner. Eng. 2003, 16, 305–321. [Google Scholar] [CrossRef]
- Rajaram, R.; Dutta, S.; Parameswaran, K. Sustainable Mining Practices: A Global Perspective; Taylor & Francis: London, UK, 2005. [Google Scholar]
- Fan, Y.V.; Varbanov, P.S.; Klemeš, J.J.; Nemet, A. Process efficiency optimisation and integration for cleaner production. J. Clean. Prod. 2018, 174, 177–183. [Google Scholar] [CrossRef]
- Severo, E.A.; de Guimarães, J.C.F.; Dorion, E.C.H. Cleaner production, social responsibility and eco-innovation: Generations’ perception for a sustainable future. J. Clean. Prod. 2018, 186, 91–103. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Luo, S.Z. Linguistic neutrosophic Hamacher aggregation operators and the application in evaluating land reclamation schemes for mines. PLoS ONE 2018, 13, e0206178. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.L.; Duan, N.; Dan, Z.G.; Shi, F.F.; Wang, H.F. An understandable and practicable cleaner production assessment model. J. Clean. Prod. 2018, 187, 1094–1102. [Google Scholar] [CrossRef]
- Tseng, M.L.; Lin, Y.H.; Chiu, A.S. Fuzzy AHP-based study of cleaner production implementation in Taiwan PWB manufacturer. J. Clean. Prod. 2009, 17, 1249–1256. [Google Scholar] [CrossRef]
- Peng, W.G.; Li, C.G. Fuzzy-Soft set in the field of cleaner production evaluation for aviation industry. Commun. Inf. Sci. Manag. Eng. 2012, 2, 39–43. [Google Scholar]
- Basappaji, K.M.; Nagesha, N. Assessment of cleaner production level in agro based industries—A fuzzy logic approach. Energy Proced. 2014, 54, 127–134. [Google Scholar] [CrossRef]
- Gong, B.G.; Guo, D.D.; Zhang, X.Q.; Cheng, J.S. An approach for evaluating cleaner production performance in iron and steel enterprises involving competitive relationships. J. Clean. Prod. 2017, 142, 739–748. [Google Scholar] [CrossRef]
- Dong, L.J.; Shu, W.W.; Li, X.B.; Zhang, J.M. Quantitative evaluation and case studies of cleaner mining with multiple indexes considering uncertainty factors for phosphorus mines. J. Clean. Prod. 2018, 183, 319–334. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Luo, S.Z. An integrated EDAS-ELECTRE method with picture fuzzy information for cleaner production evaluation in gold mines. IEEE Access 2018, 6, 65747–65759. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Luo, S.Z. Selecting the optimal mine ventilation system via a decision making framework under hesitant linguistic environment. Symmetry 2018, 10, 283. [Google Scholar] [CrossRef]
- Luo, S.Z.; Cheng, P.F.; Wang, J.Q.; Huang, Y.J. Selecting project delivery systems based on simplified neutrosophic linguistic preference relations. Symmetry 2017, 9, 151. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Wu, H. Evaluating investment risks of metallic mines using an extended TOPSIS method with linguistic neutrosophic numbers. Symmetry 2017, 9, 149. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Yager, R.R. Multicriteria decision making with ordinal/linguistic intuitionistic fuzzy sets for mobile apps. IEEE Trans. Fuzzy Syst. 2016, 24, 590–599. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Hong, C.S. Selecting the optimal mining method with extended multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) approach. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z.S. Probabilistic linguistic term sets in multi-attribute group decision making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Wei, G.W. Grey relational analysis model for dynamic hybrid multiple attribute decision making. Knowl. Based Syst. 2011, 24, 672–679. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xing, X.M. Probabilistic linguistic VIKOR method to evaluate green supply chain initiatives. Sustainability 2017, 9, 1231. [Google Scholar] [CrossRef]
- Peng, H.G.; Zhang, H.Y.; Wang, J.Q. Cloud decision support model for selecting hotels on TripAdvisor.com with probabilistic linguistic information. Int. J. Hosp. Manag. 2018, 68, 124–138. [Google Scholar] [CrossRef]
- Liao, H.C.; Jiang, L.S.; Xu, Z.S.; Xu, J.P.; Herrera, F. A linear programming method for multiple criteria decision making with probabilistic linguistic information. Inf. Sci. 2017, 415, 341–355. [Google Scholar] [CrossRef]
- Gomes, L.F.A.M.; Lima, M.M.P.P. TODIM: Basics and application to multicriteria ranking of projects with environmental impacts. Found. Comput. Decis. Sci. 1992, 16, 113–127. [Google Scholar]
- Liang, W.Z.; Zhao, G.Y.; Wu, H.; Chen, Y. Assessing the risk degree of goafs by employing hybrid TODIM method under uncertainty. Bull. Eng. Geol. Environ. 2018. [Google Scholar] [CrossRef]
- Tosun, Ö.; Akyüz, G. A fuzzy TODIM approach for the supplier selection problem. Int. J. Comput. Int. Syst. 2015, 8, 317–329. [Google Scholar] [CrossRef]
- Zindani, D.; Maity, S.R.; Bhowmik, S.; Chakraborty, S. A material selection approach using the TODIM (TOmada de Decisao Interativa Multicriterio) method and its analysis. Int. J. Mater. Res. 2017, 108, 345–354. [Google Scholar] [CrossRef]
- Wu, M.Q.; An, Y.L.; Zhou, X.D.; Xiao, Y. Establishment of the index system of cleaner production assessment of phosplate minesddphosplate mines of Guiyang a case study. Environ. Sci. Manag. 2009, 34, 189–194. [Google Scholar]
- Zhou, H.L.; Yang, S.; Chen, J.H. Research and application of cleaner production evaluation index system in gold mine. Gold Sci. Technol. 2017, 25, 93–100. [Google Scholar]
- Liang, W.Z.; Zhao, G.Y.; Hong, C.S. Performance Assessment of Circular Economy for Phosphorus Chemical Firms Based on VIKOR-QUALIFLEX Method. J. Clean. Prod. 2018, 196, 1365–1378. [Google Scholar] [CrossRef]
- Liang, W.Z.; Zhao, G.Y.; Wu, H.; Dai, B. Risk assessment of rockburst via an extended MABAC method under fuzzy environment. Tunn. Undergr. Space Technol. 2019, 83, 533–544. [Google Scholar] [CrossRef]
- Basu, A.J.; van Zyl, D.J. Industrial ecology framework for achieving cleaner production in the mining and minerals industry. J. Clean. Prod. 2006, 14, 299–304. [Google Scholar] [CrossRef]
- Xu, Z.S. Deviation measures of linguistic preference relations in group decision making. Omega 2005, 33, 249–254. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S.; Liao, H.C. Multiple criteria decision making based on Bonferroni means with hesitant fuzzy linguistic information. Soft Comput. 2017, 21, 6515–6529. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S. Novel basic operational laws for linguistic terms, hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. Inf. Sci. 2016, 372, 407–427. [Google Scholar] [CrossRef]
- Krohling, R.A.; de Souza, T.T. Combining prospect theory and fuzzy numbers to multi-criteria decision making. Expert Syst. Appl. 2012, 39, 11487–11493. [Google Scholar] [CrossRef]
- Qin, Q.D.; Liang, F.Q.; Li, L.; Chen, Y.W.; Yu, G.F. A TODIM-based multi-criteria group decision making with triangular intuitionistic fuzzy numbers. Appl. Soft Comput. 2017, 55, 93–107. [Google Scholar] [CrossRef]
- Gomes, L.F.A.M. An application of the TODIM method to the multicriteria rental evaluation of residential properties. Eur. J. Oper. Res. 2009, 193, 204–211. [Google Scholar] [CrossRef]
- Zhao, H.R.; Zhao, H.R.; Guo, S. Evaluating the comprehensive benefit of eco-industrial parks by employing multi-criteria decision making approach for circular economy. J. Clean. Prod. 2017, 142, 2262–2276. [Google Scholar] [CrossRef]
- Liu, P.D. A novel method for hybrid multiple attribute decision making. Knowl.-Based Syst. 2009, 22, 388–391. [Google Scholar]
- Fan, Z.P.; Zhang, X.; Chen, F.D.; Liu, Y. Extended TODIM method for hybrid multiple attribute decision making problems. Knowl.-Based Syst. 2013, 42, 40–48. [Google Scholar] [CrossRef]
- Hossain, M.U.; Poon, C.S.; Dong, Y.H.; Lo, I.M.; Cheng, J.C. Development of social sustainability assessment method and a comparative case study on assessing recycled construction materials. Int. J. Life Cycle Assess. 2018, 23, 1654–1674. [Google Scholar] [CrossRef]
- Wang, F.; Li, H. Novel method for hybrid multiple attribute decision making based on TODIM method. J. Syst. Eng. Electron. 2015, 26, 1023–1031. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).