1. Introduction
With the gradually increasing consumption of nonrenewable energy, such as oil, coal, and natural gas, renewable energy has become the hope of humankind to solve the current energy shortage and future energy crisis [
1,
2]. Wind energy is a well-known renewable energy source and has been used worldwide due to its advantages of clean, renewable, and large reserves [
3,
4,
5]. People capture wind energy through wind turbines, and wind speed and wind direction characteristics are therefore crucial for calculating wind power and the design and arrangement of wind turbines [
6]. The wind speed probability density distribution can be used to estimate wind power density [
7,
8] and can also be applied to determine the most dominant wind direction [
9,
10,
11]. In order to optimize wind farm layout in complex terrain, the joint probability distribution of wind direction and wind speed have gained great attention [
12,
13,
14] as it can be used to obtain wind speed characteristics under different wind directions in complex terrain. Wind speed characteristics under different wind directions play a significant role in arrangement of wind turbines. It should be noted that wind speed with the highest frequency and wind speed that can capture the maximum wind energy are different. To obtain maximum energy output, the two wind speeds should be as close as possible [
9]. In addition, the joint probability distribution is important in the construction of the measure–correlate–predict method and the calculation of structural wind load [
15,
16,
17].
Up to now, a large number of probability models have been used to fit wind velocity distribution [
18,
19,
20,
21]. However, there is no fixed optimal model for different regions. Masseran et al. [
22] investigated eight probability models to describe the wind speed probability distribution: Weibull, Rayleigh, lognormal, exponential, inverse Gaussian, gamma, Burr, and inverse gamma. Jaramillo et al. [
23] found that the Weibull–Weibull distribution was more appropriate than the two-parameter Weibull distribution for regions where wind speed presented a bimodal probability distribution. Kollu et al. [
24] used a mixture of three probability distributions—Weibull–lognormal distribution, Weibull–extreme value, and lognormal–extreme value distribution—to model wind speed distribution. The result showed that the mixed model had good fitting on both multipeak and single-peak wind speed distribution. Moreover, it is known that wind direction distribution plays a crucial role in determining the most dominant wind direction [
11]. However, compared to wind speed, there are few models that are suitable for fitting wind direction distribution [
25]. This can be attributed to two main difficulties. Firstly, the wind direction is generally divided into 16 intercardinal directions: north (N), north-northeast (NNE), northeast (NE), east-northeast (ENE), east (E), east-southeast (ESE), southeast (SE), south-southeast (SSE), south (S), south-southwest (SSW), southwest (SW), west-southwest (WSW), west (W), west-northwest (WNW), northwest (NW), and north-northwest (NNW). Second, the wind direction is a circular variable. Masseran et al. [
11] manifested that a finite mixture of von Mises function (FVMF) could be applied to describe the actual data of wind direction in Malaysia. As a result, it was found that more than 90% of wind directions could be explained by FVMF models. So far, FVMF models have been widely applied to model the angular variable, which plays an important role in many fields, such as wind energy [
26,
27,
28,
29], environment [
30], economics [
31], and video analysis [
32].
In modeling the joint probability function of wind direction and speed, Johnson and Wehrly [
12] constructed four kinds of models, and the fourth model was a combination of wind direction and speed distribution. Carta et al. [
6] derived joint distribution with isotropic Gaussian model, angular–linear model, and anisotropic Gaussian model. The conclusion was that the angular–linear model had a better degree of fit in the case of the Canary Islands. Erdem and Shi [
13] constructed bivariate joint distribution based on angular–linear model, Farlie–Gumbel–Morgenstern model, and anisotropic lognormal approaches model. The results indicated that angular–linear model had a good fit to the measured wind data in North Dakota, USA. Han et al. [
17] proposed two nonparametric models to fit joint speed and direction distributions and claimed that the novel methods performed better than parametric distributions. Up to now, very few publications have utilized joint probability distributions to simultaneously approximate wind speed and direction.
For a more accurate description of complex wind characteristics, the wind speed distribution is described by a mixture of three probability distributions: Weibull–Weibull (W–W), lognormal–lognormal (L–L), and Weibull–lognormal (W–L); the FVMF models are used to investigate the wind direction characteristics, and the joint probability distribution of wind direction and speed is obtained with angular–linear model. The suitability of the distribution is judged from the coefficient of determination R2.
5. Wind Power Density
Wind power density can be used to evaluate the potential of wind energy in a region. The mean wind power density [
35,
36,
37] can be expressed as follows (Equation (35)):
where
represent the mean wind power density (W/m
2);
N is the number of records in the set period;
is the wind speed of the
ith record (m/s);
is the density of air (kg/m
3). In this paper, the value of
ρ was 1.225 kg/m
3. The probability distribution of wind power density at different wind speed can be determined using Equation (36):
In addition, the wind power density can be estimated by Equation (37):
The joint probability distribution of wind direction and speed can be used to evaluate the wind speed distribution at different wind directions, given by Equation (38):
Moreover, two useful wind speeds parameters, namely the most probable wind speed and the wind speed carrying maximum energy, can be derived by the wind speed distribution and wind power density distribution [
38,
39]. The most probable wind speed is the wind speed of maximum point in the wind speed distribution. The wind speed carrying maximum energy is the wind speed of maximum point in the wind power density distribution [
40].
6. Results and Discussion
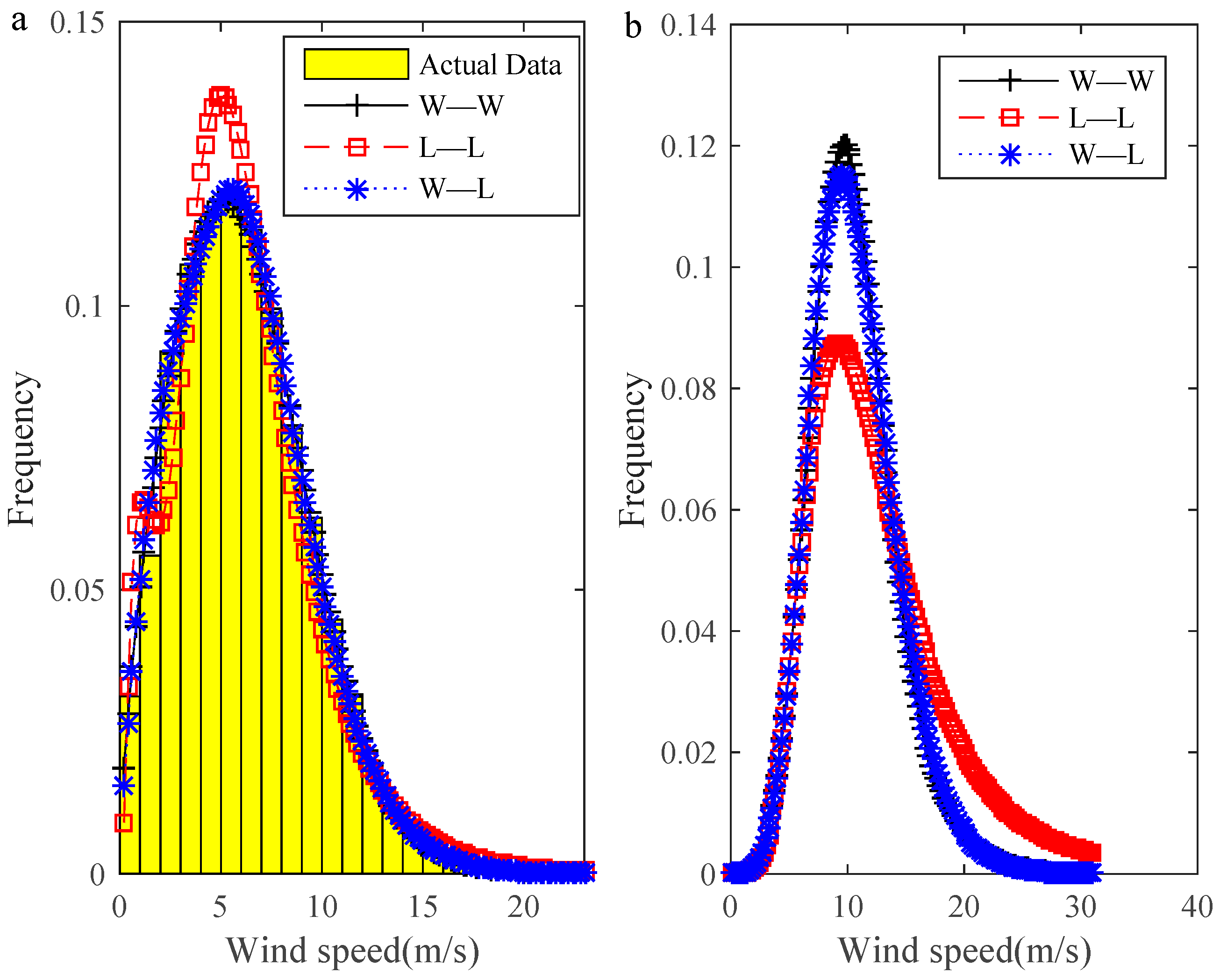
Figure 1 was drawn by analyzing the data at a height of 70 m, and it demonstrates the wind speed distributions (
Figure 1a) and the probability distribution of wind power density (
Figure 1b). The parameters in the wind speed distributions, the corresponding
R2 coefficient, and AIC are shown in
Table 1. It can be seen from
Figure 1a that W–L distribution was better than W–W and L–L distribution for the histogram of wind speed data, which is also clear from in
Table 1. Therefore, we chose W–L distribution as the marginal distribution of wind speed to construct the joint distribution.
Figure 1b illustrates the probability density distribution of wind power density. The estimated wind power density was 270.79 W/m
2, 307.34 W/m
2, and 271.97 W/m
2 corresponding to W–W, L–L, and W–L, respectively. The mean wind power density was 270.53 W/m
2.
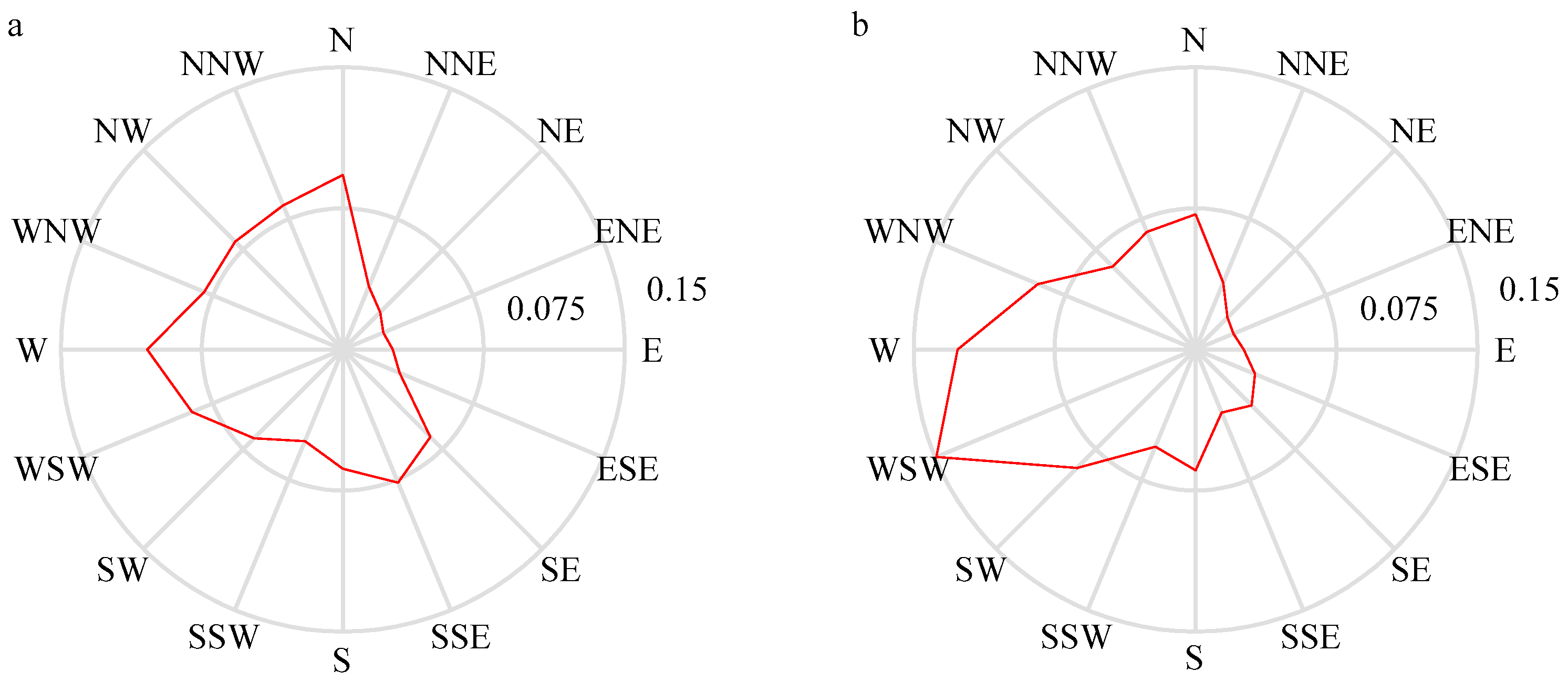
Figure 2 shows that the wind direction rose at a height of 70 m (
Figure 2a) and the wind energy rose at a height of 70 m (
Figure 2b). As shown in
Figure 2, wind direction 1, 8, and 13 (N, SSE, and W) had a large wind direction frequency of 9.28%, 7.66%, and 10.41%, respectively, while wind direction 12 (WSW) had a large wind power density frequency (
Figure 2b) of 14.92%. Therefore, in order to investigate their internal correspondence, we needed to study the wind speed characteristics under different wind directions and investigate their characteristics.
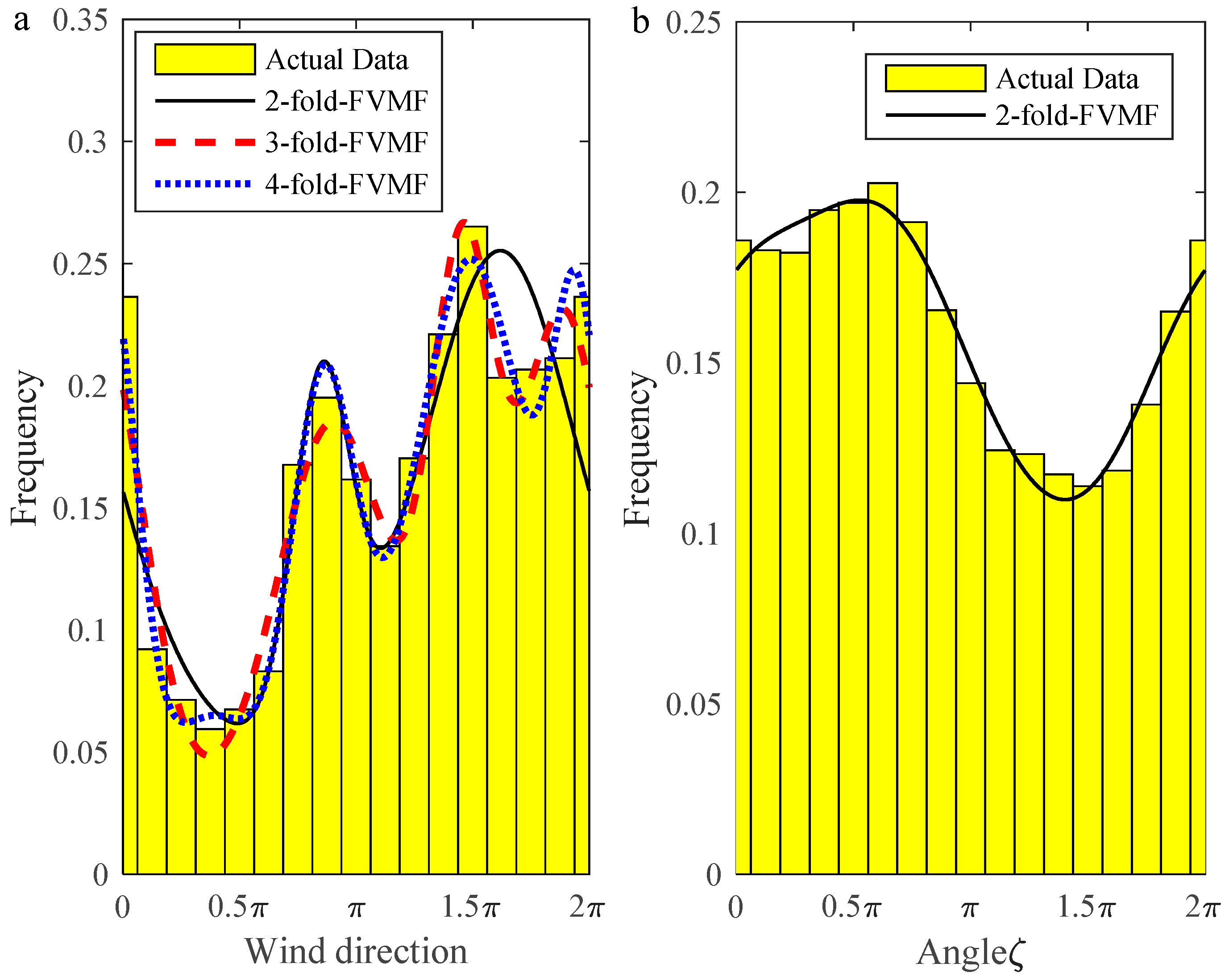
Figure 3 was obtained by numerical calculation of the circular variable, which was measured at a height 70 m.
Figure 3a shows the wind direction distributions, and
Figure 3b depicts the probability distribution of the angular variable
ζ. It can be seen from the histogram of the measured wind direction data in
Figure 3a that there were up to four main wind directions; therefore, the FVMF with
M = 2,
M = 3, and
M = 4 was chosen to fit the wind direction distribution.
Figure 3b illustrates that there were two distinct peaks in the histogram of the angular variable
ζ; Therefore, the FVMF with
M = 2 was selected to construct the probability distribution of the angular variable
ζ. The parameters in the wind direction distributions, the corresponding
R2 coefficient, and AIC are shown in
Table 2. The parameters in the angular variable
ζ distribution function and the corresponding
R2 coefficient are shown in
Table 3. From
Figure 3a and
Table 2, it can be seen that the FVMF with
M = 4 was the best fitted model for the wind direction data. In addition, in order to estimate the parameters of the FVMF model, we redefined
and
instead of
. Here, the
should be calculated by
and
to describe the mean wind direction. The FVMF with
M = 4 reflected that the most dominant wind direction was 4.69 rad (268.6°). As displayed in
Figure 3b and
Table 3, the FVMF with
M = 2 was suitable to describe the angular variable
ζ distribution.
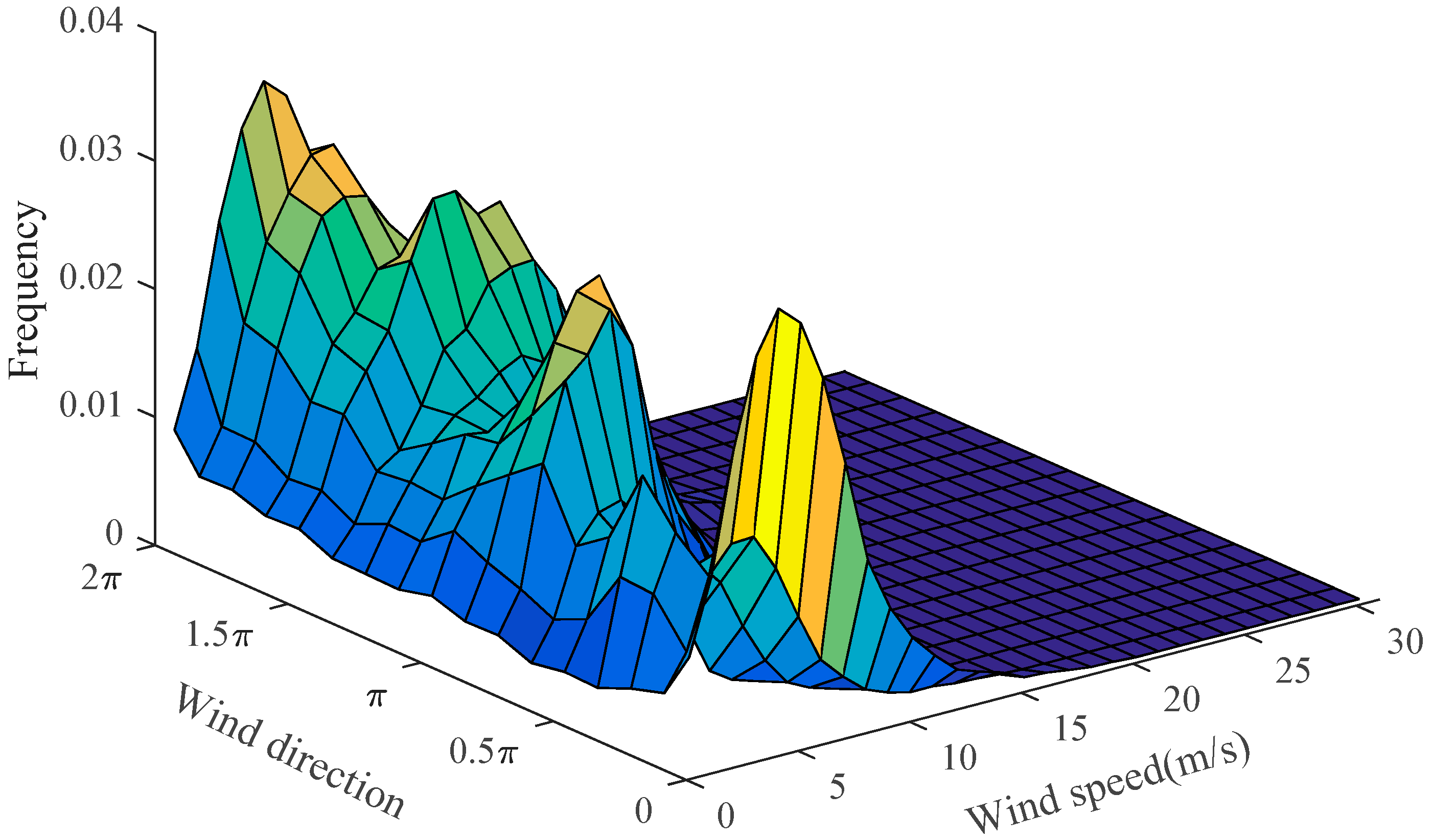
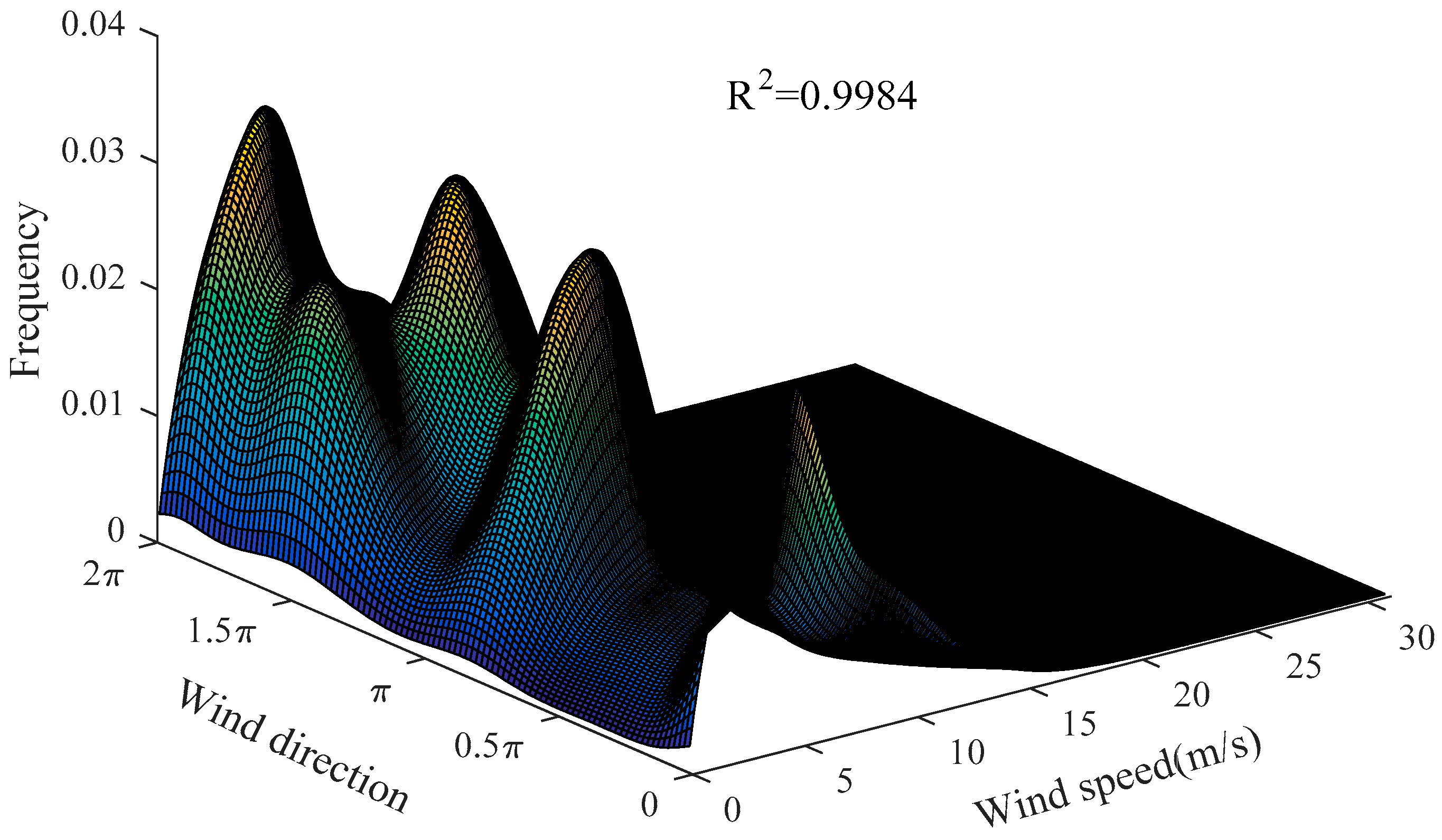
Figure 4 shows the joint probability distribution of actual wind direction and speed at a height of 70 m.
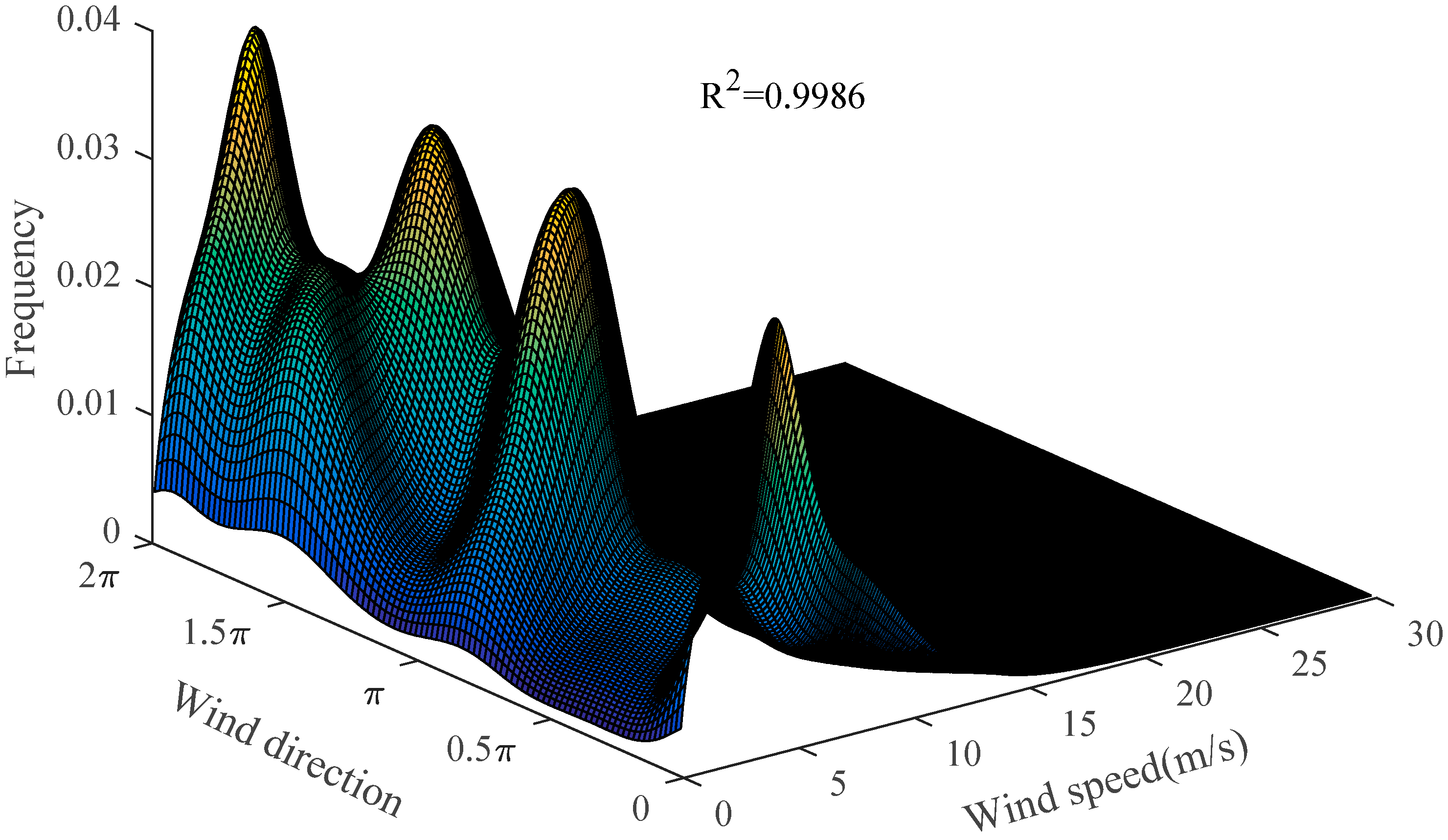
Figure 5 shows the joint probability distribution at a height of 70 m, which was obtained with the angular–linear distribution model. According to the proposed joint probability distribution at a height 70 m, the wind speed distribution under 16 wind directions could be determined. The corresponding
R2 value can be seen in
Table 4. As can be seen from
Figure 4 and
Figure 5 and
Table 4, the proposed model had a great degree of fit to the sample data at a height 70 m. Moreover, in order to verify the validity of the selected model, the proposed model was used to construct the joint probability distribution at a height of 50 m. It should be borne in mind that the wind direction varied slightly from 70 m to 50 m.
Figure 6 shows the joint probability distribution at a height of 50 m. In the proposed joint distribution model, W–L distribution was selected to process the wind speed data, and the FVMF with
M = 4 was the fitted model for the wind direction data. Moreover, the FVMF with
M = 2 was chosen to describe the angular variable
ζ distribution. The parameters in the joint probability distribution at a height of 50 m and the corresponding
R2 coefficient are shown in
Table 5. According to the proposed joint probability distribution at a height of 50 m, the wind speed distribution under 16 wind directions could be determined. The corresponding
R2 value can be seen in
Table 6. It can be seen from the above analysis that the proposed model could well present wind characteristics at different heights.
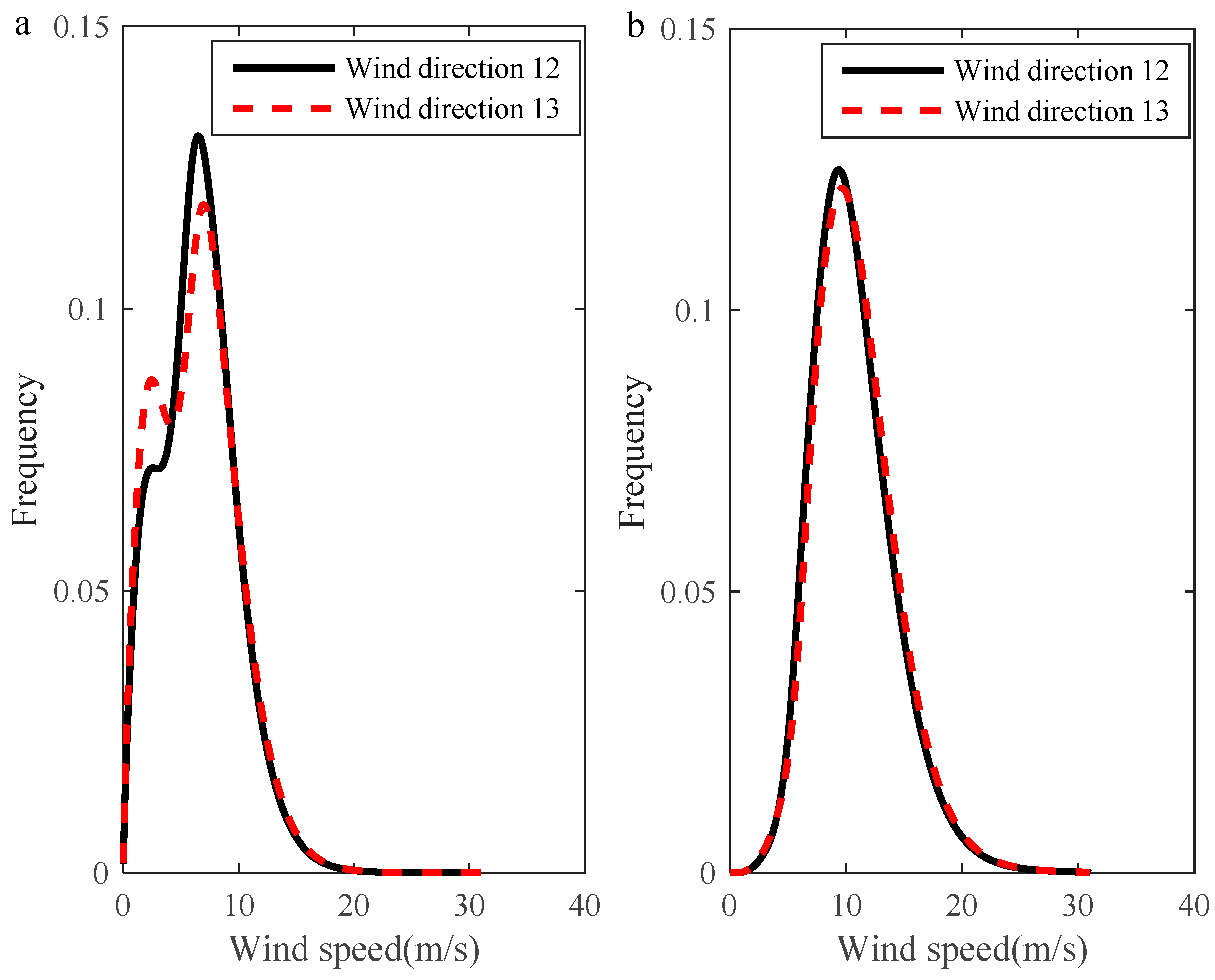
The wind direction was recorded in 16 intercardinal directions. Each wind direction of the 16 intercardinal directions had a corresponding wind speed and a wind power density distribution. Due to the limitation of space, we have only given the results of two wind directions—wind direction 12 (E) and wind direction 13 (W)—in
Figure 7. The figure was drawn by applying the joint probability density distribution at a height of 70 m. As can be seen from
Figure 7, the most probable wind speeds for wind direction 12 and 13 were 6.5 m/s and 6.95 m/s, respectively; the wind speeds carrying maximum energy were 9.34 m/s and 9.63 m/s, respectively.
The FVMF with
M = 4 was a good fitted model for the wind direction data and could be used to investigate the wind direction characteristics for four seasons. The four seasons were defined as follows: (a) spring: March, April, and May; (b) summer: June, July, and August; (c) Autumn: September, October, and November; (d) winter: December, January, and February.
Figure 8 depicts the wind direction distributions over four seasons. It was drawn using the wind direction data of 70 m for three years. The parameters in the wind direction model over four seasons and the corresponding
R2 coefficient are shown in
Table 7. As can be seen from
Figure 8, the most dominant wind direction was 5 rad (286.6°) in the spring season, 6 rad (348.8°) in the summer season, 4.5 rad (260.2°) in the autumn season, and 4.7 rad (267.1°) in the winter season. There were more than two prevailing directions in the four seasons. It was concluded from
Figure 8 that the wind direction had seasonal features.
7. Conclusions
This paper presents the analysis of wind speed and wind direction using joint probability distribution methods. The joint distribution was obtained with wind direction and speed distributions. By fitting the wind data at different heights, the proposed model could well present wind characteristics. Thus, the proposed model was used to investigate the wind direction and wind speed. The main findings of this paper are as follows:
(1) W–W, L–L, and W–L distribution with higher R2 coefficient provide a good fitting for wind speed data at a height of 70 m. In this paper, the best fitting model for wind speed was W–L distribution, which could accurately represent wind speed characteristics.
(2) The FVMF with M = 4 was a good fitted model for the wind direction data at a height of 70 m and could accurately describe the wind direction distribution with multiple peaks. Moreover, the dominant wind direction was 4.69 rad (268.6°) in the three years.
(3) The joint probability distribution provided a good fit to the measured wind data at different heights, and the R2 of the joint probability distribution was greater than 0.99, indicating that this model was able to explain more than 99% of wind data. With the joint probability distribution, the most probable wind speeds for wind direction 12 and 13 were 6.5 m/s and 6.95 m/s at a height of 70 m, respectively; the wind speed carrying maximum energy were 9.34 m/s and 9.63 m/s at a height of 70 m, respectively.
(4) The wind direction had seasonal features. The most dominant wind direction was 5 rad (286.6°) in the spring season, 6 rad (348.8°) in the summer season, 4.5 rad (260.2°) in the autumn season, and 4.7 rad (267.1°) in the winter season. Moreover, there were more than two prevailing directions in the four seasons.