A Comparison of Machine-Learning Methods to Select Socioeconomic Indicators in Cultural Landscapes
Abstract
1. Introduction
2. Methodology
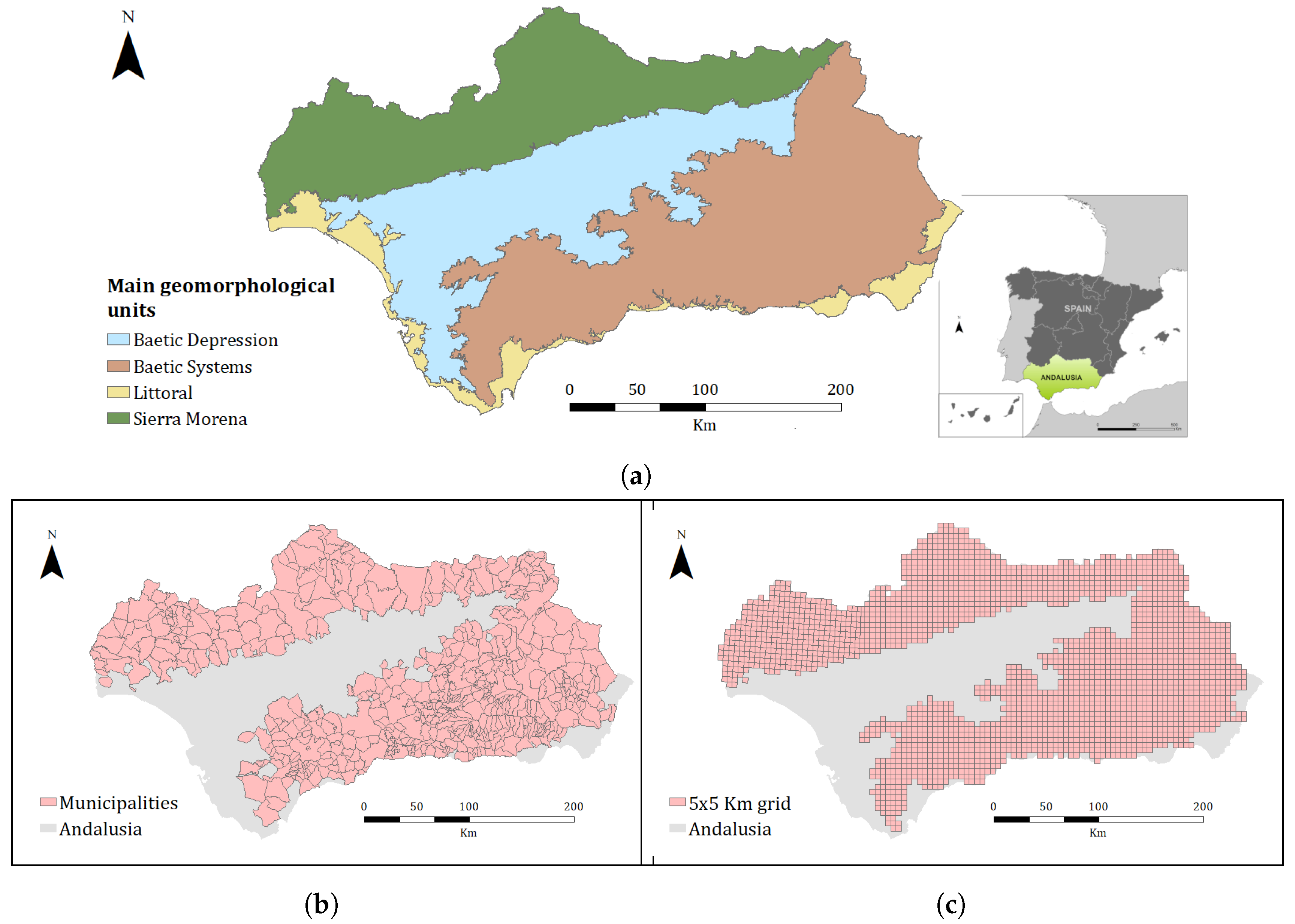
2.1. Study Area
2.2. Data Description
2.3. Methods
2.3.1. Multiple Linear Regression
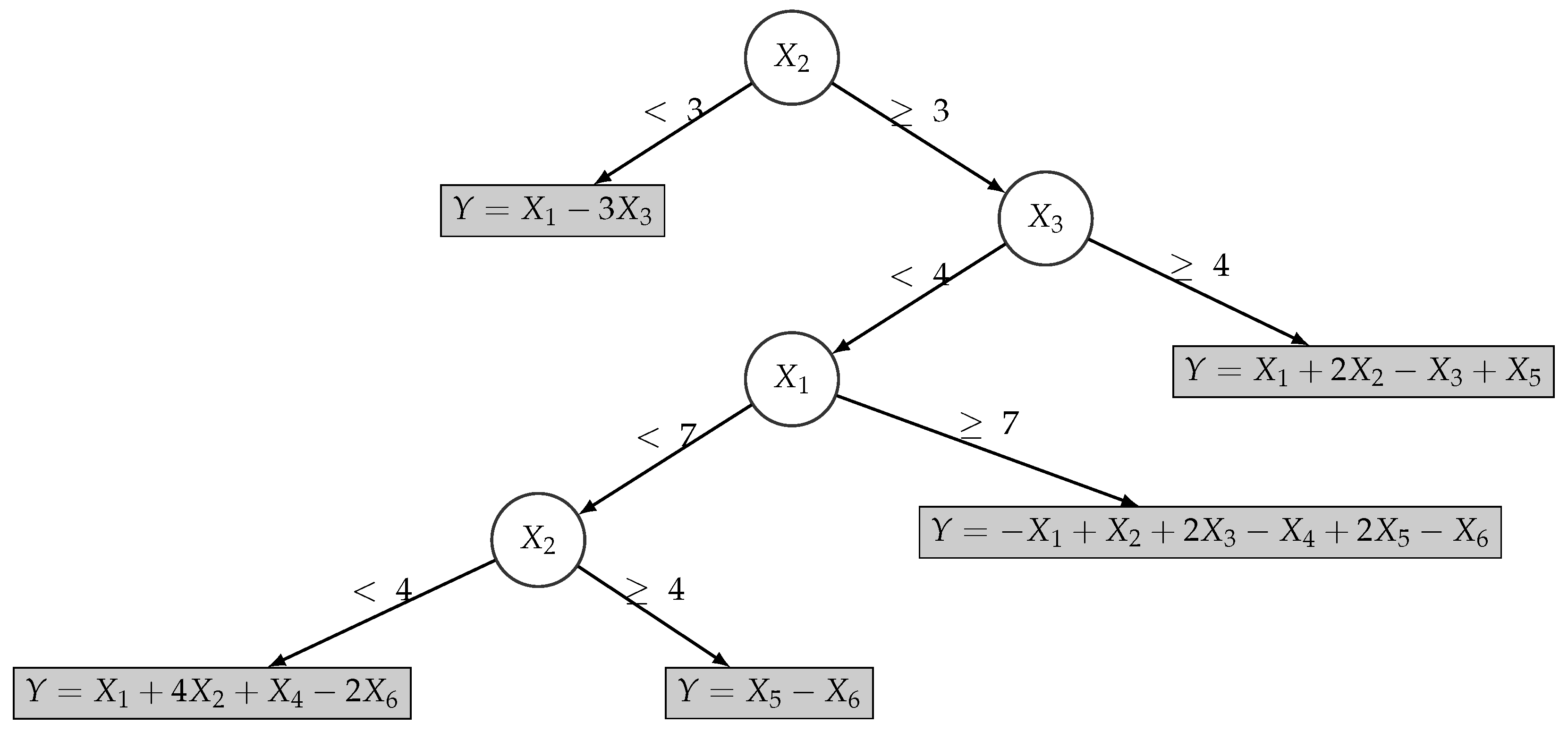
2.3.2. Model Trees
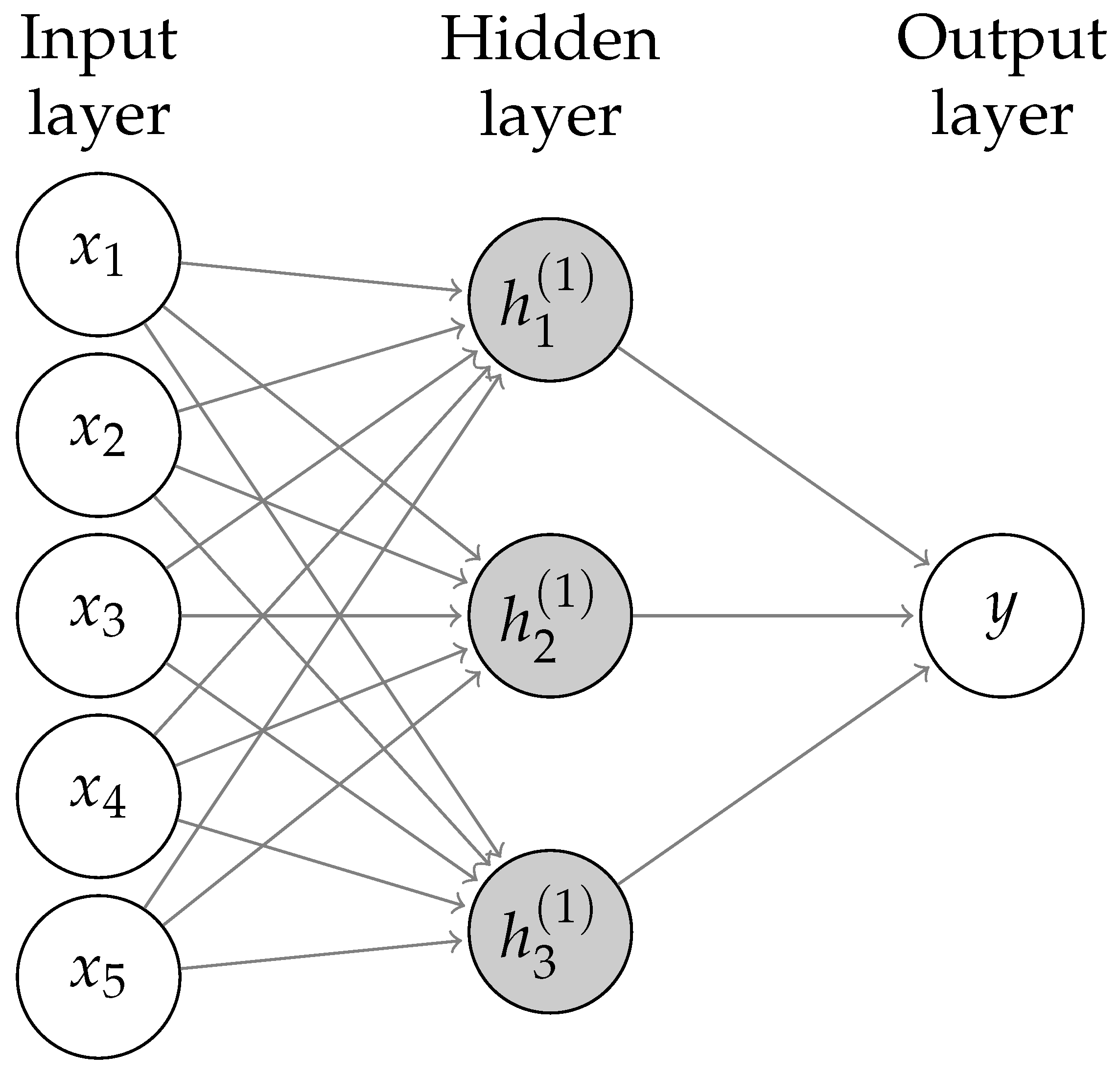
2.3.3. Neural Networks
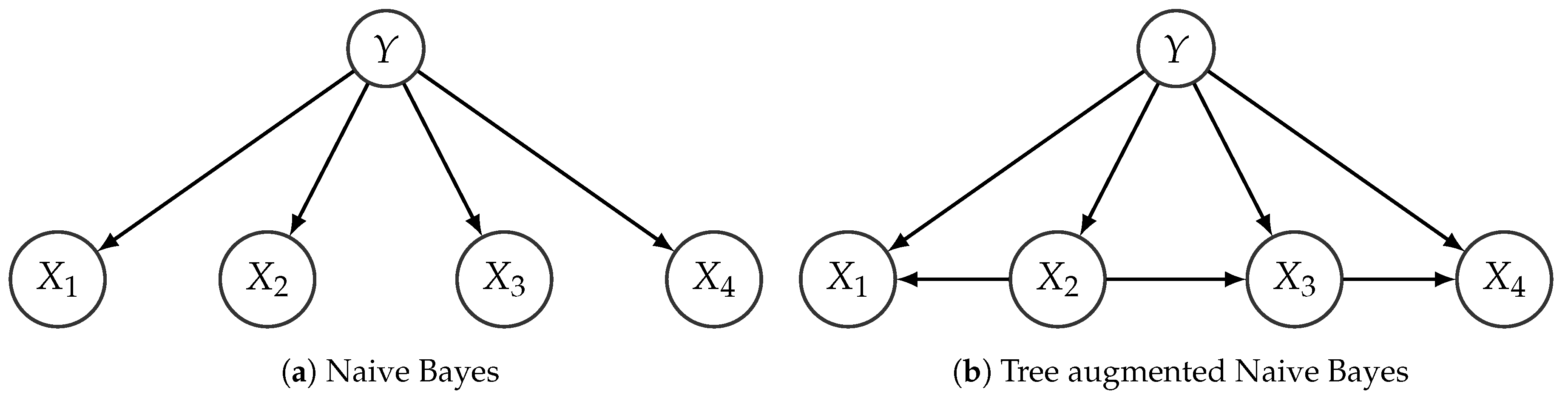
2.3.4. Bayesian Networks
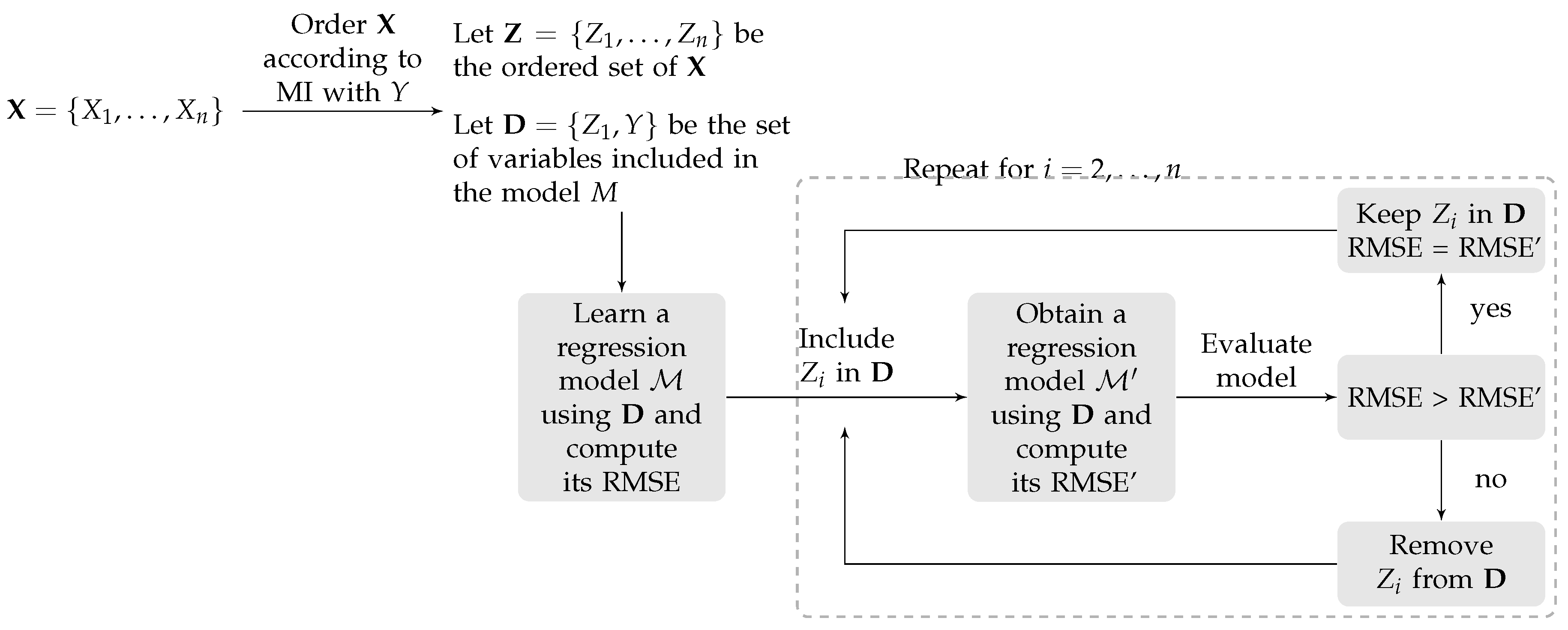
2.4. Variable Selection
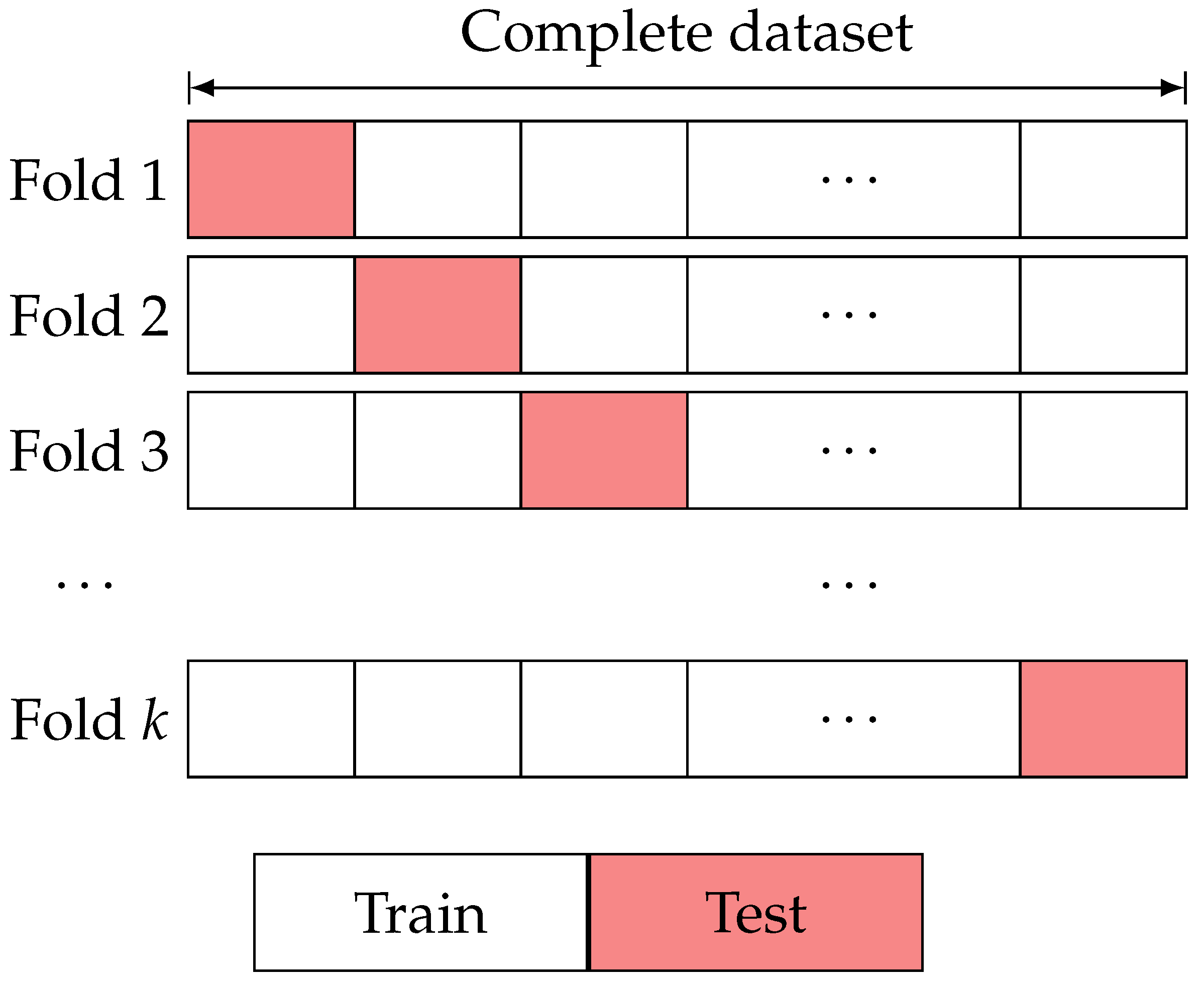
2.5. Model Validation
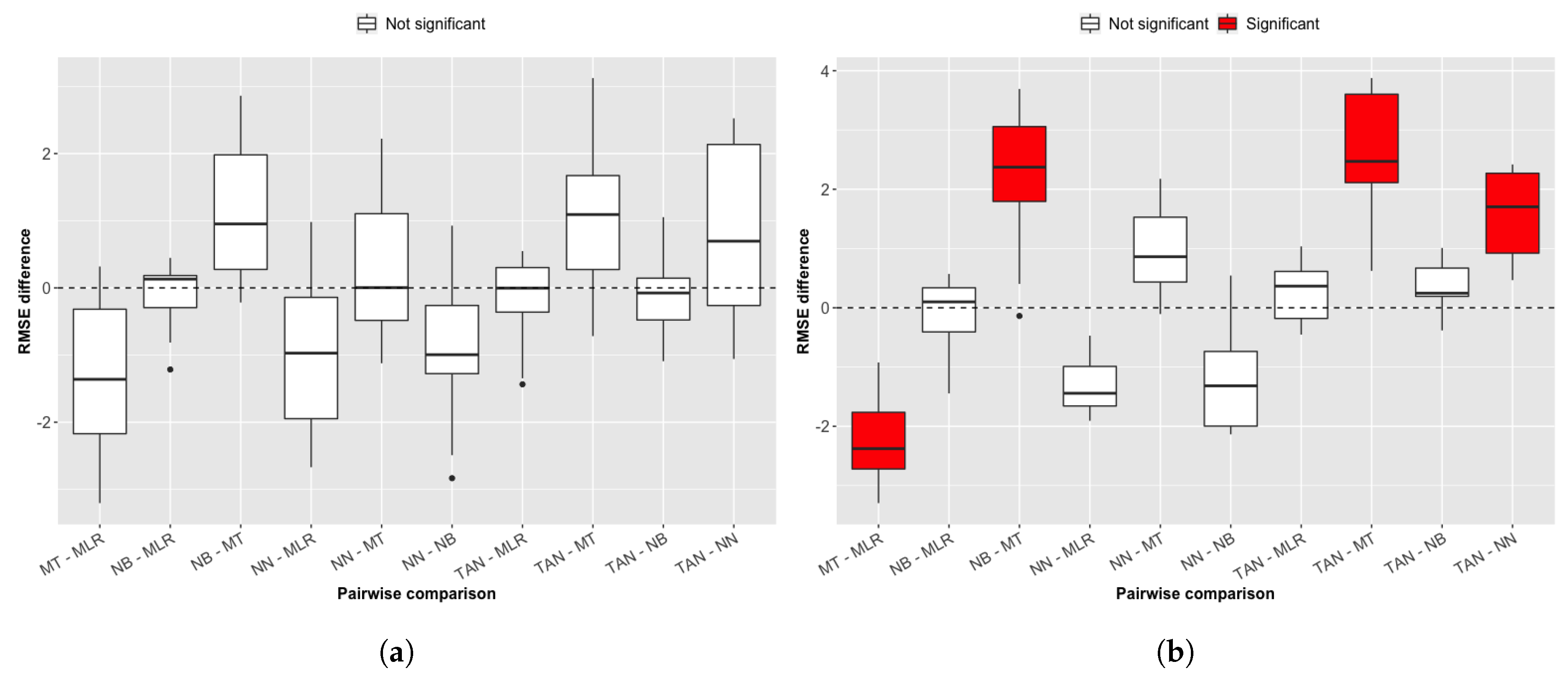
3. Results
4. Discussion
4.1. Models Comparison
4.2. Socioeconomic Variables as Indicators
- Population density (pDens) and Distance to the main city (DMC) can be considered as the most important indicators since all models selected them. Both variables can be related to land abandonment. The remoteness from big cities, where better connectivity to other cities and accessibility to public services are found, can be relevant factors of land abandonment [66]. Traditionally, emigration has abundantly occurred in cultural landscapes in Andalusia [67], especially among young people and women who seek to acquire a higher education level and better job opportunities in larger cities.
- In the past decades, these landscapes have attracted tourism [68]. The growth of tourism has changed the socioeconomic sectors, developing the tertiary (sec.T identified by the MT model) and hospitality sectors (sec.H). These sectors coexist with the primary sector through agriculture. In this sense, some authors [66,69] consider that many rural areas maintain symbiosis between tourism and agriculture. The variables related to tourism (sec.H) and agriculture (sec.P) were selected by the NN and NB models. Tourism is involved in population growth and the improvement of transportation infrastructures, such as roads [70], attenuating the abandonment process, and giving rural residents an opportunity to enhance their wellbeing [71].
- The variable related to middle-school studies (st.mid) can be considered as an important indicator since it was selected by four out of five models. Generally speaking, people with basic knowledge of writing and reading (st.no), and with middle school being their maximum level of attained education (st.mid), predominate in these landscapes. These variables emphasize the tourism–agriculture relationship. People dedicated to agriculture have basic knowledge, and people dedicated to tourism have middle professional training.
- Sex ratio (SxR) was selected by the MT and TAN models. As aforementioned, plenty of the emigrants are women who aim at obtaining a high education level and better job opportunities. As a consequence, the sex ratio is imbalanced toward men. This tendency is one of the main factors to the social and demographic sustainability of rural landscapes in Spain [70].
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farina, A. The cultural landscape as a model for the integration of ecology and economics. Biosciences 2000, 50, 313–320. [Google Scholar] [CrossRef]
- Plieninger, T.; Bieling, C. Resilience and the Cultural Landscape: Understanding and Managing Change in Human-Shaped Environments; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Schmitz, M.F.; De Aranzabal, I.; Aguilera, P.A.; Rescia, A.; Pineda, F.D. Relationship between landscape typology and socioeconomic structure: Scenarios of change in Spanish cultural landscapes. Ecol. Model. 2003, 168, 343–356. [Google Scholar] [CrossRef]
- Maldonado, A.D.; Aguilera, P.A.; Salmerón, A.; Nicholson, A.E. Probabilistic modeling of the relationship between socioeconomy and ecosystem services in cultural landscapes. Ecosyst. Serv. 2018. [Google Scholar] [CrossRef]
- De Aranzabal, I.; Schmitz, M.F.; Aguilera, P.; Pineda, F.D. Modelling of landscape changes derived from the dynamics of socio-ecological systems: A case of study in a semiarid Mediterranean landscape. Ecol. Indic. 2008, 8, 672–685. [Google Scholar] [CrossRef]
- Rescia, A.; Willaarts, B.; Schmitz, M.; Aguilera, P. Changes in land uses and management in two Nature Reserves in Spain: Evaluating the social-ecological resilience of natural landscapes. Landsc. Urban Plan. 2010, 98, 26–35. [Google Scholar] [CrossRef]
- Rescia, A.; Pérez-Corona, M.E.; Arribas-Ureña, P.; Dover, J. Cultural landscapes as complex adaptive systems: The cases of northern Spain and Northern Argentina. In Resilience and the Cultural Landscape: Understanding and Managing Change in Human-Shaped Environments; Pleninger, T., Bieling, T., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 126–145. [Google Scholar]
- Parrott, L.; Quinn, N. A complex systems approach for multiobjective water quality regulation on managed wetland landscapes. Ecosphere 2016, 7, e01363. [Google Scholar] [CrossRef]
- Parrott, L. Hybrid modelling of complex ecological systems for decision support: Recent successes and future perspectives. Ecol. Inform. 2011, 6, 44–49. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Sousa, S.; Martins, F.; Alvim-Ferraz, M.; Pereira, M. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ. Model. Softw. 2007, 22, 97–103. [Google Scholar] [CrossRef]
- Banos-Gonzalez, I.; Martínez-Fernández, J.; Esteve-Selma, M.Á.; Esteve-Guirao, P. Sensitivity analysis in socio-ecological models as a tool in environmental policy for sustainability. Sustainability 2018, 10, 2928. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Murphy, K. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Valletta, J.J.; Torney, C.; Kings, M.; Thornton, A.; Madden, J. Applications of machine learning in animal behaviour studies. Anim. Behav. 2017, 124, 203–220. [Google Scholar] [CrossRef]
- Kamenova, S.; Bartley, T.; Bohan, D.; Boutain, J.; Colautti, R.; Domaizon, I.; Fontaine, C.; Lemainque, A.; Viol, I.L.; Mollot, G.; et al. Chapter Three - Invasions Toolkit: Current Methods for Tracking the Spread and Impact of Invasive Species. In Networks of Invasion: A Synthesis of Concepts; Bohan, D.A., Dumbrell, A.J., Massol, F., Eds.; Academic Press: Cambridge, MA, USA, 2017; Volume 56, pp. 85–182. [Google Scholar] [CrossRef]
- Aguilera, P.A.; Fernández, A.; Reche, F.; Rumí, R. Hybrid Bayesian network classifiers: Application to species distribution models. Environ. Model. Softw. 2010, 25, 1630–1639. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y. Applying various algorithms for species distribution modelling. Integr. Zool. 2013, 8, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Maldonado, A.D.; Aguilera, P.A.; Salmerón, A. Modeling zero-inflated explanatory variables in hybrid Bayesian network classifiers for species occurrence prediction. Environ. Model. Softw. 2016, 82, 31–43. [Google Scholar] [CrossRef]
- Tamaddoni-Nezhad, A.; Milani, G.A.; Raybould, A.; Muggleton, S.; Bohan, D.A. Chapter Four—Construction and Validation of Food Webs Using Logic-Based Machine Learning and Text Mining. In Ecological Networks in an Agricultural World; Woodward, G., Bohan, D.A., Eds.; Academic Press: Cambridge, MA, USA, 2013; Volume 49, pp. 225–289. [Google Scholar] [CrossRef]
- Uusitalo, L.; Tomczak, M.T.; Müller-Karulis, B.; Putnis, I.; Trifonova, N.; Tucker, A. Hidden variables in a Dynamic Bayesian Network identify ecosystem level change. Ecol. Inform. 2018, 45, 9–15. [Google Scholar] [CrossRef]
- Willcock, S.; Martínez-López, J.; Hooftman, D.A.; Bagstad, K.J.; Balbi, S.; Marzo, A.; Prato, C.; Sciandrello, S.; Signorello, G.; Voigt, B.; et al. Machine learning for ecosystem services. Ecosyst. Serv. 2018, 33, 165–174. [Google Scholar] [CrossRef]
- Zickus, M.; Greig, A.J.; Niranjan, M. Comparison of Four Machine Learning Methods for Predicting Pm 10 Concentrations in Helsinki, Finland. Water Air Soil Pollut. 2002, 2, 717–729. [Google Scholar] [CrossRef]
- Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Martínez-España, R.; Bueno-Crespo, A.; Timón, I.; Soto, J.; Muñoz, A.; Cecilia, J.M. Air-Pollution Prediction in Smart Cities through Machine Learning Methods: A Case of Study in Murcia, Spain. J. Univ. Comput. Sci. 2018, 24, 261–276. [Google Scholar]
- Aguilera, P.A.; Fernández, A.; Ropero, R.F.; Molina, L. Groundwater quality assessment using data clustering based on hybrid Bayesian networks. Stoch. Environ. Res. Risk Assess. 2013, 27, 435–447. [Google Scholar] [CrossRef]
- Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef]
- Vesselinov, V.V.; Alexandrov, B.S.; O’Malley, D. Contaminant source identification using semi-supervised machine learning. J. Contam. Hydrol. 2018, 212, 134–142. [Google Scholar] [CrossRef] [PubMed]
- Belanche-Muñoz, L.; Blanch, A.R. Machine learning methods for microbial source tracking. Environ. Model. Softw. 2008, 23, 741–750. [Google Scholar] [CrossRef]
- Kim, Y.H.; Im, J.; Ha, H.K.; Choi, J.K.; Ha, S. Machine learning approaches to coastal water quality monitoring using GOCI satellite data. GISci. Remote Sens. 2014, 51, 158–174. [Google Scholar] [CrossRef]
- Maldonado, A.D.; Aguilera, P.A.; Salmerón, A. Continuous Bayesian networks for probabilistic environmental risk mapping. Stoch. Environ. Res. Risk Assess. 2016, 30, 1441–1455. [Google Scholar] [CrossRef]
- Karpatne, A.; Jiang, Z.; Vatsavai, R.R.; Shekhar, S.; Kumar, V. Monitoring Land-Cover Changes: A Machine-Learning Perspective. IEEE Geosci. Remote Sens. Mag. 2016, 4, 8–21. [Google Scholar] [CrossRef]
- Maclaurin, G.J.; Leyk, S. Temporal replication of the national land cover database using active machine learning. GISci. Remote Sens. 2016, 53, 759–777. [Google Scholar] [CrossRef]
- Gibril, M.B.A.; Idrees, M.O.; Shafri, H.Z.M.; Yao, K. Integrative image segmentation optimization and machine learning approach for high quality land-use and land-cover mapping using multisource remote sensing data. J. Appl. Remote Sens. 2018, 12, 016036. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Specht, D.F. A General Regression Neural Network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Larochelle, H.; Bengio, Y.; Louradour, J.; Lamblin, P. Exploring Strategies for Training Deep Neural Networks. J. Mach. Learn. Res. 2009, 10, 1–40. [Google Scholar]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Ciregan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J. A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning. In Proceedings of the ICML ’08 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 160–167. [Google Scholar] [CrossRef]
- Kohara, K.; Ishikawa, T.; Fukuhara, Y.; Nakamura, Y. Stock Price Prediction Using Prior Knowledge and Neural Networks. Intell. Syst. Account. Financ. Manag. 1997, 6, 11–22. [Google Scholar]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Ramos-López, D.; Masegosa, A.R.; Martínez, A.M.; Salmerón, A.; Nielsen, T.D.; Langseth, H.; Madsen, A.L. MAP inference in dynamic hybrid Bayesian networks. Prog. Artif. Intell. 2017, 6, 133–144. [Google Scholar] [CrossRef]
- Masegosa, A.; Nielsen, T.D.; Langseth, H.; Ramos-López, D.; Salmerón, A.; Madsen, A.L. Bayesian Models of Data Streams with Hierarchical Power Priors. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; PMLR, International Convention Centre: Sydney, Australia, 2017; Volume 70, pp. 2334–2343. [Google Scholar]
- Jordan, M.I. Graphical Models. Stat. Sci. 2004, 19, 140–155. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Pattern Recognition and Machine Learning. J. Electron. Imaging 2007, 16, 049901. [Google Scholar] [CrossRef]
- Larrañaga, P.; Moral, S. Probabilistic graphical models in artificial intelligence. Appl. Soft Comput. 2011, 11, 1511–1528. [Google Scholar] [CrossRef]
- Olea, L.; San Miguel-Ayanz, A. The Spanish dehesa. A traditional Mediterranean silvopastoral system linking production and nature conservation. In Proceedings of the 21st General Meeting of the European Grassland Federation, Badajoz, Spain, 3–6 April 2006. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012; ISBN 3-900051-07-0. [Google Scholar]
- Wang, Y.; Witten, I.H. Induction of model trees for predicting continuous cases. In Proceedings of the Poster Papers of the European Conference on Machine Learning, Prague, Czech Republic, 23–25 April 1997; pp. 128–137. [Google Scholar]
- Hornik, K.; Buchta, C.; Zeileis, A. Open-Source Machine Learning: R Meets Weka. Comput. Stat. 2009, 24, 225–232. [Google Scholar] [CrossRef]
- Günther, F.; Fritsch, S. neuralnet: Training of Neural Networks. R J. 2010, 2, 30–38. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan-Kaufmann (San Mateo): San Francisco, CA, USA, 1988. [Google Scholar]
- Langseth, H.; Nielsen, T.D.; Rumí, R.; Salmerón, A. Mixtures of Truncated Basis Functions. Int. J. Approx. Reason. 2012, 53, 212–227. [Google Scholar] [CrossRef]
- Moral, S.; Rumí, R.; Salmerón, A. Mixtures of Truncated Exponentials in Hybrid Bayesian Networks. In Symbolic and Quantitative Approaches to Reasoning with Uncertainty; Benferhat, S., Besnard, P., Eds.; Springer: Berlin, Germany, 2001; Volume 2143, pp. 156–167. [Google Scholar]
- Elvira Consortium. Elvira: An Environment for Creating and Using Probabilistic Graphical Models. In Proceedings of the First European Workshop on Probabilistic Graphical Models, Cuenca, Spain, 6–8 November 2002; pp. 222–230. [Google Scholar]
- Fernández, A.; Salmerón, A. Extension of Bayesian network classifiers to regression problems. In Advances in Artificial Intelligence—IBERAMIA 2008; Geffner, H., Prada, R., Alexandre, I.M., David, N., Eds.; Springer: Berlin, Germany, 2008; Volume 5290, pp. 83–92. [Google Scholar]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–147. [Google Scholar]
- Hothorn, T.; Hornik, K.; van de Wiel, M.; Zeileis, A. Implementing a Class of Permutation Tests: The coin Package. J. Stat. Softw. 2008, 28, 1–23. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A. Nonparametric Statistical Methods, 2nd ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Fleiss, J.L. Measuring nominal scale agreement among many raters. Psychol. Bull. 1971, 76, 378–382. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D. Neural networks and M5 model trees in modelling water level—Discharge relationship. Neurocomputing 2005, 63, 381–396. [Google Scholar] [CrossRef]
- Perlich, C.; Provost, F.; Simonoff, J.S. Tree induction vs. logistic regression: A learning-curve analysis. J. Mach. Learn. Res. 2003, 4, 211–255. [Google Scholar]
- Vidal-Macua, J.J.; Ninyerola, M.; Zabala, A.; Domingo-Marimon, C.; Gonzalez-Guerrero, O.; Pons, X. Environmental and socioeconomic factors of abandonment of rainfed and irrigated crops in northeast Spain. Appl. Geogr. 2018, 90, 155–174. [Google Scholar] [CrossRef]
- Rey Benayas, J.M.; Martins, A.; Nicolau, J.M.; Schulz, J.J. Abandonment of agricultural land: An overview of drivers and consequences. CAB Rev. Perspect. Agric. Vet. Sci. Nutr. Nat. Resour. 2007, 2, 1–14. [Google Scholar] [CrossRef]
- Schmitz, M.F.; Pineda, F.D.; Castro, H.; De Aranzabal, I.; Aguilera, P. Paisaje Cultural y Estructura SocioeconóMica. Valor Ambiental y Demanda TuríStica en un Territorio MediterráNeo; Junta de Andalucía: Sevilla, Spain, 2005. [Google Scholar]
- Cánoves, G.; Villarino, M.; Priestley, G.K.; Blanco, A. Rural tourism in Spain: An analysis of recent evolution. Geoforum 2004, 35, 755–769. [Google Scholar] [CrossRef]
- Consejo Económico y Social de España (CES). El Medio Rural y su VertebracióN Social y Territorial; Colección Informes: Madrid, Spain, 2018. [Google Scholar]
- Muresan, I.C.; Oroian, C.F.; Harun, R.; Arion, F.H.; Porotiu, A.; Chiciudean, G.; Todea, A.; Lile, R. Local Residents’ Attitude toward sustainable rural tourism development. Sustainability 2016, 8, 100. [Google Scholar] [CrossRef]
| Variable Name (Code) | Definition |
|---|---|
| Heterogeneous land (HET) | Percentage of heterogeneous lands, obtained as the combination of (1) patches of mixing grassland and forest and (2) crops with natural vegetation, from the Land use and land cover map of Andalusia of 2011 (at scale 1:10,000), based on the Land Occupation Information System of Spain (SIOSE). |
| Population density (pDens) | Population density of each municipality in 2011 (inhabitants/Km). |
| Sex ratio (SxR) | Proportion of males (M) to females (F) in each municipality in 2011, computed as . |
| Doubling time (DT) | Time (in years) the population takes to double or reduce to half its size, computed as , where r is the population growth rate. |
| Human Development Index (HDI) | Well-being in a population in terms of life expectancy, knowledge and standards of living, computed as , where LE is the Life expectancy index, EI is the Education index and II is the Income index. Variables LE, EI and II are described in Table 2. |
| Distance to main city (DMC) | Distance (Km) from the main settlement in a municipality to the nearest urban settlement with more than 50,000 inhabitants. |
| Population growth rate (EGR) | Exponential growth of the population, computed as , where represents the population in 2001, the population in 2011 and t the 10-year period. |
| Old-age dependency index (ODI) | Percentage of the older over the younger population in 2011, computed as , where is the population older than 65 years old and is the population younger than 15 years old. |
| Index of Migration effectiveness (IME) | Percentage of total migration for the period 2001–2011. It ranges from −100 (emigration) to 100 (immigration), with values close to 0 indicating no change in the population dynamic. It is computed as . |
| Mortality rate (MortR) | Number of deaths per 1000 inhabitants in each municipality in 2011. |
| Birth rate (BirthR) | Number of births per 1000 inhabitants in each municipality in 2011. |
| Workforce (WF) | Percentage of the municipality’s working age population (≥16) that are available to work in 2011. It is computed as ; where is the Employment Rate; is the Unemployment Rate and is the population older than 16 years old. |
| Unemployment rate (UR) | Percentage of workforce that is unemployed. |
| Earned income (earnInc) | Income declared (€) per number of declarations in 2011. |
| Illiterate (st.ill) | Number of illiterate people per 1000 inhabitants (computed from people over 16). |
| No studies (st.no) | Number of people who do not have any level of educational attainment but know how to write and read per 1000 inhabitants (computed from people over 16). |
| Elementary school (st.elem) | Number of people whose maximum level of education attained is elementary school per 1000 inhabitants (computed from people over 16). |
| Middle school (st.mid) | Number of people whose maximum level of education attained is middle school per 1000 inhabitants (computed from people over 16). |
| High school (st.high) | Number of people whose maximum level of education attained is high school per 1000 inhabitants (computed from people over 16). |
| University (st.uni) | Number of people whose maximum level of education attained is a university degree per 1000 inhabitants (computed from people over 16). |
| Primary sector (sec.P) | Number of employees in the primary sector per 1000 inhabitants. |
| Secondary sector (sec.S) | Number of employees in the secondary sector per 1000 inhabitants. |
| Hospitality sector (sec.H) | Number of employees in the hospitality sector (hotels and restaurants) per 1000 inhabitants. |
| Tertiary sector (sec.T) | Number of employees in the Freight, Trading, Banking or Service sectors, including business services, education, health care and other social services, per 1000 inhabitants. |
| Variable Name (Code) | Definition |
|---|---|
| Income index (II) | The Income Index was obtained as , where IPC is the Income Per Capita. It was used to compute the HDI. |
| Education Index (EI) | The Education Index was obtained by weight averaging the Adult Literacy Index (ALI) and the Gross Enrollment Index (GEI) as . It was used to compute the HDI. |
| Life expectancy index (LEI) | It was obtained from the Multiterritorial Information System of Andalusia at the provincial scale (since it should not be computed for small populations due to the introduction of bias). It was used to compute the HDI. |
| Adult Literacy Index | Proportion of people that know how to write and read. It was used to compute the Education Index (EI). |
| Gross Enrollment Index | Proportion of people of age 6 to 25 enrolled in school at levels from elementary school to university. It was used to compute the Education Index (EI). |
| Income Per Capita (IPC) | Total income (€) in a municipality divided by total number of inhabitants in 2011. It was used to compute the Income Index (II). |
| Municipality Dataset | 5 × 5 Km Grid Dataset | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | MLR | MT | NN | NB | TAN | Times Selected | Variables | MLR | MT | NN | NB | TAN | Times Selected |
| pDens | x | x | x | x | x | 5 | pDens | x | x | x | x | 4 | |
| SxR | x | x | 2 | SxR | x | x | x | x | 4 | ||||
| DT | x | x | x | 3 | DT | x | x | x | x | 4 | |||
| HDI | x | x | x | 3 | HDI | x | x | 2 | |||||
| DMC | x | x | x | x | x | 5 | DMC | x | x | x | x | x | 5 |
| EGR | x | 1 | EGR | x | x | x | x | 4 | |||||
| ODI | x | x | 2 | ODI | x | x | 2 | ||||||
| IME | 0 | IME | x | x | 2 | ||||||||
| MortR | x | 1 | MortR | x | x | x | x | 4 | |||||
| BirthR | 0 | BirthR | x | x | 2 | ||||||||
| WF | 0 | WF | x | x | x | 3 | |||||||
| UR | x | 1 | UR | x | x | x | 3 | ||||||
| earnInc | x | x | x | 3 | earnInc | x | x | x | 3 | ||||
| st.ill | 0 | st.ill | x | 1 | |||||||||
| st.no | x | x | 2 | st.no | x | x | 2 | ||||||
| st.elem | 0 | st.elem | x | x | x | 3 | |||||||
| st.mid | x | x | x | x | 4 | st.mid | x | x | x | 3 | |||
| st.high | 0 | st.high | x | x | x | 3 | |||||||
| st.uni | 0 | st.uni | x | x | x | x | 4 | ||||||
| sec.P | x | x | x | 3 | sec.P | x | x | 2 | |||||
| sec.S | x | 1 | sec.S | x | x | 2 | |||||||
| sec.H | x | x | x | x | 4 | sec.H | x | x | 2 | ||||
| sec.T | x | 1 | sec.T | x | x | x | x | 4 | |||||
| Total selected | 8 | 10 | 7 | 9 | 7 | Total selected | 16 | 10 | 9 | 18 | 15 | ||
| Municipality Dataset | 5 × 5 km Grid Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MLR | MT | NN | NB | TAN | MLR | MT | NN | NB | TAN | ||
| Fold 1 | 8.80 | 9.12 | 8.71 | 8.90 | 8.40 | Fold 1 | 14.80 | 12.05 | 13.12 | 15.18 | 15.42 |
| Fold 2 | 9.43 | 9.11 | 8.61 | 9.62 | 9.80 | Fold 2 | 13.80 | 12.88 | 12.77 | 13.28 | 13.50 |
| Fold 3 | 11.45 | 10.21 | 12.43 | 11.61 | 11.59 | Fold 3 | 14.73 | 12.18 | 13.75 | 14.66 | 14.27 |
| Fold 4 | 7.90 | 8.05 | 7.88 | 8.35 | 7.76 | Fold 4 | 13.54 | 10.25 | 11.64 | 13.59 | 14.06 |
| Fold 5 | 16.85 | 13.65 | 15.22 | 16.51 | 15.41 | Fold 5 | 16.42 | 13.14 | 14.82 | 16.83 | 17.02 |
| Fold 6 | 11.44 | 8.55 | 9.39 | 10.62 | 11.68 | Fold 6 | 16.38 | 14.18 | 14.70 | 15.86 | 16.60 |
| Fold 7 | 11.66 | 9.28 | 9.46 | 11.95 | 11.98 | Fold 7 | 15.44 | 14.14 | 14.54 | 14.00 | 15.01 |
| Fold 8 | 13.97 | 13.64 | 12.85 | 13.82 | 14.52 | Fold 8 | 17.38 | 15.69 | 15.82 | 17.95 | 18.20 |
| Fold 9 | 10.85 | 9.30 | 8.18 | 11.01 | 10.61 | Fold 9 | 14.07 | 11.42 | 13.59 | 14.28 | 15.10 |
| Fold 10 | 11.23 | 9.75 | 10.94 | 10.02 | 9.89 | Fold 10 | 14.39 | 12.41 | 13.07 | 14.54 | 14.57 |
| Mean | 11.36 | 10.07 | 10.37 | 11.24 | 11.16 | Mean | 15.09 | 12.83 | 13.78 | 15.02 | 15.37 |
| Municipality Dataset | 5 × 5 km Grid Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LR | M5P | NN | NB | TAN | LR | M5P | NN | NB | TAN | ||
| seconds | 0.073 | 0.895 | 196.847 | 50.334 | 260.767 | seconds | 0.114 | 2.359 | 1891.152 | 826.915 | 14,234.235 |
| minutes | 0.001 | 0.015 | 3.281 | 0.839 | 4.346 | minutes | 0.002 | 0.039 | 31.519 | 13.782 | 237.237 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, A.D.; Ramos-López, D.; Aguilera , P.A. A Comparison of Machine-Learning Methods to Select Socioeconomic Indicators in Cultural Landscapes. Sustainability 2018, 10, 4312. https://doi.org/10.3390/su10114312
Maldonado AD, Ramos-López D, Aguilera PA. A Comparison of Machine-Learning Methods to Select Socioeconomic Indicators in Cultural Landscapes. Sustainability. 2018; 10(11):4312. https://doi.org/10.3390/su10114312
Chicago/Turabian StyleMaldonado, Ana D., Darío Ramos-López, and Pedro A. Aguilera . 2018. "A Comparison of Machine-Learning Methods to Select Socioeconomic Indicators in Cultural Landscapes" Sustainability 10, no. 11: 4312. https://doi.org/10.3390/su10114312
APA StyleMaldonado, A. D., Ramos-López, D., & Aguilera , P. A. (2018). A Comparison of Machine-Learning Methods to Select Socioeconomic Indicators in Cultural Landscapes. Sustainability, 10(11), 4312. https://doi.org/10.3390/su10114312





