Export Diversification and Ecological Footprint: A Comparative Study on EKC Theory among Korea, Japan, and China
Abstract
1. Introduction
2. Literature Review
3. Data and Empirical Model
3.1. Ecological Footprint Per Capita
3.2. Real GDP Per Capita
3.3. Real GDP Per Capita Squared
3.4. Export Diversification
4. Empirical Model
- Step 1: Confirm the unit root.
- Step 2: Identify the number of lags.
- Step 3: Identify the number of cointegration relationships.
- Step 4: Fit a VECM (vector error correction model).
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
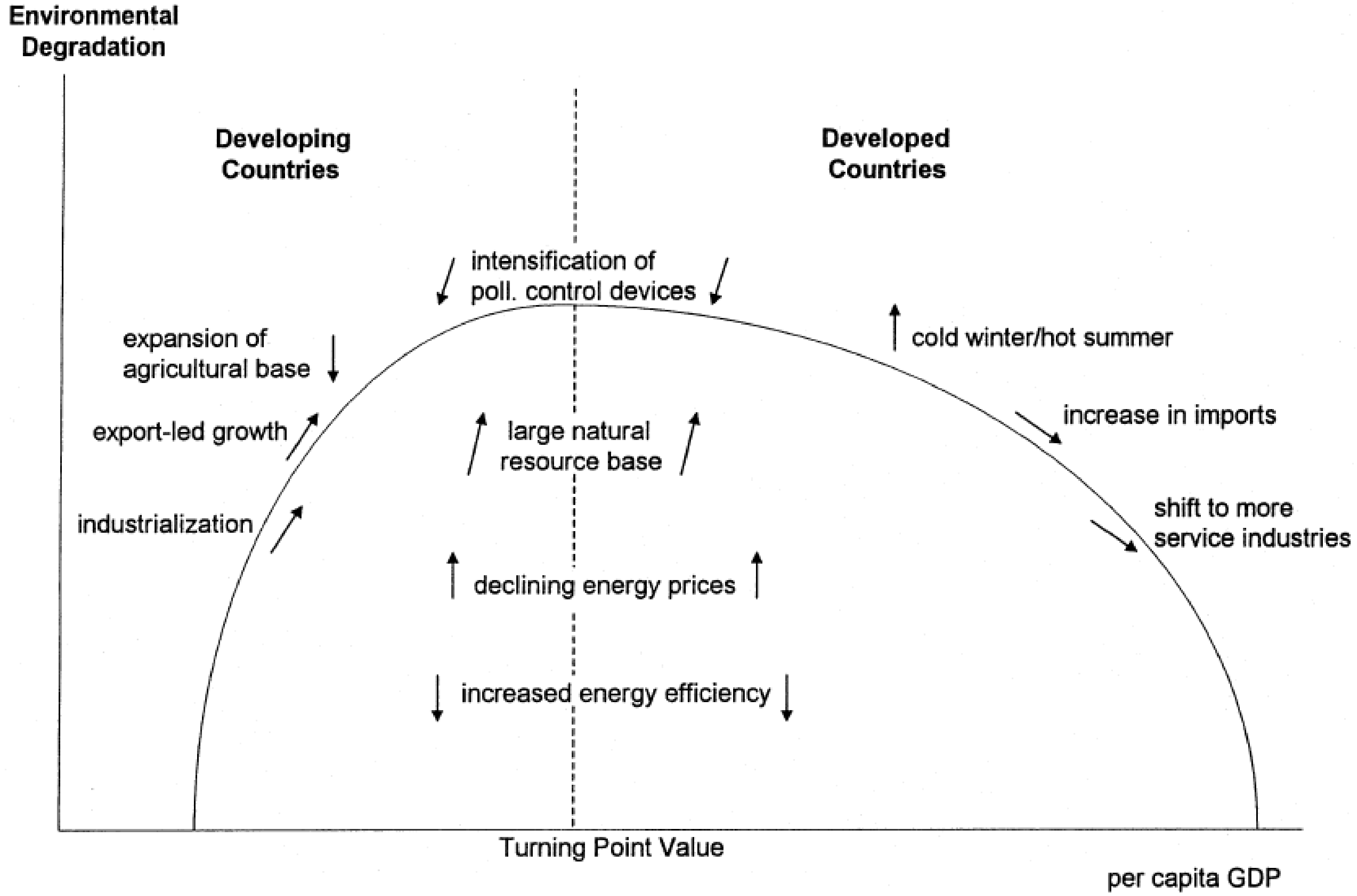
Appendix A. Depiction of the Environmental Kuznets Curve
References
- Kang, S.; Eltahir, E.A. North China Plain threatened by deadly heatwaves due to climate change and irrigation. Nat. Commun. 2018, 9, 2894. [Google Scholar] [CrossRef] [PubMed]
- Grossman, G.M.; Krueger, A.B. Environmental Impacts of a North American Free Trade Agreement; National Bureau of Economic Research; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Heil, M.T.; Selden, T.M. International trade intensity and carbon emissions: A cross-country econometric analysis. J. Environ. Dev. 2001, 10, 35–49. [Google Scholar]
- Copeland, B.R.; Taylor, M.S. Trade and the Environment: Theory and Evidence; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Grossman, G.M.; Krueger, A.B. The inverted-U: What does it mean? Environ. Dev. Econ. 2008, 1, 119–122. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Economic growth and the environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Stern, D.I. The environmental Kuznets curve after 25 years. J. Bioecon. 2017, 19, 7–28. [Google Scholar] [CrossRef]
- Stern, D.I.; Zha, D. Economic growth and particulate pollution concentrations in China. Environ. Econ. Policy Stud. 2016, 18, 327–338. [Google Scholar] [CrossRef]
- Stern, D.I. The Environmental Kuznets Curve after 25 Years; The Australian National University: Canberra, Australia, 2015; pp. 1–22. [Google Scholar]
- Stern, D.I. The rise and fall of the environmental Kuznets curve. World Dev. 2004, 32, 1419–1439. [Google Scholar] [CrossRef]
- Siemieniuk, R.A.; Fonseca, K.; Gill, M.J. Using root cause analysis and form redesign to reduce incorrect ordering of HIV tests. Jt. Comm. J. Q. Patient Saf. 2012, 38, 506–512. [Google Scholar] [CrossRef]
- Chetty, R. Sufficient Statistics for Welfare Analysis: A Bridge Between Structural and Reduced-Form Methods. Annu. Rev. Econ. 2009, 1, 451–487. [Google Scholar] [CrossRef]
- Orcutt, G.H.; Cochrane, D. A sampling study of the merits of autoregressive and reduced form transformation in regression analysis. Publ. Am. Stat. Assoc. 1949, 44, 356–372. [Google Scholar] [CrossRef]
- Özokcu, S.; Özdemir, Ö. Economic growth, energy, and environmental Kuznets curve. Renew. Sustain. Energy Rev. 2017, 72, 639–647. [Google Scholar] [CrossRef]
- Hartman, R.; Kwon, O.-S. Sustainable growth and the environmental Kuznets curve. J. Econ. Dyn. Control 2005, 29, 1701–1736. [Google Scholar] [CrossRef]
- Stern, D.I.; Common, M.S.; Barbier, E.B. Economic growth and environmental degradation: The environmental Kuznets curve and sustainable development. World Dev. 1996, 24, 1151–1160. [Google Scholar] [CrossRef]
- Selden, T.M.; Song, D. Environmental quality and development: Is there a Kuznets curve for air pollution emissions? J. Environ. Econ. Manag. 1994, 27, 147–162. [Google Scholar] [CrossRef]
- Shafik, N.; Bandyopadhyay, S. Economic Growth and Environmental Quality: Time-Series and Cross-Country Evidence; World Bank Publications: Washington, DC, USA, 1992; Volume 904. [Google Scholar]
- Agras, J.; Chapman, D. A dynamic approach to the Environmental Kuznets Curve hypothesis. Ecol. Econ. 1999, 28, 267–277. [Google Scholar] [CrossRef]
- Friedl, B.; Getzner, M. Determinants of CO2 emissions in a small open economy. Ecol. Econ. 2003, 45, 133–148. [Google Scholar] [CrossRef]
- Shen, J.; Hashimoto, Y. Environmental Kuznets curve on country level: Evidence from China. Discuss. Pap. Econ. Bus. 2004, 5, 4–9. [Google Scholar]
- Diao, X.D.; Zeng, S.X.; Tam, C.M.; Tam, V.W. EKC analysis for studying economic growth and environmental quality: A case study in China. J. Clean. Prod. 2009, 17, 541–548. [Google Scholar] [CrossRef]
- Stern, D.I.; Common, M.S. Is there an environmental Kuznets curve for sulfur? J. Environ. Econ. Manag. 2001, 41, 162–178. [Google Scholar] [CrossRef]
- Liddle, B. What are the carbon emissions elasticities for income and population? Bridging STIRPAT and EKC via robust heterogeneous panel estimates. Glob. Environ. Chang. 2015, 31, 62–73. [Google Scholar] [CrossRef]
- Lee, C.-C.; Chiu, Y.-B.; Sun, C.-H. Does one size fit all? A reexamination of the environmental Kuznets curve using the dynamic panel data approach. Rev. Agric. Econ. 2009, 31, 751–778. [Google Scholar] [CrossRef]
- Liu, H.; Kim, H. Ecological Footprint, Foreign Direct Investment, and Gross Domestic Production: Evidence of Belt & Road Initiative Countries. Sustainability 2018, 10, 3527. [Google Scholar]
- Cadot, O.; Carrère, C.; Strauss-Kahn, V. Export diversification: What’s behind the hump? Rev. Econ. Stat. 2011, 93, 590–605. [Google Scholar] [CrossRef]
- Cadot, O.; Carrere, C.; Strauss-Kahn, V. Trade diversification, income, and growth: What do we know? J. Econ. Surv. 2013, 27, 790–812. [Google Scholar] [CrossRef]
- Dutt, P.; Mihov, I.; van Zandt, T. Trade Diversification and Economic Development; Mimeograph; INSEAD: Paris, France, 2008. [Google Scholar]
- Chandra, V.; Boccardo, J.; Osorio, I. Export Diversification and Competitiveness in Developing Countries; World Bank: Washington, DC, USA, 2007. [Google Scholar]
- Imbs, J.; Wacziarg, R. Stages of diversification. Am. Econ. Rev. 2003, 93, 63–86. [Google Scholar] [CrossRef]
- Gozgor, G.; Can, M. Export product diversification and the environmental Kuznets curve: Evidence from Turkey. Environ. Sci. Pollut. Res. 2016, 23, 21594–21603. [Google Scholar] [CrossRef] [PubMed]
- Export Market Diversification and Productivity Improvements: Theory and Evidence from Argentinean Firms. Available online: https://ideas.repec.org/p/fip/fedlwp/2013-015.html (accessed on 14 April 2013).
- Świąder, M.; Szewrański, S.; Kazak, J.; van Hoof, J.; Lin, D.; Wackernagel, M.; Alves, A. Application of Ecological Footprint Accounting as a Part of an Integrated Assessment of Environmental Carrying Capacity: A Case Study of the Footprint of Food of a Large City. Resources 2018, 7, 52. [Google Scholar] [CrossRef]
- Zheng, H.; Fang, Q.; Wang, C.; Wang, H.; Ren, R. China’s carbon footprint based on input-output table series: 1992–2020. Sustainability 2017, 9, 387. [Google Scholar] [CrossRef]
- Fotis, P.; Karkalakos, S.; Asteriou, D. The relationship between energy demand and real GDP growth rate: The role of price asymmetries and spatial externalities within 34 countries across the globe. Energy Econ. 2017, 66, 69–84. [Google Scholar] [CrossRef]
- The Environmental Kuznets Curve: A Survey of the Literature. Available online: https://ideas.repec.org/p/fem/femwpa/1999.85.html (accessed on 10 February 2000).
- Becketti, S. Introduction to Time Series Using Stata; Stata Press College: Station, TX, USA, 2013. [Google Scholar]
- Elliot, B.; Rothenberg, T.; Stock, J. Efficient tests of the unit root hypothesis. Econometrica 1996, 64, 13–36. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Development in the Study of Co-Integrated Economic Variables. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1468-0084.1986.mp48003002.x (accessed on 15 July 2011).
- An Empirical Study of the Relationships between CO2 Emissions, Economic Growth and Openness. Available online: http://ftp.iza.org/dp5304.pdf (accessed on 28 February 1986).
| Author | Dependent Variable(s) | Independent Variable(s) | Type of Function | Regression Method | Turning Point | Country |
|---|---|---|---|---|---|---|
| MARK T. HEIL and THOMAS M.SELDEN (2001) | Per capita carbon emissions | Per capita GDP, Trade intensity | Income squared | Country fixed effect | USD 7000 | 132 countries from 1950 to 1992 |
| Birgit Friedl, Michael Getzner (2003) | CO2 emissions per capita | Per capita GDP, deviation of GDP from trend GDP, value added in the service sector nominal ratio to GDP, imports as a ratio to GDP, time dummy | Income cubed | Cointegrating regression | Austria from 1960 to 1999 | |
| Stern and Common (2001) | Per capita emission of sulfur | Per capita GDP, per capita GDP square, both with purchasing power parity | Income squared | Fixed and random | $101,166 | World, OECD countries, non-OECD countries |
| Junyi Shen, Yoshizo Hashimoto (2004) | Per capita pollutant emission | per capita GDP, share of the secondary industry, population density, time trend | Income cubed | Random | 69,071 CNY for dust fall case | China |
| Xiaozi Liu (2006) | Pollution index: Total Suspended Particulate (TSP), SO2, NOX, Nemerow index | Per capita GDP, per capita GDP square | Income cubed | Random | Monotonic relation, no turning point | Shenzhen, China from 1989 to 2003 |
| YUE YAGUCHI, TETSUSHI SONOBE (2007) | SO2, CO2 emission per area | Per capita GDP, per capita GDP square, three time dummies | Income squared | Fixed plus random | No turning point in China case, Japan had in SO2 | China and Japan from 1975 to 1999 |
| Tao SONG (2007) | Waste gas emission | Per capita GDP, per capita GDP square, per capita GDP cubed | Income cubed | Panel cointegration | 29,017 RMB | China |
| X.D. Diao (2009) | Sulfur oxide discharge, soot discharge, industrial dust discharge | Per capita GDP, per capita GDP square, per capita GDP cubed, environmental policies/investment strategies/contribution of industry to GDP | Income cubed | 23,218 RMB for soot discharge | Zhejiang Province, China | |
| Victor BRAJER, Robert W. MEAD, Feng XIAO | Concentration of SO2, TSP, and NO2, Nemerow index, pollution index1, pollution index2 (epidemiological index) | Real per capita gross city product (PPP in 2004), population density, city location dummies, time trend | Income | Random effect Tobit model | For SO2, 10,663 RMB; For TSP, 120,000 RMB; For NO2, two turning points of 26,754 and 42,902 RMB respectively | 139 cities in China from 1990 to 2006 |
| Usama Al-mulali el. | Ecological footprint | GDP growth | GDP growth | Fixed effect and generalized method of moments | Inverted U-shaped relationship between Ecological Footprint (EF) and GDP growth | 93 countries |
| Y wang | Ecological footprint of consumption, income and biocapacity | Economic growth | Economic growth | Ordinary Least Square (OLS) and spatial Durbin model | No evidence of inverted U-shaped EKC curve | China |
| Variables | DF-GLS Tau Test Statistic | 1% Critical Value | 5% Critical Value | 10% Critical Value |
|---|---|---|---|---|
| ln_EF_Korea | −1.355 | −3.770 | −3.476 | −2.932 |
| ln_hhi_product_Korea | −1.163 | −3.770 | −3.476 | −2.932 |
| ln_hhi_market_Korea | −0.035 | −3.770 | −3.476 | −2.932 |
| ln_gdp_Korea | −0.605 | −3.770 | −3.476 | −2.932 |
| ln_gdp2_Korea | −0.620 | −3.770 | −3.476 | −2.932 |
| Lag | LL | LR | df | p | FPE | AIC | HQIC | SBIC |
|---|---|---|---|---|---|---|---|---|
| 0 | 39.2527 | 4.80 × 10−7 | −6.04211 | −6.08699 | −5.92089 | |||
| 1 | 77.3431 | 76.181 | 9 | 0 | 4.00 × 10−9 | −10.8905 | −11.0701 | −10.4056 |
| 2 | 92.7421 | 30.798 | 9 | 0 | 2.10 × 10−9 | −11.957 | −12.2712 | −11.1084 |
| 3 | 323.447 | 461.41 | 9 | 0 | 1.00 × 10−24 * | −48.9078 | −49.3566 | −47.6956 |
| 4 | 1118.14 | 1589.4 * | 9 | 0 | −180.357 * | −180.357 * | −178.902 * |
| f | Parms | LL | Eigenvalue | Trace Statistic | 5% Critical Value |
|---|---|---|---|---|---|
| 0 | 12 | 60.83 | 29.1381 * | 29.68 | |
| 1 | 17 | 69.4 | 0.70619 | 11.9906 | 15.41 |
| 2 | 20 | 73.86 | 0.47135 | 3.0666 | 3.76 |
| 3 | 21 | 75.39 | 0.19671 |
| Log EF Per Capita | Export Product Diversification | Export Market Diversification | ||||
|---|---|---|---|---|---|---|
| China | Japan | Korea | China | Japan | Korea | |
| Error correction term | 0.749 *** (0.00) | 0.299 (1.68) | −0.157 (−0.56) | 0.945 *** (4.42) | 0.387 ** (2.11) | −0.288 (−1.09) |
| ∆lagged Log real gdp per capita | −0.872 *** (−3.00) | 3.461 (1.03) | 4.996 * (1.79) | −0.826 * (−2.04) | 3.318 (0.76) | 7.336 ** (2.67) |
| ∆lagged Log real gdp per capita sq | 0.073 *** (4.13) | −0.183 (−1.12) | −0.233 (−1.69) | 0.074 *** (3.14) | −0.173 (−0.80) | −0.354 ** (−2.57) |
| ∆lagged Log HHI | −0.028 (−0.09) | −0.110 ** (−2.30) | −0.134 (−1.32) | 0.018 (0.19) | 0.073 (0.83) | 0.272 ** (2.36) |
| Cons_ | 0.123 *** (3.58) | −15.068 (−0.88) | −25.178 * (−1.78) | 2.602 (1.57) | −14.050 (−0.63) | −35.041 ** (−2.65) |
| Adj R-squared | 0.9870 | 0.7968 | 0.7871 | 0.9773 | 0.7494 | 0.8216 |
| observations | 21 | 23 | 23 | 21 | 23 | 23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Kim, H.; Liang, S.; Kwon, O.-S. Export Diversification and Ecological Footprint: A Comparative Study on EKC Theory among Korea, Japan, and China. Sustainability 2018, 10, 3657. https://doi.org/10.3390/su10103657
Liu H, Kim H, Liang S, Kwon O-S. Export Diversification and Ecological Footprint: A Comparative Study on EKC Theory among Korea, Japan, and China. Sustainability. 2018; 10(10):3657. https://doi.org/10.3390/su10103657
Chicago/Turabian StyleLiu, Hongbo, Hanho Kim, Shuanglu Liang, and Oh-Sang Kwon. 2018. "Export Diversification and Ecological Footprint: A Comparative Study on EKC Theory among Korea, Japan, and China" Sustainability 10, no. 10: 3657. https://doi.org/10.3390/su10103657
APA StyleLiu, H., Kim, H., Liang, S., & Kwon, O.-S. (2018). Export Diversification and Ecological Footprint: A Comparative Study on EKC Theory among Korea, Japan, and China. Sustainability, 10(10), 3657. https://doi.org/10.3390/su10103657




