Predicting Phase 1 Lymphoma Clinical Trial Durations Using Machine Learning: An In-Depth Analysis and Broad Application Insights
Abstract
:1. Introduction
- Resource and Strategic Planning: Predicting trial durations helps ensure optimal distribution of personnel and funds, minimizing inefficiencies. Furthermore, this foresight enables organizations to make informed decisions about trial prioritization, resource allocation, and initiation timelines [3,4];
- Patient Involvement and Safety: estimating trial durations provides patients with clarity on their commitment, which safeguards their well-being and promotes informed participation [5];
- Transparent Relations with Regulators: Providing predictions on trial durations, whether below or above the average, fosters open communication with regulatory authorities. This strengthens compliance, builds trust, and establishes transparent relationships among all stakeholders [6].
2. Background
- Pioneering Work in Duration Prediction: our machine learning model stands as a trailblazing effort in the domain, bridging the existing gap in duration prediction applications and establishing benchmarks for future research;
- Diverse Modeling: we extensively reviewed eight machine learning models, highlighting the Random Forest model for its unparalleled efficiency in predicting durations;
- Comprehensive Variable Exploration: our model incorporates varied variables, from enrollment metrics to study patterns, enhancing its predictive capabilities;
- Insight into Data Volume: beyond mere predictions, we delve into determining the optimal data volume required for precise forecasting;
- In-Depth Model Probability: Apart from binary predictions, our model associates higher probabilities with longer average durations, along with a 95% CI. This precision offers a comprehensive range of potential trial durations, aiding informed decision-making and strategic planning;
- Broad Applicability: with proven efficacy in lung cancer trials, our model showcases its potential use across various oncology areas.
3. Materials and Methods
3.1. Dataset
3.2. Data Preprocessing
3.3. Data Exploration and Feature Engineering
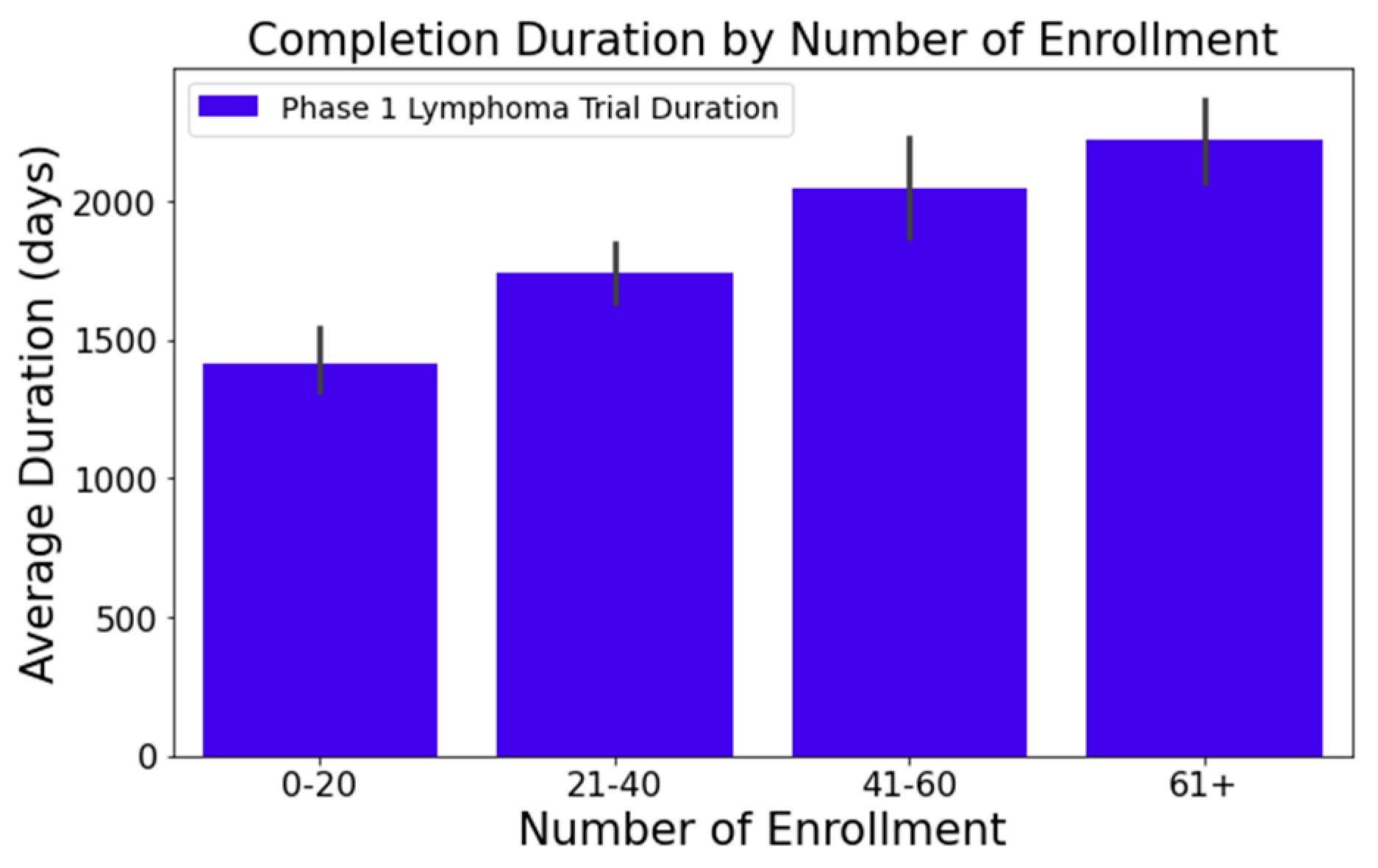
- Figure 1 illustrates that trials tend to take longer with increased enrollment. For example, trials with 0–20 enrollees averaged about 1417 days, while those with 61 or more enrollees extended to 2218 days—roughly 1.6 times longer. This difference was statistically significant at a 95% confidence level;
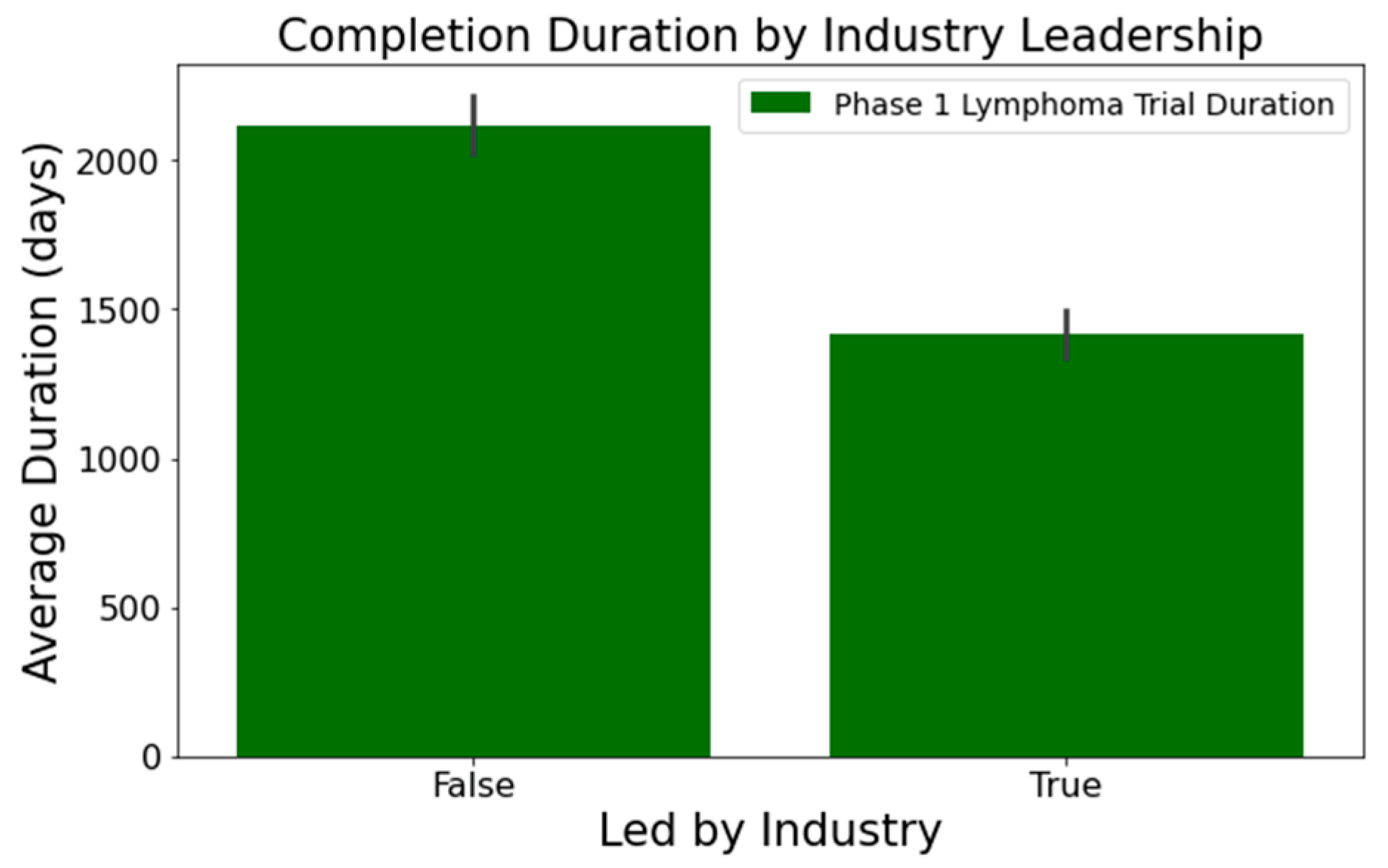
- In Figure 2, industry-led trials concluded more quickly than non-industry-led ones. On average, industry-led trials (510 trials) had a mean duration of 1414 days, notably shorter than non-industry-led trials with a mean duration of 2118 days across 579 trials. This difference was statistically significant at a 95% confidence level;
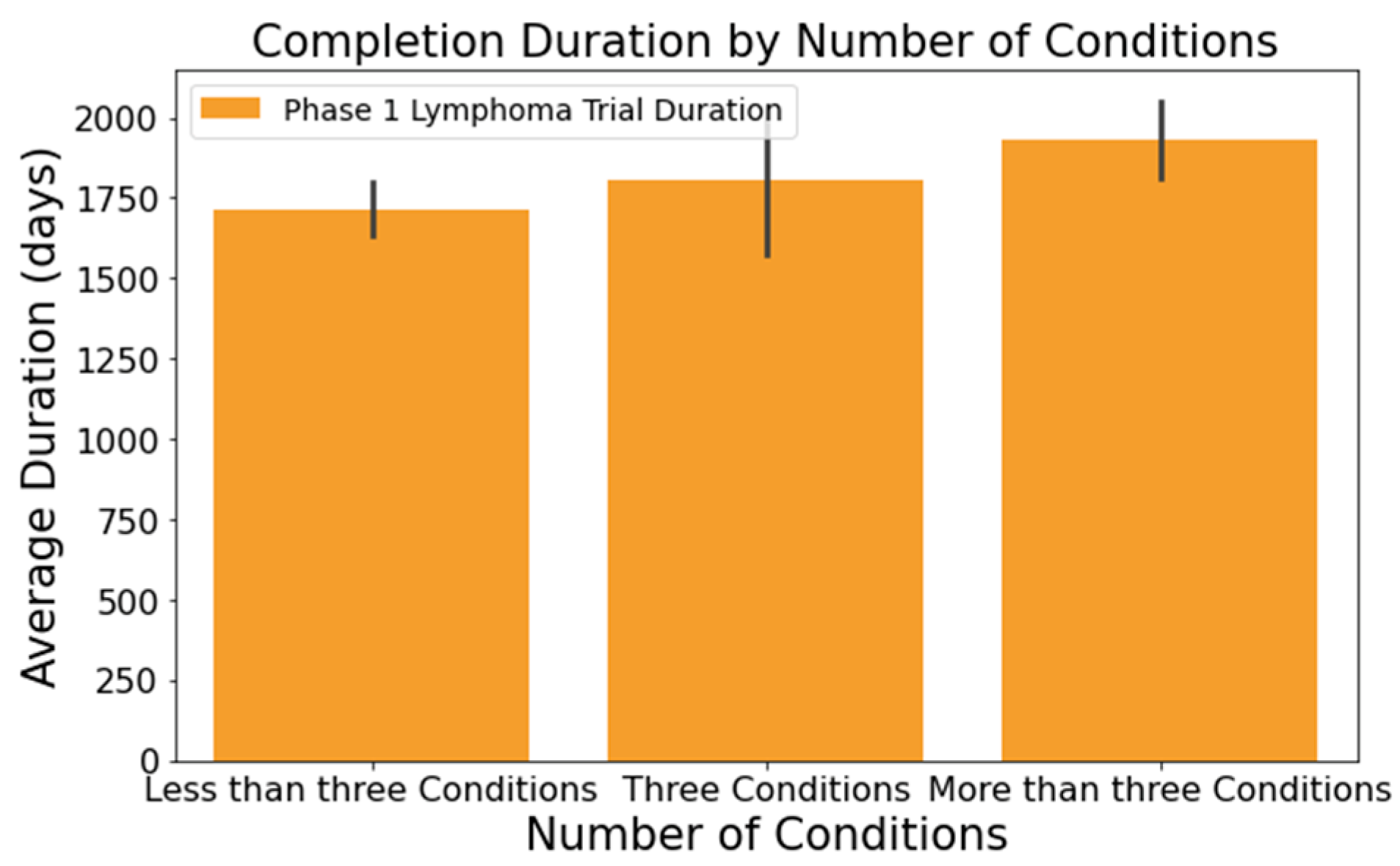
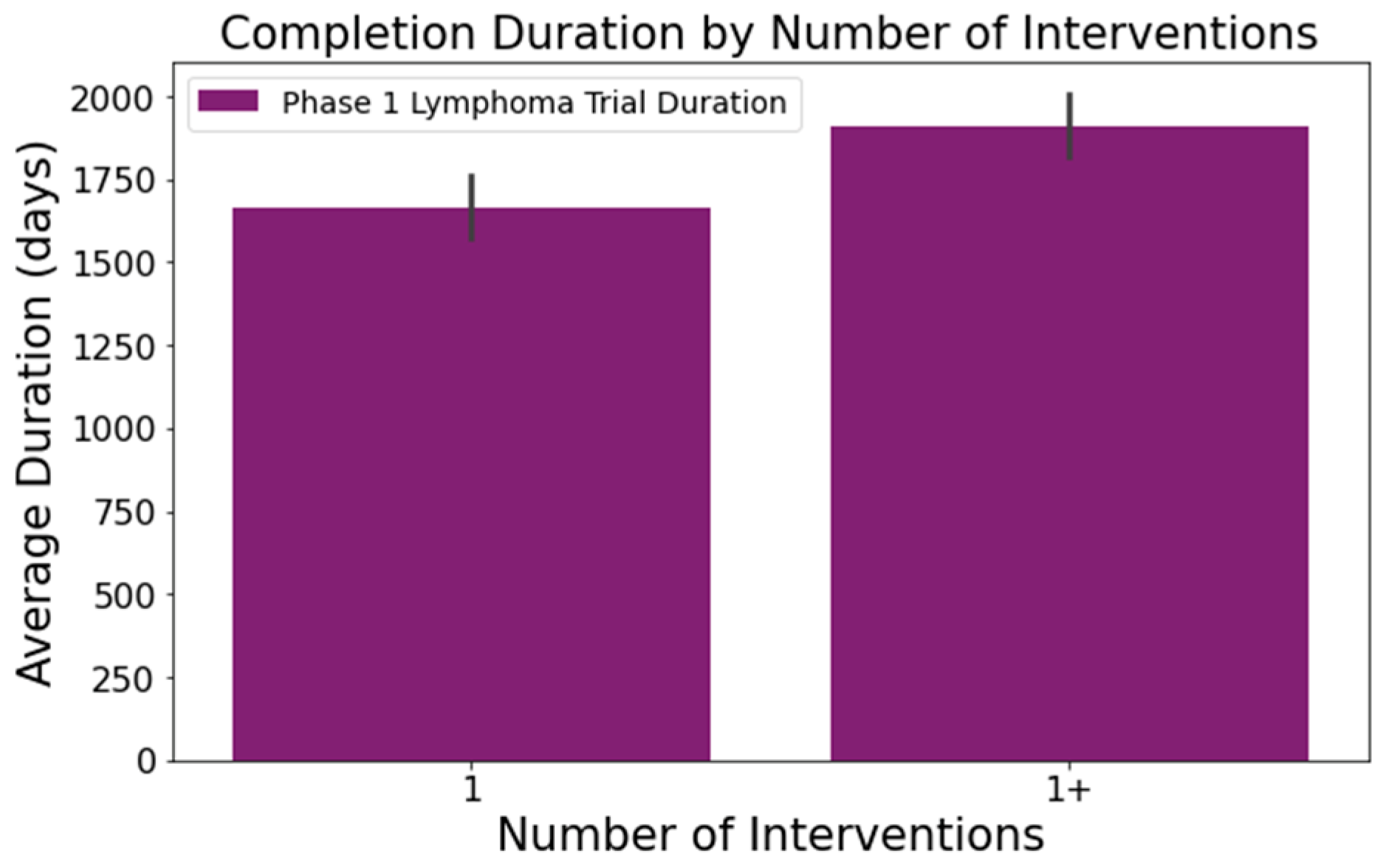
- The number of conditions or interventions in a trial correlates with its duration, as indicated in Figure 3 and Figure 4. For instance, trials with fewer than three conditions lasted about 1714 days (Figure 3). Those with more than three conditions had a 215-day longer mean duration (1929 days), with statistical significance across the three groups at a 95% confidence level. In Figure 4, trials with more than one intervention, on average, took 248 days longer to complete than those with only one intervention (1661 days), a statistically significant difference at 95%;
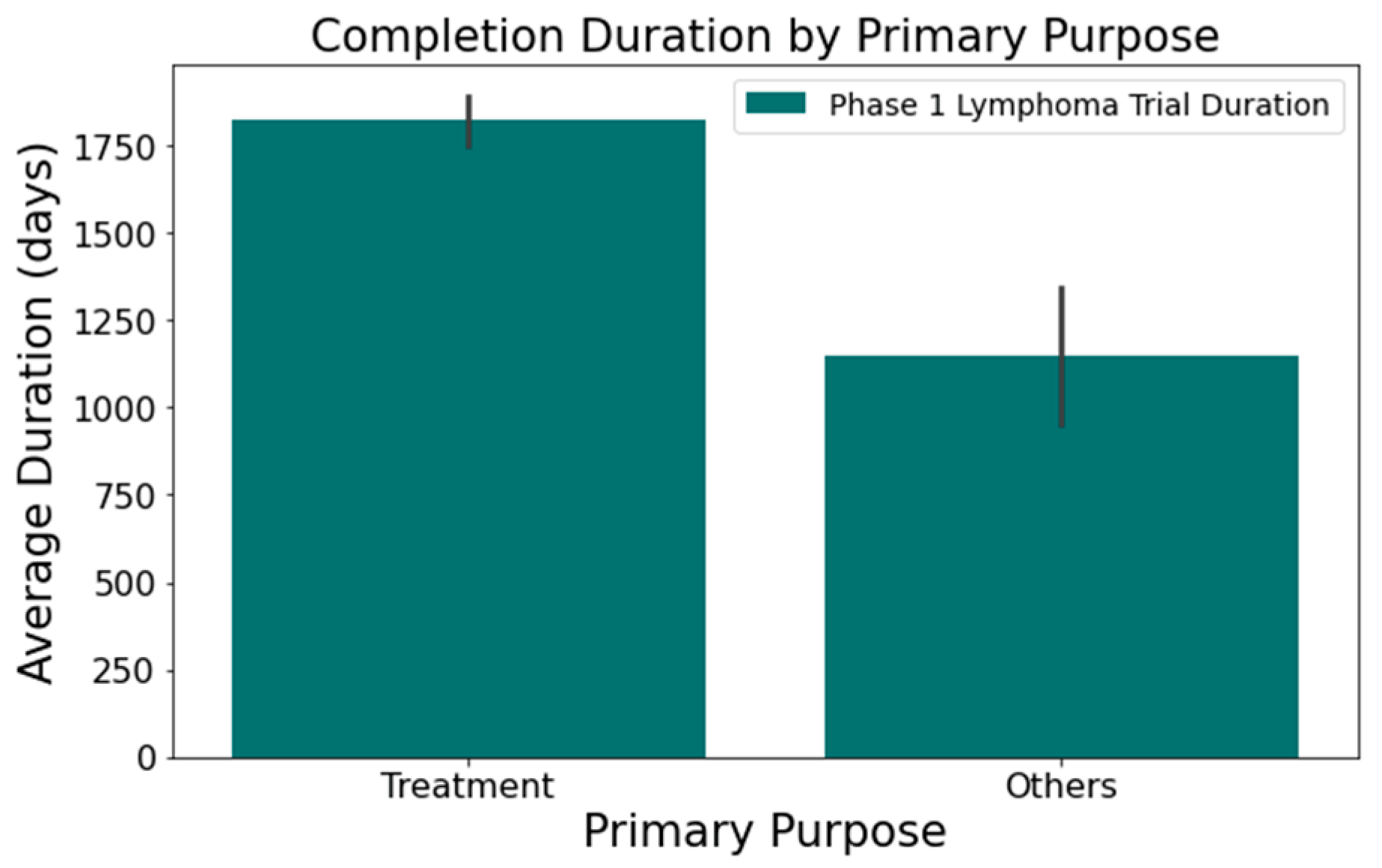
- Figure 5 shows that the primary purpose significantly affects the trial duration. ‘Treatment’ trials had a mean duration of 1821 days, while trials with other primary purposes were completed almost two years quicker, with a mean duration of 1145 days. This difference was statistically significant at a 95% confidence level.
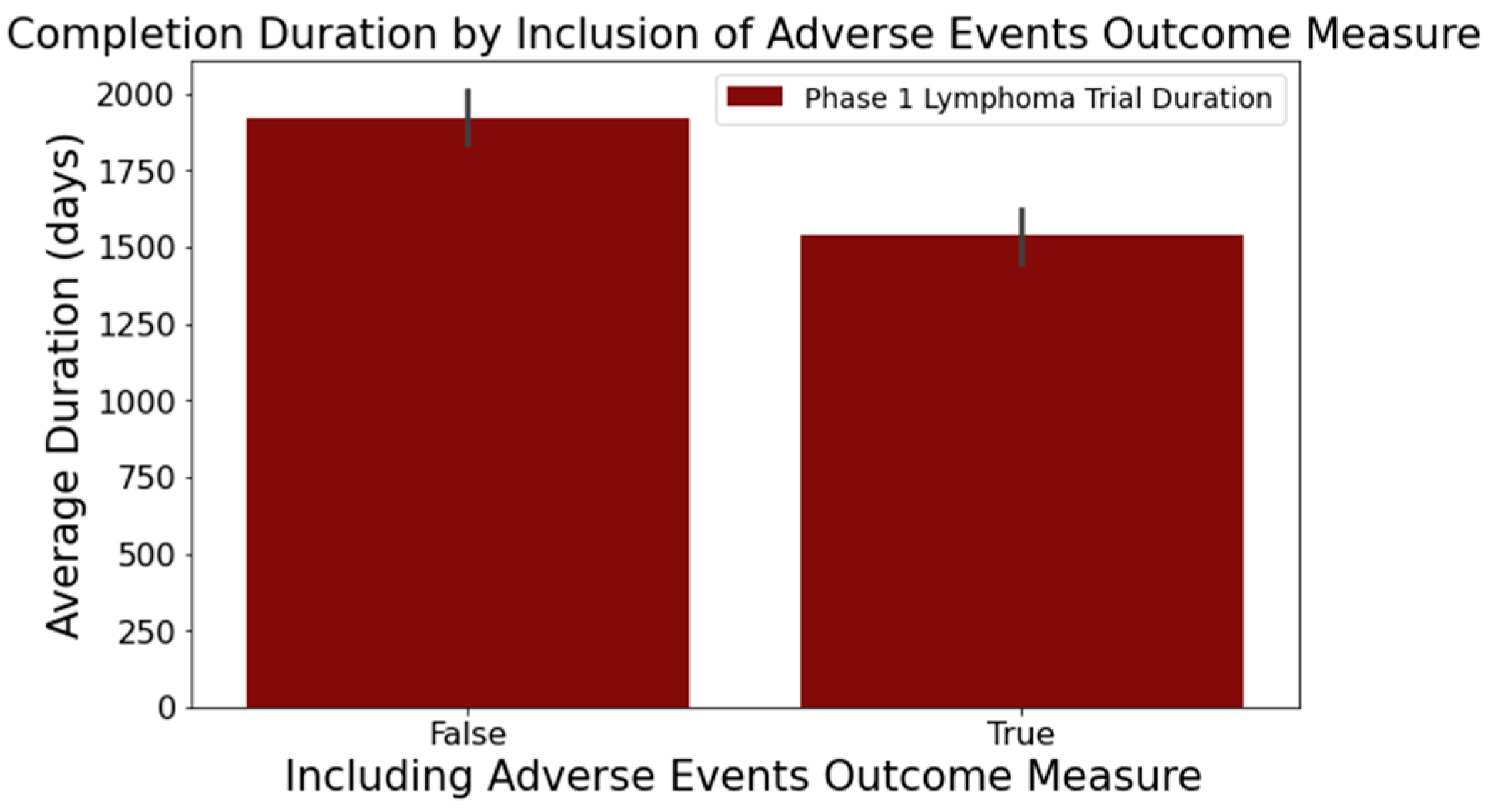
- Figure 6 reveals that trials focusing on adverse events in the ‘Outcome Measures’ column tend to conclude faster. Trials without adverse event measurement had a mean duration of 1919 days across 716 trials, while those with such measurement had a mean duration of 1537 days across 373 trials. This difference was statistically significant at a 95% confidence level;
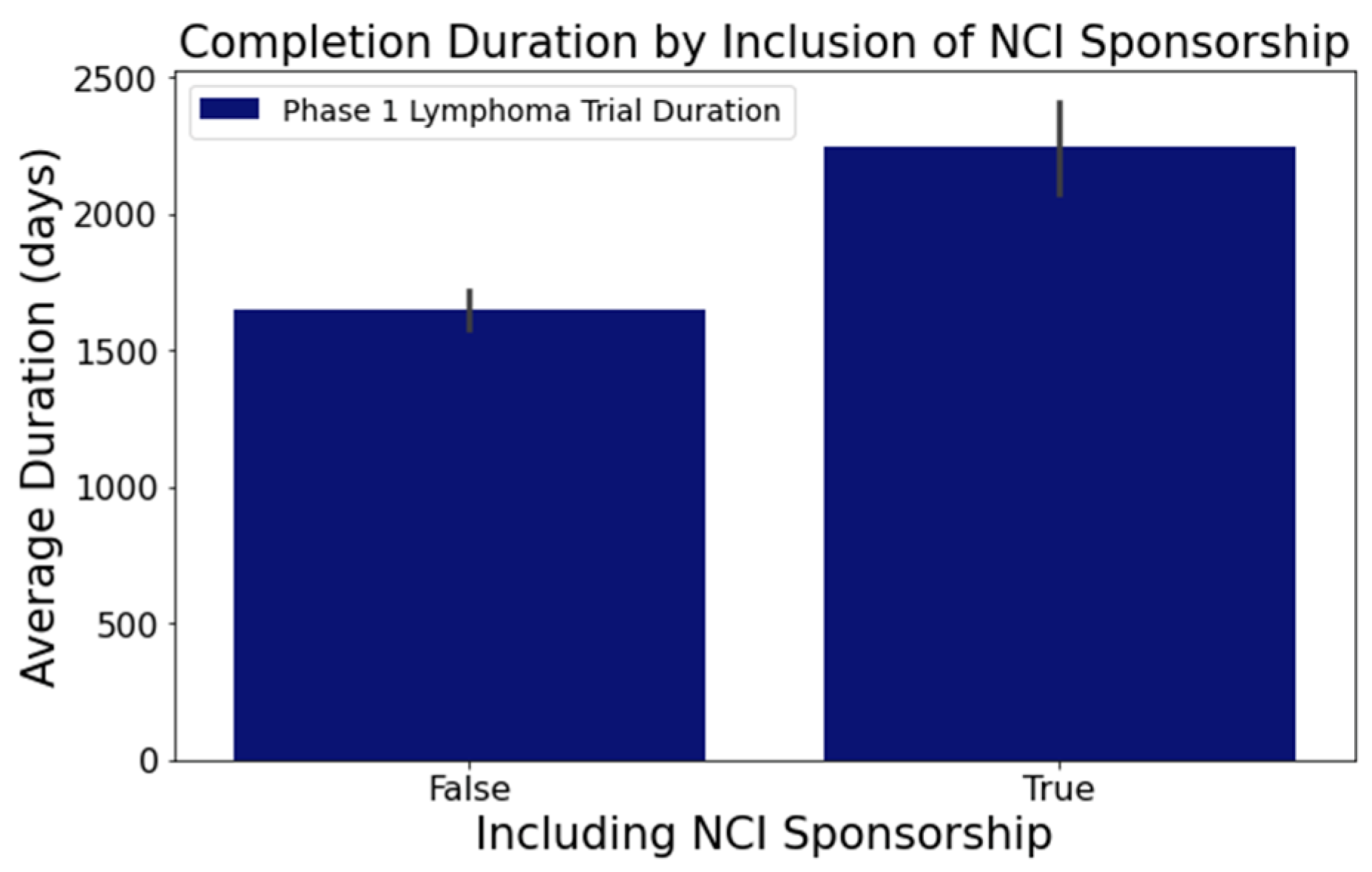
- In Figure 7, trials indicating the ‘National Cancer Institute (NCI)’ as a sponsor tended to have longer durations. Trials with NCI sponsorship had a mean duration of 2246 days, compared to trials without, which had a mean duration of 1648 days. This difference was statistically significant at a 95% confidence level;
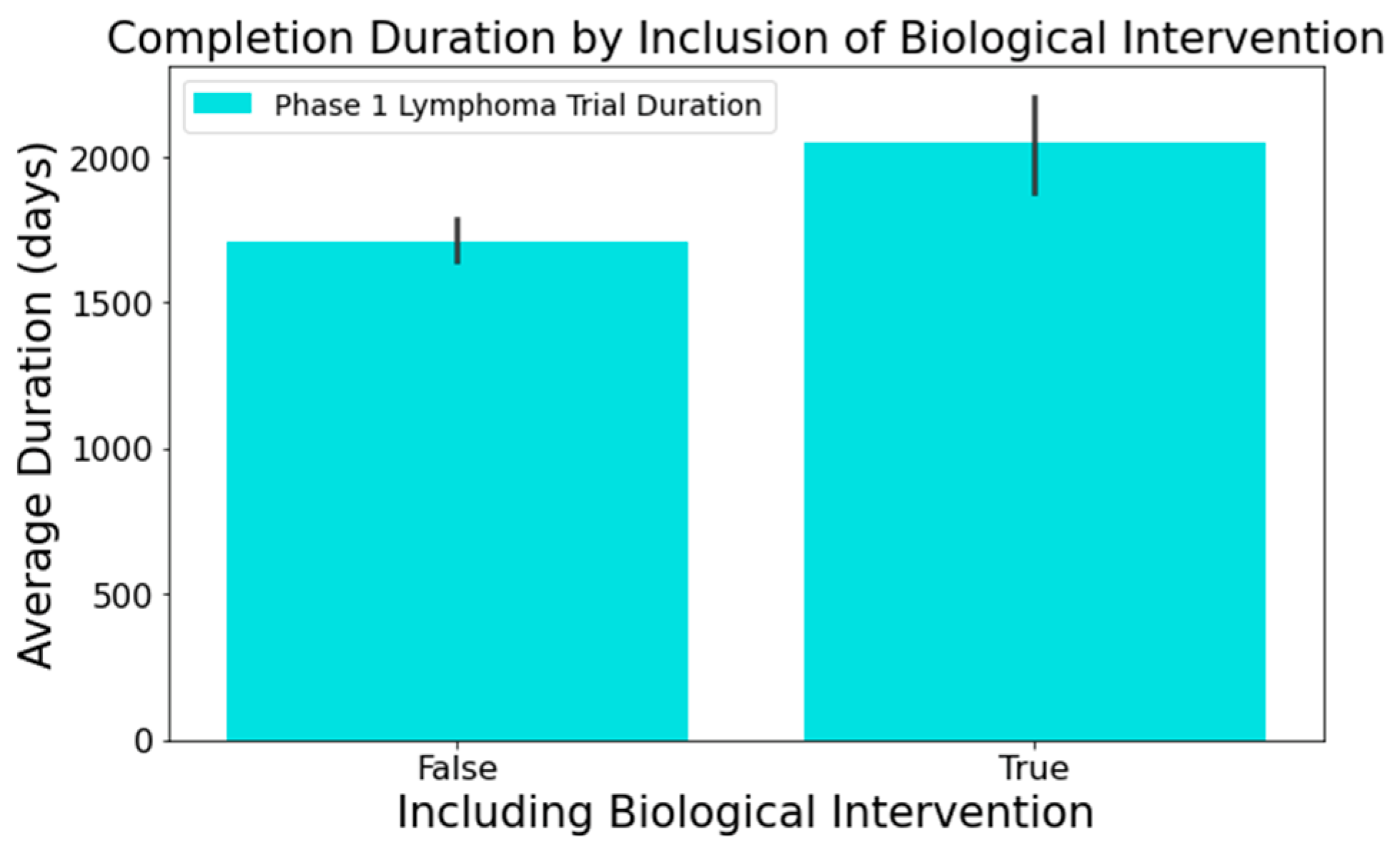
- Figure 8 highlights that the involvement of biological interventions in trials often results in extended durations, a statistically significant difference at 95%.
3.4. Machine Learning Models and Evaluation Metrics
3.4.1. Logistic Regression (LR)
3.4.2. K-Nearest Neighbors (KNN)
3.4.3. Decision Tree (DT)
3.4.4. Random Forest (RF) and XGBoost (XGB)
3.4.5. Linear Discriminant Analysis (LDA) and Gaussian Naïve Bayes (Gaussian NB)
3.4.6. Multi-Layer Perceptron (MLP)
- Accuracy measures the fraction of correct predictions (see Equation (1));
- ROC visually represents classifier performance by plotting recall against the false positive rate (see Equation (2)) across diverse thresholds. This visual representation is condensed into a metric via the AUC, a value between 0 and 1, where 1 signifies flawless classification;
- Precision gauges the reliability of positive classifications, shedding light on the inverse of the false positive rate (see Equation (3));
- Recall (or sensitivity) denotes the fraction of actual positives correctly identified, emphasizing the influence of false negatives (see Equation (4));
- F1-score provides a balance between precision and recall, acting as their harmonic mean (see Equation (5)).
4. Results and Discussion
4.1. Sample Characteristics
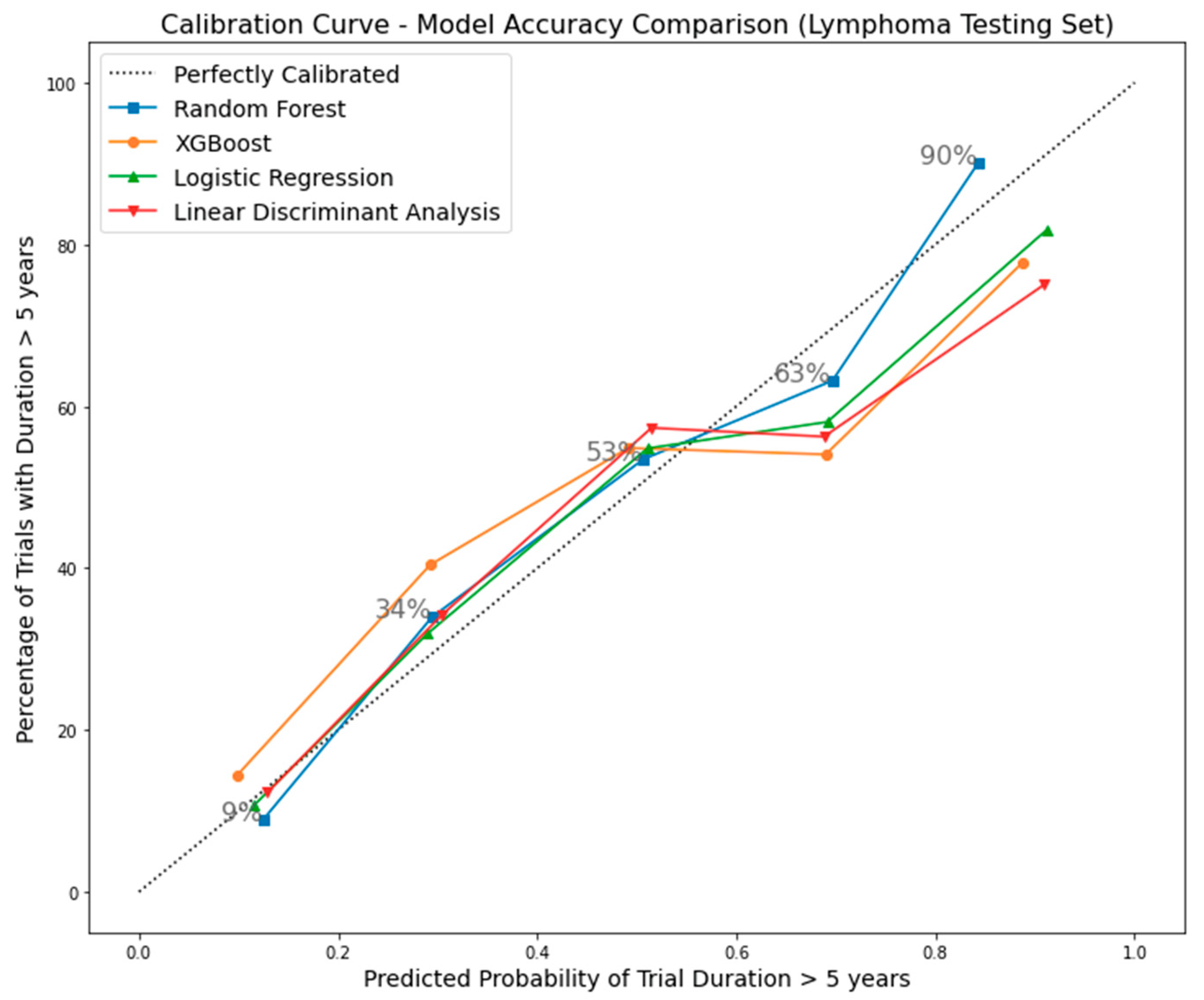
4.2. Machine Learning Classification
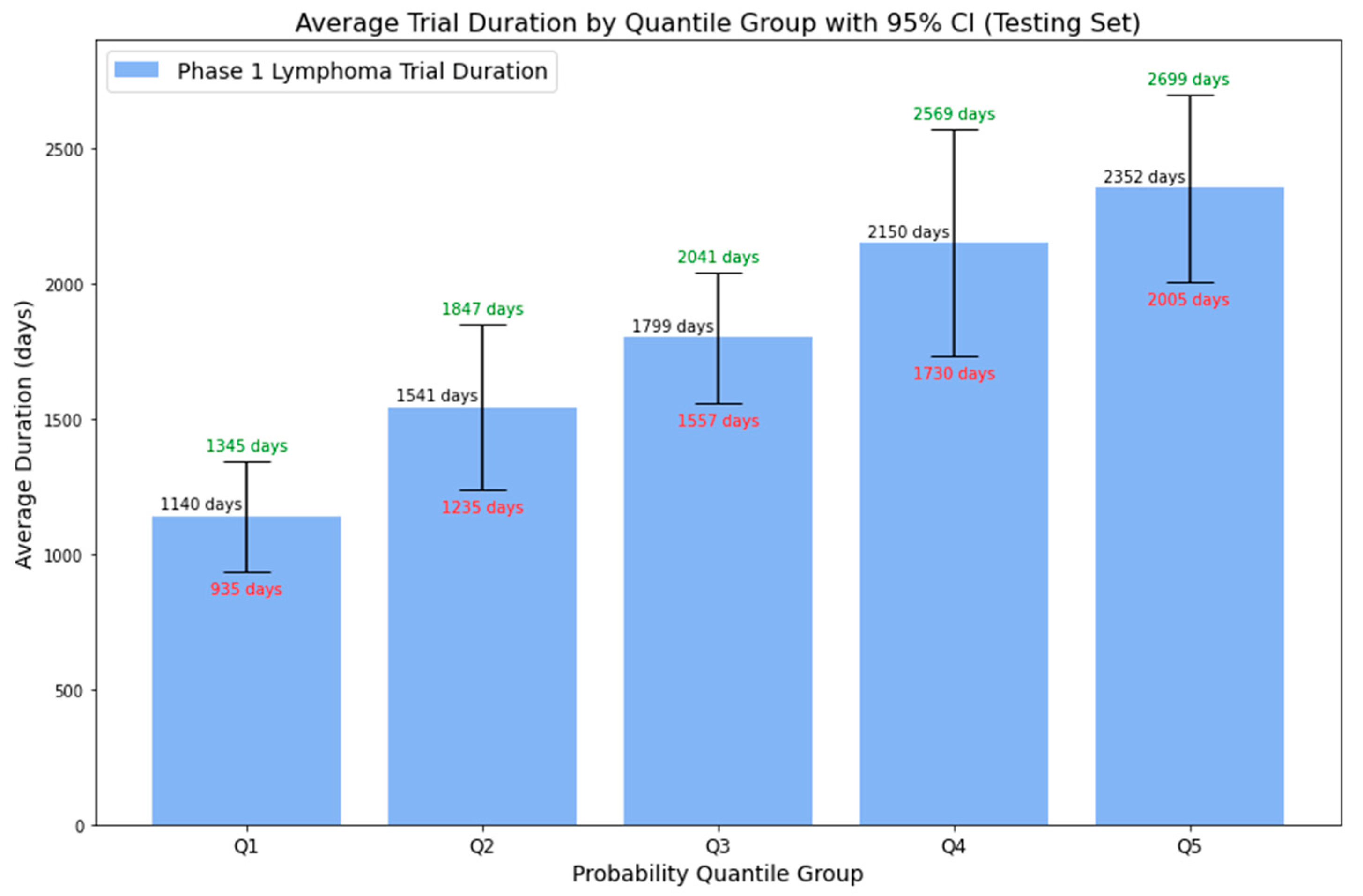
4.3. Random Forest Model Validation
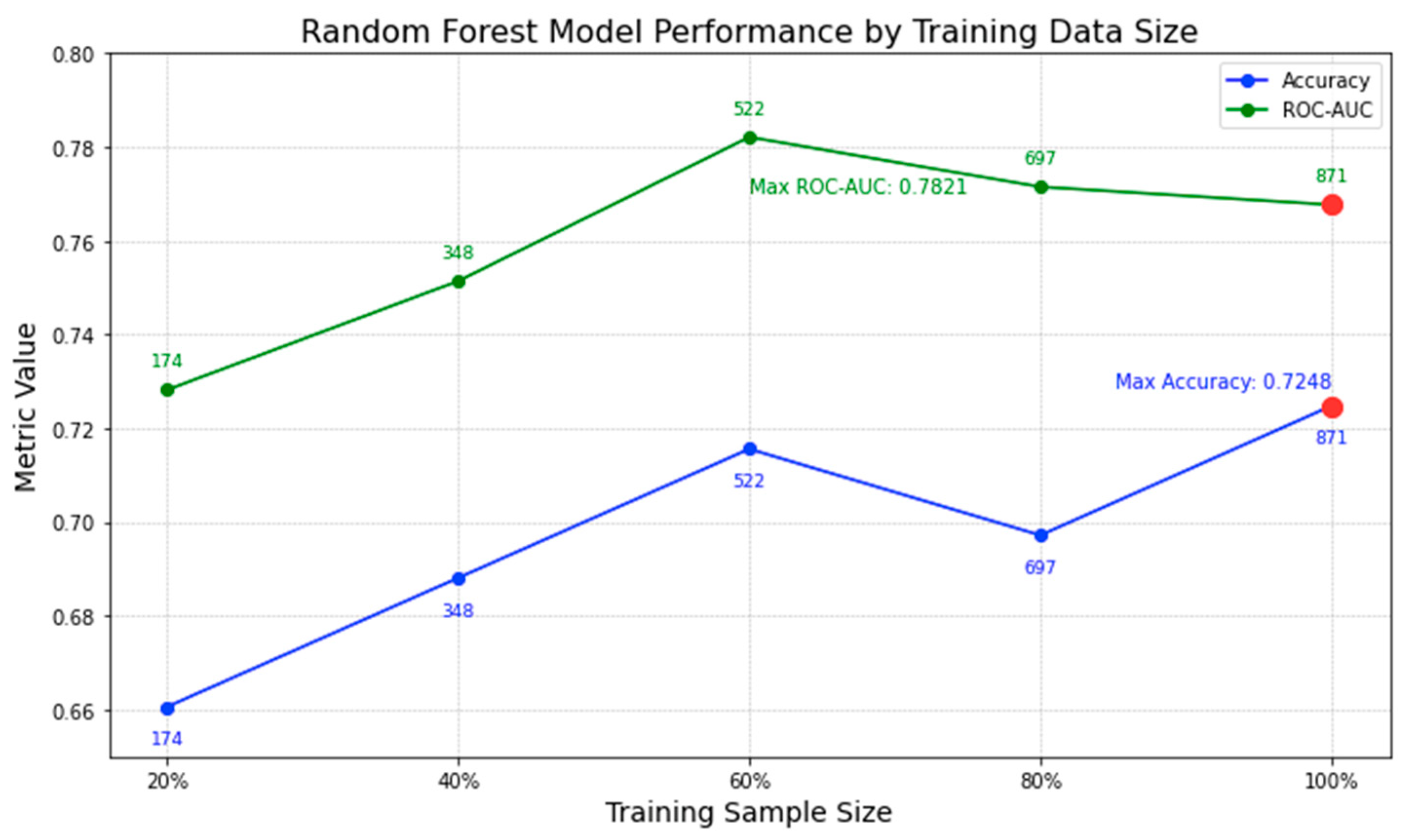
4.3.1. Impact of Varying Training Data Sizes on Model Performance
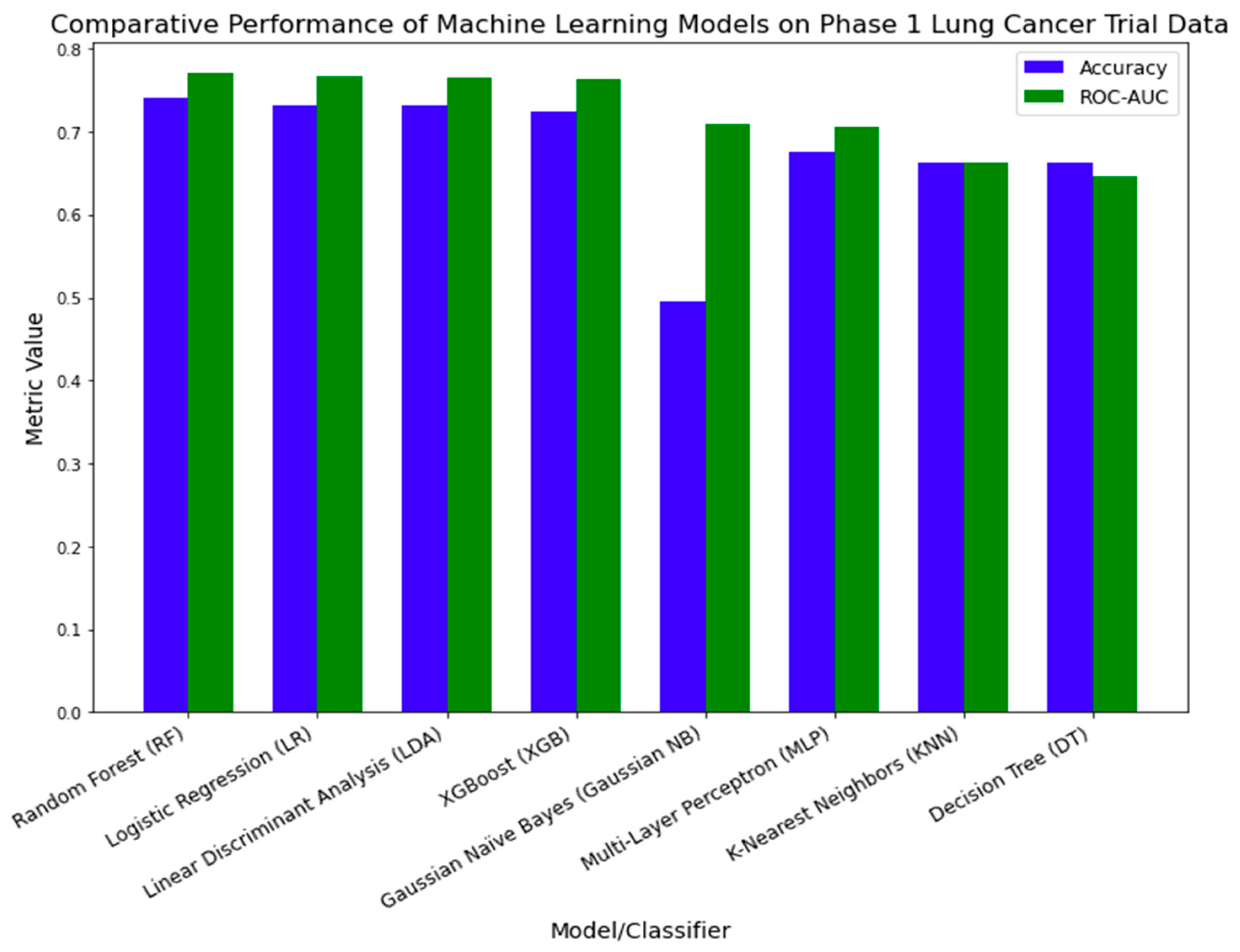
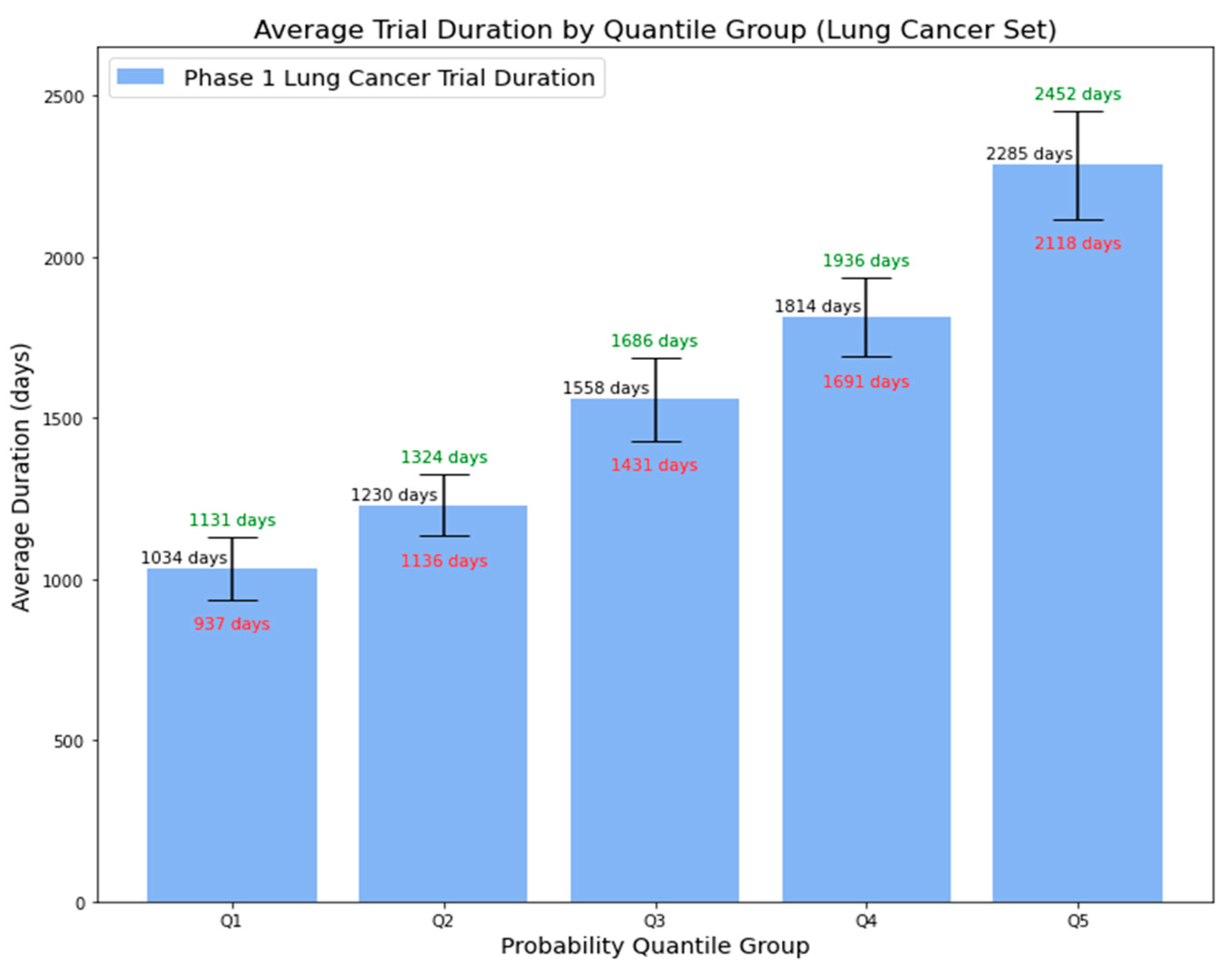
4.3.2. External Validation Using Phase 1 Lung Cancer Trial Data
Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Wagle, N.S.; Jemal, A. Cancer statistics, 2003. CA Cancer J. Clin. 2023, 73, 17–48. [Google Scholar] [CrossRef] [PubMed]
- Roberts, T.G.; Goulart, B.H.; Squitieri, L.; Stallings, S.C.; Halpern, E.F.; Chabner, B.A.; Gazelle, G.S.; Finkelstein, S.N.; Clark, J.W. Trends in the risks and benefits to patients with cancer participating in phase 1 clinical trials. JAMA 2004, 292, 2130–2140. [Google Scholar] [CrossRef] [PubMed]
- Weissler, E.H.; Naumann, T.; Andersson, T.; Ranganath, R.; Elemento, O.; Luo, Y.; Freitag, D.F.; Benoit, J.; Hughes, M.C.; Khan, F.; et al. The role of machine learning in clinical research: Transforming the future of evidence generation. Trials 2021, 22, 537. [Google Scholar] [CrossRef]
- Wu, K.; Wu, E.; Dandrea, M.; Chitale, N.; Lim, M.; Dabrowski, M.; Kantor, K.; Rangi, H.; Liu, R.; Garmhausen, M.; et al. Machine Learning Prediction of Clinical Trial Operational Efficiency. AAPS J. 2022, 24, 57. [Google Scholar] [CrossRef] [PubMed]
- Beauchamp, T.L.; Childress, J.F. Principles of Biomedical Ethics; Oxford University Press: New York, NY, USA, 2001; Available online: https://books.google.com/books?hl=en&lr=&id=_14H7MOw1o4C&oi=fnd&pg=PR9&dq=Beauchamp,+T.+L.,+%26+Childress,+J.+F.+(2013).+Principles+of+biomedical+ethics+(7th+ed.).+New+York:+Oxford+University+Press.&ots=1x_n4OBqWq&sig=pCzR4XfW0iDFmXEFsOajo6dGdU4 (accessed on 30 October 2023).
- Dri, D.A.; Massella, M.; Gramaglia, D.; Marianecci, C.; Petraglia, S. Clinical Trials and Machine Learning: Regulatory Approach Review. Rev. Recent Clin. Trials 2021, 16, 341–350. [Google Scholar] [CrossRef]
- Harrison, R.K. Phase II and phase III failures: 2013–2015. Nat. Rev. Drug Discov. 2016, 15, 817–818. [Google Scholar] [CrossRef]
- Sun, D.; Gao, W.; Hu, H.; Zhou, S. Why 90% of Clinical Drug Development Fails and How to Improve It? Acta Pharm. Sin. B 2022, 12, 3049–3062. [Google Scholar] [CrossRef]
- Fogel, D.B. Factors Associated with Clinical Trials That Fail and Opportunities for Improving the Likelihood of Success: A Review. Contemp. Clin. Trials Commun. 2018, 11, 156–164. [Google Scholar] [CrossRef]
- Uniform. How to Avoid Costly Clinical Research Delays|Blog. MESM. Available online: https://www.mesm.com/blog/tips-to-help-you-avoid-costly-clinical-research-delays/ (accessed on 30 October 2023).
- Research Methods Resources. GRT Calculator. 2023. Available online: https://researchmethodsresources.nih.gov/grt-calculator (accessed on 19 December 2023).
- OpenEpi. Sample Size for Cohort Studies. 2023. Available online: https://www.openepi.com/SampleSize/SSCohort.htm (accessed on 19 December 2023).
- ClinCalc. Sample Size Calculator. 2023. Available online: https://clincalc.com/stats/samplesize.aspx (accessed on 19 December 2023).
- Rubinstein, L.V.; Gail, M.H.; Santner, T.J. Planning the duration of a comparative clinical trial with loss to follow-up and a period of continued observation. J. Chronic Dis. 1981, 34, 469–479. [Google Scholar] [CrossRef]
- Camerlingo, N.; Vettoretti, M.; Sparacino, G.; Facchinetti, A.; Mader, J.K.; Choudhary, P.; Del Favero, S.; Hypo-RESOLVE Consortium. Design of clinical trials to assess diabetes treatment: Minimum duration of continuous glucose monitoring data to estimate time-in-ranges with the desired precision. Diabetes Obes. Metab. 2021, 23, 2446–2454. [Google Scholar] [CrossRef]
- Schwager, E.; Jansson, K.; Rahman, A.; Schiffer, S.; Chang, Y.; Boverman, G.; Gross, B.; Xu-Wilson, M.; Boehme, P.; Truebel, H.; et al. Utilizing machine learning to improve clinical trial design for acute respiratory distress syndrome. npj Digit. Med. 2021, 4, 133. [Google Scholar] [CrossRef] [PubMed]
- Kavalci, E.; Hartshorn, A. Improving clinical trial design using interpretable machine learning based prediction of early trial termination. Sci. Rep. 2023, 13, 121. [Google Scholar] [CrossRef] [PubMed]
- Harrer, S.; Shah, P.; Antony, B.; Hu, J. Artificial Intelligence for Clinical Trial Design. Trends Pharmacol. Sci. 2019, 40, 577–591. [Google Scholar] [CrossRef] [PubMed]
- Cai, T.; Cai, F.; Dahal, K.P.; Cremone, G.; Lam, E.; Golnik, C.; Seyok, T.; Hong, C.; Cai, T.; Liao, K.P. Improving the Efficiency of Clinical Trial Recruitment Using an Ensemble Machine Learning to Assist With Eligibility Screening. ACR Open Rheumatol. 2021, 3, 593–600. [Google Scholar] [CrossRef]
- Vazquez, J.; Abdelrahman, S.; Byrne, L.M.; Russell, M.; Harris, P.; Facelli, J.C. Using supervised machine learning classifiers to estimate likelihood of participating in clinical trials of a de-identified version of ResearchMatch. J. Clin. Transl. Sci. 2021, 5, e42. [Google Scholar] [CrossRef]
- Chekroud, A.M.; Zotti, R.J.; Shehzad, Z.; Gueorguieva, R.; Johnson, M.K.; Trivedi, M.H.; Cannon, T.D.; Krystal, J.H.; Corlett, P.R. Cross-trial prediction of treatment outcome in depression: A machine learning approach. Lancet Psychiatry 2016, 3, 243–250. [Google Scholar] [CrossRef]
- Schperberg, A.V.; Boichard, A.; Tsigelny, I.F.; Richard, S.B.; Kurzrock, R. Machine learning model to predict oncologic outcomes for drugs in randomized clinical trials. Int. J. Cancer 2020, 147, 2537–2549. [Google Scholar] [CrossRef]
- Tong, L.; Luo, J.; Cisler, R.; Cantor, M. Machine Learning-Based Modeling of Big Clinical Trials Data for Adverse Outcome Prediction: A Case Study of Death Events. In Proceedings of the 2019 IEEE 43rd Annual Computer Software and Applications Conference (COMPSAC), Milwaukee, WI, USA, 15–19 July 2019; pp. 269–274. [Google Scholar] [CrossRef]
- Batanova, E.; Birmpa, I.; Meisser, G. Use of Machine Learning to classify clinical research to identify applicable compliance requirements. Inform. Med. Unlocked 2023, 39, 101255. [Google Scholar] [CrossRef]
- Steyerberg, E.W. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. In Statistics for Biology and Health; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Sargent, D.J.; Conley, B.A.; Allegra, C.; Collette, L. Clinical Trial Designs for Predictive Marker Validation in Cancer Treatment Trials. J. Clin. Oncol. 2005, 23, 2020–2027. [Google Scholar] [CrossRef]
- Kola, I.; Landis, J. Can the pharmaceutical industry reduce attrition rates? Nat. Rev. Drug Discov. 2004, 3, 711–715. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Vergouwe, Y. Towards better clinical prediction models: Seven steps for development and an ABCD for validation. Eur. Heart J. 2014, 35, 1925–1931. [Google Scholar] [CrossRef]
- Mandrekar, S.J.; Sargent, D.J. Clinical Trial Designs for Predictive Biomarker Validation: One Size Does Not Fit All. J. Biopharm. Stat. 2009, 19, 530–542. [Google Scholar] [CrossRef]
- Blanche, P.; Dartigues, J.; Jacqmin-Gadda, H. Estimating and comparing time-dependent areas under receiver operating characteristic curves for censored event times with competing risks. Stat. Med. 2013, 32, 5381–5397. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005; Available online: https://books.google.com/books?hl=en&lr=&id=woaH_73s-MwC&oi=fnd&pg=PR13&dq=Rousseeuw,+P.J.,+Leroy,+A.M.+(1987).+Robust+Regression+and+Outlier+Detection.+John+Wiley+%26+Sons.&ots=TCuOR_zkjR&sig=pwLEHKv7QboOplfEIV0LO6POvdY (accessed on 30 October 2023).
- Hastie, T.; Friedman, J.; Tibshirani, R. The Elements of Statistical Learning. In Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4, Available online: https://link.springer.com/book/9780387310732 (accessed on 30 October 2023).
- Fox, J. Applied Regression Analysis and Generalized Linear Models, 2nd ed.; Sage Publications, Inc.: Thousand Oaks, CA, USA, 2008; pp. 375–378. [Google Scholar]
- ClinicalTrials.gov. National Library of Medicine. 2023. Available online: https://clinicaltrials.gov/. (accessed on 25 July 2023).
- Delgado, A.; Guddati, A.K. Clinical endpoints in oncology—A primer. Am. J. Cancer Res. 2021, 11, 1121–1131. [Google Scholar] [PubMed]
- Hirsch, B.R.; Califf, R.M.; Cheng, S.K.; Tasneem, A.; Horton, J.; Chiswell, K.; Schulman, K.A.; Dilts, D.M.; Abernethy, A.P. Characteristics of Oncology Clinical Trials: Insights from a Systematic Analysis of ClinicalTrials.gov. JAMA Intern. Med. 2013, 173, 972–979. [Google Scholar] [CrossRef] [PubMed]
- Honnibal, M.; Montani, I. spaCy 2: Natural language understanding with Bloom embeddings, convolutional neural networks and incremental parsing. Appear 2017, 7, 411–420. [Google Scholar]
- Yadav, A.; Shokeen, H.; Yadav, J. Disjoint Set Union for Trees. In Proceedings of the 2021 12th International Conference on Computing Communication and Networking Technologies (ICCCNT), IEEE, Kharagpur, India, 6–8 July 2021; pp. 1–6. Available online: https://ieeexplore.ieee.org/abstract/document/9580066/ (accessed on 30 October 2023).
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, in KDD ’16, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hasan, K.; Alam, A.; Roy, S.; Dutta, A.; Jawad, T.; Das, S. Missing value imputation affects the performance of machine learning: A review and analysis of the literature (2010–2021). Inform. Med. Unlocked 2021, 27, 100799. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Q.; Hu, Y.; Sun-Woo, K.; Zhang, X.; Zhu, H.; Jie, L.; Li, S. Novel binary logistic regression model based on feature transformation of XGBoost for type 2 Diabetes Mellitus prediction in healthcare systems. Futur. Gener. Comput. Syst. 2022, 129, 1–12. [Google Scholar] [CrossRef]
- Rajliwall, N.S.; Davey, R.; Chetty, G. Cardiovascular Risk Prediction Based on XGBoost. In Proceedings of the 2018 5th Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Nadi, Fiji, 10–12 December 2018; pp. 246–252. [Google Scholar] [CrossRef]
- Long, B.; Tan, F.; Newman, M. Ensemble DeBERTa Models on USMLE Patient Notes Automatic Scoring using Note-based and Character-based approaches. Adv. Eng. Technol. Res. 2023, 6, 107. [Google Scholar] [CrossRef]
- Barnett, V.; Lewis, T. Outliers in Statistical Data; Wiley: New York, NY, USA, 1994; Volume 3, Available online: https://scholar.archive.org/work/l4rvge57snh7fjjzpc5idiyxj4/access/wayback/http://tocs.ulb.tu-darmstadt.de:80/214880745.pdf (accessed on 30 October 2023).
- Maheswari, K.; Priya, P.P.A.; Ramkumar, S.; Arun, M. Missing Data Handling by Mean Imputation Method and Statistical Analysis of Classification Algorithm. In EAI International Conference on Big Data Innovation for Sustainable Cognitive Computing; Haldorai, A., Ramu, A., Mohanram, S., Onn, C.C., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 137–149. [Google Scholar] [CrossRef]
- Accelerating Study Start-Up: The Key to Avoiding Trial Delays. 2017. Available online: https://acrpnet.org/2017/02/01/accelerating-study-start-up-the-key-to-avoiding-trial-delays/ (accessed on 19 December 2023).
| Column | Value |
|---|---|
| NCT Number | NCT02220842 |
| Title | A Safety and Pharmacology Study of Atezolizumab (MPDL3280A) Administered With Obinutuzumab or Tazemetostat in Participants With Relapsed/Refractory Follicular Lymphoma and Diffuse Large B-cell Lymphoma |
| Acronym | |
| Status | Completed |
| Study Results | No Results Available |
| Conditions | Lymphoma |
| Interventions | Drug: Atezolizumab|Drug: Obinutuzumab|Drug: Tazemetostat |
| Outcome Measures | Percentage of Participants With Dose Limiting Toxicities (DLTs)|Recommended Phase 2 Dose (RP2D) of Atezolizumab|Obinutuzumab Minimum Serum Concentration (Cmin)|Percentage of Participants With Adverse Events (AEs) Graded According to the National Cancer Institute (NCI) Common Terminology Criteria for Adverse Events version 4.0 (CTCAE v4.0)... |
| Sponsor/Collaborators | Hoffmann-La Roche |
| Gender | All |
| Age | 18 Years and Older (Adult, Older Adult) |
| Phases | Phase 1 |
| Enrollment | 96 |
| Funded By | Industry |
| Study Type | Interventional |
| Study Designs | Allocation: Non-Randomized|Intervention Model: Parallel Assignment|Masking: None (Open Label)|Primary Purpose: Treatment |
| Other IDs | GO29383|2014-001812-21 |
| Start Date | 18 December 2014 |
| Primary Completion Date | 21 January 2020 |
| Completion Date | 21 January 2020 |
| First Posted | 20 August 2014 |
| Results First Posted | |
| Last Update Posted | 27 January 2020 |
| Locations | City of Hope National Medical Center, Duarte, California, United States|Fort Wayne Neurological Center, Fort Wayne, Indiana, United States|Hackensack University Medical Center, Hackensack, New Jersey, United States… |
| Study Documents | |
| URL | https://ClinicalTrials.gov/show/NCT02220842 (accessed on 25 July 2023) |
| Feature Name | Explanation |
|---|---|
| Enrollment | Number of trial participants |
| Industry-led | Trial led by the industry (true/false) |
| Location Count | Number of trial locations |
| Measures Count | Number of outcome measures |
| Condition Count | Number of medical conditions |
| Intervention Count | Number of interventions |
| NCI Sponsorship | Sponsorship includes NCI (true/false) |
| AES Outcome Measure | Outcome measure includes adverse events (true/false) |
| Open Masking Label | Trial uses open masking label (true/false) |
| Biological Intervention | Intervention type includes biological (true/false) |
| Efficacy Keywords | Title includes efficacy-related keywords (true/false) |
| Random Allocation | Patient allocation is random (true/false) |
| US-led | Trial primarily in the US (true/false) |
| Procedure Intervention | Intervention type includes procedure (true/false) |
| Overall Survival Outcome Measure | Outcome measure includes overall survival rate (true/false) |
| Drug Intervention | Intervention type includes drugs (true/false) |
| MTD Outcome Measure | Outcome measure includes maximally tolerated dose (true/false) |
| US-included | Trial location includes the US (true/false) |
| DOR Outcome Measure | Outcome measure includes duration of response (true/false) |
| Prevention Purpose | Primary purpose is prevention (true/false) |
| AES Outcome Measure (Lead) | Leading outcome measure is adverse events (true/false) |
| DLT Outcome Measure | Outcome measure includes dose-limiting toxicity (true/false) |
| Treatment Purpose | Primary purpose is treatment (true/false) |
| DLT Outcome Measure (Lead) | Leading outcome measure is dose-limiting toxicity (true/false) |
| MTD Outcome Measure (Lead) | Leading outcome measure is maximally tolerated dose (true/false) |
| Radiation Intervention | Intervention type includes radiation (true/false) |
| Tmax Outcome Measure | Outcome measure includes time of Cmax (true/false) |
| Cmax Outcome Measure | Outcome measure includes maximum measured concentration (true/false) |
| Non-Open Masking Label | Trial use non-open masking label (true/false) |
| Crossover Assignment | Patient assignment is crossover (true/false) |
| Characteristics | Training/Cross-Validation Sets (n = 871) | Testing Set (n = 218) |
|---|---|---|
| Percentage of Trials Exceeding 5-Year Completion Time (Target) | 40% | 40% |
| Mean Trial Participant Enrollment | 49 | 50 |
| Percentage of Industry-led Trials | 46% | 48% |
| Average Number of Trial Locations | 6 | 6 |
| Average Outcome Measures Count | 6 | 6 |
| Average Medical Conditions Addressed | 4 | 4 |
| Average Interventions per Trial | 3 | 2 |
| Percentage of NCI-Sponsored Trials | 23% | 24% |
| Percentage of Trials with AES Outcome Measure | 34% | 34% |
| Percentage of Trials with Open-Label Masking | 91% | 92% |
| Percentage of Titles Suggesting Efficacy | 50% | 51% |
| Percentage of Trials Involving Biological Interventions | 23% | 20% |
| Percentage of Randomly Allocated Patient Trials | 24% | 27% |
| Models/Classifier | Accuracy | ROC-AUC | Precision | Recall | F1-Score |
|---|---|---|---|---|---|
| XGBoost (XGB) | 0.7442 ± 0.0384 | 0.7854 ± 0.0389 | 0.7009 ± 0.0439 | 0.6286 ± 0.0828 | 0.6614 ± 0.0633 |
| Random Forest (RF) | 0.7371 ± 0.0389 | 0.7755 ± 0.0418 | 0.6877 ± 0.0403 | 0.6286 ± 0.0969 | 0.6544 ± 0.0667 |
| Logistic Regression (LR) | 0.7118 ± 0.0324 | 0.7760 ± 0.0282 | 0.6525 ± 0.0487 | 0.6171 ± 0.0506 | 0.6323 ± 0.0367 |
| Linear Discriminant Analysis (LDA) | 0.7072 ± 0.0393 | 0.7567 ± 0.0365 | 0.6457 ± 0.0545 | 0.6114 ± 0.0388 | 0.6272 ± 0.0412 |
| Multi-Layer Perceptron (MLP) | 0.6717 ± 0.0302 | 0.7071 ± 0.0593 | 0.6133 ± 0.0423 | 0.4914 ± 0.0984 | 0.5414 ± 0.0684 |
| Gaussian Naïve Bayes (Gaussian NB) | 0.5293 ± 0.0169 | 0.6980 ± 0.0274 | 0.4571 ± 0.0096 | 0.9086 ± 0.0194 | 0.6081 ± 0.0097 |
| K-Nearest Neighbors (KNN) | 0.6223 ± 0.0475 | 0.6487 ± 0.0445 | 0.5385 ± 0.0762 | 0.4286 ± 0.0619 | 0.4786 ± 0.0661 |
| Decision Tree (DT) | 0.6464 ± 0.0252 | 0.6363 ± 0.0317 | 0.5567 ± 0.0295 | 0.5771 ± 0.0780 | 0.5651 ± 0.0502 |
| Model/Classifier | Accuracy | ROC-AUC | Precision | Recall | F1-Score |
|---|---|---|---|---|---|
| Random Forest (RF) | 0.7248 | 0.7677 | 0.675 | 0.6136 | 0.6429 |
| Linear Discriminative Analysis (LDA) | 0.6927 | 0.7319 | 0.6180 | 0.6250 | 0.6215 |
| XGBoost (XGB) | 0.6881 | 0.7574 | 0.6282 | 0.5568 | 0.5904 |
| Logistic Regression (LR) | 0.6422 | 0.7281 | 0.5581 | 0.5455 | 0.5517 |
| Total Lymphoma Trials on Testing Set | Correctly Predicted Trials Using Random Forest (RF) | Chi-Square Test Results | |
|---|---|---|---|
| 218 | 158 | Correctly Predicted Trials using Linear Discriminative Analysis (LDA) | 151 |
| p-Value (RF vs. LDA) | 1.45 × 10−17 | ||
| Correctly Predicted Trials using XGBoost (XGB) | 150 | ||
| p-Value (RF vs. XGB) | 4.35 × 10−30 | ||
| Correctly Predicted Trials using Logistic Regression (LR) | 140 | ||
| p-Value (RF vs. LR) | 2.77 × 10−21 | ||
| Model/Classifier | Optimal Parameters |
|---|---|
| Random Forest (RF) | max depth: 20; min sample split: 10; number of trees: 100; bootstrap: false; and seed: 42 |
| Probability Quantile Group | Probability Range | Average Duration | Lower Bound (95% CI) | Upper Bound (95% CI) |
|---|---|---|---|---|
| Q1 | 0 to 0.1624 | 1140 days | 935 days | 1345 days |
| Q2 | 0.1624 to 0.3039 | 1541 days | 1235 days | 1847 days |
| Q3 | 0.3039 to 0.4697 | 1799 days | 1557 days | 2041 days |
| Q4 | 0.4697 to 0.6291 | 2150 days | 1730 days | 2569 days |
| Q5 | 0.6291 to 1 | 2352 days | 2005 days | 2699 days |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, B.; Lai, S.-W.; Wu, J.; Bellur, S. Predicting Phase 1 Lymphoma Clinical Trial Durations Using Machine Learning: An In-Depth Analysis and Broad Application Insights. Clin. Pract. 2024, 14, 69-88. https://doi.org/10.3390/clinpract14010007
Long B, Lai S-W, Wu J, Bellur S. Predicting Phase 1 Lymphoma Clinical Trial Durations Using Machine Learning: An In-Depth Analysis and Broad Application Insights. Clinics and Practice. 2024; 14(1):69-88. https://doi.org/10.3390/clinpract14010007
Chicago/Turabian StyleLong, Bowen, Shao-Wen Lai, Jiawen Wu, and Srikar Bellur. 2024. "Predicting Phase 1 Lymphoma Clinical Trial Durations Using Machine Learning: An In-Depth Analysis and Broad Application Insights" Clinics and Practice 14, no. 1: 69-88. https://doi.org/10.3390/clinpract14010007
APA StyleLong, B., Lai, S.-W., Wu, J., & Bellur, S. (2024). Predicting Phase 1 Lymphoma Clinical Trial Durations Using Machine Learning: An In-Depth Analysis and Broad Application Insights. Clinics and Practice, 14(1), 69-88. https://doi.org/10.3390/clinpract14010007






