Surface Waviness of EV Gears and NVH Effects—A Comprehensive Review
Abstract
1. Introduction
2. Materials and Methods
3. Gear Surface Waviness and NVH: Literature Review
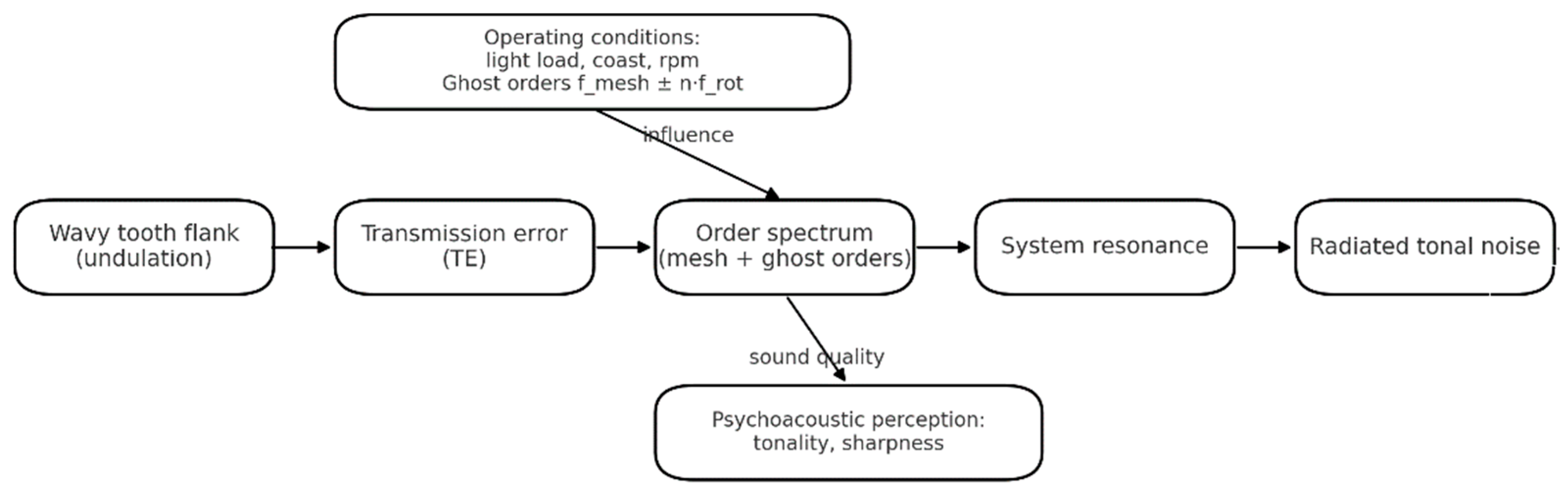
3.1. Noise Excitation Mechanisms of Waviness
3.2. Influence of Manufacturing Processes on Waviness and Noise
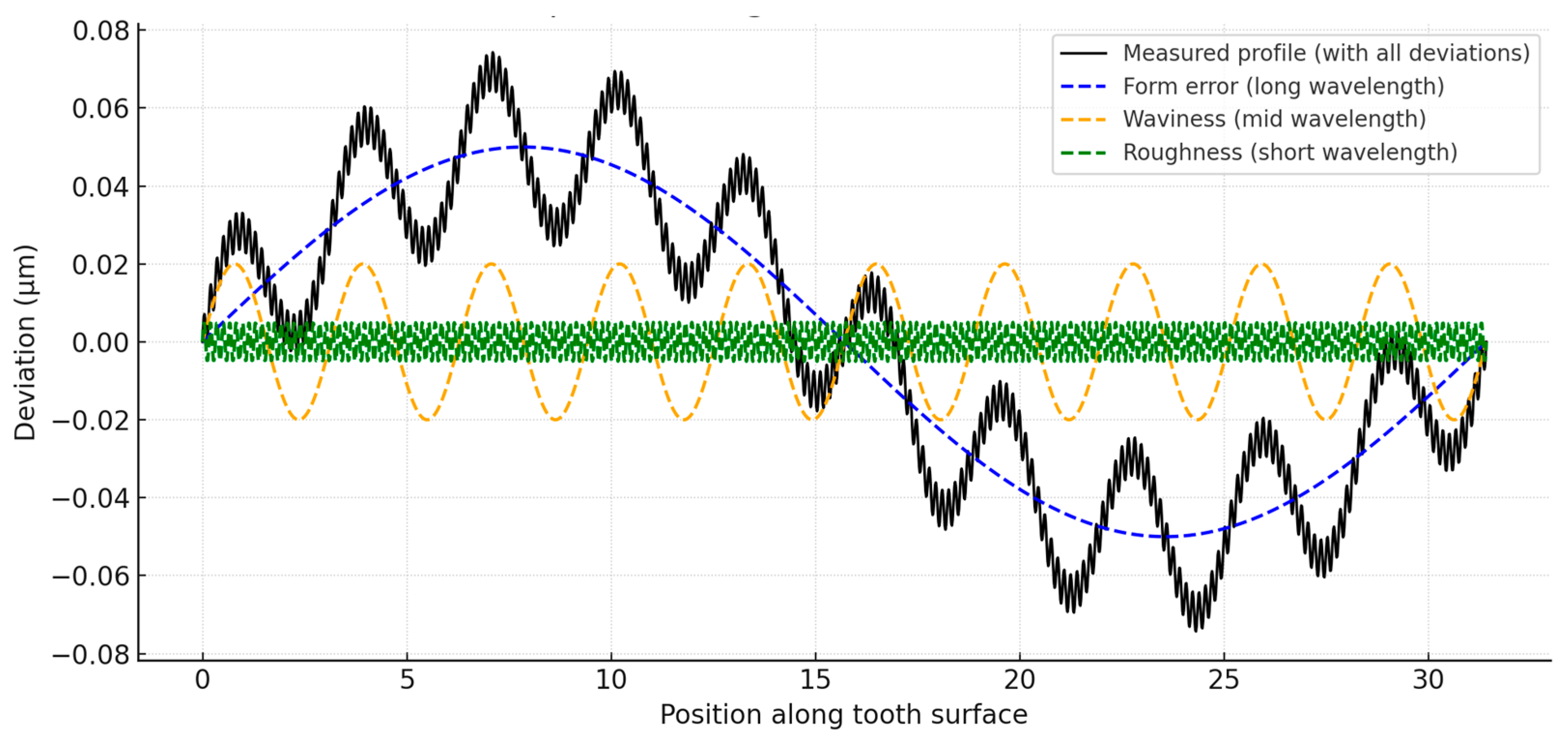
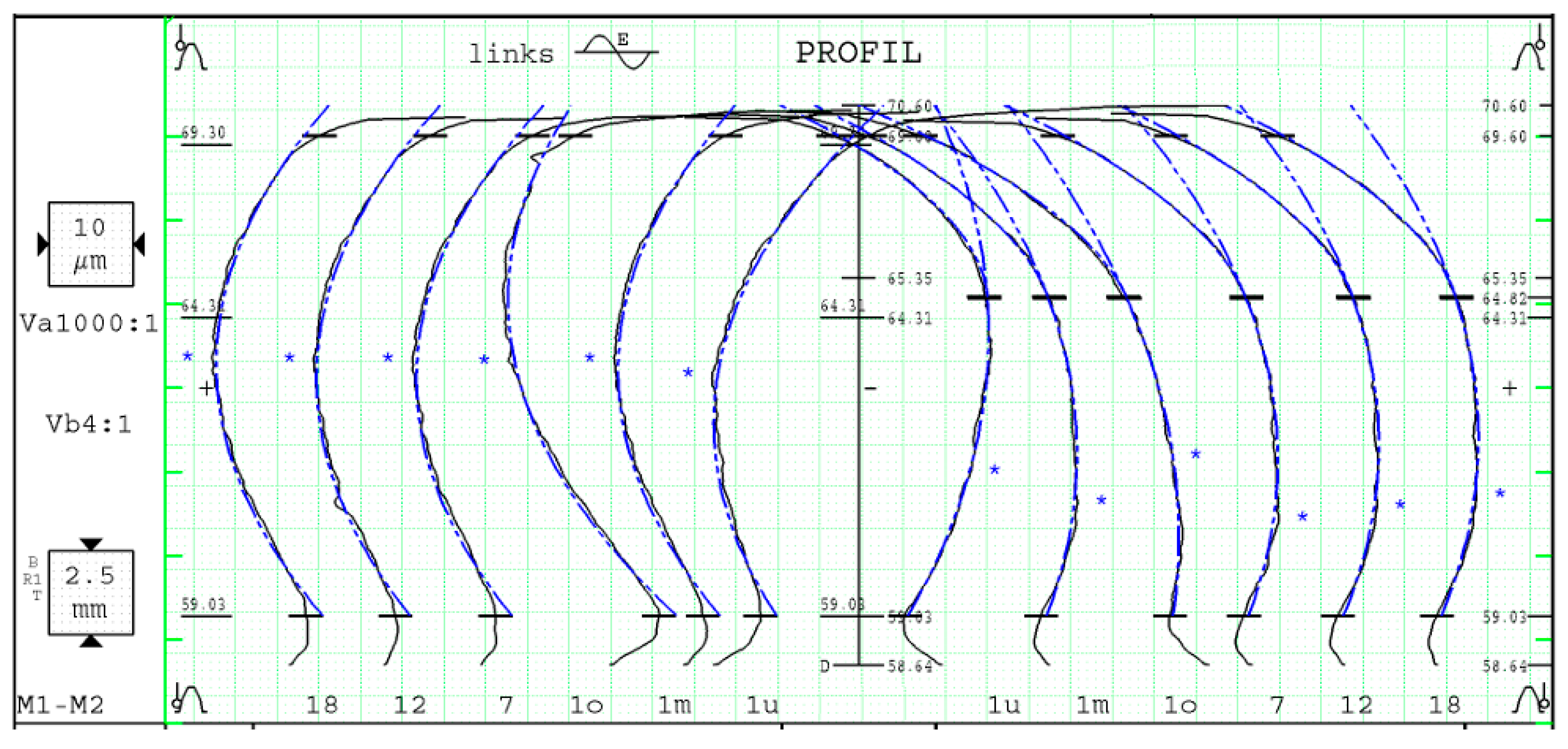
3.3. Measurement and Detection of Waviness in Gear Production
3.4. Case Studies and Industrial Examples
- Case 1: EV Reduction Gear Whine (Automaker A, circa 2020). An automotive manufacturer encountered a tonal whine around 2–3 kHz in their new EV gearbox during acceleration. Traditional TE analysis indicated nothing obviously wrong—design contact ratio was high and gears were Grade 4 (very high quality). Eventually, spectral analysis of vibration pointed to a ghost order that did not match any normal meshing harmonics. Using advanced measurement, they discovered a subtle 11-tooth waviness on the pinion, likely from a grinding wheel imbalance. The 11th order ghost coincided with a housing resonance, causing the whine. The solution was twofold. First, they tightened the balance and dressing controls on the grinder to eliminate the 11-tooth pattern. Second, as a short-term fix, they selectively mated pinions and gears such that any residual waviness on the pinion was counter-phased by a slight intentional adjustment on the gear (achieved by a minor process tweak in gear grinding). This phase cancellation approach—essentially trying to have the gear’s error negate the pinion’s error—is not commonly documented in literature but was trialed internally. It reduced the ghost tone amplitude significantly. This case underscores how even within-spec waviness can trigger NVH issues and how high-frequency ghost tones can be very detrimental in quiet EVs.
- Case 2: Sikorsky Helicopter Main Gearbox. This case involved a helicopter where cabin noise was dominated by gear mesh harmonics (the main gearbox bull gear). The gears were already of superb quality, yet noise was a critical factor for passenger comfort. A collaboration with researchers led to implementing isotropic superfinishing on the gear teeth. By removing the fine surface grind marks and any residual waviness, they achieved a notable drop in tonal vibrations. The cabin noise measurements showed reduction in the gear mesh tone. While this mostly addressed friction-related noise (since helicopter gears operate under huge loads, friction noise is non-negligible), it also removed any minor waviness left from grinding. It demonstrated in a high-stakes, real application that improved surface texture yields NVH benefits [28].
- Case 3: Automotive Differential Gear Hum (Gear Supplier B). A gear manufacturer was faced with some batches of automotive ring and pinion sets causing a “hum” at certain speeds, even though geometry was within AGMA 2000-A quality specs. Using a ripple analysis tool similar to Gravel’s method, they found that the problematic rings all had a 3nd-order ovality (the ring gear was slightly triangular shape) and the pinions had a 16th-order waviness from their grinding. Neither alone was enough to fail quality inspection, but together they produced a beating phenomenon that led to a moaning noise under light load. Countermeasure: process adjustments were made—fixturing for ring gear grinding was improved to eliminate the 3-lobed distortion, and the pinion grinder’s workrest was stiffened to remove the 16-order chatter. After these changes, subsequent gears showed clean spectra and the hum disappeared. This case illustrates that multiple waviness issues can compound, and that solving NVH may involve addressing several manufacturing aspects concurrently.
- Case 4: Inline Production Monitoring (Truck Transmission Plant). Cited in a Gleason white paper, a heavy truck gearbox manufacturer integrated the GRSL 100% inspection. A particular benefit they reported was the ability to spot when a grinding wheel or honing tool was deteriorating. As the tool wears, waviness on gears gradually increased. The inline system caught this trend and flagged parts before they became noisy. They could then change the tool proactively. In effect, the factory moved from statistical sampling to full inspection, and their reject rate for noisy gears in end-assembly dropped dramatically. This is a case of leveraging metrology for predictive maintenance of the manufacturing process itself. It highlights industry’s move toward zero-defect, zero-noise production using advanced waviness detection.
- Case 5: Patent Example—Tooth Slotting for Noise (Prototype Tests). A unique approach comes from the patent WO2019200261A1: adding a small slot in each gear tooth to reduce stiffness variation. While not about surface waviness per se, it addresses the same end goal of reducing TE fluctuations. The inventors built prototype spur gears with narrow EDM-cut slots near the tooth tips, giving the teeth a bit of compliance. Testing showed a reduction in the amplitude of the mesh frequency vibration, effectively smoothing the engagement. One might consider this a macro-geometry analog to adding waviness: instead of micro-scale waves on the surface, they altered the tooth structure to achieve a more constant mesh force. This concept reflects how far engineers will go to tackle gear noise—even changing tooth topology. The approach might be limited to low-torque applications (since slots can weaken teeth), but it is a compelling example of innovation driven by NVH demands.
3.5. Controversies and Contradictory Findings
- Gear Quality vs. Noise Paradox: As noted earlier, one counterintuitive phenomenon is that a gear manufactured to ultra-high quality (minimal deviations) can sometimes exhibit more tonal noise than one with slight, benign irregularities. This was brought out in Müller and Gorgels [3] and earlier by Smith [13] in an SAE technical paper. It challenges the assumption that “quieter gears = higher quality.” The nuance is what metric of quality we refer to. Traditional quality metrics do not capture tonality. Some engineers initially resisted the idea of purposely introducing deviations to reduce noise, as it flies in the face of conventional quality control. This topic spurred debate: is it ever wise to deliberately deviate from the perfect involute? The controversy is gradually settling as psychoacoustic metrics gain recognition—tonality can matter more than absolute SPL in perceived annoyance [3,13]. Thus, a gear that is “noisier” in terms of overall level might actually be judged “quieter” by a human if the noise is broadband. This has led to a more sophisticated view of quality: NVH-optimized quality might sometimes mean controlled non-uniformity. However, implementing this in manufacturing is tricky and not widely practiced yet (outside of experimental trials), because it complicates an already precise process.
- Older Studies: Some older studies emphasized that high-frequency gear noise is primarily caused by surface roughness, where frictional interactions at fine scales dominate the noise spectrum. In contrast, other investigations—especially at moderate operating speeds—identified waviness as the main source of tonal (periodic) noise components. Roughness-induced noise tends to occupy higher frequency bands and is often attributed to micro-scale friction. Waviness-induced excitation creates distinct tonal peaks in the noise spectrum [37]. Some earlier work, such as Ishida and Matsuda (1980), emphasized that surface roughness, mainly through frictional interactions, leads to broadband “hiss” noise and contributes to vibration at high frequencies [38]. In contrast, more recent surveys demonstrate that profile errors, including waviness introduce tonal components—distinct whine tones—in the noise spectrum, even when surfaces appear smooth. Thus, roughness and waviness play complementary roles: roughness elevates broadband noise levels, while waviness introduces tonal excitations associated with transmission error [38]. The current approach is holistic: both need addressing, but if a harsh tonal whine exists, addressing waviness (or profile error) is the key, whereas if there is a general “noisy” quality without specific tone, finishing roughness might be the key.
- Simulation vs. Experiment Discrepancies: Another area of divergence has been between predicted effects of certain deviations and measured outcomes. Some numerical studies struggled to replicate the level of noise reduction observed experimentally with, for example, superfinishing. This could be due to simplifications in models—early simulations might not model the tooth surface micro-topography in detail, thus underestimating the role of roughness/waviness. Henriksson (2020) simulated lightweight gear TE and found high sensitivity to mesh-stiffness variations [39], but when trying to simulate micro-deviations, it becomes computationally intensive. There is a known gap in purely physics-based models capturing microgeometry influences versus real tests. This discrepancy has driven interest in empirical and ML approaches that can absorb real-world complexity without needing all physics modeled.
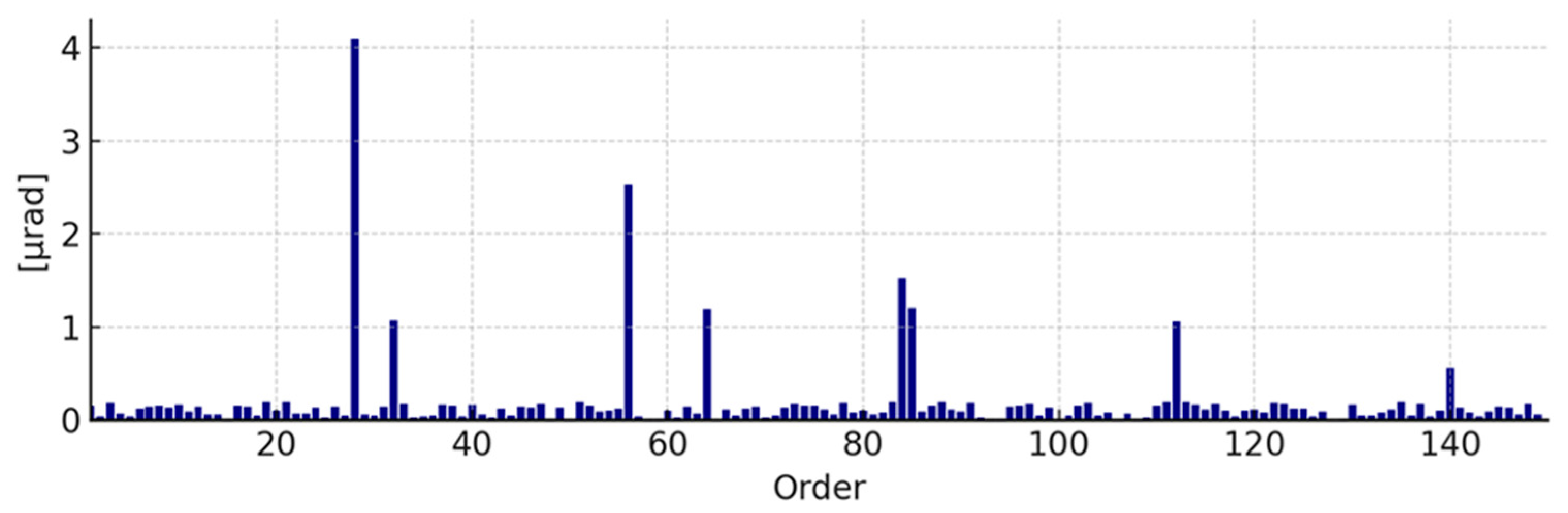
- Which Orders Matter Most: Controversy sometimes arises in deciding which waviness orders are “critical.” Some gear engineers maintain that only low-order stuff (like 1–4 per rev) really cause issues (the rumble or boom), and that anything above maybe 10th order is minor. However, in EVs, even higher orders (e.g., 10–20 per rev ghost components) can land in the mid-frequency audible range and be noticeable. The case of a ~11th order ghost causing a whine is one example. So the argument is context-dependent: in heavy-duty slow gears, low orders dominate; in high-speed quiet EV gears, higher orders can indeed be audible. Furthermore, EVs are susceptible to a mix of excitation sources—including transmission error, motor dynamics, and control switching frequencies—that can make higher-order tones more noticeable for occupant comfort [40]. There is not a single answer, and one must consider the frequency content relative to the vehicle’s acoustic sensitivity. Standards have yet to clearly prescribe which waviness orders to measure for what application, which is a gap to fill.
- Cumulative Effects vs. Single Factor: In diagnosing gear noise, multiple small factors often interact; thus, a waviness amplitude 1–2 µm may seem insignificant under perfect alignment (Situation A), yet produce significant noise under different alignment or load (Situation B). This suggests that the impact of waviness on noise is highly context-dependent, shaped by variables like load, alignment, and system resonance. Moreover, measurement results for waviness can vary depending on filter cutoffs and evaluation strategies, leading to inconsistent values from identical surface profiles. This underscores the need for clarity in how waviness is defined and measured [30,31].
3.6. Ghost Orders and Gear Tooth Surface Waviness in EV Drivetrains
3.7. Simulation of Surface Waviness for NVH Outputs (Methods and Software)
- System-level MBD injects TE or mesh-stiffness modulation into flexible drivetrains (shafts, bearings, housing) to predict order spectra at shafts/housing and to separate mesh vs. ghost components—documented in Romax/AVL/Adams workflows and widely used for EV powertrains. MBD simulations were then used to propagate the TE excitations through shafts, bearings, and housing models. This allowed comparison of ghost-order amplitudes at the housing surface with accelerometer measurements from the case studies, demonstrating how even sub-micron waviness can translate into audible tonal noise.”
- Hybrid FE → LTCA → MBD (and acoustic co-simulation). High-fidelity FE or LTCA is used to compute TE/ tables (possibly across load/speed), which are exported into an MBD driveline for fast order prediction; flexible housings/shafts enter as condensed FE superelements; optional coupling to acoustic BEM/FE estimates radiated sound/tonality. This route retains FE-level contact fidelity where needed (e.g., ghost-sensitive orders, per-tooth phases) while keeping system-level runs tractable. Typical implementations appear as: FE (or LTCA) → TE/ → MBD order maps → acoustic solver, with measured or analytical per-tooth waviness as inputs [52].
- KISSsoft applies a sinusoidal flank waviness (amplitude, wavelength/order, phase) on profile/lead to estimate TE and excitation force directly; it is intended for early design and microgeometry what-ifs.
- Romax (Enduro/Spectrum) couples LTCA (microgeometry, manufacturing deviations) to system NVH prediction, enabling a design → NVH pipeline for e-axles; industry papers also show importing measured microgeometry and comparing to TE/FFT tests [53].
- AVL EXCITE (2023R1) added explicit waviness specification along the tooth for cylindrical gears so contact considers the imposed pattern, then propagates to order spectra/radiated noise within the EXCITE environment.
- MSC Adams 2024.1.1. Multi-body dynamics (MBD) models and similar RecurDyn or SIMPACK chains accept per-tooth analytical waviness or inspection-based microgeometry (via import or calibrated tables) to reproduce measured order content.
- Recent EV studies demonstrate measured surface scans combined with pitch error fed into Adams to compare three scenarios: an ideal model, a model with measured microgeometry and pitch error, and a model with measured microgeometry but without pitch error.
- Siemens Simcenter 3D supports TE comparison against tests and an advanced FE-preprocessor stiffness route that accounts for profile/lead errors and tooth coupling, enabling FE-MBD-style hybrid predictions of whine/tonality.
- In the case studies, LTCA was not applied in abstract terms but with explicit waviness inputs. Measured or analytically imposed sinusoidal deviations were added to the nominal profile, and the LTCA computed the resulting loaded TE curves and mesh-stiffness variations [13,28]. This enabled direct quantification of how specific waviness orders contribute to dynamic excitation, in line with established formulations. The results were then coupled into MBD drivetrain models, where the TE excitations acted as inputs to flexible shafts, bearings, and housing structures [27]. Such combined LTCA–MBD workflows, as implemented in industrial software like Romax or AVL EXCITE, allowed the case studies to link micron-scale waviness patterns to measured tonal whine in EV gearboxes. The strength of this approach lies in bridging surface-level deviations with system-level NVH, while the limitation remains the high computational cost when importing full measured surface maps.
3.8. Research Gaps and Future Directions
- Standardized Waviness Metrics and Tolerances: As mentioned, there is no widely adopted standard specifically for allowable waviness on gear teeth. Gear quality standards implicitly control some waviness by form error limits, but they do not quantify it in frequency terms. The industry would benefit from a standardized metric (perhaps something like a “waviness amplitude in a specified band”) and guidelines for different applications. Establishing this requires correlating a large number of gear measurements with NVH results to set meaningful limits—an area ripe for systematic research. Recent efforts in academia to create open datasets of gears with measured topography and noise are a step in this direction. Horváth (2025) notes the lack of a benchmark dataset for gear noise prediction, which hampers direct comparison of methods [6]. The use of a large industrial dataset and modern machine learning methods is a strong point, but the models have limited interpretability and the proprietary nature of the data reduces reproducibility [6]. Future work could focus on creating such datasets, enabling researchers to test algorithms on common data.
- Integration of Design and Manufacturing Simulation: Modern analysis tools—such as Loaded Tooth Contact Analysis (LTCA) and full FE models—typically assume ideal (nominal) gear geometry, occasionally augmented with simplified errors. In several case studies, waviness patterns obtained from profilometer scans were superimposed on the ideal involute and evaluated with LTCA. This provided quantitative loaded TE values and mesh-stiffness fluctuations, which could then be linked to measured tonal noise. However, they rarely incorporate full measured microgeometry maps, as doing so presents both computational and methodological challenges. While some progress has been made, such as digital twin frameworks that use measurement data for virtual testing, simulation engineers and manufacturing metrologists often work separately. Bridging this gap—by enabling inclusion of a measured 3D surface map into a dynamic gearbox simulation to compute noise contributions—would be highly beneficial. Implementations like Romax Enduro enable LTCA with microgeometry considerations, but integration with comprehensive measured topographies remains a frontier.
- Digital Twin: Another promising development is the application of digital twin frameworks. Here, measured microgeometry and manufacturing deviations are imported directly into dynamic gearbox models to predict NVH behavior. Inline optical systems such as Gleason’s GRSL make this integration feasible by generating both roll test data and 3D surface scans. Projects like ECO-Drive have demonstrated that feeding these measurements into multi-body driveline simulations enables predictive noise control before final assembly. The strength of digital twins lies in closing the loop between design, manufacturing, and operation, yet challenges remain in computational cost and the absence of standard methods for converting surface scans into usable dynamic models. Despite these hurdles, digital twin technology is widely seen as a key enabler of proactive, data-driven NVH management in EV transmissions.
- Material Effects on NVH: Most current approaches to gear noise reduction concentrate on kinematic design, gear geometry, and surface texture. The effect of material grade on NVH performance has received far less systematic attention. Different steel grades, heat treatments, and surface coatings can alter contact stiffness and damping. These changes may reduce transmission error and radiated tonal noise. Polymer gears and hybrid contact pairs have also been shown to provide higher damping than conventional steel gears. Despite this potential, comprehensive NVH-oriented studies on material effects remain scarce. This gap suggests that future research should not only refine geometry and surface finish, but also explore material selection as a design parameter for noise reduction.
- Explainable AI and Causation: While machine learning models can highlight that “waviness matters” for gear noise, they often fail to explain why a particular pattern is problematic. This interpretability gap hampers engineer trust and actionable insight. Recent calls—such as by Horváth (2025)—advocate for integrating explainable AI (XAI) tools into gear noise diagnostics [6]. For example, if an ML model flags a specific frequency component in surface measurements, XAI techniques (e.g., SHAP or LIME) could reveal whether this feature corresponds to a particular vibration mode or a manufacturing signature—enabling engineers to adjust processes accordingly. Some initiatives have begun to apply SHAP and LIME to vibration-based fault detection, but truly interpretable, physics-aware ML systems in gear noise analysis remain an open challenge [6].
- Intentional Waviness Design: One of the more intriguing gaps is exploring in a controlled way the concept of designing microgeometry for noise cancellation. While some patents and anecdotal trials exist (as discussed in Section 3.2), there is scant published research systematically studying this. For example, can we mathematically derive an optimal micro-tooth profile that yields minimum tonality for a given gear pair? Perhaps using inverse optimization or evolutionary algorithms to tweak microgeometry (within the bounds of what manufacturing can do) for best psychoacoustic outcome. If such studies exist, they are not widely known. Filling this gap would require a multidisciplinary approach—gear geometry, manufacturing constraints, and psychoacoustic metrics combined. The payoff could be gearsets that are inherently quiet by design, not just by precision.
- High-Frequency NVH (Beyond 5 kHz): Most gear noise studies focus up to a few kHz, where the main tonal components lie. However, EV motors can spin so fast that mesh frequencies enter the ultrasonic range (>20 kHz). We might not hear those, but they can excite structural squeaks or cause fatigue issues, and some portion could down-convert to audible via modulation. The impact of microgeometry at very high orders (say 50th order and above) on such high-frequency phenomena is not well researched. Also, interior noise concerns in luxury EVs now include very-high-frequency noise (which can affect perceived sound quality even if not loud). Thus, another future direction is examining the ultra-fine waviness (maybe 0.01–0.1 µm range) and its effects in high-frequency NVH. This intersects with materials science too—at those scales, surface finish processes and material structure (grains, etc.) might matter.
- Multi-Source NVH and Trade-offs: In an EV, gears are one of several noise sources (others include electric motor electromagnetic noise, tire noise, etc.). There is a system-level gap in understanding how reducing gear tonal noise might expose other noises or whether a small gear noise might be tolerable if other noises dominate. For instance, if one completely eliminates gear whine, does inverter whine become more noticeable? These system considerations mean the absolute lowest gear noise might not always be necessary if it is below other sources. But EVs are getting so quiet that gear noise often is the loudest. Still, future work could consider NVH optimization at the vehicle level—maybe a small tonal gear noise could be masked by a complementary sound design (some EVs use sound synthesis for pedestrian warning or interior feel). This is speculative but shows NVH control is broadening in scope.
- Wider adoption of digital twin technology for gear production—virtual gearboxes continuously fed by real manufacturing data to predict NVH outcomes in real time. This will allow dynamic adjustments in manufacturing (e.g., if a certain deviation trend is creeping in, adjust machine parameters before parts go out of spec).
- Hybrid modeling approaches that combine physics-based models with data-driven corrections to account for microgeometry effects that pure physics might miss. This can improve predictive accuracy across all regimes.
- Advanced materials or coatings that might passively damp out ghost vibrations. For example, applying a thin vibro-acoustic coating on gear teeth (there is experimental work on polymer coatings or surface damping treatments—not common yet in gears due to durability concerns). With EV torque being lower (for final drives) than ICE engines in some cases, there might be room to explore such unconventional ideas.
- Additive manufacturing (AM) for gears: Though currently most high-performance gears are machined; the rise of metal AM could allow micro-topologies on gear surfaces that were impossible before. One could imagine 3D printing a gear with a deliberate micro-pattern. If AM precision reaches the micrometer level consistently, that could open a new design space for NVH optimization of gears.
- Psychoacoustic metrics integrated into waviness assessment: Moving beyond dB-level acceptance to include tonality, sharpness, and roughness in the definition of acceptable waviness patterns, particularly for EV gear whine.
- 100% inline metrology + NVH screening: Advanced laser-based rolling systems with integrated waviness analysis could enable stochastic tolerance control and rapid feedback to machining before noisy parts reach assembly.
4. Discussion
5. Conclusions
- Surface waviness is a critical microgeometry factor for gear NVH: Even extremely small periodic deviations (on the order of 0.1–1 µm) on gear flanks can induce ghost frequencies in the gearbox vibration spectrum. These ghost orders can lead to tonal noise that is clearly audible in the absence of masking engine sound, as is the case in EVs. Gears that are within traditional tolerance limits can still exhibit objectionable noise due to unmeasured waviness components, highlighting the need for dedicated waviness control.
- Manufacturing processes imprint characteristic waviness patterns: The choice of finishing process (grinding, honing, lapping, superfinishing) strongly influences the surface texture and waviness. Finishing processes like honing or superfinishing play a critical role in modifying surface waviness. As discussed in Section 3.2, properly selected and controlled finishing methods can effectively reduce tonal noise, while emerging strategies even explore introducing managed waviness for psychoacoustic benefit.
- Gear noise mitigation requires both design and manufacturing excellence: A consensus in literature is that optimal NVH cannot rely on design or manufacturing alone—both must work in concert. Designing for a high contact ratio and including appropriate profile/lead modifications lays the foundation for low transmission error, but manufacturing variations like waviness or runout can negate those benefits if not tightly controlled. On the other hand, outstanding manufacturing (ultra-precision and/or post-process finishing) can sometimes overcome a less-than-ideal design to yield acceptable noise. The quietest gear systems—such as premium EV gearboxes and aerospace drives—are achieved when designers anticipate possible error patterns and when production implements rigorous controls to minimize those errors.
- Advances in measurement and analytics are closing the loop on quality control: Traditional gear inspections were often insufficient to detect waviness [8]. New technologies like inline laser scanning coupled with rolling tests now enable detection of waviness amplitudes down to 0.1 µm and automatic correlation with noise potential. This has made 100% gear noise screening feasible in high-volume production, allowing manufacturers to prevent noisy gears from reaching assembly. Additionally, data-driven models (machine learning) have demonstrated the ability to predict noise test results from measured manufacturing data, with surface waviness identified as a key predictor. Such models, integrated into digital twin frameworks, foreshadow a future where gear NVH is managed proactively via predictive quality control rather than reactive fixes.
- Literature gaps highlight opportunities for further research: We identified several areas where understanding is incomplete or technology is lacking. Notably, there is an absence of standardized waviness metrics or tolerances in gear quality standards. There is also a need for more research on intentional microgeometry modifications for noise reduction, and for improved methods to interpret complex data and guide practical decisions. Addressing these gaps will likely involve collaborative efforts across academia and industry, combining gear engineering expertise with acoustics and data science. Future research should aim to develop quantitative relationships between specific waviness characteristics and noise outcomes, and to establish clear guidelines for acceptable waviness in different applications.
Funding
Data Availability Statement
Conflicts of Interest
References
- Horváth, K.; Zelei, A. Simulating Noise, Vibration, and Harshness Advances in Electric Vehicle Powertrains: Strategies and Challenges. World Electr. Veh. J. 2024, 15, 367. [Google Scholar] [CrossRef]
- Winkelmann, L. Tackling EV Noise Reduction. Gear Solutions Magazine. 15 October 2022. Available online: https://gearsolutions.com/departments/materials-matter/tackling-ev-noise-reduction/ (accessed on 13 August 2025).
- Müller, H.; Gorgels, C. Aspects of gear noise, quality, and manufacturing technologies for electromobility. Gear Technol. 2023, 63, 60–64. [Google Scholar]
- Gravel, G. Analysis of Ripple on Noisy Gears. Gear Solutions Magazine. 8 January 2023. Available online: https://gearsolutions.com/features/analysis-of-ripple-on-noisy-gears/ (accessed on 13 August 2025).
- Gorgels, C.; Finkeldey, M. Method and Measuring System. Publication No. US 20230003574A1, 5 January 2023. Available online: https://patents.google.com/patent/US20230003574A1/en (accessed on 13 August 2025).
- Horváth, K. Data-driven predictive modeling for investigating the impact of gear manufacturing parameters on noise levels in electric vehicle drivetrains. World Electr. Veh. J. 2025, 16, 426. [Google Scholar] [CrossRef]
- Klingelnberg, A.G. Deviation Analysis for Cylindrical Gears [Brochure]. Available online: https://klingelnberg.com/fileadmin/Business_Divisions/Precision_Measung_Centers/Downloads/DEVIATION_ANALYSIS_BROCH_EN.pdf (accessed on 13 August 2025).
- Masuda, T.; Inoue, M.; Iida, T.; Aoki, T. Prediction of gear noise considering the influence of tooth-flank finishing method. J. Vib. Acoust. Stress Reliab. Des. 1986, 108, 121–130. [Google Scholar] [CrossRef]
- Houser, D.R.; Harianto, J. Gear noise: Causes and control. Gear Technol. 2001, 18, 10–19. [Google Scholar]
- Tian, X.; Sun, Y.; Mu, W.; Xia, L.; Han, J. High-speed and low-noise gear finishing by gear grinding and honing: A review. Chin. J. Mech. Eng. 2024, 37, 10. [Google Scholar] [CrossRef]
- Türich, A.; Deininger, K. Noise Analysis for E-Drive Gears and In-Process Gear Inspection. Gear Solutions/Power Transmission Engineering. May 2023. Available online: https://www.geartechnology.com/noise-analysis-for-e-drive-gears-and-in-process-gear-inspection (accessed on 13 August 2025).
- Elder, J.T. Method of Gear Noise Reduction. Publication No. WO 2019200261A1, 17 October 2019. Available online: https://patents.google.com/patent/WO2019200261A1/en (accessed on 13 August 2025).
- Smith, J.D. Gear Noise and Vibration, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Müller, H. Noise Generation in Gearings: See No Evil, Hear No Evil, Speak No Evil; White Paper; Klingelnberg GmbH: Wuppertal, Germany, 2017; Available online: https://klingelnberg.com/fileadmin/News/White_Paper/DRIVE_TECHNOLOGY_NOISE_GENERATION_IN_GEARINGS_SEE_NO_EVIL_HEAR_NO_EVIL_SPEAK_NO_EVIL_WHITEPAPER_2017_01_09_EN.pdf (accessed on 13 August 2025).
- Bassett, D.E. The Design and Analysis of Single Flank Transmission Error Measurement Technique; NASA Contractor Report NASA-CR-176163; NASA: Washington, DC, USA, 1987. Available online: https://ntrs.nasa.gov/citations/19850026091 (accessed on 13 August 2025).
- Rotec GmbH. Upgrading a Gear Testing Machine for Use in Single Flank Testing and Airborne & Structure-Borne Noise Measurements [PDF]. Available online: https://www.misuremeccaniche.it/pdf/Upgrade_of_Gear_Tester.pdf (accessed on 13 August 2025).
- He, Z.; Lin, T.; Song, J.; Wang, Z.; Que, H. Analytical and computational method of structure-borne noise and shock resistance of gear system. J. Meas. Eng. 2014, 2, 215–224. [Google Scholar]
- Sanzenbacher, S.; Bouraui, M.W.; Bertsche, B. Reducing propagation of structure-borne noise in transmissions. In Proceedings of the ISMA 2012 Conference Proceedings, Leuven, Belgium, 9–11 September 2012; ISMA: Leuven, Belgium, 2012; pp. 1–12. [Google Scholar]
- Gear Technology. GRSL Quality Center Brings Fast Gear Inspection to the Shop Floor for Higher Quality Gears. Gear Technology. 10 May 2024. Available online: https://www.geartechnology.com/grsl-quality-center-speeding-the-way-to-quieter-gears (accessed on 13 August 2025).
- One Hundred Percent In-Process Quality Inspection for Low Noise Transmissions. Metrology News. 24 October 2023. Available online: https://metrology.news/one-hundred-percent-in-process-quality-inspection-for-low-noise-transmissions/ (accessed on 13 August 2025).
- Ahmad, M.; Brimmers, J.; Brecher, C. Influence of long-wave deviations on the quasi-static and dynamic excitation behavior at higher speeds. Appl. Acoust. 2020, 165, 107307. [Google Scholar] [CrossRef]
- Choi, W.J.; Kim, J.; Lee, Y.; Park, K.P. Effects of manufacturing errors of gear macro-geometry on gear performance. Sci. Rep. 2023, 13, 27204. [Google Scholar]
- Gleason. GRSL—Laser Inspection with Double Flank Rolling. Available online: https://www.gleason.com/en/products/metrology/metrology-systems/in-process-laser-inspection/grsl-laser-inspection-with-double-flank-rolling (accessed on 13 August 2025).
- Im, D.; Chung, W.-J.; Lee, H.; Lee, Y.-J.; Sung, H.; Lee, M.; Park, Y.-J. Analysis of gear transmission error in helical gear using enhanced tooth contact analysis model considering measured tooth profile errors. Sci. Rep. 2025, 15, 90010. [Google Scholar] [CrossRef] [PubMed]
- SmartMT. Sidebands in Gear Noise Due to Manufacturing Errors. SmartMT Blog. 2023. Available online: https://www.smartmt.com/blog/sidebands-in-gear-noise-due-to-manufacturing-errors/ (accessed on 13 August 2025).
- Singh, R.; Lim, T.C. A Review of Gear Housing Dynamics and Acoustics Literature; NASA Report NAG3 773; NASA: Washington, DC, USA, 1988. Available online: https://ntrs.nasa.gov/api/citations/19880017291/downloads/19880017291.pdf (accessed on 13 August 2025).
- ISO 16610; Geometrical Product Specifications (GPS)—Filtration. International Organization for Standardization: Geneva, Switzerland, 2015.
- Ehinger, R.T.; Kilmain, C.J. Evaluation of isotropic superfinishing on a Bell Helicopter Model 427 main rotor gearbox. In Proceedings of the American Helicopter Society 63rd Annual Forum, Virginia Beach, VA, USA, 1–3 May 2007; pp. 1–12. Available online: https://www.remchem.com/wp-content/uploads/2013/11/AHS2007-000172-Evaluation-of-Isotropic-Superfinishing-on-a-Bell-Helicopter-Model-427-Main-Rotor-Gearbox.pdf (accessed on 13 August 2025).
- Sundar, S.; Singh, R.; Jayasankaran, K.; Kim, S. Effect of the tooth surface waviness on the dynamics and structure-borne noise of a spur gear pair. SAE Int. J. Passeng. Cars—Mech. Syst. 2013, 6, 1087–1093. [Google Scholar] [CrossRef]
- Reavie, T.; Koulin, G.; Frazer, R.C.; Wilson, S.J.; A Shaw, B. A method to quantify waviness measurement capability of a gear measurement machine. Surf. Topogr. Metrol. Prop. 2019, 7, 015002. [Google Scholar] [CrossRef]
- ISO 25178; Geometrical Product Specifications (GPS)—Surface Texture: Areal. ISO: Geneva, Switzerland, 2012.
- Digital Metrology. Can a CMM Stylus Ball Actually Measure Waviness? 2019. Available online: https://digitalmetrology.com/can-i-measure-waviness-on-a-cmm/ (accessed on 13 August 2025).
- Stadtfeld, H.J. Psychoacoustic Methodology for the Noise Reduction of Bevel Gears. Gear Solutions Magazine. 15 December 2018. Available online: https://gearsolutions.com/features/psychoacoustic-methodology-for-the-noise-reduction-of-bevel-gears/ (accessed on 13 August 2025).
- Klingelnberg. R 300 The Gear Noise Finder—A Solution Featuring Single Flank Test, Structure-Borne Noise Test, and Torsional Acceleration Test for Fast, End-of-Line Gear Quality Control. 2025. Available online: https://klingelnberg.com/en/news/product-highlights/r-300-the-gear-noise-finder (accessed on 13 August 2025).
- Deutronic. Structure-Borne Sound Measurement—For a Smart Quality Assurance of the Production Process. Available online: https://www.deutronic.com/produkte/structure-borne-sound-test-system. (accessed on 13 August 2025).
- European Commission. H2020 ECO-Drive Project: System-Level NVH Optimization for Sustainable Electric Drivetrains; Grant Agreement No. 858018; European Commission: Brussels, Belgium, 2020–2024. [Google Scholar]
- Kim, S. Prediction of Transmission Error of Helical Gears Considering Surface Roughness. Tribol. Int. 2007, 40, 1406–1414. [Google Scholar] [CrossRef]
- Ishida, K.; Matsuda, T. Effect of Tooth Surface Roughness on Gear Noise and Gear Noise Transmitting Path; ASME Paper 80-C2/DET-70; American Society of Mechanical Engineers: New York, NY, USA, 1980. [Google Scholar]
- Henriksson, J. Simulation and validation of transmission error, meshing stiffness and vibration in gear systems. J. Sound Vib. 2020, 478, 115366. [Google Scholar] [CrossRef]
- Harris, O.; Langlois, P.; Gale, A. Electric Vehicle Whine Noise—Gear Blank Tuning as an Optimization Option. Gear Technology. 1 March 2019, pp. 64–73. Available online: https://www.smartmt.com/wp-content/uploads/2024/01/GT-electric-vehcile-whine-noise-gear-blank-tuning-as-an-optimisation-option.pdf (accessed on 13 August 2025).
- Kahraman, A.; Singh, A.; Vijayakar, S.M. An investigation of ghost noise in helical gear sets. J. Mech. Des. 2011, 133, 121004. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Choi, S.; Park, S. Real-Time Active Noise Control with Preservation of Desired Sound. Appl. Acoust. 2020, 157, 106971. [Google Scholar] [CrossRef]
- Baik, Y.S.; Ryu, S. Effect of manufacturing errors on gear transmission error. Mech. Mach. Theory 2012, 49, 216–233. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Liu, J.; Wu, X. Influence of grinding wheel vibration on gear surface waviness. CIRP Ann. 2021, 70, 293–296. [Google Scholar] [CrossRef]
- ISO 1328-2; Cylindrical Gears—ISO System of Flank Tolerance Classification—Part 2: Definitions and Allowable Values of Deviations Relevant to Flanks. International Organization for Standardization: Geneva, Switzerland, 2015.
- Romax Technology. Incorporating Measured Gear Waviness into NVH Simulation; Technical Note; Romax Technology: Nottingham, UK, 2020. [Google Scholar]
- Huang, Y.; Chen, L.; Zhang, Q. Method of Machining Gears to Produce Sinusoidal–Parabolic Hybrid Motion Error. U.S. Patent US11331734B2, 10 May 2022. [Google Scholar]
- Hexagon. Romax Enduro: Perform Loaded Tooth Contact Analysis (LTCA) and Micro-Geometry Optimization. Available online: https://hexagon.com/products/romax-enduro (accessed on 13 August 2025).
- Li, J. A digital twin based state monitoring method of gear test bench. Appl. Sci. 2023, 13, 3291. [Google Scholar] [CrossRef]
- Mey, O.; Neufeld, D. Explainable AI Algorithms for Vibration Data-Based Fault Detection: Use Case Adapted Methods and Critical Evaluation. Sensors 2022, 22, 9037. [Google Scholar] [CrossRef] [PubMed]
- Siemens PLM Software. Boosting Productivity in Gearbox Engineering: Simcenter 3D Transmission Builder White Paper; Siemens PLM Software: Zürich, Switzerland, 2024; Available online: https://www.apic.com.tw/proimages/pdf/Simcenter3D/12.pdf (accessed on 16 September 2025).
- Romax Technology (Hexagon). Romax Spectrum Product Flyer; Hexagon AB: Stockholm, Sweden, 2022; Available online: https://romax.s3.eu-west-2.amazonaws.com/product-flyer/Hexagon_MI_Romax_Flyer-Spectrum_A4-WEB.pdf (accessed on 16 September 2025).
- Tümosan; Hexagon MI Romax. Tümosan Case Study: Optimising Gear Microgeometry with Romax Enduro; Hexagon MI: Istanbul, Turkey, 2022; Available online: https://bias.com.tr/storage/media/2376/hexagon-mi-romax-casestudy-tumosan-a4-web-1.pdf (accessed on 16 September 2025).

| Study (Year) | Scope | Methodology | Key Findings |
|---|---|---|---|
| [8] | Tooth finishing method vs. noise | Experimental (vibration tests of gears ground vs. honed) | Honed gears showed lower excitation at mesh frequency than ground gears; finishing process affects tonal noise. Early evidence that surface condition alters noise. |
| [9] | Frictional noise and surface finish | Experimental (gearbox test with ground vs. superfinished gears; various lubricants) | Superfinishing (surface polishing) reduced high-frequency “hiss” noise by ~3–6 dB. Surface roughness and fine waviness contribute to noise; smooth surfaces notably quieter. |
| [21] | Long-wave form errors at high Ex speed | Theoretical and experimental (modeling + tests of gears with imposed eccentricity/waviness) | Low-order vibrations (e.g., runout, ovality) significantly increased dynamic TE and noise at high rpm. Emphasizes need for tighter control of long-wave errors in EV gears. |
| [10] | Review of gear grinding vs. honing for noise | Literature review (focused on finishing technologies) | Modern grinding/honing techniques can minimize waviness and tonal noise. Recommends combined processes (grind + hone) for EV gears to achieve smooth flanks and low noise. |
| [22] | Macro-geometry errors vs. performance | Simulation and analysis | Even small macro errors (lead slope, alignment) can amplify mesh excitation. Implies that in a marginal design, waviness effects are worse. Holistic tolerance of both macro and micro needed. |
| [6] | Data-driven analysis of manufacturing vs. noise | ML on production data (hundreds of gears, with features like waviness, profile error; correlated to noise tests) | Surface waviness emerged as one of top predictors of noisy gears. ML models could flag gears with high waviness that would fail NVH, enabling early intervention. Demonstrates importance of waviness in large-scale production. |
| [4] | Detection of gear ripples (waviness) | Developed sine approximation method for measurement data; case studies | Introduced a practical method to quantify waviness from standard inspection data, correlating certain waviness orders to noise. Showed that previously undetectable ripples (sub-micron) can be identified and tied to machine faults. |
| (various patents) e.g., JP5427078B2 (2014) and US2023/0003574A1 | Ghost noise detection and analysis | Patented methods (algorithmic approaches in metrology machines) | Propose advanced analysis of measured flank topography to predict ghost noise. Real-time waviness frequency analysis in inspection can identify gears prone to noise and even infer machine condition, enabling proactive quality control. |
| [12] | Gear tooth structural modification | Patent (design and manufacturing method) | Describes adding a slit/cutout in gear teeth to introduce bending compliance, thereby smoothing mesh-stiffness variation and reducing TE-induced noise. Illustrates innovation beyond surface finish—altering tooth geometry to mitigate noise. |
| Surface Treatment | Source(s) | Reported Effect on Waviness | Reported Effect on NVH (Noise Reduction) |
|---|---|---|---|
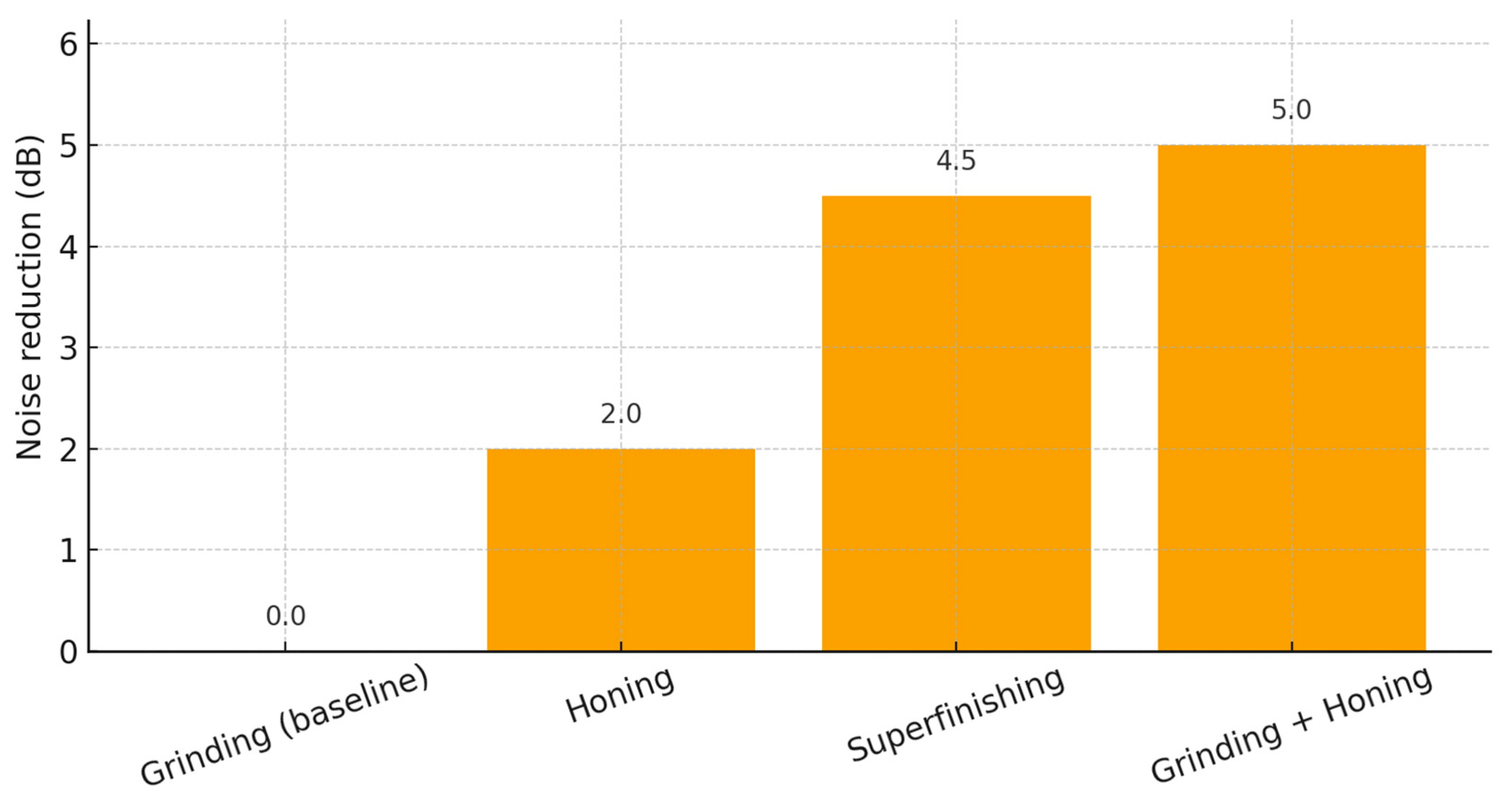
| Grinding (baseline) | Masuda et al. (1986) [8] | Residual high-frequency ripples | Reference condition (0 dB improvement) |
| Honing | Masuda et al. (1986) [8] | Reduced grinding-induced ripples | Lower tonal excitation (~1–2 dB) |
| Superfinishing | Houser et al. (2001) [9]; Ehinger and Kilmain (2007) [16] | Removed micro-undulations, smoother flanks | Reduced high-frequency “hiss” by ~3–6 dB |
| Grinding + Honing | Tian et al. (2024) [10] | Randomized surface texture, smoother finish | Tonal noise reduction up to ~5 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horvath, K.; Feszty, D. Surface Waviness of EV Gears and NVH Effects—A Comprehensive Review. World Electr. Veh. J. 2025, 16, 540. https://doi.org/10.3390/wevj16090540
Horvath K, Feszty D. Surface Waviness of EV Gears and NVH Effects—A Comprehensive Review. World Electric Vehicle Journal. 2025; 16(9):540. https://doi.org/10.3390/wevj16090540
Chicago/Turabian StyleHorvath, Krisztian, and Daniel Feszty. 2025. "Surface Waviness of EV Gears and NVH Effects—A Comprehensive Review" World Electric Vehicle Journal 16, no. 9: 540. https://doi.org/10.3390/wevj16090540
APA StyleHorvath, K., & Feszty, D. (2025). Surface Waviness of EV Gears and NVH Effects—A Comprehensive Review. World Electric Vehicle Journal, 16(9), 540. https://doi.org/10.3390/wevj16090540






