Torque Smoothness for a Modified W-Type Inverter-Fed Three-Phase Induction Motor with Finite Set Model Predictive Control for Electric Vehicles
Abstract
1. Introduction
- Evaluate the impact of the quality of voltage profiles on rotor speed and electromagnetic torque for motors. Two motors of different ratings are deployed for better generalization of applications.
- Comparatively assess rotor speed and electromagnetic torque ripples for simultaneous variations in multiple motor parameters. The motors are fed with three different voltage profiles for this purpose, and nine sets of variations have been presented.
- Validate the performance of FCSMPC for minimization of ripples, combined with the significance of the voltage quality supplied by an MWI for different driving torque patterns. The quality of stator currents is also analyzed.
2. Problem Statement
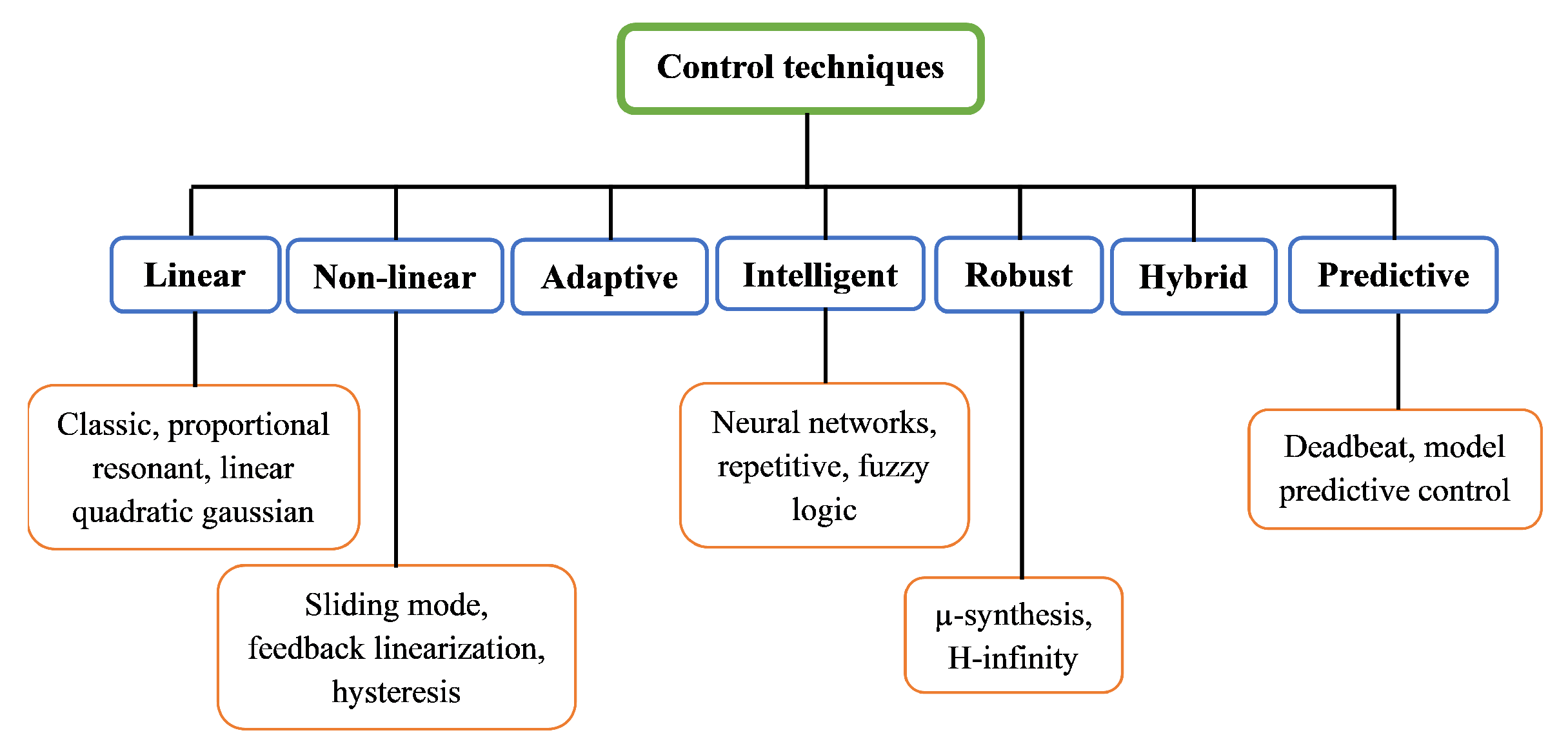
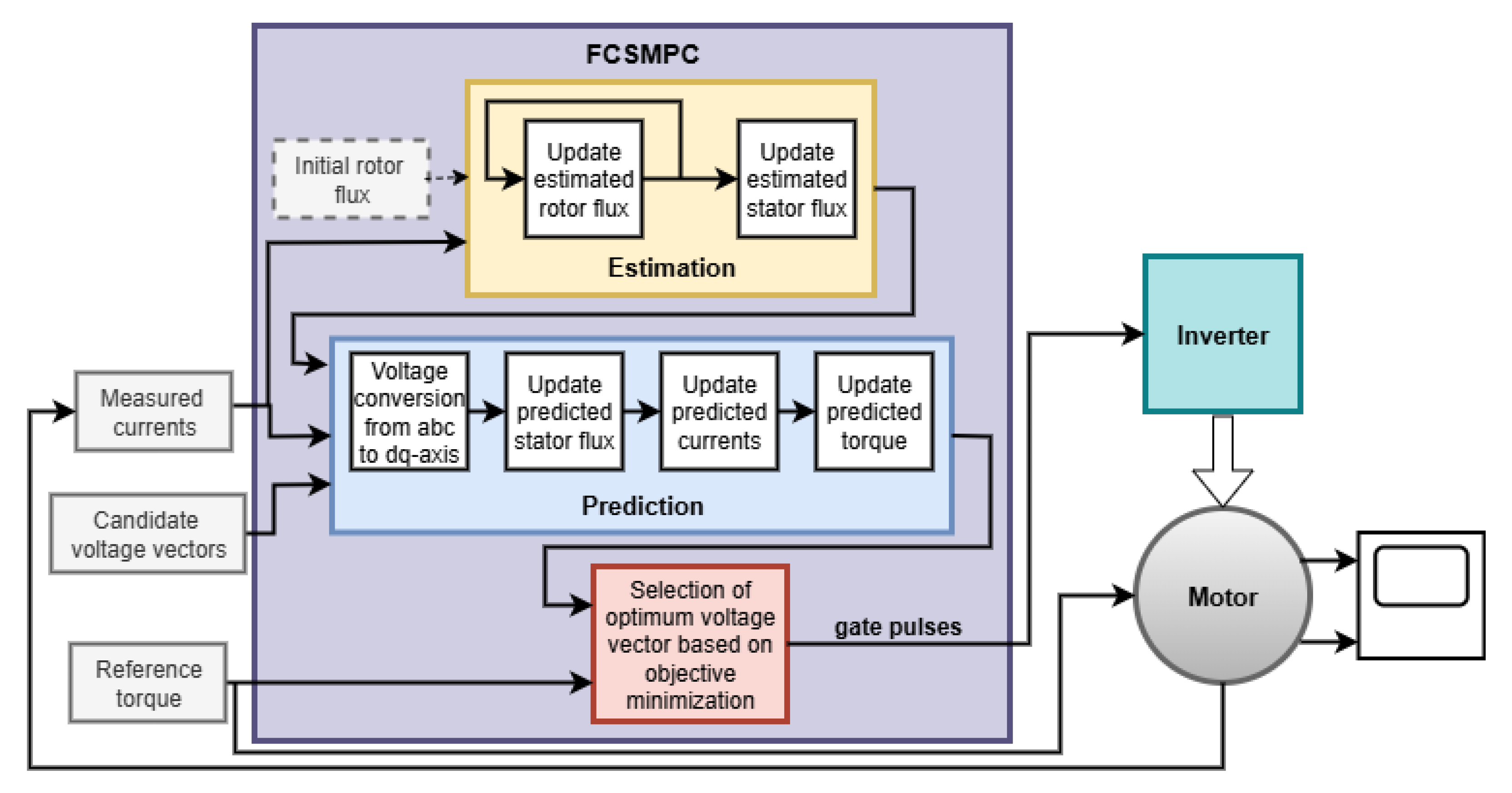
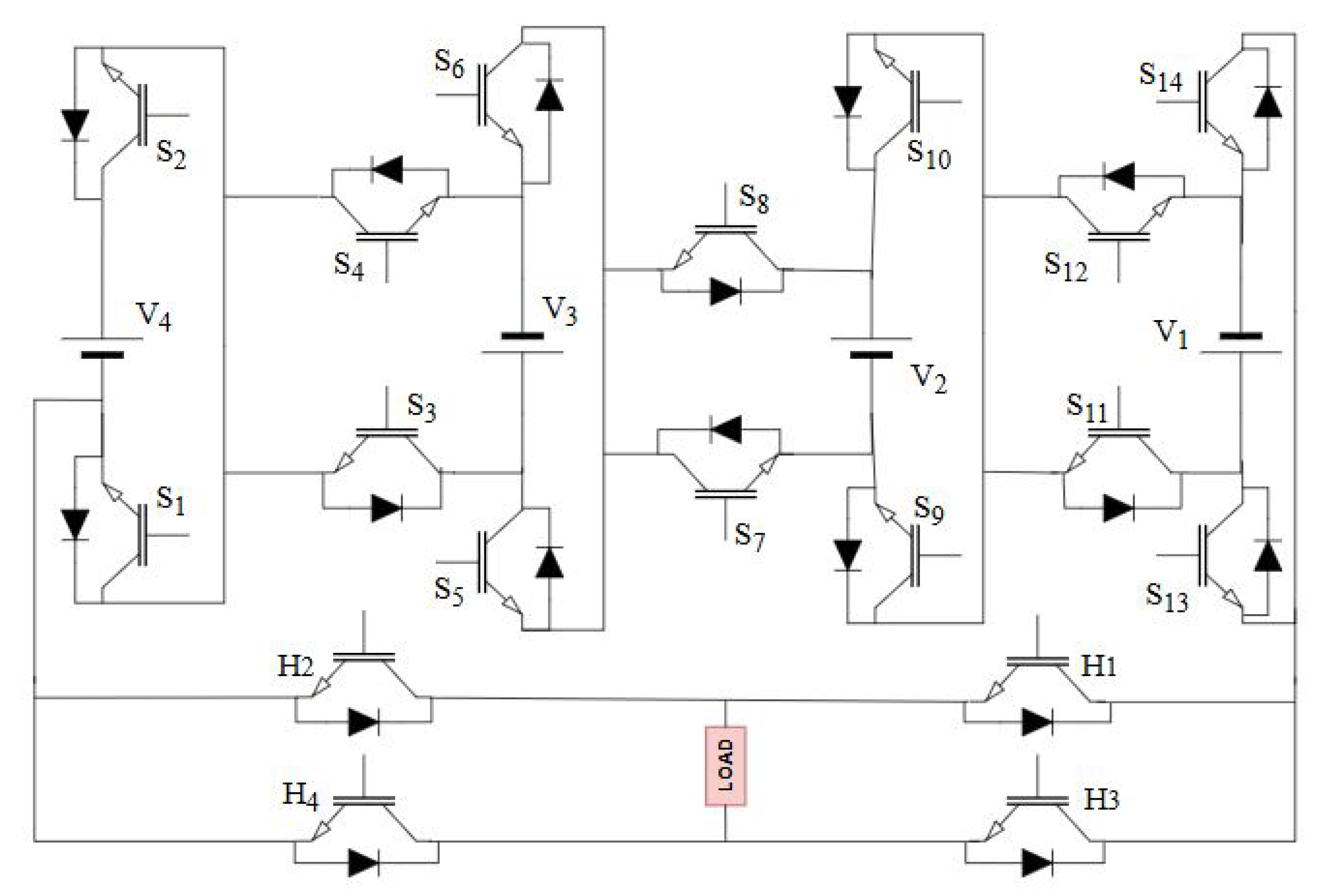
3. Methodology
4. Results and Discussion
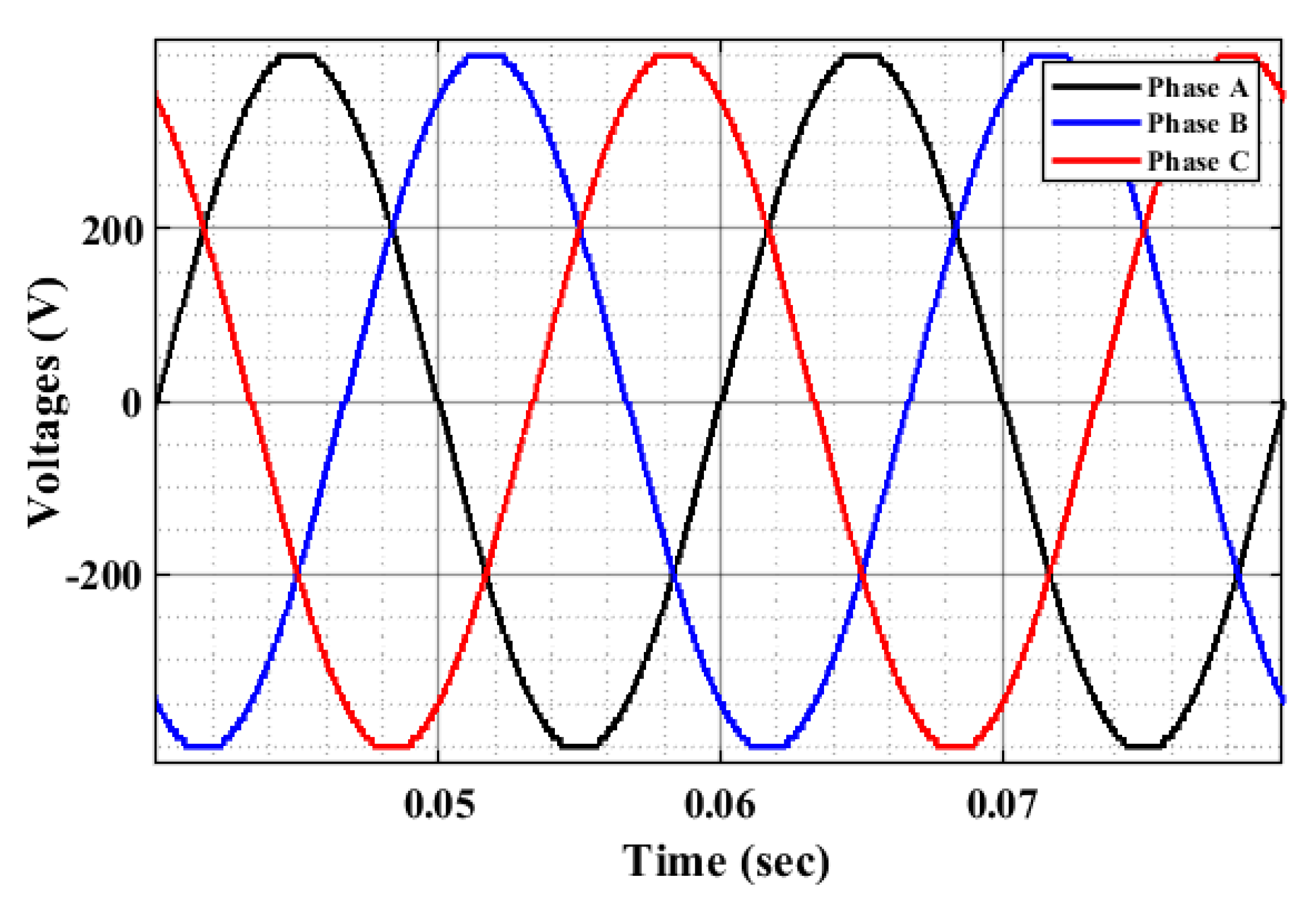
4.1. Impact of Inverter Quality
4.2. Performance of FCSMPC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols
| FCSMPC | Finite Control Set Model Predictive Control |
| MWI | Modified W-type Inverter |
| IM | Induction Motor |
| EV | Electric Vehicle |
| DCM | DC Motor |
| SRM | Switched Reluctance Motor |
| PM | Permanent Magnet |
| BLDC | Brushless DC |
| PMSM | Permanent-Magnet Synchronous Motor |
| IPMSM | Interior-Permanent-Magnetic Synchronous Motor |
| SynRM | Synchronous Reluctance Motor |
| MPC | Model Predictive Control |
| MLI | Multilevel Inverter |
| CHB | Cascaded H-Bridge |
| PIDC | Proportional–Integral–Derivative Control |
| VFC | Voltage–Frequency Control |
| PQC | Power Quality Control |
| SHE | Selective Harmonic Elimination |
| MPPT | Maximum Power Point Tracking |
| VOC | Voltage-Oriented Control |
| DTC | Direct Torque Control |
| HC | H-Infinity Control |
| SMC | Sliding Mode Control |
| DCC | Direct Current Control |
| PCC | Predictive Current Control |
| CHB11 | Eleven-Level CHB Inverter |
| THD | Total Harmonic Distortion |
| Reference Electromagnetic Torque |
| Predicted Electromagnetic Torque | |
| k | Current Time Instant |
| Next Time Instant | |
| Estimated Stator Flux Vector | |
| Estimated Rotor Flux Vector | |
| Measured Stator Current Vector | |
| Predicted Stator Current Vector | |
| Estimated Electromagnetic Torque | |
| Predicted Stator Flux Vector | |
| Stator Voltage Vector | |
| Predicted Electromagnetic Torque | |
| Stator Inductance | |
| Rotor Inductance | |
| Mutual Inductance | |
| Stator Resistance | |
| Rotor Resistance | |
| Leakage Factor | |
| p | Number of Pole Pairs |
| Rotor Electrical Speed | |
| Sample Time | |
| Motor Parameter Constant |
Appendix A
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nominal RMS voltage | 460 V | Nominal power | 18.45 kVA |
| Stator resistance | 0.5968 | Stator inductance | 0.3495 mH |
| Rotor resistance | 0.6258 | Rotor inductance | 5.473 mH |
| Mutual inductance | 0.0354 H | Inertia | 0.05 kg m2 (0.5 for Table 1) |
| Friction factor | 0.005879 Nms | Number of pole pairs | 2 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nominal RMS voltage | 460 V | Nominal power | 120 kVA |
| Stator resistance | 0.0302 | Stator inductance | 0.283 mH |
| Rotor resistance | 0.01721 | Rotor inductance | 0.283 mH |
| Mutual inductance | 0.01095 H | Inertia | 2 kg m2 |
| Friction factor | 0.02154 Nms | Number of pole pairs | 2 |
References
- Madichetty, S.; Sukumar, M.; Basu, M. New trends in electric motors and selection for electric vehicle propulsion systems. IET Electr. Syst. Transp. 2021, 11, 186–199. [Google Scholar] [CrossRef]
- Itu, C.; Sorin, V. The effect of vibrations from racing cars on the human body in formula student races. Appl. Sci. 2023, 13, 12150. [Google Scholar] [CrossRef]
- Jedryczka, C.; Danielczyk, D.; Szelag, W. Torque ripple minimization of the permanent magnet synchronous machine by modulation of the phase currents. Sensors 2020, 20, 2406. [Google Scholar] [CrossRef]
- Hazar-Yavuz, A.N.; Yavuz, A. Investigation of vehicle-induced whole-body vibration with experimental rat models. J. Res. Pharm. 2023, 27, 2310–2329. [Google Scholar] [CrossRef]
- Yang, J.; Leng, J.; Zhou, J.; Chen, R.; Yu, K.; Jiang, Z.; Zou, Y.; Zhang, Z.; Du, J. Study on the impact of vehicle-induced vibration on the flexural behavior of UHPC joints in widened bridges. Urban Lifeline 2024, 2, 20. [Google Scholar] [CrossRef]
- Huang, C.-L.; Lee, F.-C.; Liu, C.-J.; Chen, J.-Y.; Lin, J.-Y.; Yang, S.-C. Torque ripple reduction for BLDC permanent magnet motor drive using DC-link voltage and current modulation. IEEE Access 2022, 10, 51272–51284. [Google Scholar] [CrossRef]
- Prabhu, N.; Thirumalaivasan, R.; Ashok, B. Critical review on torque ripple sources and mitigation control strategies of BLDC motors in electric vehicle Applications. IEEE Access 2023, 11, 115699–115739. [Google Scholar] [CrossRef]
- Yan, L.; Liao, Y.; Lin, H.; Sun, J. Torque ripple suppression of permanent magnet synchronous machines by minimal harmonic current injection. IET Power Electron. 2019, 12, 1368–1375. [Google Scholar] [CrossRef]
- Abdel-Aziz, A.; Elgenedy, M.; Williams, B. Review of switched reluctance motor converters and torque ripple minimisation techniques for electric vehicle applications. Energies 2024, 17, 3263. [Google Scholar] [CrossRef]
- Oloo, J.; Laszlo, S. Torque ripple minimization for switched reluctance motor drives based on harris hawks–radial basis function approximation. Energies 2025, 18, 1006. [Google Scholar] [CrossRef]
- Al Quraan, L.; Szamel, L. Torque ripple reduction of switched reluctance motor using direct instantaneous torque control and adaptive turn-on technique for electric vehicle applications. IET Electr. Power Appl. 2023, 17, 1502–1514. [Google Scholar] [CrossRef]
- Jang, H.; Kim, H.; Liu, H.-C.; Lee, H.-J.; Lee, J. Investigation on the torque ripple reduction method of a hybrid electric vehicle motor. Energies 2021, 14, 1413. [Google Scholar] [CrossRef]
- Abou-ElSoud, A.M.; Nada, A.S.A.; Abdel-Aziz, A.-A.M.; Sabry, W. Torque ripples reduction of electric vehicle synchronous reluctance motor drive using the strong action controller. Ain Shams Eng. J. 2024, 15, 102428. [Google Scholar] [CrossRef]
- Yoon, H.-J.; Castano, A.F.; Voulgaris, P. Adaptive control to suppress torque ripple in electric vehicles. In Proceedings of the IFAC-PapersOnLine 3rd Modeling, Estimation and Control Conference MECC 2023, Lake Tahoe, CA, USA, 2–5 October 2023; Volume 56, pp. 223–228. [Google Scholar] [CrossRef]
- Kumar, S.; Pal, Y. Asymmetric multilevel inverter induction motor drive for fuel cell based electrical vehicles. In Proceedings of the 2019 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 17–19 July 2019; pp. 791–795. [Google Scholar] [CrossRef]
- Nayak, M.R.; Saritha, M.; Mujeer, S.A.; Devulal, B.; Kumar, T.S. A photovoltaic based multilevel inverter fed induction motor drive. Turcomat 2021, 12, 6196–6212. [Google Scholar] [CrossRef]
- Omer, P.; Kumar, J.; Surjan, B.S. A review on reduced switch count multilevel inverter topologies. IEEE Access 2020, 8, 22281–22302. [Google Scholar] [CrossRef]
- Salem, M.; Richelli, A.; Yahya, K.; Hamidi, M.N.; Ang, T.-Z.; Alhamrouni, I. A comprehensive review on multilevel inverters for grid-tied system applications. Energies 2022, 15, 6315. [Google Scholar] [CrossRef]
- Kadam, A.; Shukla, A. A multilevel transformerless inverter employing ground connection between PV negative terminal and grid neutral point. IEEE Trans. Ind. Electron. 2017, 64, 8897–8907. [Google Scholar] [CrossRef]
- Mehta, S.; Puri, V. A review of different multi-level inverter topologies for grid integration of solar photovoltaic system. Renew. Energy Focus 2022, 43, 263–276. [Google Scholar] [CrossRef]
- Jain, S.; Sonti, V. A highly efficient and reliable inverter configuration based cascaded multilevel inverter for PV systems. IEEE Trans. Ind. Electron. 2017, 64, 2865–2875. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Forouzesh, M.; Lee, S.S.; Blaabjerg, F.; Siwakoti, Y.P. Switched-capacitor multilevel inverters: A comprehensive review. IEEE Trans. Power Electron. 2022, 37, 11209–11243. [Google Scholar] [CrossRef]
- Lee, S.S. Single-stage switched-capacitor module (S3CM) topology for cascaded multilevel inverter. IEEE Trans. Power Electron. 2018, 33, 8204–8207. [Google Scholar] [CrossRef]
- Hassan, A.; Yang, X.; Chen, W. A multi-cell 21-level hybrid multilevel inverter synthesizes a reduced number of components with voltage boosting property. IEEE Access 2020, 8, 224439–224451. [Google Scholar] [CrossRef]
- Siddique, M.D.; Iqbal, A.; Memon, M.A.; Mekhilef, S. A new configurable topology for multilevel inverter with reduced switching components. IEEE Access 2020, 8, 188726–188741. [Google Scholar] [CrossRef]
- Taghvaie, A.; Jafar, A.; Rezanejad, M. A self-balanced step-up multilevel inverter based on switched-capacitor structure. IEEE Trans. Power Electron. 2018, 33, 199–209. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Rawa, M.; Wahyudie, A.; Chokaev, B.; Salamov, I. Extended multilevel inverter topology with reduced switch count and voltage stress. IEEE Access 2020, 8, 201835–201846. [Google Scholar] [CrossRef]
- Mondol, M.H.; Tür, M.R.; Biswas, S.P.; Hosain, M.K.; Shuvo, S.; Hossain, E. Compact three phase multilevel inverter for low and medium power photovoltaic systems. IEEE Access 2020, 8, 60824–60837. [Google Scholar] [CrossRef]
- Abarzadeh, M.; Al-Haddad, K. Generalized circuit topology of Qn-hybrid-NPC multilevel converter with novel decomposed sensor-less modulation method. IEEE Access 2019, 7, 59813–59824. [Google Scholar] [CrossRef]
- Ahmed, S.; Saqib, M.A.; Kashif, S.A.R.; Hashmi, K.; Aymen, F.; AboRas, K.M.; Jasińska, L.; Leonowicz, Z. A modified multi-level inverter system for grid-tied DES applications. Sustainability 2022, 14, 16545. [Google Scholar] [CrossRef]
- Saeedian, M.; Adabi, J.; Hosseini, S.M. Cascaded multilevel inverter based on symmetric–asymmetric DC sources with reduced number of components. IET Power Electron. 2017, 10, 1468–1478. [Google Scholar] [CrossRef]
- Agrawal, R.; Jain, S. Multilevel inverter for interfacing renewable energy sources with low/medium- and high-voltage grids. IET Renew. Power Gener. 2017, 11, 1822–1831. [Google Scholar] [CrossRef]
- Bughneda, A.; Salem, M.; Richelli, A.; Ishak, D.; Alatai, S. Review of multilevel inverters for PV energy system applications. Energies 2021, 14, 1585. [Google Scholar] [CrossRef]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A review of modulation and control techniques for multilevel inverters in traction applications. IEEE Access 2021, 9, 24187–24204. [Google Scholar] [CrossRef]
- Ahmed, S.; Saqib, M.A.; Kashif, S.A.R. Modified W-type configuration for a single-phase reduced parts count 81-level inverter. PLoS ONE 2022, 17, e0269714. [Google Scholar] [CrossRef]
- Sedhom, B.E.; El-Saadawi, M.M.; Hatata, A.Y.; Abd-Raboh, E.-H.E. H-Infinity versus model predictive control methods for seamless transition between islanded- and grid-connected modes of microgrids. IET Renew. Power Gener. 2020, 14, 856–870. [Google Scholar] [CrossRef]
- Sarwar, M.I.; Sarwar, A.; Farooqui, S.A.; Tariq, M.; Fahad, M.; Beig, A.R. A hybrid nearest level combined with PWM control strategy: Analysis and implementation on cascaded H-bridge multilevel inverter and its fault tolerant topology. IEEE Access 2021, 9, 44266–44282. [Google Scholar] [CrossRef]
- Ko, Y.; Tcai, A.; Liserre, M. DC-link voltage balancing modulation for cascaded H-bridge converters. IEEE Access 2021, 9, 103524–103532. [Google Scholar] [CrossRef]
- Jamma, M.; Barara, M.; Akherraz, M.; Enache, B.A. Voltage oriented control of three-phase PWM rectifier using space vector modulation and input output feedback linearization theory. In Proceedings of the 2016 8th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Ploiesti, Romania, 30 June–2 July 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Dyanamina, G.; Kakodia, S.K. Adaptive neuro fuzzy inference system based decoupled control for neutral point clamped multi level inverter fed induction motor drive. Chin. J. Electr. Eng. 2021, 7, 70–82. [Google Scholar] [CrossRef]
- Fatima, A.; Almas, T.; Biabani, M.A.K.A.; Imran, M. Sliding mode control of induction motor used in traction. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 3336–3343. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Yaramasu, V.; Fuentes, R.L.; Zargari, N.R. Model predictive control of high-power modular multilevel converters—An overview. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 168–183. [Google Scholar] [CrossRef]
- Ghauri, M.A.; Abbasi, M.A.; Shahid, M.B.; Noman, M.; Hakeem, M.A. Finite control set model predictive field-oriented control for three-phase induction motor drives. J. Eng. Res. 2022. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Xia, B. Model-predictive control of induction motor drives: Torque control versus flux control. IEEE Trans. Ind. Appl. 2016, 52, 4050–4060. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M. Model-predictive control of multilevel inverters: Challenges, recent advances, and trends. IEEE Trans. Power Electron. 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Y.; Yang, H. A universal multiple vector-based model predictive control of induction motor drives. IEEE Trans. Power Electron. 2018, 33, 6957–6969. [Google Scholar] [CrossRef]
- Mohapatra, S.R.; Agarwal, V. Model predictive controller with reduced complexity for grid-tied multilevel inverters. IEEE Trans. Ind. Electron. 2019, 66, 8851–8855. [Google Scholar] [CrossRef]
- Baig, M.A.; Kashif, S.A.R.; Khan, I.A.; Abbas, G. Quick search algorithm-based direct model predictive control of grid-connected 289-level multilevel inverter. Electronics 2023, 12, 3312. [Google Scholar] [CrossRef]
- Alkhaldi, A.; Elkhateb, A.; Laverty, D. Voltage lifting techniques for non-isolated DC/DC converters. Electronics 2023, 12, 718. [Google Scholar] [CrossRef]
- Zerdali, E.; Rivera, M.; Wheeler, P. A review on weighting factor design of finite control set model predictive control strategies for AC electric drives. IEEE Trans. Power Electron. 2024, 39, 9967–9981. [Google Scholar] [CrossRef]
- Penthala, T.; Kaliaperumal, S. Predictive control of induction motors using cascaded artificial neural network. Electr. Eng. 2024, 106, 2985–3000. [Google Scholar] [CrossRef]
- Kasri, A.; Ouari, K.; Belkhier, Y.; Bajaj, M.; Zaitsev, I. Optimizing electric vehicle powertrains peak performance with robust predictive direct torque control of induction motors: A practical approach and experimental validation. Sci. Rep. 2024, 14, 14977. [Google Scholar] [CrossRef]
- Fang, X.; Lin, S.; Wang, X.; Yang, Z.; Lin, F.; Tian, Z. Model predictive current control of traction permanent magnet synchronous motors in six-step operation for railway application. IEEE Trans. Ind. Electron. 2022, 69, 8751–8759. [Google Scholar] [CrossRef]
- Kousalya, V.; Rai, R.; Singh, B. Sliding model-based predictive torque control of induction motor for electric vehicle. IEEE Trans. Ind. Appl. 2022, 58, 742–752. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F. Latest advances of model predictive control in electrical drives—part II: Applications and benchmarking with classical control methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Usha, S.; Geetha, P.; Geetha, A.; Palanisamy, R.; Thentral, T.M.T.; Mahato, B.; Giri, N.C.; Alharbi, M. Performance enhancement of sensorless induction motor drive using modified direct torque control techniques for traction application. Alex. Eng. J. 2024, 108, 518–538. [Google Scholar] [CrossRef]
- Kim, D.-K.; Kim, D.-M.; Park, J.-C.; Lee, S.-G.; Yoo, J.; Lim, M.-S. Torque ripple reduction of BLDC traction motor of electric wheelchair for ride comfort improvement. J. Electr. Eng. Technol. 2022, 17, 351–360. [Google Scholar] [CrossRef]
- Zhao, W.; Lu, B.; Liu, Z.; Zhang, G. An improved passivity-based control for suppressing the traction motor torque ripples due to traction network voltage fluctuation in high-speed railways. IET Power Electron. 2023, 16, 2287–2300. [Google Scholar] [CrossRef]
- Holczer, A.; Freijedo, F.D.; Bojoi, R. Optimal high-frequency injection minimizing high-frequency torque ripple for sensorless control of electric vehicle IPM traction motors. IEEE Trans. Ind. Electron. 2025, 72, 4424–4435. [Google Scholar] [CrossRef]
- Yue, H.; He, H.; Han, M. Study on torsional vibration characteristics and suppression of electric vehicles with dualmotor drive system. J. Frankl. Inst. 2023, 360, 380–402. [Google Scholar] [CrossRef]
- Liu, W.; He, H.; Sun, F.; Wang, H. Optimal design of adaptive shaking vibration control for electric vehicles. Veh. Syst. Dyn. 2019, 57, 134–159. [Google Scholar] [CrossRef]
- Rezig, A.; Boudendouna, W.; Djerdir, A.; N’Diaye, A. Investigation of optimal control for vibration and noise reduction in-wheel switched reluctance motor used in electric vehicle. Math. Comput. Simul. 2020, 167, 267–280. [Google Scholar] [CrossRef]
- Zhao, Z.; Taghavifar, H.; Du, H.; Qin, Y.; Dong, M.; Gu, L. In-wheel motor vibration control for distributed-driven electric vehicles: A review. IEEE Trans. Transp. Electrif. 2021, 7, 2864–2880. [Google Scholar] [CrossRef]
- M, D.; Samithas, D.; Balachandran, P.; Selvarajan, S. Experimental analysis of enhanced finite set model predictive control and direct torque control in SRM drives for torque ripple reduction. Sci. Rep. 2024, 14, 16805. [Google Scholar] [CrossRef]
- Varvolik, V.; Buticchi, G.; Prystupa, D.; Wang, S.; Aboelhassan, A.; Peresada, S. Comparative study on torque ripple reduction considering minimum losses for synchronous reluctance motor drives. IEEE Trans. Transp. Electrif. 2024, 10, 6527–6538. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z. Harmonic injection-based torque ripple reduction of PMSM With improved DC-link voltage utilization. IEEE Trans. Power Electron. 2023, 38, 7976–7981. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Midgley, W.; Steffen, T. A review of the state of the art of torque ripple minimization techniques for permanent magnet synchronous motors. IEEE Trans. Ind. Inform. 2024, 20, 1019–1031. [Google Scholar] [CrossRef]
- Cortes, P.; Wilson, A.; Kouro, S.; Rodriguez, J.; Abu-Rub, H. Model predictive control of cascaded H-bridge multilevel inverters. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–9. [Google Scholar]
- Baek, J.-Y.; Lee, K.-B. Model predictive current control strategy for improved dynamic response in cascaded H-bridge multilevel inverters. J. Electr. Eng. Technol. 2024, 19, 1395–1405. [Google Scholar] [CrossRef]
- Varga, T.; Benšić, T.; Jerković Štil, V.; Barukčić, M. Continuous control set predictive current control for induction machine. Appl. Sci. 2021, 11, 6230. [Google Scholar] [CrossRef]
- Arias-Esquivel, Y.; Cárdenas, R.; Urrutia, M.; Diaz, M.; Tarisciotti, L.; Clare, J.C. Continuous control set model predictive control of a modular multilevel converter for drive applications. IEEE Trans. Ind. Electron. 2023, 70, 8723–8733. [Google Scholar] [CrossRef]
- Habibullah, M.; Lu, D.D.-C.; Xiao, D.; Rahman, M.F. A simplified finite-state predictive direct torque control for induction motor drive. IEEE Trans. Ind. Electron. 2016, 63, 3964–3975. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; Wiley: Santiago, Chile, 2012. [Google Scholar]
- Tariq, M.A.; Kashif, S.A.R. Impact of the voltage profiles of CHB vs. MW-type inverters on torque and speed ripples for 3-phase induction motors. In Proceedings of the 2024 IEEE Workshop on Control and Modeling for Power Electronics (COMPEL), Lahore, Pakistan, 24–27 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Tariq, M.A.; Shami, U.T.; Fakhar, M.S.; Kashif, S.A.R.; Abbas, G.; Ullah, N.; Mohammad, A.; Farrag, M.E. Dragonfly algorithm-based optimization for selective harmonics elimination in cascaded H-bridge multilevel inverters with statistical comparison. Energies 2022, 15, 6826. [Google Scholar] [CrossRef]
- Schlemmer, E.; Laussegger-Rauch, H. E-drive component tests derived from vehicle master test cases in the SyrNemo collaborative research project. Renew. Energies Power Qual. J. 2016, 14, 166–171. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, S.; Dong, Y. A novel model-based driving behavior recognition system using motion sensors. Sensors 2016, 16, 1746. [Google Scholar] [CrossRef]

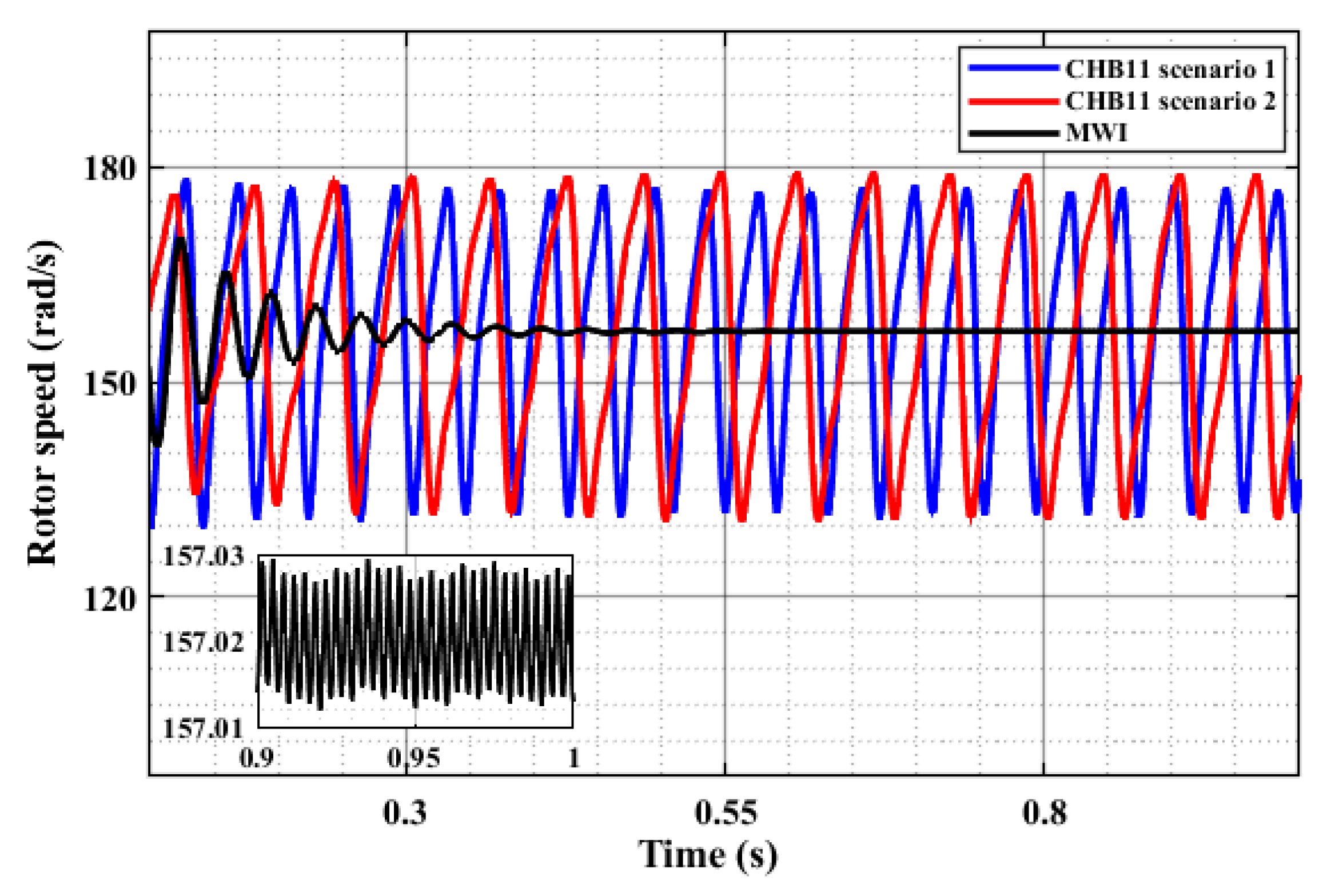
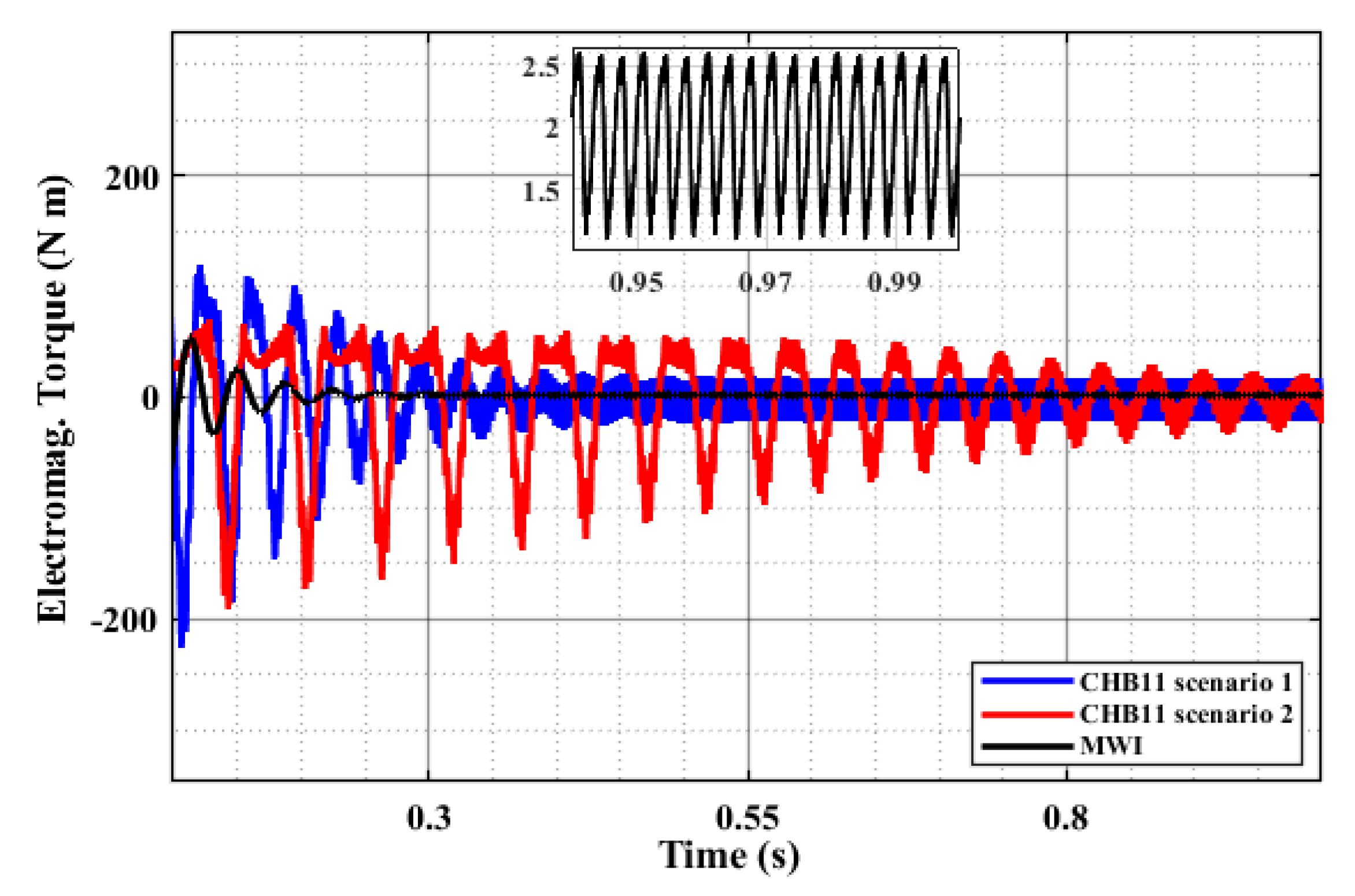

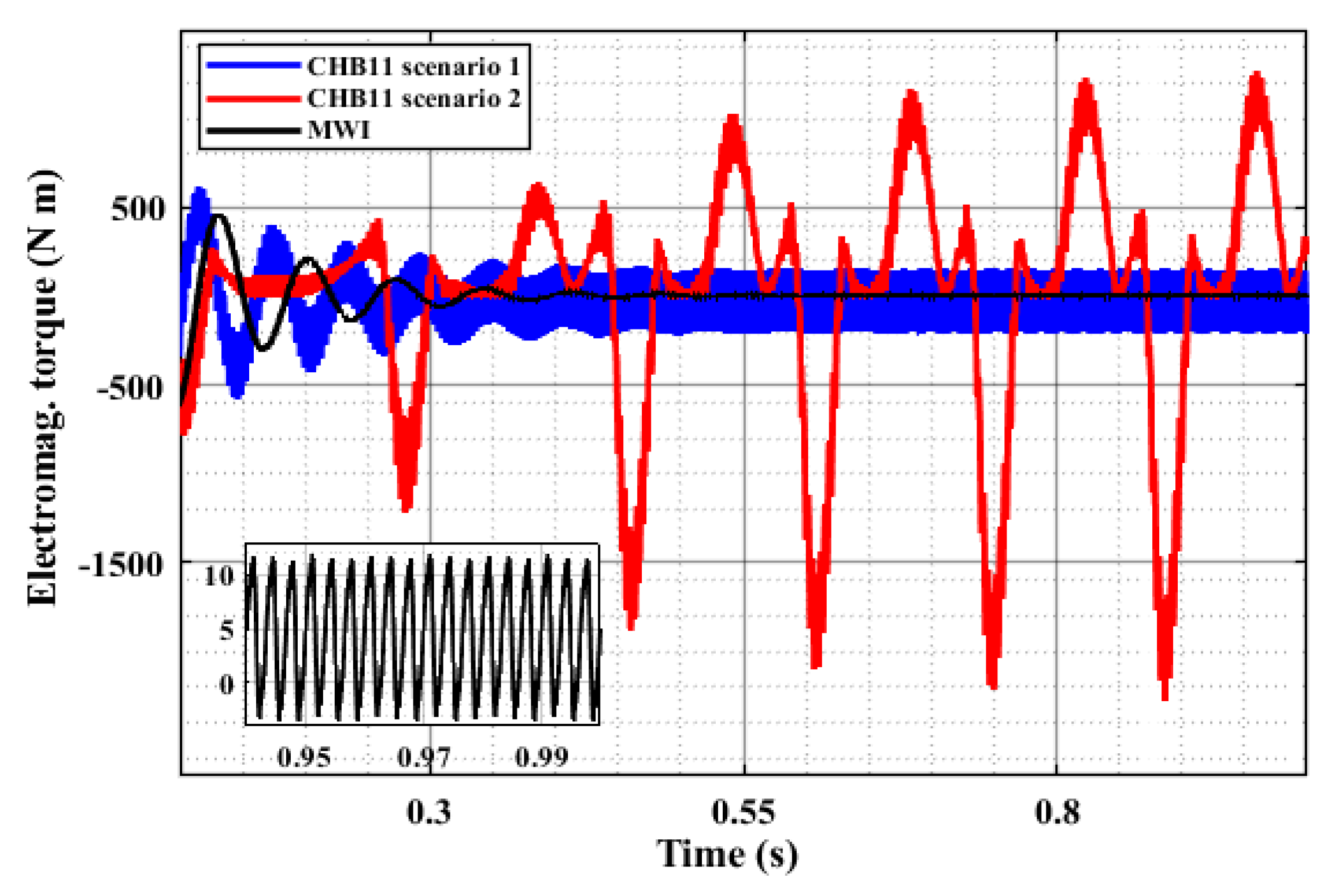



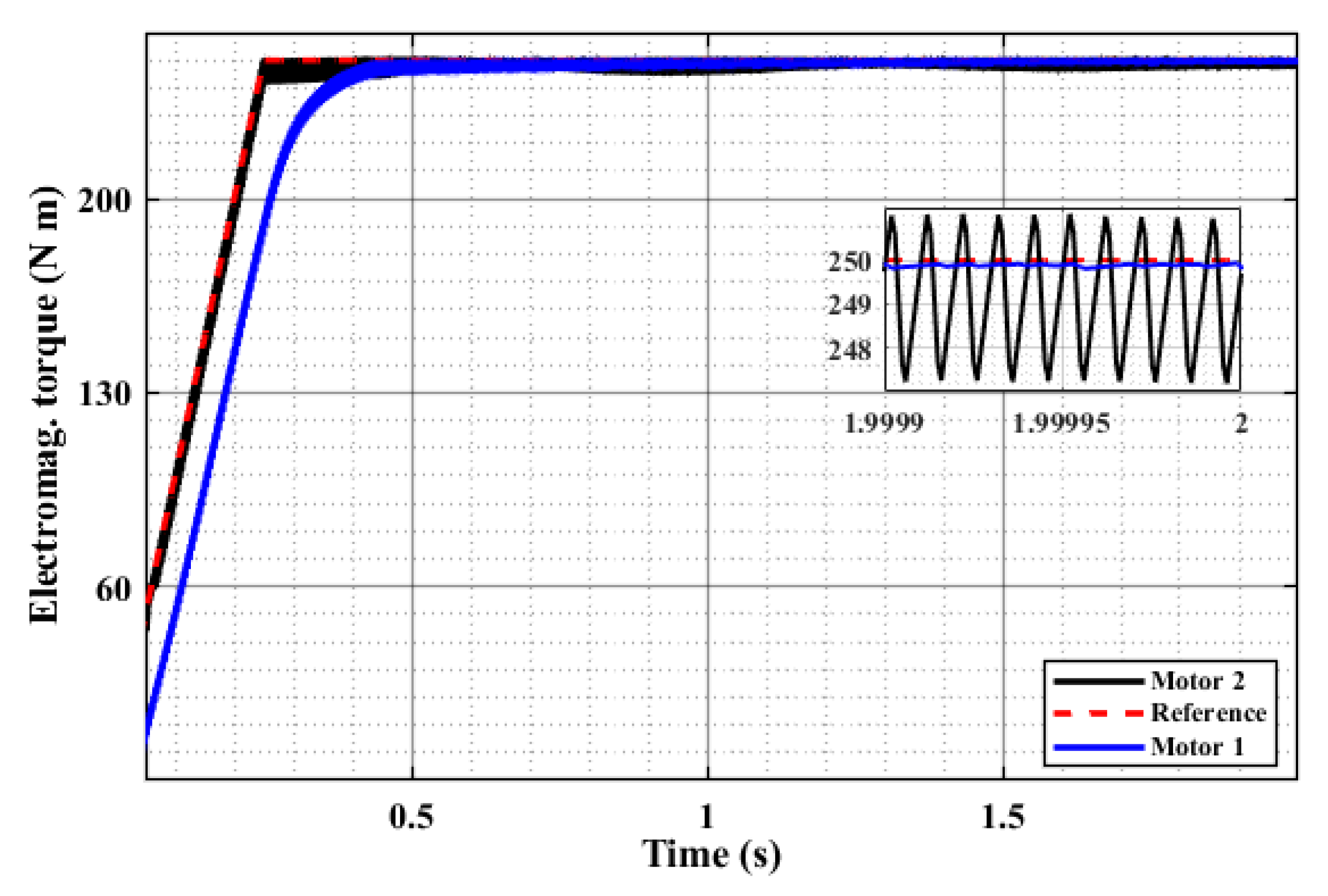
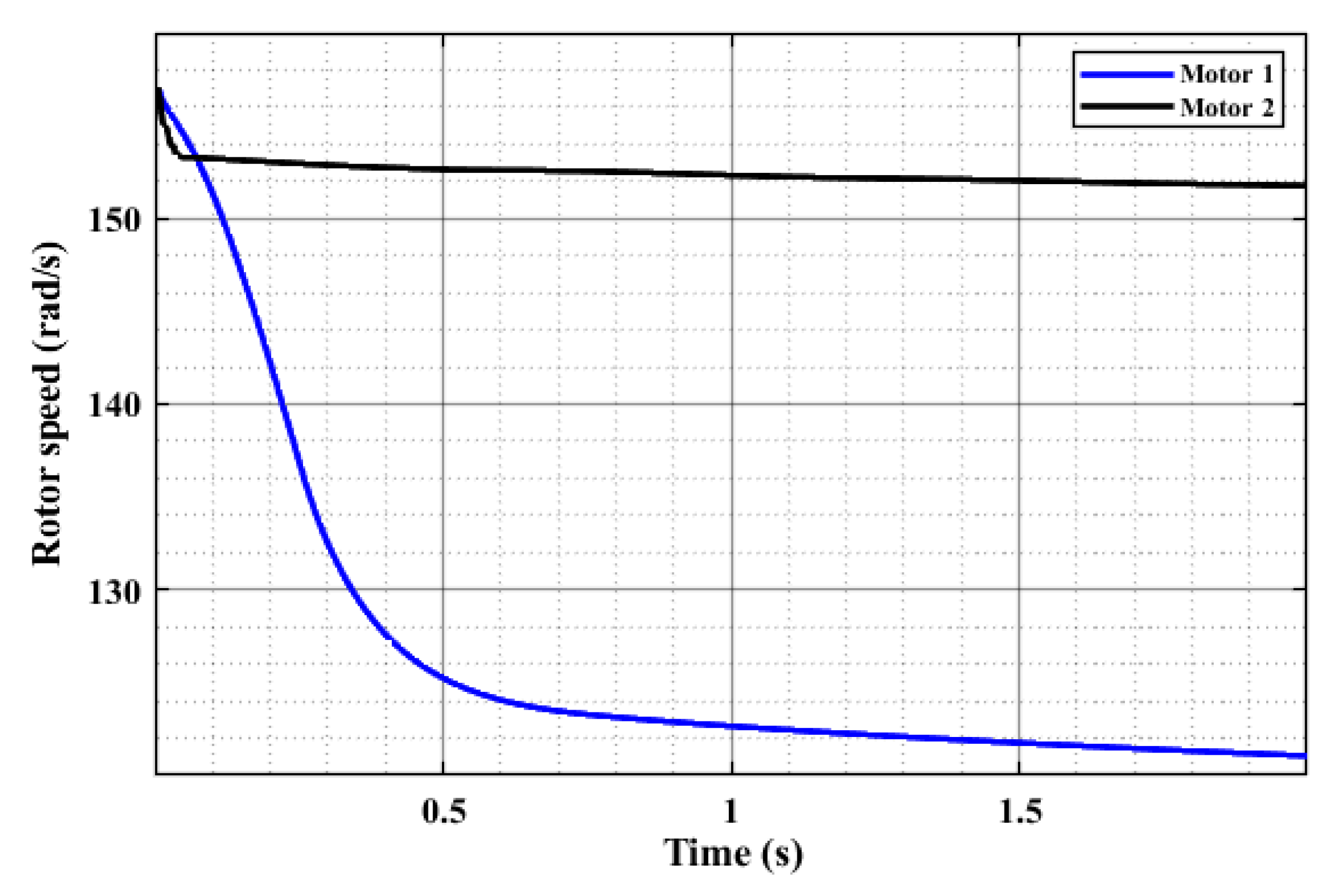
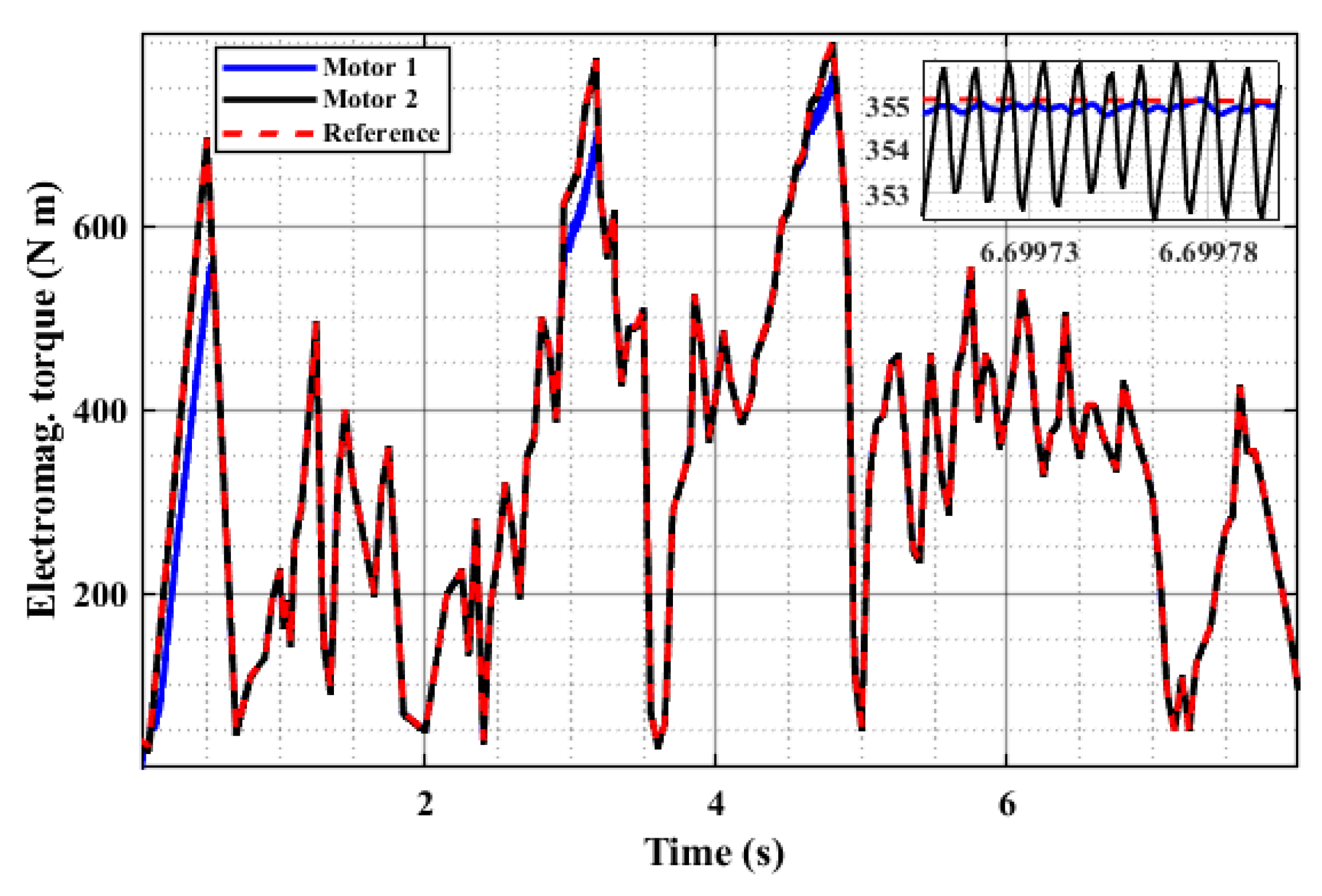
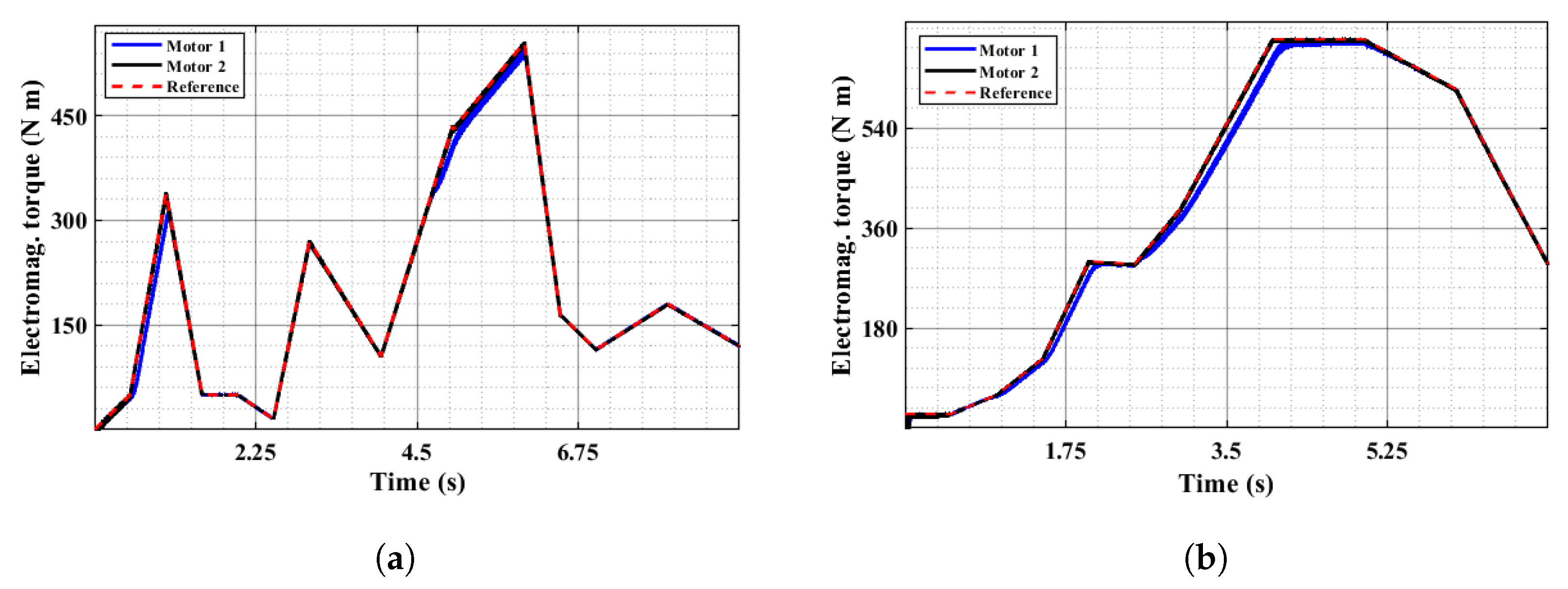
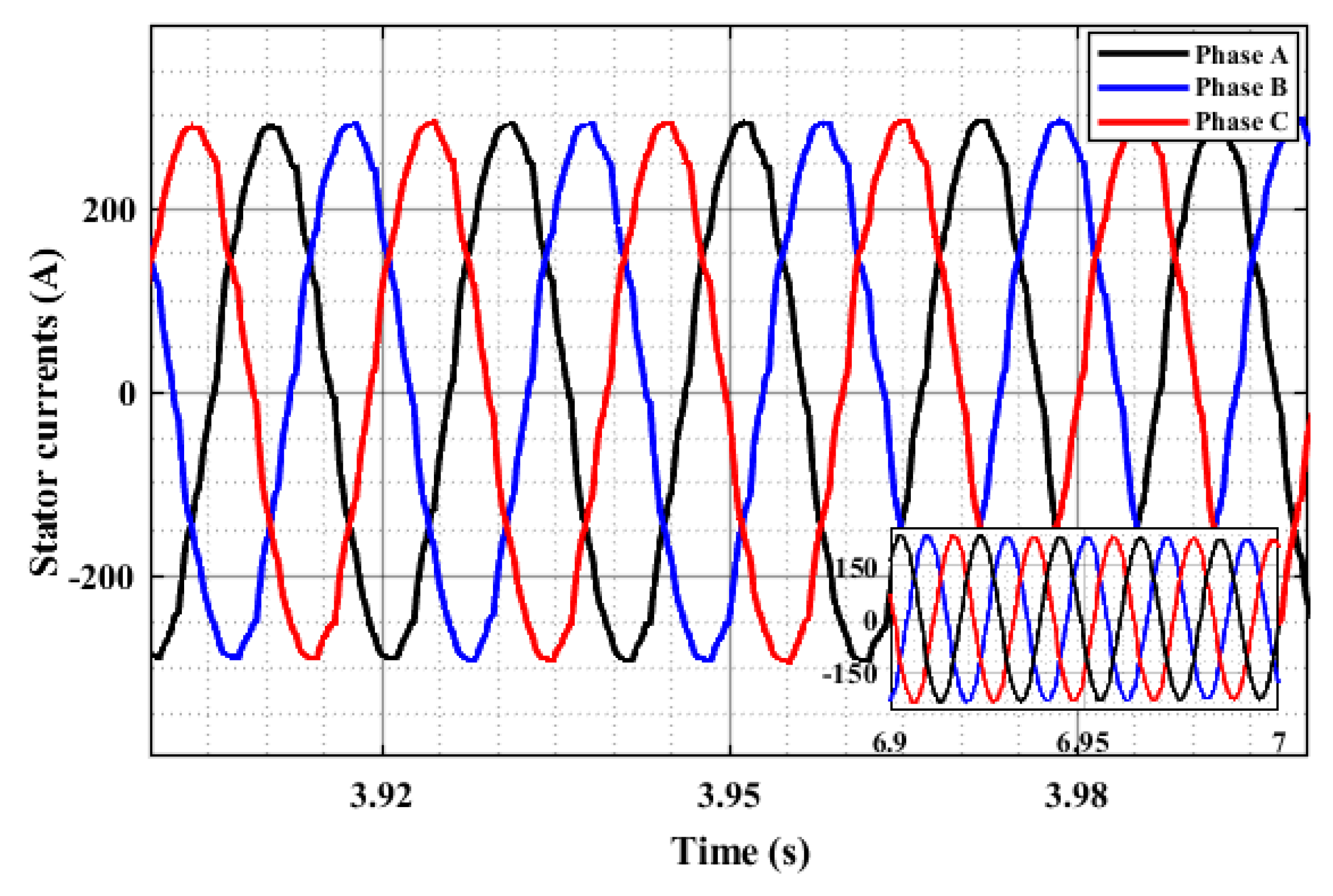
| Driving Profile | Maximum Ripple for Motor 1 at Peak Load | Maximum Ripple for Motor 2 at Peak Load |
|---|---|---|
| Pattern 2 | 1.72% | 3.07% |
| Pattern 3 | 1.9% | 0.63% |
| Pattern 4 | 2.22% | 0.9% |
| Pattern 5 | 1.87% | 0.7% |
| Driving Profile | THD |
|---|---|
| Pattern 2 | 3.41% |
| Pattern 3 | 4.64% |
| Pattern 4 | 3.09% |
| Pattern 5 | 3.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tariq, M.A.; Kashif, S.A.R.; Rasool, A.; Ali, A. Torque Smoothness for a Modified W-Type Inverter-Fed Three-Phase Induction Motor with Finite Set Model Predictive Control for Electric Vehicles. World Electr. Veh. J. 2025, 16, 539. https://doi.org/10.3390/wevj16090539
Tariq MA, Kashif SAR, Rasool A, Ali A. Torque Smoothness for a Modified W-Type Inverter-Fed Three-Phase Induction Motor with Finite Set Model Predictive Control for Electric Vehicles. World Electric Vehicle Journal. 2025; 16(9):539. https://doi.org/10.3390/wevj16090539
Chicago/Turabian StyleTariq, Muhammad Ayyaz, Syed Abdul Rahman Kashif, Akhtar Rasool, and Ahmed Ali. 2025. "Torque Smoothness for a Modified W-Type Inverter-Fed Three-Phase Induction Motor with Finite Set Model Predictive Control for Electric Vehicles" World Electric Vehicle Journal 16, no. 9: 539. https://doi.org/10.3390/wevj16090539
APA StyleTariq, M. A., Kashif, S. A. R., Rasool, A., & Ali, A. (2025). Torque Smoothness for a Modified W-Type Inverter-Fed Three-Phase Induction Motor with Finite Set Model Predictive Control for Electric Vehicles. World Electric Vehicle Journal, 16(9), 539. https://doi.org/10.3390/wevj16090539









