Cooperative Estimation Method for SOC and SOH of Lithium-Ion Batteries Based on Fractional-Order Model

Abstract

To overcome the limitations of traditional integer-order models, which fail to accurately capture the dynamic behavior of lithium-ion batteries, and to improve the insufficient accuracy of state of charge (SOC) and state of health (SOH) collaborative estimation, this study proposes a cooperative estimation framework based on a fractional-order model. First, a fractional-order second-order RC equivalent circuit model is established, and the whale optimization algorithm is applied for offline parameter identification to improve model accuracy. Second, a strong tracking strategy is introduced into the improved unscented Kalman filter to address the convergence speed issue under inaccurate initial SOC conditions. Meanwhile, the extended Kalman filter is employed for SOH estimation and online parameter identification. Furthermore, a multi-time-scale collaborative estimation algorithm is proposed to enhance overall estimation accuracy. Experimental results under three dynamic operating conditions driving cycles demonstrate that the proposed method effectively solves the SOC/SOH collaborative estimation problem, achieving a mean SOC estimation error of 0.45% and maintaining the SOH estimation error within 0.25%.

1. Introduction

With the rapid development of China’s new energy vehicle (NEV) industry, the ownership of NEVs has been steadily increasing [1]. As the primary power source for new energy vehicles (NEVs), lithium-ion batteries require precise state monitoring—a core function of the battery management system (BMS) that critically impacts the driving experience and overall performance of electric vehicles [2]. In lithium-ion battery state estimation, state of charge (SOC) and state of health (SOH) estimation have become not only a key research focus in the electric vehicle field but also one of the most critical functions for operational vehicle fleets [3,4].

High-precision battery models serve as the foundation for accurate SOC and SOH estimation, playing a crucial role in lithium-ion battery state estimation [5]. Currently, equivalent circuit models (ECMs) are the most widely used approach, with the Thevenin model being the predominant representative [6], followed by the integer-order second-order RC model [7] and fractional-order second-order RC model [8]. The fractional-order model employs a constant phase element (CPE) to characterize the fractional-order dynamics of lithium-ion diffusion in electrolytes during charge/discharge processes, thereby achieving higher modeling accuracy [9]. For offline parameter identification of fractional-order models, global optimization algorithms such as adaptive genetic algorithms [10], ant colony optimization [11], and particle swarm optimization [12] are commonly adopted. Online parameter identification primarily utilizes recursive least squares (RLS) [13], RLS with variable forgetting factor [14], and extended Kalman filter (EKF) algorithms [15,16].

Lithium-ion battery SOC is one of the most critical parameters in BMS. SOC estimation methods primarily include open-loop algorithms (Ah integration method, open-circuit voltage method), data-driven approaches, and filtering-based algorithms. The Ah integration method is simple and convenient, but its main drawback lies in the inability to obtain an accurate initial SOC value. Moreover, prolonged use of this method leads to cumulative integration errors, resulting in SOC estimation distortion [17]. The open-circuit voltage (OCV) method relies on the assumption that the terminal voltage equals the OCV after prolonged rest. By referencing the OCV-SOC lookup table, the current SOC can be determined [18]. However, this method requires the battery to remain idle for an extended period, a condition rarely met in practical applications, making it unsuitable for standalone SOC estimation [19]. Data-driven approaches mainly include neural networks, support vector machines (SVMs), and machine learning methods. These techniques eliminate the need for complex equivalent circuit models or electrochemical relationships, instead relying on self-learning from training datasets to estimate SOC. Nevertheless, they are highly dependent on training samples, computationally intensive, and challenging to implement on resource-constrained BMS hardware [20]. Kalman filtering-based methods estimate SOC by constructing an equivalent circuit model and establishing a state observation equation, enabling accurate state estimation through measurement tracking. Reference [21] employed an improved unscented Kalman filter (UKF) for SOC estimation, enhancing algorithm robustness. Similarly, another reference combined a strong tracking algorithm with UKF to achieve rapid convergence even with inaccurate initial states.

The accuracy of Kalman filter-based SOC estimation heavily depends on battery model precision. When lithium-ion batteries undergo variations in operating temperature, aging state, charge/discharge rates, or operate within different SOC ranges, the parameters of their equivalent circuit models (ECMs) will correspondingly change. Inaccurate model parameters can significantly degrade SOC estimation performance. To address this challenge, reference [22] proposed a dual extended Kalman filter (DEKF) approach that enables a cooperative estimation of SOC, SOH, and online parameter identification. This method establishes a dynamic coupling mechanism between SOC estimation and model parameter updating, thereby enhancing both the robustness and adaptability of state estimation under varying operational conditions [23].

Building upon this foundation, this paper proposes an enhanced unscented Kalman filter (UKF) algorithm with strong tracking capability based on a fractional-order model for SOC estimation, combined with an extended Kalman filter (EKF) for model parameter identification.

2. Fractional-Order Second-Order RC Equivalent Circuit Model (FSO-ECM)

2.1. Experimental Setup and Test Objects

The battery testing system employed in this study is the UPC-5V6A-8C model manufactured by YouNeng Technology, with detailed specifications presented in

Table 1. Specifications of UPC-5V6A-8C battery testing system.

Model Specifications	Current Accuracy	Current Resolution	Voltage Accuracy	Voltage Resolution	Data Sampling Period
5V6A	±0.05%	0.1 mA	±0.05%	0.1 mV	100 ms

. This equipment was utilized to perform controlled charge/discharge tests on individual battery cells, acquiring current and voltage data under various operating conditions. The collected datasets serve as the fundamental source for subsequent parameter identification and state estimation validation.

The experimental subject selected for this study is a lithium nickel manganese cobalt oxide (NMC) battery produced by Samsung, model INR-18650-30Q. The detailed specifications of the individual cell are presented in

Table 2. Single-cell parameters.

Battery Model	Battery Type	Nominal Voltage	Maximum Voltage	Minimum Voltage	Nominal Capacity
INR18650-30Q	Ternary Lithium-Ion Battery	3.6 V	4.2 V	2.5 V	3 Ah

.

2.2. Experimental Conditions

Pulse discharge tests and urban dynamometer driving schedule (UDDS) tests were conducted on the battery pack under investigation. The pulse discharge tests were employed for the subsequent offline parameter identification of the battery model, while the UDDS tests were utilized to validate the state estimation algorithms. The procedures of the pulse discharge and UDDS tests are described below.

2.2.1. Pulse Discharge Test

The purpose of this experiment is to establish the correlation between the open-circuit voltage (OCV) and the state of charge (SOC), thereby providing data support for subsequent parameter identification and state estimation. The procedure of the pulse discharge test is shown in Figure 1.

(1) The battery was charged at 0.5 C constant current to 4.2 V, then at constant voltage until current fell to 0.05 C, indicating full charge, followed by a 2-h rest.

(2) The battery was discharged at a constant current of 1 C for 3 min, followed by a rest period of 2 h;

(3) Step (2) was repeated until the cell voltage reached the discharge cutoff voltage of 2.5 V, after which the battery was left to for 2 h.

2.2.2. UDDS Driving Cycle Test

This experiment was designed to simulate the charge and discharge behavior of a battery under the UDDS, which represents urban driving conditions in the United States. The collected data serve as a basis for validating the accuracy of the state estimation algorithms. The UDDS test procedure is as follows:

(1) The battery was charged at a constant current of 0.5 C until the cutoff voltage of 4.2 V was reached. Subsequently, constant voltage charging was applied until the current decreased to 0.05 C, at which point the battery was considered fully charged. The battery was then left to rest for 2 h;

(2) The UDDS current profile data were imported into the battery tester to control the battery to charge and discharge according to the UDDS current profile;

(3) The UDDS current profile was cycled until the cell voltage reached the discharge cutoff voltage of 2.5 V, and the current-voltage curves of the test are shown in Figure 2.

2.3. Supplementary Experimental Parameters

To ensure reproducibility, the battery tests were conducted using the UPC-5V6A-8C battery testing system (YouNeng Technology, Lishui, China). The system specifications are as follows: current accuracy $\pm 0.05\%$, current resolution $0.1$ mA, voltage accuracy $\pm 0.05\%$, voltage resolution $0.1$ mV, and data sampling period 100 ms.

The experimental cell was a Samsung INR18650-30Q lithium nickel manganese cobalt oxide (NMC) battery with a nominal voltage of $3.6$ V, a maximum voltage of $4.2$ V, a cutoff voltage of $2.5$ V, and a nominal capacity of 3 Ah. For the pulse discharge procedure, each discharge step was carried out at 1 C for 3 min, followed by a 2 h rest period until the terminal voltage reached 2.5 V. For dynamic condition validation, three standard driving cycles were selected, namely UDDS, NEDC, and HWFET. The current profiles were directly imported into the tester to simulate real driving loads.

2.4. Establishment of the Fractional-Order Model

The second-order RC circuit model is widely employed as an equivalent representation of lithium-ion batteries. Nevertheless, during charge and discharge processes, the diffusion of lithium ions within the electrolyte exhibits fractional-order dynamics, which cannot be fully captured by integer-order models. Based on the consensus that high-precision battery models lead to high-accuracy state estimation, this paper selects the fractional-order second-order RC equivalent circuit model as the research object. As shown in the figure below, UT represents the terminal voltage of the battery, I denotes the current, and Uoc is the open-circuit voltage, which exhibits a nonlinear relationship with the state of charge (SOC). R0 is the ohmic resistance, representing the external characteristic that describes the rapid change in terminal voltage under sudden current. R1 and R2 are the polarization resistances, while CPE1 and CPE2 are the fractional-order capacitors. U1 and U2 represent the polarization voltages, describing concentration polarization and electrochemical polarization, respectively.

Based on the fractional-order second-order RC model in Figure 3, the state observation equation is established as follows:

State Equation:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^m{U}_1}{d{t}^m}}=-{\displaystyle \frac{1}{R_1{C}_1}}{U}_1+{\displaystyle \frac{1}{C_1}}I\hfill \\ {\displaystyle \frac{d^n{U}_1}{d{t}^n}}=-{\displaystyle \frac{1}{R_2{C}_2}}{U}_2+{\displaystyle \frac{1}{C_2}}I\hfill \\ S\dot{O}C=-{\displaystyle \frac{1}{Q_0}}I\hfill \end{array}\right.$$

(1)

Observation Equation:

$$U_T=U_{OC}(SOC)-R_{0}I-U_1-U_2$$

(2)

Here, m and n represent the orders of the fractional-order capacitors and Q0 is the current maximum available capacity of the battery pack.

Based on the G-L definition, the discrete form of the state equation after discretizing Equation (1) is as follows:

$$x_{k+1}=A{x}_k+B{I}_k-\sum _{j=1}^{k+1}{K}_j{x}_{k+1-j}$$

(3)

where $A=\left[\begin{array}{ccc}-{\displaystyle \frac{T^m}{{\tau }_1}}& 0& 0\\ 0& -{\displaystyle \frac{T^n}{{\tau }_2}}& 0\\ 0& 0& 1\end{array}\right]$, ${\tau }_1=R_1{C}_1$, ${\tau }_2=R_2{C}_2$, $B=\left[\begin{array}{c}{\displaystyle \frac{T^m}{C_1}}\\ {\displaystyle \frac{T^n}{C_2}}\\ -{\displaystyle \frac{T}{Q_0}}\end{array}\right]$, $K_j=\left[\begin{array}{ccc}{{\omega }_j}^m& 0& 0\\ 0& {{\omega }_j}^n& 0\\ 0& 0& 0\end{array}\right]$

T denotes the sampling interval, ${{\omega }_0}^m=1$, ${{\omega }_j}^m={(-1)}^j\left(\begin{array}{c}m\\ j\end{array}\right)$.

2.5. Offline Parameter Identification and Model Validation of Fractional-Order Model

The whale optimization algorithm (WOA) is a global optimization algorithm derived from observing the hunting behavior of whales. Meta-heuristic technology is considered a universal method for solving global optimization problems, with its core being to obtain optimal solutions by simulating human and natural intelligence. It has significant advantages in computational efficiency and accuracy and is currently the most widely used method. As illustrated in Figure 4, it achieves the optimization process through three main strategies, namely encircling prey, bubble net attacking, and searching for prey. During the iterative process, the positions of the whales represent the set of possible solutions to the problem. The fitness function is used to convert the positions of the whales into fitness values, and the optimal solution of the current iteration is computed. This solution is then used to update the positions of the whales for the next iteration. Through several iterations, the optimal solution of the function can be determined.

Based on the state observation equations of the fractional-order second-order RC model established by Equations (2) and (3), the variance of the terminal voltage error is used as the fitness function. The whale optimization algorithm is applied to identify the parameters of the fractional-order model, with the specific results presented in

Table 3. Parameters of the integer-order and fractional-order models.

Battery Model	${\mathit{R}}_{\mathbf{0}}/\mathsf{\Omega }$	${\mathit{R}}_{\mathbf{1}}/\mathsf{\Omega }$	${\mathit{C}}_{\mathbf{1}}/\mathit{F}$	${\mathit{R}}_{\mathbf{2}}/\mathsf{\Omega }$	${\mathit{C}}_{\mathbf{2}}/\mathit{F}$	m	n
Integer-Order Model	0.037	0.019	2334	0.035	50135	/	/
Fractional-Order Model	0.037	0.021	1105	0.085	24835	0.9674	0.9554

.

In order to compare the accuracy of the fractional-order model, this paper also uses the whale optimization algorithm to identify the parameters of the integer-order model for comparison. As illustrated in Figure 5, pulse discharge data are used to validate the errors of both the integer-order and fractional-order models.

As shown in

Table 4. Error comparison between the integer-order model and the fractional-order model.

Battery Model	Average Terminal Voltage Error (V)	Maximum Terminal Voltage Error (V)
Integer-Order Model	0.0051	0.0551
Fractional-Order Model	0.0047	0.0363

, it can be observed that by comparing the estimated terminal voltage with the actual terminal voltage, the average error of the integer-order model is 0.0051 V and the maximum error is 0.0551 V. The average error of the fractional-order model is 0.0047 V and the maximum error is 0.0363 V. The error of the fractional-order model is smaller than that of the integer-order model, indicating higher model accuracy, which makes it more suitable for subsequent state estimation.

2.6. Supplementary Details of Parameter Identification

The whale optimization algorithm (WOA) was applied for fractional-order model parameter identification. The terminal voltage error variance was used as the fitness function to evaluate the candidate parameter sets. The algorithm iteratively updated the solution space, with the maximum number of iterations set to 500 and the convergence threshold set to ${10}^{-5}$ for the fitness value.

The parameter vector to be optimized included

$$\theta =\{R_0,R_1,C_1,R_2,C_2,m,n\}.$$

The optimization process terminated when either the maximum iteration count was reached or the tolerance threshold was satisfied, ensuring both accuracy and computational efficiency.

3. Collaborative Estimation of SOC and Model Parameters Based on Fractional-Order Model

3.1. Framework Overview of Collaborative Estimation Algorithm

The overall SOC/SOH collaborative estimation procedure is summarized as follows:

• Initialization: Define the state vector including SOC, polarization voltages, and model parameters and set the initial error covariance matrices for state and parameter estimation.
• Improved UKF Estimation: Apply the unscented Kalman filter (UKF) with singular value decomposition (SVD) to generate sigma points, improving numerical stability.
• Strong Tracking Strategy: Introduce an adaptive fading factor when innovation values are large, allowing the SOC estimate to rapidly converge when the initial SOC is inaccurate.
• Online Parameter Update: Use the extended Kalman filter (EKF) to update model parameters in real time, with the Jacobian observation derived from the sensitivity of terminal voltage to parameter variations.
• Multi-Time-Scale Collaboration: Implement different update frequencies for SOC and model parameters. SOC is updated at every sampling interval (100 ms), while parameter updates are performed once every 60 SOC updates, reflecting their slower dynamics.
• Iteration: Repeat the above steps throughout the charge/discharge process until termination conditions (voltage $\le 2.5$ V or SOC $\le 0\%$) are met.

This design ensures that the proposed algorithm can achieve both high-accuracy SOC estimation and robust SOH tracking under dynamic operating conditions.

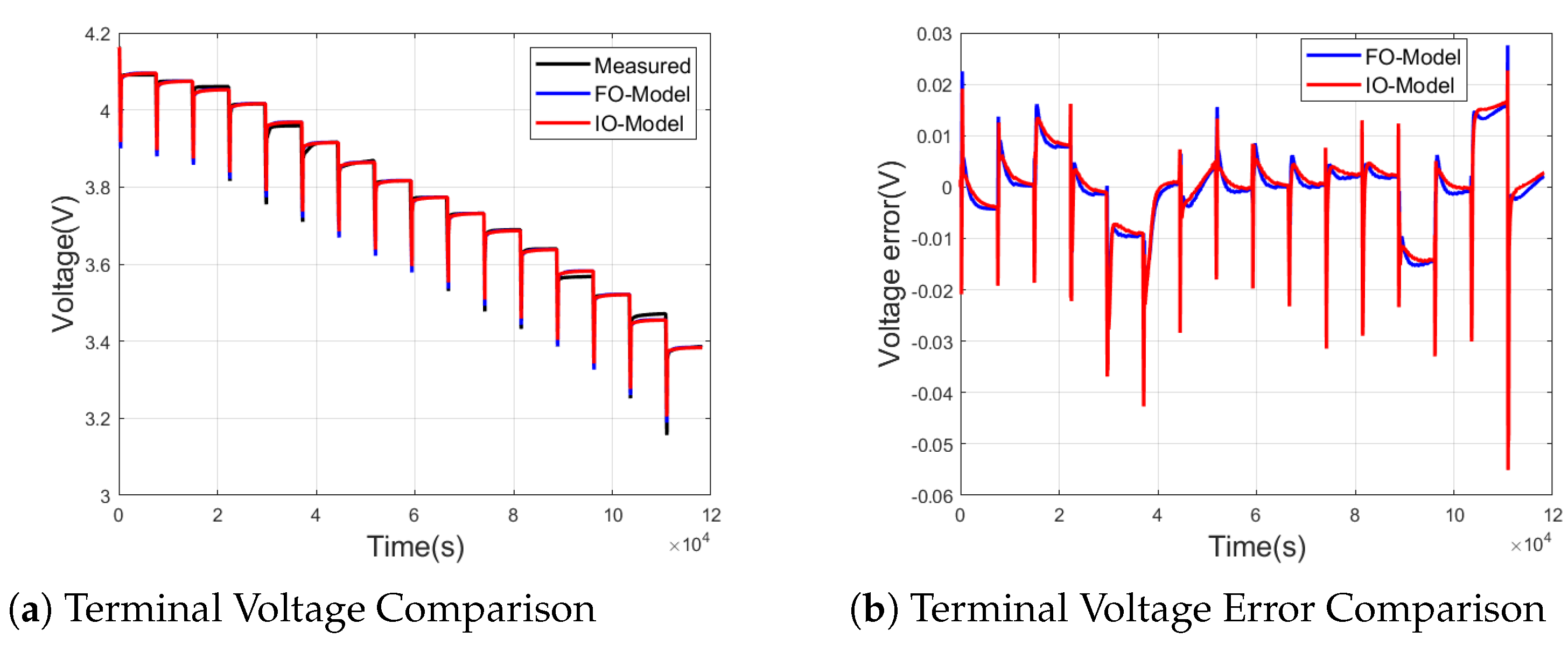
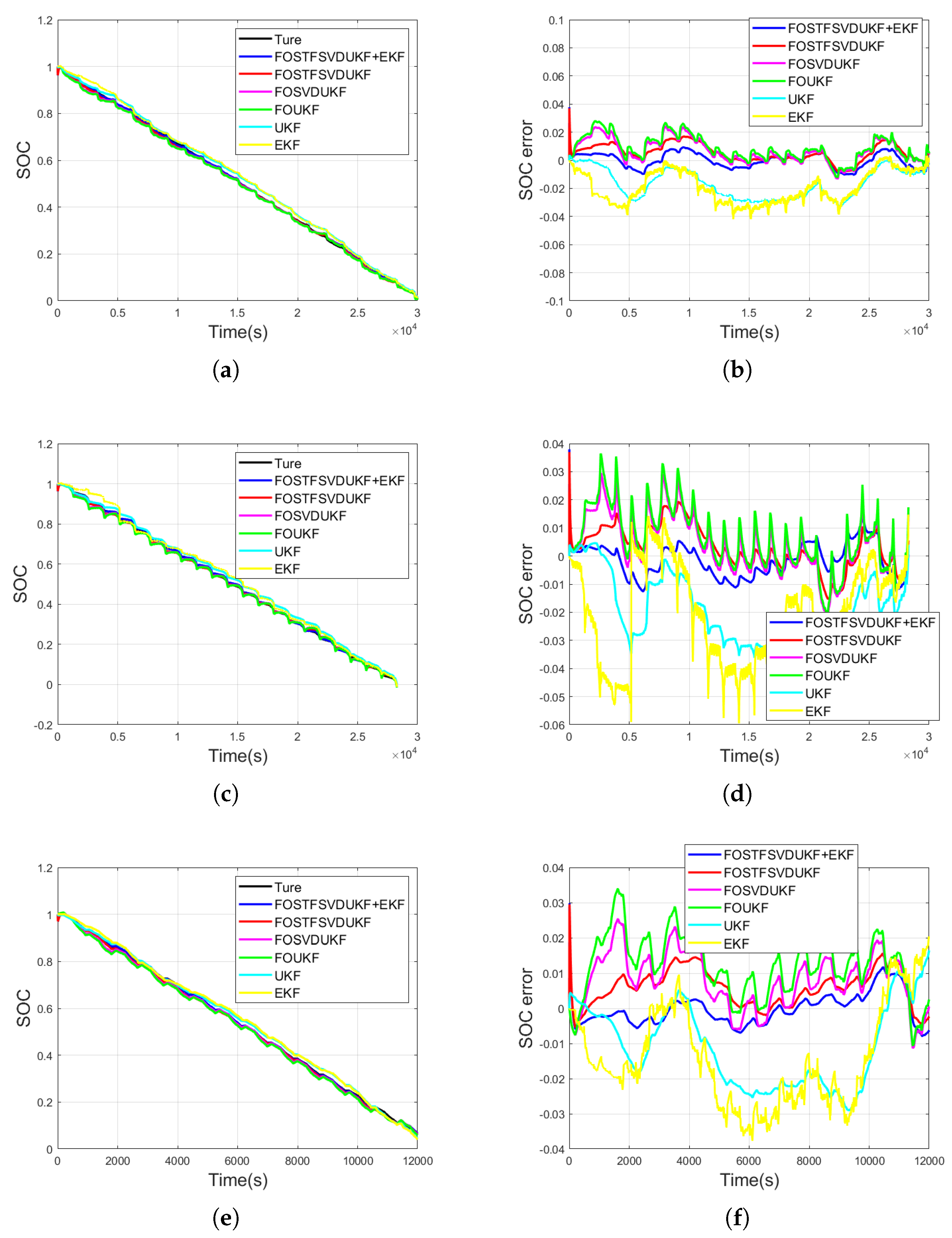
3.2. Improved UKF Algorithm

The extended Kalman filter (EKF) is a commonly used method for SOC estimation. Based on the established state observation equations, the EKF uses terminal voltage measurements for correction to achieve optimal SOC estimation. Lithium-ion batteries are nonlinear systems, and during the SOC estimation process, the EKF linearizes the system using the Jacobian matrix, which increases SOC estimation errors. The UKF (unscented Kalman filter) algorithm generates a set of sampling points using the unscented transform to capture the distribution characteristics of nonlinear systems, thereby improving the accuracy loss caused by the linearization process in the EKF. When calculating the sigma sampling points, the UKF algorithm uses Cholesky decomposition on the covariance matrix. However, when the system is disturbed by measurement noise, which leads to abnormal observations, the covariance matrix may lose its positive definiteness, potentially causing the UKF algorithm to halt or terminate. To overcome this issue, singular value decomposition (SVD) is used to replace the Cholesky decomposition in the traditional UKF algorithm. The process of the improved UKF algorithm is shown below.

(1) Set the initial values of the state vector $x_0$, the initial posterior state estimation error covariance $P_0$, the system noise covariance matrix Q, and the measurement noise covariance R.

(2) At any arbitrary time k, perform singular value decomposition (SVD) on the posterior state estimation error covariance matrix $P_k$.

$$P_k=V_k{D}_k^2{V_k}^T$$

(4)

(3) Update the sigma sampling points.

$$\left\{\begin{array}{c}{x}_k^0={\widehat{x}}_k\hfill \\ x_k^i=x_k+\sqrt{(L+\lambda )}{V}_k{D}_k,i=1,2\dots L\hfill \\ x_k^i=x_k-\sqrt{(L+\lambda )}{V}_k{D}_k,i=L+1,L+2,\dots 2L\hfill \end{array}\right.$$

(5)

Here, L represents the dimension of the state vector, and the other weight values are calculated as follows:

$$\left\{\begin{array}{c}\lambda ={\alpha }^2(L+k_i)-L\hfill \\ W_m^0={\displaystyle \frac{\lambda }{L+\lambda }},W_m^i={\displaystyle \frac{1}{2(L+\lambda )}},i=1,2\dots 2L\hfill \\ W_c^0={\displaystyle \frac{\lambda }{L+\lambda }}+1-{\alpha }^2+\beta ,W_c^i={\displaystyle \frac{1}{2(L+\lambda )}},i=1,2\dots 2L\hfill \end{array}\right.$$

(6)

Here, take $\alpha =0.01$, $k_i=0$, $\beta =2$.

(4) Update the prior state vector ${\overline{x}}_{k+1}$ and the system variance prediction $P_{xx}$.

$$\begin{array}{c}{\overline{x}}_{k+1}=\sum _{i=0}^{2L}{W}_m^i{x}_k^i-\sum _{j=1}^{k+1}{K}_j{\widehat{x}}_{k+1-j}\end{array}$$

(7)

$$\begin{array}{c}{P}_{xx}=\sum _{i=0}^{2L}(W_c^i(x_k^i-{\overline{x}}_{k+1}){(x_k^i-{\overline{x}}_{k+1})}^T)+Q\end{array}$$

(8)

(5) Update the observation value ${\widehat{y}}_{k+1}$ and the predicted observation variance $P_{yy}$.

$$\begin{array}{c}{\widehat{y}}_{k+1}=\sum _{i=0}^{2L}{W}_m^i{y}_k^i\end{array}$$

(9)

$$\begin{array}{c}{P}_{yy}=\sum _{i=0}^{2L}(W_c^i(y_k^i-{\widehat{y}}_{k+1}){(y_k^i-{\widehat{y}}_{k+1})}^T)+R\end{array}$$

(10)

Here, $R_k$ denotes the observation noise covariance matrix.

(6) Update the covariance $P_{xy}$ and the Kalman gain $K_{k+1}$.

$$\begin{array}{c}{P}_{xy}=\sum _{i=0}^{2L}{W}_c^i(x_k^i-{\overline{x}}_{k+1}){(y_k^i-{\widehat{y}}_{k+1})}^T\end{array}$$

(11)

$$\begin{array}{c}{K}_{k+1}={\displaystyle \frac{P_{xy}}{P_{yy}}}\end{array}$$

(12)

(7) Update the posterior state vector ${\widehat{x}}_{k+1}$ and the posterior state estimation error covariance $P_{k+1}$.

$$\begin{array}{c}{\widehat{x}}_{k+1}={\overline{x}}_{k+1}+K_{k+1}(y_{k+1}-{\widehat{y}}_{k+1})\end{array}$$

(13)

$$\begin{array}{c}{P}_{k+1}=P_{xx}-K_{k+1}{P_{xy}}^T\end{array}$$

(14)

3.3. Strong Tracking Algorithm

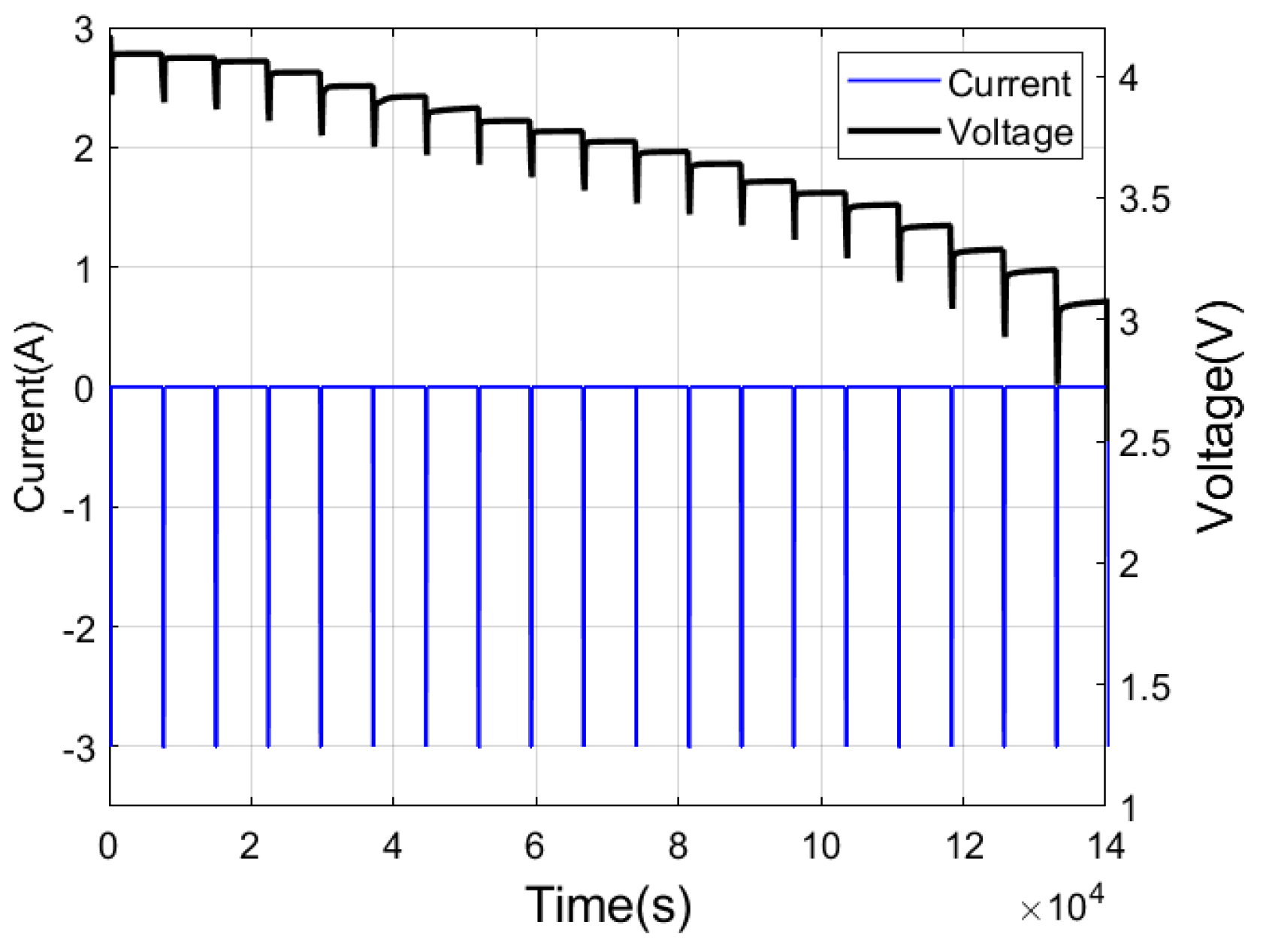
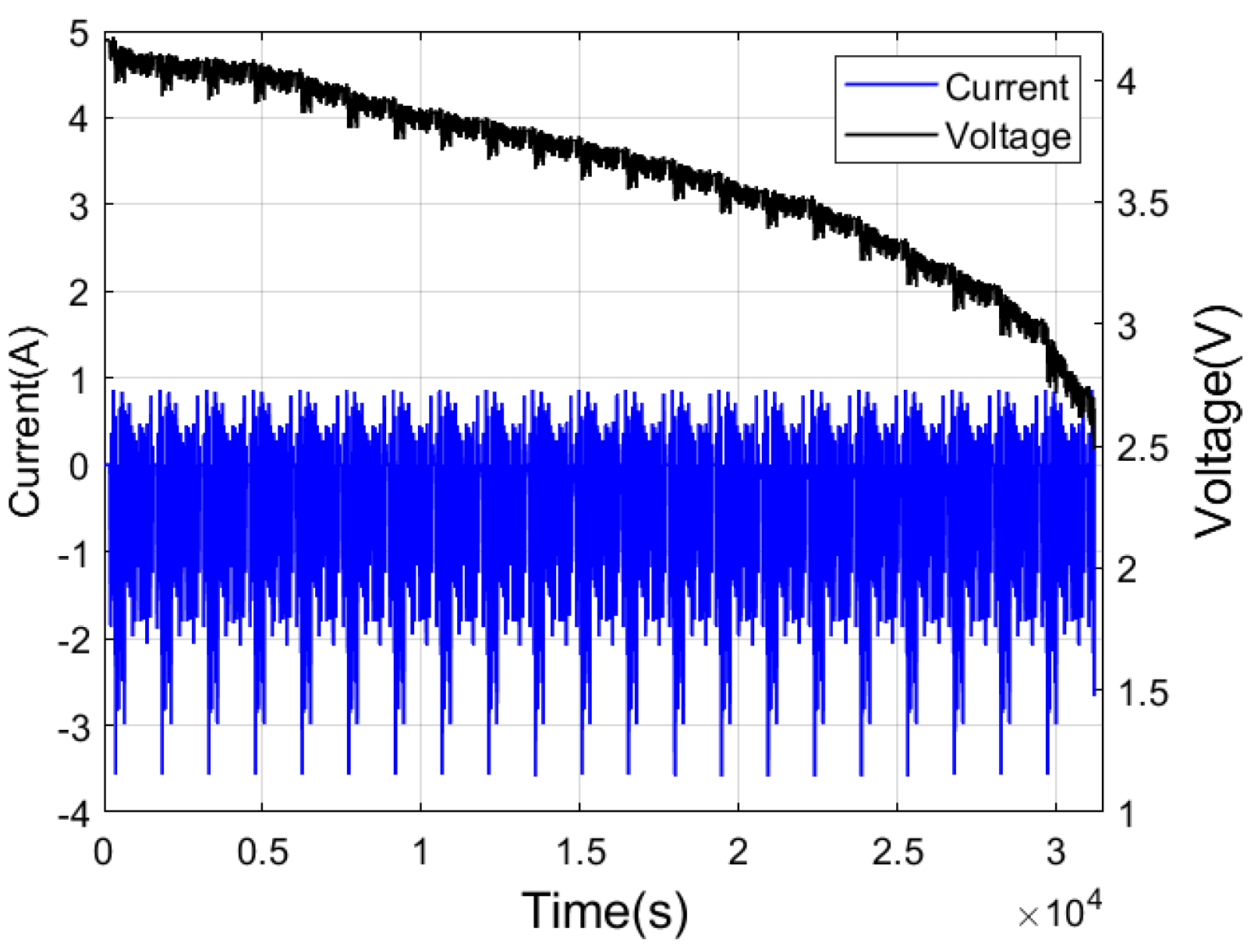
During the operation of lithium-ion batteries, the charge and discharge currents are highly variable, the operating temperature range is wide, and the usage conditions are complex. When the system is subjected to external disturbances that lead to increased SOC estimation errors, the algorithm needs to have the capability of rapidly tracking and converging the SOC estimate. In other words, when the initial SOC is inaccurate, the algorithm should be able to make the SOC estimate converge to the true state value within a small number of iterations so as to provide more accurate battery state information. To achieve this objective, this paper introduces the strong tracking algorithm to enable fast convergence under inaccurate initial SOC conditions. During the initial operating stage, a large SOC error results in increased innovation. The strong tracking algorithm adjusts the covariance and Kalman gain based on the innovation magnitude, enhancing the sensitivity of the algorithm to terminal voltage errors. As a result, the SOC estimate can rapidly track the true SOC value. The modified covariance matrix is expressed as follows:

$$P_{xx}={\gamma }_k\sum _{i=0}^{2L}(W_c^i(x_k^i-{\overline{x}}_{k+1}){(x_k^i-{\overline{x}}_{k+1})}^T)+Q$$

(15)

Here, ${\gamma }_k$ denotes the strong tracking coefficient. When the innovation value is large, it indicates that the algorithm has not yet completed the convergence process and a fading factor needs to be introduced so that the strong tracking coefficient becomes ${\gamma }_k>1$. When the innovation value is small, it indicates that the algorithm has entered a converged state and the fading factor is no longer required, allowing the algorithm to proceed in the conventional manner. The expression of the strong tracking coefficient ${\gamma }_k$ is as follows:

$$\begin{array}{c}{\gamma }_k=\left\{\begin{array}{cc}& {\gamma }_{0k},\gamma >1\hfill \\ & 1,\gamma \le 1\hfill \end{array}\right.\end{array}$$

(16)

$$\begin{array}{c}{\gamma }_{0k}={\displaystyle \frac{Tr({\overline{P}}_{yy})}{Tr(P_{yy})}}\end{array}$$

(17)

$Tr({\overline{P}}_{yy})$ denotes the trace of matrix ${\overline{P}}_{yy}$ and ${\overline{P}}_{yy}$ represents the variance of the true innovation. The innovation window size is M.

$${\overline{P}}_{yy}={\displaystyle \frac{1}{M}}\sum _{j=k+2-M}^{k+1}{e}_j{e_j}^T,e_j=y_j-{\widehat{y}}_j$$

(18)

3.4. SOC and Parameter Collaborative Estimation Algorithm

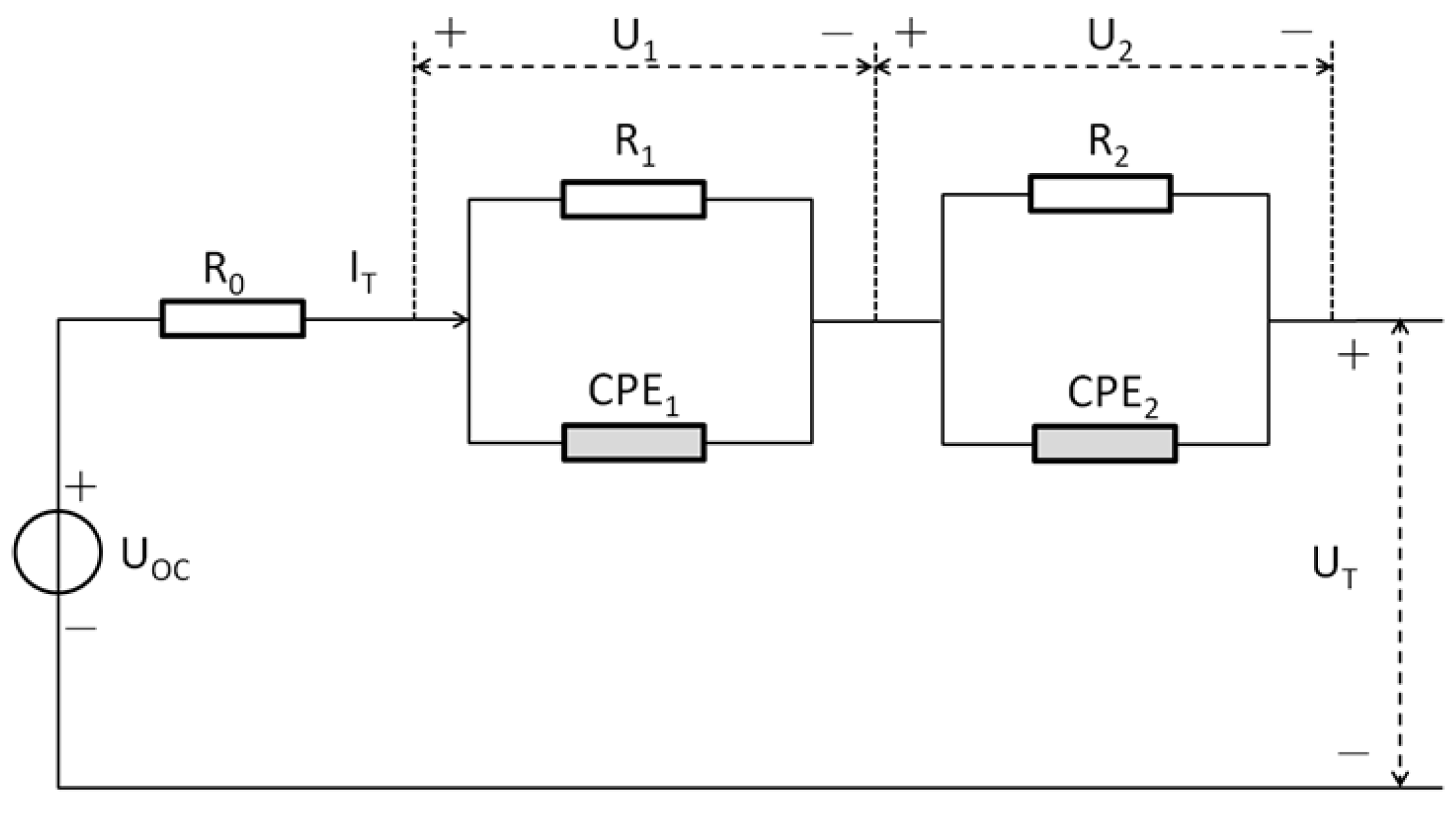
Accurate SOC estimation relies on a high-precision battery model, which includes parameters such as the battery’s ohmic resistance, polarization resistance, polarization capacitance, fractional-order parameters, and the current maximum available capacity. Offline parameter identification is based on existing data, where optimization algorithms are used to obtain the equivalent circuit model parameters for the battery’s current state. However, the parameters of the equivalent circuit model change with variations in environmental temperature, battery aging, SOC, and charge/discharge current rates. When the battery’s state undergoes significant changes, the previously established model parameters may result in larger errors compared to the current state, which leads to increased SOC estimation errors and distorted state estimates.

To address the issue of SOC estimation accuracy under full operating conditions and throughout the battery’s entire service life, it is necessary to track the changes in battery model parameters in real time to ensure model accuracy and enable precise SOC estimation. Based on this, this paper develops an SOC and parameter collaborative estimation algorithm, in which the EKF (extended Kalman filter) algorithm is employed to update the model parameters in real time and track their variations during the battery charge and discharge processes. The procedure of EKF-based parameter estimation is as follows:

(1) Set the initial values of the parameter vector ${\theta }_0$, the initial posterior parameter estimation error covariance $P_0^{\theta }$, the system noise covariance matrix $Q^{\theta }$, and the measurement noise covariance $R^{\theta }$. Here, $\theta =\left[R_0,R_1,C_1,R_2,C_2,m,n,Q_n\right]$.

(2) Update the prior parameter vector ${\overline{\theta }}_{l+1}$.

$${\overline{\theta }}_{l+1}={\widehat{\theta }}_l$$

(19)

(3) Update the prior parameter estimation error covariance ${\overline{P}}_{l+1}^{\theta }$.

$${\overline{P}}_{l+1}^{\theta }=P_l^{\theta }+Q^{\theta }$$

(20)

(4) Compute the Kalman gain $K_{l+1}^{\theta }$ for the parameter vector.

$$K_{l+1}^{\theta }={\overline{P}}_{l+1}^{\theta }{C_{l+1}^{\theta }}^T{(C_{l+1}^{\theta }{\overline{P}}_{l+1}^{\theta }{C_{l+1}^{\theta }}^T+R^{\theta })}^{-1}$$

(21)

Here, $C_{l+1}^{\theta }$ denotes the derivative of the terminal voltage with respect to the parameter vector at time $l+1$.

(5) Update the posterior parameter vector ${\widehat{\theta }}_{l+1}$.

$${\widehat{\theta }}_{l+1}={\overline{\theta }}_{l+1}+K_{l+1}^{\theta }(y_{l+1}-{\widehat{y}}_{l+1})$$

(22)

(6) Update the posterior parameter estimation error covariance.

$$P_{l+1}^{\theta }=(E-K_{l+1}^{\theta }{C}_{l+1}^{\theta }){\overline{P}}_{l+1}^{\theta }$$

(23)

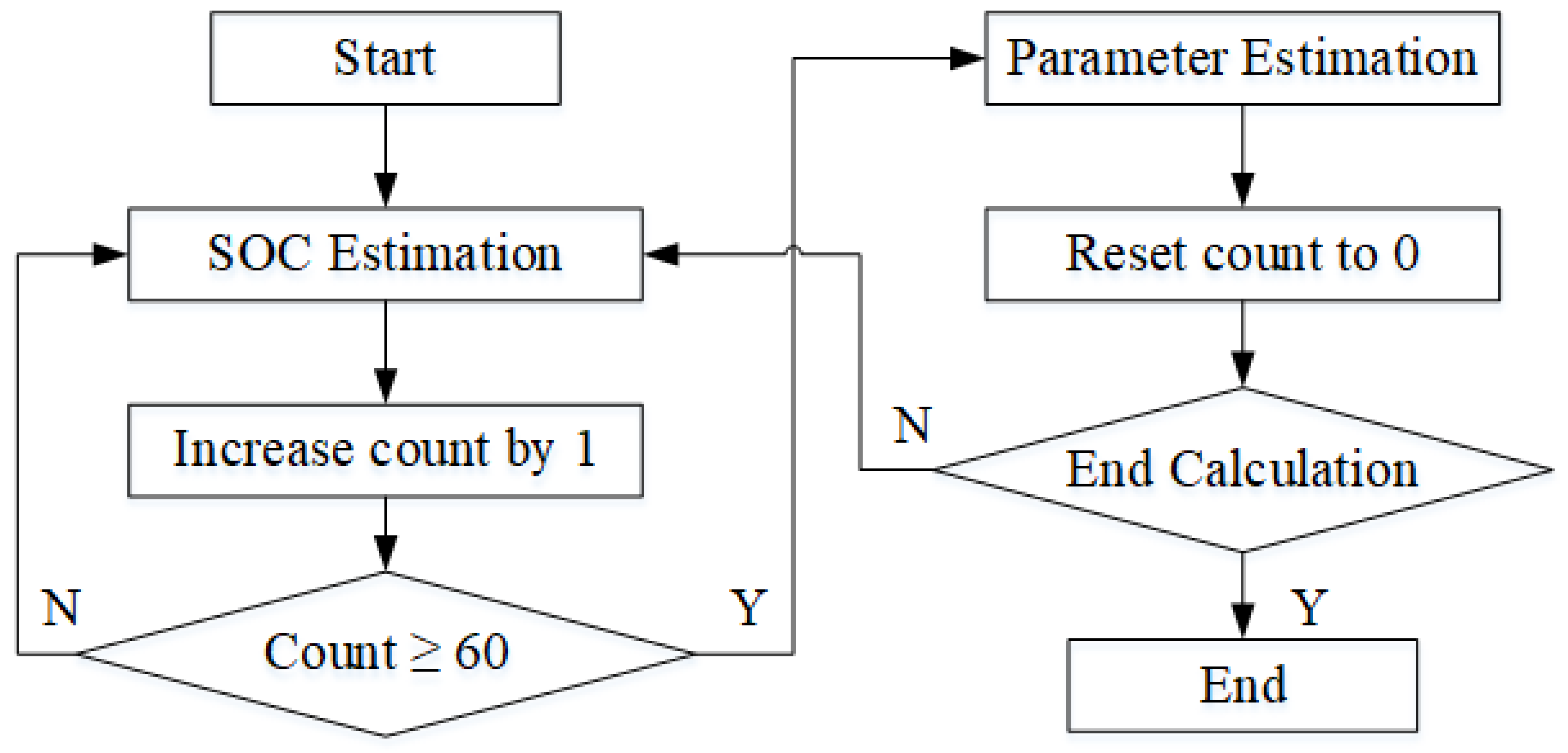
For time-varying battery systems, during the charge and discharge processes, the SOC is highly sensitive to temporal variations, whereas the model parameters are less sensitive to changes over time. In other words, SOC is considered a fast time-varying parameter, while the model parameters are regarded as slow time-varying parameters. As illustrated in Figure 6, based on the time-varying characteristics of SOC and the model parameters, different estimation frequencies need to be set for SOC estimation and parameter estimation. Specifically, the estimation frequency for SOC should be higher than that for the parameters, thereby establishing a multi-time-scale collaborative estimation algorithm. For the slowly varying model parameters, estimation is performed on a macro time scale. In contrast, for the rapidly varying SOC, estimation is performed on a micro time scale. That is, within a function operating cycle of TTT, for every 60 state estimations, the algorithm performs one parameter estimation.

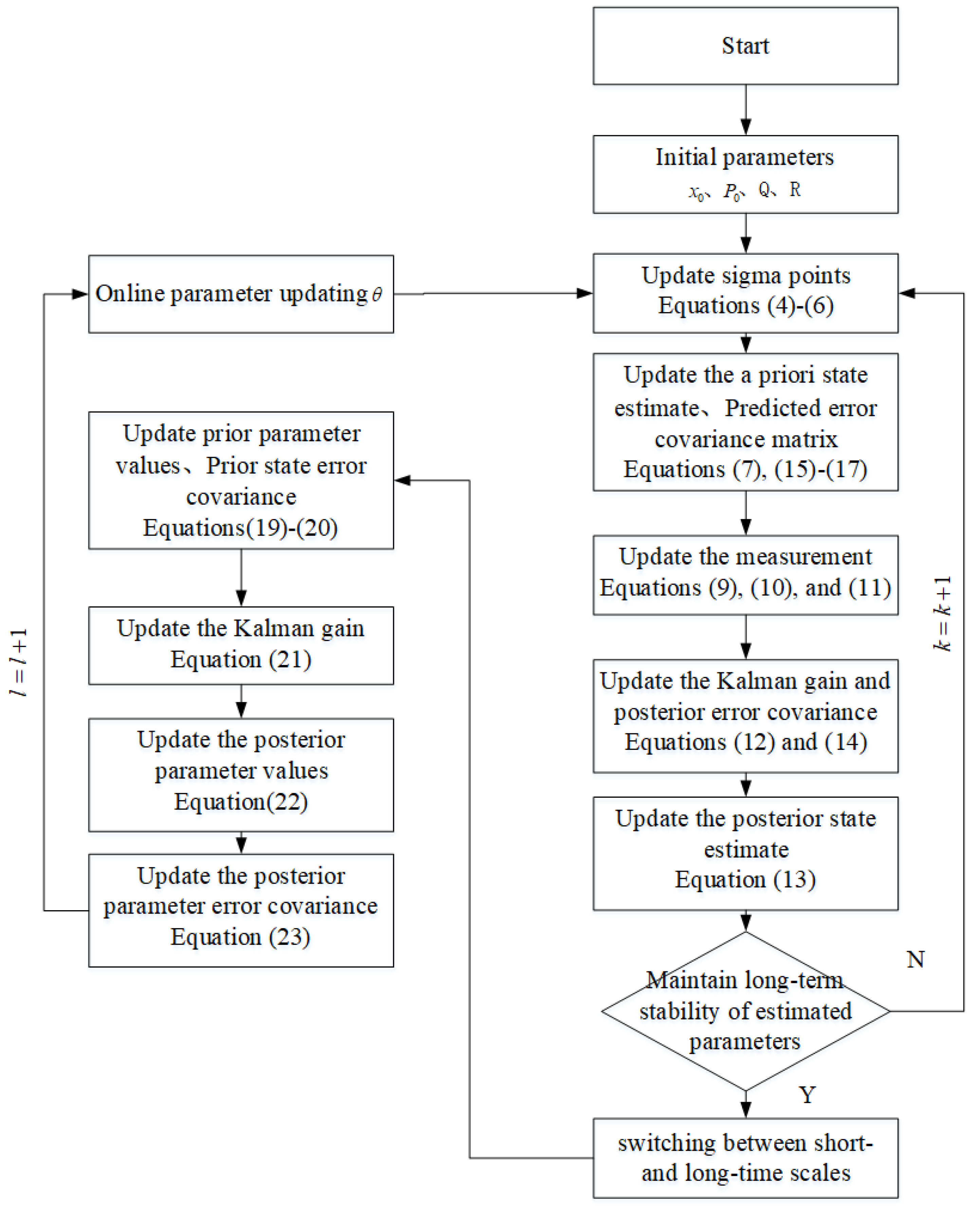
The procedure of the SOC and model parameter collaborative estimation algorithm based on the fractional-order model is as follows:

The procedure of the SOC and model parameter collaborative estimation algorithm based on the fractional-order model is visually summarized in Figure 7 and can be described as follows:

4. Simulation Validation

4.1. Accuracy Validation of the Collaborative Estimation Algorithm

To verify the effectiveness of the proposed collaborative estimation algorithm, this study employs the UDDS, NEDC, and HWFET driving cycles to validate the accuracy of the state estimation. In addition, a series of comparison algorithms are selected to comprehensively evaluate the estimation accuracy of the target algorithm, including the fractional-order strong tracking SVD-UKF (FOSTFSVDUKF), the fractional-order SVD-UKF (FOSVDUKF), the fractional-order UKF (FOUKF), the conventional UKF, and the EKF. In the two selected dynamic operating conditions, the battery is initially fully charged. Considering that the single discharge duration is relatively short and the cumulative current error can be almost neglected, the true SOC values under these conditions can be calculated by ampere-hour integration, providing a reference for assessing the SOC estimation errors of different algorithms. The SOC initial values for each algorithm are set to be accurate. The SOC estimation results under the two dynamic conditions are compared, as shown in the Figure 8.

As shown in Figure 9, the collaborative estimation algorithm achieves the highest SOC estimation accuracy, with the mean SOC error around 0.5% and the maximum SOC error not exceeding 1.4%. Additionally, the SOH estimation values produced by the collaborative estimation algorithm fluctuate around the true value, with an SOH estimation error within 0.25%. The statistics of the mean SOC estimation error and the maximum SOC error for the different algorithms are summarized in

Table 5. Comparative analysis of average and maximum SOC estimation errors across different algorithms.

Operating Profile	Algorithm	Mean SOC Error	Maximum SOC Error
UDDS	FOSTFSVDUKF + EKF	0.45%	1.03%
	FOSTFSVDUKF	0.63%	1.69%
	FOSVDUKF	0.80%	2.81%
	FOUKF	0.96%	3.31%
	UKF	1.61%	3.45%
	EKF	1.77%	4.41%
NEDC	FOSTFSVDUKF + EKF	0.51%	1.39%
	FOSTFSVDUKF	0.65%	1.92%
	FOSVDUKF	0.85%	2.98%
	FOUKF	0.96%	3.69%
	UKF	2.28%	3.94%
	EKF	1.98%	5.95%
HWFET	FOSTFSVDUKF + EKF	0.35%	1.17%
	FOSTFSVDUKF	0.66%	1.55%
	FOSVDUKF	0.89%	2.31%
	FOUKF	1.24%	2.88%
	UKF	1.84%	2.91%
	EKF	2.17%	3.77%

.

As shown in the results of Table 5, the collaborative estimation algorithm achieves the highest SOC estimation accuracy. Under the UDDS operating condition, the mean SOC error is 0.45%, and the maximum SOC error is 1.03%. Under the NEDC operating condition, the mean SOC error is 0.51% and the maximum SOC error is 1.39%. Compared with the FOSTFSVDUKF algorithm, incorporating model parameter identification reduces the mean SOC estimation error by approximately 0.16% and decreases the maximum SOC estimation error by about 0.58%.

4.2. Robustness Validation of the Collaborative Estimation Algorithm

4.2.1. Robustness Validation of SOC Estimation

During the operation of pure electric vehicles, the charge and discharge conditions are complex and intermingled. Additionally, current sensor measurements contain sampling errors, and full-charge calibration is rarely triggered, which makes it impossible for the BMS to accurately acquire the initial SOC after startup. To validate the robustness of the collaborative estimation algorithm under inaccurate initial SOC conditions, this study selects initial SOC values of 40%, 60%, and 80% for comparison.

As shown in Figure 10, the larger the initial SOC error, the longer it takes to converge to the vicinity of the true value. The collaborative estimation algorithm is able to converge to the true SOC within approximately 300 seconds. Under different levels of initial SOC error, the algorithm consistently converges rapidly to the true value. After convergence, the estimation errors of the collaborative estimation algorithm are nearly identical regardless of the initial SOC. Under different initial SOC conditions, the differences in the mean SOC error and maximum SOC error of the collaborative estimation algorithm are minimal, indicating that the algorithm demonstrates strong robustness in SOC estimation.

To comprehensively evaluate the performance of the proposed cooperative estimation algorithm under initial SOC uncertainty, this study conducted systematic validation under three typical driving cycle conditions: UDDS, NEDC, and HWFET.

Table 6. Error comparative analysis of cooperative estimation algorithms under initial SOC uncertainty.

Operating Profile	Initial SOC of the Algorithm	Mean SOC Error	Maximum SOC Error
UDDS	40%	0.50%	1.55%
	60%	0.46%	1.03%
	80%	0.45%	1.03%
NEDC	40%	0.53%	1.39%
	60%	0.52%	1.39%
	80%	0.51%	1.39%
HWFET	40%	0.38%	1.17%
	60%	0.35%	1.17%
	80%	0.33%	1.17%

provides a comprehensive quantitative comparison of the error characteristics of each algorithm, offering essential data support for the subsequent analysis.

4.2.2. Robustness Validation of SOH Estimation

As the battery is used, its current maximum available capacity exhibits an irreversible degradation trend, which reflects the decline of battery life. If the current maximum available capacity deviates from the actual value, the accuracy of the battery model decreases, thereby affecting the accuracy of state estimation. To validate the robustness of the collaborative estimation algorithm under conditions of inaccurate initial SOH, this study selects initial SOH values of 90% and 95% for comparison.

The aforementioned analytical results demonstrate significant differences in the SOH estimation performance of each algorithm under the three testing conditions. The quantitative data provided in

Table 7. Estimation error comparison of cooperative algorithms under initial SOH uncertainties.

Operating Profile	Initial SOH of the Algorithm	Mean SOH Error	Maximum SOH Error
UDDS	90%	0.24%	0.97%
	95%	0.24%	0.93%
NEDC	90%	0.26%	0.75%
	95%	0.31%	1.23%
HWFET	90%	0.33%	1.08%
	95%	0.33%	1.09%

clearly illustrates the specific performance of different algorithms across various error metrics. These comparative results provide important basis for evaluating the robustness and accuracy of the algorithms under initial SOH uncertainty conditions. Particularly under extreme operating conditions, the error distribution characteristics and stability variations among the algorithms indicate directions for further optimization of cooperative estimation algorithms.

As shown in Figure 11 and

Table 8. Comparison of SOC/SOH estimation accuracy between the proposed method and the existing literature.

Method/Reference	Mean SOC Error	Max SOC Error	SOH Error
Proposed method (FOSTFSVDUKF + EKF)	0.45–0.51%	≤1.39%	≤0.25%
BiLSTM framework [1]	≈1.2%	≤3.5%	≤0.8%
AR-ECM + data-driven fusion [2]	≈0.9%	≤2.7%	≤0.6%
Temperature-dependent EKF + DL [4]	0.7–1.0%	≤2.5%	≤0.5%
Dual EKF (DEKF) [11]	0.8–1.1%	≤3.0%	≤0.7%

, the larger the initial SOH error, the longer it takes to converge to the vicinity of the true value. The collaborative estimation algorithm is able to converge to the true SOH within approximately 1600 s. After convergence, the estimation errors of the collaborative estimation algorithm are similar across different initial SOH conditions. Under varying levels of initial SOH error, the algorithm can rapidly converge to the true value, demonstrating strong robustness in SOH estimation.

5. Conclusions

In this study, a cooperative estimation method for the state of charge (SOC) and state of health (SOH) of lithium-ion batteries based on a fractional-order model was proposed. A fractional-order second-order RC equivalent circuit model was established, and the whale optimization algorithm (WOA) was employed for offline parameter identification. On this basis, an improved unscented Kalman filter (UKF) with singular value decomposition (SVD) and a strong tracking algorithm was combined with an extended Kalman filter (EKF) to form a multi-time-scale collaborative estimation framework.

The main advantages of the proposed approach are as follows:

• High SOC estimation accuracy: Across UDDS, NEDC, and HWFET driving cycles, the proposed algorithm achieved mean SOC errors of approximately 0.45–0.51%, with the maximum SOC error remaining below $1.4\%$. This represents a significant improvement compared with conventional UKF and EKF methods.
• High SOH estimation accuracy: The SOH estimation error was maintained within $0.25\%$, with estimation values fluctuating stably around the ground truth across all dynamic operating conditions.
• Robustness under uncertain initial conditions: When the initial SOC (40%, 60%, 80%) or SOH (90%, 95%) was inaccurate, the proposed algorithm rapidly converged to the true values within short time intervals (approximately 300 s for SOC and 1600 s for SOH). This demonstrates strong adaptability in real-world applications where accurate initialization is rarely available.
• Practical applicability: By combining fractional-order modeling with a multi-time-scale estimation strategy, the framework balances model accuracy with computational efficiency, making it well-suited for real-time battery management systems (BMSs).

In summary, the proposed cooperative estimation framework provides an effective solution for accurate and robust SOC/SOH monitoring of lithium-ion batteries. The results highlight its potential for improving the safety, reliability, and performance of battery management systems in electric vehicles and other energy storage applications.