Tire Contact Pressure Distribution and Dynamic Analysis Under Rolling Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Establishment of the Finite Element Model
2.2. Validation of Finite Element Models
3. Results
4. Mechanical Response Under Rolling Conditions
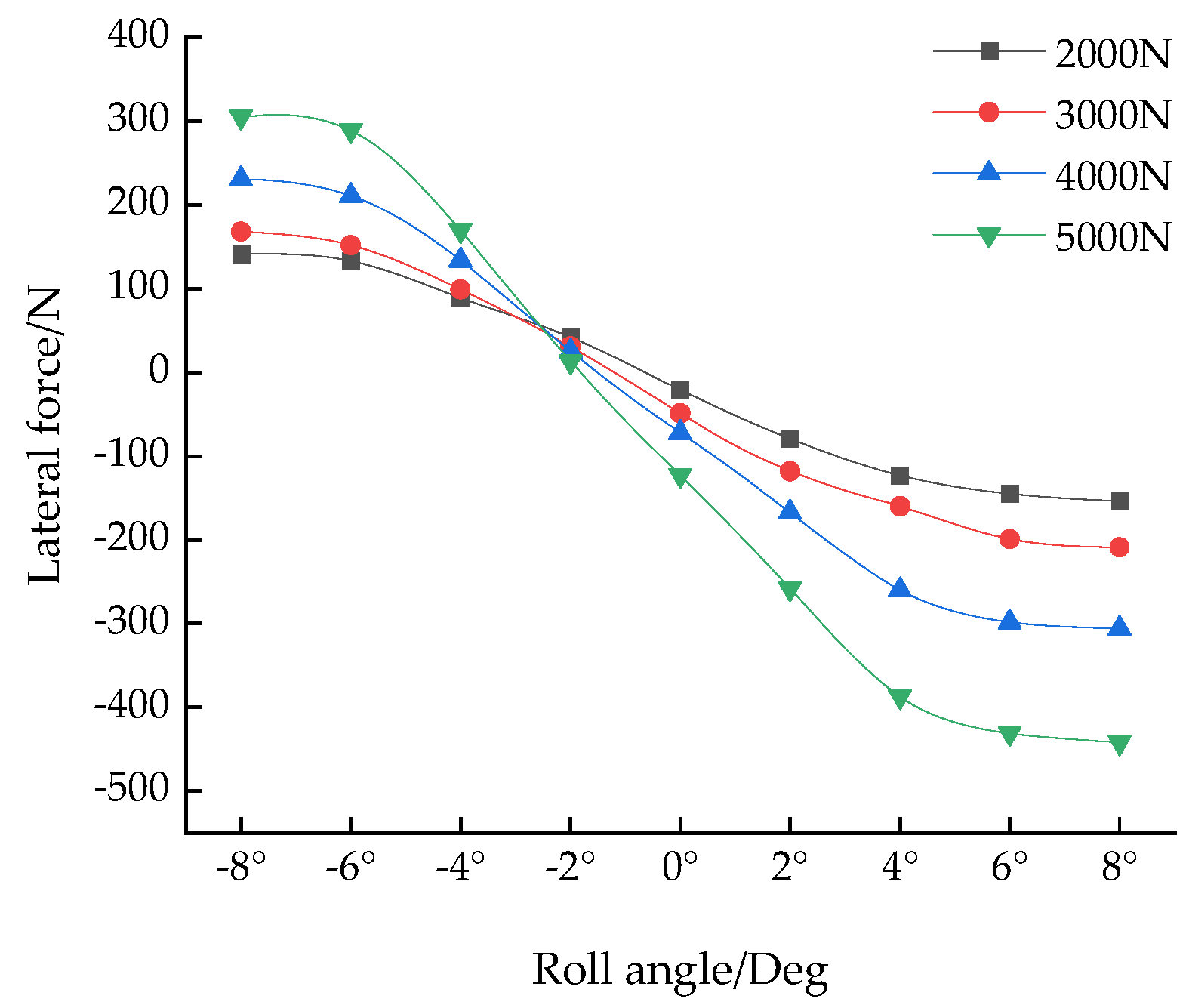
4.1. Lateral Force
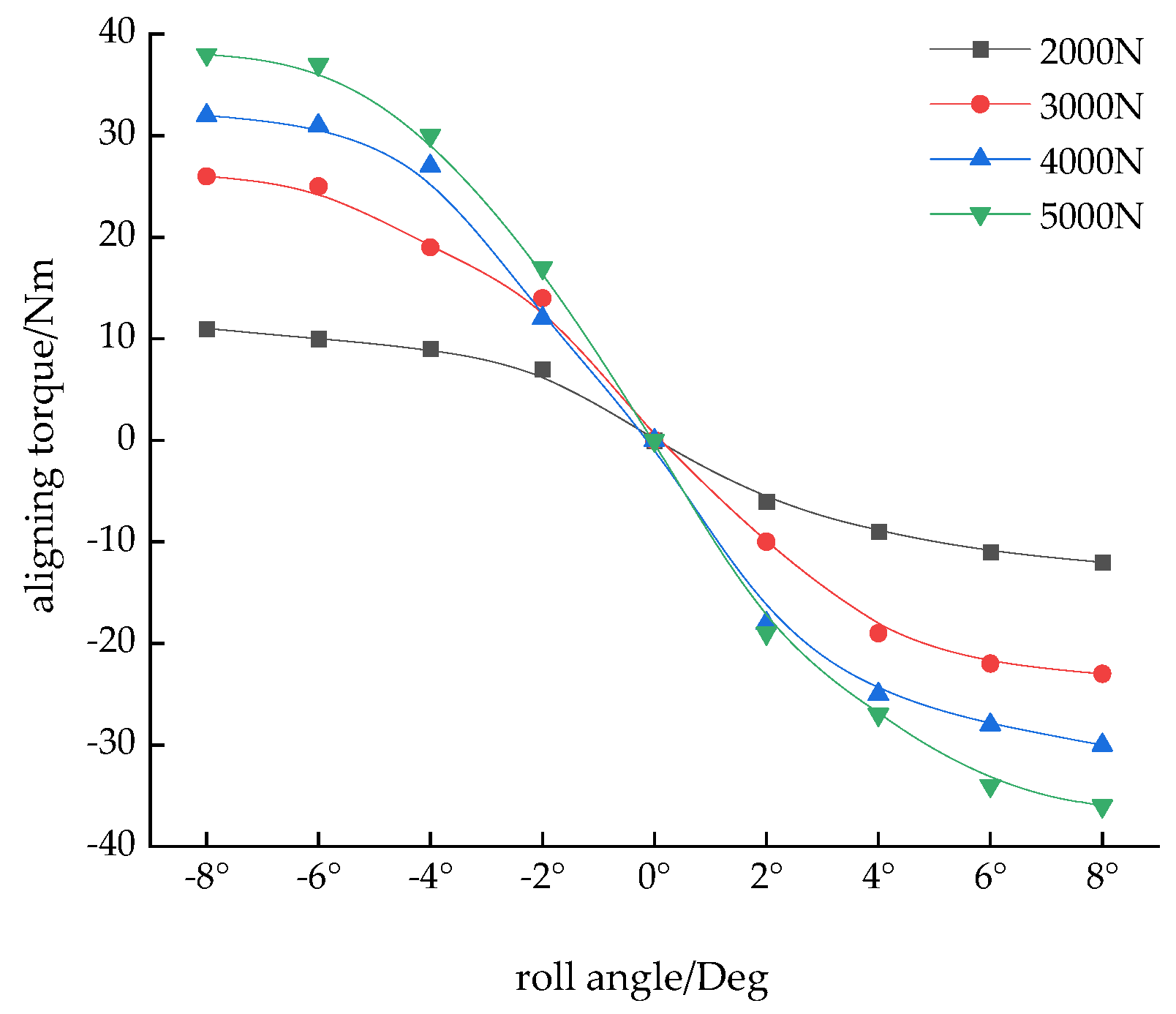
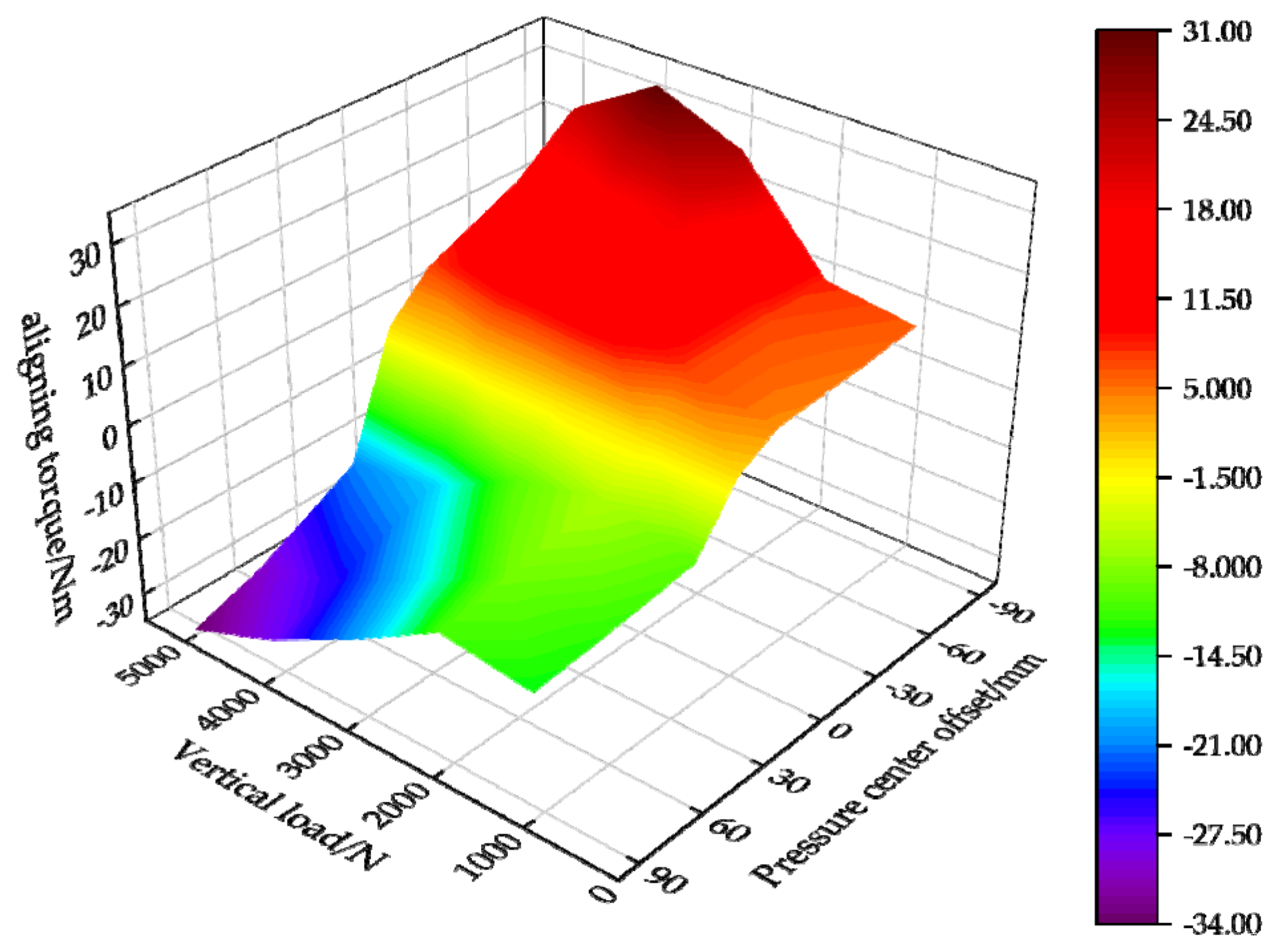
4.2. Aligning Torque
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ricco, M.; Percolla, A.; Rizzo, G.C.; Zanchetta, M.; Tavernini, D.; Dhaens, M.; Geraerts, M.; Vigliani, A.; Tota, A.; Sorniotti, A. On the model-based design of front-to-total anti-roll moment distribution controllers for yaw rate tracking. Veh. Syst. Dyn. 2020, 60, 569–596. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, C.; Gao, Q.; Ma, D.; Liu, S. Study on intelligent tyre force estimation algorithm based on strain analysis. Adv. Mech. Eng. 2024, 16. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, L.; Li, Y.; Sun, P.; Su, G.; Meng, J. Study on the influence of different tire cord structures on tire grounding characteristics. J. Eng. Fibers Fabr. 2022, 17. [Google Scholar] [CrossRef]
- Sun, Y.; Li, B.; Bei, S.Y. Tire force analysis considering the characteristics of stress distribution in grounding area. J. Jiangsu Inst. Technol. 2024, 30, 60–72. [Google Scholar]
- Ricco, M.; Zanchetta, M.; Rizzo, G.C.; Tavernini, D.; Sorniotti, A.; Chatzikomis, C.; Velardocchia, M.; Geraerts, M.; Dhaens, M. On the Design of Yaw Rate Control via Variable Front-to-Total Anti-Roll Moment Distribution. IEEE Trans. Veh. Technol. 2019, 69, 1388–1403. [Google Scholar] [CrossRef]
- Liang, C.; Shan, M.; Wang, G.; Zhu, D.; Chen, X. A method for tire wet grip performance evaluation based on grounding characteristics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 109–117. [Google Scholar] [CrossRef]
- Meng, J.-L.; Sun, P.-F.; Zhou, S.-T.; Li, Y.; Chen, L.-W.; Mao, R. Study on the influence of belt angle on tire grounding characteristics under longitudinal slip conditions. J. Eng. Fibers Fabr. 2024, 19. [Google Scholar] [CrossRef]
- Romano, L. Advanced Brush Tyre Modelling; Springer Nature: Dordrecht, The Netherlands, 2022; ISBN 9783030984342. [Google Scholar]
- Zhang, S.P.; Chen, Y.X.; Zhou, H.C.; Zhang, W.; Liu, Y.; Shi, H.P. Study on the factors affecting the asymmetric characteristics of radial tire grounding region under lateral inclination. J. Chongqing Univ. Technol. Nat. Sci. 2023, 37, 56–62. [Google Scholar]
- Xie, Y.; Yang, Q. Tyre–pavement contact stress distribution considering tyre types. Road Mater. Pavement Des. 2018, 20, 1899–1911. [Google Scholar] [CrossRef]
- Zang, L.G.; Wang, X.Y.; Wang, Z.; Li, Y.W. Grounding characteristics of non-pneumatic tires under side dumping conditions. J. Chongqing Univ. Technol. Nat. Sci. 2021, 35, 49–55. [Google Scholar]
- Liu, Z.; Liu, Y.; Gao, Q. In-plane flexible ring modeling and a nonlinear stiffness solution for heavy-load radial tires. Mech. Syst. Signal Process. 2022, 171. [Google Scholar] [CrossRef]
- Romano, L.; Bruzelius, F.; Jacobson, B. Brush tyre models for large camber angles and steering speeds. Veh. Syst. Dyn. 2020, 60, 1341–1392. [Google Scholar] [CrossRef]
- Huang, T.; Gao, Q.H.; Liu, Z.H.; Wang, D. Study on nonlinear characteristics and model modification of heavy-duty radial tires. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2021, 49, 42–46. [Google Scholar]
- Yin, H.F.; Lu, D.; Min, H.T.; Wu, H.D.; Zhang, Y.D. Study on the effect of lateral inclination angle on the mechanical characteristics of tire deflection. Automot. Eng. 2025, 47, 342–355. [Google Scholar]
- Yao, X.; Wang, Z.; Ma, L.; Miao, Z.; Su, M.; Han, X.; Yang, J. Temperature Dependence of Rubber Hyper-Elasticity Based on Different Constitutive Models and Their Prediction Ability. Polymers 2022, 14, 3521. [Google Scholar] [CrossRef] [PubMed]
- Wu, X. Research on the Design of Carcass and Tread Structure to Reduce the Rolling Resistance of Tires; Jiangsu University: Zhenjiang, China, 2018. [Google Scholar]
- Liu, H. Research on the Effect of Radial Tire Tread Partition Variability on Tire Stiffness; Jiangsu University: Zhenjiang, China, 2022. [Google Scholar]
- Xiao, F.; Hu, J.; Jia, M.; Zhu, P.; Deng, C. A novel integrated control framework of AFS, ASS, and DYC based on ideal roll angle to improve vehicle stability. Adv. Eng. Inform. 2022, 54. [Google Scholar] [CrossRef]
- Lin, F.; Wang, S.; Zhao, Y.; Cai, Y. Research on autonomous vehicle path tracking control considering roll stability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 235, 199–210. [Google Scholar] [CrossRef]
- Sun, P.; Feng, G.; Zhou, S.; Qiu, C.; Fan, J. Experimental Analysis of Radial Tire Stiffness and Grounding Characteristics. IOP Conf. Ser. Mater. Sci. Eng. 2019, 677, 022111. [Google Scholar] [CrossRef]
- Zheng, B.; Huang, X.; Ma, J.; Hong, Z.; Chen, J.; Zhao, R.; Zhu, S.; Heidarzadeh, A. Evaluation on Distribution Characteristics of Pore Water Pressure within Saturated Pavement Structure Based on the Proposed Tire-Fluid-Pavement Coupling Model. Adv. Mater. Sci. Eng. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Tang, C.Y.; Pan, L.; Li, J.H.; Zhang, M.L. Vehicle path tracking control considering stability boundary and lateral stability. J. Northeast. Univ. Nat. Sci. Ed. 2024, 45, 1123–1134. [Google Scholar]
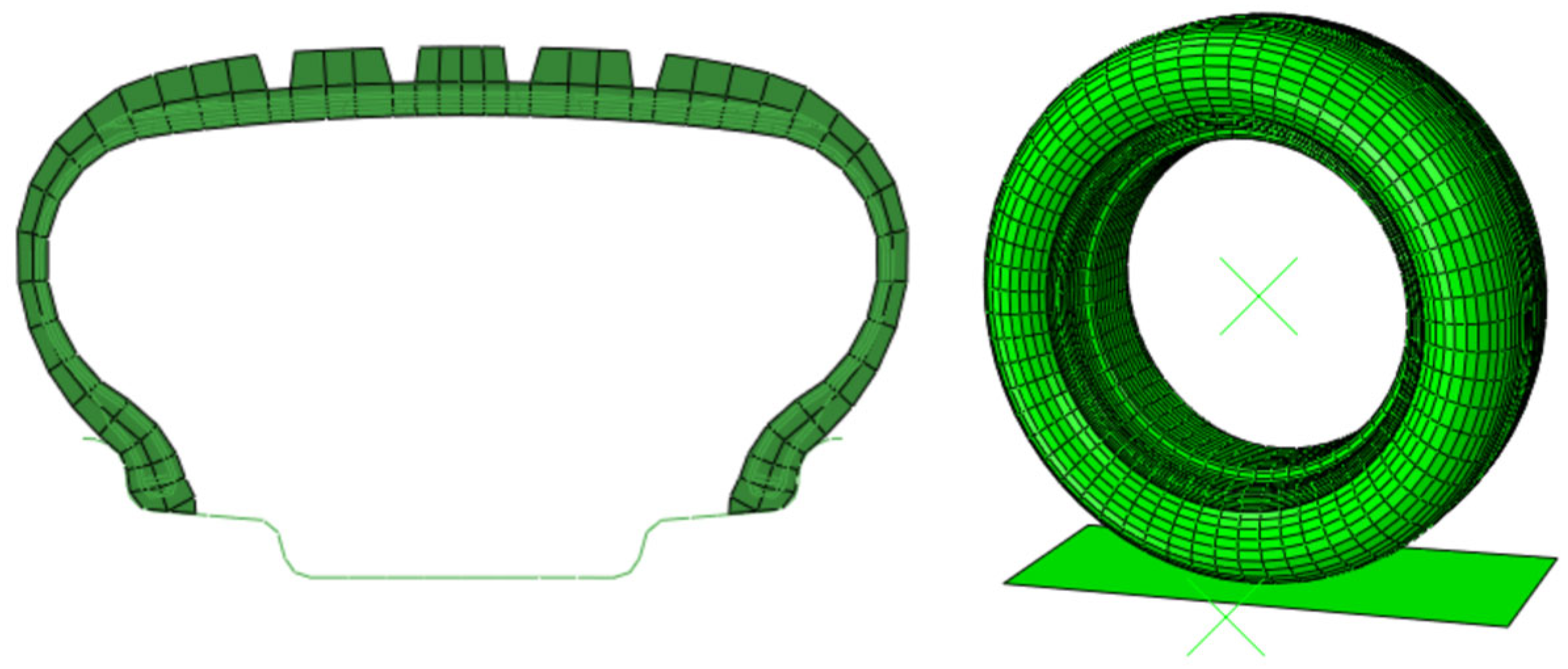

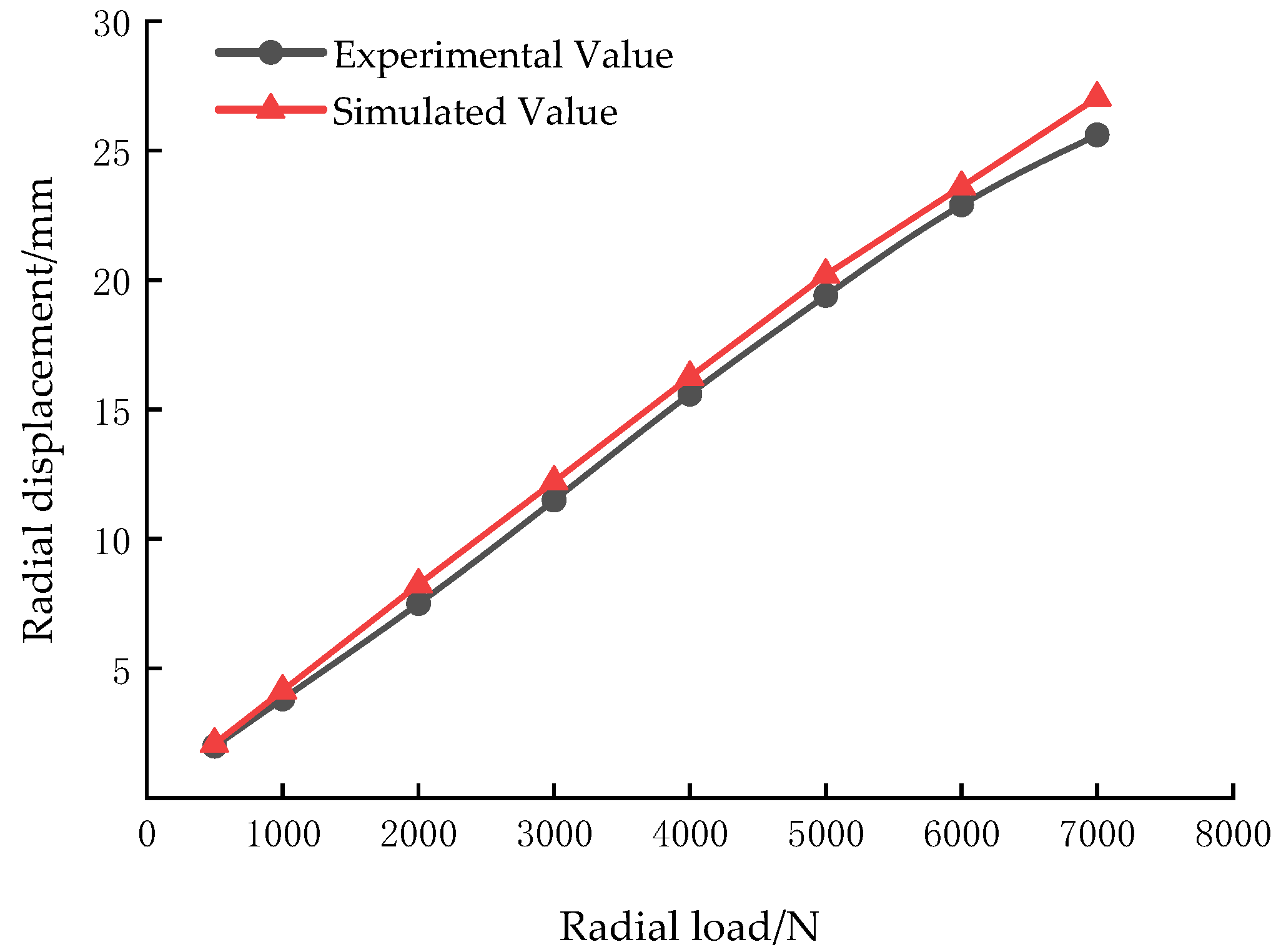
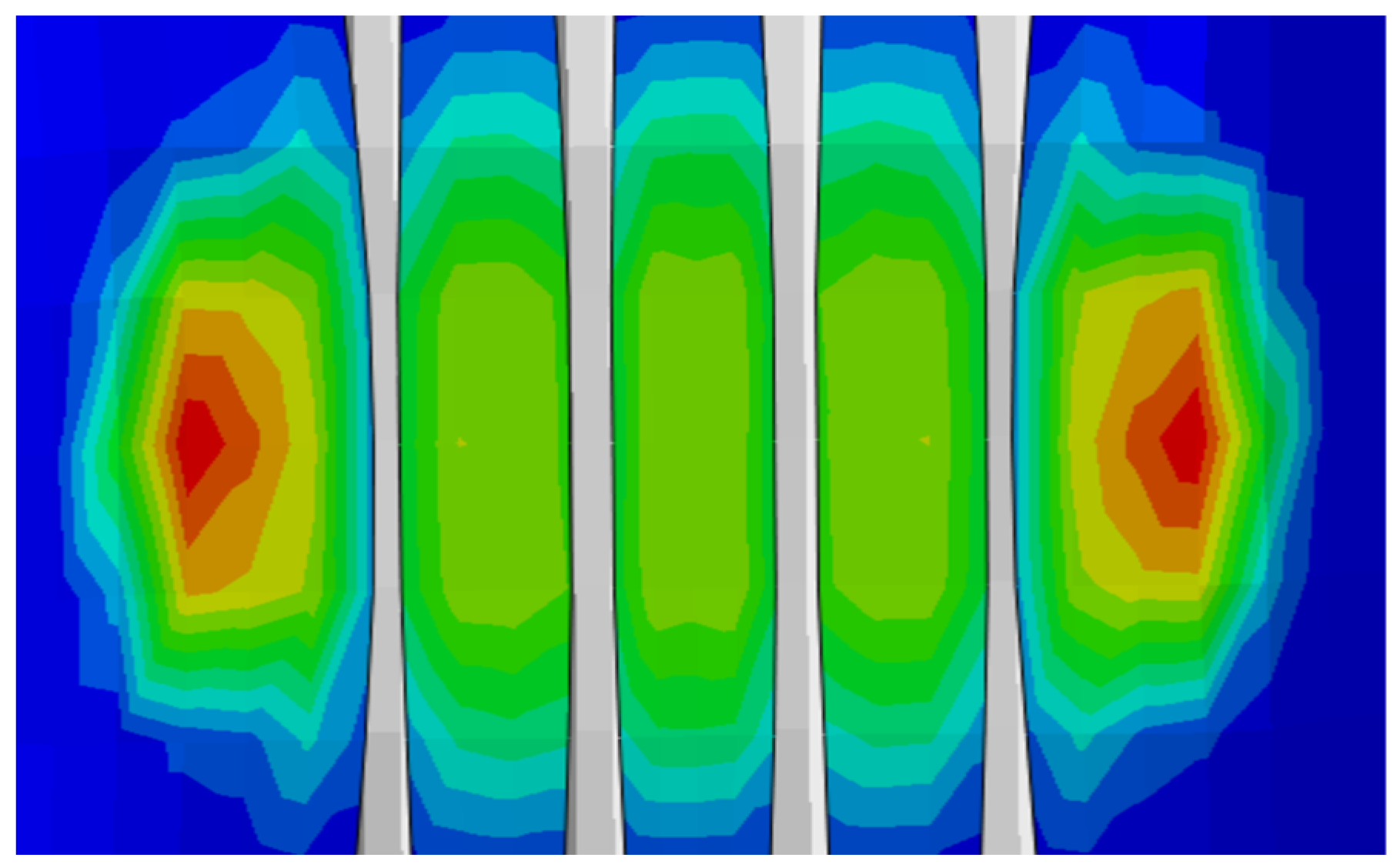
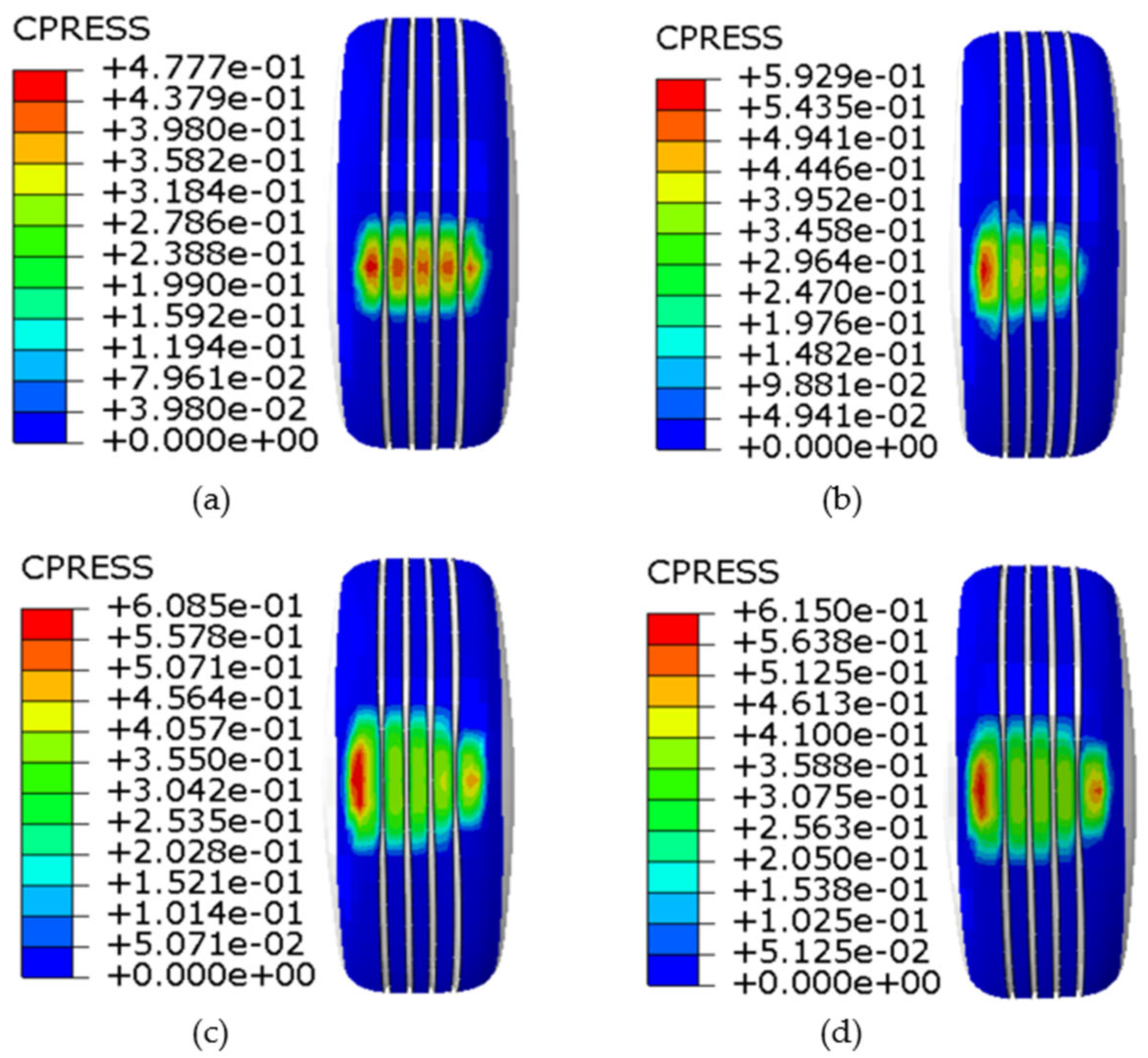
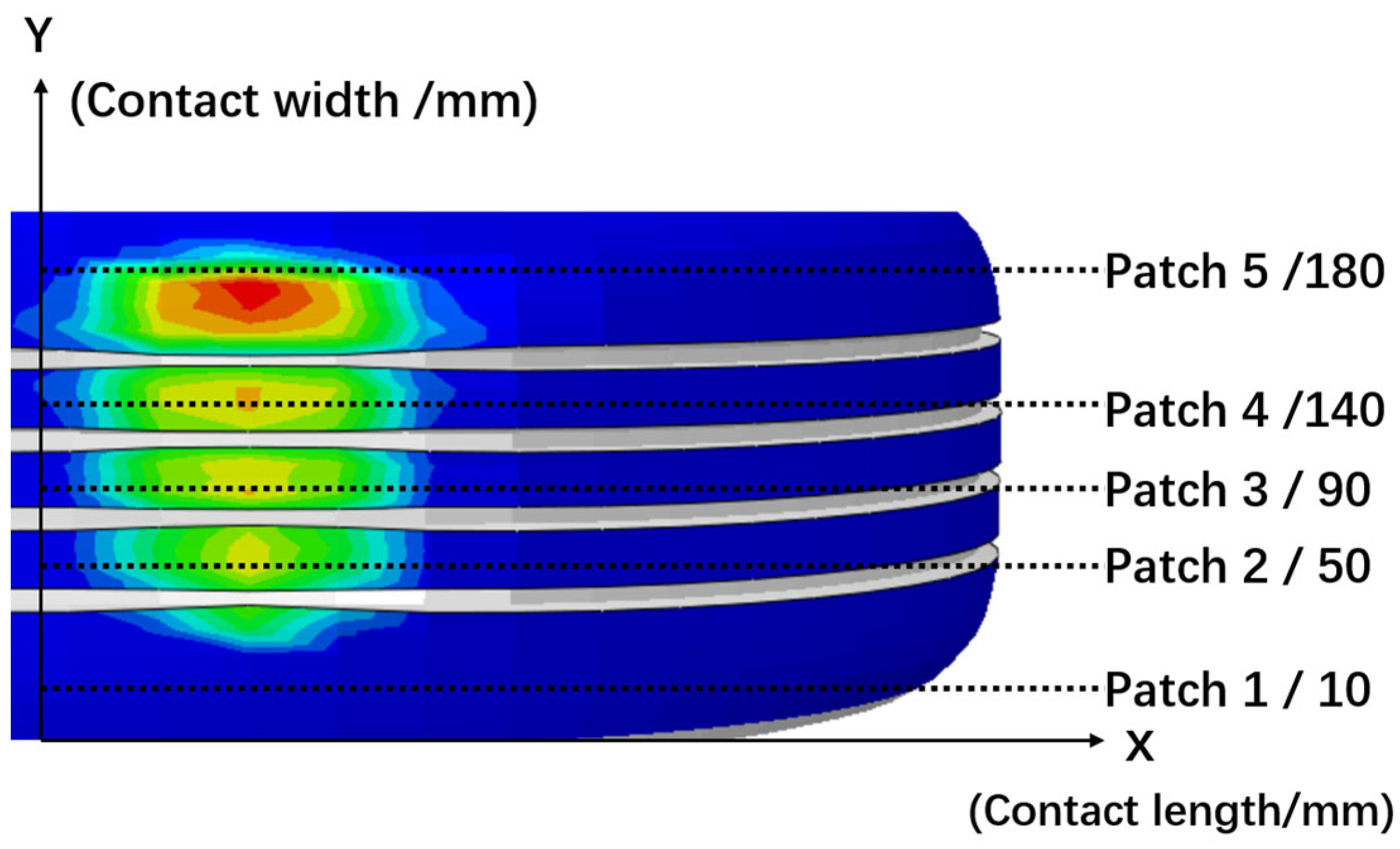
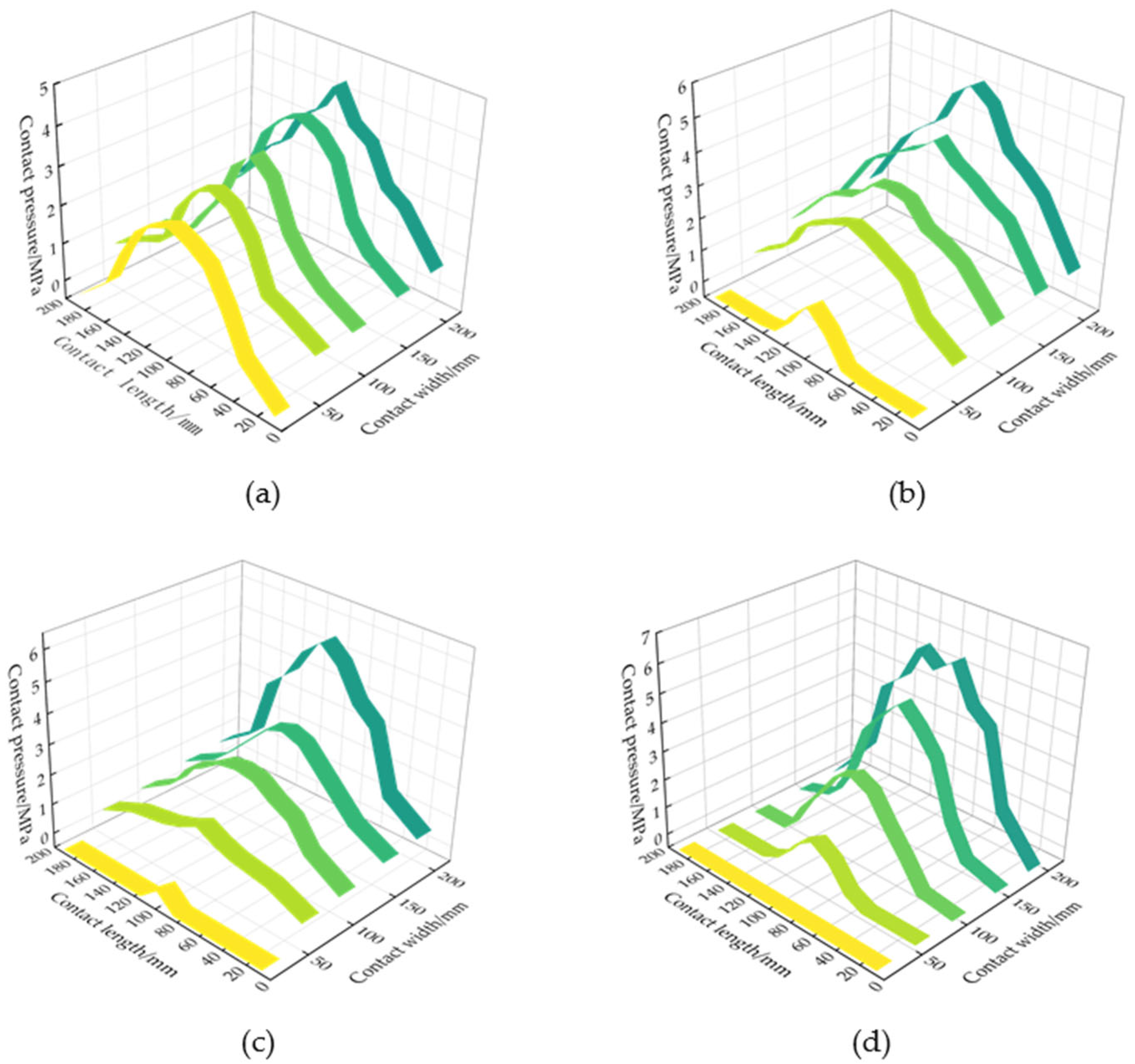
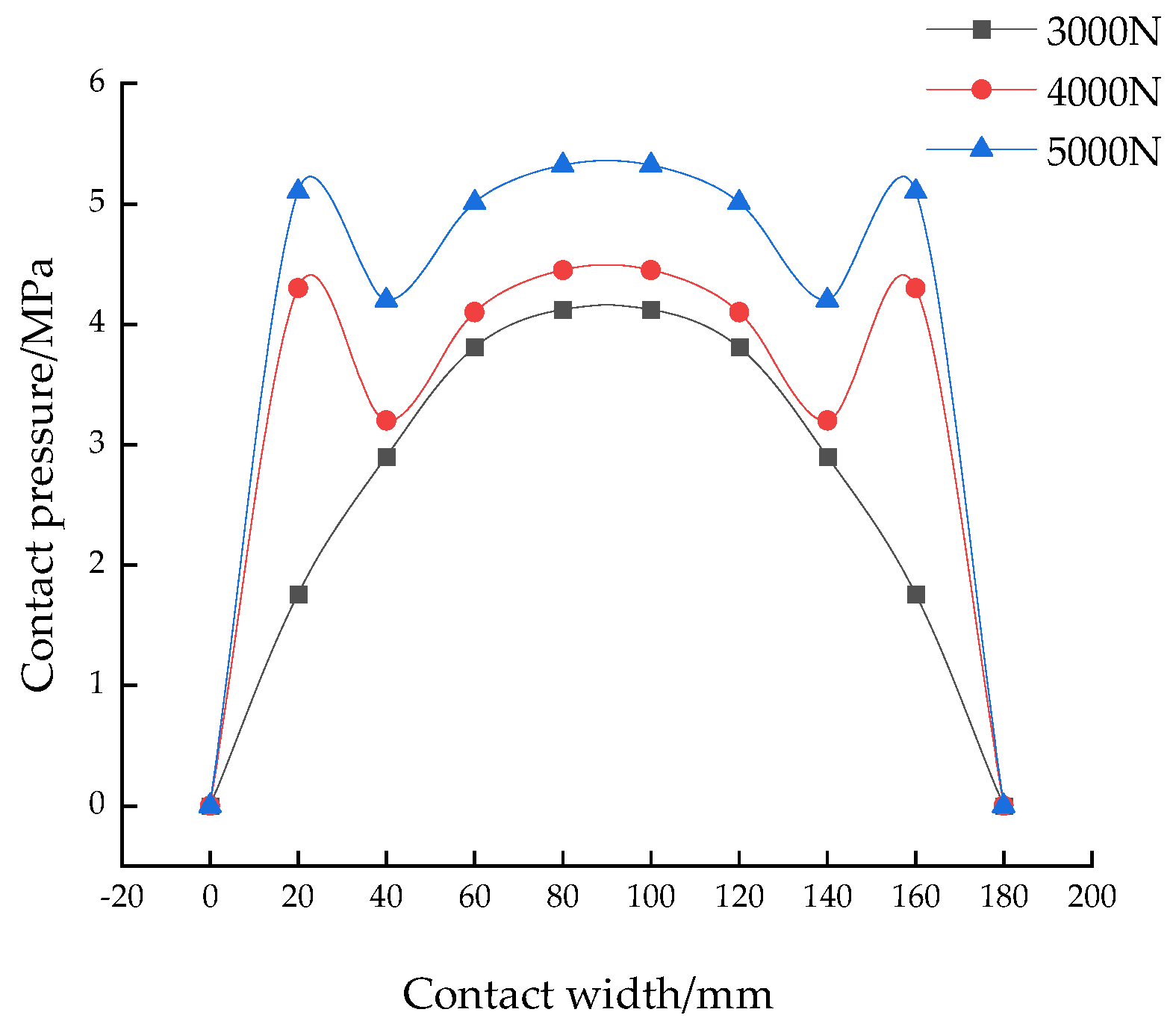

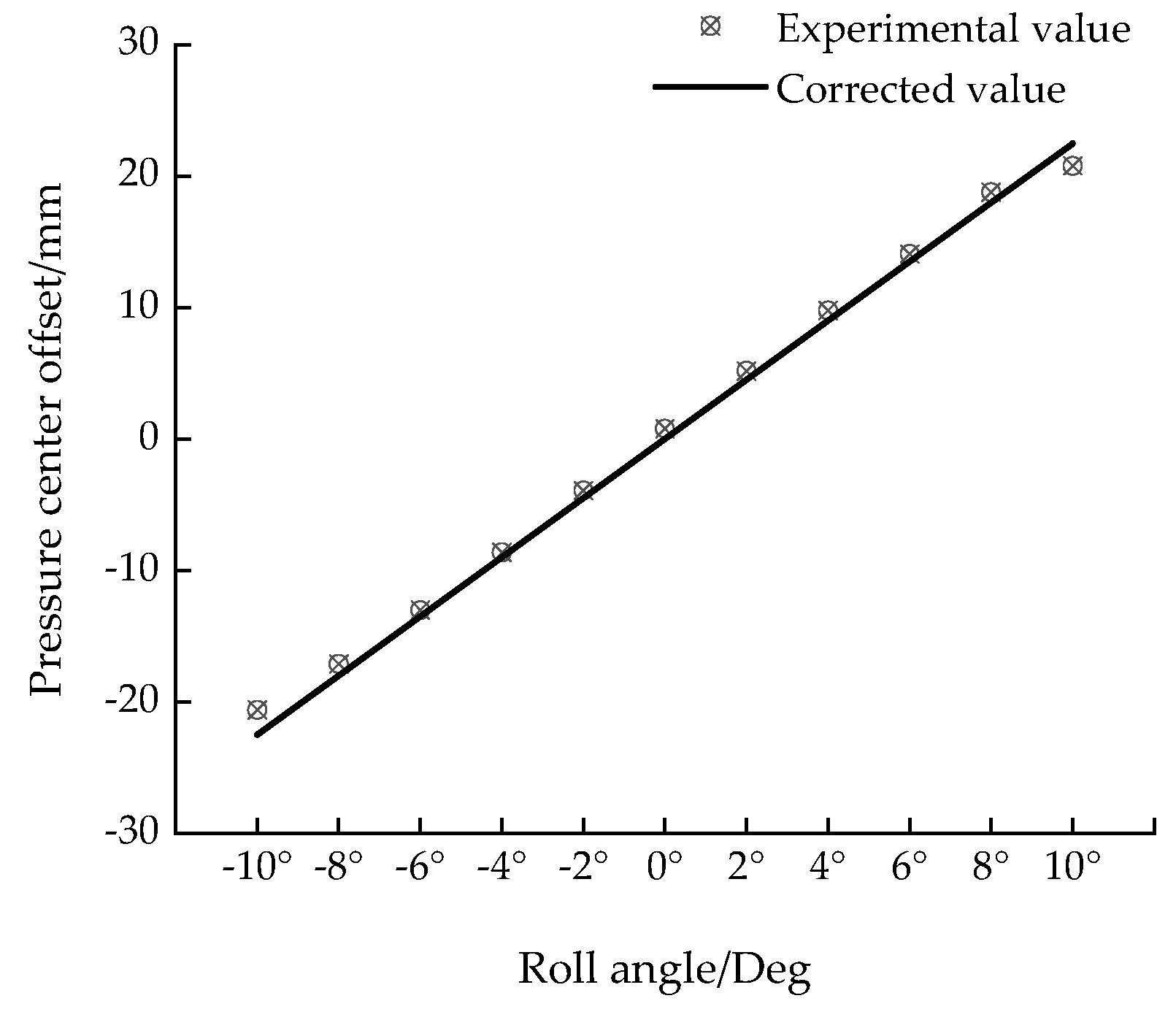
| Item | Contact Width/mm | Contact Length/mm |
|---|---|---|
| Experimental Value | 169.02 | 149.11 |
| Simulated Value | 177.45 | 154.47 |
| Relative Error | 4.51% | 3.24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Wang, Y.; You, H. Tire Contact Pressure Distribution and Dynamic Analysis Under Rolling Conditions. World Electr. Veh. J. 2025, 16, 525. https://doi.org/10.3390/wevj16090525
Ma X, Wang Y, You H. Tire Contact Pressure Distribution and Dynamic Analysis Under Rolling Conditions. World Electric Vehicle Journal. 2025; 16(9):525. https://doi.org/10.3390/wevj16090525
Chicago/Turabian StyleMa, Xintan, Yugang Wang, and Haitao You. 2025. "Tire Contact Pressure Distribution and Dynamic Analysis Under Rolling Conditions" World Electric Vehicle Journal 16, no. 9: 525. https://doi.org/10.3390/wevj16090525
APA StyleMa, X., Wang, Y., & You, H. (2025). Tire Contact Pressure Distribution and Dynamic Analysis Under Rolling Conditions. World Electric Vehicle Journal, 16(9), 525. https://doi.org/10.3390/wevj16090525





