Fusing Direct and Indirect Visual Odometry for SLAM: An ICM-Based Framework
Abstract
1. Introduction
- We propose a novel, modular approach for the unified fusion of direct and feature-based odometry. This integration improves pose estimation reliability and reduces tracking failure, particularly in challenging conditions.
- Novel potential functions are introduced to enable 6-DoF pose estimation using ICM.
- Dynamically adjusted gain values are integrated into the ICM algorithm to enhance robustness against tracking loss in visually degraded or low-texture environments.
2. Materials and Methods
2.1. System Overview
2.2. Theoretical Background on Iterated Conditional Modes
2.3. Potential Functions Definition
2.3.1. Odometry Potential
2.3.2. Continuity Potential
2.3.3. Mapping and Observations Potential
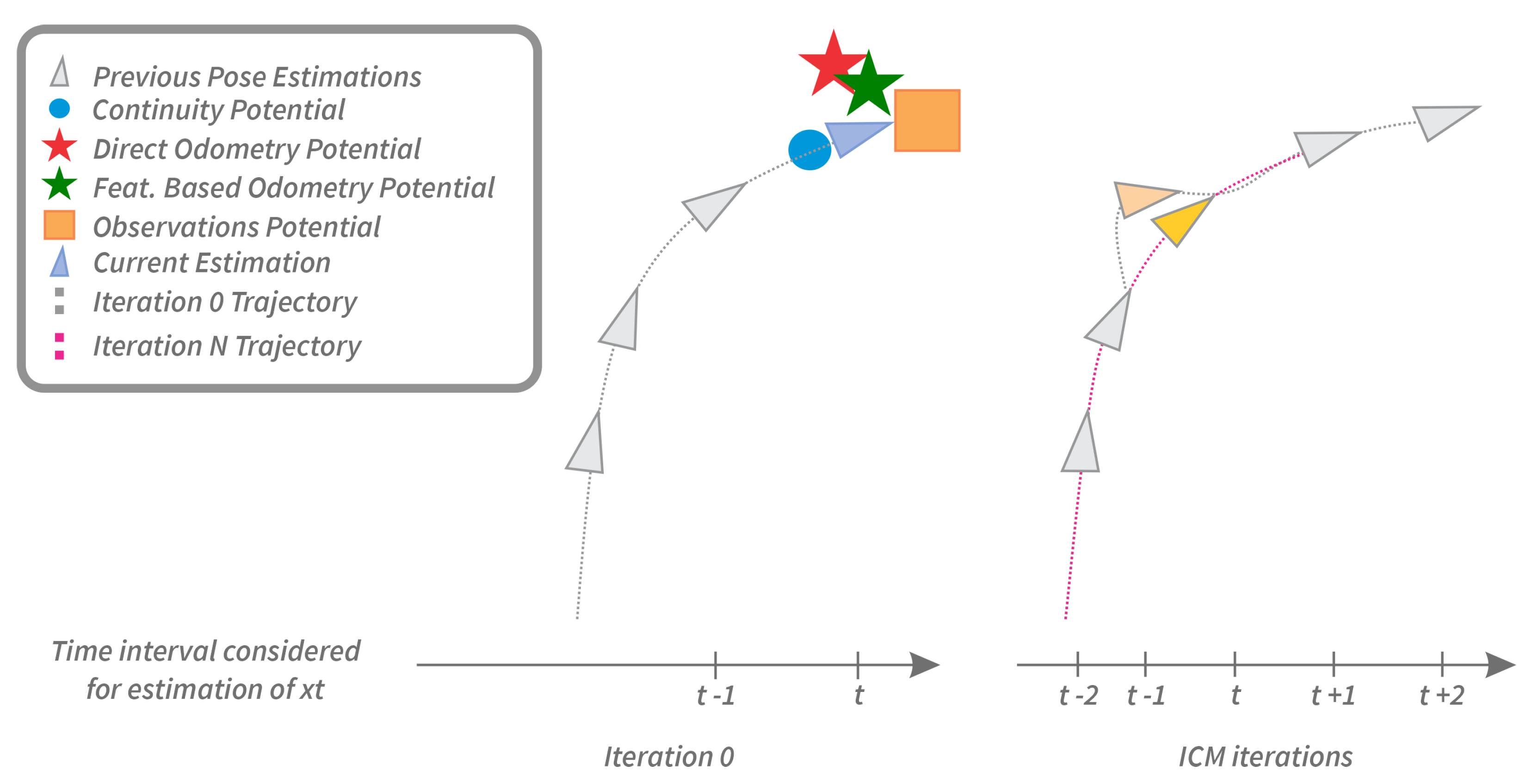
2.4. Data Fusion via ICM
2.4.1. Initialization
| Algorithm 1 Online ICM initialization. |
|
2.4.2. ICM Iterations
| Algorithm 2 ICM iterations. |
|
2.5. Adaptable Gain Values
3. Results
3.1. TUM Dataset
3.2. Field Tests
3.2.1. Indoor Test
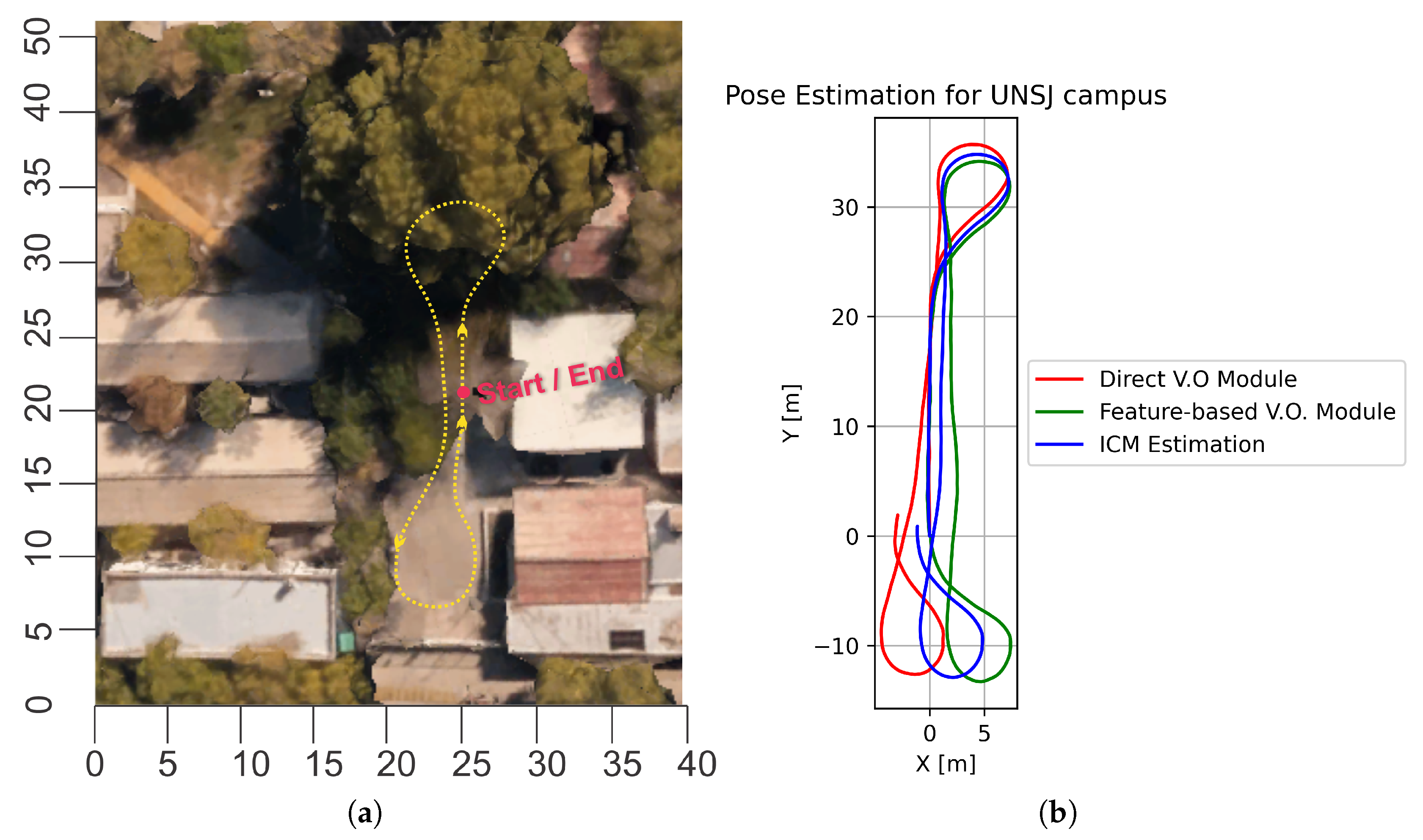
3.2.2. Outdoor Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Pixel Selection Algorithm
Appendix A.1. Texture Descriptors
- High SRE values correspond to a predominance of short gray-level runs, which are indicative of the fine textures with frequent intensity transitions.
- Low SRE values reflect a higher occurrence of longer runs, suggesting a coarser texture with less frequent intensity changes.
- High LRE values signify a predominance of long gray-level runs, typical of coarse textures with large homogeneous areas or gradual transitions in intensity.
- Low LRE values indicate a larger proportion of short runs, which are characteristic of finer textures.
Appendix A.2. Maximum Gradients Image
Appendix A.3. Adaptive Reference Point Selection Algorithm
Appendix A.3.1. Adaptive Threshold Adjustment (Thcurr)
Appendix A.3.2. Adaptive Search Window Adjustment (Spatch)
- An excessively large window may result in too few extracted keypoints, failing to meet the minimum requirement.
- A window that is too small increases computational cost and may cause significant delays.
- In regions rich in texture or structure, a large window may underutilize the information, yielding few keypoints.
- Conversely, very small windows may lead to excessive keypoint extraction, slowing down subsequent pose estimation steps.
References
- Yang, K.; Cheng, Y.; Chen, Z.; Wang, J. Slam meets nerf: A survey of implicit slam methods. World Electr. Veh. J. 2024, 15, 85. [Google Scholar] [CrossRef]
- Lluvia, I.; Lazkano, E.; Ansuategi, A. Active Mapping and Robot Exploration: A Survey. Sensors 2021, 21, 2445. [Google Scholar] [CrossRef]
- Placed, J.A.; Strader, J.; Carrillo, H.; Atanasov, N.; Indelman, V.; Carlone, L.; Castellanos, J.A. A survey on active simultaneous localization and mapping: State of the art and new frontiers. IEEE Trans. Robot. 2023, 39, 1686–1705. [Google Scholar] [CrossRef]
- Gaia, J.; Orosco, E.; Rossomando, F.; Soria, C. Mapping the Landscape of SLAM Research: A Review. IEEE Lat. Am. Trans. 2023, 21, 1313–1336. [Google Scholar] [CrossRef]
- Li, Y.; An, J.; He, N.; Li, Y.; Han, Z.; Chen, Z.; Qu, Y. A Review of Simultaneous Localization and Mapping Algorithms Based on Lidar. World Electr. Veh. J. 2025, 16, 56. [Google Scholar] [CrossRef]
- Wu, D.; Ma, Z.; Xu, W.; He, H.; Li, Z. Visual Odometry Based on Improved Oriented Features from Accelerated Segment Test and Rotated Binary Robust Independent Elementary Features. World Electr. Veh. J. 2024, 15, 123. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Fraundorfer, F. Visual odometry [tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Tardif, J.P.; Pavlidis, Y.; Daniilidis, K. Monocular visual odometry in urban environments using an omnidirectional camera. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2531–2538. [Google Scholar] [CrossRef]
- Bescos, B.; Fácil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar] [CrossRef]
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Peng, S.; Larsson, V.; Xu, W.; Bao, H.; Cui, Z.; Oswald, M.R.; Pollefeys, M. Nice-slam: Neural implicit scalable encoding for slam. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12786–12796. [Google Scholar]
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct sparse odometry with loop closure. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2198–2204. [Google Scholar] [CrossRef]
- Yang, N.; Stumberg, L.v.; Wang, R.; Cremers, D. D3vo: Deep depth, deep pose and deep uncertainty for monocular visual odometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1281–1292. [Google Scholar] [CrossRef]
- Matsuki, H.; Murai, R.; Kelly, P.H.; Davison, A.J. Gaussian splatting slam. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 18039–18048. [Google Scholar]
- Schlegel, D.; Grisetti, G. Visual localization and loop closing using decision trees and binary features. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 4616–4623. [Google Scholar] [CrossRef]
- Nobis, F.; Papanikolaou, O.; Betz, J.; Lienkamp, M. Persistent Map Saving for Visual Localization for Autonomous Vehicles: An ORB-SLAM 2 Extension. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Elvira, R.; Tardós, J.D.; Montiel, J.M. ORBSLAM-Atlas: A robust and accurate multi-map system. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 6253–6259. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Li, S. Spherical-model-based SLAM on full-view images for indoor environments. Appl. Sci. 2018, 8, 2268. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Folkesson, J.; Christensen, H. Graphical SLAM-a self-correcting map. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Proceedings, ICRA’04. Volume 1, pp. 383–390. [Google Scholar]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Akai, N.; Akagi, Y.; Hirayama, T.; Morikawa, T.; Murase, H. Detection of localization failures using Markov random fields with fully connected latent variables for safe LiDAR-based automated driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17130–17142. [Google Scholar] [CrossRef]
- Kindermann, R.; Snell, J.L. Markov Random Fields and Their Applications; American Mathematical Society: Providence, RI, USA, 1980; Volume 1. [Google Scholar]
- Jadaliha, M.; Choi, J. Fully Bayesian simultaneous localization and spatial prediction using Gaussian Markov random fields (GMRFs). In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 4592–4597. [Google Scholar]
- Wang, C.; Li, T.; Meng, M.Q.H.; De Silva, C. Efficient mobile robot exploration with Gaussian Markov random fields in 3D environments. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5015–5021. [Google Scholar]
- Gimenez, J.; Amicarelli, A.; Toibero, J.M.; di Sciascio, F.; Carelli, R. Iterated conditional modes to solve simultaneous localization and mapping in Markov random fields context. Int. J. Autom. Comput. 2018, 15, 310–324. [Google Scholar] [CrossRef]
- Gimenez, J.; Amicarelli, A.; Toibero, J.M.; di Sciascio, F.; Carelli, R. Continuous probabilistic SLAM solved via iterated conditional modes. Int. J. Autom. Comput. 2019, 16, 838–850. [Google Scholar] [CrossRef]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. Ser. B Stat. Methodol. 1986, 48, 259–279. [Google Scholar] [CrossRef]
- Jaime, F.; Marzola, T.; Baldoni, M.; Mattoccia, S. HoloSLAM: A novel approach to virtual landmark-based SLAM for indoor environments. SN Comput. Sci. 2024, 5, 469. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Horn, B.K. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Sero Electric Sedan Electric Vehicle. Available online: https://www.seroelectric.com/modelo-sedan/ (accessed on 7 May 2025).
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man, Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Galloway, M.M. Texture analysis using grey level run lengths. Nasa Sti/Recon Tech. Rep. N 1974, 75, 18555. [Google Scholar]



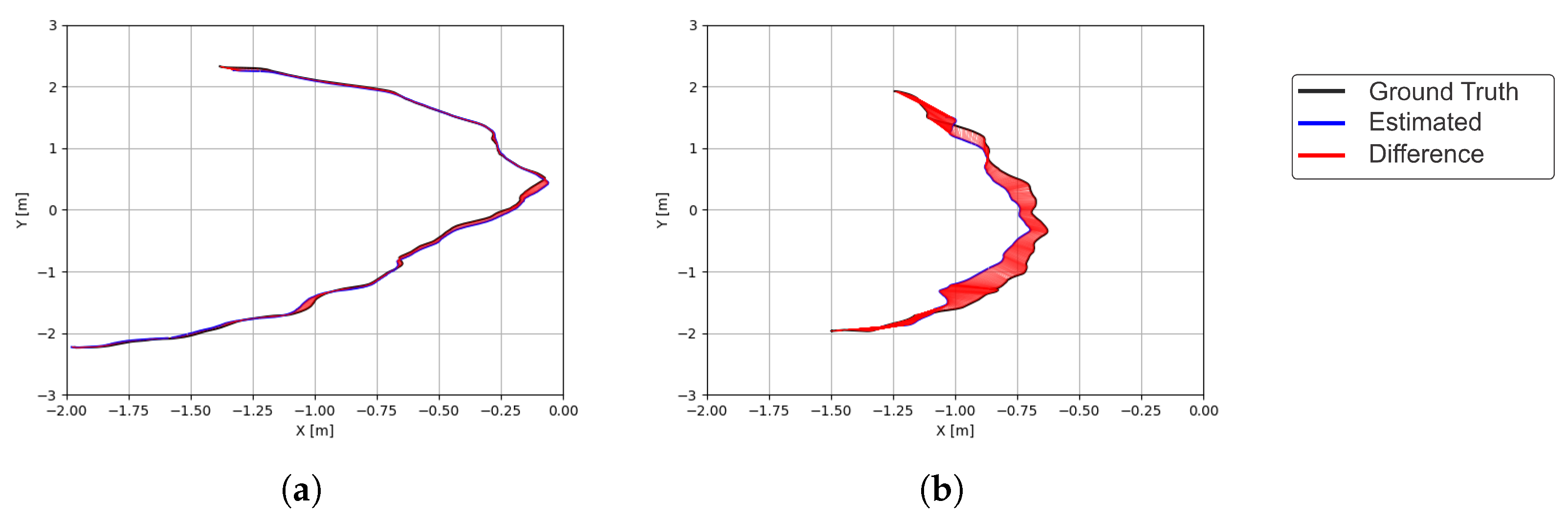
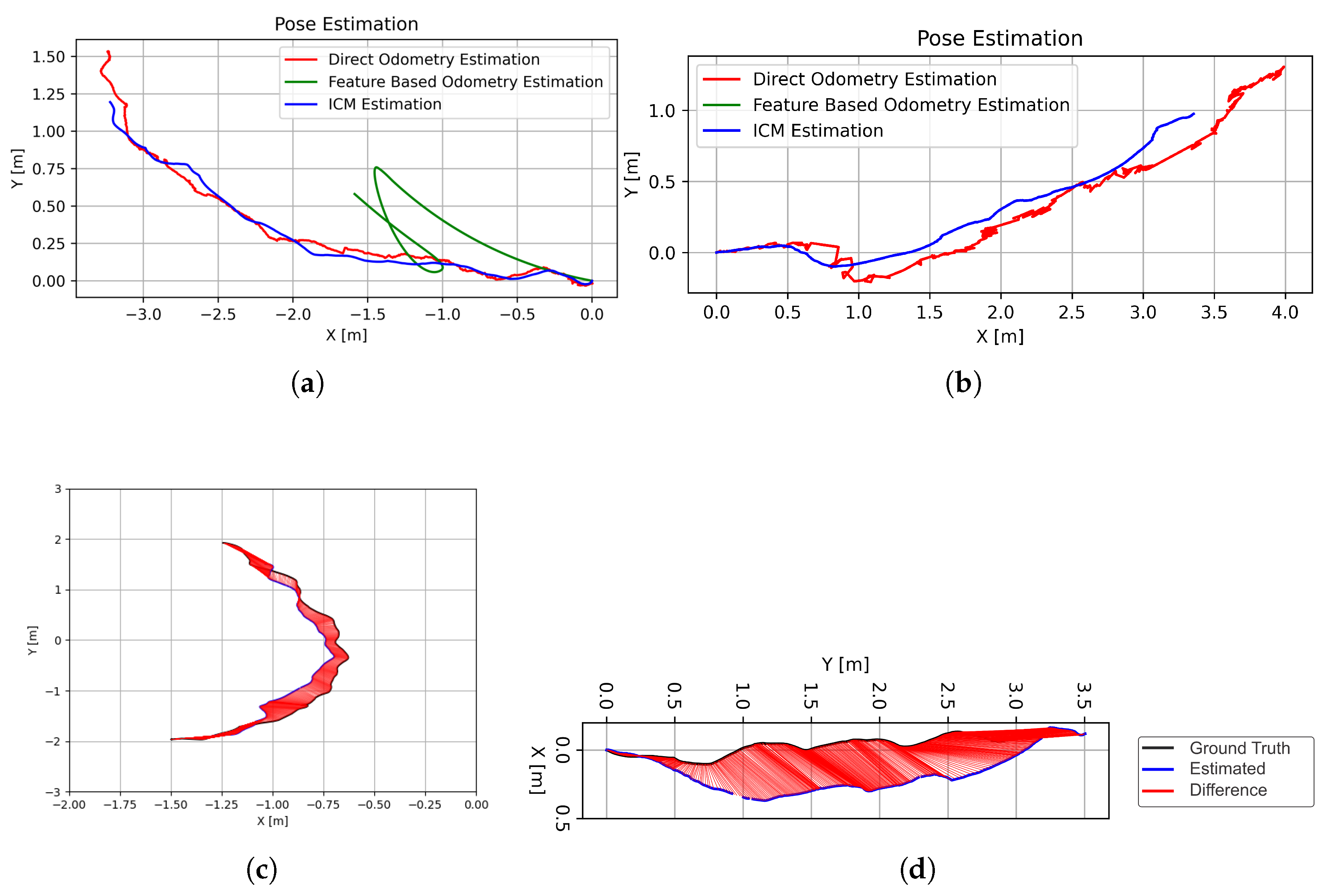
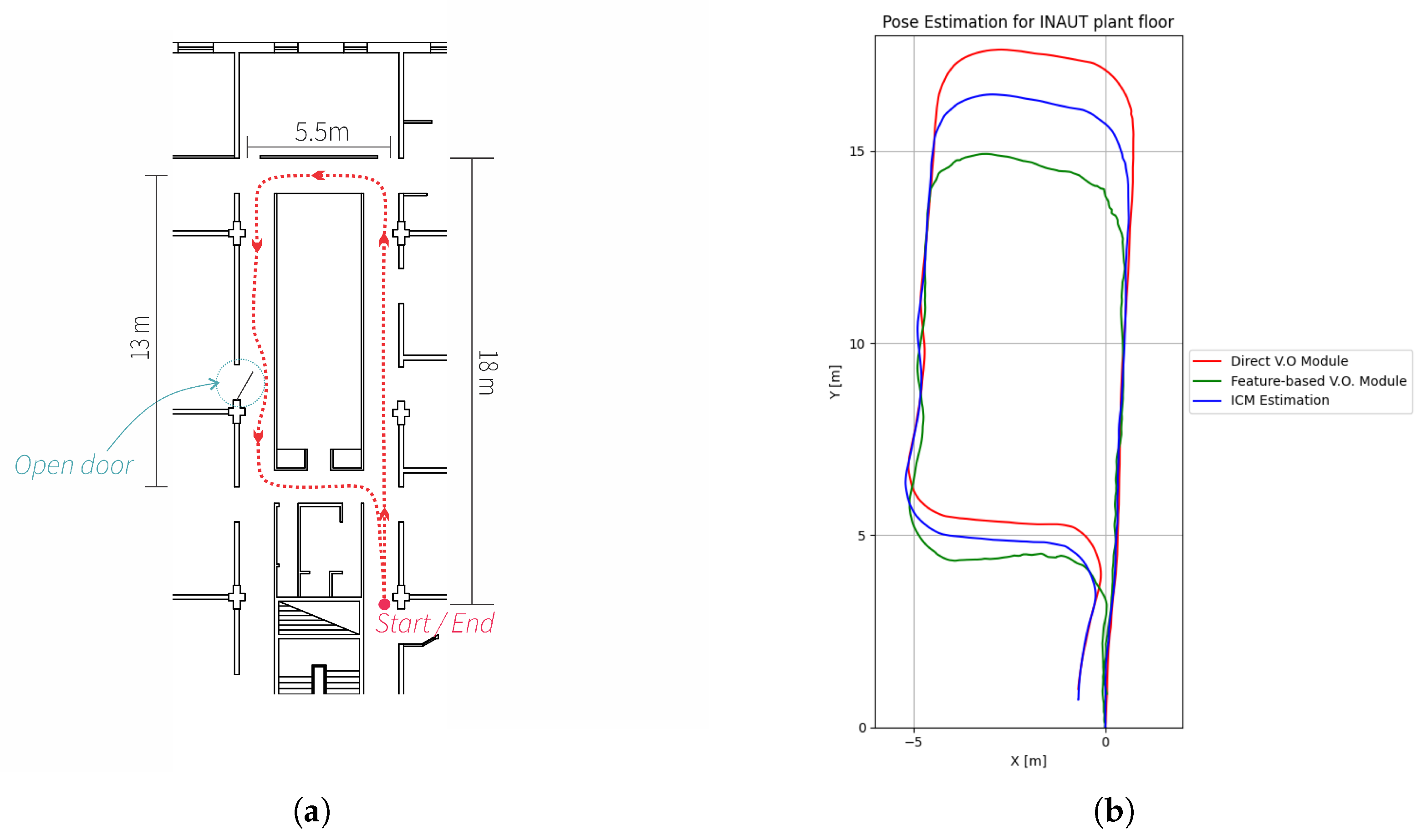
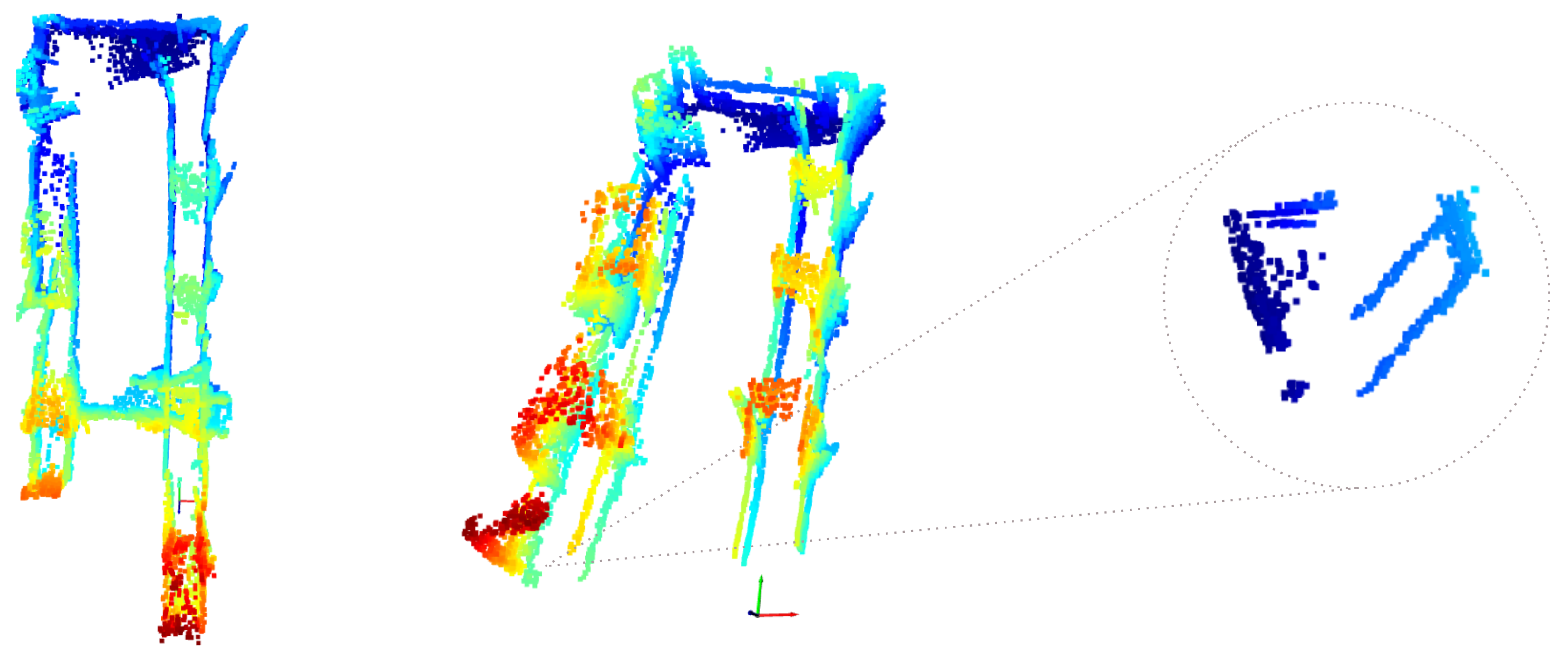

| Sequence | ATE RMSE [m] | ATE Mean [m] | ATE Median [m] | ATE Std [m] | ATE min [m] | ATE max [m] |
|---|---|---|---|---|---|---|
| fr1/plant | 0.5567 | 0.4989 | 0.4895 | 0.2470 | 0.0185 | 1.0784 |
| fr2/desk | 0.4344 | 0.3900 | 0.3743 | 0.1914 | 0.0321 | 0.7947 |
| fr3/s-t | 0.0296 | 0.0275 | 0.0266 | 0.0108 | 0.0035 | 0.0619 |
| fr3/s-Nt | 0.1933 | 0.1795 | 0.1821 | 0.0715 | 0.0692 | 0.4366 |
| fr3/Ns-t | 0.0574 | 0.0529 | 0.0486 | 0.0222 | 0.0041 | 0.1155 |
| fr3/Ns-Nt | 0.3361 | 0.3121 | 0.2990 | 0.1246 | 0.1115 | 0.5243 |
| Sequence | Mean Cost Value |
|---|---|
| fr1/plant it 0 | |
| fr1/plant it N | |
| fr2/desk it 0 | |
| fr2/desk it N | |
| fr3/s-t it 0 | |
| fr3/s-t it N | |
| fr3/s-Nt it 0 | |
| fr3/s-Nt it N | |
| fr3/Ns-t it 0 | |
| fr3/Ns-t it N | |
| fr3/Ns-Nt it 0 | |
| fr3/Ns-Nt it N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaia, J.; Gimenez, J.; Orosco, E.; Rossomando, F.; Soria, C.; Ulloa-Vásquez, F. Fusing Direct and Indirect Visual Odometry for SLAM: An ICM-Based Framework. World Electr. Veh. J. 2025, 16, 510. https://doi.org/10.3390/wevj16090510
Gaia J, Gimenez J, Orosco E, Rossomando F, Soria C, Ulloa-Vásquez F. Fusing Direct and Indirect Visual Odometry for SLAM: An ICM-Based Framework. World Electric Vehicle Journal. 2025; 16(9):510. https://doi.org/10.3390/wevj16090510
Chicago/Turabian StyleGaia, Jeremias, Javier Gimenez, Eugenio Orosco, Francisco Rossomando, Carlos Soria, and Fernando Ulloa-Vásquez. 2025. "Fusing Direct and Indirect Visual Odometry for SLAM: An ICM-Based Framework" World Electric Vehicle Journal 16, no. 9: 510. https://doi.org/10.3390/wevj16090510
APA StyleGaia, J., Gimenez, J., Orosco, E., Rossomando, F., Soria, C., & Ulloa-Vásquez, F. (2025). Fusing Direct and Indirect Visual Odometry for SLAM: An ICM-Based Framework. World Electric Vehicle Journal, 16(9), 510. https://doi.org/10.3390/wevj16090510







