Optimization of Prefabricated Building Component Distribution Under Dynamic Charging Strategy for Electric Heavy-Duty Trucks

Abstract

To align with the adoption of electric vehicles in the transportation sector, this paper proposes the use of electric heavy-duty trucks for the logistics and distribution of large prefabricated building components. This approach aims to address the problems of high total costs and significant energy waste in prefabricated component transportation. Focusing on the multi-to-multi distribution mode, a two-level optimization model is constructed. The upper-level model is responsible for the reasonable allocation of demand points. The lower-level model optimizes the selection of road network nodes and charging stations along the delivery routes. It also dynamically adjusts charging timing and volume according to the real-time power situation. To enhance solution performance, a two-level multi-objective evolutionary algorithm based on Pareto theory is designed. This algorithm simultaneously optimizes distribution costs while coordinating path planning and charging strategies. Comparative experiments across different cases show that, compared with traditional single-level and multi-stage models, the proposed algorithm improves both solution accuracy and quality. Additionally, when compared with the scheduling scheme based on the full-charge capacity strategy, the dynamic charging strategy proposed in this paper reduces the total distribution cost by approximately 15.83%. These findings demonstrate that the constructed model and algorithm can effectively optimize the logistics and distribution of prefabricated components. They also provide a feasible solution for the practical application of electric vehicles in engineering logistics.

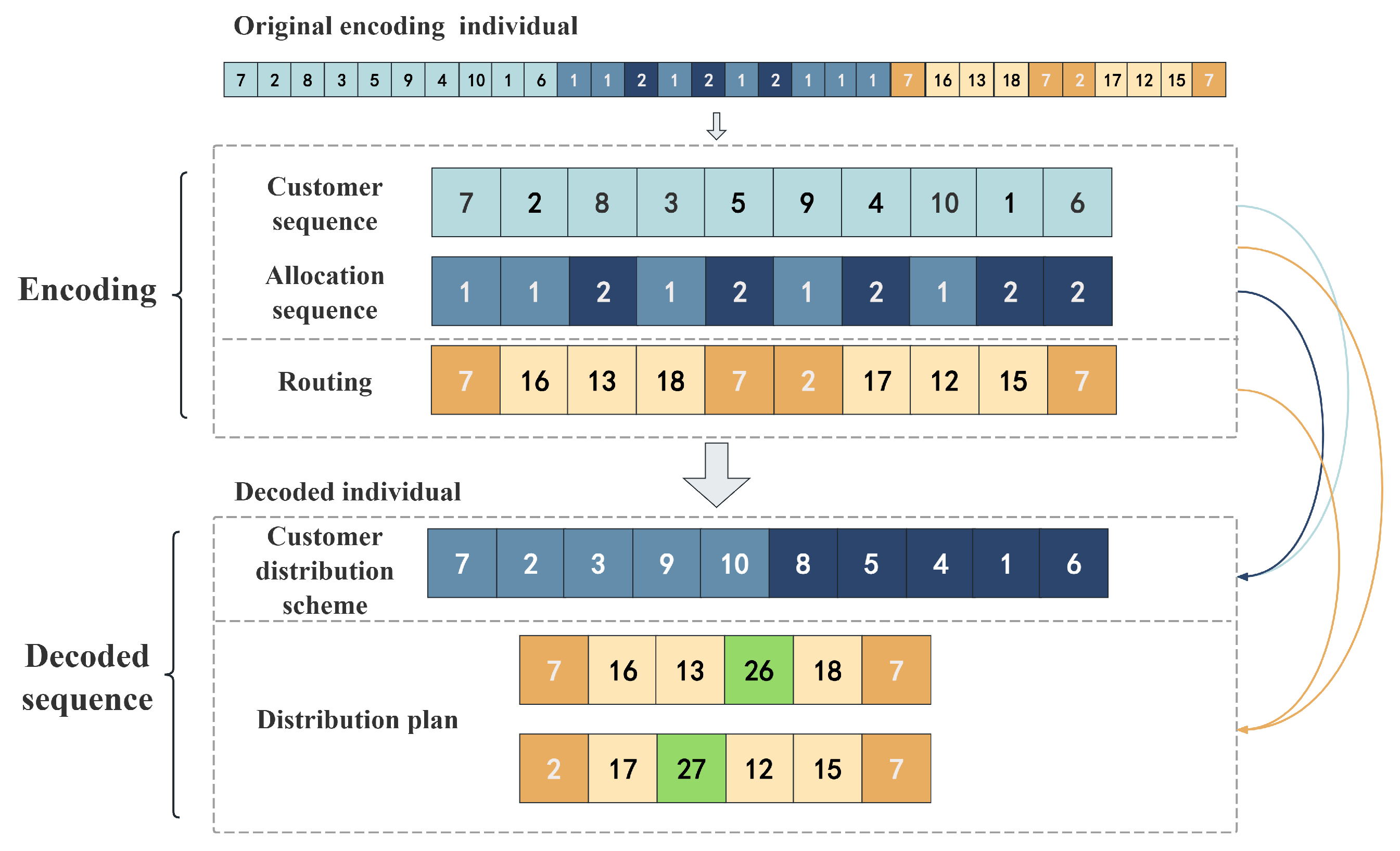
1. Introduction

The automobile industry is a crucial pillar of the national economy, playing a significant role in both economic growth and social development. However, with the rapid increase in the production and sales of fuel vehicles, issues such as energy shortages and environmental pollution have become increasingly prominent. The resulting energy crisis and environmental degradation have severely constrained human survival and development, making environmental protection and sustainable development urgent global concerns. Compared to traditional fuel vehicles, electric vehicles offer notable advantages, including high energy utilization, low maintenance costs, and substantial reductions in exhaust emissions. As such, they have emerged as an effective means to address resource scarcity and environmental pollution. Against this backdrop, the development of energy-saving and environmentally friendly electric vehicles has become an urgent necessity. In recent years, electric vehicles have been reshaping the traditional market landscape at an unprecedented pace. This transformation not only reflects the widespread acceptance and proactive adoption of green mobility concepts by consumers, but also underscores the determination and effectiveness of global efforts to mitigate climate change and promote sustainable development. Gradually becoming a focal point in the transportation sector, electric vehicles carry the vision of transforming travel modes and advancing renewable energy utilization, thus signaling the advent of a cleaner, smarter, and more efficient era of green transportation.

In recent years, the introduction of policies on carbon peaking and carbon neutrality has led scholars in various fields to increasingly focus on strategies to effectively reduce carbon emissions and achieve the ’dual carbon’ goals. In line with the national “dual carbon” policy, the construction industry has identified prefabricated buildings—characterized by greenness, efficiency, and energy conservation—as the core technology and product in the modernization of the sector [1,2,3]. Powered by strong national policies and sustained market demand, the market share of prefabricated buildings has grown steadily year by year. However, because of the large volume and weight of individual pre-fabricated components, their transportation still heavily depends on traditional large fuel-powered vehicles for frequent deliveries, making the logistics and distribution of prefabricated components a critical area for emission reduction. The official delivery approval of Tesla’s electric truck, Semi, has been widely considereda significant step for the future of the transportation sector. The release of Tesla’s electric truck, Semi, not only promotes the accelerated adoption of electric vehicle strategies by logistics enterprises worldwide but also fosters the development of new energy logistics vehicles. These vehicles are characterized by large capacity, high load, and extended driving range, making them suitable for a variety of operational scenarios. This trend is progressively driving the green transformation of the logistics and transportation industry, signaling that the large-scale adoption of electric vehicles in prefabricated component distribution is imminent [4].

Most existing research on the logistics distribution of prefabricated components in prefabricated buildings has focused on reducing logistics costs. Owing to the large weight and volume of prefabricated components, vehicle transportation costs account for a relatively high proportion of total logistics expenses. Consequently, researchers have sought to apply advanced logistics optimization concepts to prefabricated component distribution, aiming to minimize total transportation costs while ensuring delivery efficiency. Dan Y [5] proposed a production and transportation scheduling method that simultaneously considers delivery timeliness and transportation economy, thereby reducing both delivery penalties and transportation costs. Almashaqbeh M [6] enhanced the cost-effectiveness of modular construction projects by optimizing the transportation of prefabricated modules from factories to construction sites. Qi R [7] addressed the multi-frequency vehicle routing problem for prefabricated components, minimizing total transportation costs and completion time under service time and vehicle load constraints. Yi W [8] developed a mathematical programming model to optimize prefabricated component transportation plans, minimizing the combined vehicle transportation and inventory costs. Wang H [9] applied mathematical programming techniques to design minimum-cost transportation plans, achieving on-time delivery while reducing overall transportation costs by 10.13%. Zhang H [10] investigated the flexible coordination between prefabricated component supply chain planning and construction schedules. A multi-objective optimization model was proposed to balance planning flexibility and cost trade-offs, thereby achieving efficient deliveries while considering transportation costs. Dan Y [11] further explored the integrated production and transportation scheduling problem for multiple production lines of prefabricated components. Their mathematical model, solved using a genetic algorithm, aims to ensure on-time delivery while reducing costs, thereby improving efficiency, lowering expenses, and enhancing the practicality of production–transportation scheduling schemes in multi-line assembly plants.

With the increase in project scale and transportation complexity, truck delivery, as the primary mode for transporting prefabricated components, has attracted growing attention in terms of route planning and scheduling. Zhou J [12] incorporated practical constraints such as road conditions and weight limitations into the transportation of large prefabricated components. They developed a truck–trailer routing optimization model with time windows. To solve the model, an adaptive hybrid intelligent algorithm was employed. The results show that this approach effectively reduces both transportation and carbon emission costs, thus offering theoretical support for low-carbon logistics route optimization for large cargo. In parallel, declining battery costs, wider commercial adoption, and the global push for emission reductions have spurred interest in transitioning from internal combustion engines to electric vehicles in the transportation sector. Xu K [13] made a detailed comparison of the carbon emissions generated by the three energy consumption methods of diesel, gasoline, and electricity during the transportation of composite beam components. The results showed that the carbon emissions of electric trucks were the lowest, at only 12.24 kg.

Against this backdrop, the electric vehicle industry has advanced rapidly under the dual drivers of technological innovation and policy support, with its applications expanding from passenger vehicles to the commercial vehicle market. Stopka O [14] analyzed the development trends of electric transportation in the road passenger and freight sectors. He highlighted that improvements in battery energy density, charging infrastructure, and the declining cost of electrification technology have made the adoption of electric vehicles in road transport an irreversible trend. Among them, electric heavy-duty trucks, with their advantages in load capacity and environmental performance, demonstrate particularly significant potential in the freight sector. They also create opportunities for innovating transportation modes for large objects.

However, due to the lag in battery technology, limited driving range has become a barrier to medium and long-distance transportation. Consequently, scholars have begun to focus on the issue of en-route charging in distribution. Vanitha V [15] applied machine learning to identify fast-charging stations with minimal waiting time and coordinated charging schedules for electric vehicles under range constraints. An Y [16] proposed a coordinated charging mathematical model aimed at minimizing the total charging time for a given fleet of urban electric vehicles, thereby improving charging efficiency and alleviating users’ range anxiety. Chen J [17] developed a hierarchical model for electric vehicles that considers shared charging stations to address the matching problem between large-scale charging demand and available facilities. Kumar V M [18] proposed a dual-objective model that integrates dynamic schedulable time, energy demand fluctuations, and user priorities. Taking into account travel requirements and battery characteristics, the model allocates each electric vehicle to an optimal charging station with the goal of minimizing total time, queuing time, charging time, and energy costs. Devendiran R [19] addressed the problem of charging station selection by incorporating factors such as average waiting time, remaining energy, number of vehicles, and travel distance. Their study demonstrated that this approach significantly improves performance in the context of large-scale charging demand.

In solving logistics distribution models, most existing studies either focus solely on single-stage problems or decompose multi-stage problems into multiple single-stage problems for independent optimization. Tofighi S [20] developed a two-stage possibilistic-stochastic programming approach for systems involving multiple central warehouses and local distribution centers. In the first stage, the optimal locations of warehouses and logistics centers, along with preset inventory levels of relief materials, are determined. In the second stage, rescue distribution plans are formulated under various disaster scenarios. Basso R [21] introduced the two-stage electric vehicle routing problem, where the first stage determines the optimal route to the destination, and the second stage refines the plan by considering vehicle time window constraints to identify optimal charging routes. Abid M [22] proposed a three-stage method to sequentially address customer allocation, route selection, and charging station placement, aiming to minimize total travel time, travel distance, energy consumption, and the number of deployed vehicles. Liu H [23] addressed a heterogeneous fixed-fleet vehicle routing problem with varying vehicle capacities and mixed time windows. Using an improved ant colony algorithm combined with the Dijkstra algorithm, a two-stage solution strategy was designed to achieve minimum transportation costs while ensuring optimal vehicle routing.

Additionally, several studies have proposed solution methods for multi-objective optimization problems in prefabricated building logistics scheduling. Attajer A [24] simulated the operational process of modular integrated construction using a hybrid method that combines multi-agent simulation and deep learning. Their study optimized fleet scheduling through machine learning algorithms and achieved simultaneous improvements in carbon reduction, timeliness, and cost efficiency. Zhang C [25] employed an improved NSGA-II algorithm to solve a dual-objective optimization model for prefabricated component logistics under a Just-In-Time strategy. Their study realized the co-optimization of carbon emissions and delivery efficiency, while also enhancing the robustness of scheduling schemes. Dong C Y [26] optimized the scheduling of modular integrated construction transport vehicles using integer programming and operations research methods. The empirical results demonstrated superior performance compared with traditional empirical scheduling and showed improvements in overall project efficiency. Liu D [27] integrated 4D Building Information Modeling, Global Navigation Satellite System, and Radio Frequency Identification technologies to construct a transportation optimization model driven by real-time construction progress. Their results showed that this model significantly reduced on-site transportation time and enhanced construction efficiency.

The existing literature indicates that although numerous studies have examined the logistics distribution of prefabricated building components, significant gaps remain in addressing the practical scenario of using new energy heavy-duty trucks for transporting large prefabricated components. First, mainstream research has predominantly focused on conventional fuel vehicles or small-scale electric vehicles. In contrast, optimization strategies specifically designed for electric heavy-duty trucks in the transportation of large and heavy components remain insufficiently explored. In practice, electric heavy-duty trucks face constraints such as limited battery capacity and the necessity for en-route charging, which impose more stringent requirements for the coordinated optimization of delivery routes, charging station selection, and charging strategies. However, most existing studies adopt a “full charging at every stop” strategy, overlooking the combined effects of charging costs, delivery time windows, and charging efficiency. As a result, they fail to meet the dual objectives of cost minimization and timeliness in real-world logistics scenarios. Second, in terms of optimization methodology, the majority of existing work relies on single-level evolutionary algorithms to solve single-stage or single-objective distribution problems. Such approaches are often inadequate for addressing the complexity of multi-distribution-center, multi-demand-point, and multi-stage decision-making in prefabricated component distribution. As a result, they lead to insufficient solution diversity and suboptimal global performance.

To address these limitations, this paper introduces the following innovations:

Firstly, Dynamic charging decision optimization model for electric heavy-duty trucks. For the first time, a dynamic charging decision optimization model is developed for the practical scenario of using electric heavy-duty trucks to transport large prefabricated components. In this model, vehicles dynamically select charging stations and determine charging amounts en route based on real-time battery levels, delivery time windows, and remaining travel distances, thereby balancing economic and timeliness objectives. This strategy differs significantly from the traditional full-charging approach, as it is more consistent with real engineering application scenarios and enhances both the applicability and optimization potential of the model.

Secondly, Two-level multi-objective evolutionary algorithm for large-scale, multi-stage decision-making. To address the complexity of multi-to-multi deliveries and multi-stage collaborative decision-making, a two-level multi-objective evolutionary algorithm is proposed. In this framework, the upper-level plans routes and distribution schemes to optimize global objectives such as total cost and delivery timeliness, while the lower level dynamically adjusts charging station selection and charging amounts. The proposed two-level collaborative mechanism broadens the search space and improves global solution quality. It further exhibits superior scalability and adaptability over conventional single-level evolutionary algorithms, particularly in solving large-scale, high-dimensional, and strongly constrained real-world problems.

In summary, the core innovation of this paper lies in the integrated modeling of dynamic charging and multi-objective distribution optimization for electric heavy-duty trucks. Combined with full-process collaborative optimization through a two-level evolutionary algorithm, this approach effectively improves both the economy and timeliness of logistics distribution for prefabricated building components.

2. Methodology

2.1. Problem Description

There are multiple prefabricated building production plants in a certain place, which need to use electric heavy trucks to transport prefabricated components to multiple construction sites within a specified time. However, due to the limited battery capacity of such vehicles, their maximum driving range often fails to satisfy the requirements of long-distance delivery tasks. As a result, when the remaining battery range is insufficient to complete a delivery, vehicles must stop at en-route charging stations to replenish energy. Consequently, the production plants must develop a scheduling plan that accounts for both order information and vehicle battery capacity, while incorporating charging decisions during transit, to ensure that all prefabricated components are delivered to their respective construction sites in a timely and reliable manner.

In order to clarify the scope of application of the study, the following assumptions are made:

• The basic information of each distribution center and demand point, such as coordinates, order information, and time window constraints, is known.
• Since the dimensions of electric heavy-duty trucks meet the maximum size requirements of mainstream prefabricated components (such as floor slabs, stairs, and wall panels), it is assumed that the cargo boxes of all vehicles can accommodate the length, width, and height of these components. Additionally, all vehicles are considered identical in terms of carrying capacity, load capacity, and battery capacity.
• Each construction site has a time window for receiving components. Early delivery or late delivery will result in fines. The specific penalty amount is calculated according to the deviation time.
• Disregarding order variations and temporary assignments during delivery, each vehicle is assumed to return to the factory upon completing a single delivery and to wait for the subsequent task.
• In the process of scheduling scheme planning, it is necessary to select the appropriate time node to go to the designated charging station according to the real-time range of the vehicle, so as to ensure that the vehicle can arrive at the target charging station in time along the way to supplement the power, and avoid the situation that the vehicle power is exhausted during the distribution.
• Each production plant is equipped with a consistent number of dedicated charging piles, which only serve the vehicles of the enterprise itself. The number of charging piles is limited and vehicles are served on a first-come, first-served basis. There may be queues due to multiple vehicles returning simultaneously. The vehicle was fully charged when it left the production plant.
• The commercial charging stations along the way are shared charging piles, which need to compete with other social vehicles for resources. Charging services follow a first-come, first-served principle, and the queuing time is affected by external traffic demand.
• The charging prices at commercial charging stations along the route are different from those at charging stations in distribution centers. The charging prices at commercial charging stations are higher than those at distribution centers.

2.2. Parameter Definition and Relationship

To ensure a clear understanding of the key parameters in this study,

Table 1. Constant parameters.

Parameter	Parameter Meaning	Unit
M	A set of distribution centers, $M\in \left(1,\dots ,m\right)$	/
$P^{\left(m\right)}$	The set of charging piles at distribution center m, $P^{\left(m\right)}\in \left(1,\dots ,p^m\right)$	/
N	A set of demand points, $N\in \left(1,\dots ,n\right)$	/
S	A set of commercial charging stations, $S\in \left(1,\dots ,s\right)$	/
$P^{\left(s\right)}$	The set of charging piles at commercial charging station, $P^{\left(s\right)}\in \left(1,\dots ,p^s\right)$	/
U	The set of intermediate nodes in the road network (non-functional nodes)	/
V	The set of all nodes, $V=M\cup N\cup S\cup R$	/
E	The set of road network edges, $(i,j)$ indicates that $i\to j$ is reachable	/
$R_n$	The total demand quantity of demand point n	ton
Q	Vehicle load capacity	ton
B	Maximum battery capacity of the vehicle	kWh
$[a_n,b_n]$	The service time window of demand point n	h
${\lambda }_1$	The unit charging price of vehicles at the distribution center	¥/kWh
${\lambda }_2$	The unit charging price of vehicles at commercial charging stations	¥/kWh
${\varpi }_1$	Constant charging power at the distribution center	kw
${\varpi }_2$	Constant charging power at the commercial charging stations	kw
$\epsilon$	The speed of the vehicle under constant travel	km/h
$SO{C}_{min}$	The minimum tolerable power threshold for a vehicle	kWh
$\beta$	Penalty coefficient for early delivery before the time window	¥
$\gamma$	Penalty coefficient for delayed delivery later than the time window	¥
$E{V}_1$	Vehicle power consumption per 100 km	kWh/100 km
$E{V}_2$	The actual power consumption of the vehicle after calculating the proportion of kinetic energy recovery, $E{V}_2=E{V}_1·(1-\alpha )$	kWh/100 km
$\alpha$	Kinetic energy recovery ratio	%

and

Table 2. Variable parameters.

Parameter	Parameter Meaning	Unit
$K_{mn}$	The number of vehicles center m dispatches to serve demand point n.	trips
$MK$	The set of all available vehicles, with each vehicle marked as $(m,k)$, represents the k-th vehicle dispatched by distribution center	/
$d_{ij}$	The distance from node i to node j	km
$ROUT{E}^{(m,k)}$	It is the ordered node sequence of the k-th vehicle’s distribution path from center m, $ROU{T}^{(m,k)}=[v_1,v_2,\dots ,v_l]$	/
$q_n^{(m,k)}$	The actual delivery volume of the k-th vehicle dispatched by distribution center m to the demand point n, $q_n^{(m,k)}\in [0,Q]$	ton
$T_n^{(m,k)}$	The time point when the k-th vehicle of distribution center m completes the delivery to demand point n	h
$T_n$	The time point when the delivery of demand point n is completed. If demand point n requires multiple services, the latest service time among the most times will be taken	h
$W^{(m,k)}$	The queuing time for vehicle k to charge at the distribution center m	h
$W_s^{(m,k)}$	The queuing waiting time for vehicle k to charge at charging station s	h

summarize the main constants and variables used in the route planning model of electric heavy-duty trucks. Table 1 lists the constants that define the fixed system parameters. These constants are helpful for establishing a realistic and feasible optimization model. Meanwhile, Table 2 shows the main variables, which are crucial for modeling vehicle routes, energy consumption and charging strategies. These variables capture aspects such as vehicle status, charging behavior, and delivery constraints. The detailed descriptions in these two tables lay the foundation for the subsequent implementation of mathematical formulas and algorithms. Based on the existing basic information in the delivery process, relevant parameters can be derived to obtain more parameter information.

Based on the existing basic information in the delivery process, relevant parameters can be derived to obtain more parameter information. The relationship between each parameter is described as follows: In the model of this paper, each requirement point has a clear list of component requirements, in which the quantity and individual weight of each component are listed. To meet the transportation constraints, this paper calculates the number of required transport trips based on the maximum load capacity of each vehicle and the total weight needed. The component demand list of a certain demand point n is as follows: the quantity of the g-th component is $R_{ng}$, and the weight of a single component of the g-th component is $w_g$. Then the total demand weight $R_n$ of this demand point is as follows:

$$R_n=\sum _{g=1}^{G_n}{R}_{ng}·w_g$$

(1)

In Formula (1), $G_n$ represents the total number of component types required by the demand point n.

Based on the vehicle’s maximum load capacity Q, the number of vehicles required from distribution center m to deliver components to demand point n is the following:

$$K_{mn}=⌈{\displaystyle \frac{R_n}{Q}}⌉$$

(2)

Here, $⌈{\displaystyle \frac{R_n}{Q}}⌉$ represents an upward rounding operation.

2.3. Model Construction

(1) Minimization of the total transportation distance

$$MinF\left(1\right)=\sum _{m=1}^M\sum _{k=1}^{K_{mn}}\sum _{(i,j)\in E}{d}_{(i,j)}·x_{(i,j)}^{(m,k)}$$

(3)

$$x_{(i,j)}^{(m,k)}\in \left\{0,1\right\}$$

(4)

Formula (4) indicates whether the k-th vehicle of distribution center m passes by edge $(i,j)$.

(2) Minimization of the total vehicle charging cost

$$MinF\left(2\right)=\sum _{m=1}^M\sum _{k=1}^{K_{mn}}\left({\lambda }_1·Q_m^{(m,k)}+\sum _{s=1}^S{\lambda }_2·Q_s^{(m,k)}·y_s^{(m,k)}\right)$$

(5)

$$Q_m^{(m,k)}=B-B_{cur,m}^{(m,k)}$$

(6)

Formula (6) represents the charging amount of the k-th vehicle at distribution center m after returning to the distribution center. It is calculated by subtracting the battery capacity when the vehicle returns to the distribution center from the maximum battery capacity of the vehicle. Here, it implies that the battery must be fully charged before the next task can begin.

$$y_s^{(m,k)}\in \left\{0,1\right\}$$

(7)

Formula (7) indicates whether the k-th vehicle of distribution center m is charging at charging station s.

$$Q_s^{(m,k)}=\left\{\begin{array}{cc}min\left(B-B_{cur,s_h}^{(m,k)},B_{remain,s_h}^{(m,k)}-B_{cur,s_h}^{(m,k)}\right)\hfill & \mathrm{if}{s}_h\mathrm{is}\mathrm{last}\mathrm{charger}\hfill \\ min\left(B-B_{cur,s_h}^{(m,k)},B_{s_h:s_{h+1}}^{(m,k)}\right)\hfill & \mathrm{if}\mathrm{future}\mathrm{clients}\mathrm{exist}\hfill \\ B-B_{cur,s_h}^{(m,k)}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

Formula (8) represents the charging volume distribution strategy, and the charging volume is calculated based on the dynamic charging strategy. Specifically, it is divided into the following three situations:

(a) The current charging station is the last one on the route. The vehicle will be recharged to exactly meet the energy consumption demand of the remaining route, ensuring that no additional charging is required after completing the transportation task.

(b) If there are still demand points after the current charging station (i.e., the route still requires delivery), the replenished power at this time must be sufficient to complete the delivery tasks of subsequent demand points, and the remaining power can support the vehicle to reach the nearest feasible charging station.

(c) If there is no demand point after the current charging station (i.e., only for the return journey), the vehicle will be fully charged directly to ensure sufficient energy during the return journey. In the $ROUT{E}^{(m,k)}$, $s_h$ represents the sequence number of the charging stations visited by the k-th delivery vehicle of the distribution center m when performing the current task. In a single delivery task, this vehicle may pass through multiple charging stations for charging.

In the Formula (8), $B_{cur,s_h}^{(m,k)}$ represents the remaining power of the k-th vehicle of the distribution center m when it reaches the charging station $s_h$ on the current distribution route. $B_{remain,s_h}^{(m,k)}$ represents the amount of electricity still needed to complete the remaining distance of this distribution task when the k-th vehicle of distribution center m arrives at the charging station $s_h$. $B_{s_h:s_{(h+1)}}^{(m,k)}$ represents the power required for the k-th vehicle of distribution center m to travel from charging station $s_h$ to the next charging station $s_{(h+1)}$.

$$B_{cur,s_h}^{(m,k)}=B+B_{acc,m}^{(m,k)}-{\displaystyle \frac{{\displaystyle \sum _{(i,j)\in E}}{d}_{(i,j)}·x_{(i,j)}^{(m,k)}}{100}}·E{V}_2$$

(9)

$$B_{remain,s_h}^{(m,k)}={\displaystyle \frac{{\displaystyle \sum _{c=1}^L}{d}_{l_c,l_{c+1}}}{100}}·E{V}_2$$

(10)

$$B_{s_h:s_{(h+1)}}^{(m,k)}={\displaystyle \frac{{\displaystyle \sum _{h=1}^{s_{(h+1)}}}{d}_{s_h,s_{(h+1)}}}{100}}·E{V}_2$$

(11)

Formulas (9)–(11) detail the calculation methods for charging amounts at different stages. Among them, all the nodes in path $ROUT{E}^{(m,k)}$ are numbered as $l(l=l_1,l_2,..,l_L)$, and L represents the number of nodes in path $ROUT{E}^{(m,k)}$.

(3) Minimization of the penalty cost for delivery time deviations

$$MinF\left(3\right)=\sum _{n=1}^N{H}_n$$

(12)

$$H_n=\left\{\begin{array}{c}0 if{T}_n\in [a_n,b_n]\hfill \\ \beta ·(a_n-T_n)if{T}_n<a_n\hfill \\ \gamma ·(T_n-b_n)if{T}_n>b_n\hfill \end{array}\right.$$

(13)

Formula (13) represents the penalty cost for the deviation of the delivery time $T_n$ from the time window at the demand point n.

$$T_n^{(m,k)}=T_{start}^{(m,k)}+W^{(m,k)}+{\displaystyle \frac{Q_m^{(m,k)}}{{\varpi }_1}}+{\displaystyle \frac{{\displaystyle \sum _{(i,j)\in E}}{d}_{ij}·x_{ij}^{(m,k)}}{\epsilon }}+W_s^{(m,k)}+\sum _{s=1}^S{\displaystyle \frac{Q_s^{(m,k)}}{{\varpi }_2}}·y_s^{(m,k)}$$

(14)

Formula (14) represents the calculation formula for the time when the k-th vehicle of distribution center m completes the delivery to demand point n.

$$W^{(m,k)}=T_{start,m}^{(m,k)}-T_{arr,m}^{(m,k)}$$

(15)

Formula (15) represents the charging queue waiting time of vehicle k at the distribution center m. The distribution center only serves internal transportation vehicles. After the vehicle is transported, it returns to the distribution center to be fully charged before the next delivery. If all the charging piles are occupied during charging, it will enter the queue and wait until there is an idle charging pile before charging can start. In the formula, $T_{start,m}^{(m,k)}$ represents the charging start time of vehicle k at the distribution center m. $T_{arr,m}^{(m,k)}$ represents the time when vehicle k arrives at the distribution center.

$$W_s^{(m,k)}=\left\{\begin{array}{c}0 if{T}_{arr,s}^{(m,k)}\ge T_{available}^{\left(p^s\right)}\hfill \\ T_{start,s}^{(m,k)}-T_{arr,s}^{(m,k)}if{T}_{arr,s}^{(m,k)}<T_{available}^{\left(p^s\right)}\hfill \end{array}\right.$$

(16)

In Formula (16), $W_s^{(m,k)}$ represents the queuing waiting time of vehicle k when it is charging at the charging station s. Since the charging station is an open commercial facility and needs to serve external vehicles simultaneously, this study adopts the queue simulation method: a separate queue for the arrival of charging vehicles is established for each charging pile, and the queuing waiting time of vehicle k is dynamically calculated based on the specific time when vehicle k arrives at the charging station s. For each charging pile $p^s$ in charging station s, there is a charging service queue ${\Omega }_{s,p}=\{(t_{11},t_{12}),(t_{21},t_{22}),\dots ,(t_{n1},t_{n2})\}$. $(t_{n1},t_{n2})$ represents the charging time interval of each vehicle, where $t_{n1}$ is the start time and $t_{n2}$ is the end time. The queue is sorted in ascending order according to the estimated charging completion time $t_{n2}$. This method avoids the complexity of directly simulating the vehicle arrival process while ensuring the accuracy of queue time calculation. $T_{start,s}^{(m,k)}$ represents the start charging time of vehicle k at charging station s. $T_{arr,s}^{(m,k)}$ represents the time when vehicle k arrives at the charging station s and will be allocated to the charging pile with the earliest completion time of the load $T_{available}^{\left(p^s\right)}$. After the charging task is assigned, the charging queue ${\Omega }_{s,p}$ of the corresponding charging pile is updated. Tasks after $T_{arr,s}^{(m,k)}$ will be extended backward according to the charging time required by the inserted charging task.

$$T_{end,s}^{(m,k)}=\left\{\begin{array}{cc}{T}_{arr,s}^{(m,k)}+{\displaystyle \frac{Q_s^{(m,k)}}{{\varpi }_2}}\hfill & if{W}_s^{(m,k)}=0\hfill \\ T_{arr,s}^{(m,k)}+W_s^{(m,k)}+{\displaystyle \frac{Q_s^{(m,k)}}{{\varpi }_2}}\hfill & if{W}_s^{(m,k)}\ne 0\hfill \end{array}\right.$$

(17)

Formula (17) represents the charging completion time of vehicle k at the charging pile $p^s$.

s.t

$$\sum _{m=1}^M\sum _{k=1}^K{q}_n^{(m,k)}·z_n^{(m,k)}=R_n\left(\forall n\in N\right)$$

(18)

$$z_n^{(m,k)}\in \left\{0,1\right\}$$

(19)

$$\sum _{n=1}^N{z}_n^{(m,k)}=1$$

(20)

$$q_n^{(m,k)}\le Q$$

(21)

$$SO{C}_{min}\le SO{C}^{(m,k)}\le B$$

(22)

$$T_{start,m}^{(m,k)}\ge T_{arr,m}^{(m,k-1)}+W^{(m,k-1)}$$

(23)

$$T_{start,s}^{(m,k)}\ge T_{end,s}^{(m,k-1)}$$

(24)

Formula (18) represents an assurance that the customer demands, which must be fully met and which is allowed to be achieved through multi-vehicle collaborative delivery. Formula (19) indicates whether the k-th vehicle of distribution center m serves the demand point n. Formula (20) indicates that the k-th vehicle of distribution center m serves only one demand point n at a time. Formula (21) represents the capacity constraint of a single vehicle delivery. Formula (22) represents the charge boundary constraint of vehicle k at any moment. Formulas (23) and (24) represent the tight front and tight rear constraints for vehicle charging.

2.4. Overview of Optimization Solution Methods

This paper studies the many-to-many distribution model of logistics distribution from multiple distribution centers to multiple demand points. In order to better solve the optimization scheduling problem of this distribution model, we divide the problem into two stages for processing. The first stage is used to solve the problem of demand point allocation, which is to match distribution centers that provide delivery services for each demand point. In the second stage, a distribution plan will be formulated based on the geographical locations of the distribution center and demand points, as well as the delivery demand time window, including the delivery sequence of each distribution center providing delivery services to each demand point and the delivery path of vehicles. The problems dealt with in the two stages are interdependent, and the scheduling optimization of the distribution plan in the second stage depends on the demand point allocation results in the first stage.

The numerical experimental results show that if clustering algorithms are directly used in the first stage to match demand points with distribution centers based on the principle of nearest distance, it will actually result in the loss of some high-quality solutions during the optimization of the lower-level distribution plan. This will make the algorithm more prone to premature convergence and fall into local optima. Therefore, based on the NSGA-III algorithm theory [28,29], this paper designs a two-level multi-objective evolutionary algorithm (TC-NSGA-III) based on Pareto theory. This algorithm uses a dual-level transfer structure to transfer individuals from the upper-level algorithm to the lower-level algorithm. In this two-level structure, all individuals in the upper-level algorithm will be passed to the lower-level algorithm through the population transmission mechanism for the next stage of optimization calculation. The final calculation results will be separately returned to the corresponding individuals in the upper-level algorithm, used to evaluate the quality of the individuals in the upper-level algorithm. This will serve as a basis for continuing to guide the iteration of the upper-level algorithm, thereby obtaining a larger search space and improving the solution effect.

2.5. Encoding and Decoding Mechanisms

In this paper, integer coding is used in individuals at each level, as shown in Figure 1. This figure shows the encoding of allocation-distribution individuals in a two-level algorithm, which includes the allocation scheme and distribution sequence of demand points, as well as the sequence of delivery path nodes, which can be used to calculate individual fitness values. The upper-level of the algorithm is used to solve the problem of demand point allocation, so the individual decoding of TC-NSGA-III in the upper-level can obtain the demand point allocation scheme. The lower-level algorithm is used to optimize the order in which each distribution center implements delivery for each demand point and the delivery path for vehicles from each distribution center to reach the target demand point. That is, to determine the order in which each distribution center delivers goods to demand points, as well as the road network nodes and charging stations that vehicles pass through when delivering goods to each demand point.

2.6. Process of Many-Objective Two-Level Co-Evolution Algorithm

The optimization scheduling model under the many-to-many distribution mode consists of two levels. In the upper-level optimization model, it is necessary to optimize the demand point allocation scheme and determine which distribution center will deliver each demand point. The second level optimization model needs to optimize the demand point distribution sequence and plan the distribution route based on the demand point allocation results generated by the first optimization model. The two-level model is progressive and highly coupled. For this type of two-level programming problem, the common single-level solution method of multi-chromosome joint coding [30] often fails to achieve good results. The hierarchical model and hierarchical algorithm can achieve a larger solution range and solution accuracy.

The main process of the TC-NSGA-III algorithm is shown in Figure 2. The individuals of the upper-level model will be passed into the lower-level for iterative optimization. After the iteration of the lower-level model is completed, the selected Pareto center solutions from the final population will be passed back to the upper-level model, so that the individuals in the population of the upper-level model have the optimization objectives of the lower-level model. Afterward, in the upper-level model, crossover, mutation, non-dominated sorting, and other operations are performed again based on the three optimization objectives to complete population evolution.

The overall process of the algorithm is shown in Algorithm 1, and the process of population return is shown in Algorithm 2. The extraction process of the Pareto center solution in the lower-level algorithm is detailed in Algorithm 3.

Algorithm 1 TC-NSGA-III

Require:  Population size N, generations G Ensure:  Final non-dominated solutions of upper-level population   1: Initialize upper-level population $P_1$ (customer allocation plans)   2: Evaluate each individual in $P_1$ using upper-level objective $F_1$   3: for $g=1$ to G do   4:       for each individual $x_i$ in $P_1$ do   5:             Initialize lower-level population $P_2$ for delivery routing   6:             Optimize $P_2$ using NSGA-II on objectives $F_2$ and $F_3$   7:             Extract Pareto front of $P_2$   8:             Select center solutions and return to upper level   9:       end for 10:       Combine $F_1$, $F_2$, $F_3$ for all returned solutions 11:       Perform non-dominated sorting and selection in upper-level population 12:       Generate next generation $P_1$ using NSGA-II 13: end for 14: return Final non-dominated solutions of $P_1$

Algorithm 2 Feedback-Based NSGA-III Optimization

Require:  upper-level model population Ensure:  Population after feedback 1: for each individual i in the population do 2:       Initialize a new population based on individual i 3:       for $iter=1$ to $max\_iterations$ do 4:             Perform NSGA-III iterative calculation on the population 5:             Select middle solution individual j from the population 6:             Transfer individual j back and merge into individual i 7:       end for 8:       Obtain the population after the feedback 9: end for

Algorithm 3 Selection of Middle Solution in Pareto Front

Require:  upper-level model population F Ensure:  Middle solution m 1: for each solution in Pareto front F do 2:       Normalize objectives to [0, 1] range 3:       Compute distance: $d=\sqrt{{\mathrm{obj}}_1^2+{\mathrm{obj}}_2^2+{\mathrm{obj}}_3^2}$ 4: end for 5: Sort Pareto front F based on distance 6: middle_index $\leftarrow \lfloor \mathrm{length}(F)/2\rfloor$ 7: $m\leftarrow F[middle\_index]$ 8: return  m

2.7. The Evaluation of Pareto Front

The shape of the Pareto front represents the balance between different optimization objectives, and the calculation result of the NSGA-III algorithm is only an approximation of the Pareto front. The true Pareto front of NP-hard problems is usually difficult to obtain. Therefore, this paper evaluates the algorithm based on the following three evaluation indicators [31]:

(1) The proximity between the points on the approximate front and the true Pareto front

The hypervolume(HV) estimates the volume of the target space dominated by a set of Pareto optimal solutions. It is defined as the volume of the region enclosed by all solutions on the reference point and non-dominated solution set. The method of calculation of the hypervolume metric is shown in Formula (25). The larger the value, the better the approximation performance.

$$HV=\delta \left({\cup }_{i=1}^{\left|S\right|}{v}_i\right)$$

(25)

(2) Diversity of the Pareto front

The inverse generation distance (IGD) is used to measure the closeness and coverage quality between the non-dominated solution set and the true Pareto front. The smaller its value, the better the solution set. The calculation method is shown in Formula (26).

$$IGD={\displaystyle \frac{1}{\left|P^{*}\right|}}\sum _{P\in P^{*}}\underset{q\in A}{min}\sqrt{\sum _{i=1}^m{\left(p_i-q_i\right)}^2}$$

(26)

(3) Uniformity of Pareto solution

The dispersion index (Spread) is used to measure the diversity of the solution set in the target space, reflecting whether the solution set is evenly distributed on the true Pareto front. The smaller the value, the better the distribution of the solution set. The calculation method is shown in Formulas (27) and (28).

$$Spread={\displaystyle \frac{{\sum }_{i=1}^{N-1}\left|d_i-\overline{d}\right|+d_f+d_l}{d_f+d_l+\left(N-1\right)\overline{d}}}$$

(27)

$$\overline{d}={\displaystyle \frac{1}{N-1}}\sum _{i=1}^{N-1}{d}_i$$

(28)

3. Experiments

The data used in this study was simulated based on the actual locations of prefabricated component production plants and demand construction sites, as well as daily distribution tasks. The specific data has been published on Github (https://github.com/zxc20121234/Electric-truck, accessed on 28 November 2024). The numerical experiment first verified the correlation between the two-level of algorithms through Monte Carlo experiments [32,33]. Then, the optimal algorithm parameters are determined through orthogonal experiments. Finally, scheduling simulations were conducted based on case data and compared with conventional single-level algorithms to demonstrate the superiority of the algorithm.

The experimental design in this section was developed with reference to existing studies on similar vehicle transportation scheduling problems. In particular, we adopted parameter settings, benchmark instance structures, and evaluation metrics inspired by related works in freight vehicle routing and scheduling optimization [34,35,36]. These references provide established modeling assumptions and test instance configurations, which ensure that our numerical experiments are comparable to prior research and allow for meaningful performance evaluation of the proposed method.

In the numerical experiments, programming development was carried out in the Python 3.9.1 environment, and multi-process technology was employed to achieve parallel computation. The use of multi-process technology significantly improved computational efficiency, enabling faster solution times for large-scale optimization problems. All numerical experiments were performed on a workstation equipped with an Intel Core i7-13700KF CPU. In order to optimize the overall performance of the algorithm, parallel computing was implemented through multiprocessing and multithreading techniques throughout the computation process.

3.1. Monte Carlo Coordination Experiment of Multi-Stage Scheduling Scheme

In the many-to-many distribution mode with multiple distribution centers and demand points, the optimization problem needs to be coordinated and optimized in multiple stages. If the allocation of demand points is solely based on minimizing the distance between customers and factories, it will lead to excessive optimization of the results in the first stage. This restriction reduces the feasible solution space for subsequent delivery plans. As a result, a large number of high-quality solutions may be lost. Such losses hinder the second-stage algorithm iteration and prevent the model from effectively optimizing the overall delivery plan. Consequently, it becomes difficult to achieve global optimality, which in turn reduces overall delivery efficiency. To further illustrate the problem, we design a Monte Carlo coordination experiment based on the two-stage scheduling scheme. The objective of this setup is to analyze how over-optimization in the demand point allocation stage influences the optimization of the distribution plan in the second stage.

In the Monte Carlo coordination experiment, we first construct demand point allocation plans with different values based on the objective function of the upper-level model. Each generated allocation plan is then fed into the second stage to carry out the optimization of the distribution plan. Through this iterative process, the optimal vehicle distribution scheme corresponding to each allocation plan is obtained. Finally, the objective function values of all solution sets are recorded for subsequent analysis. In the experiment, the NSGA-III algorithm was used to solve the scheduling scheme for the second stage. The algorithm was iterated 100 times, with a population size of 100, a crossover rate of 80, and a mutation rate of 10. Reflecting the degree of coordination through the correspondence between the average objective function values of individual populations.

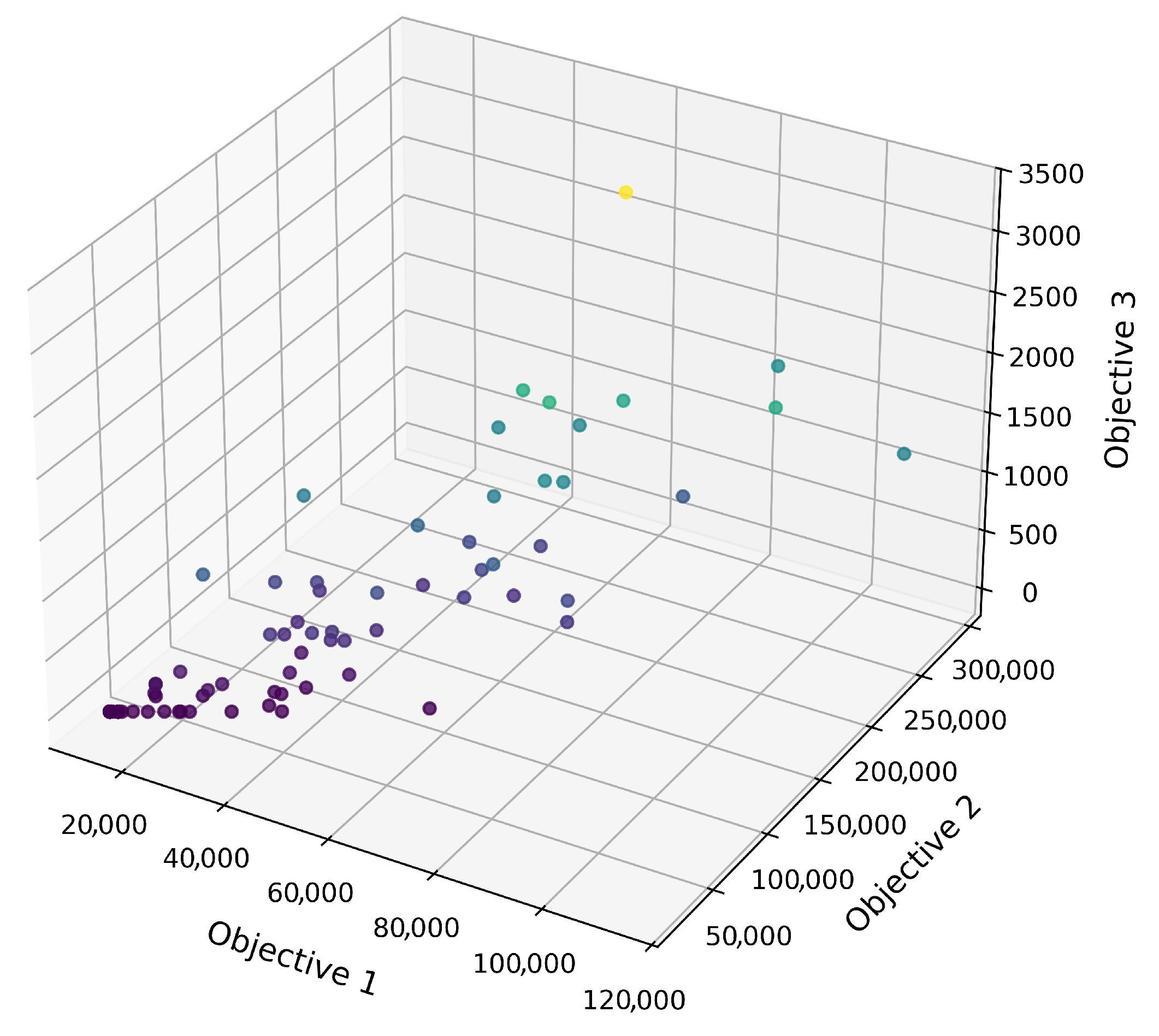
Figure 3 shows the relationship between the optimization objective function $F_1$ and its lower model optimization objectives $F_2$ and $F_3$ during the customer allocation phase. It can be seen from the figure that the high-quality solutions of the lower model are not completely distributed below the minimum value of $F_1$, but are distributed in a larger range. As shown in Figure 3, the optimal solution of the lower-level model is distributed near the median value of the entire solution space with respect to the objective function of the upper-level model. This result shows that when dealing with this kind of multi-stage optimization problem, the optimal solution of the upper-level model cannot be directly introduced into the lower-level model. Instead, collaborative optimization is required to avoid the situation where the lower-level model is trapped in the local optimum due to the upper-level model solution limiting the algorithm’s operating space when solving the lower-level model.

To verify the observations in Figure 3 from a statistical perspective, we conducted a multi-sample t-test. Based on 10 different distribution cases, we respectively extracted the lower-level objective function values ($F_2$, $F_3$) corresponding to the optimal solutions of the upper-level model’s objective function, and compared them with the optimal solutions obtained by the lower-level model under the collaborative optimization algorithm. By comparing the performance of the two types of solutions on the lower-level objectives and conducting a statistical significance analysis using a paired t-test, we evaluate whether their differences are statistically significant. The results indicate that there is a significant difference in the overall solution space distribution between the target value of the lower-level model solution and the global optimal value of the upper-level objective function. Statistically, the former is more likely to occur near the median value in the upper-level objective space, which supports the conclusion drawn from Figure 3. The detailed statistical results are summarized in

Table 3. Summary of t-test analysis results.

Target	Upper-Guided Lower-Level Mean	Lower-Level Optimum	t Value	p Value
$F_2$	40,703.51	20,327.65	3.530	0.002
$F_3$	3620.06	860.13	3.393	0.003

.

3.2. Adjustment of Orthogonal Experimental Parameters

In the two-level objective evolutionary algorithm, the population size, maximum iteration times, crossover probability, and mutation probability of each level will all affect the algorithm’s running time and final solution results. In order to find the optimal parameter combination, population size (NP), maximum number of iterations (MI), crossover probability (PC), and mutation probability (PM) are used as variable parameters. This paper sets up 16 groups of experiments, and the comparative experimental parameters designed according to different factor levels are shown in

Table 4. Orthogonal experimental parameters design.

Exp. No.	NP	MI	PC	PM
1	50	200	0.75	0.15
2	100	200	0.70	0.10
3	150	200	0.90	0.25
4	200	200	0.85	0.20
5	50	300	0.85	0.20
6	100	300	0.90	0.25
7	150	300	0.70	0.10
8	200	300	0.75	0.15
9	50	400	0.90	0.25
10	100	400	0.85	0.20
11	150	400	0.75	0.15
12	200	400	0.70	0.10
13	400	50	0.90	0.25
14	400	100	0.85	0.20
15	400	150	0.75	0.15
16	400	200	0.70	0.10

. HV, IGD, Spread, algorithm running time, and the average value of the final population objective function are used as evaluation indicators of the algorithm.

The results of the orthogonal experiments presented in Table 4 and

Table 5. Evaluation indices of orthogonal experiment.

Exp. No.	TIME	SP	IGD	HV
1	186.52	2.732051	0.044025	0.959997
2	206.42	2.653240	0.043391	0.969555
3	234.78	2.154987	0.035491	0.978416
4	254.32	2.887651	0.039882	0.979523
5	370.95	2.565487	0.050730	0.964958
6	457.49	2.326549	0.042504	0.958750
7	501.45	1.959845	0.041052	0.982515
8	765.43	1.879540	0.033458	0.972737
9	984.44	1.859877	0.045067	0.982562
10	1336.89	1.851329	0.039164	0.977808
11	1578.21	1.802051	0.031445	0.977351
12	1789.03	1.793246	0.028932	0.988260
13	2245.04	1.762051	0.049911	0.981063
14	2648.54	1.745798	0.037811	0.968569
15	2987.24	1.732575	0.034372	0.972739
16	3635.15	1.738795	0.032498	0.981547

indicate that when the population size reaches 400 and the number of iterations reaches 200, the running time of the algorithm increases by over 100% compared to the parameters utilized in Experiment 12. However, the Hypervolume (HV), Inverted Generational Distance (IGD), and Spread of the algorithm do not exhibit significant improvements. Consequently, this study adopts the parameter combination from Experiment 12, as it strikes an optimal balance between the optimization effect and the running time.

3.3. Algorithm Comparison Experiment

3.3.1. Comparison of Solutions for Different Structural Algorithms

In order to effectively reflect the advantages of the TC-NSGA-III algorithm, this paper compares the TC-NSGA-III algorithm with the other two algorithms that use a single-level structure. These two single-level solving algorithms include the NSGA-II algorithm based on multi-chromosome joint encoding (C-NSGA-II) and the NSGA-III algorithm using two-stage stepwise solving (S-NSGA-III). The multi-chromosome joint encoding method refers to representing the relevant chromosomes of demand point allocation, demand point delivery order, and delivery path as a single individual, and performing the corresponding evolutionary operations on multiple chromosomes simultaneously during algorithm iteration. The two-stage, step-by-step solution optimizes the demand point allocation plan according to the minimization of the total distance as the optimization goal. After obtaining the Pareto frontier, the distribution plan of each individual in all Pareto frontiers is optimized separately. The obtained distribution plan is then combined with the corresponding allocation plan to form a complete solution. In the comparative experiments, each experiment was repeated 10 times, and the average value was taken as the final result. The initial population of the NSGA-II and NSGA-III algorithms used in the comparative experiment is 100, and the number of algorithm iterations is 100. The other parameters are consistent with those of the two-level multi-objective genetic algorithm in this paper.

As shown in

Table 6. Evaluation indexes under different calculation examples and solution methods.

Solution Method	TIME	SP	IGD	HV
TC-NSGA-III	1958.54	1.933246	0.028932	0.99998
C-NSGA-II	412.78	1.842311	0.031256	0.97128
C-MOEAD	315.93	1.902874	0.036028	0.96693

, the IGD and HV metrics of the TC-NSGA-III algorithm are significantly better than those of other algorithms, but it takes a longer time, and the performance of SP is relatively backward, which may be related to the collaborative optimization strategy of two-level models. According to the results in

Table 7. Average value of the final population objective function of the algorithm under different examples and solution methods.

Solution Method	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$
TC-NSGA-III	54,350.14	48,100.13	656.7921
C-NSGA-II	58,531.15	50,680.76	700.3398
S-NSGA-II	64,492.78	60,586.43	866.5465

,

Table 8. Max value of the final population objective function of the algorithm under different examples and solution methods.

Solution Method	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$
TC-NSGA-III	136,677.5	155,750.1	3907.386
C-NSGA-II	141,732.5	172,477.0	5348.073
S-NSGA-II	152,071.5	198,718.0	5310.187

and

Table 9. Min value of the final population objective function of the algorithm under different examples and solution methods.

Solution Method	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$
TC-NSGA-III	12,522.02	20,229.79	252.64
C-NSGA-II	19,353.17	30,190.95	309.72
C-MOEAD	20,975.64	32,722.01	347.44

, the average population objective function value of the TC-NSGA-III algorithm has a larger optimization range than other comparison algorithms, and the maximum and minimum values of the population individuals are lower than those of the other two algorithms. This result shows that the final population obtained by the TC-NSGA-III algorithm has better population quality. Figure 4 shows the final Pareto front obtained by the TC-NSGA-III algorithm, indicating that TC-NSGA-III can obtain a uniform and effective solution set in the solution space.

The above data confirm the advantages of the two-level collaborative optimization strategy adopted by the designed algorithm in solving this type of two-stage optimization problem. The TC-NSGA-III algorithm can effectively improve the search performance and depth in a larger solution space. Although it takes a longer time, it can still obtain better optimization results within an acceptable time range and has higher application value.

3.3.2. Comparison of Scheduling Scheme Effects Between Dynamic Charging Strategy and Full Charging Strategy

The traditional full charging strategy lacks consideration of the vehicle’s real-time remaining driving range. Regardless of the length of the subsequent journey, once the vehicle needs to be charged, it will be fully charged at a commercial charging station in one go. Although this simplifies charging management, it results in vehicles spending more time charging at commercial charging stations. The charging price of commercial charging stations is often higher than that of distribution center charging facilities, and the longer the charging time at commercial charging stations, the higher the overall charging cost. Therefore, this paper sets up a method to dynamically adjust the charging power according to the distance of the delivery task and employs it to develop the vehicle charging strategy. This strategy can accurately calculate the amount of charging power required for vehicles to complete delivery tasks, reducing the amount of charging power at commercial charging stations and thus reducing overall charging costs.

Table 10. Comparison of optimization effects between dynamic charging strategy and full charging strategy.

Objective	Dynamic Charge Level	Fully Charged	Optimization Range (%)
$F_1$	45,200.25	45,200.25	0.0
$F_2$	135,200.80	160,628.12	15.83
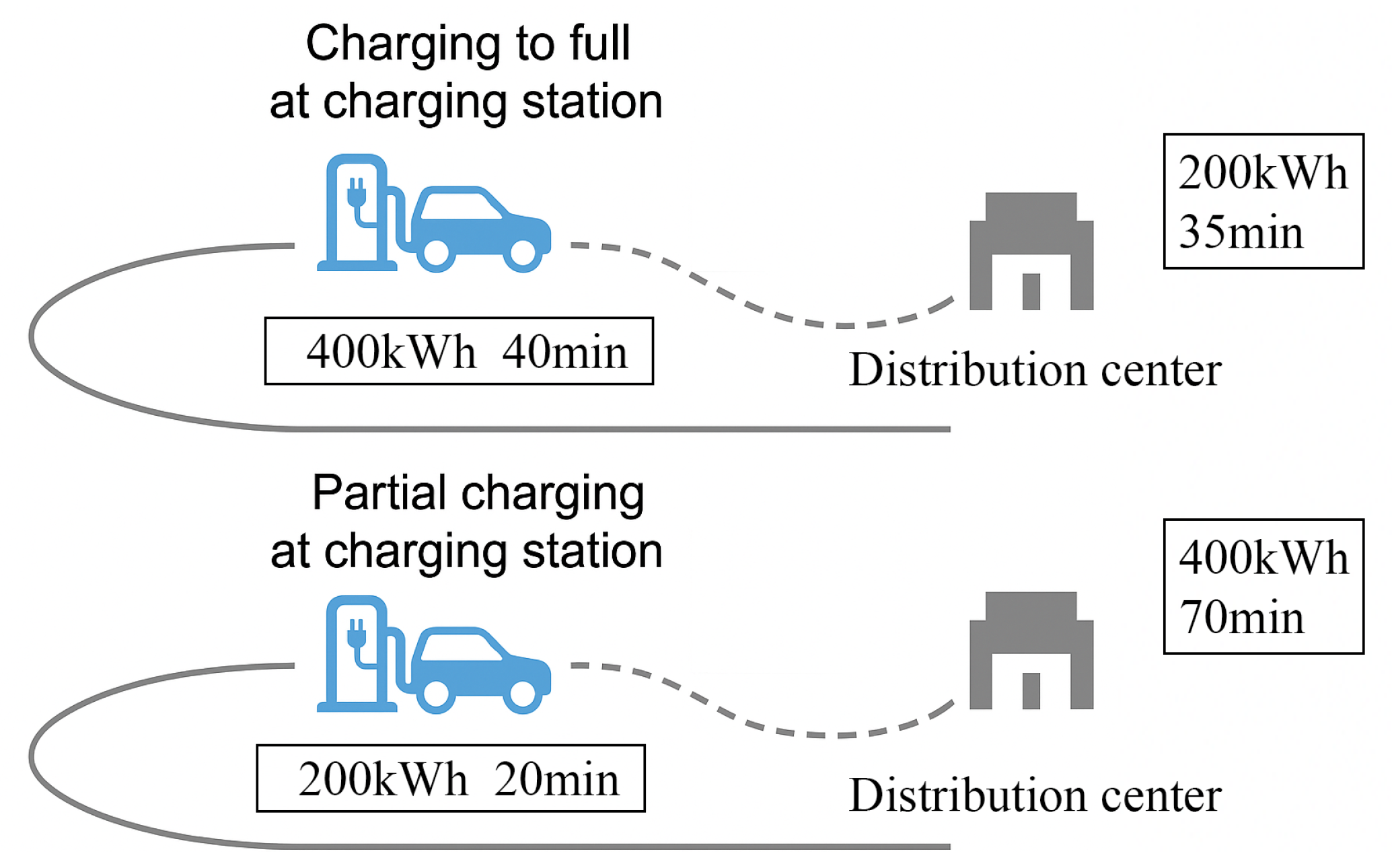
$F_3$	1121.64	1096.87	−2.26

presents the comparison of objective values between the distribution schemes using the dynamic programming charging strategy and the full charging strategy. The comparison is made under the condition that the number of vehicles at the distribution station remains the same for a given customer allocation scheme. Comparative experimental data show that the method of dynamically adjusting charging power can effectively reduce the overall charging cost while ensuring task completion, and the charging cost reduction rate can reach more than 15%. At the same time, the charging stations inside the distribution center operate at a much lower speed compared with commercial supercharging stations. Consequently, when a dynamic charging strategy is adopted, the charging time of vehicles at the distribution center increases. This extended charging time postpones the departure of vehicles for the next task and results in higher delivery penalties. As shown in the case in Figure 5, when the vehicle arrives at the charging station on its return journey, the maximum rechargeable capacity is 400 kWh, and the remaining mileage requires the consumption of 200 kWh of electricity. If the full charging strategy is adopted, 400 kWh of charging is required at the charging station, which takes 40 min. After returning to the distribution center, it takes 35 min to charge 200 kWh to fully charge the battery. The overall charging time is 75 min. If the dynamic charging strategy is adopted, it takes 20 min to charge 200 kWh at the charging station. After returning to the distribution center, it takes 70 min to charge 400 kWh. The total charging time is 90 min. According to the data in Table 10, the penalty amount of the dynamic charging strategy is 2.26% higher than that of the full charging strategy. Dynamic charging strategies will cause a 15 min delay in vehicle departure time, resulting in an increase in delay penalties. However, although the penalty associated with dynamic charging strategies increases slightly, a substantial reduction in overall charging cost can be achieved. Consequently, the comprehensive transportation cost is significantly reduced, which holds great importance for enterprise operations. Figure 5 shows the optimization results of the vehicle delivery routes assigned by the completed customers.

In order to further address the issue of increasing penalty amounts, we have performed tests and found that adding a small number of vehicles can solve this problem. According to the data in

Table 11. Comparison of changes in total penalty value after increasing the number of delivery vehicles.

Objective	Additional Vehicles	No Additional Vehicles	Optimization Range (%)
Delay Penalty	1121.64	1083.17	3.43

, if the delivery plan and vehicle number remain unchanged, and the number of vehicles in each delivery center is increased by one under the dynamic charging plan, the total charging cost remains unchanged. However, the total penalty amount for delivery has decreased due to the increase in the number of vehicles, which reduces the waiting time for departure, and can be basically the same as the penalty amount under the original full charging strategy.

Overall, the dynamic charging scheme can effectively reduce the total cost during the delivery process and has high application value.

3.4. Sensitivity Analysis

In actual applications, the deployment of charging equipment on a scale comparable to commercial supercharging stations is often not feasible at distribution stations due to cost and space limitations. Additionally, the charging costs of self-built charging piles are considerably different from those of commercial supercharging stations. During the numerical experimental research process, it was found that when the dynamic charging strategy is adopted for scheduling optimization, the difference between charging cost and charging rate had an impact on the final cost optimization effect. Therefore, in order to further examine the impact of charging price differences and charging rates on scheduling optimization, 20 distribution scheme examples were selected. The optimization effects under different parameters were then calculated. The resulting influence degrees were finally assessed and validated through charts and statistical tests.

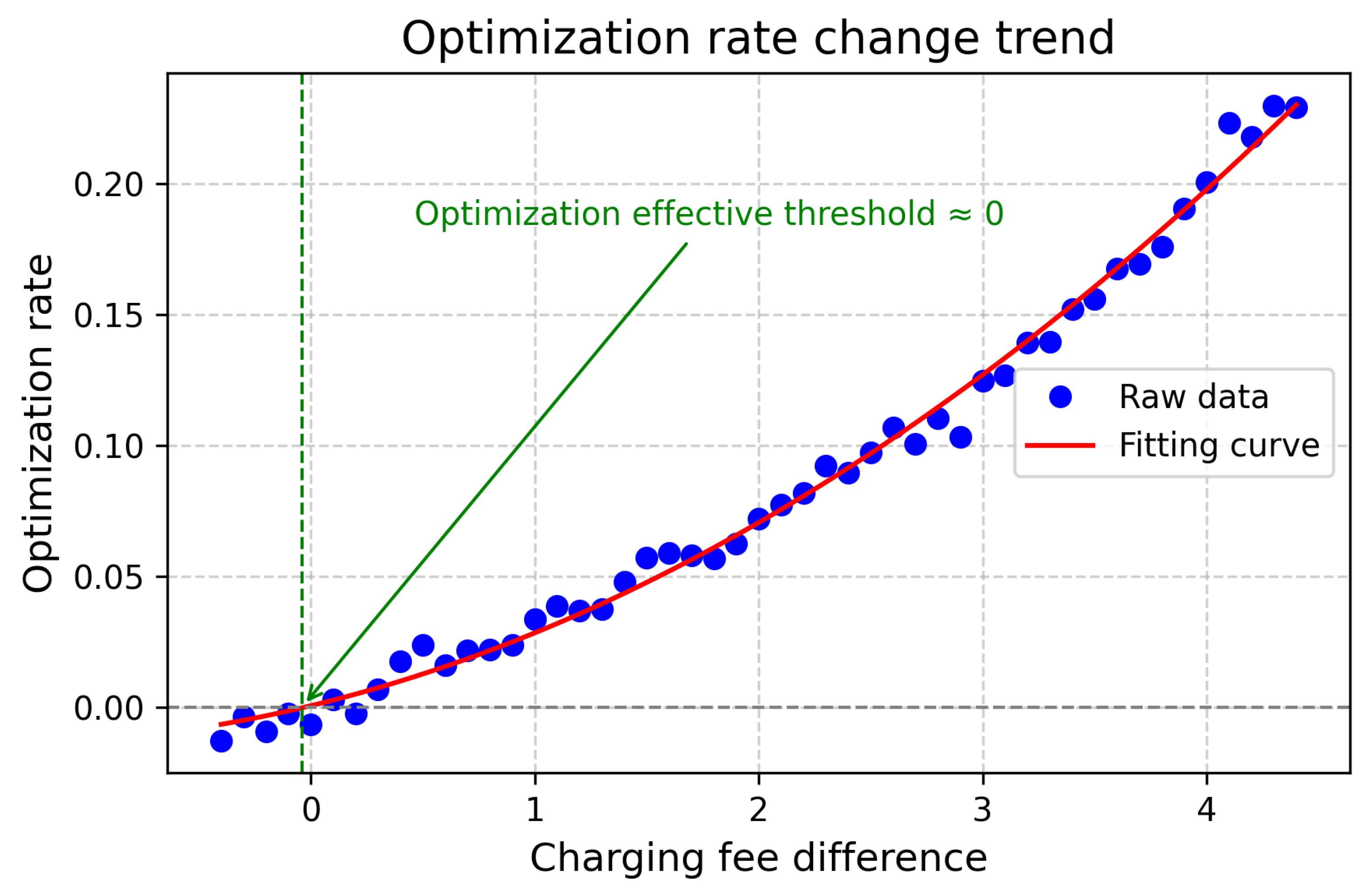
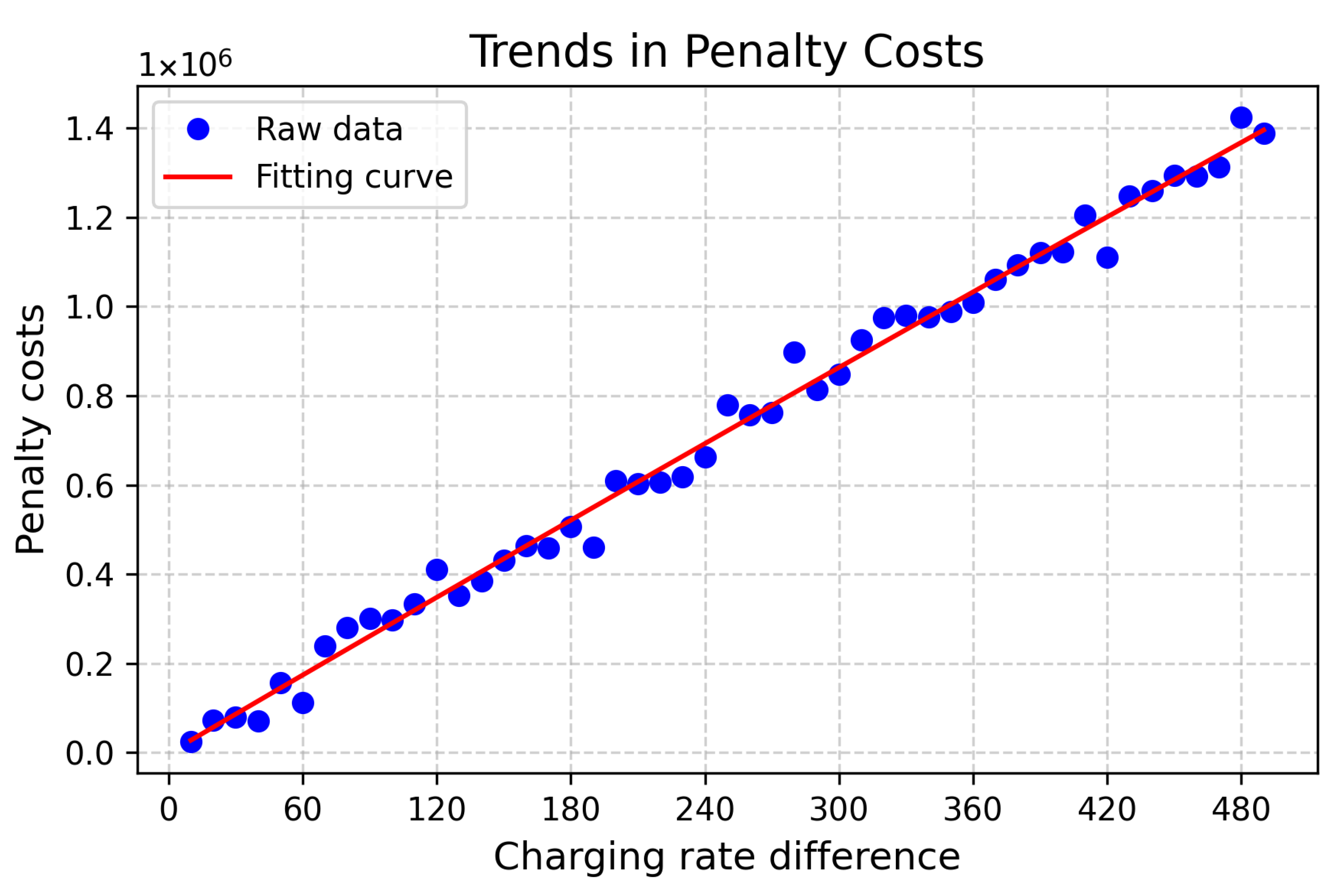
Figure 6 shows the impact of different charging cost differences on the optimization rate when the distribution plan is the same. When the rate difference is 0, the charging location is not affected by the charging cost, and the dynamic charging strategy will not be able to effectively optimize the overall charging cost. Additionally, as the difference in charging rates increases, the overall optimization rate also rises accordingly.

Table 12. Results of t-test for charging costs of dynamic charging strategy and full charging strategy under different charging cost differences.

Dynamic Charging Strategy Charging Cost (Average)	Full Charging Strategy Charging Cost (Average)	Standard Deviation	t Value	p Value
188,734.676	203,628.589	53,820.285	−9.944	0.02

presents the charging cost data for both dynamic and full charging strategies under varying charging price differentials, aiming to assess whether the impact of charging price differences on charging costs is significant. The results show that the optimization advantages of the dynamic charging strategy also exhibit significant differences in a statistical sense, further confirming the effectiveness of the strategy.

To analyze the impact of charging speed differences on penalty costs, multiple simulation experiments for charging power levels were designed. Different charging speed levels were set for the distribution center and external charging stations, and the variations in total penalty costs under each condition were recorded. For each group of experiments, only the charging speed was changed while other parameters were kept constant to ensure the comparability of the results. Figure 7 illustrates the impact of charging speed differences on the overall penalty cost. Since the charging speed at the distribution center is lower than that at commercial charging stations, the waiting time for vehicles charging at the distribution center increased, leading to more delayed orders and higher penalty costs. Moreover, the greater the charging speed difference, the longer the overall waiting time for vehicles at the distribution center, further exacerbating distribution delays and increasing the total penalty cost.

Table 13. Pearson correlation analysis results of penalty costs under different charging rate differences.

Correlation Coefficient	p Value	Sample Size
0.864	0.01	100

presents the results of the statistical analysis of the penalty cost under different charging speed differences. Pearson correlation analysis is used to test whether the charging speed difference has a significant impact on the penalty cost. The analysis results show that the difference in charging speed and penalty cost exhibits a significance level of 0.01, thus indicating a significant positive correlation between them.

In conclusion, the dynamic charging solution can effectively help enterprises save overall distribution costs, and it can also be used to guide enterprises in configuring the number of required transport vehicles based on distribution order tasks.

3.5. Case Studies and Simulation Experiments

3.5.1. Dataset Construction

To verify the proposed optimization model and assess its applicability and effectiveness in real-world scenarios, a case dataset based on actual component distribution requirements was constructed. On this basis, simulation experiments were carried out. The data of this case is derived from the actual engineering dispatching background, combined with key factors such as the urban road network structure, the range performance of electric heavy-duty trucks, the status of dynamic charging stations, customer orders, and time windows, fully covering the optimization dimensions involved in the model design.

Table 14. Data configuration list.

Category	Parameter Item	Description
Network structure	Number of road network nodes	200 (ID: 1–200)
	Number of distribution centers	3 (ID: 201–203)
	Number of demand points	31 (ID: 225–255)
	Commercial charging stations	18 (ID: 207–224)
Vehicle configuration	Electric trucks per station	8–10
	Battery capacity	1000 kWh
	Max driving range	800 km
	Kinetic energy recovery rate	20%
	Unit energy consumption	1.3 kWh/km
	Loading capacity	36 t
Charging system	Charging power (distribution center)	350 kW
	Electricity price (distribution center)	1.2 ¥/kWh
	Charging power (commercial station)	600 kW
	Electricity price (commercial station)	4.5 ¥/kWh
Requirement configuration	Total customer demand	200–800 t
	Customer time window	[20, 150]
Optimal settings	Penalty coefficient	$\beta =50$, $\gamma =100$

lists the actual configurations used in the simulation experiment.

3.5.2. Design and Operation Mode of Simulation Experiment

Based on the completion of the case dataset construction, this paper conducts simulation experiments based on the optimization model and algorithm. The system automatically completes three key decisions: customer allocation, vehicle route planning, and energy replenishment dispatching. Orders at each demand point can be completed by multiple vehicles in coordination. Each node in the vehicle path (including demand points and charging stations) undergoes power detection and dynamic decision-making on charging strategies.

The queuing behavior of commercial charging stations is jointly simulated by the vehicle arrival sequence controlled by a Poisson distribution and the actual queue state. Internal charging at the distribution center is dynamically maintained through the task queues of each charging pile and allocated to returning vehicles based on the earliest idle time strategy. Each path automatically takes into account the kinetic energy recovery effect. Based on the remaining demand analysis strategy of the path segment, it is determined whether to charge halfway, the amount of charging, and the location of the selected charging station. For each simulation run, performance indicators, including the total vehicle routing distance of each distribution center, energy consumption, charging queue time, internal and external charging costs, customer service completion time, and time window penalties, are recorded, which are then used to evaluate the overall performance of the model.

3.5.3. Experimental Results and Analysis

Table 15. Summary of scheduling optimization results of distribution centers.

DC	Distance (km)	Commercial Charge (kWh)	DC Charge (kWh)	Total Cost (¥)	Time Window Penalty (¥)
S201	99,778.64	36,277.95	93,434.28	275,371.94	23,513.69
S202	87,306.31	31,743.21	81,754.99	240,950.44	20,571.73
S203	62,361.65	22,673.72	58,396.43	172,107.46	14,694.81
Total	249,446.61	90,694.89	233,585.70	688,429.85	58,780.24

summarizes a set of scheduling results from the experiment during the simulation process. These results are derived from the Pareto preface of the final solution set and include the total distribution distance, internal and external charging capacity, comprehensive charging cost, service time window penalty, and the comprehensive charging cost optimization rate compared to the full charge strategy. The experimental results show that the model can provide an integrated scheduling solution for complex component demand scenarios, effectively controlling the charging cost.

Table 16. Evaluation of simulated scheduling performance indicators.

Indicator	Value	Explanation
Total number of tasks	328 vehicle trips	Each demand point is accomplished by several train services
Time window penalty	179.2 ¥ per customer	The average delay cost generated
Average mileage per vehicle	9238.7 km	The average total mileage of all vehicle paths
Proportion of charging at commercial stations	27.91%	The proportion of total charging from commercial charging stations
Optimization rate of total charging cost	13.12%	The total cost optimization rate compared to the full charging strategy
Time window penalty optimization rate	−5.87%	The total penalty optimization rate compared to the full charging strategy

presents the evaluation results of the simulation scheduling performance indicators based on the actual case data. The dispatching task involves a total of 328 vehicle trips, covering 93 complete delivery routes. Each customer’s demand is fulfilled by several vehicle trips. With respect to charging strategies, external charging stations contribute 27.91% of the total charged energy. This result suggests that, during the optimization of vehicle delivery tasks, the model tends to give priority to the cost advantages of on-station charging. In terms of optimization effect, compared with the full charging strategy, the proposed dynamic charging strategy can achieve a 13.12% reduction in the total charging cost in real cases. However, the time window penalty optimization rate is −5.87%, indicating that while the cost is reduced, the delay penalty has slightly increased. Overall, this scheduling strategy significantly reduces charging costs while maintaining a high completion rate of distribution tasks and a reasonable distribution of path lengths, providing a feasible reference for practical applications.

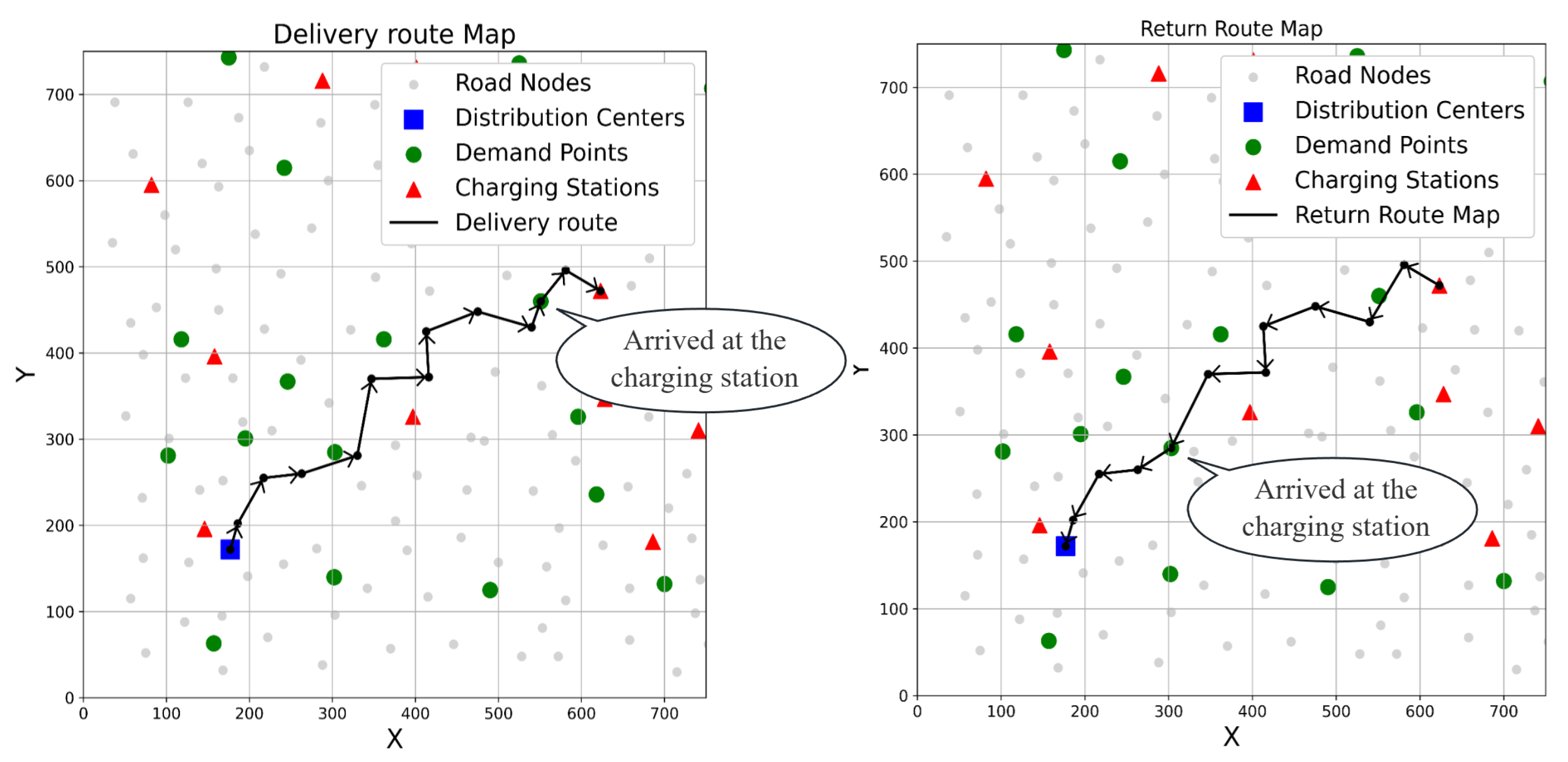
Figure 8 shows a typical path planning scheme for electric heavy-duty trucks in urban component distribution tasks. The figure contains four types of node elements: gray dots represent road network nodes, which form the basic transportation network accessible to vehicles; the blue square nodes represent the distribution centers (starting points), from where vehicles depart and eventually return. The red triangles represent commercial charging stations where vehicles can be recharged during the journey. The green dots represent the customer’s demand points (construction site locations), and the vehicles need to complete the component delivery tasks within the time window constraints. The black lines represent the complete delivery route of a specific vehicle. The route dynamically alternates between demand points and charging stations, demonstrating the model’s comprehensive optimization capabilities for range constraints, kinetic energy recovery, and charging queue states during the path planning process.

The simulation results of this case indicate that the proposed model is capable of effectively addressing the coupled problem of demand allocation, routing, and charging planning in high-complexity scenarios. Additionally, the improvements in scheduling efficiency and cost control are significant. In terms of charging allocation, the system tends to prioritize the advantageous in-station electricity prices. However, in long-distance distribution, external charging is flexibly activated, which demonstrates good dispatching flexibility. Overall, this model has the potential to be deployed and applied in real component distribution projects.

4. Conclusions and Discussion

The logistics industry is currently placing increasing emphasis on environmental protection. Within this context, the transportation sector plays a pivotal role in driving green transformation. At the same time, electric vehicle technologies are advancing and reaching higher levels of maturity. Consequently, the electrification of logistics fleets has drawn significant attention, given its potential to enable low-carbon operation and long-term sustainable development. Nevertheless, existing research remains notably insufficient with respect to the distribution of large-volume, heavy-load items such as prefabricated components. In particular, in-depth investigations into the charging strategies and scheduling optimization of electric vehicles in this context are still lacking. As a result, the application potential of electric vehicles in engineering logistics has yet to be fully realized. Therefore, this paper conducts the following research on the logistics transportation optimization of prefabricated components for electric vehicles:

Firstly, This paper sets up a logistics model for the delivery of prefabricated components by electric heavy trucks. Considering the actual delivery situation, this paper conducts research on the delivery of prefabricated components from multiple production plants to multiple construction sites.

Secondly, In this study, factors such as the distribution scheme of prefabricated component plants, vehicle routing, selection of en-route charging stations, and real-time adjustment of charging power are comprehensively considered, and a two-level optimization model is developed. The upper-level model addresses the allocation of demand points. The lower-level focuses on overcoming the short driving range limitation of electric heavy-duty trucks in logistics transportation. Specifically, it optimizes vehicle charging and distribution routes from multiple production plants to target construction sites and dynamically determines the charging amount for vehicles at each charging station.

Thirdly, In the process of solving the model, a two-level multi-objective evolutionary algorithm is developed on the basis of Pareto theory. The collaborative optimization between the two levels is realized by incorporating a population transfer mechanism. This design enhances both the accuracy and the overall quality of the obtained solutions.

Fourthly, In the example experiment, the evaluation was conducted from two perspectives. On the one hand, the proposed two-level model was benchmarked against traditional single-level and multi-stage algorithms. The findings indicate that the two-level model can achieve a broader search space and deliver improved solution outcomes. On the other hand, the performance of the dynamic charging capacity strategy was compared with that of the full charging capacity strategy. The results show that the dynamic strategy is able to reduce total charging costs by 15.83% while ensuring the completion of delivery tasks, thereby achieving a marked reduction in overall transportation costs. These results demonstrate the practical effectiveness of the proposed model in cost reduction and highlight its considerable potential for engineering applications.

Finally, In the case simulation, the proposed model algorithm ensured the completion of all 328 vehicle trips. Under this condition, the dynamic charging strategy reduced the total charging cost from 811,942.55 yuan to 688,429.85 yuan, achieving an optimization rate of 13.12%. Although the optimization rate of the time window penalty was −5.87% and the average delay cost per customer increased to 179.2 yuan, the overall transportation cost still declined significantly. This improvement was mainly attributed to the reduced proportion of external charging and the lower overall charging expenditure. These results confirm the effectiveness and engineering feasibility of the proposed model in reducing operating costs and improving resource utilization efficiency, highlighting its application advantages in complex component distribution scenarios.

It can be seen that the two-level model and algorithm proposed in this study can not only effectively assist enterprises in allocating customers, optimizing vehicle charging strategies, and determining optimal delivery routes, but also play a significant role in controlling overall distribution costs. It is worth noting that the transportation of prefabricated components differs from the traditional Vehicle Routing Problem (VRP). Since the goods are large and heavy, multiple trips or even multiple vehicles are often required to fulfill the demand of a single customer. This introduces additional constraints related to loading capacity and multi-trip scheduling, making the problem more complex and closer to real-world scenarios. Although this study focuses on prefabricated components, the proposed model and algorithm are also applicable to the transportation of heavy or bulky goods such as steel products, large industrial equipment, and renewable energy components, thereby demonstrating potential applicability in a broader range of logistics fields.

Nevertheless, it should be acknowledged that, owing to the theoretical nature of this study, the validation of the proposed model currently relies on simulation data. This inevitably creates a gap compared with the complex and dynamic factors present in real-world logistics scenarios, meaning that its direct applicability in practical operations has yet to be fully verified. Future research will therefore focus on the progressive refinement and implementation of the model. On the one hand, multi-dimensional real-world data from operational logistics systems will be continuously collected and integrated to optimize parameter calibration and constraint settings, thereby improving the model’s fidelity to actual conditions. On the other hand, collaboration with logistics enterprises or industry associations is planned to design simplified pilot projects based on the theoretical framework. By conducting small-scale field distribution tests, practical experience can be accumulated, and the model’s deviations under complex operational environments can be progressively corrected. Ultimately, this will enable a smooth transition from theoretical results to practical applications, providing more targeted and operational guidance for the deployment of dynamic charging logistics systems for electric vehicles.

Furthermore, although the proposed TC-NSGA-III algorithm performs well in the IGD and HV metrics, we also notice that its performance in the SP metric is relatively limited. Enhancing the diversity of the Pareto frontier is of great significance for decision-makers in different application scenarios, as it provides richer optimal solutions. Therefore, in the future, we will be committed to improving the methods for generating solution set diversity and systematically documenting the related achievements [37]. At the same time, future research will further expand the scope by incorporating renewable energy charging strategies into the optimization framework. We will explore the coordinated optimization of renewable energy structure, delivery cost, and carbon emission objectives, thereby further enhancing the applicability of the model in green logistics systems [38]. Additionally, cargo loading and unloading operations will be incorporated into the model to better capture the practical constraints and operational characteristics of real-world logistics systems [39].