Optimal Air Gap Magnetic Flux Density Distribution of an IPM Synchronous Motor Using a PM Rotor Parameter-Stratified Sensitivity Analysis
Abstract
1. Introduction
2. Analysis of Air Gap Flux Density and Parametric Sensitivity Modeling
2.1. Analysis of Air Gap Flux Density
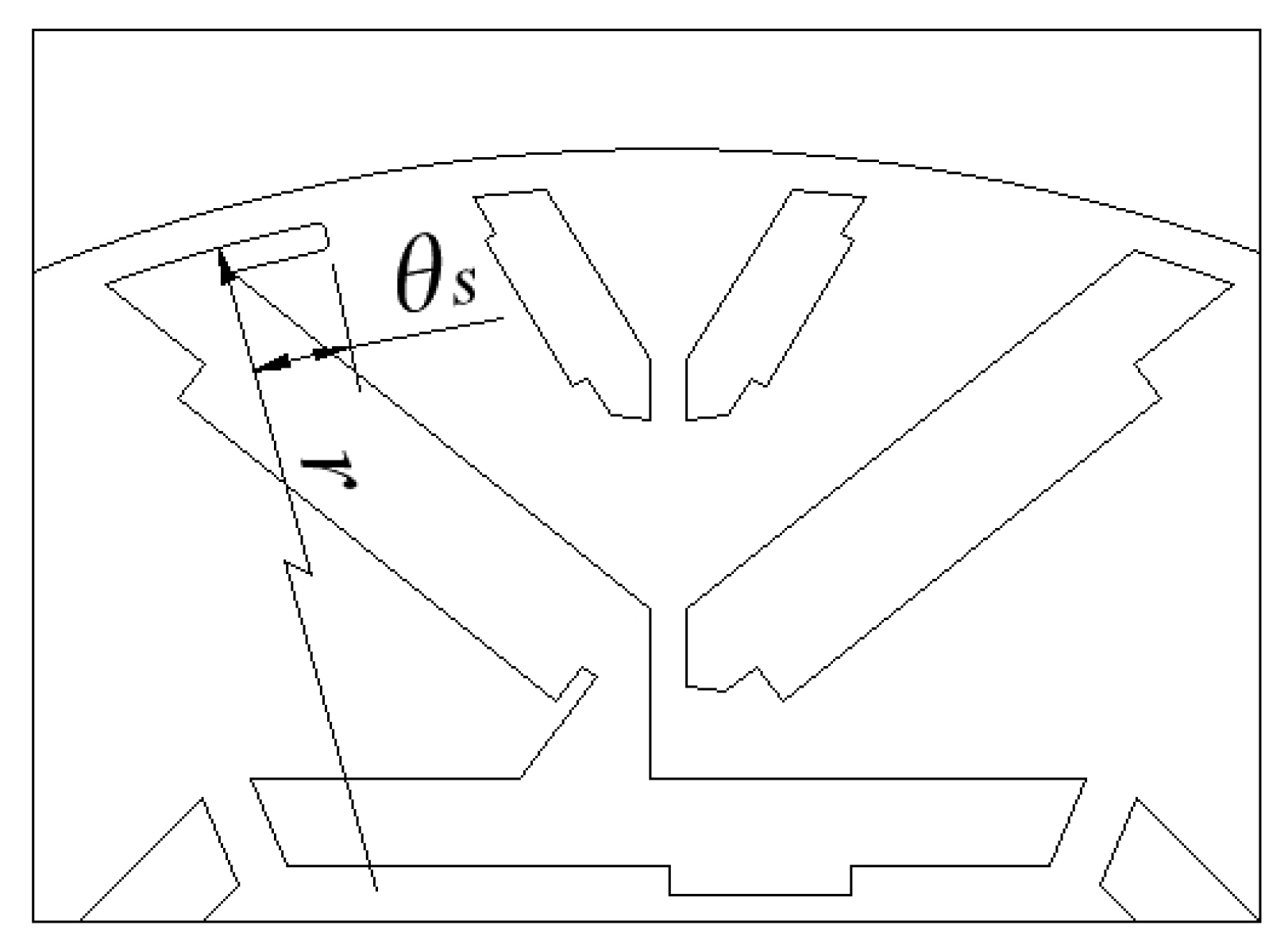
2.2. Model and Main Parameters
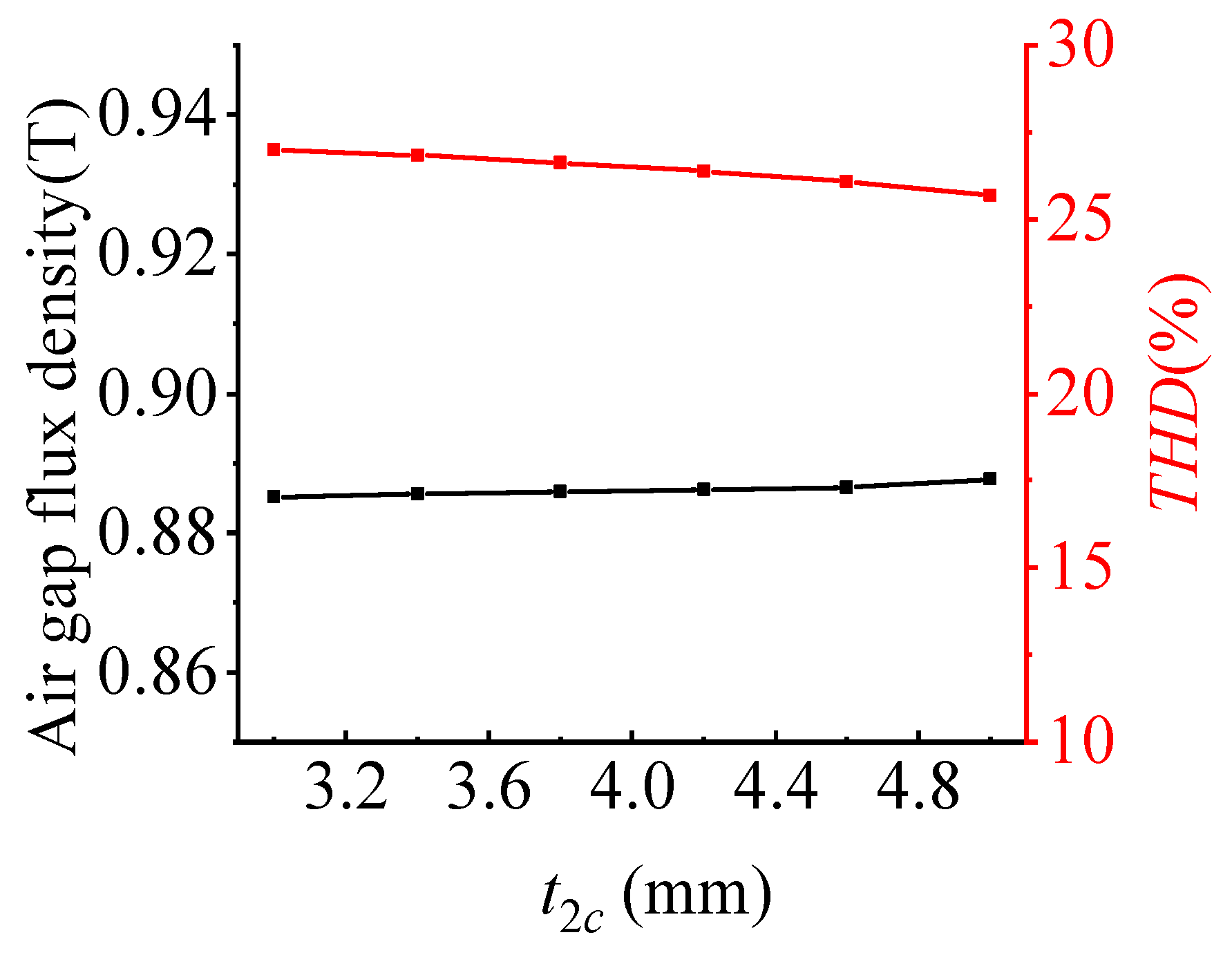
2.3. Second-Layer Parameter Scanning
2.3.1. Influence of the Second V-Shaped PM
2.3.2. Influence of the Second Radial PM
2.3.3. Influence of the First V-Shaped PM
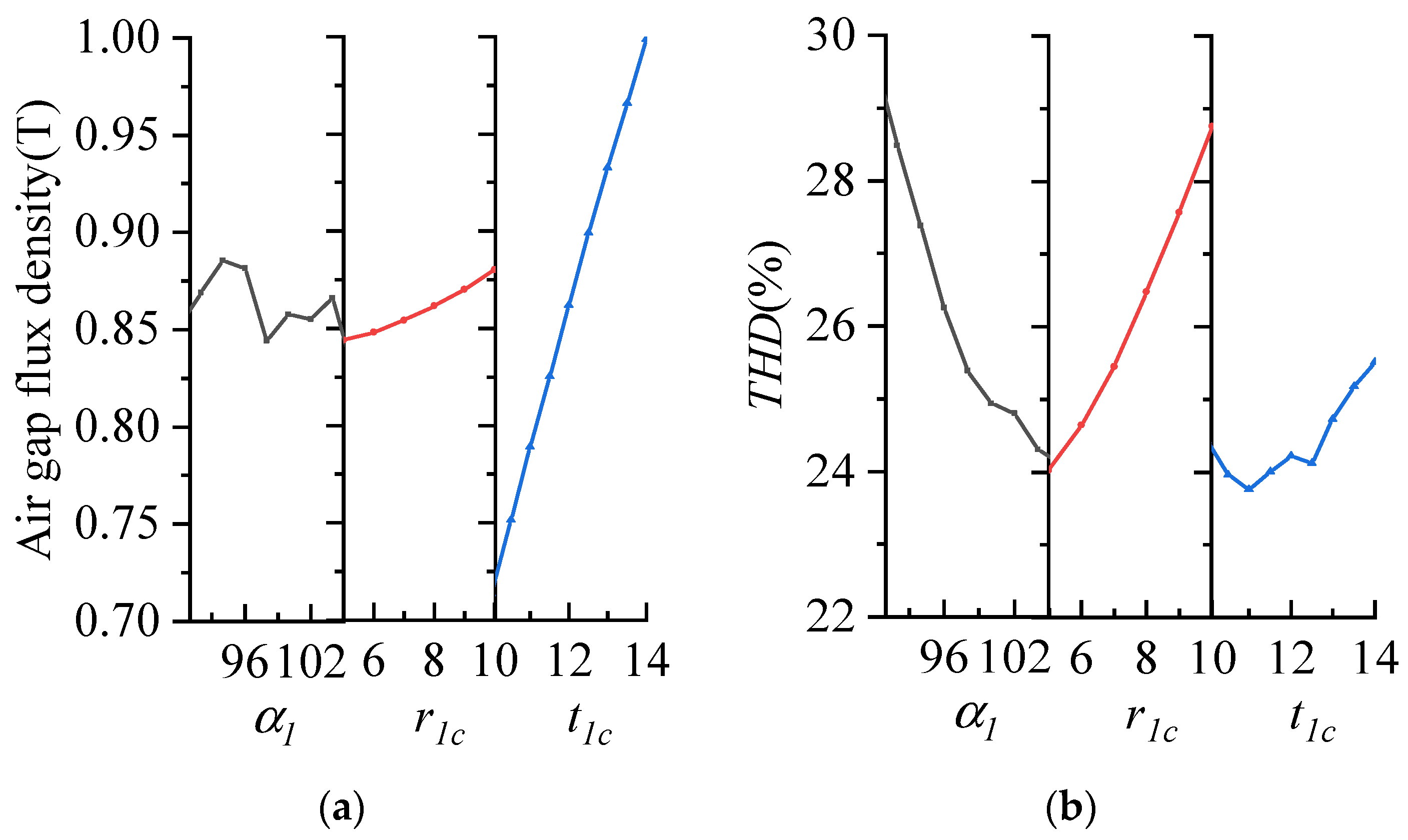
3. High-Sensitivity Parameter Optimization Based on Taguchi Method
3.1. Non-Standard Orthogonal Experimental Design
3.2. Result Analysis and Parameter Selection
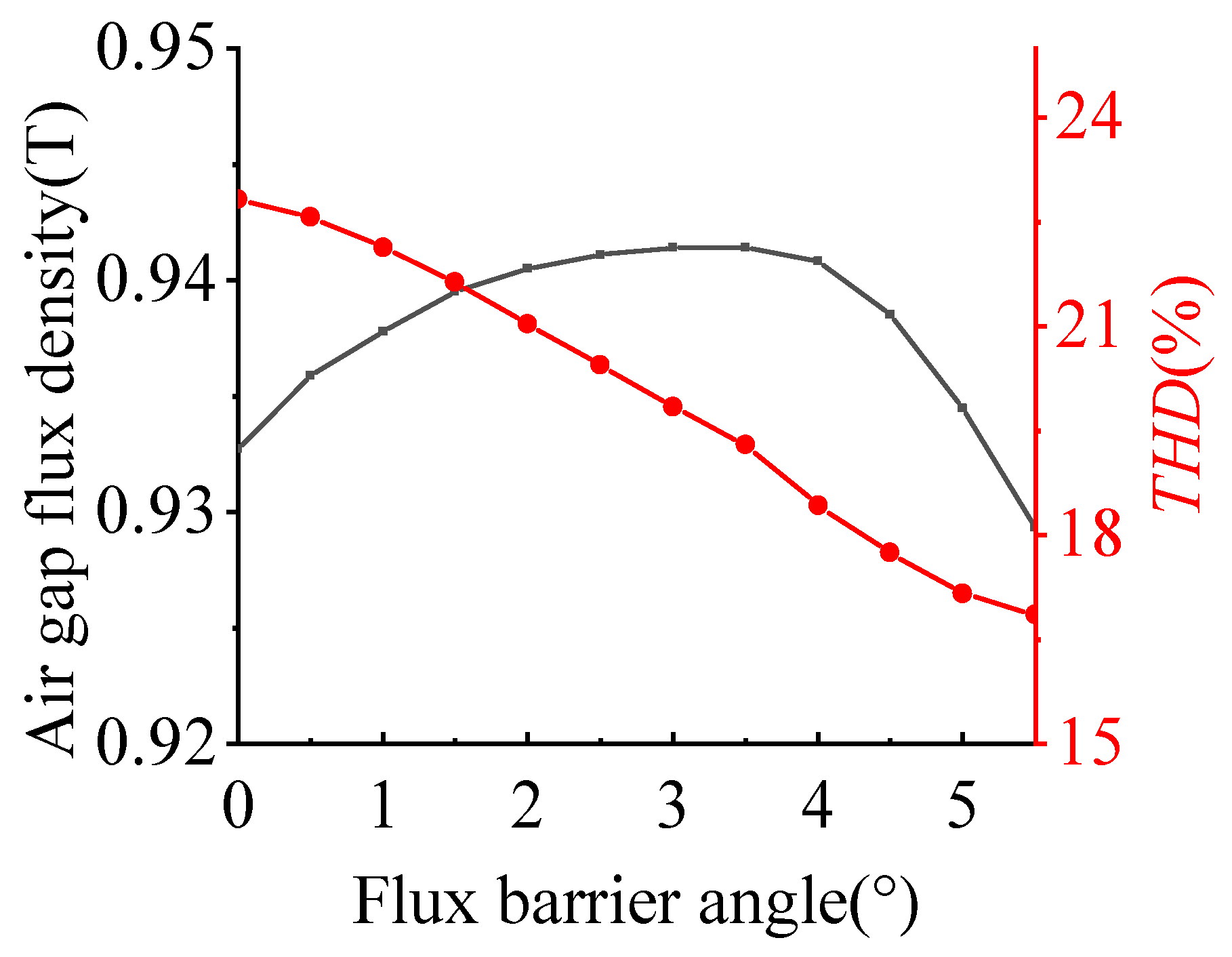
3.3. Optimization of Magnetic Isolation Slots and Thickness of the First V-Shaped PM
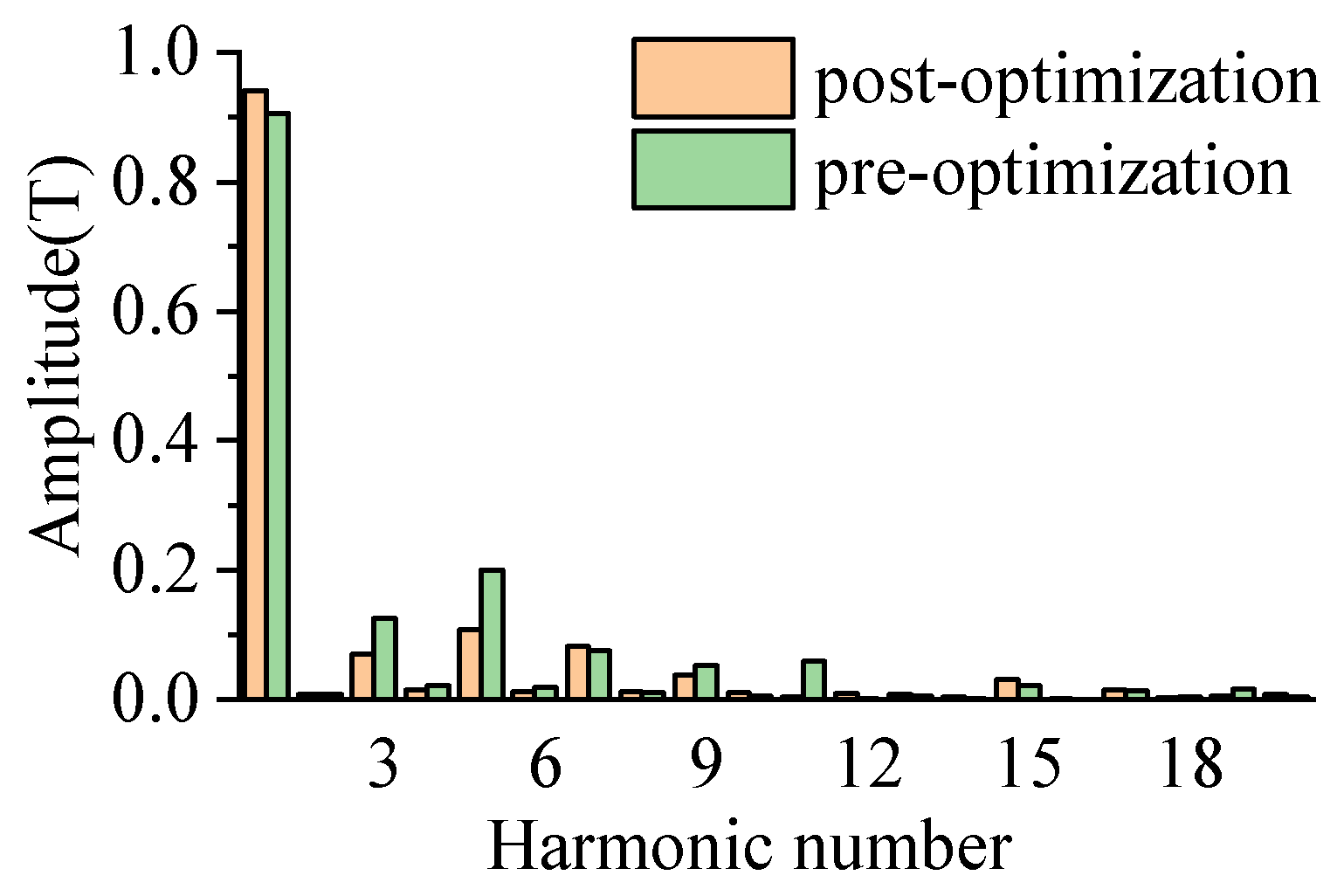
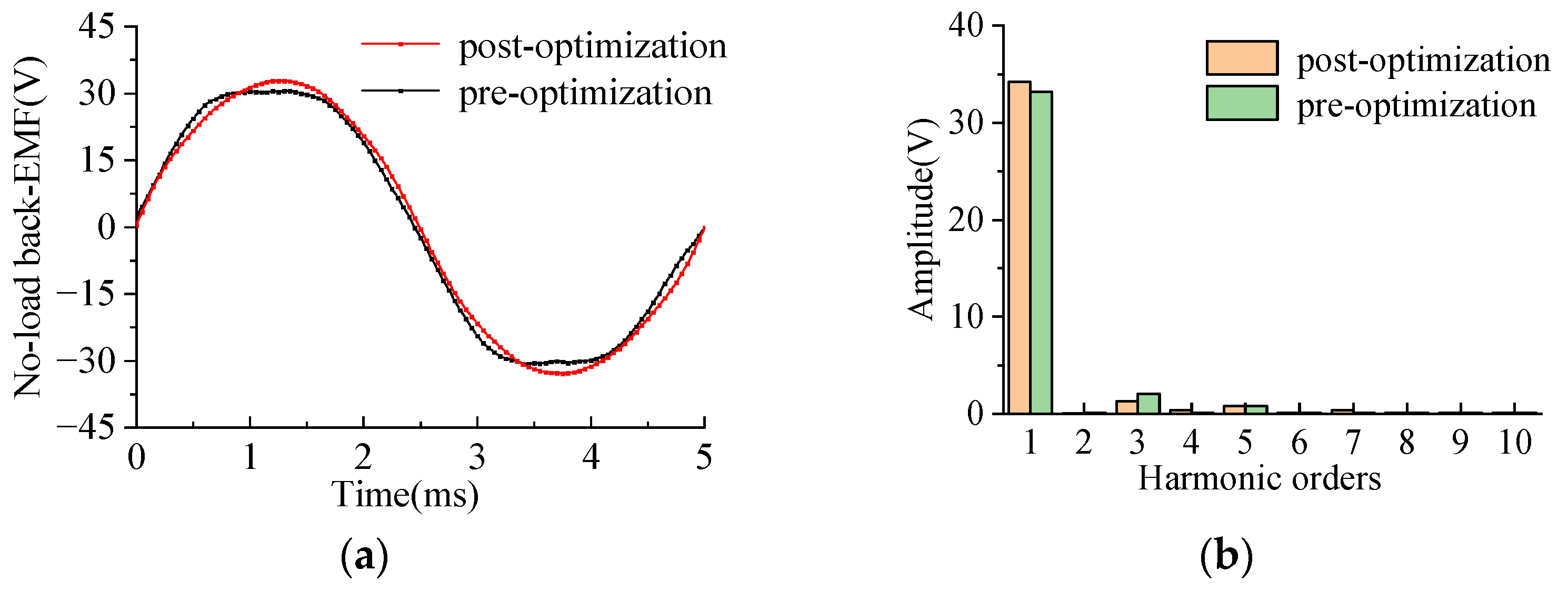
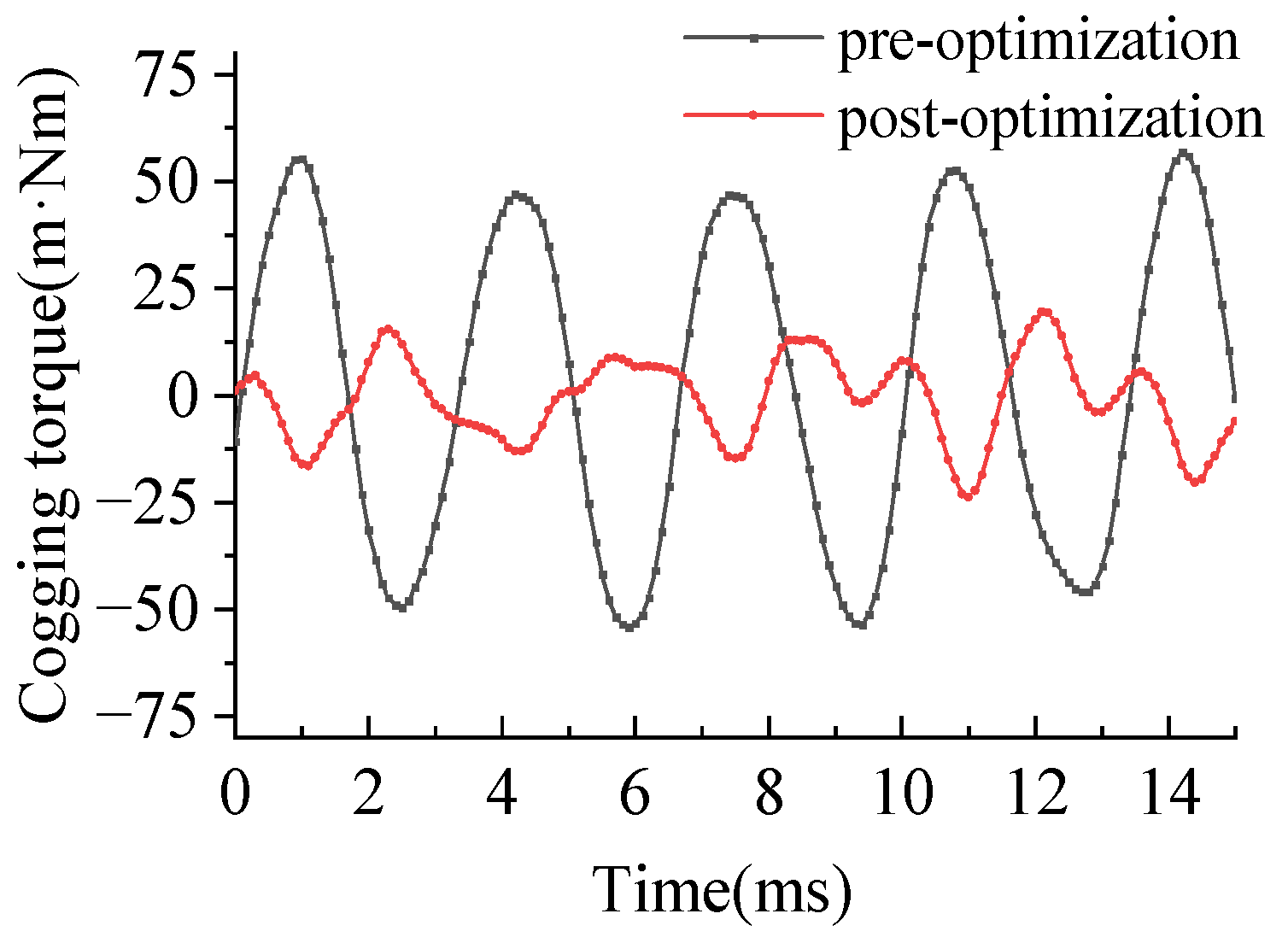
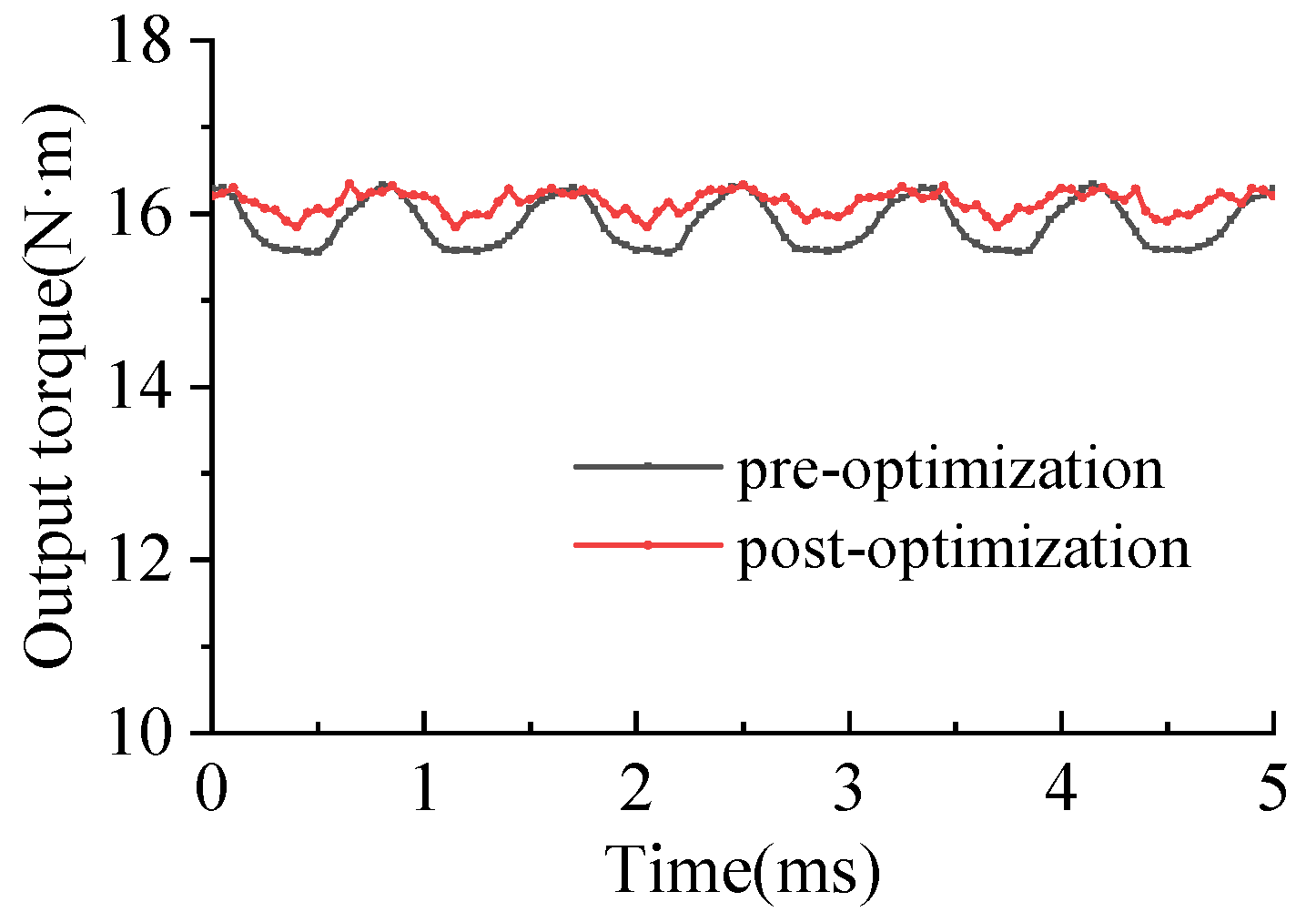
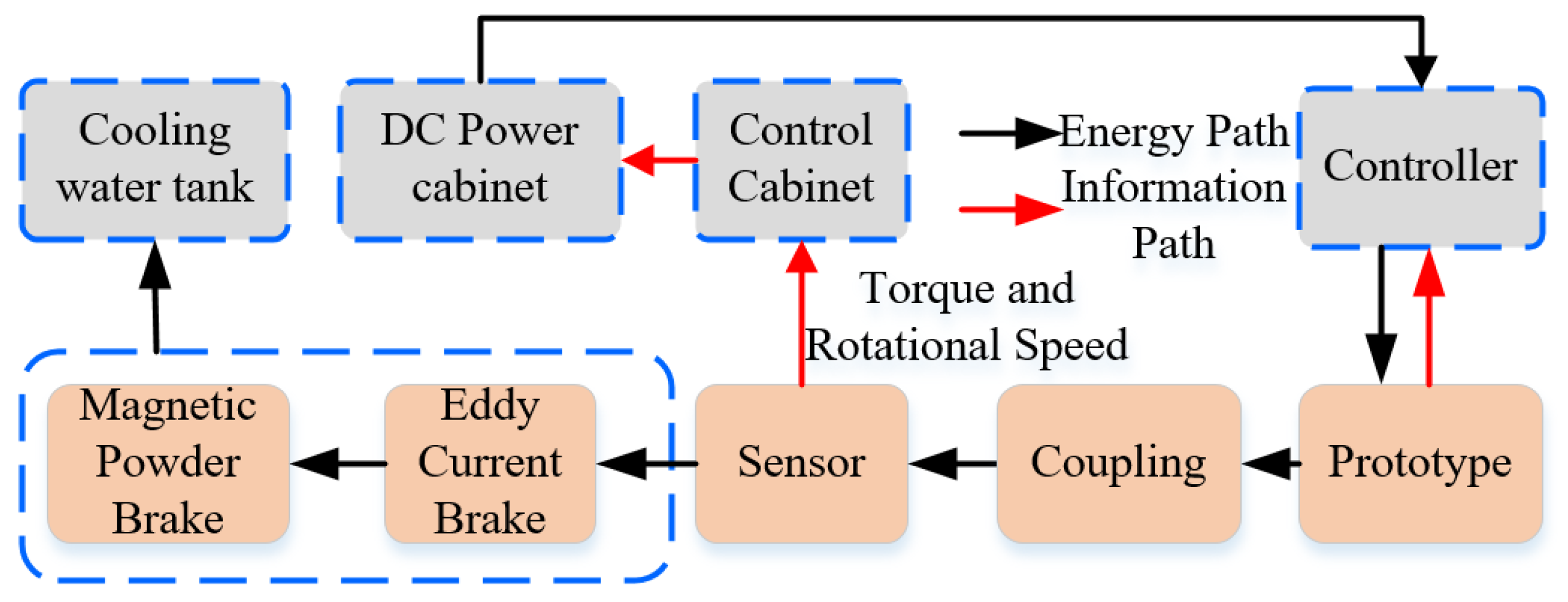
4. Comparison of Electromagnetic Characteristics and Test
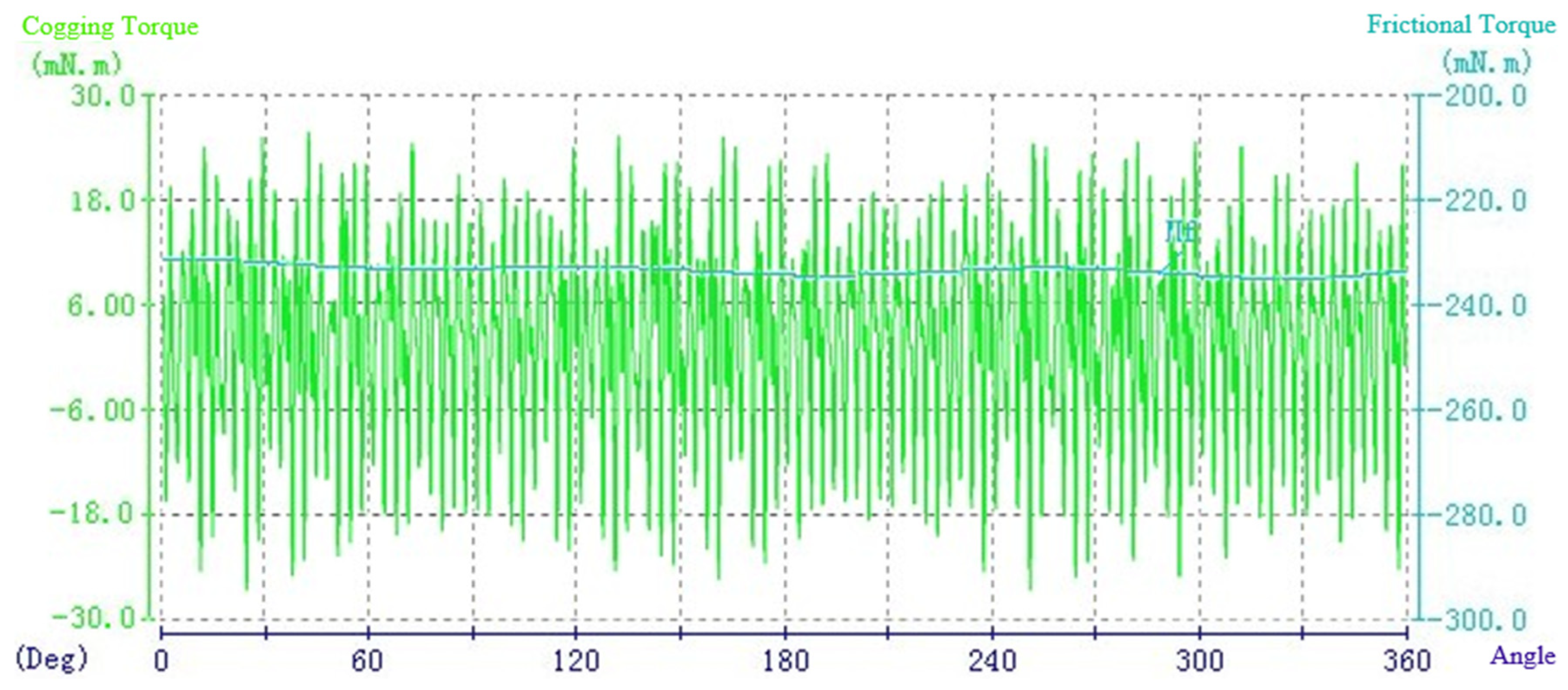
4.1. The Cogging Torque Test
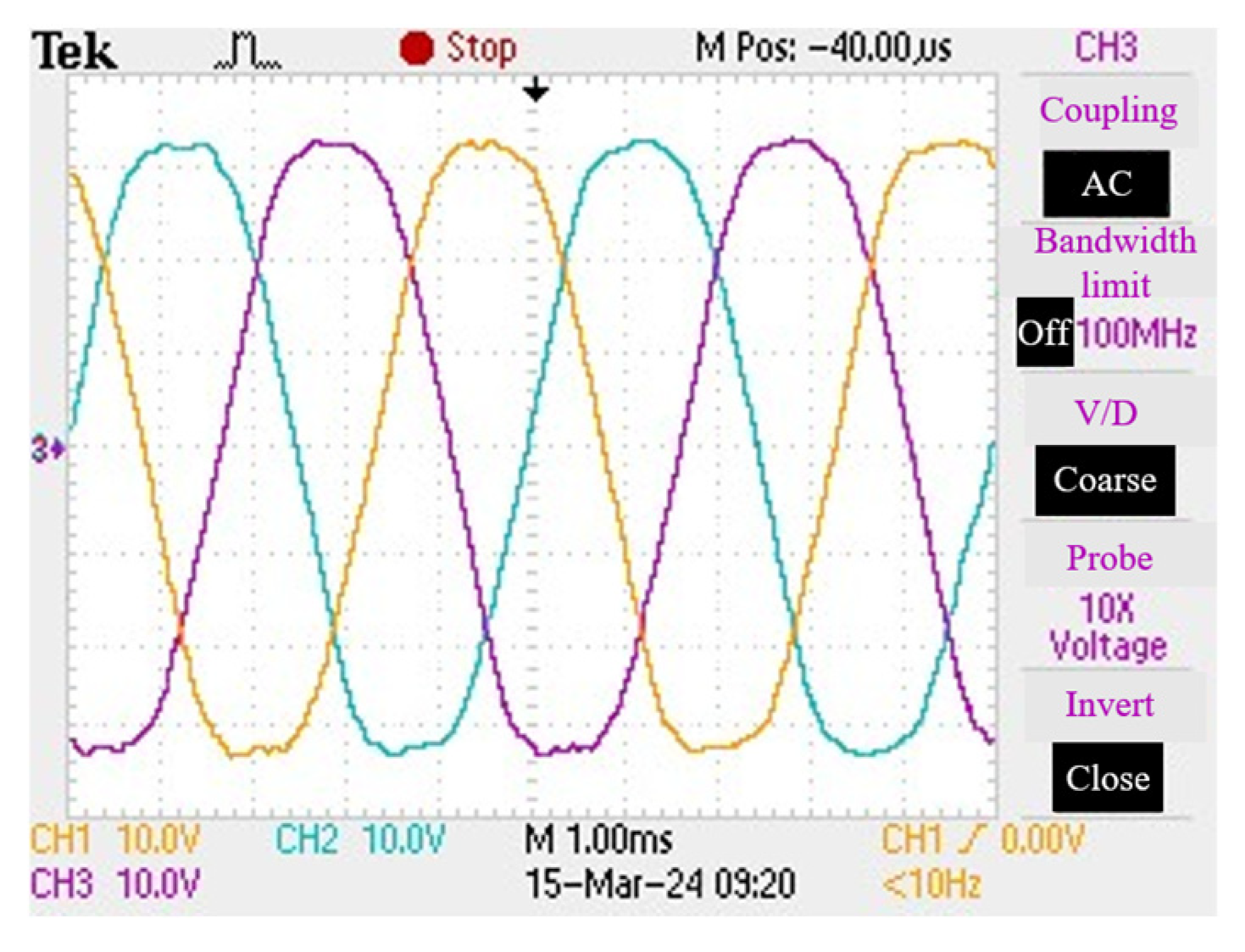
4.2. No-Load Back Electromotive Force Test
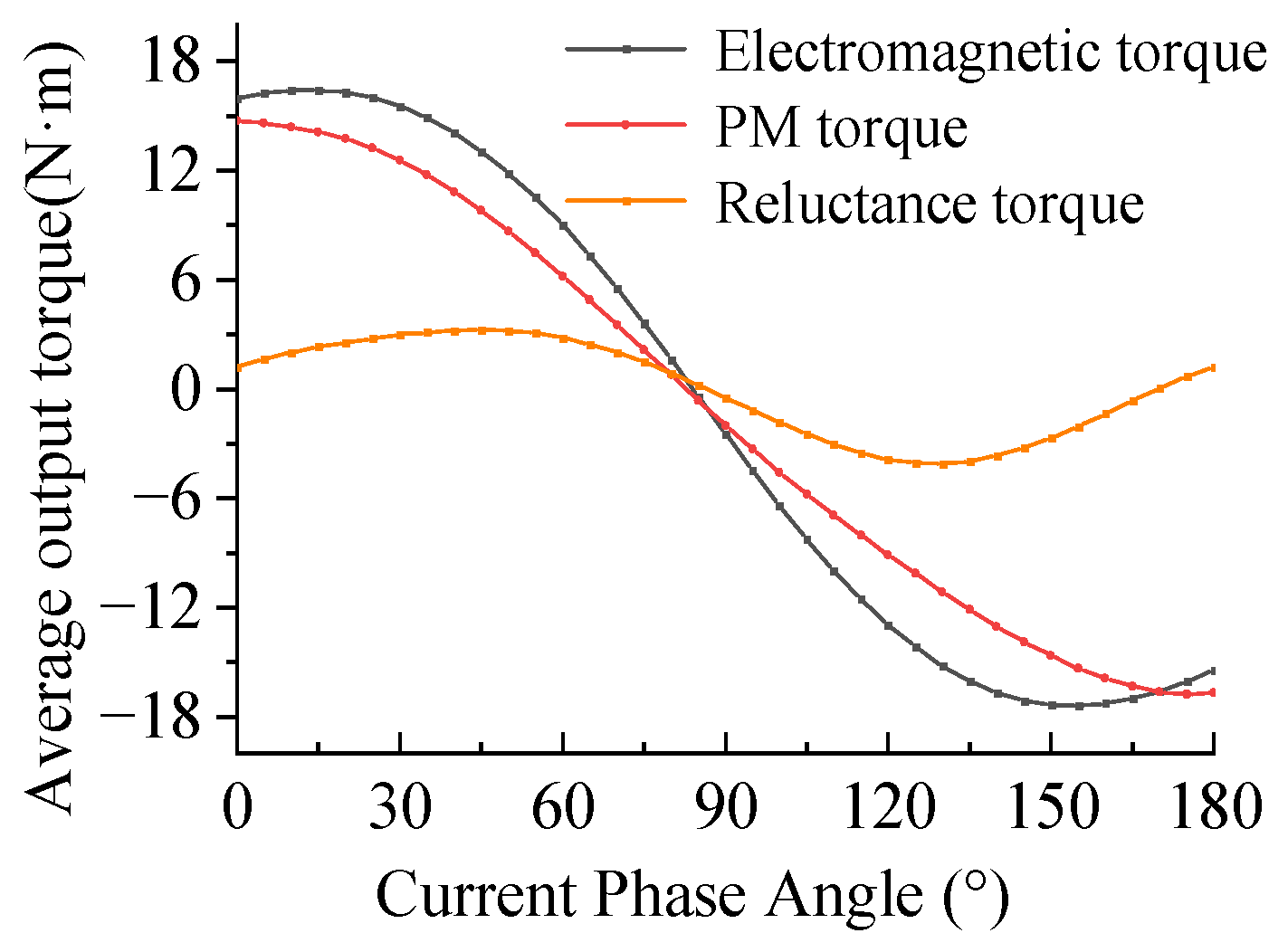
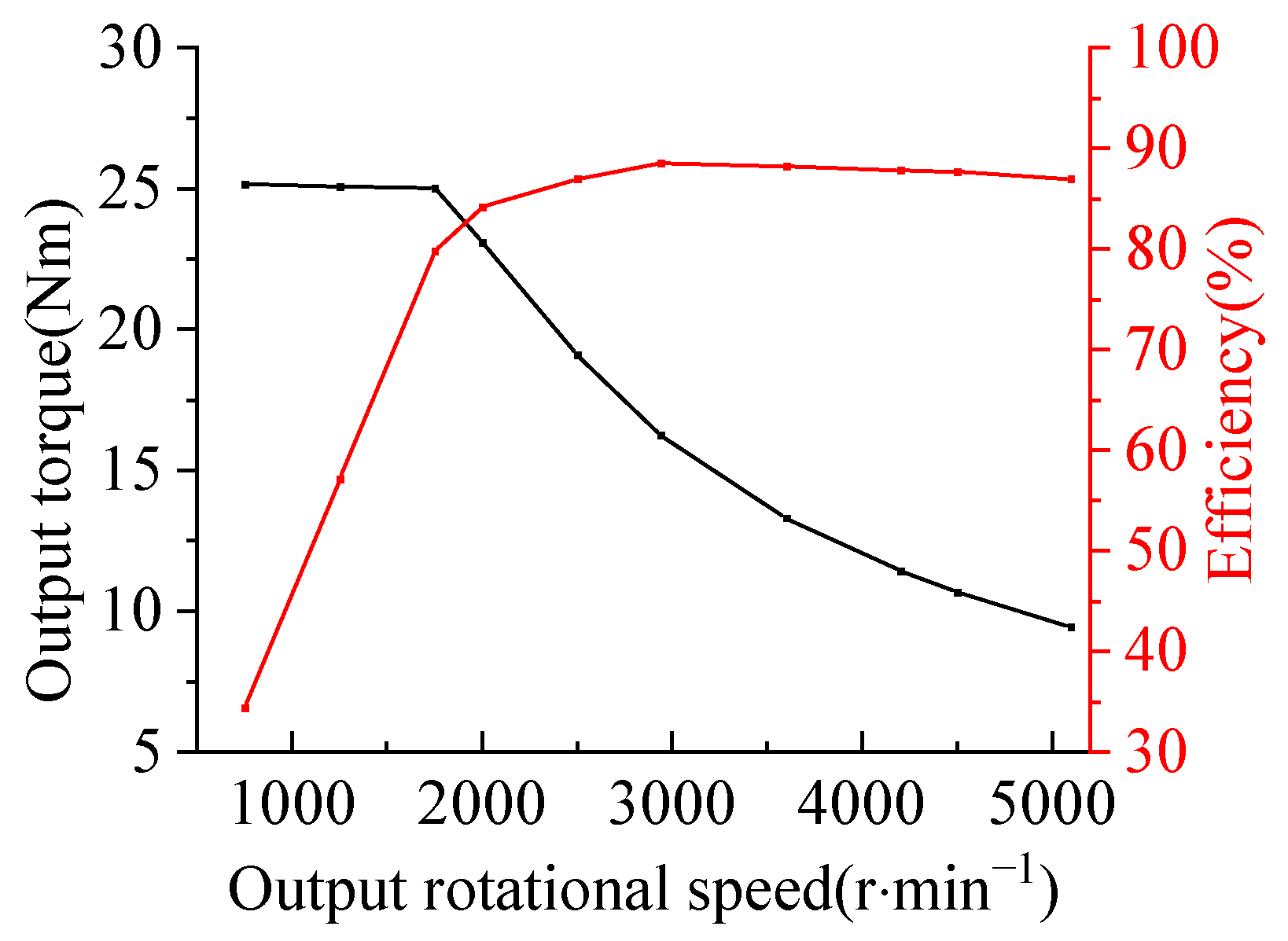
4.3. Output Characteristic Test
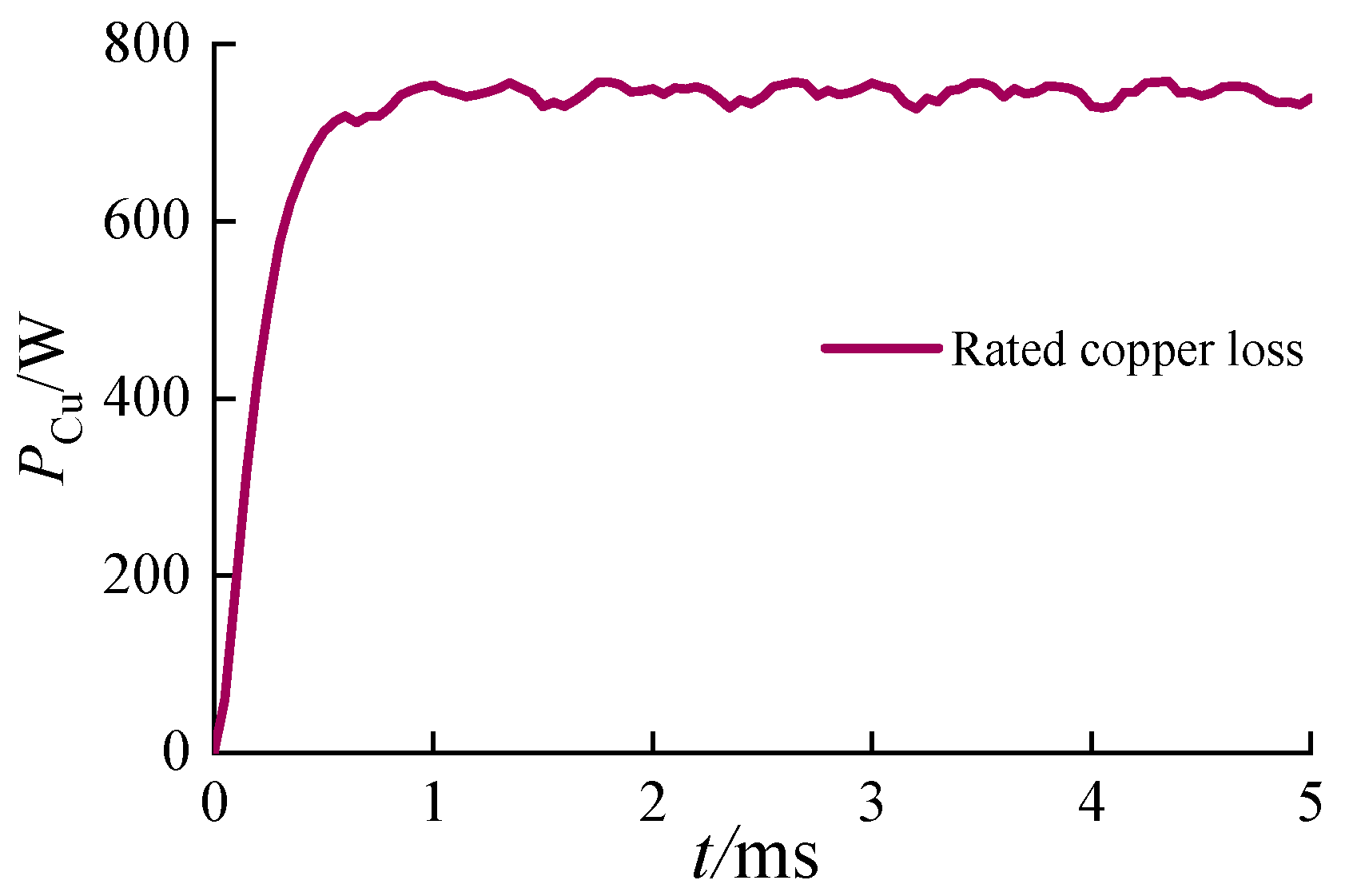
4.4. Simulation Analysis of Motor Losses
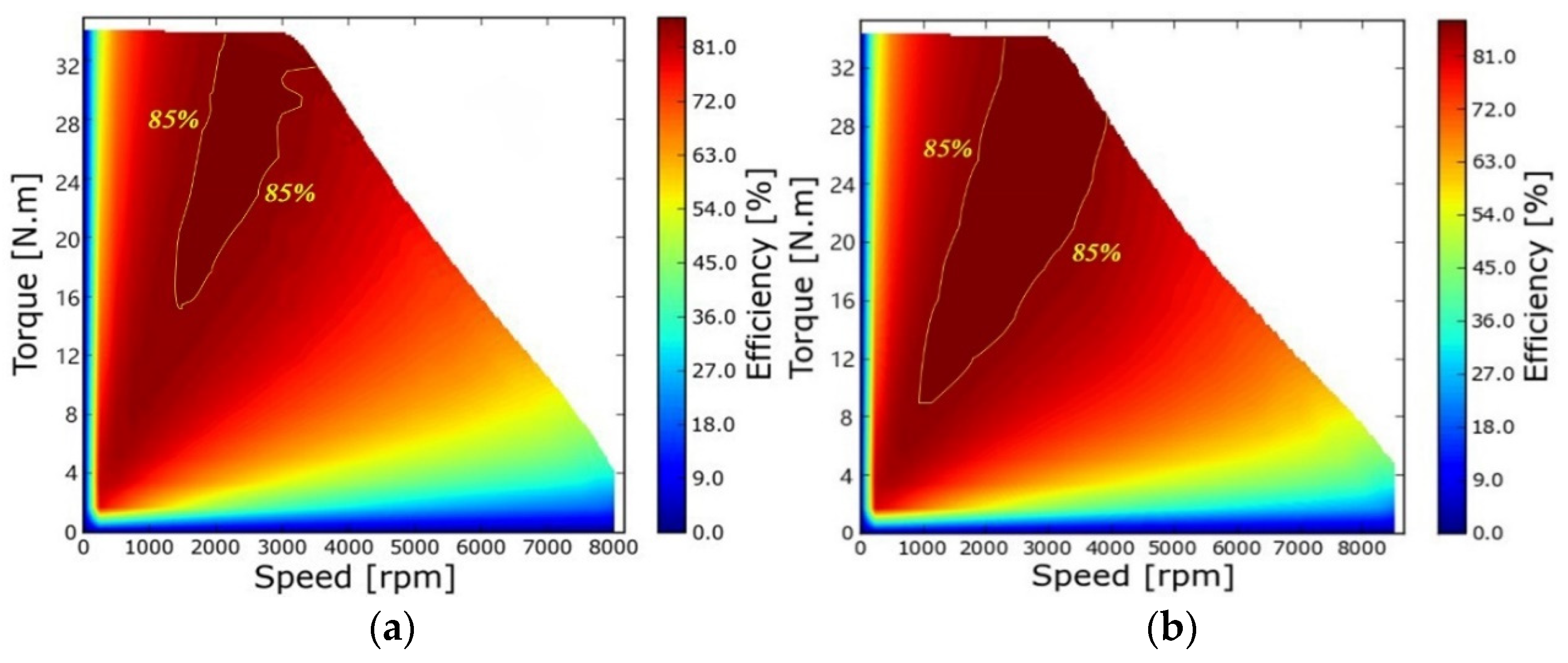
4.5. Test of Map Diagram of Motor Efficiency
5. Conclusions
- •
- Low-sensitivity parameters (α2, r1w, r2w, t2w) were resolved via metamodel prediction, eliminating unnecessary iterations;
- •
- Medium-sensitivity variables (r2c, t2c, t1w) underwent parametric sweeping to identify Pareto-optimal values;
- •
- High-sensitivity parameters (α1, t1c, r1c) were optimized using a non-standard Taguchi orthogonal array (L81(93), reducing simulation cases by 70% versus full-factorial approaches while resolving cross-variable couplings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, G.; Zhang, H.; Feng, Y.; Jia, H.; Zhang, C.; Jiang, Z. Operation patterns analysis of automotive components remanufacturing industry development in China. J. Clean. Prod. 2017, 164, 1363–1375. [Google Scholar] [CrossRef]
- Zahra, A.; Rahmat-Allah, H.; Soodabeh, S. Energy management considering simultaneous presence of demand responses and electric vehicles in smart industrial grids. Sustain. Energy Technol. Assess. 2021, 45, 101127. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, S. Analytical Magnetic Field Method of Permanent Magnet Synchronous Machine Considering Step-Skewed Magnets and Magnetic Slot Wedge. Trans. China Electr. Soc. 2019, 34, 11–22. [Google Scholar] [CrossRef]
- Shao, N.; Zhu, L.; Luo, X.; Huang, Z. Analytical Methods for Optimal Rotor Step-Skewing To Minimize Cogging Torque in Permanent Magnet Motors. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Tan, L.; Wang, Y.; Xiao, W.; Cui, J.; Zhou, Y.; Ren, C.; Guo, J.; Zhen, D. Design and Optimization of Submersible Permanent Magnet Synchronous Motor with External Rotor and Integrated Pump. Small Spec. Electr. Mach. 2023, 51, 30–39. [Google Scholar] [CrossRef]
- Zhao, H. Topology Optimization of Synchronous Reluctance Motor Based on Standardized Gaussian Network. Henan Sci. Technol. 2023, 42, 12–16. [Google Scholar] [CrossRef]
- Li, S.; Shuai, K.; Sun, L.; Wang, J. Multi-objective Optimization Design of Ferrite Permanent Magnet Assisted Synchronous Reluctance Motor. Micromotors 2023, 56, 14–20. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, W.; Yang, N.; Li, J. Parameter Optimization of Stator Auxiliary Groove of Permanent Magnet Motor Using Surrogate. J. Nanjing Inst. Technol. Nat. Sci. Ed. 2023, 21, 44–50. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.; Yang, N.; Wang, Y. Noise Optimization of Octagonal Enclosure of Door Motors Based on Surrogate Method. J. Nanjing Inst. Technol. Nat. Sci. Ed. 2023, 21, 68–73. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Y. Multi Objective Optimization of Structural Parameters of Interior Permanent Magnet Vernier Wheel Hub Motor. Small Spec. Electr. Mach. 2024, 52, 20–25. [Google Scholar] [CrossRef]
- Xu, Z.; Cheng, H.; Su, J.; Li, C.; Cheng, Y. Multi-Objective Optimization of Partitioned-Primary Permanent Magnet Linear Motor. Small Spec. Electr. Mach. 2025, 53, 7–13. [Google Scholar] [CrossRef]
- Zuo, S.; Liu, X.; Yu, M.; Wu, X.; Zhang, G. Numerical Prediction and Analysis of Electromagnetic Vibration in Permanent Magnet Synchronous Motor. Trans. China Electr. Soc. 2017, 32, 159–167. [Google Scholar] [CrossRef]
- Luo, C.; Zhao, S.; Qiu, X.; Yang, X. Research on Electromagnetic Excitation Force Weakening of PMSM Based on Stator Auxiliary Slot. Micromotors 2024, 57, 1–7. [Google Scholar] [CrossRef]
- Song, T. Electromagnetic Vibration and Noise Characteristics and its Suppression of Permanent Magnet Synchronous Motor used for Electric Vehicles. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, S.; Fu, W. Sensitivity Analysis and Design Optimization of a New Hybrid-Excited Dual-PM Generator with Relieving-DC-Saturation Structure for Stand-Alone Wind Power Generation. IEEE Trans. Magn. 2020, 56, 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Wan, D.; Huang, S.; Cui, H. Parametric Sensitivity Analysis and Torque Characteristic Optimization of the PMSM with Non-uniformly Partitioned Halbach Array. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, F.; Gao, J.; Li, M.; Yao, P.; Song, Z.; Yang, K.; Gao, H. Optimization Design of Halbach Interior Permanent Magnet Synchronous Motor Based on Parameter Sensitivity Stratification. J. Xi’an Jiaotong Univ. 2022, 56, 180–190. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, W.; Shi, Q.; Meng, Q.; Du, G. Optimization Design of Dual-Redundancy Permanent Magnet Synchronous Motor Based on Improved Iterations Taguchi Method. Trans. China Electr. Soc. 2022, 38, 2637–2647. [Google Scholar] [CrossRef]
- Pan, Y. Multi-objective Optimization Design of Interior Permanent Magnet Synchronous Motor Based on Combined Surrogate Model. Ph.D. Thesis, East China Jiaotong University, Nanchang, China, 2023. [Google Scholar] [CrossRef]
- Gu, Y.; Gu, D.; Feng, L.; Zhang, W.; Li, K.; Mao, R. Multi-objective preference optimization of yokeless axial-flux wind generator. Electr. Mach. Control 2023, 27, 148–156. [Google Scholar] [CrossRef]
- Xie, Y.; Jiang, J.; Cai, W.; Ren, S.; Sun, C. Demagnetization Failure of Surface-Mounted High-Speed Permanent Magnet Synchronous Motor and Local Infiltration of Heavy Rare Earth. Electr. Mach. Control 2024, 28, 44–53. [Google Scholar] [CrossRef]
- Liu, Y. Research on Demagnetization Mechanism and Anti-Local Demagnetization Optimization of Permanent Magnets in Permanent Magnet Synchronous Motors. Ph.D. Thesis, Harbin University of Science and Technology, Harbin, China, 2023. [Google Scholar]
- Xie, Y.; Sun, C.; Cai, W.; Ren, S.; Jiang, J. Demagnetization Mechanism and Local Infiltration of Heavy Rare Earth for Permanent Magnet Synchronous Motors in Electric Vehicles. Electr. Mach. Control 2024, 28, 75–83. [Google Scholar] [CrossRef]
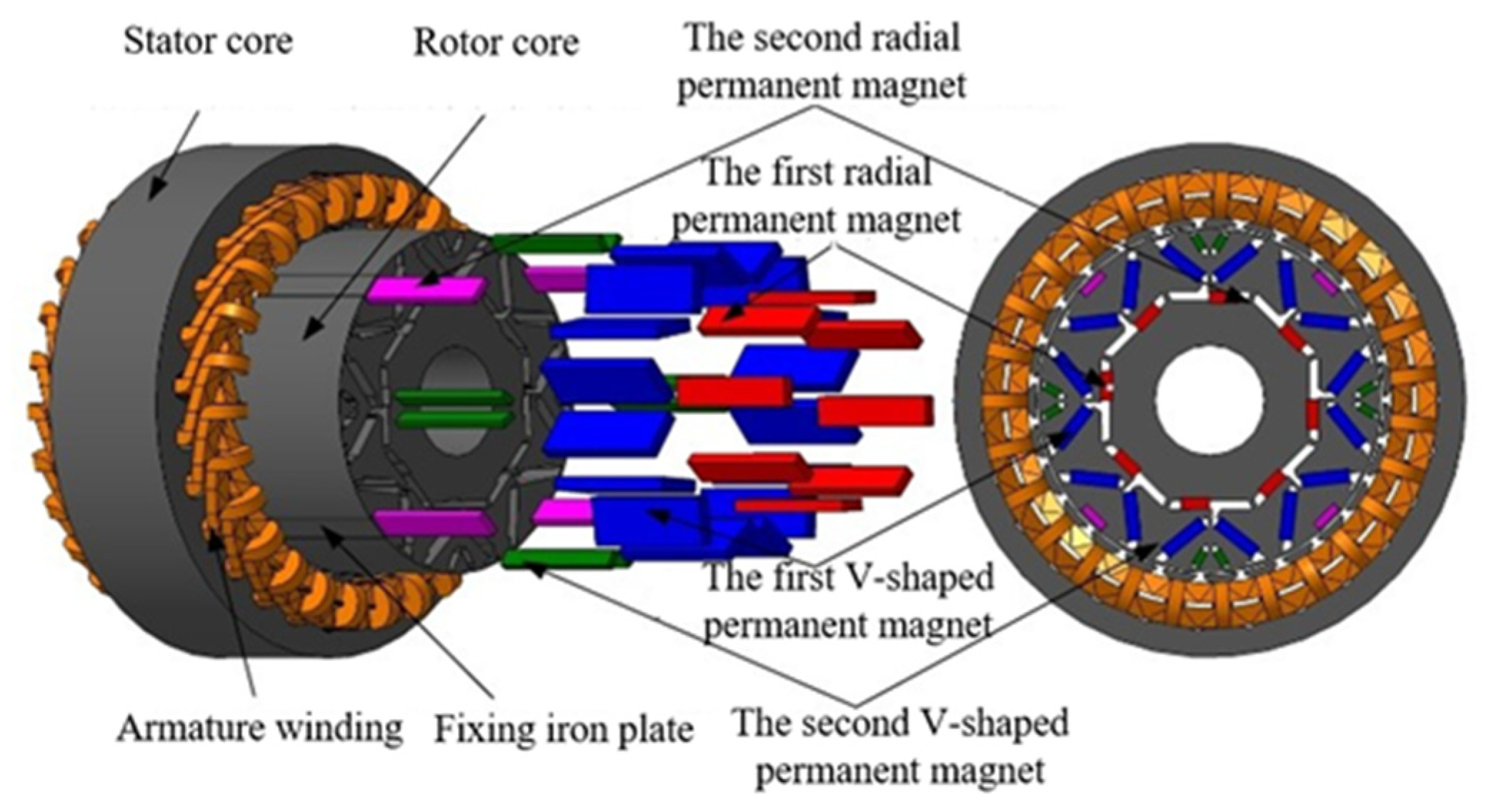
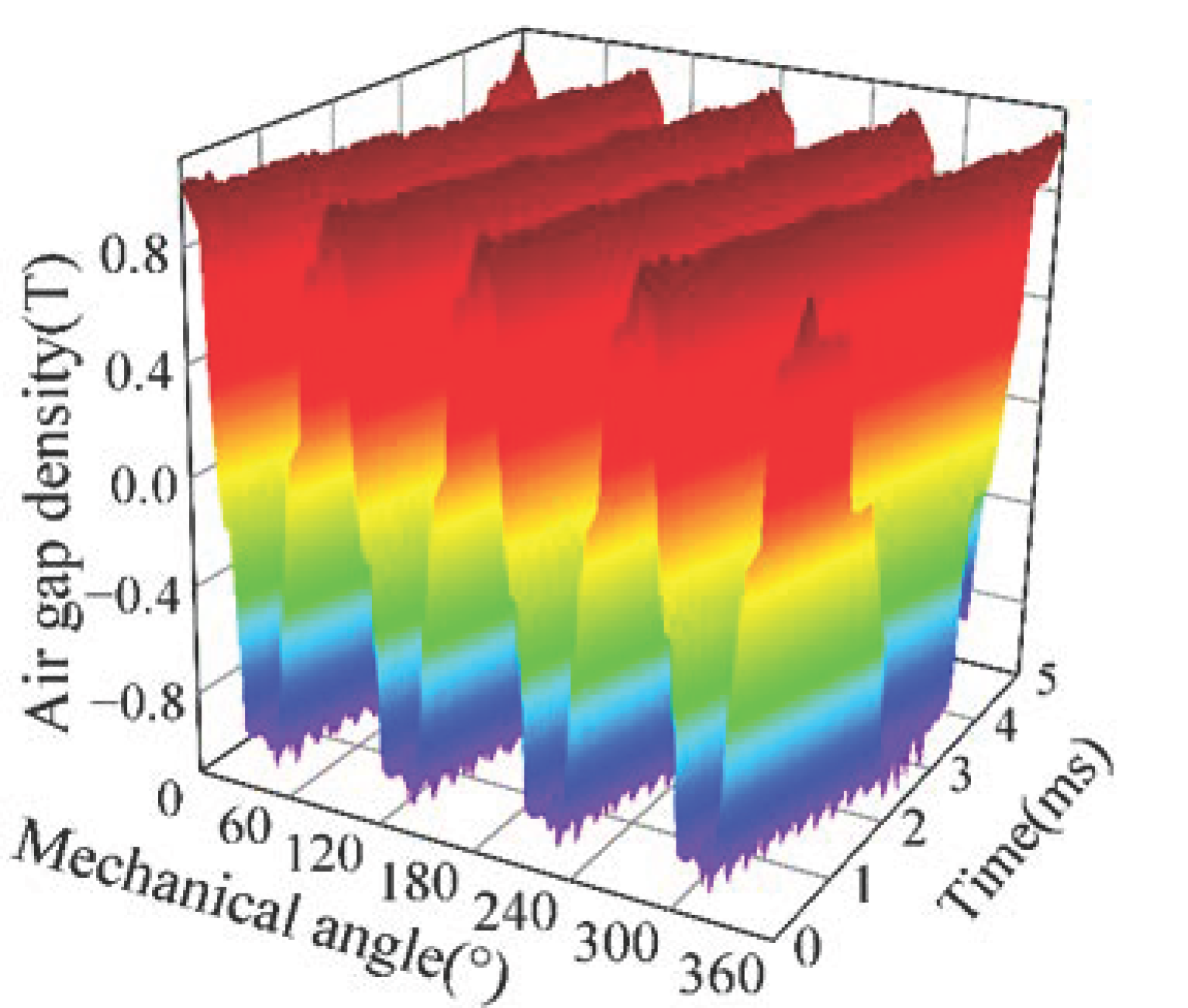
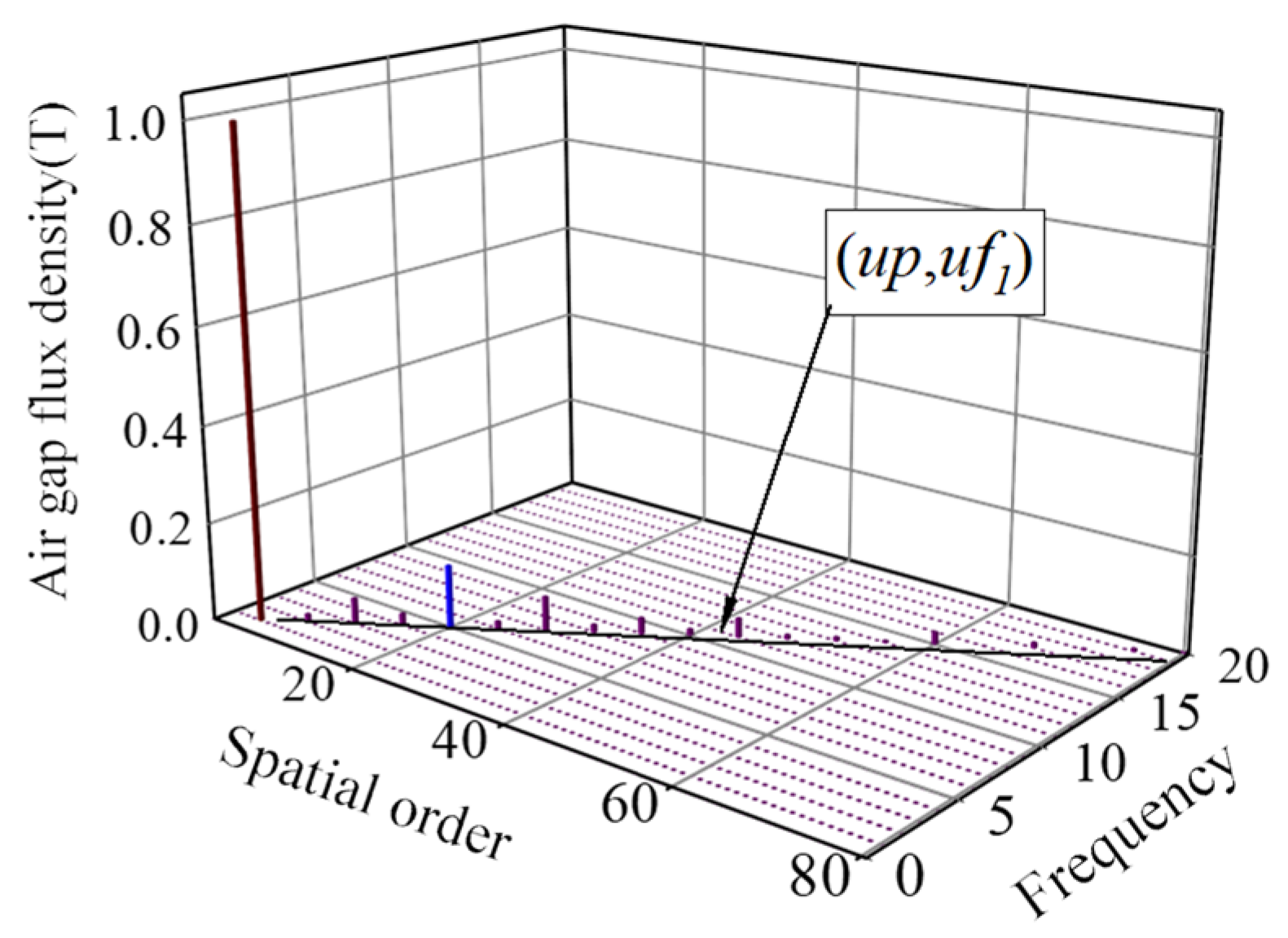

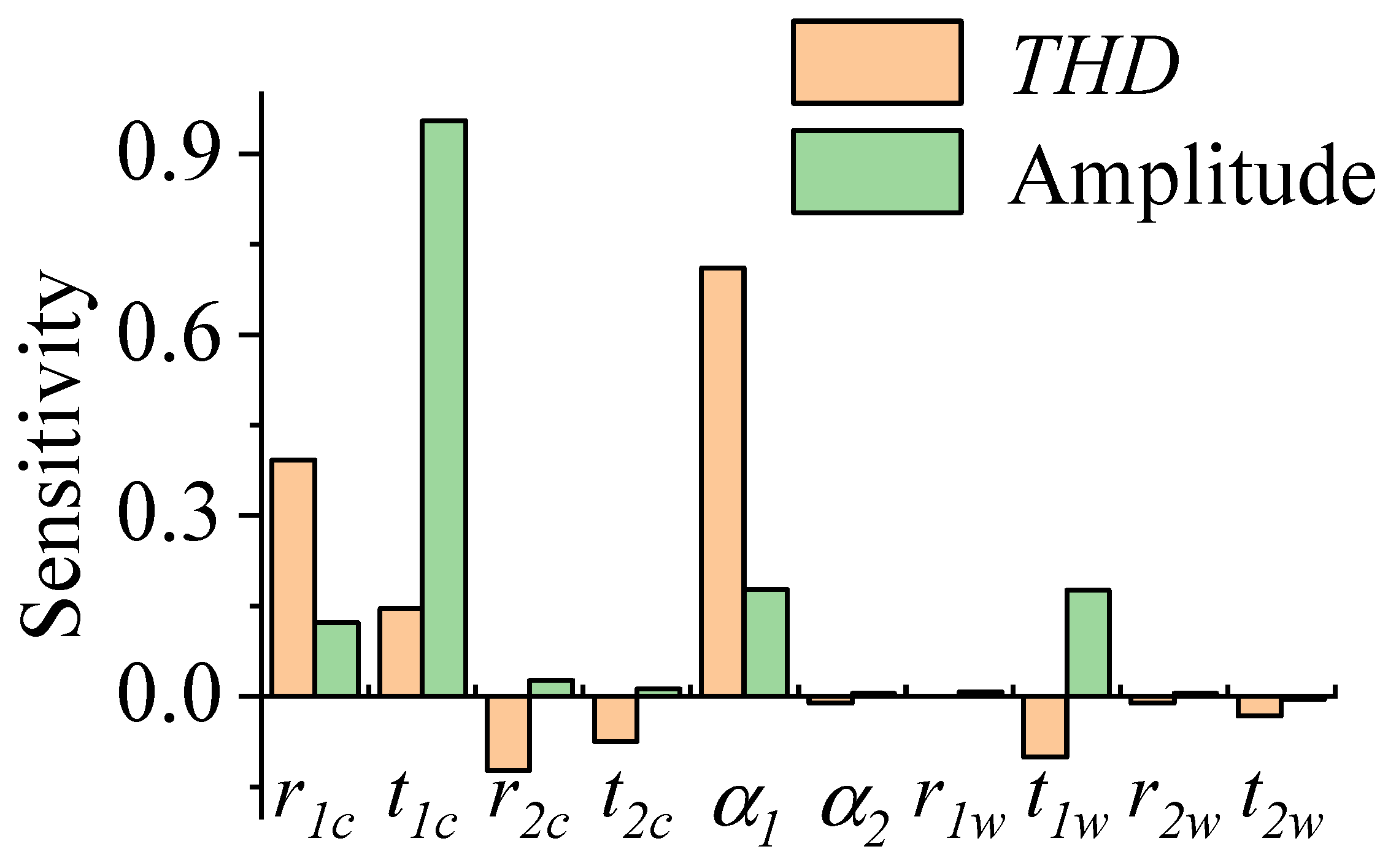


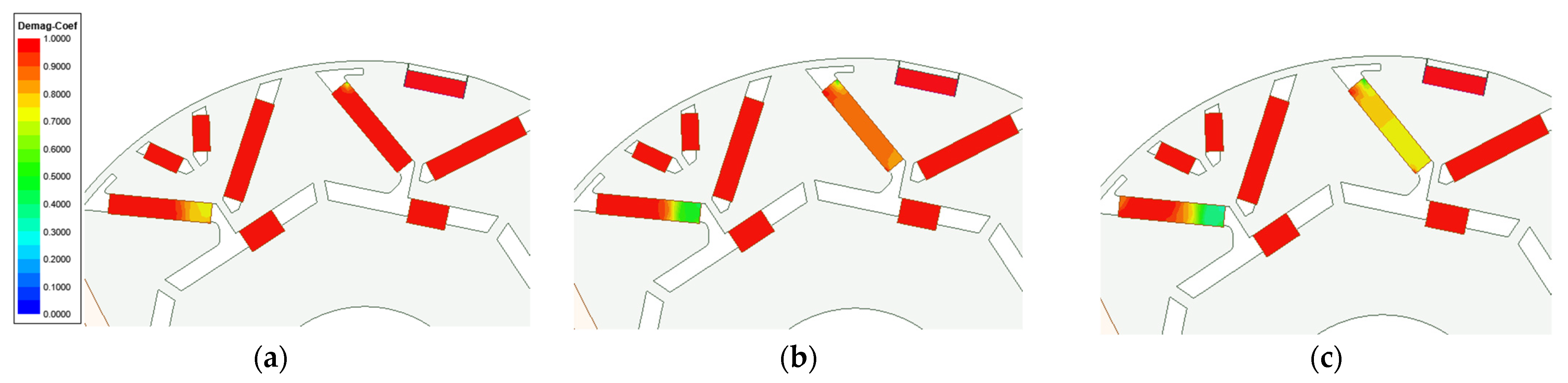
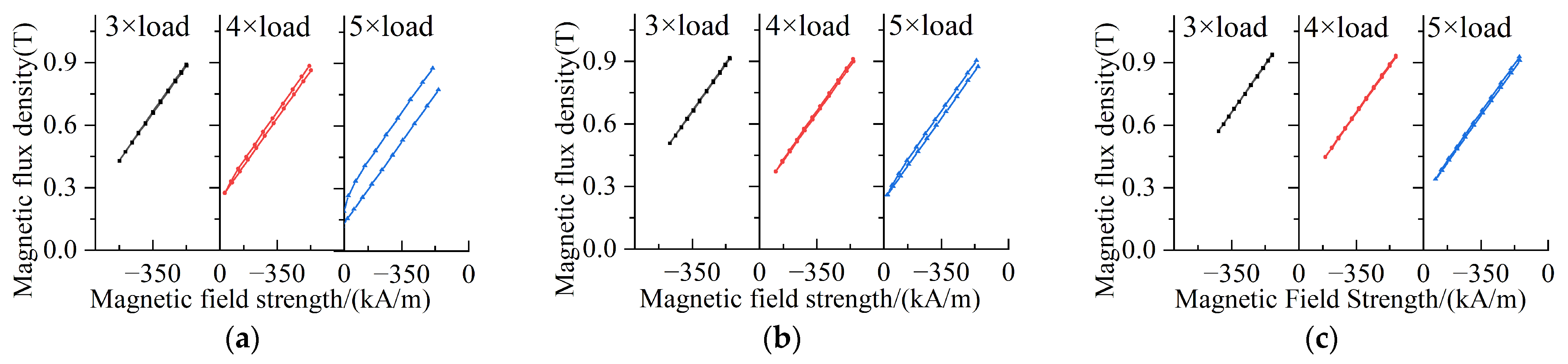
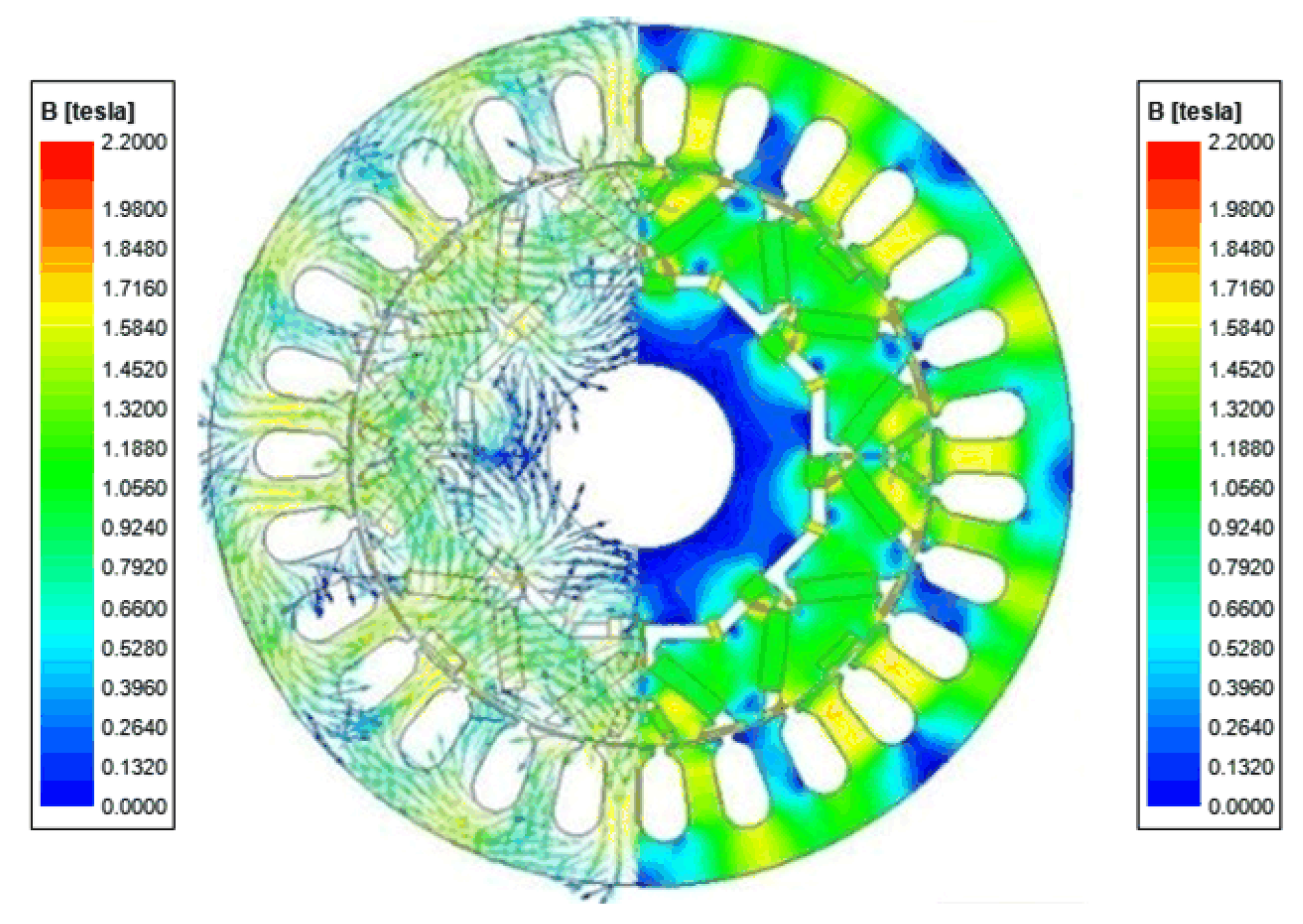
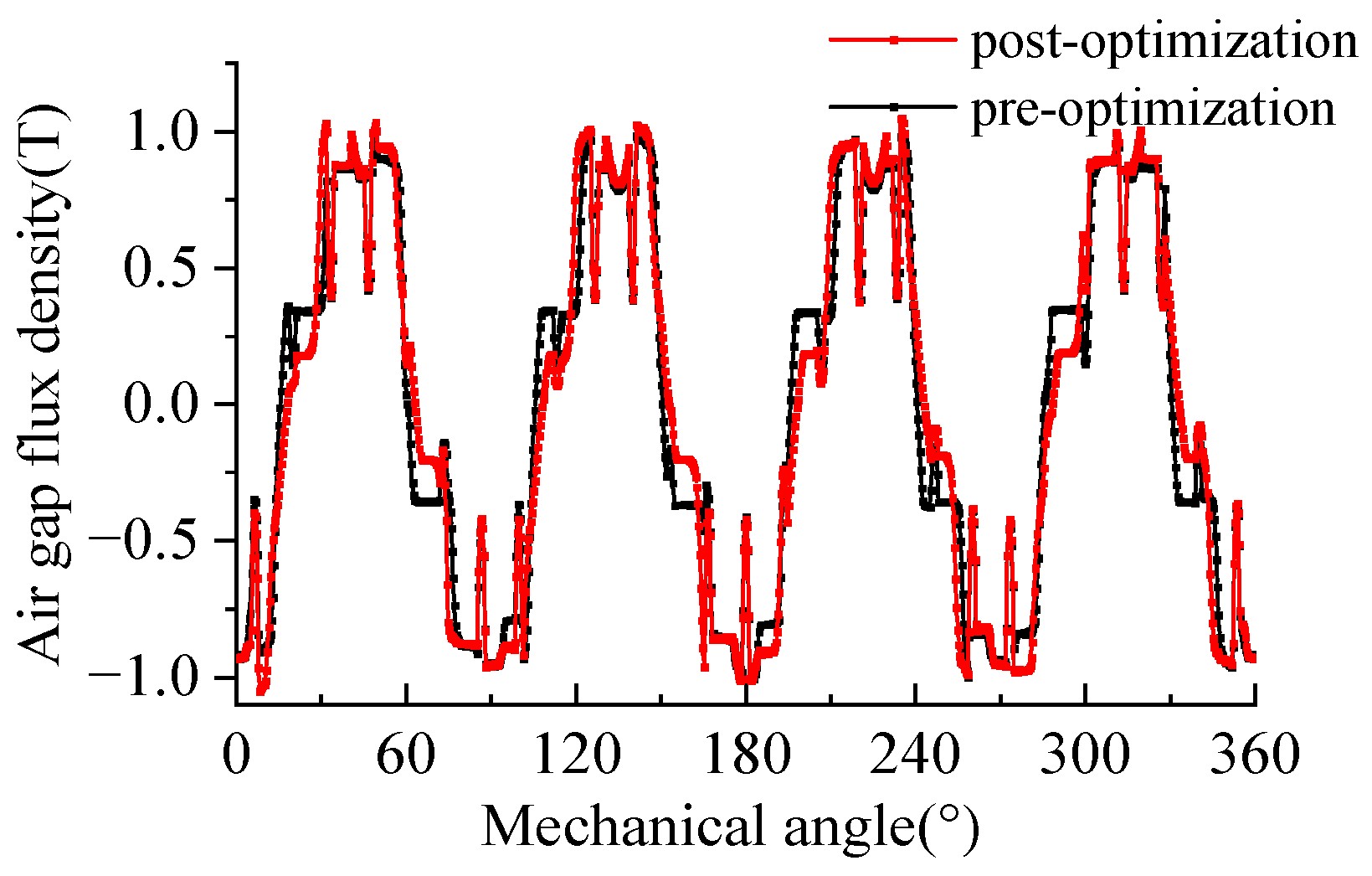




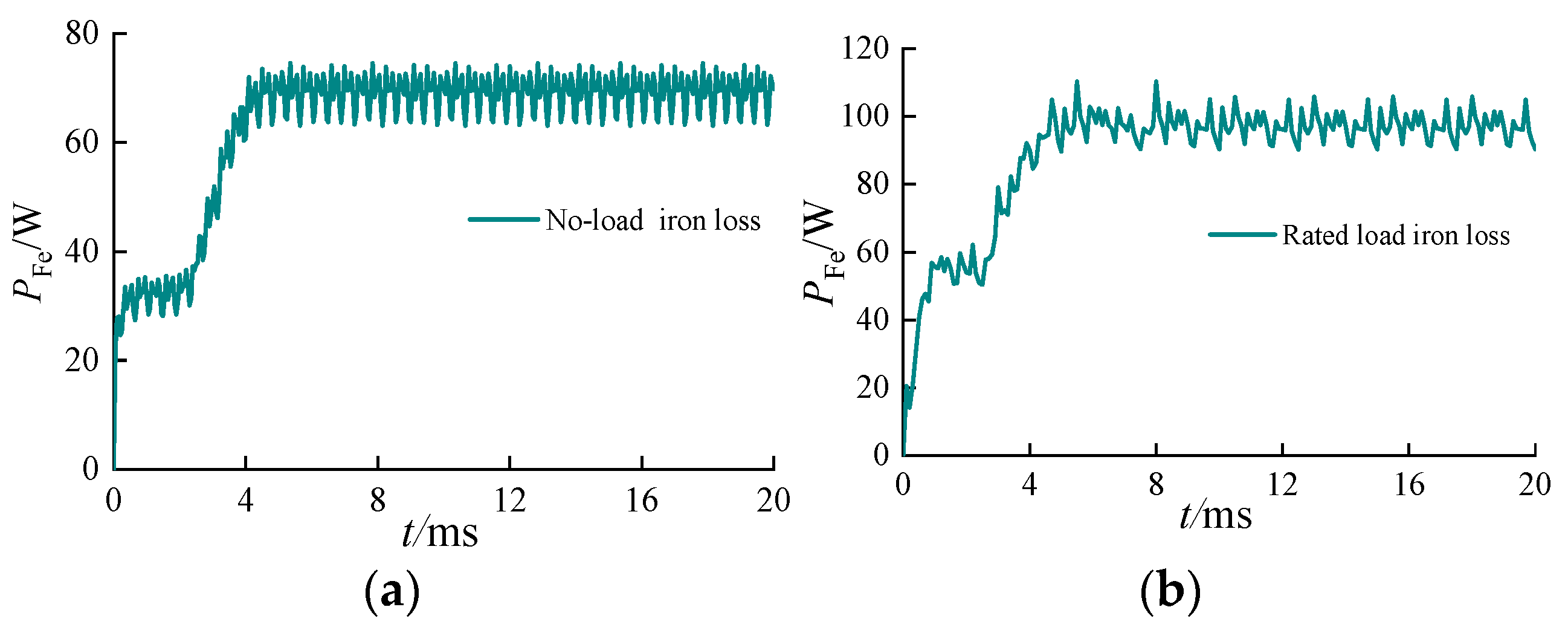
| Parameter Name/Unit | Value |
|---|---|
| Rated Power/kW | 5 |
| Rated Line Voltage/V | 72 |
| Rated Speed/r·min−1 | 3000 |
| Rated Torque/Nm | 16 |
| Stator Inner Diameter/mm | 97 |
| Air Gap Length/mm | 0.5 |
| Symbol | Variable Name | Value Range | Unit |
|---|---|---|---|
| First radial PM width | 2~4 | mm | |
| First radial PM length | 5~10 | mm | |
| Second radial PM width | 2~3 | mm | |
| Second radial PM length | 4~8 | mm | |
| First V-shaped PM included angle | 80~110 | ° | |
| First V-shaped PM width | 2~3.4 | mm | |
| First V-shaped PM length | 10~14 | mm | |
| Second V-shaped PM width | 2~2.5 | mm | |
| Second V-shaped PM length | 3~5 | mm | |
| Second V-shaped PM included angle | 60~90 | ° |
| Parameter | α1 | r1c | t1c |
|---|---|---|---|
| Level 1 | 90 | 5 | 10 |
| Level 2 | 92 | 6 | 10.5 |
| Level 3 | 94 | 7 | 11 |
| Level 4 | 96 | 8 | 11.5 |
| Level 5 | 98 | 9 | 12 |
| Level 6 | 100 | 10 | 12.5 |
| Level 7 | 102 | - | 13 |
| Level 8 | 104 | - | 13.5 |
| Level 9 | 106 | - | 14 |
| Serial No. | α1 (°) | r1c (mm) | t1c (mm) | Fundamental Amplitude (T) | THD |
|---|---|---|---|---|---|
| 1 | 104 | 5 | 12 | 0.836316 | 0.209758 |
| 2 | 106 | 5 | 10 | 0.681718 | 0.196844 |
| 3 | 100 | 9 | 10 | 0.724552 | 0.266451 |
| 4 | 98 | 7 | 10 | 0.707399 | 0.243277 |
| 5 | 102 | 7 | 11 | 0.776453 | 0.225925 |
| 6 | 94 | 6 | 12 | 0.858584 | 0.25555 |
| 7 | 102 | 8 | 13 | 0.928288 | 0.252764 |
| … | … | … | … | … | … |
| 50 | 102 | 9 | 11.5 | 0.829696 | 0.256099 |
| 51 | 94 | 7 | 10.5 | 0.751322 | 0.26077 |
| 52 | 96 | 7 | 12 | 0.862093 | 0.250752 |
| 53 | 96 | 6 | 13.5 | 0.962478 | 0.261571 |
| 54 | 94 | 9 | 12.5 | 0.916229 | 0.280312 |
| Mean Value | 0.859665 | 0.26152 | |||
| Optimization Variables | On Fundamental Amplitude | On Distortion Rate | ||
|---|---|---|---|---|
| Variance | % | Variance | % | |
| α1 | 0.000303090 | 3.37 | 0.000346573 | 4.20 |
| r1c | 0.000155859 | 1.65 | 0.000269413 | 3.27 |
| t1c | 0.008533845 | 94.98 | 0.007630398 | 92.53 |
| Symbol | Value Range | Post-Optimization Value | Unit |
|---|---|---|---|
| r1w | 2~4 | 3.2 | mm |
| r1c | 5~10 | 5 | mm |
| r2w | 2~3 | 2.2 | mm |
| r2c | 4~8 | 8 | mm |
| α1 | 80~110 | 106 | ° |
| t1w | 2~3.4 | 2.6 | mm |
| t1c | 10~14 | 14 | mm |
| t2w | 2~2.5 | 2.2 | mm |
| t2c | 3~5 | 4.8 | mm |
| α2 | 60~90 | 63 | ° |
| Characteristic Point | Voltage (V) | Current (A) | Input Power (W) | Torque (Nm) | Speed (R·min−1) | Output Power (W) | Efficiency (%) |
|---|---|---|---|---|---|---|---|
| No-load point | 72.46 | 10.93 | 792.4 | 1.3 | 3235 | 440.3 | 55.6 |
| Rated point | 72.39 | 78.03 | 5649 | 16.3 | 2938 | 5000 | 88,5 |
| Max efficiency point | 72.36 | 85.48 | 6186 | 18.2 | 2906 | 5538 | 89.5 |
| Max output power pt | 72.24 | 143.5 | 10,360 | 32.4 | 2686 | 9112 | 88.0 |
| Max torque point | 72.24 | 143.5 | 10,360 | 32.4 | 2686 | 9112 | 88.0 |
| End point | 72.24 | 143.5 | 10,360 | 32.4 | 2686 | 9112 | 88.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Hu, W.; Gao, Y.; Hua, S.; Zhou, X.; Geng, H.; Liu, Y. Optimal Air Gap Magnetic Flux Density Distribution of an IPM Synchronous Motor Using a PM Rotor Parameter-Stratified Sensitivity Analysis. World Electr. Veh. J. 2025, 16, 508. https://doi.org/10.3390/wevj16090508
Zhang J, Hu W, Gao Y, Hua S, Zhou X, Geng H, Liu Y. Optimal Air Gap Magnetic Flux Density Distribution of an IPM Synchronous Motor Using a PM Rotor Parameter-Stratified Sensitivity Analysis. World Electric Vehicle Journal. 2025; 16(9):508. https://doi.org/10.3390/wevj16090508
Chicago/Turabian StyleZhang, Jun, Wenjing Hu, Yanhong Gao, Sizhan Hua, Xin Zhou, Huihui Geng, and Yixin Liu. 2025. "Optimal Air Gap Magnetic Flux Density Distribution of an IPM Synchronous Motor Using a PM Rotor Parameter-Stratified Sensitivity Analysis" World Electric Vehicle Journal 16, no. 9: 508. https://doi.org/10.3390/wevj16090508
APA StyleZhang, J., Hu, W., Gao, Y., Hua, S., Zhou, X., Geng, H., & Liu, Y. (2025). Optimal Air Gap Magnetic Flux Density Distribution of an IPM Synchronous Motor Using a PM Rotor Parameter-Stratified Sensitivity Analysis. World Electric Vehicle Journal, 16(9), 508. https://doi.org/10.3390/wevj16090508






