Design of Coordinated EV Traffic Control Strategies for Expressway System with Wireless Charging Lanes
Abstract
1. Introduction
2. Related Works
3. Problem Definition and Model Formulation
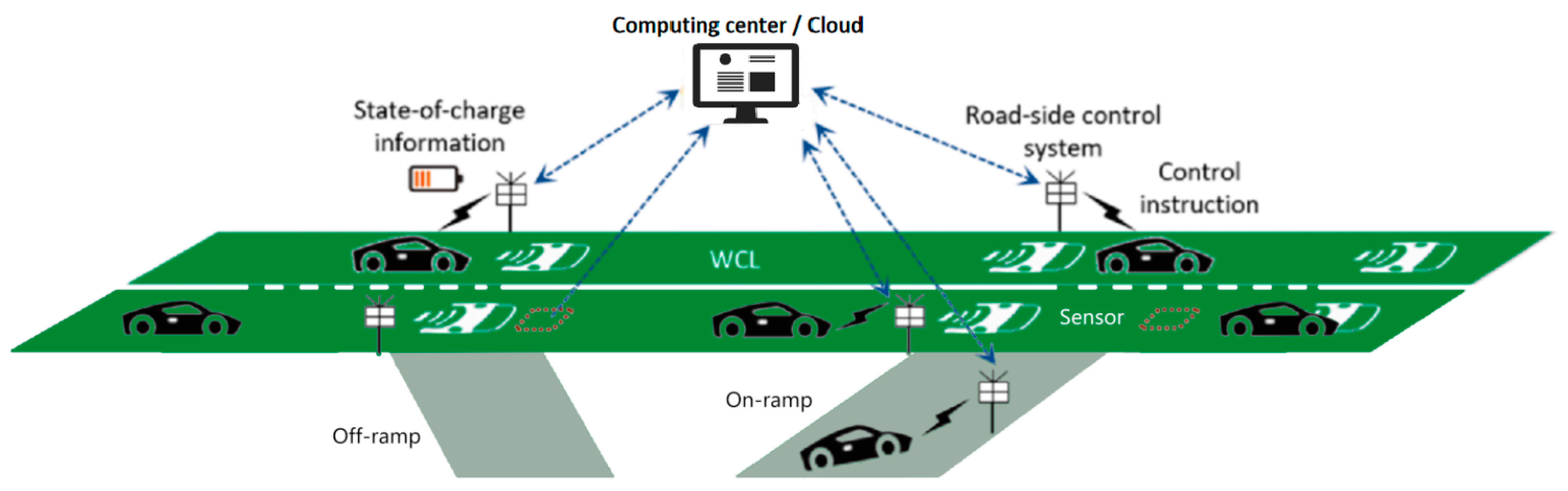
3.1. Basic Considerations
- The entire expressway is equipped with WCLs and is composed of a set of segments, each contains an on-ramp at the beginning and an off-ramp at the end. The traffic demand for the expressway consists of only EVs, each of which will enter the WCL from an on-ramp and leave via an off-ramp that is no further than the destination off-ramp of the very EV, a piece of information known to the control system based on real-time communication when the vehicle approaches the system.
- Roadside control systems are installed at the on-ramp, off-ramp, and end of each highway segment to record the information about the entry and exit of EVs as well as their SOC information. These systems are connected to the computing center with two-way information transfer, including (1) each roadside control system uploads all recorded information to the cloud for data analysis, and (2) the cloud sends traffic management information to each roadside control system. The control instructions received are then sent by the roadside control system to each EV passing by it.
- All EVs have the same battery size but several groups of initial SOC levels (e.g., low and high with 20% and 50% of the battery capacity, respectively). Each group of EVs with specific initial SOC levels has a minimum requirement for the number of WCL segments to travel after entering the system. For example, low initial SOC may be required to stay in the WCL throughout, as they are at risk of failing to reach the destination without charging. EVs with high initial SOC may be required to stay in the WCL only for the first segment where they enter the system.
- All EVs travel at a stable speed on the expressway after entering from an on-ramp and before exiting via an off-ramp, which can be achieved via onboard cruise control. Cruise control is a function that enables drivers to maintain the vehicle at a set speed without controlling the accelerator pedal when the vehicle speed exceeds 40 km/h [35]. Currently, many EVs already have the function of adaptive cruise control (ACC) on board, an advanced driver assistance system that adds the functionality that controls the distance between the vehicle and the preceding vehicle in addition to cruise control [36]. With the effect of ACC, EVs can keep the same speed in the charging lane, simultaneously identifying and minimizing the probability of a crash as soon as an accident occurs in the preceding vehicle. However, EVs may experience typical speed variation in ramp merging, entering, or leaving the expressway system.
- EVs are charged for the entire duration of driving on the WCL, with the amount of energy charged proportional to the time spent in the WCL [29]. This is reasonable since the DWPT facility is normally evenly distributed along the WCL, and the energy replenished is commonly assumed to be proportional to the recharging time [37]. Furthermore, the energy received by EVs is only related to the power received by its secondary coil from the primary coil embedded in the WCL and the time duration of energy transmission by the DWPT system [38].
3.2. Notation
3.3. Model Formulation
3.3.1. Expressway Traffic Model
3.3.2. Wireless Power Transmission Model
3.3.3. The WCL Traffic Control Model
4. Numerical Example
4.1. Parameter Setting
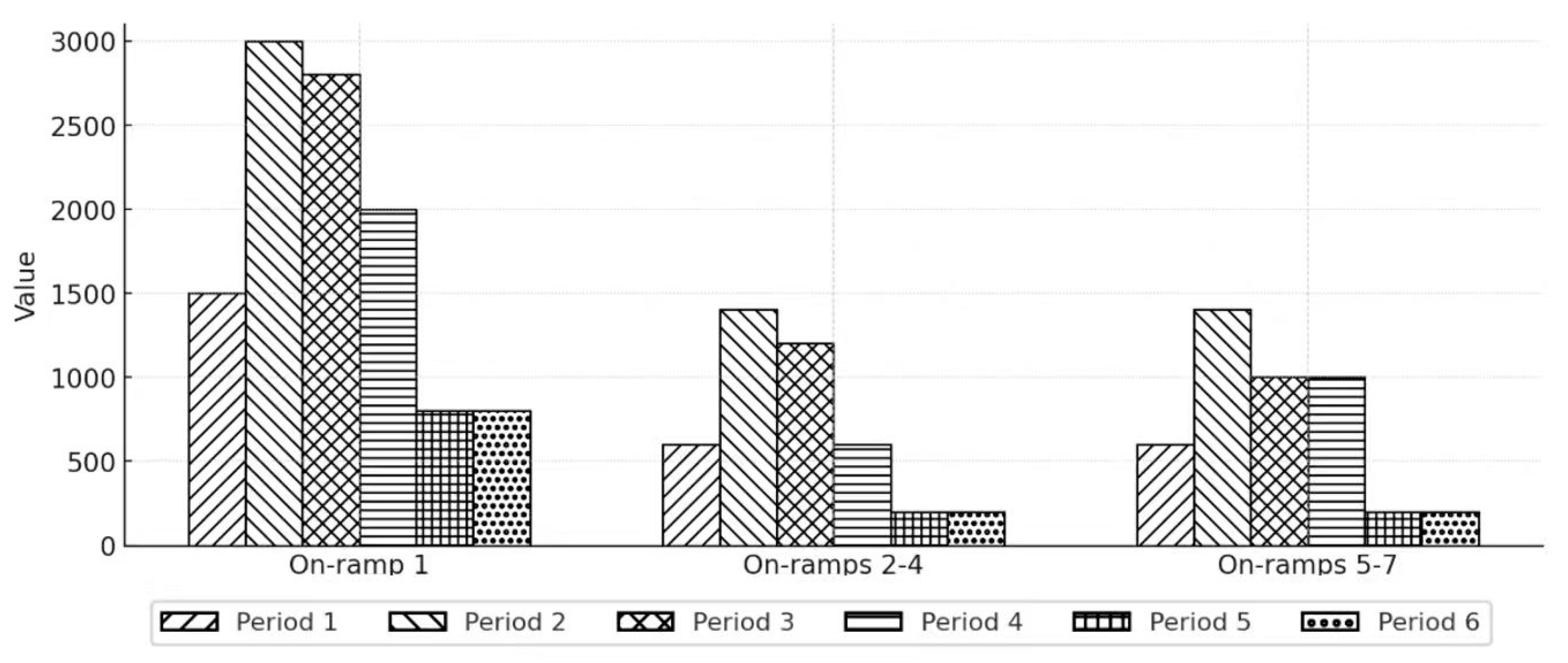
- Traffic demand: referring to the assumption by Papageorgiou [44], the demand profile for seven on-ramps over six time periods is given in Figure 3, which shows that demand peaks rapidly in the second period and decreases significantly in the fifth period, reflecting the process of change in actual traffic flows from peak to off-peak periods. Demand from high initial SOC vehicles and demand from low initial SOC vehicles are shared in 50% at each on-ramp of each period.
- Origin-destination ratio: the values of the vehicle passing ratios for seven on-ramps on seven segments are given in Table 2 For simplicity, the ratios remain constant over the six time periods in this example.
- Vehicle carrying capacity of the WCL: capacity for all segments is taken to be 3300 veh/h due to the setting of one WCL.
- Vehicle speed: travel speed of 80 km/h on the expressway mainline, which is less than the current speed limit for expressways (~100 km/h), given the need for EV charging. Though EVs may experience speed variation during ramp merging, the speed of an EV after entering or before exiting the mainline is assumed to be 80 km/h.
- Vehicle battery capacity: battery capacity for all EVs is set at 55 kWh according to the average battery capacity data from the IEA [45].
- Initial SOC types: we consider two groups of SOC levels to illustrate the usage and insights of our model: those with low SOC levels (20%) and those with high SOC levels (50%). The demand for the two groups is equal at every on-ramp. This setting considers the statistics that most stationary charging events of EVs started with 20~80% SOC, and the most frequent starting SOC levels are 50~60% [46], and the fact that range anxiety can be reduced with DWC.
- Charging efficiency: is set at 88%, which is about the average DWC efficiency of a few real projects summarized in Bi et al. [47].
- EV energy consumption: is set at 10.4 kW (or equivalently per distance consumption of 0.13 kWh/km) in reference to the simulation results for five popular vehicle models (Nissan Leaf S, Renault Zoe R110, Kia Niro, Hyundai IONIQ, and BMW i3) by Sagaria et al. [48]. Note that this value is also close to the data samples generated by Wu et al. (2015) [42]. We use 0.04 kWh and 0.01 kWh based on the consumption rate data by Wu et al. [42] and the assumption that the EV has an acceleration/deceleration of about 4 ft/sec2 [49] with a duration of about 7 s, a speed increase/decrease of 20 km/h.
- Power transmitted by the DWPT system: the receiver coil can receive energy up to kW from the transmitter coil based on the setting by García-Vázquez et al. [38].
- Minimum entry flow and passing-through segment: the minimum number of EVs with both initial SOC levels to be serviced is set to be 10% of the corresponding demand, i.e., Parameter is simply set as and for EVs with low and high SOC levels, respectively, to reflect their different charging needs and how our controller prioritizes between EVs with high and low initial SOC levels.
- DWPT layout: the layout is referenced to García-Vázquez et al. [38], which is based on one of the layouts proposed by Transport Research Laboratory [50]. This configuration provides a power transfer segment with a total length of m, each consisting of three coils with length spaced by a gap m. The distance between segments is the same as the gap, m. Recall that these DWPT layout parameters are depicted as in Figure 2.
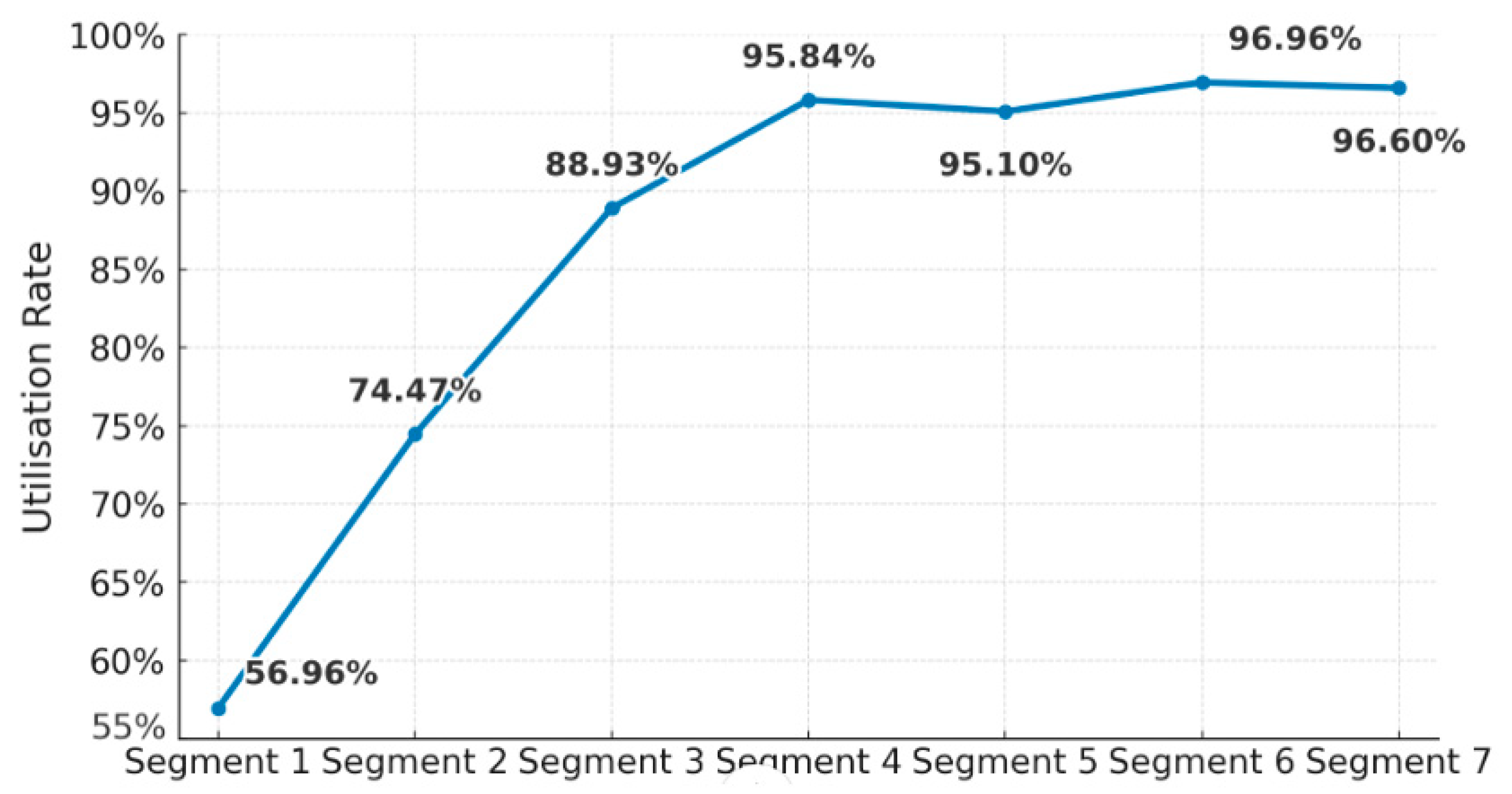
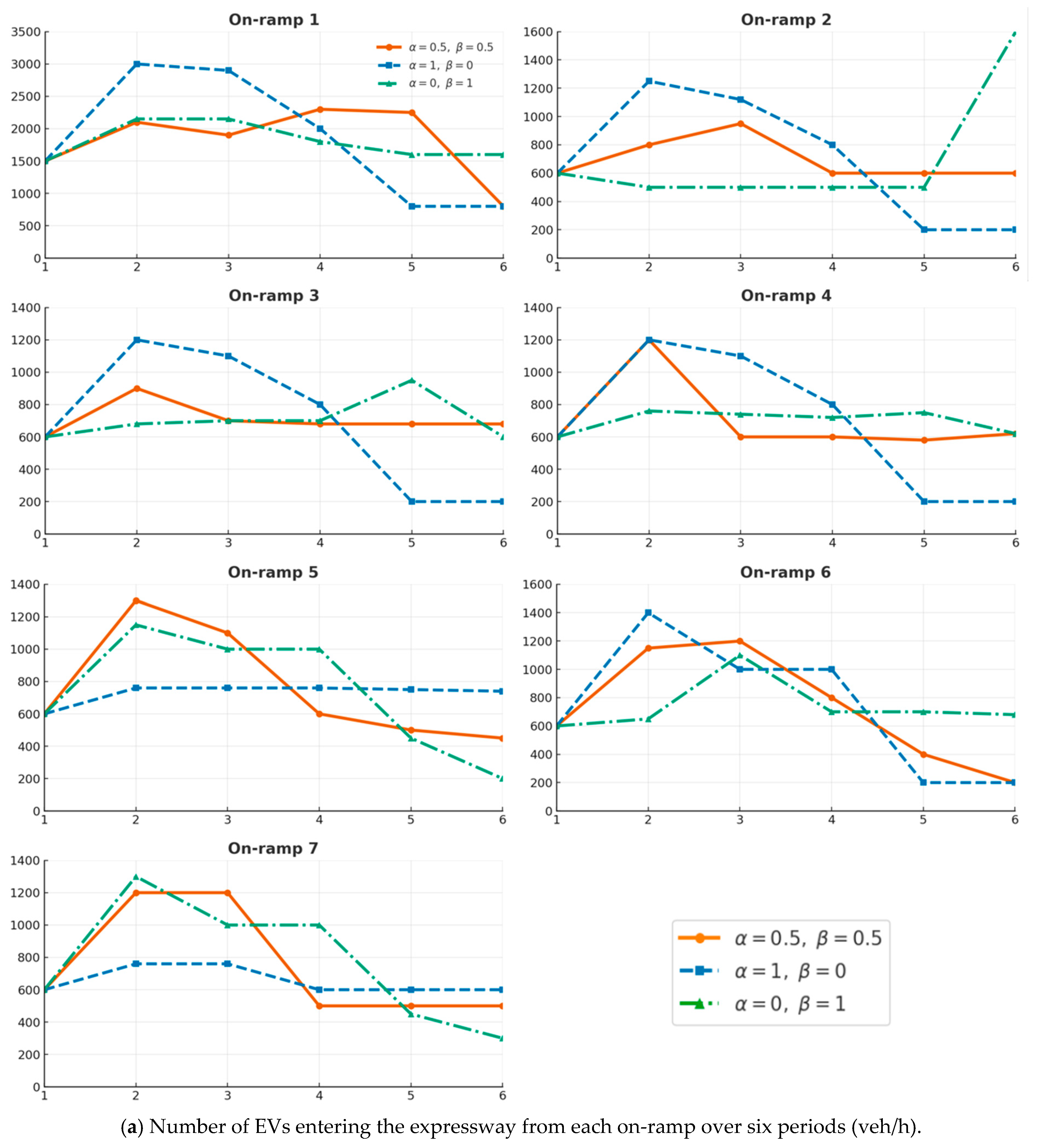
4.2. Model Analysis
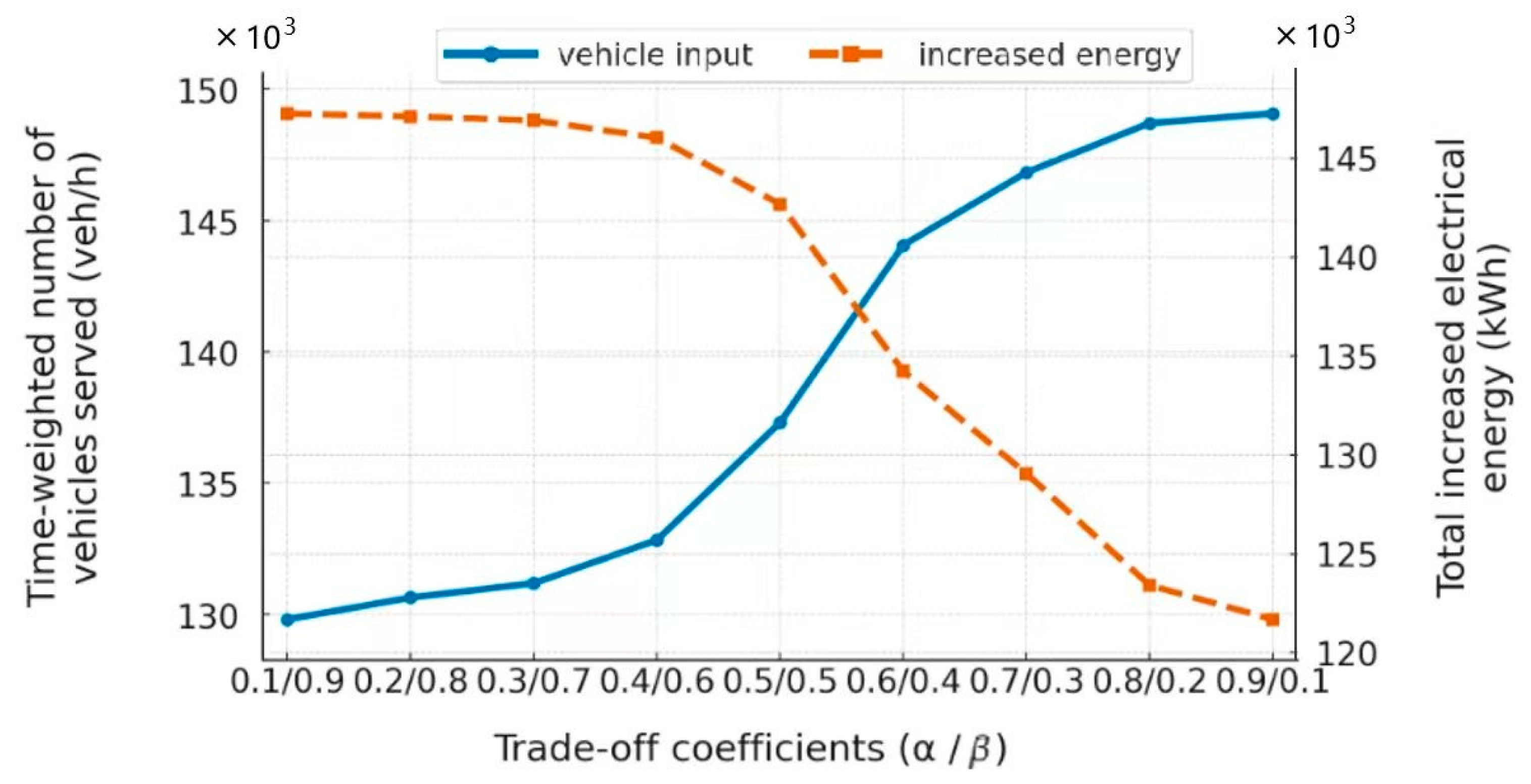
4.3. Impact of Trade-Offs
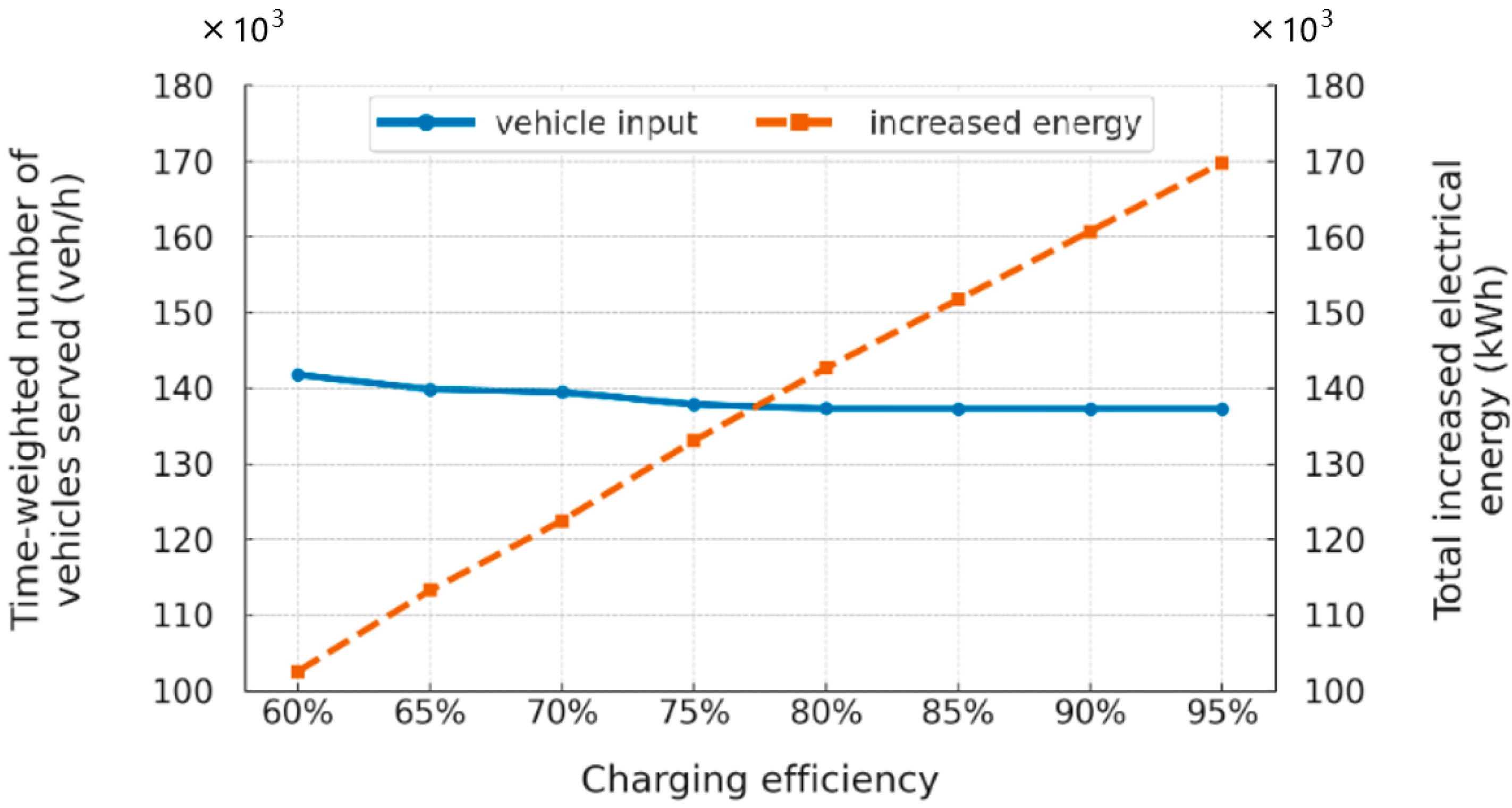
4.4. Impact of Charging Efficiency
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DWPT | dynamic wireless power transfer |
| WCL | wireless charging lane |
| EV | electric vehicle |
| ICEV | internal combustion engine vehicle |
| DWC | dynamic wireless charging |
| SOC | state-of-charge |
| OLEV | online electric vehicle |
| ACC | adaptive cruise control |
| GPL | general-purpose lane |
References
- Leach, F.; Kalghatgi, G.; Stone, R.; Miles, P. The scope for improving the efficiency and environmental impact of internal combustion engines. Transp. Eng. 2020, 1, 100005. [Google Scholar] [CrossRef]
- Liu, Z.; Song, J.; Kubal, J.; Susarla, N.; Knehr, K.W.; Islam, E.; Nelson, P.; Ahmed, S. Comparing total cost of ownership of battery electric vehicles and internal combustion engine vehicles. Energy Policy 2021, 158, 112564. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Linares-Mena, A.-R.; Borge-Diez, D.; Quinto-Alemany, C.-D. Impact assessment of electric vehicles on islands grids: A case study for Tenerife (Spain). Energy 2017, 120, 385–396. [Google Scholar] [CrossRef]
- Towoju, O.A. Fuels for Automobiles: The Sustainable Future. J. Energy Res. Rev. 2021, 7, 8–13. [Google Scholar] [CrossRef]
- He, J.; Yang, H.; Tang, T.-Q.; Huang, H.-J. Optimal deployment of wireless charging lanes considering their adverse effect on road capacity. Transp. Res. Part C Emerg. Technol. 2020, 111, 171–184. [Google Scholar] [CrossRef]
- IEA. Trends in Electric Car Markets. 2024. Available online: https://www.iea.org/reports/global-ev-outlook-2025/trends-in-electric-car-markets-2 (accessed on 10 June 2025).
- Rietmann, N.; Hügler, B.; Lieven, T. Forecasting the trajectory of electric vehicle sales and the consequences for worldwide CO2 emissions. J. Clean. Prod. 2020, 261, 121038. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Wu, F.; Sioshansi, R. A stochastic flow-capturing model to optimize the location of fast-charging stations with uncertain electric vehicle flows. Transp. Res. Part D Transp. Environ. 2017, 53, 354–376. [Google Scholar] [CrossRef]
- Arif, S.M.; Lie, T.T.; Seet, B.C.; Ayyadi, S.; Jensen, K. Review of Electric Vehicle Technologies, Charging Methods, Standards and Optimization Techniques. Electronics 2021, 10, 1910. [Google Scholar] [CrossRef]
- Dharmakeerthi, C.; Mithulananthan, N.; Saha, T. Impact of electric vehicle fast charging on power system voltage stability. Int. J. Electr. Power Energy Syst. 2014, 57, 241–249. [Google Scholar] [CrossRef]
- Habib, S.; Khan, M.M.; Abbas, F.; Sang, L.; Shahid, M.U.; Tang, H. A Comprehensive Study of Implemented International Standards, Technical Challenges, Impacts and Prospects for Electric Vehicles. IEEE Access 2018, 6, 13866–13890. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.; Niu, L.; Jiang, J. Coordinated charging strategy for electric taxis in temporal and spatial scale. Energies 2015, 8, 1256–1272. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Zhang, Y.; Jiang, L.; Li, B.; Yan, D.; Ma, C. An Optimal Design and Analysis of a Hybrid Power Charging Station for Electric Vehicles Considering Uncertainties. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE In-dustrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 5147–5152. [Google Scholar] [CrossRef]
- Martínez-Lao, J.; Montoya, F.G.; Montoya, M.G.; Manzano-Agugliaro, F. Electric vehicles in Spain: An overview of charging systems. Renew. Sustain. Energy Rev. 2017, 77, 970–983. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Inductive Power Transfer. Proc. IEEE 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- Cirimele, V.; Diana, M.; Freschi, F.; Mitolo, M. Inductive Power Transfer for Automotive Applications: State-of-the-Art and Future Trends. IEEE Trans. Ind. Appl. 2018, 54, 4069–4079. [Google Scholar] [CrossRef]
- Lukic, S.; Pantic, Z. Cutting the Cord: Static and Dynamic Inductive Wireless. IEEE Electrif. Mag. 2013, 1, 57–64. [Google Scholar] [CrossRef]
- Jansuwan, S.; Liu, Z.; Song, Z.; Chen, A. An evaluation framework of automated electric transportation system. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102265. [Google Scholar] [CrossRef]
- Duarte, G.; Silva, A.; Baptista, P. Assessment of wireless charging impacts based on real-world driving patterns: Case study in Lisbon, Portugal. Sustain. Cities Soc. 2021, 71, 102952. [Google Scholar] [CrossRef]
- Tan, Z.; Liu, F.; Chan, H.K.; Gao, H.O. Transportation systems management considering dynamic wireless charging electric vehicles: Review and prospects. Transp. Res. Part E Logist. Transp. Rev. 2022, 163, 102761. [Google Scholar] [CrossRef]
- Jang, Y.J. Survey of the operation and system study on wireless charging electric vehicle systems. Transp. Res. Part C Emerg. Technol. 2018, 95, 844–866. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Bock, S.; Boysen, N.; Briskorn, D. Optimizing the electrification of roads with charge-while-drive technology. Eur. J. Oper. Res. 2022, 299, 1111–1127. [Google Scholar] [CrossRef]
- Ko, Y.D.; Jang, Y.J. The Optimal System Design of the Online Electric Vehicle Utilizing Wireless Power Transmission Technology. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1255–1265. [Google Scholar] [CrossRef]
- Jang, Y.J.; Jeong, S.; Ko, Y.D. System optimization of the On-Line Electric Vehicle operating in a closed environment. Comput. Ind. Eng. 2015, 80, 222–235. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, Y.J.; Kum, D. Economic Analysis of the Dynamic Charging Electric Vehicle. IEEE Trans. Power Electron. 2015, 30, 6368–6377. [Google Scholar] [CrossRef]
- Hwang, I.; Jang, Y.J.; Ko, Y.D.; Lee, M.S. System Optimization for Dynamic Wireless Charging Electric Vehicles Operating in a Multiple-Route Environment. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1709–1726. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Z. Robust planning of dynamic wireless charging infrastructure for battery electric buses. Transp. Res. Part C Emerg. Technol. 2017, 83, 77–103. [Google Scholar] [CrossRef]
- Fuller, M. Wireless charging in California: Range, recharge, and vehicle electrification. Transp. Res. Part C Emerg. Technol. 2016, 67, 343–356. [Google Scholar] [CrossRef]
- Wang, T.; Yang, B.; Chen, C.; Guan, X. Wireless charging lane deployment in urban areas considering traffic light and regional energy supply-demand balance. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–5. [Google Scholar]
- He, J.; Huang, H.-J.; Yang, H.; Tang, T.-Q. An electric vehicle driving behavior model in the traffic system with a wireless charging lane. Phys. A Stat. Mech. Its Appl. 2017, 481, 119–126. [Google Scholar] [CrossRef]
- Li, D.; Leung, M.-F.; Tang, J.; Wang, Y.; Hu, J.; Wang, S. Generative Self-Supervised Learning for Cyberattack-Resilient EV Charging Demand Forecasting. IEEE Trans. Intell. Transp. Syst. 2025, 3545577. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Kiakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y.; Diakaki, C. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Liu, F.; Tan, Z.; Chan, H.K.; Zheng, L. Ramp metering control on wireless charging lanes considering optimal traffic and charging efficiencies. IEEE Trans. Intell. Transp. Syst. 2024, 25, 11590–11601. [Google Scholar] [CrossRef]
- Xiao, C. Design and Research of Cruise Control System Based on Pure Electric Vehicle. Automot. Electr. Appl. 2020, 9, 13–18. [Google Scholar]
- Madhusudhanan, A.K. A method to improve an electric vehicle’s range: Efficient Cruise. Eur. J. Control. 2019, 48, 83–96. [Google Scholar] [CrossRef]
- Deflorio, F.P.; Castello, L.; Pinna, I.; Guglielmi, P. “Charge while driving” for electric vehicles: Road traffic modeling and energy assessment. J. Mod. Power Syst. Clean Energy 2015, 3, 277–288. [Google Scholar] [CrossRef]
- García-Vázquez, C.A.; Llorens-Iborra, F.; Fernández-Ramírez, L.M.; Sánchez-Sainz, H.; Jurado, F. Comparative study of dy-namic wireless charging of electric vehicles in motorway, highway and urban stretches. Energy 2017, 137, 42–57. [Google Scholar] [CrossRef]
- Tan, Z.; Gao, H.O. Traffic control for air quality management and congestion mitigation in complex urban vehicular tunnels. Transp. Res. Part C Emerg. Technol. 2015, 58, 13–28. [Google Scholar] [CrossRef]
- Trung, N.K.; Diep, N.T.; Venet, P. A Maximum Transfer Efficiency Tracking Method for Dynamic Wireless Charging Systems of Electric Vehicles. J. Electr. Comput. Eng. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Tran, C.Q.; Keyvan-Ekbatani, M.; Ngoduy, D.; Watling, D. Dynamic wireless charging lanes location model in urban networks considering route choices. Transp. Res. Part C Emerg. Technol. 2022, 139, 103652. [Google Scholar] [CrossRef]
- Wu, X.; Freese, D.; Cabrera, A.; Kitch, W.A. Electric vehicles’ energy consumption measurement and estimation. Transp. Res. Part D Transp. Environ. 2015, 34, 52–67. [Google Scholar] [CrossRef]
- Tan, Z.; Gao, H.O. Hybrid model predictive control based dynamic pricing of managed lanes with multiple accesses. Transp. Res. Part B Methodol. 2018, 112, 113–131. [Google Scholar] [CrossRef]
- Papageorgiou, M. A new approach to time-of-day control based on a dynamic freeway traffic model. Transp. Res. Part B Methodol. 1980, 14, 349–360. [Google Scholar] [CrossRef]
- IEA. 2021. Top 5 barriers to EV adoption reported by EV100 member companies. Available online: https://www.iea.org/data-and-statistics/charts/top-5-barriers-to-ev-adoption-reported-by-ev100-member-companies (accessed on 20 July 2022).
- Smart, J.; Schey, S. Battery electric vehicle driving and charging behavior observed early in the EV project. SAE Int. J. Altern. Powertrains 2012, 1, 27–33. [Google Scholar] [CrossRef]
- Bi, Z.; Kan, T.; Mi, C.C.; Zhang, Y.; Zhao, Z.; Keoleian, G.A. A review of wireless power transfer for electric vehicles: Prospects to enhance sustainable mobility. Appl. Energy 2016, 179, 413–425. [Google Scholar] [CrossRef]
- Sagaria, S.; Neto, R.C.; Baptista, P. Modelling approach for assessing influential factors for EV energy performance. Sustain. Energy Technol. Assess. 2021, 44, 100984. [Google Scholar] [CrossRef]
- Yang, G.; Xu, H.; Tian, Z.; Wang, Z.; Zhao, Y. Acceleration Characteristics at Metered On-Ramps. Transp. Res. Rec. J. Transp. Res. Board 2015, 2484, 1–9. [Google Scholar] [CrossRef]
- Transport Research Laboratory. Feasibility Study: Powering Electric Vehicles on England’s Major Roads; Highways England Company: Birmingham, UK, 2015. [Google Scholar]
- Qian, T.; Fang, M.; Hu, Q.; Shao, C.; Zheng, J. V2Sim: An Open-Source Microscopic V2G Simulation Platform in Urban Power and Transportation Network. IEEE Trans. Smart Grid 2025, 16, 3167–3178. [Google Scholar] [CrossRef]



| Indices | |
| Index used for the expressway segments | |
| Index used for the origin on-ramps | |
| Index used for the destination off-ramps | |
| Index used for the time periods | |
| Index used for the initial SOC types of EVs | |
| Traffic model variables and parameters | |
| Total number of vehicles on the expressway during period , [veh per hour, veh/h] | |
| Number of vehicles allowed to enter the expressway from on-ramp during period p and will pass the end of segment s, [veh/h] | |
| Total number of vehicles leaving the expressway via off-ramp d during period p, [veh/h] | |
| Total number of vehicles passing the end of the expressway segment s during period p, [veh/h] | |
| Total vehicle demand in period p for entering the expressway from on-ramp o, [veh/h] | |
| Ratio of vehicles entering the expressway from on-ramp during period and will pass through the beginning of expressway segment , with | |
| Vehicle carrying capacity of expressway segment , [veh/h] | |
| Length of the expressway segment , [kilometer, km] | |
| Average travel time through the expressway segment , [hour] | |
| Average speed of an EV traveling on the expressway segment , [kilometer per hour, km/h] | |
| Average travel time from on-ramp to the end of expressway segment , with , [hour] | |
| EV charging model variables and parameters | |
| Number of EVs with initial SOC type allowed to enter the expressway from on-ramp during period and will pass the end of segment , [veh/h] | |
| The minimum number of EVs with initial SOC type required to enter the expressway from on-ramp during period , [veh/h] | |
| Demand of EVs with initial SOC type in period for entering the expressway from on-ramp , [veh/h] | |
| The index of the segment that any EV with initial SOC type entering the expressway from on-ramp must at least pass through if no further than its destination off-ramp, which is generally bigger for a lower SOC level. | |
| Electrical energy increased by an EV which enters and leaves the WCL system from on-ramp o and off-ramp d, [kilowatt-hours, kWh] | |
| Electrical energy received by an EV which enters and leaves the WCL system from on-ramp o and off-ramp d, [kWh] | |
| Electrical energy consumed by an EV which enters and leaves the WCL system from on-ramp o and off-ramp d, [kWh] | |
| Electrical energy consumption of an EV by traveling throughout segment with stable speed, [kWh] | |
| Electrical energy additional to consumed by an EV due to speed variation in merging traffic entering the system via on-ramp o, [kWh] | |
| Electrical energy additional to consumed by an EV due to speed variation in merging traffic leaving the system via off-ramp d, [kWh] | |
| Total number of segmented transmitter arrays on expressway segment | |
| Time for the EV to receive electrical energy from the DWPT system on expressway segment , [hour] | |
| o | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| s | ||||||||
| 1 | 100% | |||||||
| 2 | 90% | 100% | ||||||
| 3 | 80% | 90% | 100% | |||||
| 4 | 70% | 80% | 90% | 100% | ||||
| 5 | 60% | 70% | 80% | 90% | 100% | |||
| 6 | 50% | 60% | 70% | 80% | 90% | 100% | ||
| 7 | 40% | 50% | 60% | 70% | 80% | 90% | 100% | |
| Energy received | |||||||
| 1.54 | 3.08 | 3.08 | 3.08 | 1.54 | 2.46 | 3.69 | |
| Energy consumed | |||||||
| 0.65 | 1.30 | 1.30 | 1.30 | 0.65 | 1.04 | 1.56 |
| o | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| p | ||||||||
| 1 | 1500 | 600 | 600 | 600 | 600 | 600 | 600 | |
| 2 | 2164 | 770 | 875 | 1230 | 1300 | 1178 | 1200 | |
| 3 | 1904 | 967 | 681 | 580 | 1100 | 1221 | 1183 | |
| 4 | 2300 | 621 | 679 | 580 | 482 | 796 | 472 | |
| 5 | 2230 | 621 | 681 | 580 | 481 | 403 | 472 | |
| 6 | 802 | 621 | 684 | 630 | 437 | 202 | 473 | |
| o | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| p | ||||||||
| 1 | 750 (750) | 300 (300) | 300 (300) | 300 (300) | 300 (300) | 300 (300) | 300 (300) | |
| 2 | 665 (1499) | 70 (700) | 499 (376) | 600 (630) | 600 (700) | 700 (478) | 500 (700) | |
| 3 | 1514 (390) | 422 (545) | 60 (621) | 520 (60) | 600 (500) | 500 (721) | 683 (500) | |
| 4 | 290 (2010) | 591 (30) | 649 (30) | 32 (548) | 127 (355) | 500 (296) | 50 (422) | |
| 5 | 1829 (401) | 611 (10) | 10 (671) | 118 (462) | 471 (10) | 100 (303) | 442 (30) | |
| 6 | 402 (400) | 106 (515) | 582 (102) | 530 (100) | 102 (335) | 100 (102) | 225 (248) | |
| o | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| s | ||||||||
| 1 | 100% | |||||||
| 2 | 100% | 100% | ||||||
| 3 | 100% | 100% | 100% | |||||
| 4 | 88% | 97% | 82% | 100% | ||||
| 5 | 68% | 42% | 86% | 67% | 100% | |||
| 6 | 52% | 67% | 80% | 70% | 45% | 100% | ||
| 7 | 59% | 52% | 70% | 70% | 45% | 42% | 100% | |
| Measure | Time-Weighted Number of Vehicles Served (veh/h) | Total Increased Electrical Energy (kWh) | |
|---|---|---|---|
| Case | |||
| 137,295 (−7.9%) | 142,666 (−3.1%) | ||
| 149,078 (0%) | 99,017 (−32.8%) | ||
| 124,498 (−16.5%) | 147,303 (0%) | ||
| Time-Weighted Number of Vehicles Served (veh/h) | Total Increased Electrical Energy (kWh) | ||
|---|---|---|---|
| 0.1 | 0.9 | 129,795 (87.07%) | 147,260 (99.97%) |
| 0.2 | 0.8 | 130,624 (87.62%) | 147,103 (99.86%) |
| 0.3 | 0.7 | 131,170 (87.99%) | 146,908 (99.73%) |
| 0.4 | 0.6 | 132,819 (89.09%) | 146,034 (99.14%) |
| 0.5 | 0.5 | 137,295 (92.10%) | 142,666 (96.85%) |
| 0.6 | 0.4 | 144,060 (96.63%) | 134,219 (91.12%) |
| 0.7 | 0.3 | 146,835 (98.50%) | 129,041 (87.60%) |
| 0.8 | 0.2 | 148,709 (99.75%) | 123,401 (83.77%) |
| 0.9 | 0.1 | 149,078 (100%) | 121,682 (82.61%) |
| Charging Efficiency | Time-Weighted Number of Vehicles Served (veh/h) | Total Increased Electrical Energy (kWh) |
|---|---|---|
| 60% | 141,741 | 102,586 |
| 65% | 139,847 | 113,263 |
| 70% | 139,473 | 122,495 |
| 75% | 137,841 | 133,071 |
| 80% | 137,295 | 142,666 |
| 85% | 137,288 | 151,691 |
| 90% | 137,286 | 160,734 |
| 95% | 137,290 | 169,769 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hong, Y.; Tan, Z. Design of Coordinated EV Traffic Control Strategies for Expressway System with Wireless Charging Lanes. World Electr. Veh. J. 2025, 16, 496. https://doi.org/10.3390/wevj16090496
Zhang Y, Hong Y, Tan Z. Design of Coordinated EV Traffic Control Strategies for Expressway System with Wireless Charging Lanes. World Electric Vehicle Journal. 2025; 16(9):496. https://doi.org/10.3390/wevj16090496
Chicago/Turabian StyleZhang, Yingying, Yifeng Hong, and Zhen Tan. 2025. "Design of Coordinated EV Traffic Control Strategies for Expressway System with Wireless Charging Lanes" World Electric Vehicle Journal 16, no. 9: 496. https://doi.org/10.3390/wevj16090496
APA StyleZhang, Y., Hong, Y., & Tan, Z. (2025). Design of Coordinated EV Traffic Control Strategies for Expressway System with Wireless Charging Lanes. World Electric Vehicle Journal, 16(9), 496. https://doi.org/10.3390/wevj16090496






