Fault Identification Method for Flexible Traction Power Supply System by Empirical Wavelet Transform and 1-Sequence Faulty Energy
Abstract
1. Introduction
- (1)
- A composite sequence network model based on the generalized symmetric component method is established, incorporating EMUs, faults and ATs. This model reveals three fault distribution characteristics in FTPSS. Meanwhile, one-sequence faulty energy signal significantly suppresses the effects of ATs, parallel wires, and noise, enhancing faulty feature clarity and enabling more accurate time-frequency analysis.
- (2)
- A fault identification method combining EWT and one-sequence faulty energy is proposed to directly distinguish the TPSS fault from the EMUs load. EWT is used to decompose 1-sequence faulty energy, while permutation entropy is introduced to select the fault component. The fault variance calculated by the selected fault component can identify the TPSS fault while avoiding interference from system disturbances such as excitation inrush current from AT, non-linear current from AC-DC-AC converters and EMUs harmonic current. The method does not require synchronization signals or low sampling rates, making it practical and easy to implement.
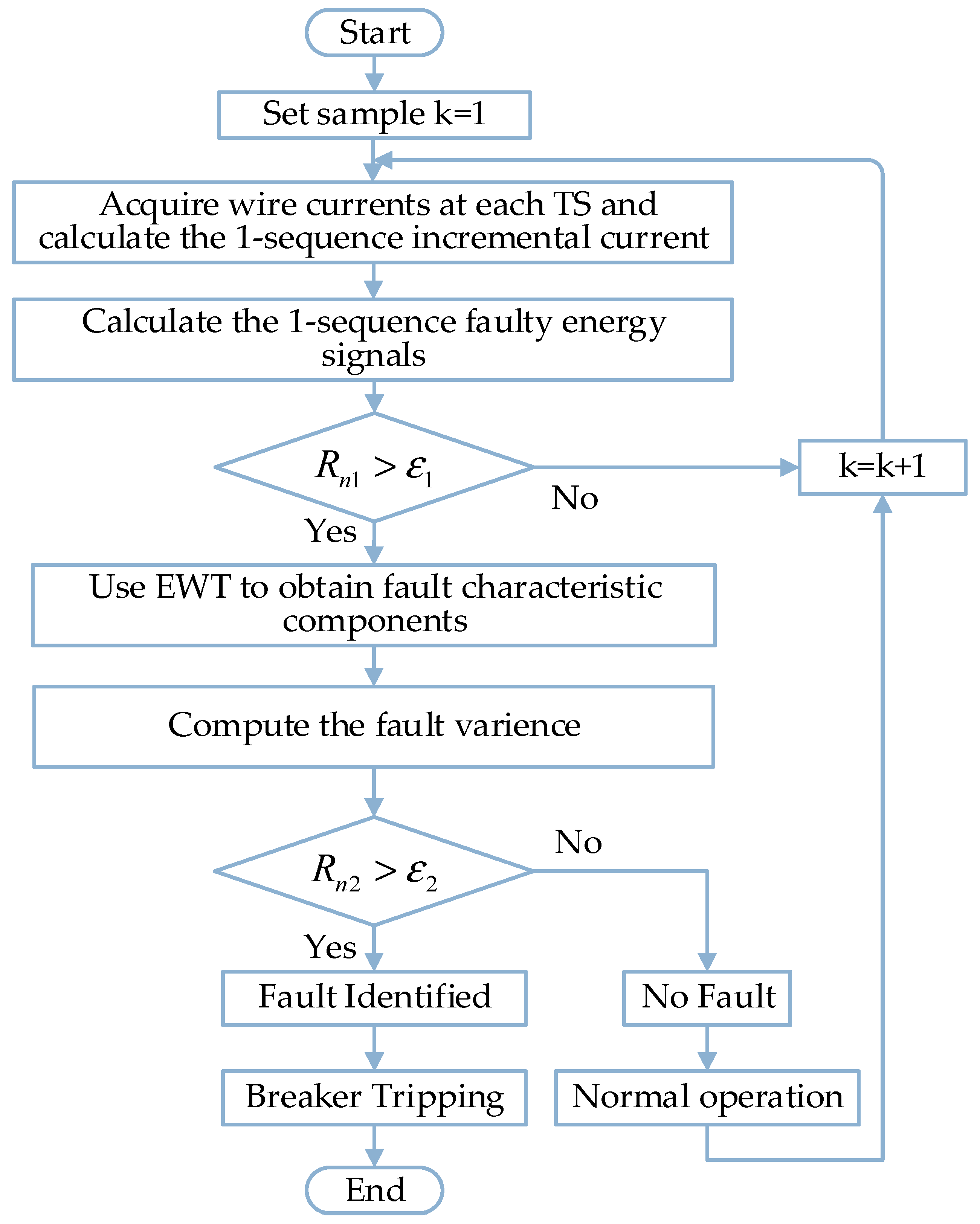
2. Fault Identification Method for FTPSS
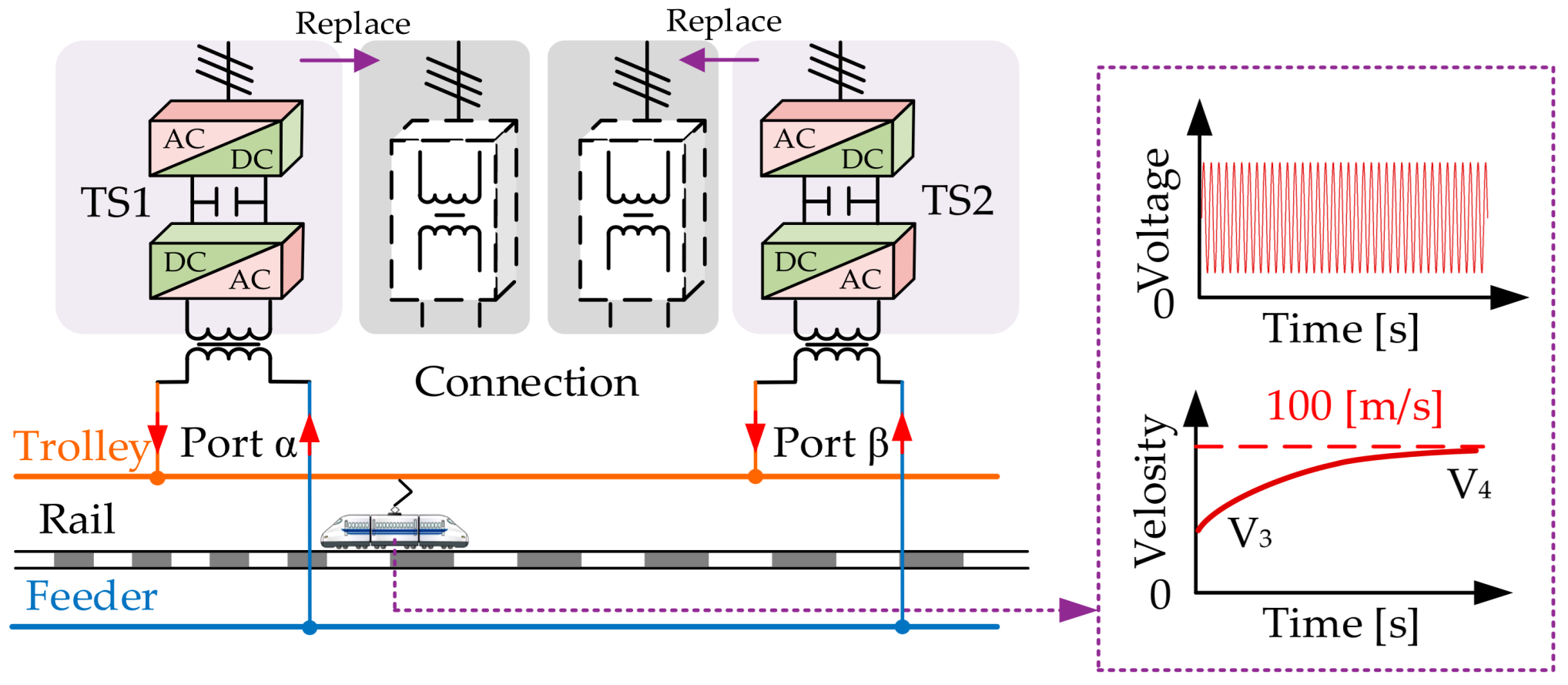
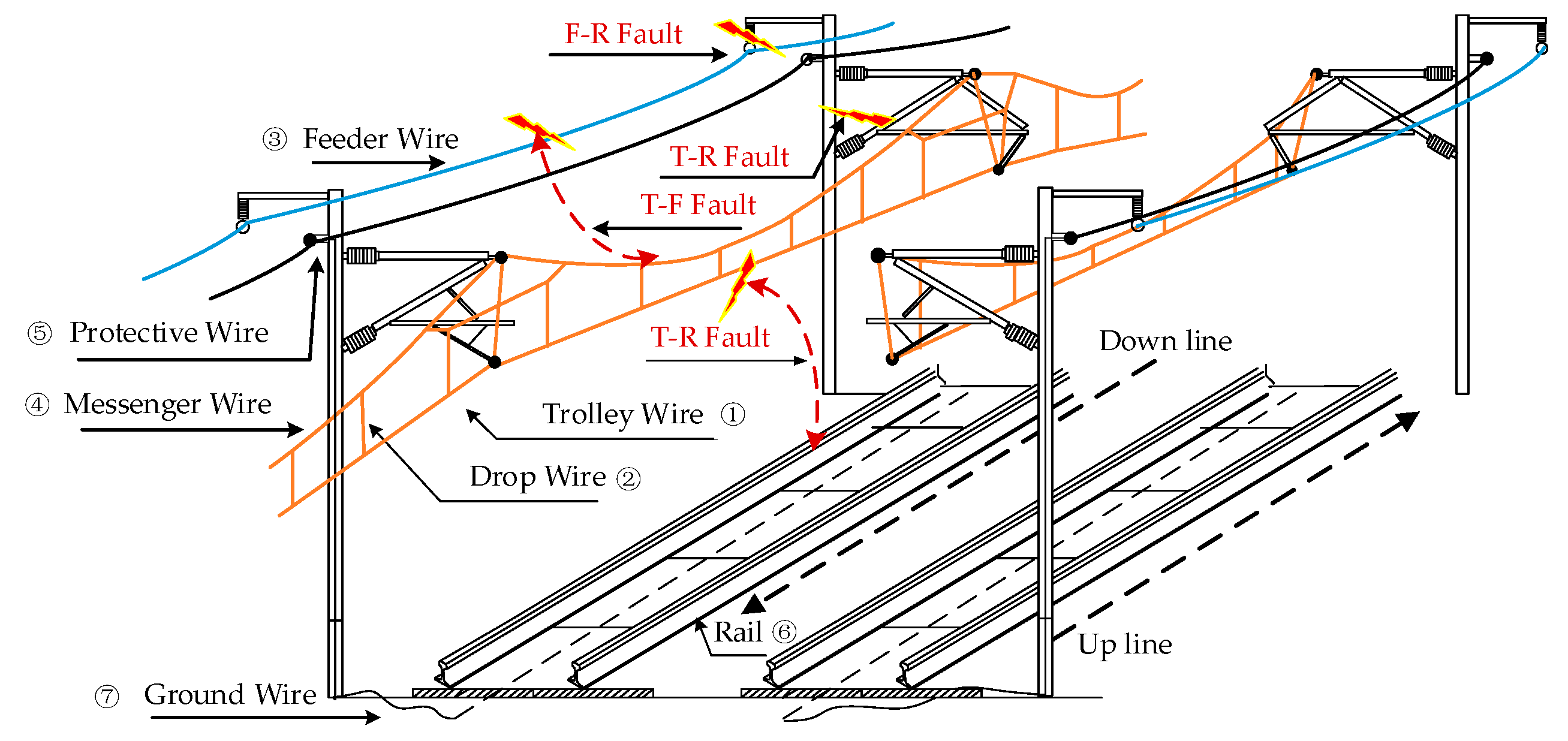
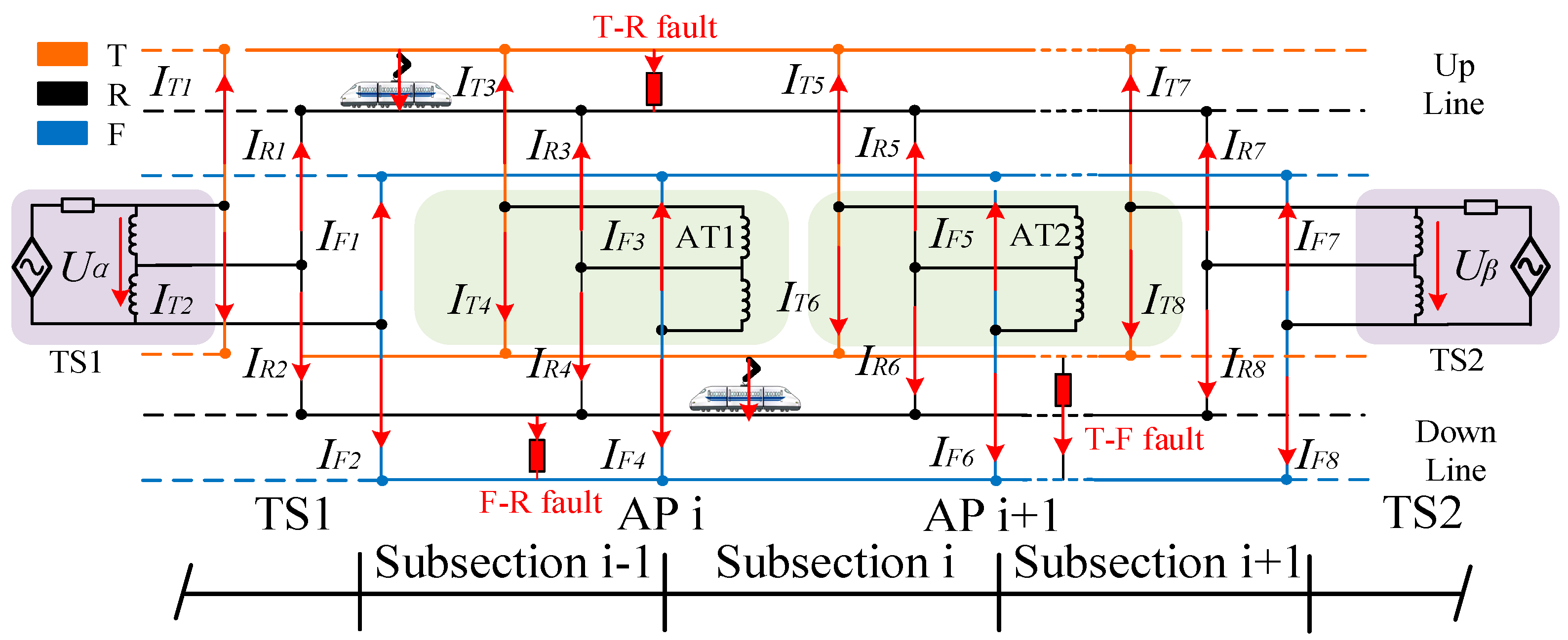
2.1. Simplified Analysis of FTPSS Faults
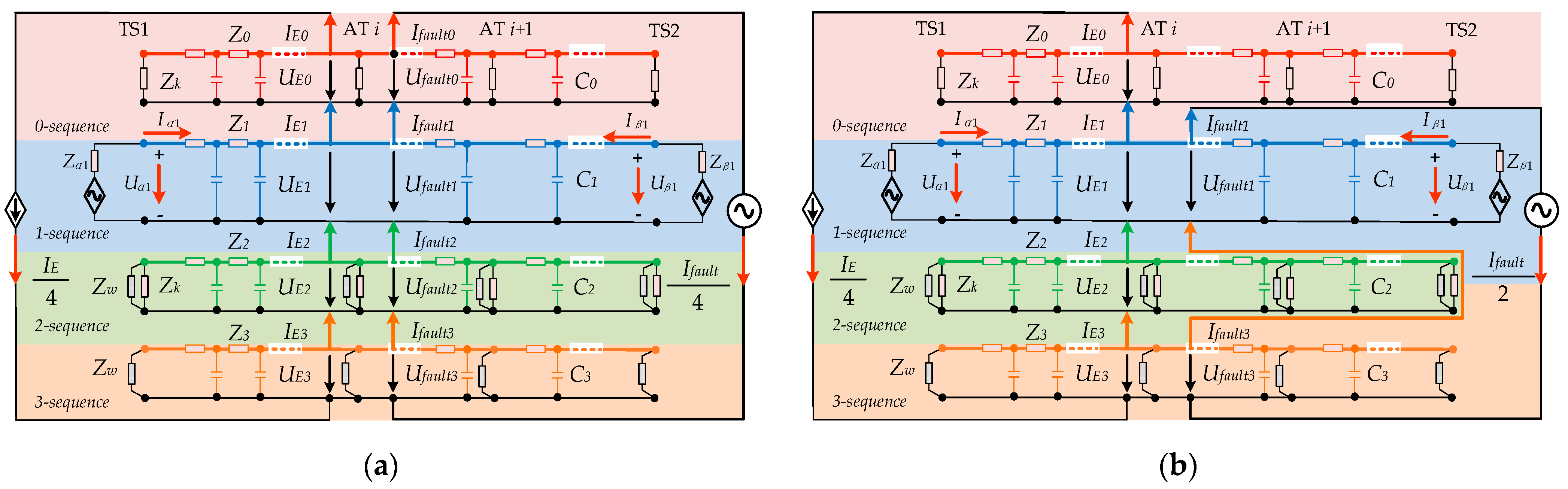
2.2. Composite Sequence Network Model
2.3. Signal Pre-Processing
2.4. Signal Decomposition Methods
2.5. Signal Selection Method
2.6. Fault Detection Methods
3. Case Studies
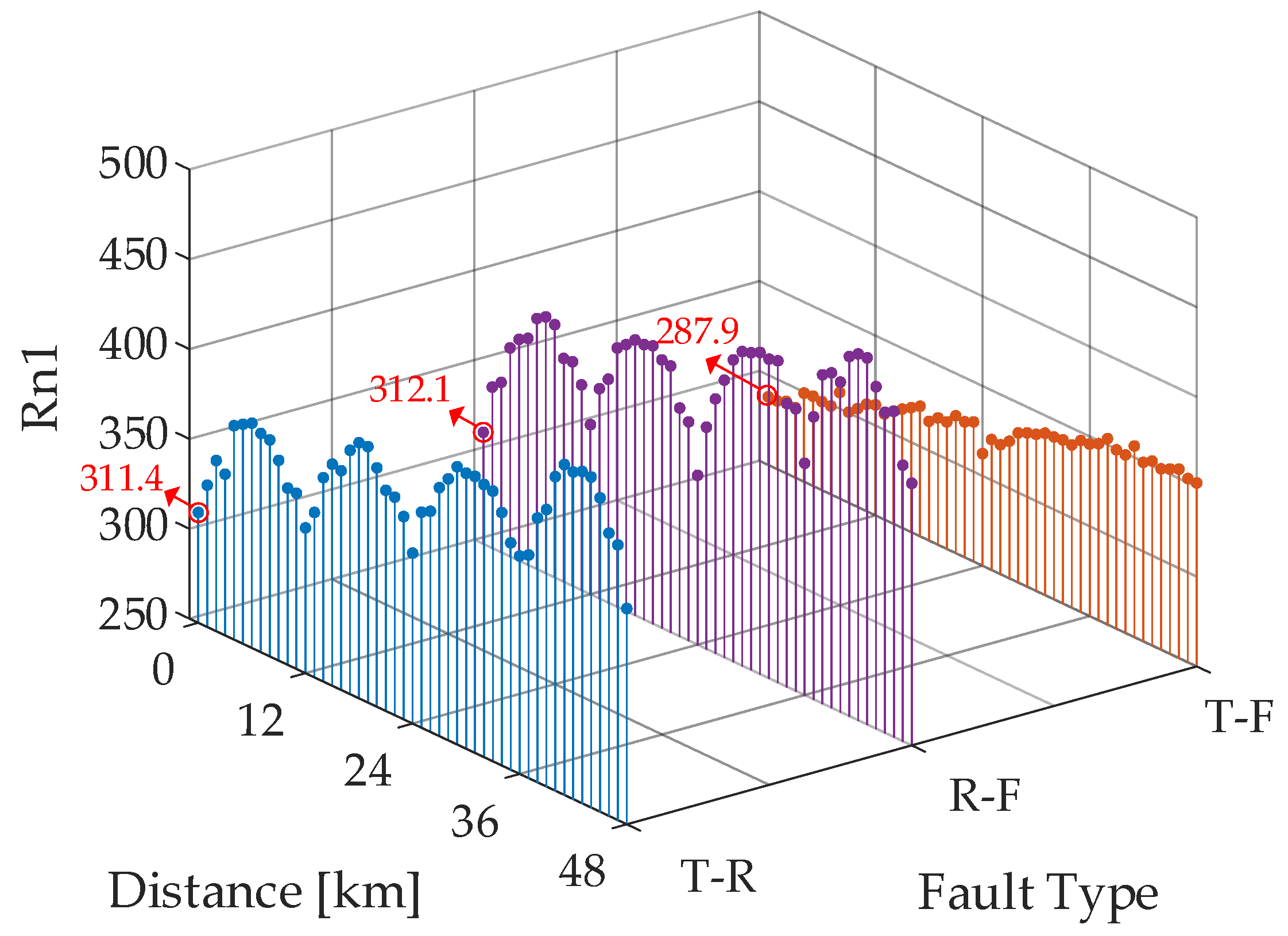
3.1. Testing with Fault Position and Metallic Fault Types
3.2. Testing with Fault Inception Angle and Fault Impedance
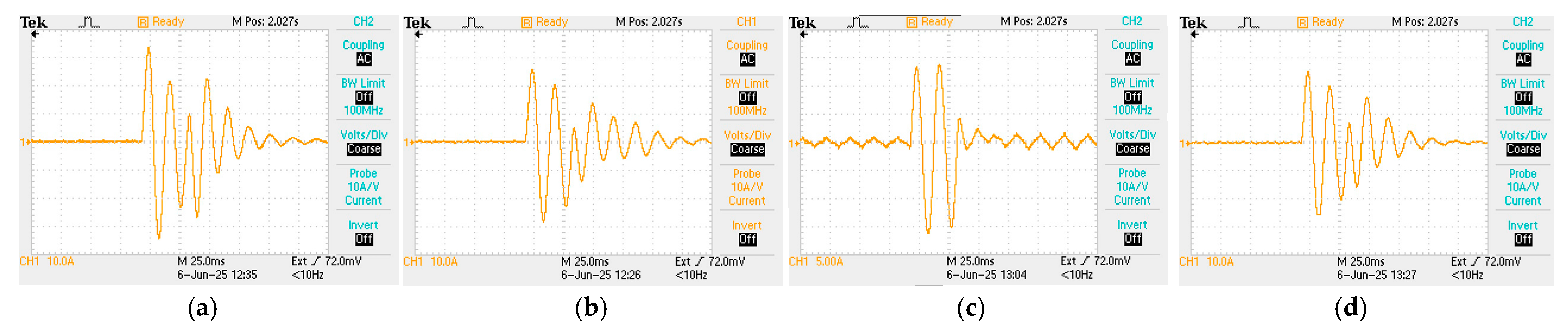
3.3. Impact of Inrush Current
3.4. Impact of EMUs Current
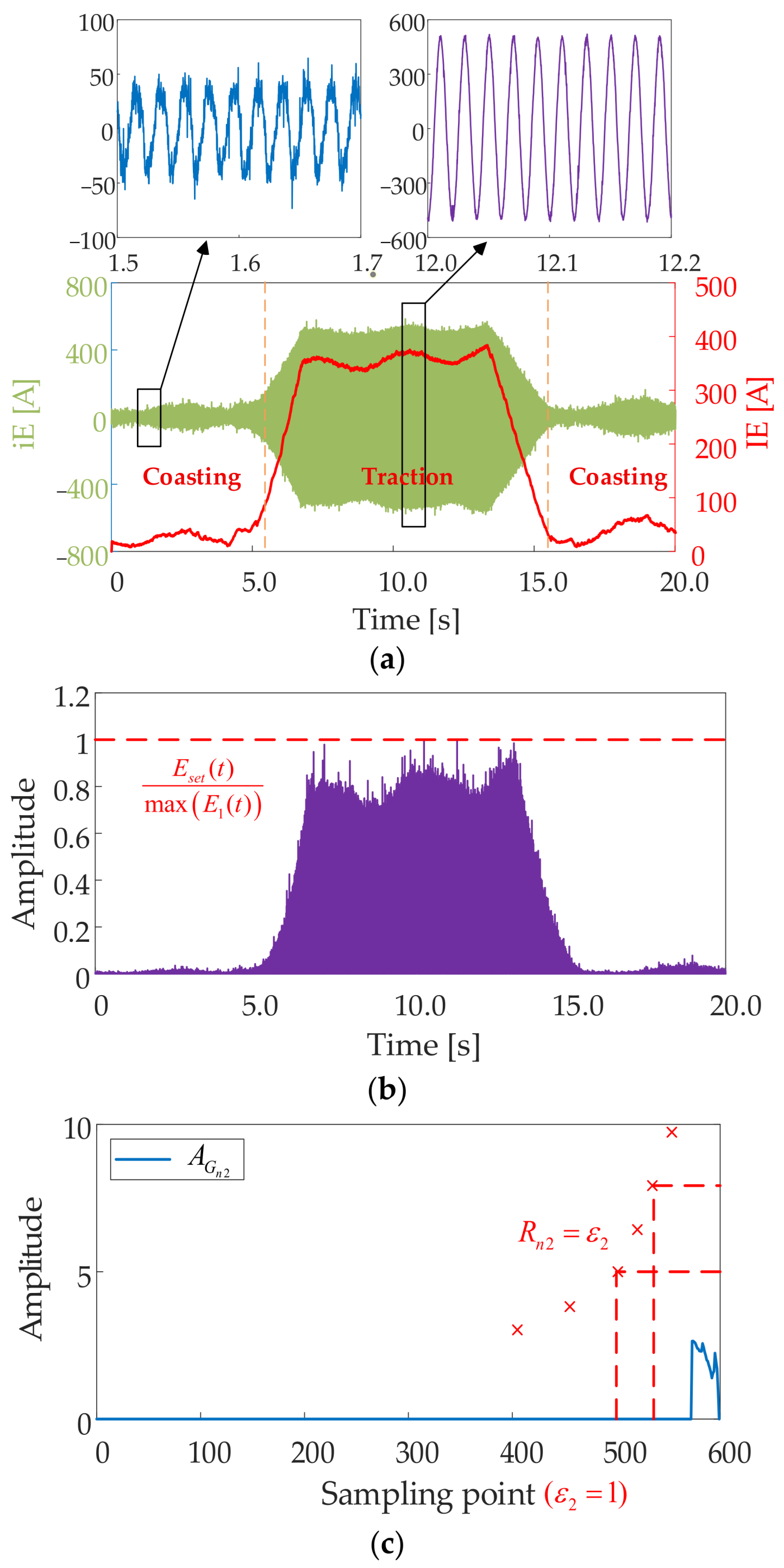
3.5. Analysis of Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Battistelli, L.; Pagano, M.; Proto, D. 25-kV 50 Hz high-speed traction power system: Short-circuit modeling. IEEE Trans. Power Deliv. 2011, 26, 1459–1466. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, M.; Cheng, Z.; Chen, Y.; Li, Q. Robust energy management of high-speed railway co-phase traction substation with uncertain PV generation and traction load. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5079–5091. [Google Scholar] [CrossRef]
- Wang, S.; Chen, M.; Kou, Z.; Sun, Z.; Zhao, N.; Li, Q. Fault Location of AT Traction Network Adopting Bilateral Power Supply Mode Based on Generalized Symmetrical Components Method. IEEE Trans. Transp. Electrif. 2023, 10, 5103–5118. [Google Scholar] [CrossRef]
- Luo, A.; Wu, C.; Shen, J.; Shuai, Z.; Ma, F. Railway static power conditioners for high-speed train traction power supply systems using three-phase V/V transformers. IEEE Trans. Power Electron. 2011, 26, 2844–2856. [Google Scholar] [CrossRef]
- He, X.; Shu, Z.; Peng, X.; Zhou, Q.; Zhou, Y.; Zhou, Q.; Gao, S. Advanced cophase traction power supply system based on three-phase to single-phase converter. IEEE Trans. Power Electron. 2013, 29, 5323–5333. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Wei, Y.; Lu, C.; Lin, Y.; Li, Z. Ground fault analysis and grounding method of static power converters in flexible AC traction power supply systems. IEEE Trans. Power Electron. 2021, 37, 5535–5546. [Google Scholar] [CrossRef]
- Shen, R.; Han, Z.; Liu, S.; Gao, S. An Adaptive Reclosing Scheme for All-Parallel Autotransformer Traction Network of High-Speed Railway Based on Multisource Information. IEEE Trans. Transp. Electrif. 2023, 10, 407–420. [Google Scholar] [CrossRef]
- Saini, D.K.; Nair, R.; Yadav, M.; Prasad, R. Modified algorithm for fault detection on AC electrical traction line: An Indian climate case study. IEEE Trans. Transp. Electrif. 2018, 4, 936–950. [Google Scholar] [CrossRef]
- Wu, S.; Wu, M.; Li, L.; Wang, S.; Song, K.; Wang, Y. Analysis and Comparison of MMC-Based Co-Phase Traction Power Supply Topology for Auto-Transformer Power Supply System. IEEE Trans. Power Deliv. 2022, 37, 4053–4063. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Xu, G.; Ran, L.; Yu, S.; Yang, Q. A new fault-impedance algorithm for distance relaying on a transmission line. IEEE Trans. Power Deliv. 2010, 25, 1384–1392. [Google Scholar] [CrossRef]
- Han, Z.; Li, S.; Liu, s.; Liu, J.; Gao, S. A Reactance-Based Fault Location Method for Overhead Lines of AC Electrified Railway. IEEE Trans. Power Deliv. 2020, 35, 2558–2560. [Google Scholar] [CrossRef]
- Han, Z.; Liu, S.; Gao, S.; Bo, Z. Protection scheme for China high-speed railway. In Proceedings of the 10th IET International Conference on Developments in Power System Protection (DPSP 2010). Managing the Change, Manchester, UK, 29 March–1 April 2010; pp. 1–5. [Google Scholar]
- Liu, S.; Han, Z.; Gao, S. Inter-tripping protection scheme for feeding sections of high-speed railway based on current features. Proc CSEE 2014, 34, 4437–4442. [Google Scholar]
- Wang, D.; He, X.; Gao, S. Protection Scheme Based on Current Limiting Control of Flexible Traction Power Supply System. In Proceedings of the 2024 IEEE 19th Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 5–8 August 2024; pp. 1–6. [Google Scholar]
- Wang, S.; Chen, M.; Li, Q.; Huang, W.; Wu, B. A new hybrid fault identification method based on multiterminals synchronous measure information for all parallel at traction power supply system. Energies 2018, 11, 2698. [Google Scholar] [CrossRef]
- Lin, G.; Hong, B.; Wu, Z.; Fu, X. Power supply arm protection scheme of high-speed railway based on wide-area current differential. Railw. Eng. Sci. 2023, 31, 281–292. [Google Scholar] [CrossRef]
- Li, B.; Chen, D.; He, J.; Wang, C.; Song, J.; Lyu, H. Fault analysis and protection in flexible DC traction power supply system. IEEE Trans. Transp. Electrif. 2023, 10, 5599–5613. [Google Scholar] [CrossRef]
- Naidu, O.; Pradhan, A.K. A traveling wave-based fault location method using unsynchronized current measurements. IEEE Trans. Power Deliv. 2018, 34, 505–513. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Gao, J.; Song, G.; Kheshti, M.; Guo, L. High-impedance fault detection method based on stochastic resonance for a distribution network with strong background noise. IEEE Trans. Power Deliv. 2021, 37, 1004–1016. [Google Scholar] [CrossRef]
- AsghariGovar, S.; Pourghasem, P.; Seyedi, H. High impedance fault protection scheme for smart grids based on WPT and ELM considering evolving and cross-country faults. Int. J. Electr. Power Energy Syst. 2019, 107, 412–421. [Google Scholar] [CrossRef]
- Song, X.; Gao, F.; Chen, Z.; Liu, W. A negative selection algorithm-based identification framework for distribution network faults with high resistance. IEEE Access 2019, 7, 109363–109374. [Google Scholar] [CrossRef]
- Fulin, Z.; Feifan, L.; Ruixuan, Y. Identification of abnormal phenomenon of vehicle-network coupling in electrified railway. Proc. CSEE 2021, 41, 7937–7950. [Google Scholar]
- Lin, G.; Fu, X.; Quan, W.; Hong, B. Improved fault location method for AT traction power network based on EMU load test. Railw. Eng. Sci. 2022, 30, 532–540. [Google Scholar] [CrossRef]
- Fan, B.; Liu, T.; Zhao, F.; Wu, H.; Wang, X. A review of current-limiting control of grid-forming inverters under symmetrical disturbances. IEEE Open J. Power Electron. 2022, 3, 955–969. [Google Scholar] [CrossRef]
- He, X.; Peng, J.; Han, P.; Liu, Z.; Gao, S.; Wang, P. A novel advanced traction power supply system based on modular multilevel converter. IEEE Access 2019, 7, 165018–165028. [Google Scholar] [CrossRef]
- Lin, G.-S.; Li, Q.-Z. Impedance calculations for AT power traction networks with parallel connections. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–5. [Google Scholar]
- Wang, S.; Li, Q.; Han, J.; Chen, M.; Sun, Z. Ground fault identification and location of autotransformer traction network for high-speed railway based on multi-terminals synchronous measure information. IET Gener. Transm. Distrib. 2023, 17, 5458–5472. [Google Scholar] [CrossRef]
- Gao, J.; Wang, X.; Wang, X.; Liu, J.; Yang, A.; Yuan, H.; Wei, X. A High-Impedance Fault Detection Method for Distribution Systems Based on Empirical Wavelet Transform and Differential Faulty Energy. IEEE Trans. Smart Grid 2021, 13, 900–912. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Z.; Cai, W.; Zhuang, Q.; Bi, G.; Deng, J.; Chen, S.; Kan, X. Research on the longitudinal protection of a through-type cophase traction direct power supply system based on the empirical wavelet transform. Glob. Energy Interconnect. 2024, 7, 206–216. [Google Scholar] [CrossRef]
- Sun, S.; Liu, J.; Wang, J.; Chen, F.; Wei, S.; Gao, H. Remaining useful life prediction for AC contactor based on MMPE and LSTM with dual attention mechanism. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Shu, L.; Gallimore, M. A new bearing fault diagnosis method based on fine-to-coarse multiscale permutation entropy, laplacian score and SVM. IEEE Access 2019, 7, 17050–17066. [Google Scholar] [CrossRef]
- Shen, R.; Han, Z.; Liu, S.; Gao, S. A Novel Distance Protection Method for Out-of-Phase Faults of AC Traction Power Supply System. IEEE Trans. Power Deliv. 2023, 38, 3729–3732. [Google Scholar] [CrossRef]

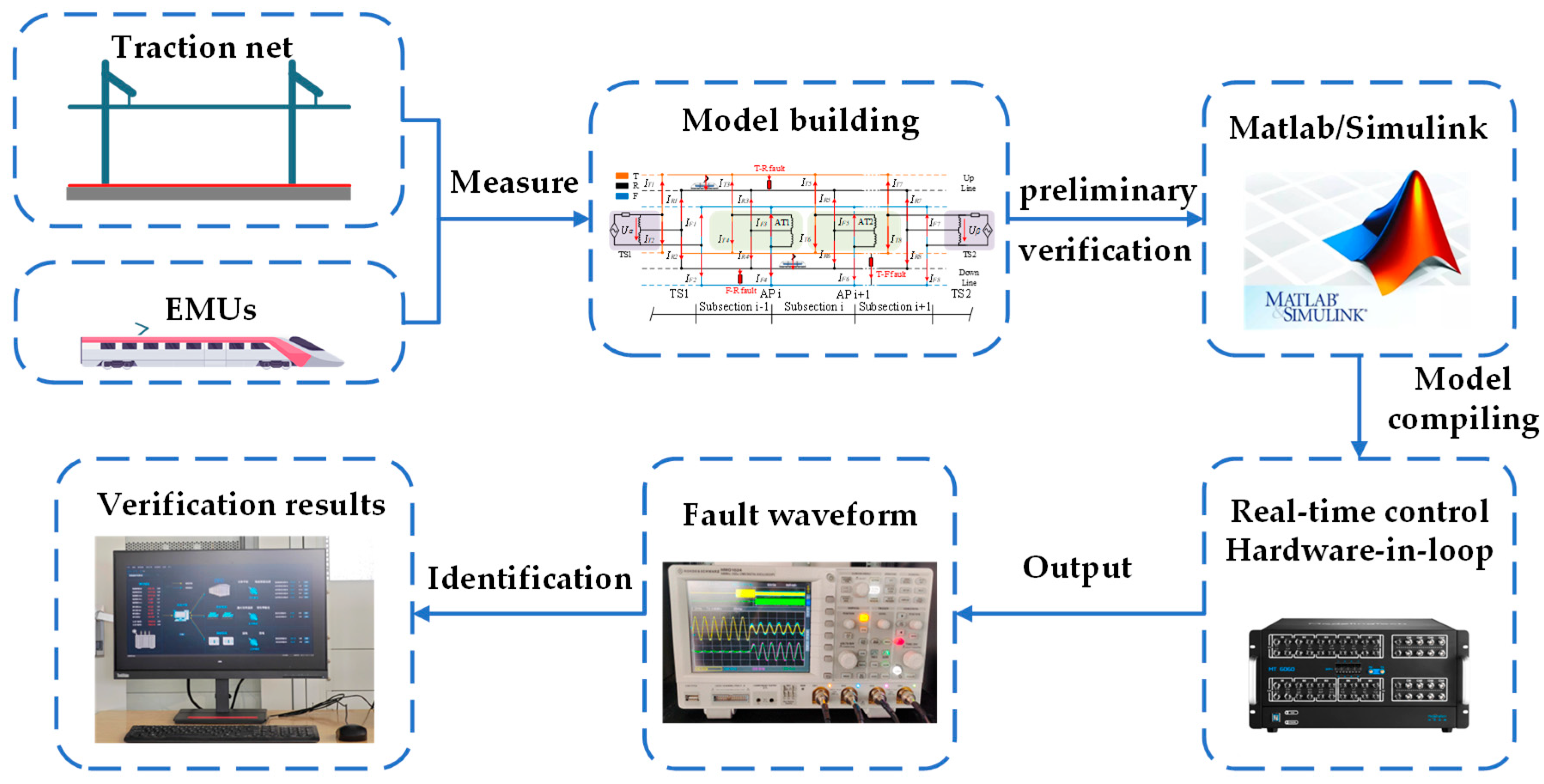
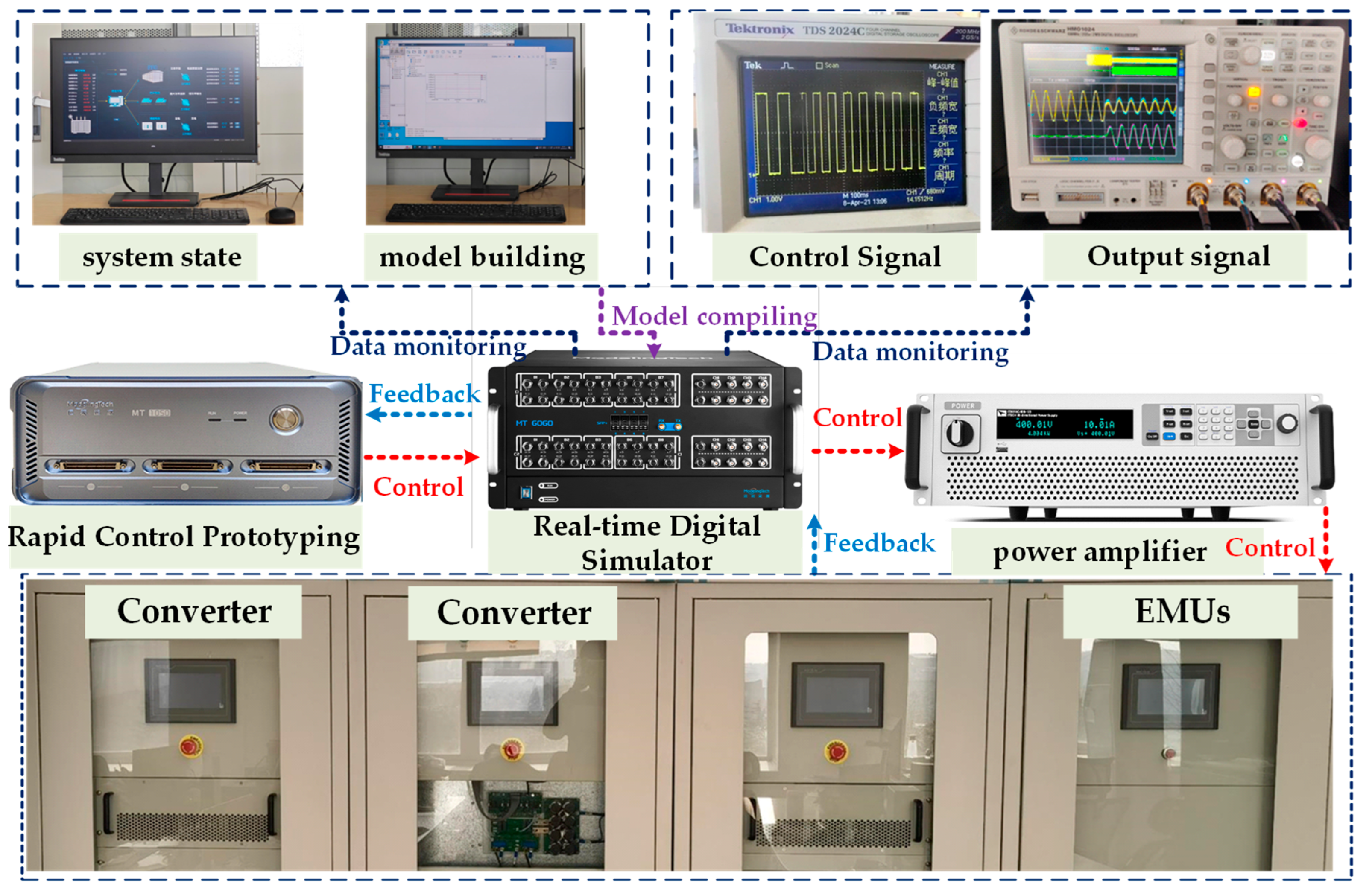

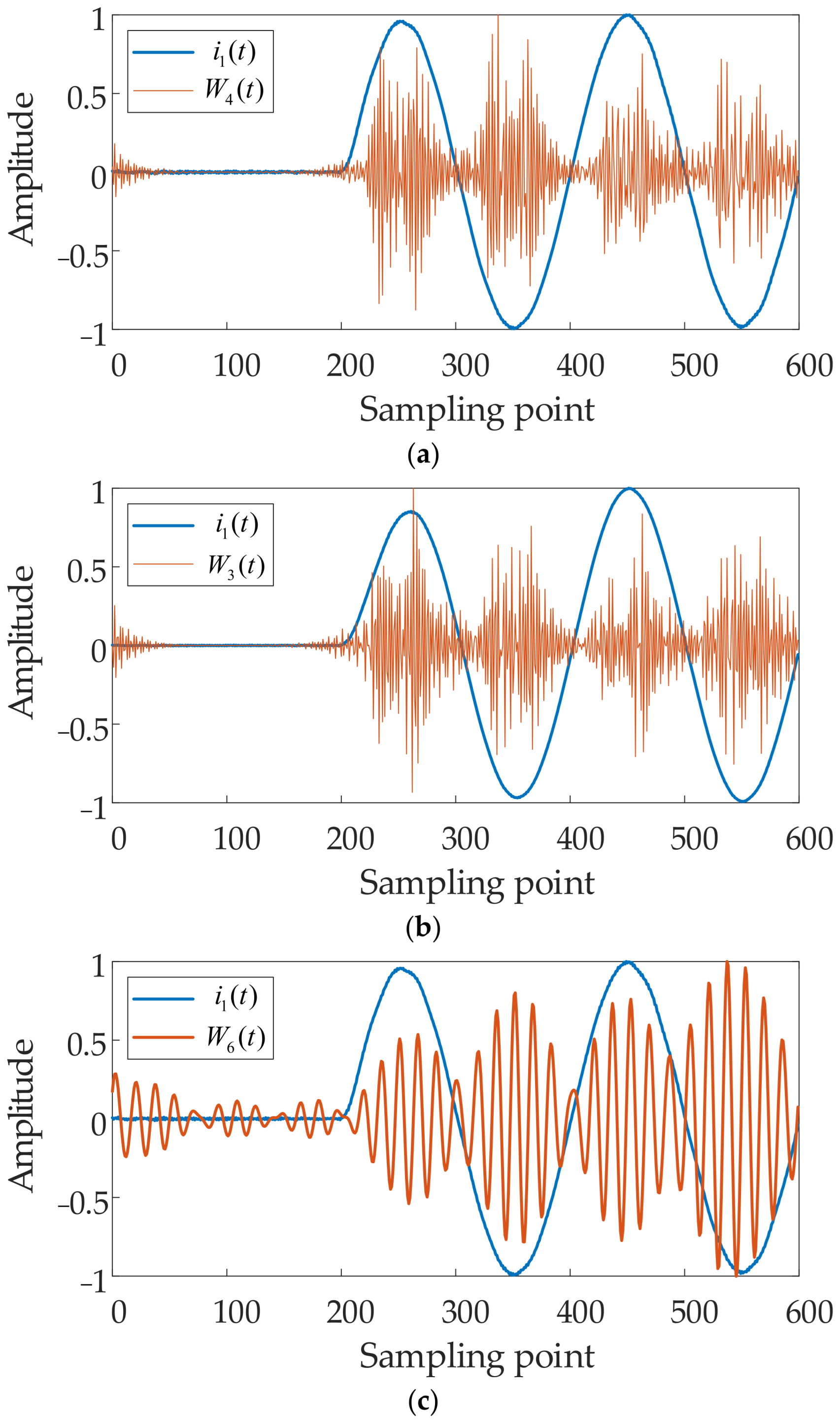
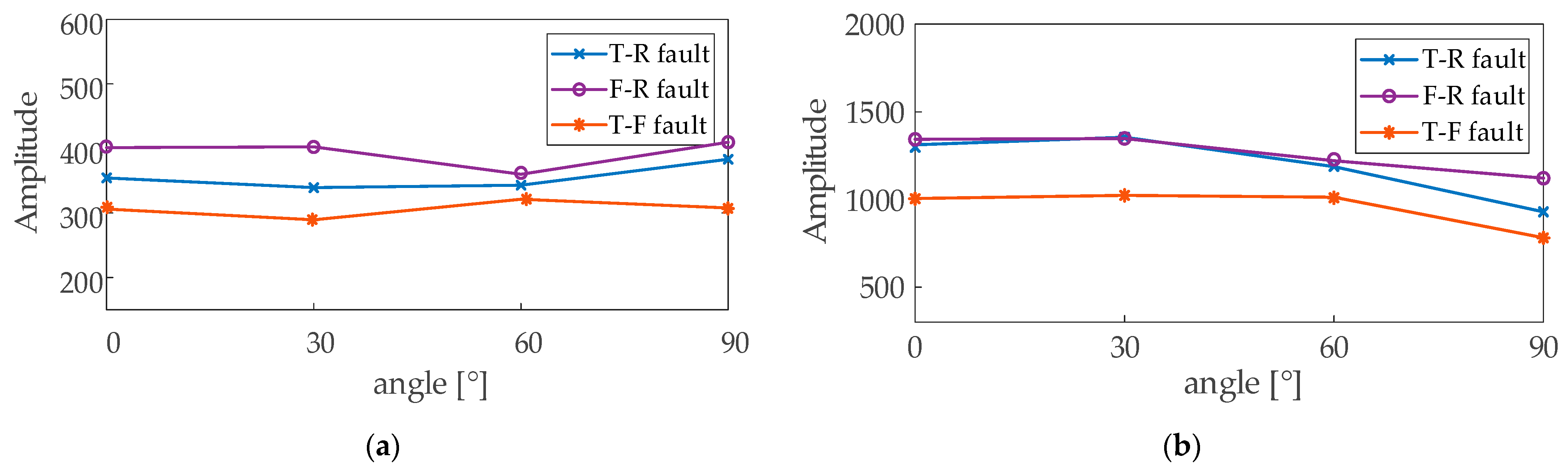
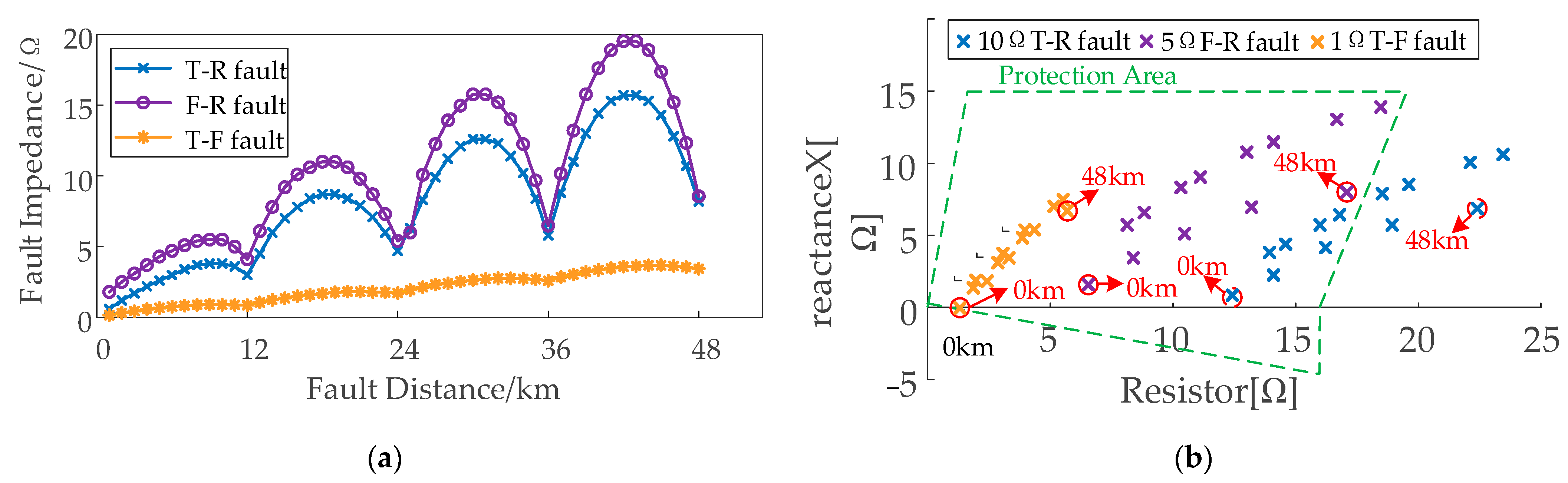
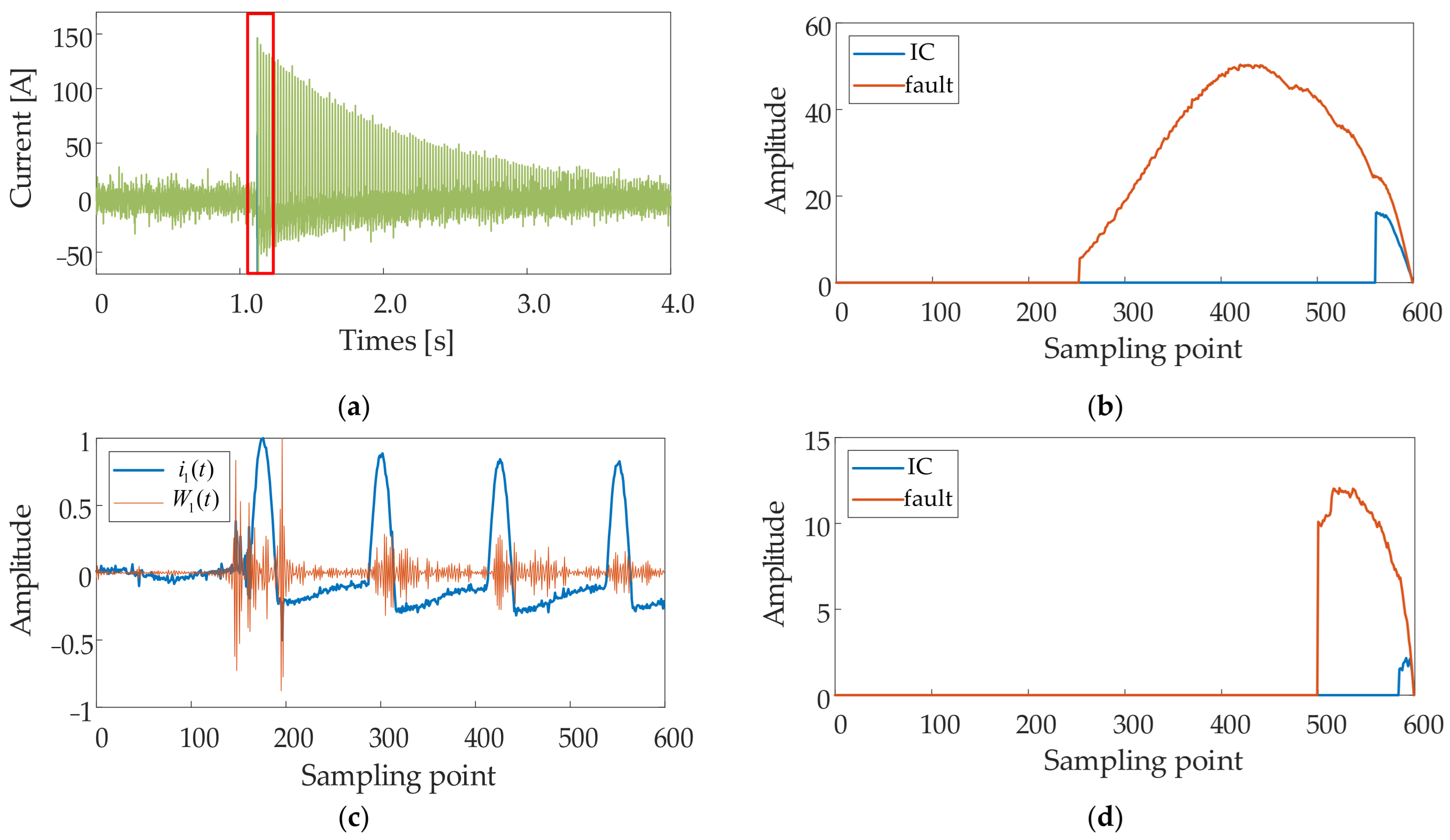
| Parameters | Conductor | Symbol | Value [Ω/km] |
|---|---|---|---|
| Impedances | T | Zt | 0.115 + j0.384 |
| F | Zf | 0.150 + j0.420 | |
| R | Zr | 0.165 + j0.481 | |
| Between T and R | Ztr | 0.048 + j0.164 | |
| Between T and F | Ztf | 0.048 + j0.178 | |
| Between F and R | Zfr | 0.048 + j0.150 | |
| Capacitances | Value [F/km] | ||
| Upline T | Ct1 | 16.420 × 10−9 | |
| Upline F | Cf1 | 10.350 × 10−9 | |
| Downline T | Ct2 | 16.420 × 10−9 | |
| Downline F | Cf2 | 16.350 × 10−9 |
| Fault Type | Fault Impedance 50 Ω |
|---|---|
| [W1, W2, W3, W4, W5, W6, W7, W8, W9, W10] | |
| T-R | [0.95, 0.94, 0.94, 0.98, 0.95, 0.93, 0.89, 0.89, 0.91, 0.87] |
| F-R | [0.95, 0.94, 0.94, 0.98, 0.95, 0.91, 0.89, 0.88, 0.90, 0.87] |
| T-F | [0.95, 0.94, 0.98, 0.96, 0.93, 0.92, 0.95, 0.92, 0.91, 0.87] |
| Fault Type | [W1, W2, W3, W4, W5, W6, W7, W8, W9, W10] |
|---|---|
| Inrush Current | [0.98, 0.97, 0.95, 0.96, 0.97, 0.96, 0.90, 0.92, 0.93, 0.89] |
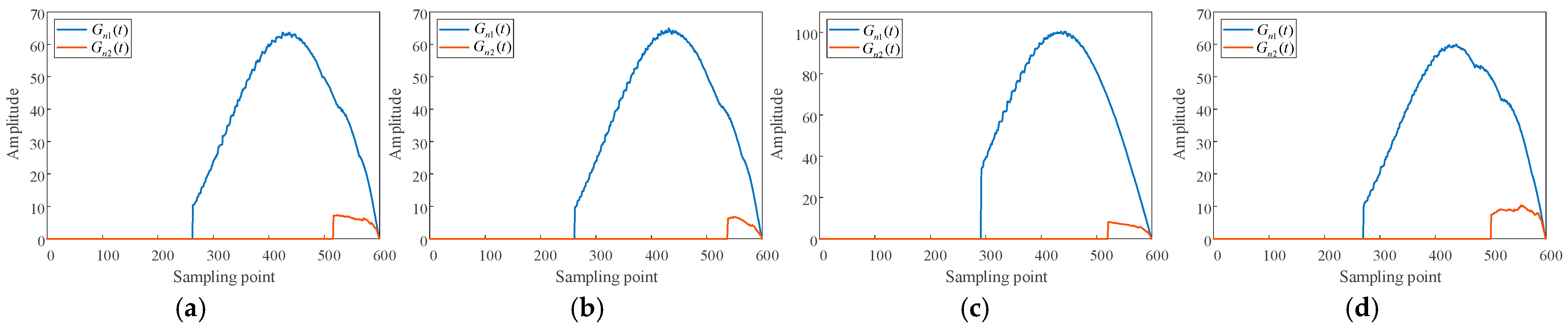
| Cases | Fault Type | Fault Impedance | Fault Position | EMUs Position | Rn1 | Rn2 | Identify Correctly? |
|---|---|---|---|---|---|---|---|
| 1 | T-R | 0.75 Ω | Up line 6.2 km | \ | 589.5 | 4.33 | √ |
| 2 | F-R | 0.75 Ω | Up line 15.1 km | Down line 29.1 km | 606.7 | 2.46 | √ |
| 3 | F-R | 35 Ω | Down line 21.6 km | \ | 1563.3 | 4.59 | √ |
| 4 | T-F | 35 Ω | Down line 39.4 km | Down line 26.2 km | 537.5 | 9.71 | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wang, S.; Yan, S.; Chen, N.; Tan, D.; Sun, Z. Fault Identification Method for Flexible Traction Power Supply System by Empirical Wavelet Transform and 1-Sequence Faulty Energy. World Electr. Veh. J. 2025, 16, 495. https://doi.org/10.3390/wevj16090495
Lu J, Wang S, Yan S, Chen N, Tan D, Sun Z. Fault Identification Method for Flexible Traction Power Supply System by Empirical Wavelet Transform and 1-Sequence Faulty Energy. World Electric Vehicle Journal. 2025; 16(9):495. https://doi.org/10.3390/wevj16090495
Chicago/Turabian StyleLu, Jiang, Shuai Wang, Shengchun Yan, Nan Chen, Daozheng Tan, and Zhongrui Sun. 2025. "Fault Identification Method for Flexible Traction Power Supply System by Empirical Wavelet Transform and 1-Sequence Faulty Energy" World Electric Vehicle Journal 16, no. 9: 495. https://doi.org/10.3390/wevj16090495
APA StyleLu, J., Wang, S., Yan, S., Chen, N., Tan, D., & Sun, Z. (2025). Fault Identification Method for Flexible Traction Power Supply System by Empirical Wavelet Transform and 1-Sequence Faulty Energy. World Electric Vehicle Journal, 16(9), 495. https://doi.org/10.3390/wevj16090495





