Formal Modelling and Verification of Multi-Parameter Context and Agent Transition Systems: Application to Urban Delivery Zone and Autonomous Electric Vehicle

Abstract

The increasing integration of autonomous electric vehicles (EVs) into Intelligent Transportation Systems (ITSs) needs rigorous mechanisms to ensure their safe and effective operation in dynamic environments. The reliability of such vehicles depends not only on their internal capabilities but also on the suitability and safety of the environments in which they operate. This paper introduces a formal modelling framework that captures independently the dynamic evolution of the environmental context and the EV agent using multi-parameter transition systems. Two distinct models are defined: the Context Transition System (CTS), which models changes in environmental states, and the Agent Transition System (ATS), which captures the internal state evolution of the EV. Safety and liveness properties are formally specified in Computation Tree Logic (CTL) and verified using the nuXmv model checker. The framework is validated through two representative use cases: a dynamic urban delivery zone and an autonomous electric delivery vehicle. The results highlight the framework’s effectiveness in detecting unsafe conditions, verifying mission objectives, and supporting the reliable deployment of EVs in ITS.

1. Introduction

Electric vehicles (EVs) are becoming central to the future of urban mobility and are increasingly integrated into Intelligent Transportation Systems (ITSs) to enable autonomous driving, smart energy management, and safe navigation [1,2]. Their increasing deployment requires that EV operations meet rigorous safety, efficiency, and adaptability requirements, particularly in dynamic environments [3]. These environments often involve various parameters that change over time. As such, ensuring the safe operation of EVs, as well as the safety and suitability of the environment in which they operate, is essential.

To guarantee safe and correct behaviours, two key components must be modelled and monitored: the context which captures dynamic environmental information, and the autonomous agent that interacts within the environment and manages its behaviour and internal state to accomplish predefined goals [4]. The continuous evolution of the two components increases their complexity and makes them susceptible to failures or undesired behaviours.

Recent studies highlight the importance of incorporating context-awareness mechanisms in ensuring the safe operation of EVs. For instance, Kumari et al. (2025) [5] introduces an ontology-based security framework that dynamically adapts to contextual changes during EV charging to prevent potential threats. Similarly, other studies integrate contextual data into safety models to reduce risks related to fire hazards or sensor vulnerabilities [6,7].

EVs can be viewed as autonomous agents operating within ITS environments. Several studies underline the critical role of formal methods and model-based approaches in ensuring the safe and reliable operation of EVs. In the context of smart grids, Wooding et al. (2020) [8] demonstrates how formal controller synthesis based on temporal logic and symbolic abstraction ensures safe frequency regulation by incorporating EVs as controllable resources. Their approach provides a mathematical guarantee that system-level specifications are maintained even in the presence of power disturbances. Likewise, Goswami et al. (2013) [9] underlines the growing importance of model-based development and formal verification in EV control software. The authors support the integrated design flows that co-optimise control logic and embedded platform parameters to meet stringent timing and safety requirements. These works reflect the application of formal techniques to manage the complexity, performance, and safety of EV systems in real-world applications.

Despite these advancements, a significant challenge remains in EVs advancement: ensuring that EVs operate safely under all possible environmental and operational changes, and that the surrounding context remains suitable for their deployment. Formal verification offers a rigorous approach to ensure that these components behave as expected over all possible changes, which is crucial in safety-critical scenarios like those involving ITSs and autonomous vehicles [10].

A central issue lies in capturing the dynamic nature of both the environmental context and the agent (EV). A key question is how to formally represent the evolution of these components using parameter-driven models that reflect their continuous change over time. This raises the need for structured, state-based formalisms capable of modelling transitions in context and agent states in a precise and analysable manner. Developing such models is important not only to represent these evolutions clearly but also to enable formal reasoning and automated verification of critical properties.

In this paper, we propose the following key contributions:

• Symbolic modelling of context and agent dynamics: we propose a formal and symbolic representation of the dynamic nature of the environmental context and the EV (agent) using two distinct transition systems:
  • The CTS models the evolution of the environmental context by capturing changes in the values of its defining parameters over time, such as changes in traffic congestion or the availability of charging stations.
  • The ATS is defined for an EV situated within a given context, and it represents the internal evolution of the EV as a function of the values of its parameters changing.
• Context monitoring based on Edge Node: An Edge Node, embedded within the environment, is responsible for capturing parameter changes and constructing the corresponding CTS.
• Formal verification using model checking: The two transition systems are the basis for verifying properties using model checking techniques. We specify safety and liveness properties in Computation Tree Logic (CTL) and verify them using the nuXmv model checker [11].

The remainder of the paper is organized as follows: Section 2 introduces the fundamental definitions and concepts required for our work. Section 3 presents our contribution, including the proposed architecture, the formal definitions of the CTS and ATS, and the verification process. Section 4 presents the use cases. Section 5 reviews related works and discusses their relevance to our proposed approach. Section 6 concludes the paper by summarising the key findings and outlining future research directions. The results of the formal verification performed using the nuXmv tool are provided in Appendix A.

2. Background

This section introduces the core concepts required to support the contributions of this work. We first present the environmental context and its role regarding the safety of ambient systems. Then, we define ambient agents, focusing on electric vehicles (EVs) as intelligent entities that act and adapt within dynamic environments. Finally, we present Computation Tree Logic (CTL) as a formal method for verifying system properties, including safety and liveness.

2.1. Environmental Context

Ling Feng et al. [12] distinguish two broad classes of context: user-centric context and environmental context. The user-centric context concerns information about the user, including background (e.g., habit and preference), dynamic behaviour (e.g., intentions and tasks), physiological state (e.g., body temperature), and emotional state (e.g., happiness and calmness). Environmental context concerns information about the surroundings, including physical environment (e.g., time and location), social environment (discount policies and traffic congestion), and computational environment (e.g., surrounding devices).

Our work focuses on modelling and verifying the environmental context, as it provides essential information about the surrounding environment needed for its characterisation.

Definition 1 

(Environmental Context [12]). A context is defined as an n-dimensional set of attributes, represented as the Cartesian product of these attributes, where each attribute has an interpretation domain specifying the range of values it can take.

2.2. Ambient Agent

The agent is defined as an entity that makes autonomous decisions and acts to achieve its goals. There are several definitions of the term “agent” in the literature. Tapia et al. [13] define an agent as a computational system embedded within an environment, capable of acting autonomously to achieve its intended goals. Similarly, Dorri et al. [14] describe an agent as an entity situated within an environment that senses various parameters, enabling it to make decisions aligned with its goals. Based on these decisions, the entity performs appropriate actions that affect its surrounding environment. Furthermore, Mahela et al. [15] characterise agents as intelligent entities capable of acting autonomously and adaptively, making informed decisions based on their reasoning and experiences.

2.3. Electric Vehicle

Electric vehicles (EVs) represent an emerging and rapidly evolving technology within Intelligent Transportation Systems. They are widely regarded as a technological advancement that offers a sustainable mobility alternative and addresses environmental issues associated with conventional automobile usage [16]. EVs replace the internal combustion engine with an electric motor powered by electricity stored in an onboard battery pack [17].

2.4. Computation Tree Logic

Computation Tree Logic (CTL) is widely used to formally specify system properties, particularly in the domains of model checking and formal verification. CTL is a branching-time temporal logic in which path quantifiers A (for all paths) and E (there exists a path) are combined with temporal operators X (neXt state), F (eventually/in the Future), G (Globally/always), and U (Until) to express properties over possible system executions [18].

2.4.1. CTL Syntax

Let $AP$ be a set of atomic propositions. The syntax of CTL formulas is defined inductively as follows:

• Every $p\in AP$ is a CTL formula.
• If $\phi$ and $\psi$ are CTL formulas, then so are

  $$\neg \phi ,\phi \wedge \psi ,\phi \vee \psi ,\phi \to \psi ,$$

  $$AX\phi ,EX\phi ,AF\phi ,EF\phi ,AG\phi ,EG\phi ,A\left[\phi U\psi \right],E\left[\phi U\psi \right].$$

2.4.2. CTL Semantics

CTL formulas are interpreted over a Kripke structure $M=(S,R,L)$, where:

• S is a set of states;
• $R\subseteq S\times S$ is a total transition relation;
• $L:S\to 2^{AP}$ assigns to each state the set of atomic propositions true in that state.

The satisfaction relation $M,s\vDash \phi$ is defined inductively:

• $M,s\vDash p$ iff $p\in L\left(s\right)$.
• $M,s\vDash \neg \phi$ iff not $(M,s\vDash \phi )$.
• $M,s\vDash \phi \wedge \psi$ iff $(M,s\vDash \phi )$ and $(M,s\vDash \psi )$.
• $M,s\vDash EX\phi$ iff there exists $s^{\prime }$ such that $(s,s^{\prime })\in R$ and $M,s^{\prime }\vDash \phi$.
• $M,s\vDash AX\phi$ iff for all $s^{\prime }$ such that $(s,s^{\prime })\in R$, $M,s^{\prime }\vDash \phi$.
• $M,s\vDash E\left[\phi U\psi \right]$ iff there exists a path $\pi$ from s and some $i\ge 0$ such that $M,\pi \left[i\right]\vDash \psi$ and $M,\pi \left[j\right]\vDash \phi$ for all $0\le j<i$.
• $M,s\vDash A\left[\phi U\psi \right]$ iff for all paths $\pi$ from s there exists some $i\ge 0$ such that $M,\pi \left[i\right]\vDash \psi$ and $M,\pi \left[j\right]\vDash \phi$ for all $0\le j<i$.

3. Proposal

In this section, we introduce a formal framework for modelling and verifying a dynamic environmental context and an autonomous agent. The evolution of the context is captured by an Edge Node integrated within the environment, which monitors parameter changes and generates the corresponding context states. The evolution of the agent is treated as a formal specification based on changes in its internal parameters. The objective is to ensure safe and correct operation by enabling formal verification of the context and agent dynamics using CTL and nuXmv model checker.

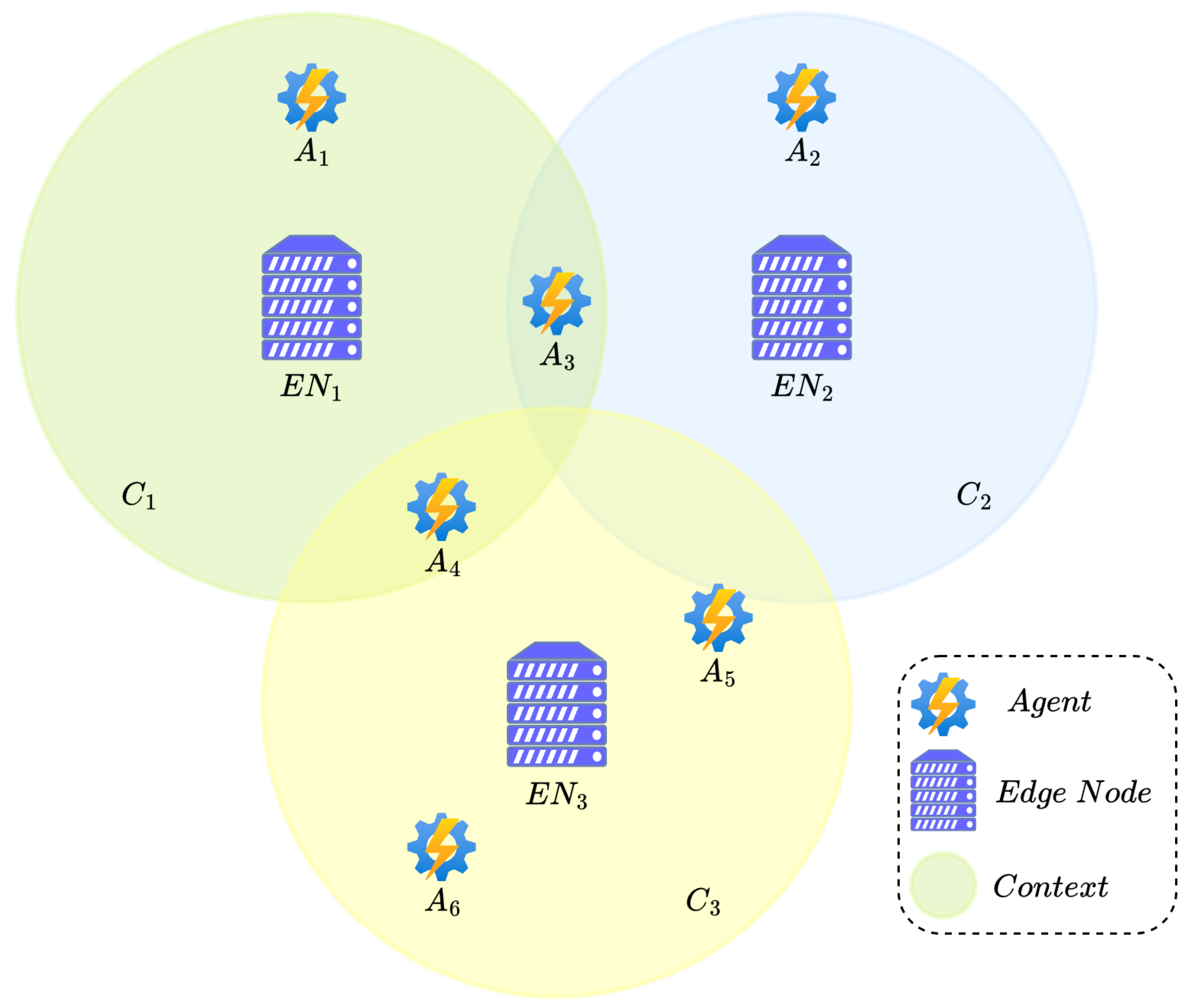
Figure 1 presents three distinct contexts, labelled ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$. Each one is linked to an Edge Node (EN) that captures contextual information and generates the corresponding CTS. These CTSs illustrate how contexts evolve by capturing the changes from one state to another.

An agent operates within a given context and is associated with its own specification Agent Transition System (ATS), which formally captures the evolution of the agent through transitions between distinct internal states over time.

3.1. Data Types Definition

A data type defines a set of values that variables of that type can take. This subsection provides the necessary preliminaries on the syntax and semantics of types, based on [19]. These concepts are fundamental to our modelling approach, which is built around parameters. Each parameter is associated with a specific type, and its possible values are taken from the interpretation domain defined by that type.

3.1.1. Syntax

Types may be divided into two categories: basic and composite types. The names of some of the basic types are specified in the following:

• $nat$: represents the type of natural numbers.
• $real$: refers to the real type.
• $bin$: is the binary type.
• $char$: defines the type of single characters, like single letters, punctuation marks, etc.
• $string$: represents a sequence of characters.

In addition, the composite types are built from several other types, and they are described using the definition of Cartesian product in [19]:

$$\prod _{i\in I}{A}_i=\{f:I\to \bigcup _{i\in I}{A}_i|f\left(i\right)\in A_i\forall i\in I\}$$

(1)

such that I is the set of index sets $A_i$ and for every $i\in I$ the Cartesian product is the set of functions $f\left(i\right)\in A_i$, where each function is considered a finite or infinite tuple composed of elements, and each one of them is from an $A_i$, $foreveryi\in I$.

3.1.2. Semantics and Meanings

To describe the semantics of the represented syntax, we opt for the definition of the interpretation domain for each type $\tau$ [19].

Definition 2 

(interpretation domains). The interpretation domain of a data type is a non-empty set of possible values described as follows:

$$⟦\tau ⟧=\{v_0,v_1\dots \}$$

(2)

For every data type $\tau$, $⟦\tau ⟧$ is a set of the matching possible values $v_i$. Based on this, the interpretation domains of certain simple types are as follows:

$$\begin{array}{cc}\hfill ⟦bin⟧& =\{\mathit{true},\mathit{false}\}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill ⟦nat⟧& =\{0,1,2,\dots \}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill ⟦char⟧& =\{a,b,c,\dots ,z,!,?,\dots \}\hfill \end{array}$$

(5)

3.2. Bnf-Based Specification of Types

In this paper, types are defined using the Backus–Naur Form (BNF) as follows:

$$\begin{array}{cc}\hfill {\mathit{simple}}_{\tau }& ::=\mathit{nat}\left|\mathit{real}\right|\mathit{bin}\left|\mathit{char}\right|\mathit{string}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \tau & ::={\mathit{simple}}_{\tau }|{\mathit{simple}}_{\tau }\tau \hfill \end{array}$$

(7)

That is, $\tau$ represents either simple or composite types.

3.3. Context Transition System

In this section, we formally define the concept of context, formalising the definition introduced in [12], and present it in Definition 3. We then introduce several key concepts needed to built the CTS, based on [19], which is formally described in Definition 5.

Definition 3 

(A context). A context $\mathcal{C}$ is defined through a non-empty finite set of parameters ${\mathcal{P}}_c$ ranged over by $\{p_c^1,p_c^2,p_c^3,\dots ,p_c^n\}$. Each $p_c^i$ ($1\le i\le n$) in ${\mathcal{P}}_c$ is a parameter identifier with a type ${\tau }_{p_c^i}$ and a value in the corresponding type domain $⟦{\tau }_{p_c^i}⟧$.

3.3.1. Interpretation Domain

The interpretation domain of a context is

$$⟦\mathcal{C}⟧=\prod _{p_c^i\in {\mathcal{P}}_c}⟦{\tau }_{p_c^i}⟧$$

(8)

That is, $⟦\mathcal{C}⟧$ is the Cartesian product of parameter values. It is a particular set of states such that each tuple of $⟦\mathcal{C}⟧$ is a state.

3.3.2. Assignment Command

The following syntactic rules are given over context parameters:

Value of parameter identifier $p_c^i\in {\mathcal{P}}_c$:

$$\overline{p_c^i:v\left[{\tau }_{p_c^i}\right]}$$

Parameter assignment operation:

$$\frac{v:\left[{\tau }_{p_c^i}\right]}{p_c^i:=v}$$

such that $v\left[{\tau }_{p_c^i}\right]$ denotes a value of type ${\tau }_{p_c^i}$, and $p_c^i:v\left[{\tau }_{p_c^i}\right]$ describes a value expression for a parameter $p_c^i$. $p_c^i:=v$ is considered a parameter assignment operation. A value expression depends on the actual state $s\in ⟦\mathcal{C}⟧$ of context $\mathcal{C}$. However, an assignment operation changes the context state.

3.3.3. Set of Functions

The interpretation domain of a context $⟦\mathcal{C}⟧$ is regarded as a set of functions s from context parameters to values, where

$$\forall p_c^i\in {\mathcal{P}}_c:s\left(p_c^i\right)\in ⟦{\tau }_{p_c^i}⟧$$

(9)

Therefore, the semantic equations are specified as follows:

$$⟦p_c^i⟧s=s\left(p_c^i\right)$$

(10)

$$⟦p_a^i:=v⟧s=\left(s\mid p_c^i\mapsto ⟦v⟧\right)//\mathrm{extended}\mathrm{function}\mathrm{of}s$$

(11)

where the value of a parameter $p_c^i$ at a particular state $s\in ⟦\mathcal{C}⟧$ is obtained through $s\left(p_c^i\right)$. However, the application of an assignment operation generates the transition from a state s to a state $s^{\prime }\left(s\right|p_c^i\mapsto ⟦v⟧)$ that is identical to s except that the value of $p_c^i$ is replaced by v, such that

$$⟦p_a^i:=v⟧s=\left(s\right|p_c^i\mapsto ⟦v⟧)\left\{\begin{array}{c}{s}^{\prime }\left(p_c^i\right)=⟦p_c^i⟧s^{\prime }\hfill \\ s^{\prime }\left(p_c^j\right)=s\left(p_c^j\right),\forall p_c^j\ne p_c^i\hfill \end{array}\right.$$

(12)

Definition 4 

(Assignment chain over context parameter). Let $s\in ⟦\mathcal{C}⟧$ be a context state and let $⟦p_c^i:=v⟧s$ be a semantics of a parameter assignment operation, where $p_c^i\in {\mathcal{P}}_c$ and $v\in ⟦{\tau }_{p_c^i}⟧$. An assignment chain is a sequence of semantics of parameters assignment operations representing changes in parameter values from state s. Inductively it is defined as follows:

$$\left\{\begin{array}{c}{\sigma }_c=⟦p_c^i:=v⟧s\hfill \\ {\sigma }_c^{\prime }={\sigma }_c.{\sigma }_c^{\prime }\mid {\sigma }_c\hfill \end{array}\right.$$

(13)

3.3.4. Extended Date Variable

To associate each change in context state with a specific temporal reference, a particular variable named Extended Date ($ED$) is introduced. This variable captures both the date and the time of the context update, where the date is represented as a tuple $day/month/year$ and the time as hour:minute. The values assigned to $ED$ correspond to real-world physical time.

Formally, for every context state transition, the variable $ED$ is updated accordingly. Given an assignment chain ${\sigma }_c^{\prime }$ representing parameters update from a context state s, the extended assignment chain $\sigma$ is defined as

$$\sigma ={\sigma }_c^{\prime }.⟦ED=D_v{T}_v⟧$$

(14)

where:

• $D_v$ is the assigned date value.
• $T_v$ is the assigned time value.
• $⟦ED=D_v{T}_v⟧$ is the assignment of the combined temporal value to $ED$.

Let ${\Sigma }_{{\mathcal{P}}_c}$ be the set of all extended assignment chains. Then, ${\Sigma }_{{\mathcal{P}}_c}=\{\sigma \mid \sigma ={\sigma }_c^{\prime }.⟦ED=D_v{T}_v⟧\}$.

The potential changes in a context $\mathcal{C}$ lead to the production of several context states. To represent the dynamic nature of $\mathcal{C}$ based on states and transitions, a CTS (for Context Transition System) is built. In the following, a formal definition is given.

Definition 5 

(CTS). Let $\mathcal{C}$ be a context. Its associated CTS is a tuple $(\mathcal{Q},\Delta ,q_0)$ where we have the following:

• $\mathcal{Q}$: is a countable set of context states labels such that for each state label $q_c^i\in \mathcal{Q}$, its corresponding state in $⟦\mathcal{C}⟧$ is noted $⟦q_c^i⟧$.
• Δ: is a transition relation between context states labels such that $\Delta \subseteq \mathcal{Q}\times {\Sigma }_{{\mathcal{P}}_c}\times \mathcal{Q}$. A transition $(q_c^i,{\sigma }^i,q_c^j)$ describes the shift between $q_c^i$ and $q_c^j$ when, at least, one parameter value of $⟦q_c^i⟧$ changes. ${\sigma }^i$ indicates the corresponding extended assignment chain for parameters whose values have changed in this transition and for the $ED$ variable that is updated with the extended date at which the change occurs. For the sake of clarity, the transition $(q_c^i,{\sigma }^i,q_c^j)$ will be noted $q_c^i\underset{⟦ED=D_v{T}_v⟧}{\overset{{{\sigma }_c^{\prime }}^i}{\to }}{q}_c^j$.
• $q_c^0$: is the context initial state label.

3.4. Agent Transition System

In this section, we present the formal definition of an agent in Definition 6 followed by the definition of ATS in Definition 7.

Definition 6 

(An agent). An agent $\mathcal{A}$ is defined through a non-empty finite set of parameters ${\mathcal{P}}_a$ ranged over by $\{p_a^1,p_a^2,\dots ,p_a^m\}$. A type ${\tau }_{p_a^i}$ and a value in $⟦{\tau }_{p_a^i}⟧$ are associated to every parameter $p_a^i(1\le i\le m)$ in ${\mathcal{P}}_a$.

The set ${\mathcal{P}}_a$ parameters are assumed to be named components, with identifier $p_a^i$ assigned to each parameter.

3.4.1. Interpretation Domain

The interpretation domain of an agent is

$$⟦\mathcal{A}⟧=\prod _{p_a^i\in {\mathcal{P}}_a}⟦{\tau }_{p_a^i}⟧$$

(15)

$⟦\mathcal{A}⟧$ is the Cartesian product of the values of agent $\mathcal{A}$ parameters, and each tuple of $⟦\mathcal{A}⟧$ is considered an agent internal state.

3.4.2. Assignment Chain over Agent Parameters

The description of the agent assignment commands is the same as the definition provided above in Section 3.3, except that the considered parameters here are $p_a^i\in {\mathcal{P}}_a$ and $⟦\mathcal{A}⟧$ represents a specific set of agent internal states.

From a state $s_a\in ⟦\mathcal{A}⟧$, the values of one or more parameters can change, leading to a chain of assignment operations for these parameters. The structure of assignment chains is defined as

$$\left\{\begin{array}{c}{\sigma }_a=⟦p_a^i:=v⟧s_a\hfill \\ {\sigma }_a^{\prime }={\sigma }_a.{\sigma }_a^{\prime }\mid {\sigma }_a\hfill \end{array}\right.$$

(16)

3.4.3. Extended Date Variable for Agent

It is used, in this instance, with the same properties defined before and for the same purposes, so that

$$\sigma ={\sigma }_a^{\prime }.⟦ED:=DvTv⟧$$

(17)

where $Dv$ and $Tv$ are the day and time values, respectively, assigned to $ED$ at the moment the agent state changes.

In order to represent the dynamic nature of an agent in terms of states and transitions, an Agent Transition System $\left(ATS\right)$ is built. The $ATS$ formal definition is given below.

Definition 7 

(ATS). Let $\mathcal{A}$ be an agent, and its associated Agent Transition System (ATS) is a tuple $({\mathcal{Q}}_a,{\Delta }_a,q_a^0)$ where we have the following:

• ${\mathcal{Q}}_a$: is a countable set of agent states labels such that for each state label $q_a^i\in {\mathcal{Q}}_a$ its corresponding state in $⟦\mathcal{A}⟧$ is noted $⟦q_a^i⟧$.
• ${\Delta }_a$: is a transition relation between agent states labels such that ${\mathcal{Q}}_a\times {\Sigma }_{\mathcal{P}a}\times {\mathcal{Q}}_a$. A transition $(q_a^i,{\sigma }^i,q_a^j)$ describes a shift between $q_a^i$ and $q_a^j$ when at least one parameter value of $⟦q_a^i⟧$ changes. ${\sigma }^i$ is the corresponding assignment chain for parameters whose values have changed in this transition and for the $ED$ variable that is updated with the extended date at which the change occurs. For the sake of clarity, the transition $(q_a^i,{\sigma }^i,q_a^j)$ is noted $q_a^i\underset{⟦ED:=D_v{T}_v⟧}{\overset{{\sigma }_a^{\prime i}}{\to }}{q}_a^j$.
• $q_a^0:$ is the initial state label.

3.5. Formal Verification and Validation

The CTS and ATS provide a foundational framework for verifying safety and liveness properties. Such verification can be carried out by leveraging temporal logics, such as CTL, applied over the corresponding Labelled Transition Systems (LTSs). The use of CTL is well-suited in this context, as it is specifically designed to express and verify properties of systems modelled as state transition systems, precisely the case for both CTS and ATS.

The nuXmv model checker [11] is employed to perform model-based verification by checking whether a given system model satisfies formally specified properties. In particular, nuXmv supports the verification of CTL formulas. If a property is violated, the tool generates a counterexample trace, which facilitates the identification and analysis of unsafe or undesired system states.

The process to verify a system model using nuXmv includes the following steps:

• The system model and the property to be checked are encoded using the nuXmv input language and saved in a $.smv$ file.
• From the command line, the verification process is initialised by executing the command $nuXmv.exemodel\_file\_name.smv$. This starts the verification process and checks whether the specified CTL property holds for the model.

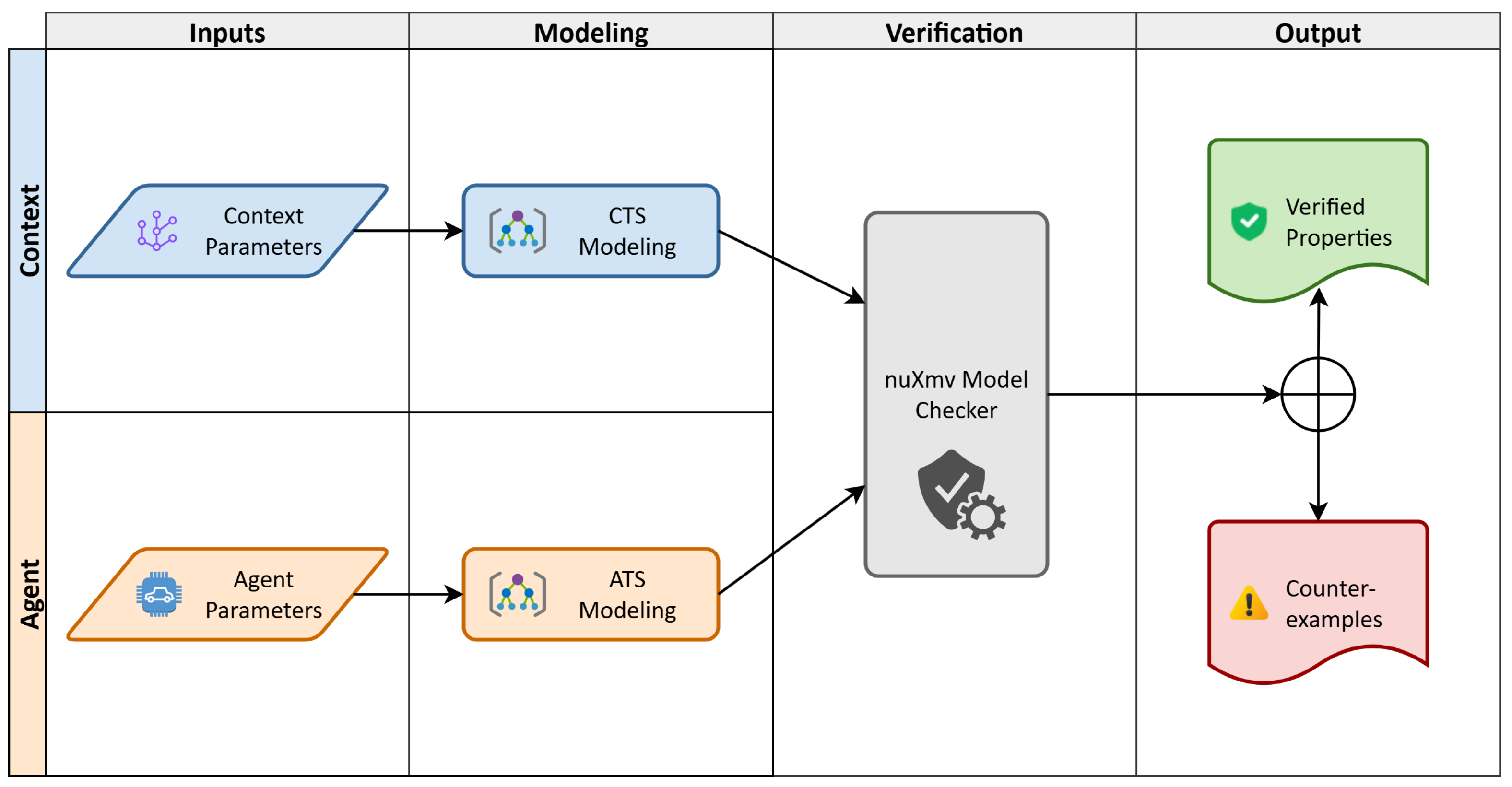
Figure 2 illustrates a unified diagram that captures the complete workflow from modelling to formal verification.

4. Use Case: Formal Verification of an Autonomous Electric Delivery Vehicle and a Dynamic Urban Delivery Zone

To show the applicability of our models, we present two examples that reflect real-world scenarios in ITS. The first example illustrates the dynamic nature of an urban delivery zone, highlighting how context parameters evolve and impact its safety. The second models an autonomous electric delivery vehicle whose internal state is determined by its parameters. The two models are specified independently, and then the safety and liveness properties are verified over them.

4.1. Part 1: Dynamic Urban Delivery Zone

A city authority aims to evaluate the feasibility and safety of an urban delivery zone before deploying autonomous electric vehicles in last-mile deliveries. The subject area is susceptible to changing environmental and traffic conditions throughout the day, such as rush-hour congestion, adverse weather, or heavy pedestrian traffic. To anticipate unsafe conditions and make informed deployment decisions, the city decides to formally model the dynamic evolution of the urban context. This modelling serves several purposes: to analyse whether the delivery zone is safe for all typical variations of the context; to verify that no evolution of the context leads to unsafe or unacceptable working conditions; and to support infrastructure planning by determining whether more control measures, like traffic redirection, time limits on delivery, and access restriction, are necessary to provide safe and efficient operation.

In order to achieve this, the city authority decides to observe the state evolution of the urban delivery zone for five days, generated by an Edge Node, which is integrated into the zone. On each day, the states are captured for 8 h from 8:00 AM to 16 h:00 PM.

The Edge Node models the urban zone (context) dynamics by capturing the evolution of its states over time. The captured states form the basis for verifying whether safety properties hold throughout the context evolution. Figure 3 illustrates a schematic representation of this urban zone.

4.1.1. Urban Delivery Zone-Defining Parameters

The urban delivery zone is considered the context defined by five parameters $p_c^1$, $p_c^2$, $p_c^3$, $p_c^4$, and $p_c^5$.

Let $p_c^1$ represent the traffic_density parameter. Its type is denoted by ${\tau }_{p_c^1}$, with an interpretation domain defined as $⟦{\tau }_{p_c^1}⟧=\{low,medium,high\}$.

Let $p_c^2$ represent the pedestrian_desity parameter, with type ${\tau }_{p_c^2}$ and interpretation domain defined as $⟦{\tau }_{p_c^2}⟧=\{low,medium,high\}$.

Let $p_c^3$ denote the $visibility$ parameter. Its type is ${\tau }_{p_c^3}$, and its interpretation domain is given by $⟦{\tau }_{p_c^3}⟧=\{good,medium,poor\}$.

Let $p_c^4$ represent the $public\_light$ parameter. Its type is ${\tau }_{p_c^4}$, and its interpretation domain is given by $⟦{\tau }_{p_c^4}⟧=\{on,off\}$.

Let $p_c^5$ denote the $road\_accessibility$ parameter. Its type is ${\tau }_{p_c^5}$, and its interpretation domain is given by $⟦{\tau }_{p_c^5}⟧=\{open,limited\}$.

4.1.2. Urban Zone Context Transition System

The contextual parameters evolve due to environmental conditions and human activity. During peak hours, increased vehicle circulation leads to a rise in traffic density, which affects pedestrian density around the delivery zone. Simultaneously, weather changes impact visibility conditions. These visibility changes affect road accessibility decisions, such as whether to restrict access for safety reasons. These variations in parameter values cause the context to evolve from one state to another over the observation period.

To monitor and track these changes, the Edge Node continuously generates, in real time, the respective context states and transitions between them.

At 8:00 AM, the Edge Node starts to capture contextual information related to the five parameters. Figure 4 presents a partial graphical representation of the $CTS$ related to the urban delivery zone on day 1. Each node represents a distinct context-labelled state, while each directed arrow denotes a state transition resulting from one or more parameter changes. The transitions are labelled with the corresponding assignment operations and a timestamp (ED), which indicates the time at which the changes occurred. For example, the transition from state $q_c^5$ to $q_c^6$ captures an increase in traffic and pedestrian density, along with a decrease in the visibility parameter to $poor$.

Remark 1. 

It is noted that for the consecutive transitions $(q_c^i,{\sigma }_c^{\prime i+1}.⟦ED:=v_{i+1}⟧,q_c^{i+1}),(q_c^{i+1},$ ${\sigma }_c^{\prime i+2}.⟦ED:=v_{i+2}⟧,q_c^{i+2})$, between the time interval $[v_{i+1},v_{i+2}]$, no changes are observed on the context parameters. The presented $CTS$ in Figure 4 is considered an aggregated timed graph.

The captured information is as follows:

• $\mathcal{Q}=\{q_c^0,q_c^1,q_c^2,q_c^3,q_c^4,q_c^5,q_c^6\}$.
• Each labelled state $q_c^i$ value is given by $⟦q_c^i⟧$, where $⟦q_c^i⟧$ is defined as a tuple of parameter values. For instance, in state $q_c^1$, the corresponding value is given by $⟦q_c^1⟧=(medium,medium,medium,on,open)$. Each value in the tuple represents, in order, the values of $traffic\_density$, $pedestrian\_density$, $visibility$, $public\_light$, and $road\_accessibility$.

Table 1. Parameter values captured at each context state during the observation of the urban delivery zone on day 1.

	Urban Delivery Zone Parameters
State Value	Traffic_Density	Pedestrian_Density	Visibility	Public_Light	Road_Accesibility
$⟦q_c^0⟧$	low	low	medium	on	open
$⟦q_c^1⟧$	medium	medium	medium	on	open
$⟦q_c^2⟧$	medium	medium	good	off	open
$⟦q_c^3⟧$	high	high	good	off	open
$⟦q_c^4⟧$	medium	medium	good	off	open
$⟦q_c^5⟧$	medium	medium	medium	off	open
$⟦q_c^6⟧$	high	high	poor	off	open

summarises the parameter values of the urban delivery zone at each state. It presents the values of the traffic_density, pedestrian_density, visibility, public_light, and road_accessibility parameters, illustrating the context evolution during day 1 of observation.

• ${\Sigma }_{{\mathcal{P}}_c}=\{{\sigma }^1,{\sigma }^2,{\sigma }^3,{\sigma }^4,{\sigma }^5,{\sigma }^6\}$ denotes the set of extended assignment chains associated with the transitions in the urban delivery zone context. Each assignment chain captures the parameters whose values change during a transition, along with the timestamp indicating when the change occurs. For example, the assignment ${\sigma }^2$ is defined as ${\sigma }^2=⟦p_c^3:=good⟧q_c^1.⟦p_c^4:=off⟧q_c^1.⟦ED:=20/06/202510:00⟧$, where $⟦p_c^3:=good⟧q_c^1.⟦p_c^4:=off⟧q_c^1$ specifies the updates applied to parameters $p_c^3$ and $p_c^4$ resulting in a transition from state $q_c^1$ to the state $q_c^2$. The component $⟦ED:=20/06/202510:00⟧$ denotes the time and date at which these parameter changes occur.

Table 2. Context transitions representing changes in the urban delivery zone on day 1.

From → To	Parameters Updates	Extended Date Stamp
$q_c^0\to q_c^1$	$⟦p_c^1:=medium⟧q_c^0$. $⟦p_e^2:=medium⟧q_c^0$	20/06/2025 08:15
$q_c^1\to q_c^2$	$⟦p_c^3:=good⟧q_c^1$. $⟦p_c^4:=off⟧q_c^1$	20/06/2025 10:00
$q_c^2\to q_c^3$	$⟦p_c^1:=high⟧q_c^2$. $⟦p_c^2:=high⟧q_c^2$	20/06/2025 12:15
$q_c^3\to q_c^4$	$⟦p_c^1:=medium⟧q_c^3$. $⟦p_c^2:=medium⟧$	20/06/2025 13:30
$q_c^4\to q_c^5$	$⟦p_c^3:=medium⟧q_c^4$	20/06/2025 15:00
$q_c^5\to q_c^6$	$⟦p_c^1:=high⟧q_c^5$. $⟦p_c^2:=high⟧q_c^5$. $⟦p_c^3:=poor⟧q_c^5$	20/06/2025 16:00

offers a summary of the context transitions observed on day 1. The first column, labelled From → To, indicates the transitions between context states. The second column, Parameters updates, lists the updates on the parameter values at each transition. The final column, Extended date stamp, specifies the date and time at which each transition occurred.

4.1.3. Safety Property Verification

The delivery zone is considered in a safe state if:

• $traffic\_density\in \{low,medium\}$.
• $pedestrian\_density\in \{low,medium\}$.
• $visibility\in \{good,medium\}$
• $public\_light\in \{on,off\}$
• $road\_accessibility=open$.

A state is unsafe if any of these parameters is outside its allowed range or value.

Property 1 

(Urban delivery zone safety). The context is always in a safe state along the execution path.

CTL formula: $AG\left(\right(traffic\_density=low\vee traffic\_density=medium)\wedge$

$(pedestrian\_density=low\vee pedestrian\_density=medium)\wedge (visibility=good\vee$

$visibility=medium)\wedge (public\_light=on\vee public\_light=off)\wedge (road\_accessibility=$

$open\left)\right)$.

Listing A1, in Appendix A, illustrates the smv code formalising the CTS of the urban delivery zone in nuXmv language.

Let us break down the represented model in this listing:

• MODULE main declares the main module, which is the entry point of the nuXmv model.
• The block VAR contains the variables of the model and their values. The $ctx\_state$ represents the states labels of the CTS as a symbolic variable ranging over states $q0$ to $q6$.
• The block ASSIGN contains several parts:

  -

  The first part INIT defines the initial values of the declared variables.

  -

  The second part next(ctx_state) defines the state transitions of $ctx\_state$, which progress sequentially from $q0,q1,\dots ,q6$.

  -

  The third part defines how $traffic\_density$ changes across states. As an example, from $q0$ to $q1$, the traffic density changes from $low$ to $medium$.

  -

  The same case applies for $pedestrian\_density$, $visibility$, $public\_light$, and $road\_accessibility$ parts.

  -

  The last part defines a CTL specification written for nuXmv to be verified, and it specifies the safety property defined above.

After launching the model checker, nuXmv reports that the specified property is violated and provides a counterexample trace illustrating the execution path leading to the violation. Listing A2, in Appendix A, shows the verification result.

Violation trace: Based on the provided model and verification output, the context state labelled $q_c^3$ violates the safety property. The relevant parameter values at this state are as follows:

state label $q_c^3$:

• traffic_density $high$, violates the constraint $traffic\_density\in \{low,medium\}$.
• pedestrian_density $high$, violates the constraint $pedestrian\_density\in \{low,medium\}$.

4.2. Part 2: Autonomous Electric Vehicle

After conducting a preliminary evaluation of the urban zone where electric vehicles will make deliveries, the company specialising in the development of autonomous electric vehicles has introduced a new model designed to operate in an ITS for urban delivery missions. To formally observe the vehicle behaviour and ensure the safety and efficiency of its operation, the technical team initiates an observation phase for 5 days. During this test phase, the autonomous EV, modelled as an autonomous agent, is tasked with transporting goods over middle-range distances from Zone A (departure) to Zone B (destination).

Throughout the mission, the autonomous vehicle’s internal state is defined by several parameters, which change dynamically.

The primary goal is to formally model the agent dynamics as a transition system and to verify the critical safety and liveness properties using model-checking techniques. Figure 5 illustrates the EV within the urban zone.

4.2.1. EV Definition

The agent dynamism is specified formally through a transition system that models the evolution of its operational states during delivery mission. The resulting state space is analysed to evaluate the agent behaviour during task execution and to ensure the absence of failures across all reachable states. The specification relies on parameters that define the vehicle, allowing precise representation of its dynamism through state transitions.

The agent EV is defined by three parameters $p_e^1$, $p_e^2$, and $p_e^3$.

The parameter $p_e^1$ represents the locality parameter. Its type is ${\tau }_{p_e^1}$, with the interpretation domain $⟦{\tau }_{p_e^1}⟧=\{zoneA,path1,path2,zoneB,charging\_station\}$, where we have the following:

• $zoneA$ indicates the agent departure and return zone, representing the location from which it is initially launched and to which it returns after completing its delivery mission.
• $path1$ denotes that the vehicle has selected path 1 to reach its destination or to return to $zoneA$ and is currently traversing this path.
• $path2$ indicates that the vehicle has selected path 2 to reach its destination or to return to $zoneA$ and is currently traversing this path.
• $zoneB$ represents the target delivery locality.
• $charging\_station$ denotes that the vehicle is currently at the charging station.

The parameter $p_e^2$ describes the status of the vehicle. Its type is ${\tau }_{p_e^2}$, with interpretation domain $⟦{\tau }_{p_e^2}⟧=\{stopped,moving,charging\}$. $stopped$ denotes that the EV is either located in $zoneA$, in $zoneB$, or is temporarily stopped due to traffic conditions or battery charging.

The parameter $p_e^3$ represents the vehicle battery status. Its type is ${\tau }_{p_e^3}$, with the interpretation domain $⟦p_e^3⟧=\{high,medium,low\}$, such that the following hold:

• $high$: the battery level is in the range $[60\%,100\%]$.
• $medium$: the battery level is in the range $[25\%,59\%]$.
• $low$: the battery level is in the range $[10\%,24\%]$.

4.2.2. Vehicle-Agent Transition System

The vehicle state may change if the value of at least one parameter is affected by events or conditions such as start, stop, etc.

On day 1 of the observation phase, the vehicle is launched for its first delivery mission at $10:00\mathrm{AM}$. Throughout the mission, the evolution of the agent internal state is tracked. This evolution is interpreted and represented by the ATS, which serves as a formal specification of the EV. Figure 6 presents a subgraph of the $ATS$ representing the transition sequence related to the first delivery task. Each node corresponds to a unique labelled internal state, while each directed arrow represents a state transition triggered by one or more parameter changes. The labels on the arrows indicate the updated parameter values along with their associated timestamps. For instance, the transition from $q_e^5$ to $q_e^6$ shows that the vehicle returns to its starting locality, $zoneA$, after completing the delivery, along with a change in its status to $stopped$.

The extracted information is

• ${\mathcal{Q}}_e=\{q_e^0,q_e^1,q_e^2,q_e^3,q_e^4,q_e^5,q_e^6\}$.
• Each labelled state $q_e^i$ value is given by $⟦q_e^i⟧$, where $⟦q_e^i⟧$ is defined as a tuple of parameter values. For instance, in state $q_e^3$, the corresponding value is given by $⟦q_e^3⟧=(path2,moving,high)$. Each value in the tuple represents, in order, the values of $locality$, $status$, and $battery\_status$.

Table 3. Parameter values of the autonomous EV captured at each state during its delivery mission.

	Electric Vehicle Parameters
State Value	Locality	Status	Battery_Status
$⟦q_e^0⟧$	zoneA	stopped	high
$⟦q_e^1⟧$	path2	moving	high
$⟦q_e^2⟧$	path2	sopped	high
$⟦q_e^3⟧$	path2	moving	high
$⟦q_e^4⟧$	zoneB	stopped	high
$⟦q_e^5⟧$	path1	moving	high
$⟦q_e^6⟧$	zoneA	stopped	high

provides a summary of the EV parameter values at each state. It details the values of the locality, status, and battery_status parameters, illustrating the internal evolution of the vehicle during its mission.

• ${\Sigma }_{{\mathcal{P}}_e}=\{{\sigma }^1,{\sigma }^2,{\sigma }^3,{\sigma }^4,{\sigma }^5,{\sigma }^6\}$ denotes the set of extended assignment chains associated with the transitions in the autonomous electric vehicle. Each assignment chain captures the parameters whose values change during a transition, along with the timestamp indicating when the change occurs. For example, the assignment ${\sigma }^4$ is defined as ${\sigma }^4=⟦p_e^1:=zoneB⟧q_e^3.⟦p_e^2:=stopped⟧q_e^3.⟦ED:=01/07/202510:35⟧$, where $⟦p_e^1:=zoneB⟧q_e^3.⟦p_e^2:=stopped⟧q_e^3$ specifies the updates applied to parameters $p_e^1$ and $p_e^2$ resulting in transition from state $q_e^3$ to the state $q_e^4$. The component $⟦ED:=01/07/202510:35⟧$ denotes the time and date at which these parameter changes occur.

Table 4. Agent transitions representing internal state evolution of the autonomous EV.

From → To	Parameters Updates	Extended Date Stamp
$q_e^0\to q_e^1$	$⟦p_e^1:=path2⟧q_e^0$. $⟦p_e^2:=moving⟧q_e^0$	01/07/2025 10:05
$q_e^1\to q_e^2$	$⟦p_e^2:=stopped⟧q_e^1$	01/07/2025 10:15
$q_e^2\to q_e^3$	$⟦p_e^2:=moving⟧q_e^2$	01/07/2025 10:20
$q_e^3\to q_e^4$	$⟦p_e^1:=zoneB⟧q_e^3$. $⟦p_e^2:=stopped⟧q_e^3$	01/07/2025 10:35
$q_e^4\to q_e^5$	$⟦p_e^1:=path1⟧q_e^4$. $⟦p_e^2:=moving⟧q_e^4$	01/07/2025 10:45
$q_e^5\to q_e^6$	$⟦p_e^1:=zoneA⟧q_e^5$. $⟦p_e^2:=stopped⟧q_e^5$	01/07/2025 11:05

offers a summary of the EV transitions during its mission. Each transition shows updated parameters and an extended date stamp of change.

4.2.3. Safety Property Verification

The electric vehicle is considered to operate safely under the following conditions:

• When the battery status is $high$, the vehicle should not be charging.
• When the vehicle locality is $zoneB$, its status should be $stopped$.

Property 1 

(Electric Vehicle safety). The vehicle always operates safely along the execution path.

CTL formulas: The following formulas describe the safety conditions, respectively:

• $AG(battery\_status=high\to status\ne charging)$.
• $AG(locality=zoneB\to status=stopped)$

4.2.4. Livensess Property Verification

The electric vehicle is considered to satisfy the liveness requirement, if along any execution path, the vehicle must eventually reach $zoneB$, ensuring that the destination is attainable.

Property 2 

(Electric Vehicle liveness). In every possible execution path, the vehicle eventually reaches its destination zone $zoneB$.

CTL formula:$AF(locality=zoneB)$

The ATS of the autonomous EV and the properties to verify are encoded in the nuXmv input language as shown in Listing A3 in Appendix A. After running the nuXmv model checker over the encoded model, the results indicate that the specified safety and liveness properties are true as shown in Listing A4 in Appendix A. This means that in all reachable states, if the value of $battery\_status$ is $high$, the vehicle is not in $charging$ status, and there exists at least one reachable state where the vehicle locality is $locality=zoneB$. Therefore, the drone operates safely in this mission and successfully reaches its intended destination.

Remark 2. 

These models (CTS/ATS) are designed to be generic and adaptable. They can be instantiated for any type of environmental context and agent by specifying appropriate parameters. For example, a smart chemical laboratory can be modelled as an environmental context using parameters such as temperature, humidity, and CO₂ level to define it, construct its CTS, and verify safety properties. Similarly, a drone delivery agent can be modelled with parameters such as locality, battery_level, status (eg., on, off, charging, and flying), and energy_consumption, which are used to define the corresponding ATS and verify its safety properties. This flexibility demonstrates the applicability of our modelling approach across diverse domains.

5. Related Work and Discussion

Several research studies have addressed the modelling and verification of context and agent entities within ITS. This section discusses key contributions in the areas of context and agent modelling, context-aware EV control, and formal verification, and compares them to our proposed approach.

Context and agent modelling are essential for capturing and reasoning about their properties and behaviours based on their information. For context modelling, several techniques are proposed in the literature. Perera et al. in [20] surveyed six popular techniques—key–value, markup schemes, and object-based, graphical, logic, and ontology-based modelling—and provided a comparative analysis based on their advantages, disadvantages, and applicability.

Ontology-based modelling is widely used to represent context for its semantic richness and hierarchical abstraction. Dimitropoulos and Hatzilygeroudis in [21] present a hybrid approach that combines ontologies and knowledge graphs to represent static robotic environments. Their method supports semantic modelling, consistency checking, and user-friendly querying. Madkour and Maach in [22] address the modelling of dynamic vehicular context for ITS applications. Their ontology-based middleware integrates heterogeneous data from vehicle, driver, and environment into a unified OWL-based representation. Through semantic reasoning and inference rules, autonomous adaptation is supported. In the EV security domain, Kumari et al. in [5] propose a context-aware security framework for EV charging. Their OWL 2 RL ontology captures vehicle state, location, and vulnerabilities, while SWRL rules allow semantic reasoning to detect malicious charging sessions in real time. Their approach provides adaptive security by reasoning over dynamic context.

While ontology-based frameworks such as [21,22] exceed in semantic consistency, they typically lack the explicit state transition modelling and formal temporal semantics needed for behaviour verification, making them less suitable for scenarios that require low-level traceability and model-checking. Some works, such as Garanin et al. in [23], address this by transforming ontology-based requirements into CTL formulas to enable formal verification using model checking tools. Our CTS formalism provides a complementary strength: it enables tracking state evolution by substituting parameter values and verifying properties over explicit state sequences.

In the domain of safety verification, Haupt and Liggesmeyer in [24] propose a context-aware framework for autonomous vehicles safety. The authors develop a context meta-model that identifies and classifies safety-relevant context entities and associates them with autonomous vehicle goals. Using Hazard Analysis and Risk Assessment (HARA), they extract a safety-state space that supports runtime monitoring through system-contextual safety rules, enabling adaptive safety responses. Their approach integrates context modelling, ontologies, and risk analysis to improve the safety of autonomous vehicles. In contrast, our approach models context evolution explicitly through parameter changes and uses model checking to detect unsafe states in the defined state space.

Agent-based models are often used to represent the EV behaviour. Torres et al. in [25] propose an agent-based model that simulates electric vehicle mobility and charging behaviour using spatial and activity pattern modelling, highlighting emergent load behaviour in decentralised electric vehicle. Kamali et al. in [26] present a hybrid agent-based architecture for autonomous vehicle platooning. Their model combines Belief–Desire–Intention (BDI) agents with formal verification techniques, checking individual agent decisions using AJFP and global timing properties using UPPAAL. Fernandes et al. in [27] implement a rational BDI agent to control an autonomous vehicle in a simulated environment. Agent behaviours are specified using LTL and verified through Gwendolen and the AJPF model checker. These works ensure correctness in decision-making but often operate at a high symbolic abstraction level and require complex verification tools. Our ATS, by contrast, focuses on the low-level, parameter-driven evolution of the agent, making it suitable for verifying the operational constraints essential in EV deployments.

Overall, our formal framework offers a structured and analysable approach for modelling the dynamic evolution of contextual environments and autonomous agents through parameter-based transition systems. The proposed CTS and ATS models enable the explicit tracking of parameter-based state changes over time and support formal verification using CTL and the nuXmv model checker. By defining these models separately, the approach respects the semantic independence between context and agent.

To evaluate the strengths and limitations of the proposed CTS and ATS models, a comparison is conducted with methods in the field of context and agent modelling.

Table 5. A comparative evaluation of the proposed CTS/ATS formalism and existing methods based on several metrics.

Metrics	CTS/ATS (Proposed Method)	Ontology-Based Models [21,22]	BDI Agent Model Verification [26,27]
Modelling type	Labelled transition systems based on parameters evolution.	Semantic-based modelling using ontologies (OWL, SWRL).	High-level symbolic agent modelling based on BDI architecture.
Context modelling	Symbolic CTS	Ontology, semantic rules	Partial
Agent modelling	Parameter-based ATS	Not explicitly modelled	BDI plan-based
State definition	Tuple of parameter values (e.g., <$traffic\_density$, $visibility$,…>).	Semantic instances (class and properties).	Agent mental state is defined by beliefs, desires, and intentions.
State transitions	Assignment chains with extended timestamp (ED), fully explicit.	No explicit transition model. Inference-based updates.	Transitions occur via plan execution.
Temporal handling	Explicit time via ED variable	implicit time	Time reasoning supported via LTL/ timed automata.
Specificity	low-level, parameter- specific	High-level contextual notions.	Symbolic abstraction over goals and tasks.
Verification support	Full formal verification using CTL and nuXmv.	No formal model checking Use OWL reasoners for consistency/inference.	AJPF for agent-level, UPPAAL for timing verification.
Multi-agent scalability	To be extended	Not addressed	Addressed in platooning
Strengths	Formal semantics, traceable, verifiable	Rich semantic modelling	Goal-based reasoning
Limitations	Deterministic only	No formal verification. Limited to ontology and semantic reasoning.	Complex modelling, hard to verify

presents a comparative overview over several key metrics, including modelling type, state definition, temporal handling, verification support, strengths, and limitations.

The metrics presented in Table 5 are systematically converted into numerical ratings on a scale from 1 to 5, where 5 indicates full support for the criterion and 1 indicates no support. Ratings reflect the extent to which each method satisfies the corresponding metric, based on a synthesis of related literature [21,22,26,27]. The meaning of each value is defined as follows:

• 5–Full support: the method fully satisfies the evaluation criterion.
• 4–Strong support: the method largely satisfies the criterion with minor limitations.
• 3–Moderate support: the method partially satisfies the criterion with noticeable limitations.
• 2–Limited support: the method provides minimal coverage or addresses the criterion indirectly.
• 1–No support: the method does not satisfy the evaluation criterion.

Table 6. Numerical evaluation (1–5) of CTS/ATS, ontology-based models, and BDI agent models across the metrics defined in Table 5. Ratings are derived from the qualitative assessment and indicate the degree to which each method satisfies the corresponding criterion.

Metric	CTS/ATS	Ontology-Based Model	BDI Agent Model
Modelling type	5	5	5
Context modelling	5	5	2
Agent modelling	5	1	5
State definition	5	3	4
State transitions	5	3	4
Temporal handling	5	2	4
Specificity	5	3	4
Verification support	5	4	4
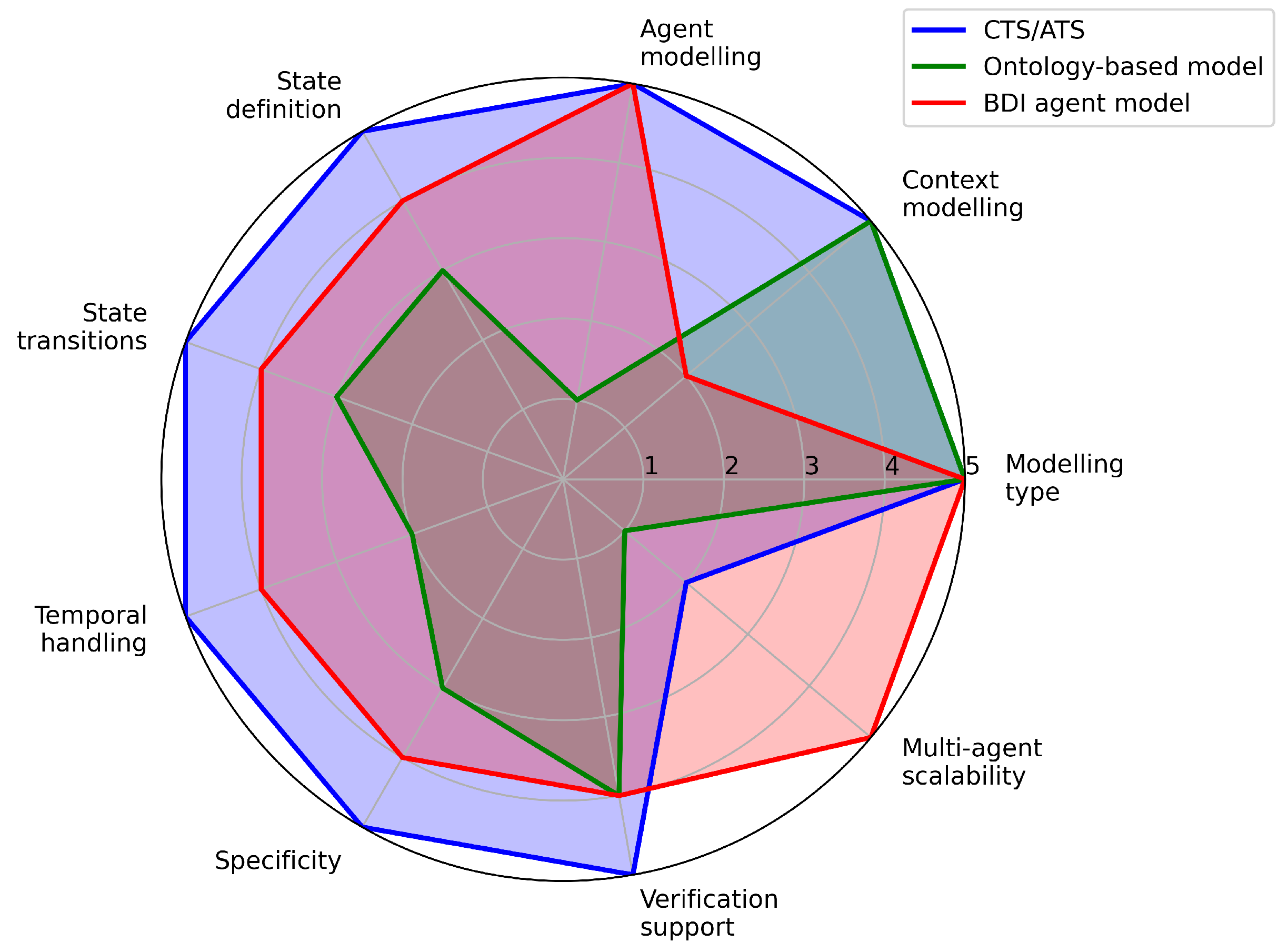
Multi-agent scalability	2	1	5

presents the resulting numerical evaluation for CTS/ATS, ontology-based models, and BDI agent models, providing a clear basis for comparative analysis. These ratings highlight the relative strengths and weaknesses across various metrics, including modelling type, context handling, agent representation, state definition, state transitions, temporal reasoning, specificity, verification support, and multi-agent scalability.

The same data form the basis for the spider chart in Figure 7, which offers a visual summary of the comparative performance of the three methods.

6. Conclusions and Future Work

This paper presents a formal approach to model the dynamic evolution of context and agent entities in ITS using multi-parameter transition systems. Through the presentation of the CTS and ATS, the work captures the temporal evolution of system states as a result of parameter changes. With the use of the nuXmv tool and the integration of CTL, rigorous verification of safety and liveness properties is allowed, ensuring that the modelled systems behave correctly along the possible execution path.

The application of our CTS and ATS models to two representative models, an urban delivery zone and an autonomous electric delivery vehicle, demonstrates the operational value of our formalism. In the urban context, the CTS captures how changes in traffic density, pedestrian presence, visibility, lighting, and road accessibility contribute to state evolution throughout a normal day. Verification of a safety property requiring all parameters to take acceptable values reveals a violation. The nuXmv tool generates a counterexample trace identifying a specific state where the traffic and pedestrian density exceeds safe levels. This highlights the CTS model ability to identify unsafe environmental conditions.

In contrast, the ATS captures the autonomous EV internal evolution across its delivery mission, defined by parameters such as $locality,status,$ and $battery\_level$. The verified CTL properties include safety conditions, for example, the vehicle should not charge when its battery is high, and liveness requirements, for example, the vehicle must eventually reach its destination. All properties are satisfied, validating the model’s capacity to guarantee correct behaviour under defined assumptions.

The integration of CTS and ATS in real-world-inspired scenarios underlines the applicability of the proposed method in practice. It allows safer EV operations and reliable delivery zone management by enabling the early detection of unsafe conditions.

Regarding future directions, the actual models are based on deterministic transitions, which may not fully capture the uncertainties or sensor variability commonly found in real deployments. Extending the models to integrate probabilistic or nondeterministic transitions using frameworks such as Markov chains is a promising future direction.

Moreover, while this framework models a single agent and context instance, Intelligent Transportation System environments often involve multiple agents interacting or competing within a shared context. This raises the need for synchronising the composition of multiple ATS and CTS, with verification extended to capture multi-agent safety.

In addition, binding this formal framework with adaptive learning techniques, like reinforcement learning, is a possible and promising extension. This would allow agents to adapt to context changes while remaining within formally verified safety limits.

Although the framework is validated using formal verification of qualitative properties, future work will include simulation-based experiments and empirical validation to further evaluate quantitative agent and context performance.