Research on Energy Saving for Hybrid Tractor Based on Working Condition Prediction and DDPG-Fuzzy Control

Abstract

To significantly reduce fuel consumption and improve fuel economy in hybrid tractor under complex working conditions, an energy—saving strategy based on working condition prediction and Deep Deterministic Policy Gradient and Fuzzy control (DDPG-Fuzzy) was proposed. Firstly, a hybrid tractor system dynamics model containing diesel, motor, and power battery was established. Secondly, a working condition prediction model for plowing velocity and resistance was constructed based on the adaptive cubic exponential smoothing method. Finally, a two-layer control architecture was designed. The upper layer adopted the DDPG algorithm, which takes demand torque, equivalent fuel consumption, and the State of Charge (SOC) as state inputs to optimize energy consumption by generating the diesel benchmark torque through the policy network. The lower layer introduced a fuzzy control compensation mechanism that calculates the torque correction based on the plowing velocity error and the plowing resistance deviation to adjust the power allocation. In light of on this, an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control was proposed. Under a standard 140 s plowing cycle, the results showed that the working condition prediction model achieved mean prediction accuracies of 97% for plowing velocity and 96.8% for plowing resistance. Under plowing conditions, the proposed strategy reduced the equivalent fuel consumption by 9.7% compared to the power-following strategy, and reduced SOC by 4.4% while maintaining it within a reasonable range. By coordinating the operation of the diesel and motor within high-efficiency regions, this approach enhances fuel economy under complex working conditions.

1. Introduction

Under the background of global climate change and intensifying resource constraints, energy transition in agriculture has become the focus of international attention. The traditional fuel tractor power system leads to serious energy waste due to low combustion efficiency, while its exhaust contains a large amount of incomplete combustion products, which further exacerbates greenhouse gas emissions and atmospheric pollution in the agricultural sector [1,2,3,4]. In order to cope with these problems, hybrid tractors have emerged, which, as an effective alternative to traditional energy-intensive tractors, is gradually becoming a key breakthrough in the energy—saving upgrading of global agricultural machinery [5,6]. The energy—saving and emission-reduction potential of hybrid tractors relies on the synergistic work of diesel and motor drive systems. However, the energy—saving control strategies of existing hybrid tractors still face problems such as poor adaptability to complex working conditions and insufficient optimization of fuel economy [7]. The reason for this is that the working conditions of farmland operations are complex and variable, and the existing strategies find it difficult to distribute power reasonably, resulting in the synergistic advantages not being fully utilized [8,9]. Therefore, there is an urgent need to develop new control methods that can adapt to the changes in complex working conditions in the farmland, coordinate the power distribution of diesel and motor, and reduce fuel consumption and emissions for agricultural machinery under the premise of ensuring the power performance of hybrid tractors [10].

The energy—saving control strategy is the core technology of hybrid tractor, which directly affects fuel economy and power by coordinating the power distribution between diesel and motor, and is the key to improve the efficiency and environmental performance of the whole machine [11]. Current energy—saving control strategies can be divided into two main categories: rule-based control strategies [12] and optimization-based control strategies [13,14]. The rule-based control strategy uses preset empirical parameters and fixed logic judgment to realize power allocation, which is a mature technology widely used in hybrid tractor at present; although it is computationally efficient in real time, it lacks adaptive ability to complex working conditions. Fang et al. [15] took the series hybrid tractor as the research object, established a simulation system based on ADVISOR secondary development, and formulated three energy management strategies: thermostat type, power-following type, and fuzzy control type. The results showed that all three strategies could effectively maintain the State of Charge (SOC) in the specified range; working under the plowing condition for 1 h, the fuzzy control strategy had the smoothest SOC curve, and the fuel economy was improved by 4.16% compared with the power-following type and 8.10% compared with the thermostat type. Wang et al. [16] proposed a fuzzy logic-based energy allocation control strategy based on the analysis of hybrid tractor working conditions, and established a simulation model of the whole vehicle using MATLAB 2013a (Primary Developer: MathWorks; Location: Natick, MA, USA). The results showed that the fuzzy logic control strategy could reasonably allocate the torque of diesel and motor, and it could make the diesel work in the high-efficiency region. Although the fuzzy strategy is better than the fixed rule in fuel economy, its nature of relying on preset rules still limits the complex working condition adaptability. To overcome the lack of adaptiveness in fuzzy rules, Zhu et al. [17] used the fuzzy adaptive equivalent fuel consumption minimization strategy (FA-ECMS) to optimize the power allocation for the problem of high fuel consumption and poor emission of high-horsepower tractor. The results showed that FA-ECMS reduced fuel consumption by 6.71% and 5.04% compared to conventional ECMS under tilling and transportation conditions, respectively. Although this strategy improves the energy efficiency of the hybrid tractor, it still suffers from insufficient adaptability under complex working conditions.

The optimization-based control strategy calculates the optimal power distribution scheme in real time through mathematical models and algorithms, which significantly outperforms the strategy that relies on preset rules in terms of responsiveness to changes in operating conditions, and has higher fuel economy and emission control capability, which is the current research hotspot and the future direction of technological development. Lee et al. [18] proposed the optimization based on the power distribution ratio for the problem of fuel consumption of a parallel hybrid tractor. By analyzing key traction performance parameters such as diesel, wheel and PTO (power take-off axis) speed, the rule-based control strategy was compared with the traction power source control scheme. The results showed that the fuel economy was significantly enhanced, while the vehicle traction performance and work point efficiency were improved. Miao et al. [19] proposed a tandem hybrid tractor plowing condition dynamic planning control strategy solution method for the fuel inefficiency problem of a tandem hybrid tractor. The results showed that the fuel consumption was reduced by about 6.3% compared with the power-following control strategy. However, this strategy has significant defects in global optimization and cannot respond to the sudden changes in disturbances in plowing conditions in real time. For this reason, Zhao et al. [20] proposed a model predictive control (MPC) energy management strategy based on dynamic programming (DP) solving. A coupled dynamics model was constructed for three typical working conditions, namely, plowing, rototilling and transporting, and the global optimal SOC trajectory solved by DP was used as the MPC constraint design strategy. The results showed that, compared with the power-following strategy, the DP-MPC strategy reduced the fuel consumption in the three working conditions by 7.97%, 13.06%, and 11.03%, respectively. Although this strategy makes up for the real-time defect of dynamic planning, it leads to difficulties in balancing long time horizon optimization and adaptability due to over-reliance on models and short-sighted decision making. Nan et al. [21] proposed a working condition prediction energy management strategy based on the RBF neural network and designed a rolling optimization energy management strategy based on velocity prediction to address the problem that dynamic planning algorithms cannot be optimized online. The results showed that the fuel consumption was improved by 5.18% compared with the rule-based EMS, which verified the effectiveness and adaptability of this working condition prediction method. Although the strategy compensates for the short-sightedness defect of MPC by predicting the information, the traditional optimization framework is not robust enough to the prediction error and is computationally inefficient. In order to break through this bottleneck, Wu et al. [22] addressed the problems of complex parameter adjustment and difficult online control algorithms for energy management strategies of hybrid tractor, adopted the DDQN(Double Deep Q-Network) algorithm to design a deep reinforcement learning-based energy management strategy, and validated it through the HIL(Hardware-in-the-Loop) test platform. The results showed that compared with the power-following strategy, the DDQN strategy reduced the equivalent fuel consumption by 10.40%, 9.78%, and 9.57% under plowing, rotary plowing, and transporting conditions, respectively, and the overall energy—saving effect was remarkable.

Overall, the development of hybrid tractor energy—saving control research still faces significant constraints: rule-based control strategies are difficult to adapt to sudden changes in complex working conditions; global optimization strategies are sensitive to prediction errors because of their dependence on precise working condition information, resulting in real-time demand being difficult to satisfy and unable to effectively allocate power; and despite the strong adaptive ability of deep reinforcement learning online, there is the problem of poor interpretability and difficulty in constructing strategies. In order to meet the control requirements of hybrid tractor under complex operating conditions, there is an urgent need to develop a new type of control strategy based on working condition prediction that combines strong interpretability and online adaptive optimization capability, so as to solve the problems of high fuel consumption and poor fuel economy.

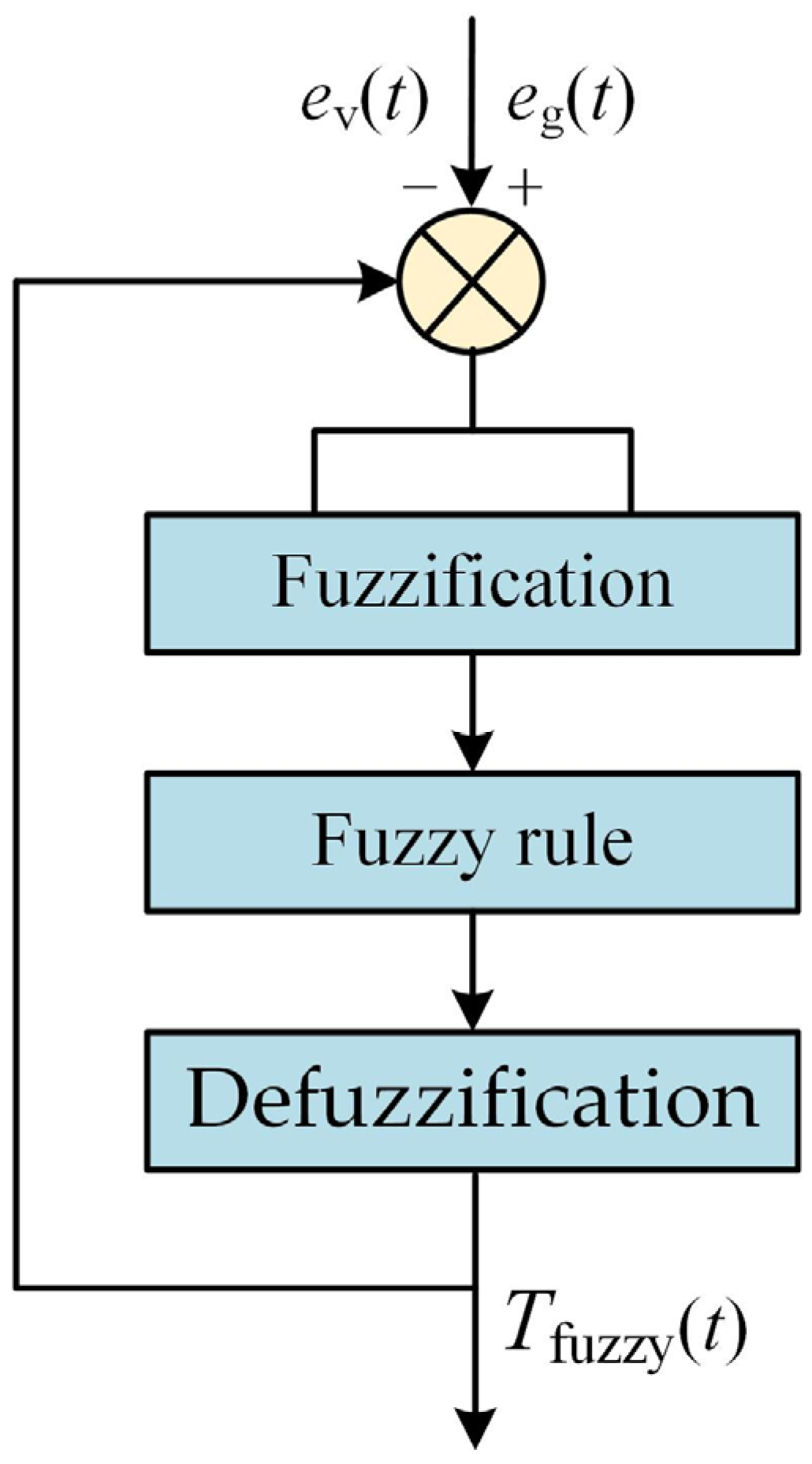
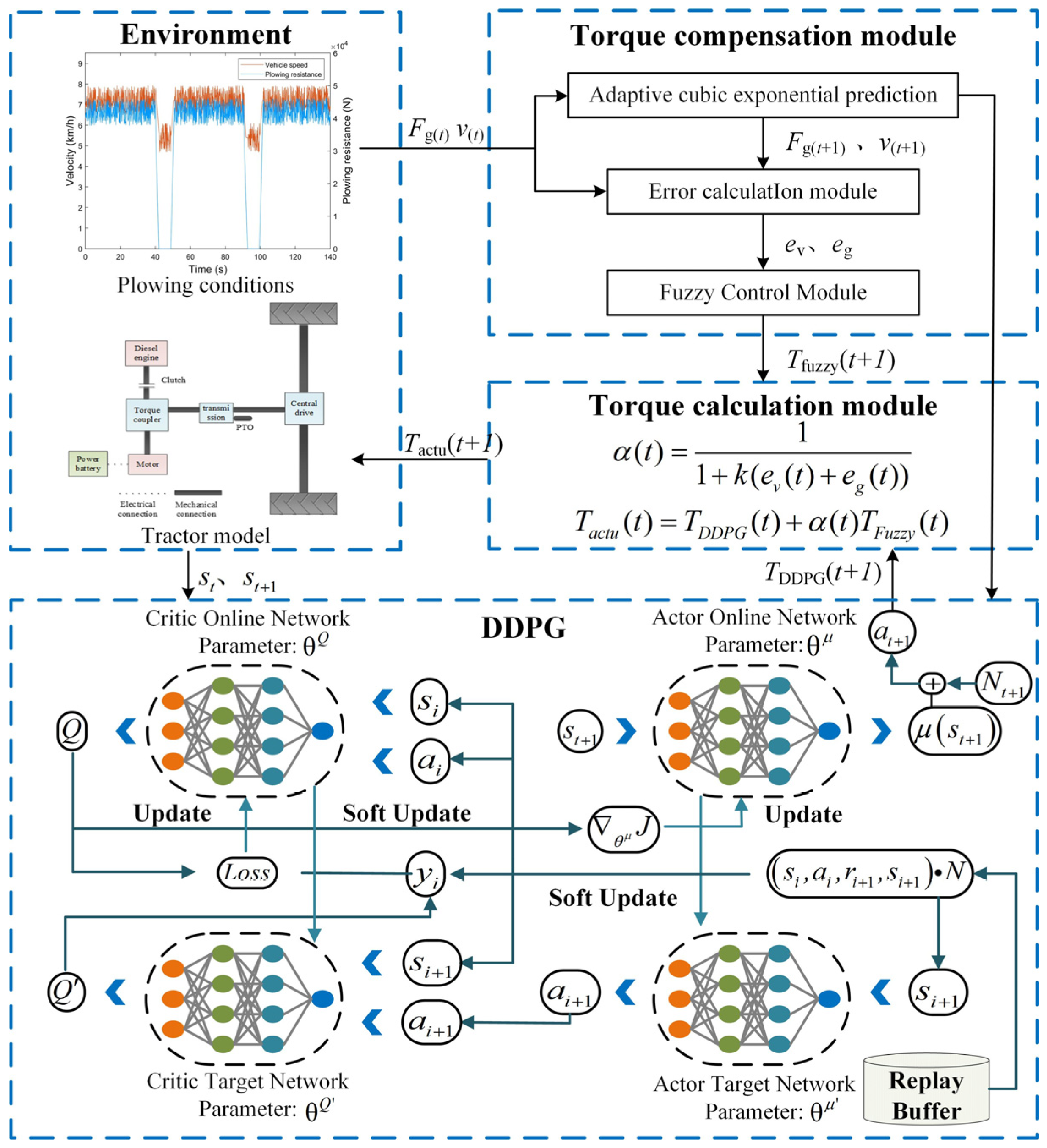
In response to the poor energy—saving performance of hybrid tractors under complex working conditions, an energy—saving strategy for hybrid tractor based on working condition prediction and Deep Deterministic Policy Gradient and Fuzzy control (DDPG-Fuzzy) is proposed in this study [23,24,25].

The main contributions of this study are as follows:

(a)

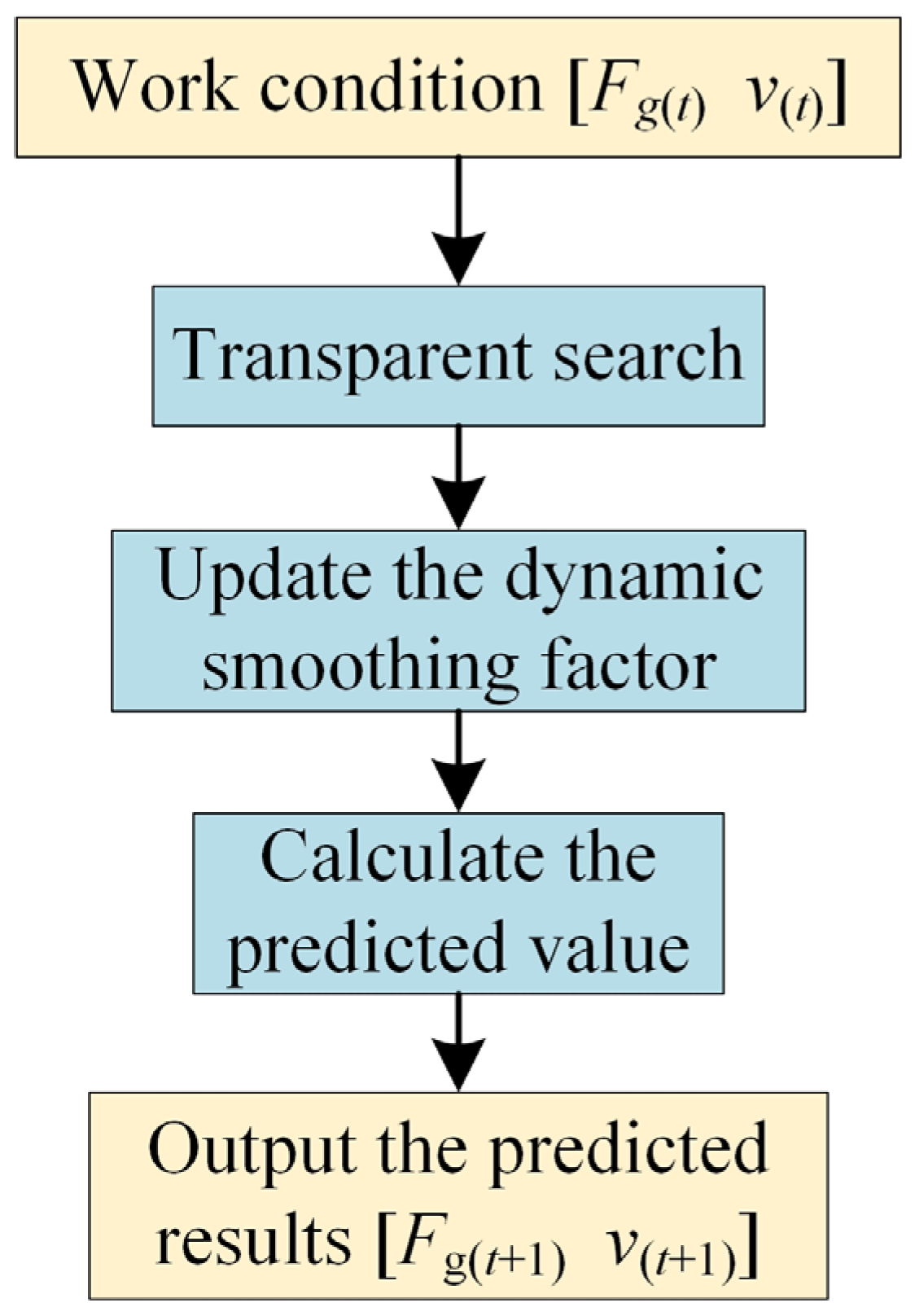
Aiming at the problem of decreasing accuracy and insufficient adaptability of the prediction model due to the change in complex working conditions in hybrid tractor plowing operation, a working condition prediction model based on the adaptive cubic exponential smoothing method is constructed to realize future working condition prediction by using historical operation data.

(b)

To remarkably reduce fuel consumption and improve fuel economy in hybrid tractor under complex working conditions, an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control is proposed to realize the optimization of energy consumption and compensation of power, to improve the adaptability of the complex working conditions, and to effectively reduce the equivalent fuel consumption rate.

The structure of this paper is as follows. Section 2 introduces the hybrid tractor power structure and main parameters. Section 3 performs simulation modeling of the main components of the hybrid tractor. Section 4 carries out the control strategy design and proposes an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control. Section 5 verifies the effectiveness of the control strategy through simulation. Section 6 provides the conclusions of this paper.

2. Hybrid Tractor Power Structure and Main Parameters

2.1. Hybrid Tractor Topology

The parallel hybrid tractor drive system studied in this paper, as illustrated in Figure 1, consists of dual drive systems for diesel and motor, with core components including a diesel, power battery, motor, power output shaft, torque coupler, transmission, and central drive unit. The diesel and the motor can be driven independently as well as output power at the same time. The output torque of the diesel and the motor is integrated through the torque coupler and then transferred to the transmission input shaft; the power output from the transmission is divided into two ways: one way as the power input of the central drive unit to drive the main body of the hybrid tractor for the operation, and the other way is connected to the PTO (Power Take Off) power output shaft to provide power support for the agricultural implements.

2.2. Performance Parameters of Main Components of Hybrid Tractor

A certain type of the diesel–electric parallel hybrid tractor is used as the research object of the energy—saving control strategy, and the specific parameters of the main components of this hybrid tractor are shown in

Table 1. Main performance parameters of hybrid tractor.

Project	Parameters	Numerical Value
Entire machine	Overall quality/kg	7200
	Drive wheel radius/m	0.8
Diesel	Rated power/kW	105
	Rated speed/(min−1)	2200
	Maximum torque/(N·m)	610 (1600)
Motor	Rated power/kW	32
	Rated torque/(N)	110
	Rated speed/(r·min−1)	2800
Central drive	Gear ratio	19.1
transmission	Gear ratio	4.1

Source: [26].

[26].

3. Hybrid Tractor Model Construction

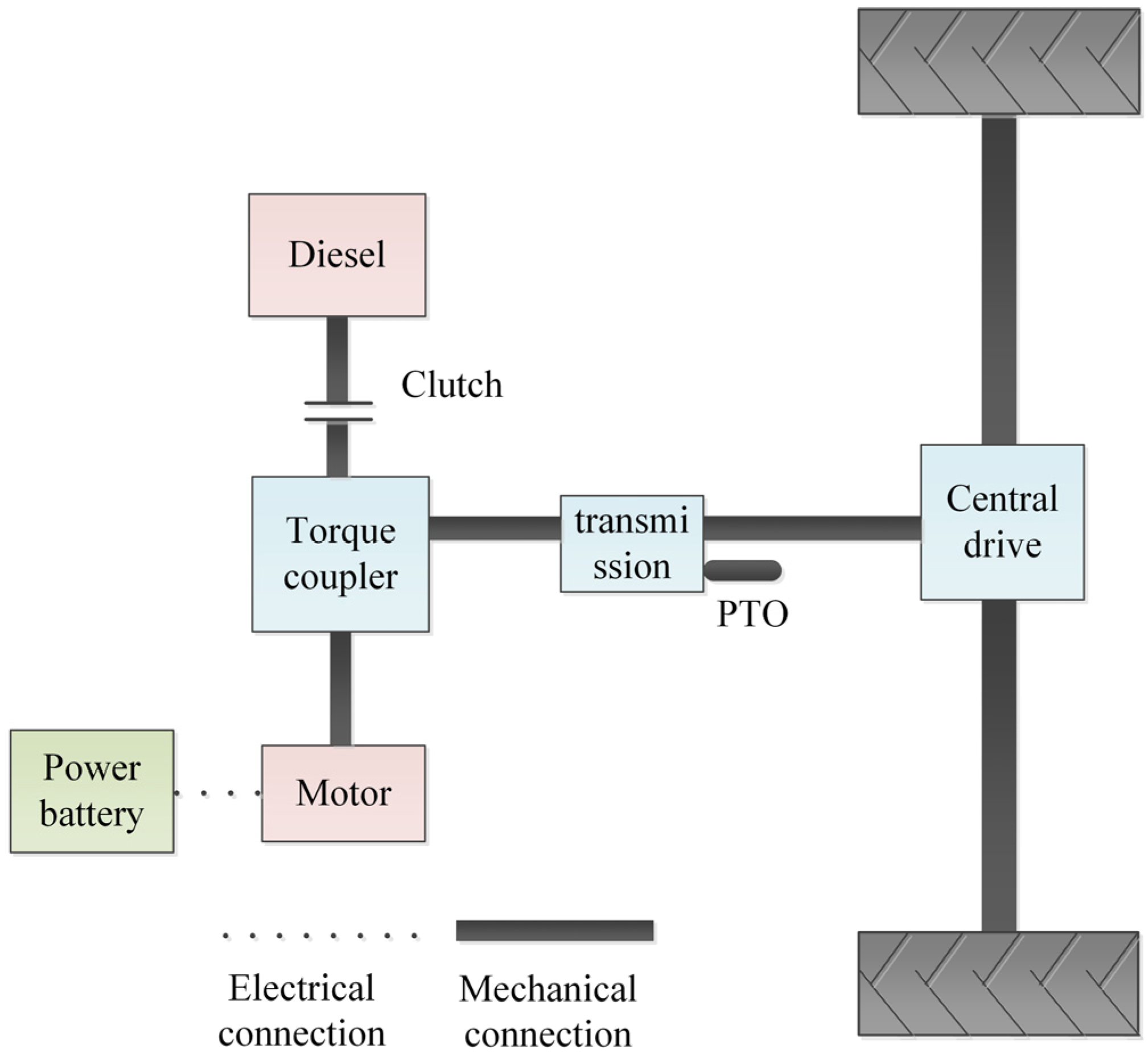
According to the topology of the hybrid tractor, its main component models were established, including transmission system model, plowing dynamics model, diesel model, power battery model, motor model, and finally the whole machine simulation model was built.

3.1. Hybrid Tractor Driveline Modeling

The transmission system consists of the torque coupler, transmission and central drive, and its core function is to transfer the mechanical energy output from the power source (diesel and motor) to the drive wheels [27]. Among them, the torque coupler, as a key component of power integration, realizes the coupling superposition of the diesel output torque T_e and the motor output torque T_m, and its coupling relationship satisfies the following kinetic equation:

$$T_{in}=T_e+T_m$$

(1)

where T_in is the torque at the input of the torque coupler, N∙m; T_e is the torque of the diesel, N∙m; and T_m is the torque of the motor, N∙m.

The total torque T_in output from the torque coupler is transferred to the drive wheels through the transmission system, and the transfer process satisfies the following torque relationship:

$$T_{in}={\displaystyle \frac{T_w}{i_z{i}_b{\eta }_z{\eta }_b{\eta }_c}}={\displaystyle \frac{F_{t}r}{i_z{i}_b{\eta }_z{\eta }_b{\eta }_c}}$$

(2)

where T_w is the drive wheel torque, N∙m; i_z is the central drive ratio; i_b is the transmission ratio; η_z is the central drive efficiency; η_b is the transmission efficiency; η_c is the torque coupler efficiency; F_t is the drive force, N; and r is the radius of the drive force, m.

The equation for the relationship between the diesel speed and the drive wheel speed is as follows:

$$n_e=n_{tire}{i}_z{i}_b$$

(3)

included among these

$$n_{tire}={\displaystyle \frac{v}{0.377r}}$$

(4)

where n_tire is the rotational speed of the driving wheel, r/min; n_e is the rotational speed of the diesel, r/min; and v is the velocity of the plowing operation, km/h.

It should be noted that the proposed driveline model focuses on the idealized power flow from the hybrid power sources through the torque coupler and transmission system to the drive wheels. While the model accurately reflects the torque distribution and mechanical efficiency of the driveline components (e.g., torque coupler, gearbox, central drive), it does not account for real-world losses associated with soil–tire interaction, such as wheel slip, particularly under varying soil conditions. In practical farming operations, soil slip can significantly reduce the effective traction torque available for propulsion, thereby affecting the overall vehicle performance and energy efficiency. This simplification was made to maintain model clarity and analytical tractability, as the primary objective of the current study was to establish the foundational relationships in the hybrid driveline system. Nevertheless, the potential impact of slip should be considered in future modeling efforts, especially for traction control and field operation optimization.

3.2. Dynamic Modeling of the Plow Unit

When the hybrid tractor works, its driving force needs to overcome the rolling resistance of the hybrid tractor itself as well as other driving resistances [28], and the equilibrium relationship between the driving force F_t and the various resistances is as follows:

$$F_t=F_f+F_i+F_j+F_A+F_g$$

(5)

where F_f is the rolling resistance, N; F_i is the ramp resistance, N; F_A is the air resistance, N; F_j is the acceleration resistance, N; and F_g is the plowing resistance, N.

3.3. Diesel Model

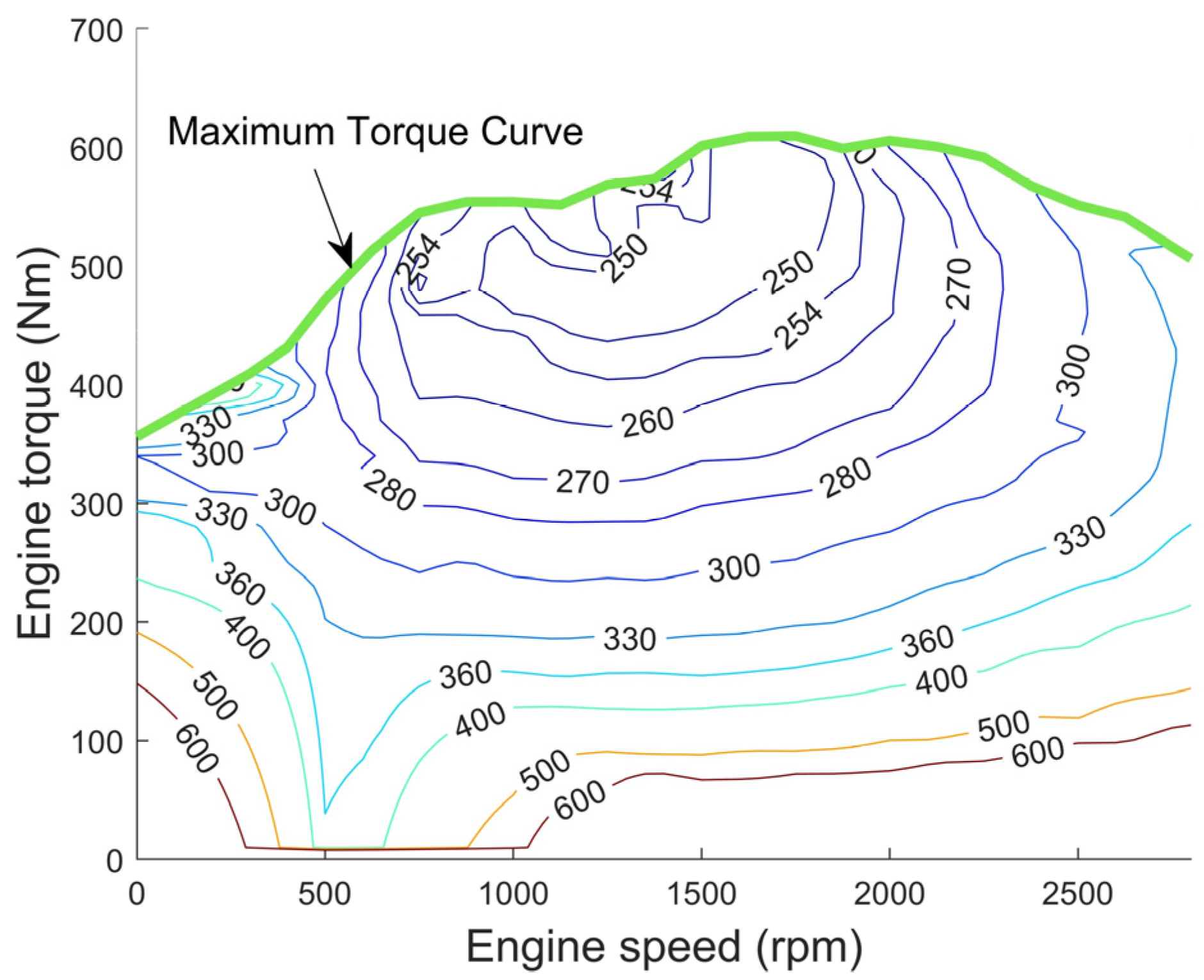
Diesel modeling methods are divided into two categories: theoretical modeling (constructing mathematical models based on theories of thermodynamics/combustion, etc.) and numerical modeling (testing the load/speed characteristic curves and fitting them through bench tests). In this study, since only the diesel input and output parameters are required and the internal combustion heat transfer process is ignored, numerical modeling is used to obtain the fuel consumption rate model, as shown in Figure 2 [29].

The diesel with the appropriate power is selected according to the conditions of use of the hybrid tractor, and only the relationship between the input and output parameters of the diesel is considered:

$$P_e={\displaystyle \frac{n_e\times T_e}{9550}}$$

(6)

where P_e is the diesel power, kW.

3.4. Power Cell Model

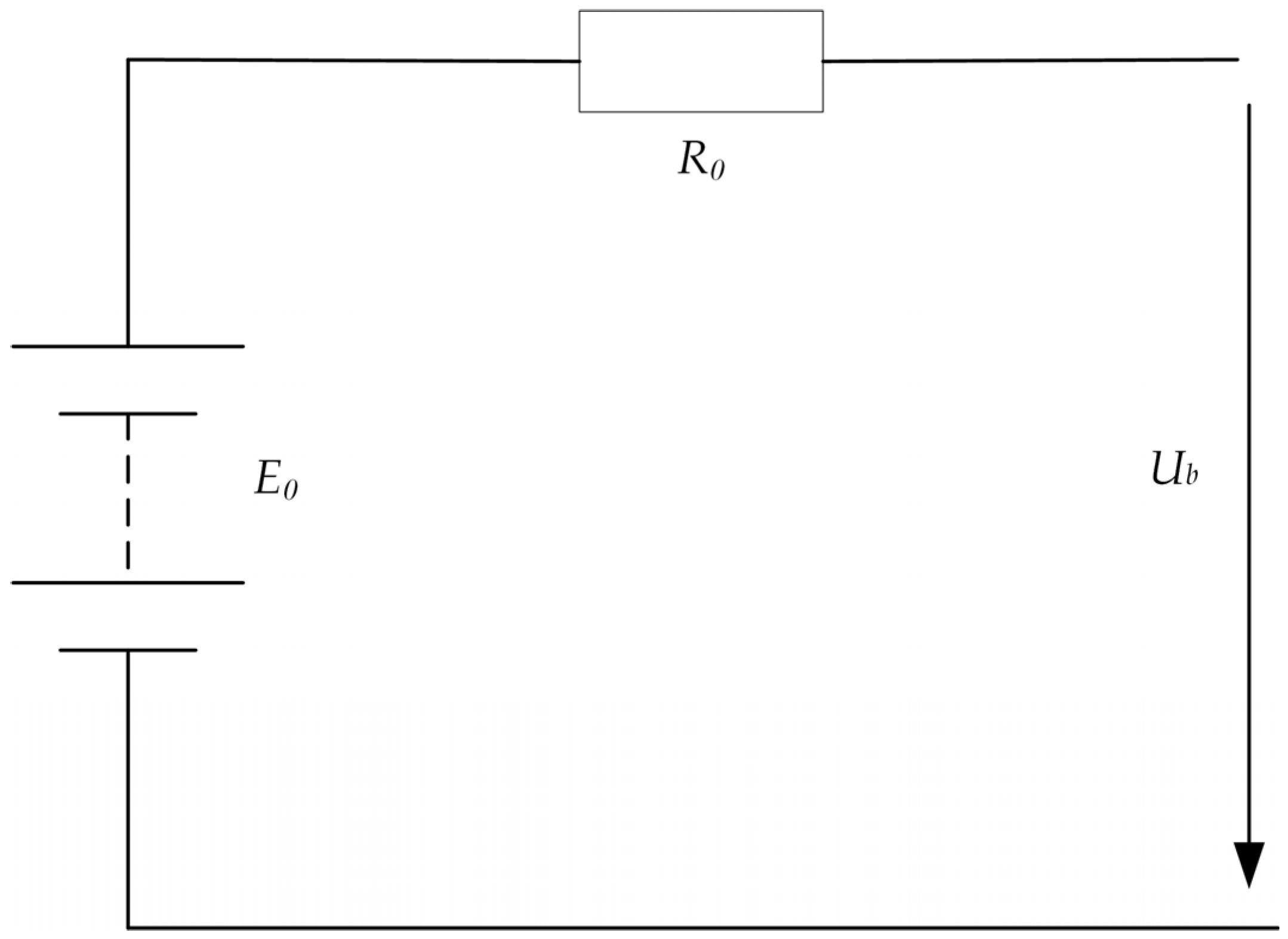
The internal resistance model (first-order equivalent circuit) and the resistance-capacitance model (second-order equivalent circuit) are commonly used for power batteries. The internal resistance model simplifies the battery pack as an ideal voltage source in series with the internal resistance, which has a simple structure and wide applicability; therefore, this model (Figure 3) is chosen in this paper to construct the equivalent circuit of the power battery, and its mathematical equations are concise and easy to calculate [30].

According to Ohm’s law, the power cell voltage characteristic equation is as follows:

$$U_b=E_0-I_b{R}_0$$

(7)

where U_b is the power cell output voltage, V; E₀ is the power cell terminal voltage, V; I_b is the power cell output current, A; and R₀ is the internal resistance of the power cell, Ω.

The power cell demand power is as follows:

$$P_{bat}=\left\{\begin{array}{l}{\displaystyle \frac{P_m}{{\eta }_{bat }}},P_m>0\\ P_m{\eta }_{bat },P_m<0\end{array}\right.$$

(8)

where P_m is the motor power, kW; and η_bat denotes the battery charging and discharging efficiency.

The calculation equation of the whole loop current is as follows:

$$I_b={\displaystyle \frac{E_0-\sqrt{{E_0}^2-4R_0{P}_m}}{2R_0}}$$

(9)

The change in the State of Charge (SOC) value of the power battery is calculated using the ampere-time integration method with the formula:

$$SOC(t)=SO{C}_0-{\displaystyle \frac{{\int }_0^t{I}_b(t)dt}{Q_b}}$$

(10)

where SOC is the battery charge state; SOC₀ is the initial value; and Q_b is the rated capacity of the power battery, Ah.

3.5. Motor Model

In order to improve the performance of the hybrid tractor electric drive system, a high-performance permanent magnet synchronous motor is selected as the power source in this study [31]. The output characteristics of this motor follow the basic motor dynamics relationship, and its power, speed and torque satisfy the following relationship:

$$P_m={\displaystyle \frac{n_m{T}_m}{9550}}$$

(11)

where n_m is the motor speed, r/min.

The motor model is established by the numerical modeling method. Through the experimental data of motor efficiency, the spline interpolation method is used to obtain the relationship between the efficiency of the motor system, torque, and rotational speed. And the relationship is determined and unique, which is suitable for the study of the control strategy. The numerical model of the motor efficiency is shown in Figure 4.

3.6. Simulation Model of the Whole Machine

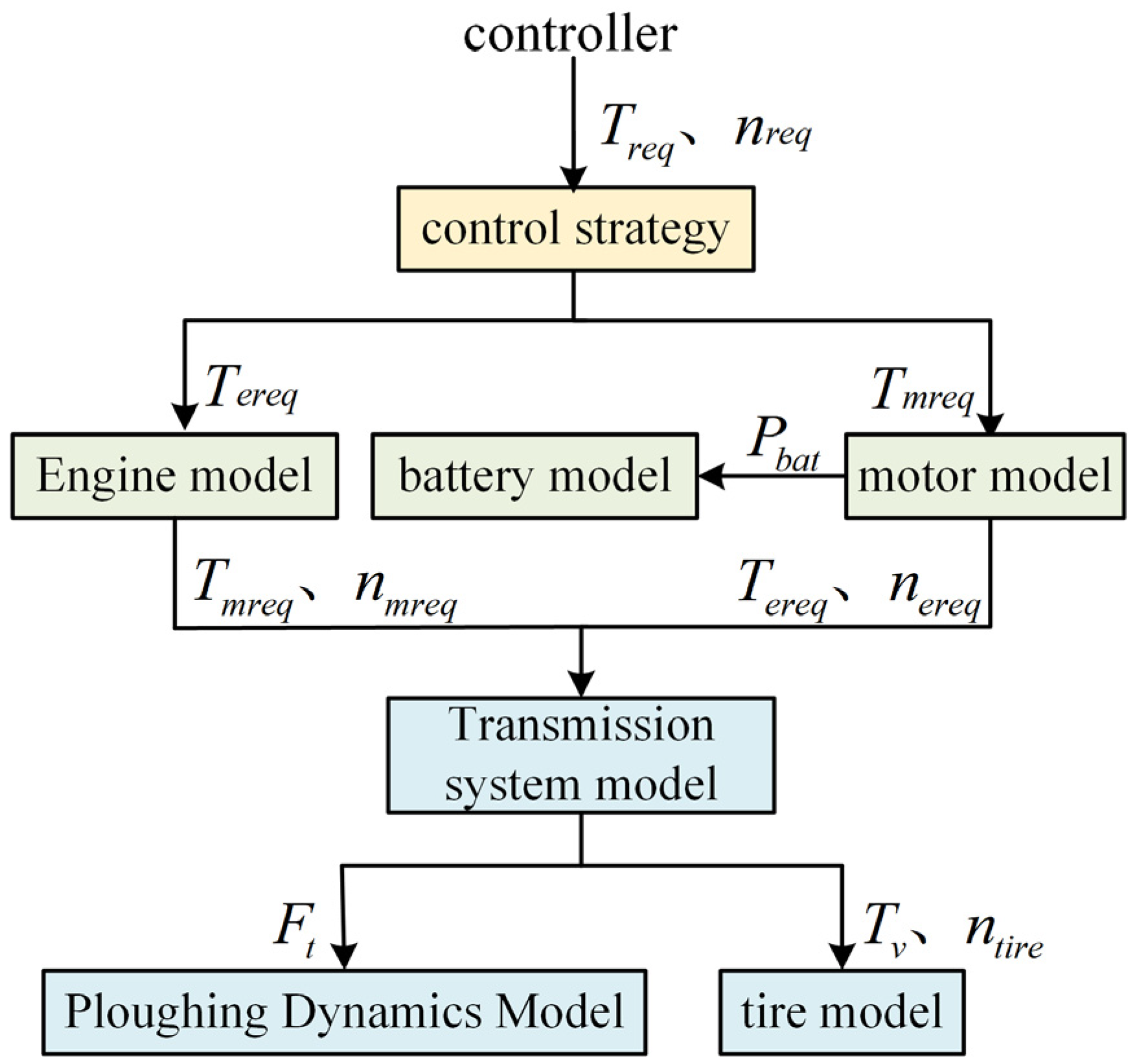
In this study, for the characteristics of the whole machine drive system of the parallel hybrid tractor, a simulation model of the whole machine is built based on MATLAB 2024b (Primary Developer: MathWorks; Location: Natick, MA, USA), as shown in Figure 5, and the model architecture contains modules such as the dynamics model of the plowing dynamics model, the model of the diesel, the model of the battery, the model of the motor, and the model of the tires. Under the typical operating conditions of the hybrid tractor, the controller collects the vehicle running signals in real time, and obtains the demand torque T_req and demand speed n_req of the whole machine through the calculation and processing of Equations (1)–(3).

Inside the controller, the demand torque of the whole machine is allocated according to the established torque allocation strategy (including the strategy proposed and compared in this paper), and then combined with the demand speed. The corresponding diesel demand torque and speed and motor demand torque and speed are output as inputs to the diesel model and motor model. The diesel model and motor model generate the target torque and speed according to the instructions, which are transferred to the plow unit dynamics model and driving resistance through the drive train model, while the battery model performs charge/discharge management according to the motor demand power.

4. Control Strategy Design

4.1. Adaptive Cubic Index Forecasting

In the hybrid tractor plowing operation, for traditional prediction models, such as the simple moving average method [32], there are problems of decreasing accuracy and insufficient adaptability when dealing with complex and dynamically changing working condition data. The exponential smoothing method, as a special form of the weighted average method, has significant advantages over the simple moving average method. The weight allocation of the simple moving average method follows a fixed decreasing pattern. The exponential smoothing method innovatively adopts the exponential decreasing pattern to allocate weights, so that the data near the current moment obtain higher weights, while the data far from the current moment have exponential decay. According to the smoothing order, it is divided into primary, secondary and tertiary smoothing, which are applicable to smooth, linear, and non-linear series, respectively. Compared with traditional methods such as exponential smoothing, data-driven methods such as LSTM and RBF networks can better model complex non-linear data, but they require large data sets, high computing power, and careful tuning, which limits their real-time use [33]. In view of the highly non-linear and irregular variation characteristics of hybrid tractor plowing operation velocity and plowing resistance, the cubic exponential smoothing method is a better choice because of its adaptability to complex trends [34].

The adaptive cubic exponential smoothing method optimizes the smoothing coefficients in real time through the dynamic adjustment mechanism, which significantly improves the prediction performance of time-varying data, and its mathematical model is as follows:

$$\left\{\begin{array}{l}{S}_{k,t}^{(1)}={\lambda }_k{X}_{k,t}+(1-{\lambda }_k)S_{k,t-1}^{\left(1\right)}\\ S_{k,t}^{\left(2\right)}={\lambda }_k{S}_{k,t}^{\left(1\right)}+(1-{\lambda }_k)S_{k,t-1}^{\left(2\right)}\\ S_{k,t}^{\left(3\right)}={\lambda }_k{S}_{k,t}^{\left(2\right)}+(1-{\lambda }_k)S_{k,t-1}^{\left(3\right)}\end{array}\right.$$

(12)

where $s_{k,t}^{\left(1\right)}$, $s_{k,t}^{\left(2\right)}$, $s_{k,t}^{\left(3\right)}$ are the primary exponential smoothing value, the secondary exponential smoothing value, and the tertiary exponential smoothing value of the data at moment t of the kth prediction, respectively; X_k,t is the actual data at moment t of the kth prediction; and λ is the smoothing coefficient of the kth prediction (0 < λ_k < 1).

Predictions for future data. a_k,t, b_k,t, and c_k,t are the prediction coefficients for the kth prediction:

$$\begin{gathered} a_{k,t}=3S_{k,t}^{(1)}-3S_{k,t}^{(2)}+S_{k,t}^{(3)} \\ {b}_{k,t}={\displaystyle \frac{\lambda }{2{(1-\lambda )}^2}}((6-5\lambda )S_{k,t}^{(1)}-(10-8\lambda )S_{k,t}^{(2)}+(4-3\lambda )S_{k,t}^{(3)}) \\ {c}_{k,t}={\displaystyle \frac{{\lambda }^2}{{(1-\lambda )}^2}}(S_{k,t}^{(1)}-2S_{k,t}^{(2)}+S_{k,t}^{(3)}) \end{gathered}$$

(13)

The kth period t + T predicted value Y_k,t+T is as follows:

$$Y_{k,t+T}=a_{k,t}+b_{k,t}T+c_{k,t}{T}^2$$

(14)

where T is the prediction step, i.e., the interval between the target prediction period and the current period, T = 1, 2, 3…; and Y_k,t+T is the predicted value of the kth t + T th period. The shorter the prediction step, the more accurate the prediction is, and T = 1 is chosen in this study.

The prediction accuracy is the basis for evaluating the good or bad prediction effect, and the sum of error squares is used as the basis for the evaluation in this study:

$$f=\min {\displaystyle \sum _{i=4}^N(Y_{k,i}}-X_{k,i}{)}^2$$

(15)

where f represents the sum of error squares; Y_k,i represents the predicted value of the i-th data for the kth prediction; X_k,i represents the actual value of the i-th data for the kth prediction; and N is the number of discrete samples in the sliding window.

The adaptive exponential smoothing method dynamically optimizes the smoothing coefficients by traversing the search with the expression:

$${\epsilon }_{k,t}={\displaystyle \frac{{\lambda }_k}{1-{(1-{\lambda }_k)}^t}}$$

(16)

where ε_k,t is a function of time t, which represents the dynamic smoothing coefficient at the kth prediction; and λ_k is the smoothing coefficient after optimization of the kth prediction.

The prediction flowchart of the adaptive exponential smoothing method is shown in Figure 6. Figure 6 demonstrates the adaptive three-time exponential prediction process: at the moment t, the plowing resistance F_g(t) and the plowing operation velocity v_(t), the smoothing coefficients are optimized by global search (the objective function is to minimize the squared error), the dynamic coefficients are updated according to Equation (13), and the one-step prediction values F_g(t+1) and v_g(t+1) are outputted with the predicted data vectors [F_g(t), v_(t), F_g(t+1), v_g(t+1)] as the basis for decision making.

4.2. Fuzzy Control Compensation Strategy

In the research of energy—saving control of hybrid tractor, the complex change in working conditions will significantly reduce the energy utilization rate and cannot effectively distribute the power. The fuzzy control can dynamically compensate for non-linear disturbances under complex working conditions without relying on an accurate mathematical model, which can better distribute power and improve the energy utilization of hybrid tractor. The plowing operation velocity and plowing resistance can reflect the power demand of hybrid tractor operation. Therefore, the plowing operation velocity error and plowing resistance error are taken as the input variables of the fuzzy control algorithm, reflecting the interpretability of the fuzzy control. And then the torque correction quantity is output through fuzzification, rule inference, and defuzzification. The model uses the affiliation function to quantify the fuzzy attribution degree of the input variables, and the control actions are determined and converted into precise commands by logical operations based on fuzzy rules [35].

The input plowing operation velocity error e_v(t) and plowing resistance error e_g(t) of the fuzzy control at time t are calculated as follows:

$$e_v(t)=v_{(t+1)}-v_{\left(t\right)}$$

(17)

$$e_g(t)=F_{g(t+1)}-F_{g(t)}$$

(18)

where v_(t+1) is the predicted velocity at time t; v_(t) is the plow operation velocity at time t; F_g(t+1) is the predicted plow resistance at time t; and v_(t+1) is the plow resistance at time t.

The fuzzy controller structure is shown in Figure 7.

From Figure 7, it can be seen that there are three key steps in fuzzy control, i.e., fuzzification, control rules, and defuzzification.

(1)

Fuzzification

The plowing operation velocity error and plowing resistance error are obtained as fuzzy values by the form of the thesis domain, and the fuzzy thesis domains are {−0.3 −0.2 −0.1 0 0.1 0.2 0.3} and {−1500 −1000 −200 0 200 1000 1500}; the fuzzy thesis domains of torque modification are {−20 −15 −10 0 10 15 20}. The corresponding language values in the thesis domain are NB, NS, Z, PS, and PB.

(2)

Generate fuzzy control rules

The fuzzy control rule is shown in

Table 2. Fuzzy control rules.

ev\eg	NB	NS	Z	PS	PB
NB	PB	PB	PS	PS	Z
NS	PB	PS	PS	Z	PS
Z	PS	PS	Z	NS	NS
PS	Z	NS	NS	NS	NB
PB	NS	NS	NB	NB	NB

.

Table 2 shows the fuzzy rule set constructed based on expert experience and empirical parameter tuning: initial rules were established based on agricultural machinery experts’ understanding of the plowing operation (the influence of velocity error and plowing resistance error on torque), followed by simulation-based adjustment of input variables (velocity error and plowing resistance error) to optimize membership functions and rule weights. By altering the range of input variable values and observing changes in the output torque correction values, the results indicate that the rules are insensitive to minor input fluctuations, effectively ensuring the robustness and stability of the control strategy.

(3)

Defuzzification

Defuzzification converts the fuzzy control rule output of the affiliation function into an accurate torque correction amount, in order to complete the line control stability control. In this paper, the center of gravity method is used to complete the defuzzification of fuzzy control variables, and the specific calculation formula is as follows:

$$T_{fuzzy}(t)={\displaystyle \frac{{\displaystyle \sum _{i=1}^n}\mu (e_t)\cdot E_c}{E}}$$

(19)

where T_fuzzy(t) is the torque correction at time t; E is the system error; E_c is the system error change rate; and μ(e_t) is the defuzzification operation.

4.3. DDPG-Fuzzy Control Energy—Saving Control Strategy Based on Working Condition Prediction

In the energy—saving control of hybrid tractor, the discrete strategy of traditional reinforcement learning is difficult to adjust the control parameters in real time due to its complex working conditions, while deep reinforcement learning (DRL) combines the continuous spatial processing capability of deep learning with the decision optimization of reinforcement learning to provide an effective solution to the energy—saving control problem of hybrid tractor under complex working conditions [36]. However, DRL lacks the incorporation of physical a priori knowledge, resulting in poor interpretability of its control logic. In contrast, fuzzy control effectively compensates for the shortcomings of DRL in terms of the lack of physical a priori and poor interpretability through the rule base established by experts. Therefore, for the complex working conditions faced by the hybrid tractor in field operations, this paper proposes an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control. The upper DDPG algorithm takes the demand torque and equivalent fuel consumption as well as the battery SOC as state variables, and outputs the diesel baseline torque through the strategy network, while the lower fuzzy controller calculates the torque modification based on the plowing operation velocity error and the plowing resistance deviation to adjust the power allocation.

4.3.1. Energy—Saving Control Optimization Model

The hybrid tractor adopts dual energy sources (electrical energy and fuel), and in order to unify the evaluation index, the equivalent fuel consumption model is constructed as the total energy consumption evaluation standard. The core objective of energy—saving control is to minimize the equivalent fuel consumption by optimizing the allocation of the operating states of the diesel and the motor [37]. The equivalent fuel consumption during the hybrid tractor operation can be expressed as follows:

$$Q_c(t)={\int }_0^{t}f\left(Q_f(t)+{\displaystyle \frac{j_m{P}_b(t)}{j_e{\eta }_{bat}}}\right)dt$$

(20)

included among these

$$Q_f(t)={\displaystyle \frac{f_e{P}_e}{1000\times 3600\times 0.84}}$$

(21)

where Q_c(t) is equivalent fuel consumption, L; t_f is the terminal moment; j_e is the oil price, yuan/L; j_m is the electricity price, yuan/degree; Q_f(t) is fuel consumption at t moment, L; P_b(t) is the battery charging and discharging power at t moment, which is greater than 0 during discharging and less than 0 during charging, kW; and f_e is the diesel fuel consumption at t moment, g/(kW-h).

According to Equation (10), the battery SOC value can be calculated to obtain the system state equation:

$$S\dot{O}C(t)=-{\displaystyle \frac{I_b(t)}{Q_b}}=-{\displaystyle \frac{U_b(t)-\sqrt{U_b^2-4P_b(t)R_0(t)}}{2R_0(t)Q_b}}$$

(22)

Since the working capacity of each component is limited by realistic conditions, the following constraints need to be satisfied:

$$\left\{\begin{array}{l}{P}_{m\min }\le P_m(t)\le P_{m\max }\\ P_{e\min }\le P_e(t)\le P_{e\max }\\ SO{C}_{\min }\le SOC(t)\le SO{C}_{\max }\end{array}\right.$$

(23)

4.3.2. DDPG Energy—Saving Control Strategy Module

The DDPG algorithm is based on the actor–critic framework and uses a deep neural network to approximate the actor network and the critic network, both of which are composed of an online network and a target network. The strategy network maximizes the expected cumulative reward through gradient ascent and adjusts the parameters using the Q-value provided by the critic network for the action gradient, while the value network minimizes the mean-square error through gradient descent, and updates the parameters based on the future reward estimation of the target network to improve the Q-value prediction accuracy [38].

The study of energy—saving control strategies for hybrid tractor using DDPG assumes that the diesel torque is optimized using a strategy μ, which is a deterministic strategy that directly maps the state to a specific action, i.e., as follows:

$$a_t=\mu \left(s_t\right)$$

(24)

where a_t is the output action at moment t and s_t is the state variable at moment t.

In this paper, the demand torque and equivalent fuel consumption of a hybrid tractor and battery SOC are used as state variables to construct the state space:

$$s_t=\{T_{req},Q_c,SOC\}$$

(25)

Diesel torque as output action:

$$a_t=T_{DDPG}(t)$$

(26)

where T_DDPG(t) is the reference torque of the diesel at the output of the agent at moment t.

The optimal control objective of the DDPG is to find the policy, which maximizes the cumulative reward obtained in the long run, and the expected value of the cumulative reward is as follows:

$$\max J_{\mu }(s_0)=E\left[{\displaystyle \sum _{t=0}^{\infty }{\gamma }^{t}r\left(s_t,a_t\right)}\right]$$

(27)

where J_μ(s₀) is a function of the initial state s₀; γ is a discount factor; and (s_t,a_t) denotes a state–action pair.

In the DDPG algorithm, the discount factor γ (range [0, 1]) is used to balance the weights of current and future rewards. The larger γ is, the more emphasis is placed on long-term returns. For the energy—saving control of hybrid tractors, which requires balancing immediate fuel consumption and long-term battery SOC management, this paper selects γ = 0.99 to ensure that the strategy is sensitive to current actions while effectively guiding the agent to optimize long-term cumulative returns, thereby achieving a balance between energy saving and system stability.

For the hybrid tractor energy—saving control problem, the reward function takes the minimization of equivalent fuel consumption as the primary goal, while maintaining the power battery SOC in a reasonable range. Then, the reward function is as follows:

$$r(t)=r\left(s(t),a(t)\right)=-\left(C_1{Q}_c(t)+C_2{\left(0.9-SOC(t)\right)}^2\right)$$

(28)

where C₁ and C₂ denote the weight of each reward.

It is recommended to select appropriate values for C₁ and C₂ based on the relative importance of fuel economy and battery SOC management, by normalizing the target items and conducting simulation experiments or sensitivity analyses. C₁ = 2 and C₂ = 0.5 are selected to balance energy—saving goals and battery health status.

The DDPG algorithm is represented by the Q-value function in order to better measure the action that should be taken in the next state:

$$Q\left(s_t,a_t\right)=r\left(s_t,a_t\right)+\gamma \max \left(Q\left(s_{t+1},\mu \left(s_{t+1}\right)\right)\right)$$

(29)

where Q(S_t,a_t) is the value function when the action a_t is taken in the state s_t; and max(Q(s_t+1,μ(s_t+1))) is the maximum value of all the actions in the state s_t+1 when the action is selected according to the policy μ function.

To avoid training instability, a target network is introduced and the target Q-value is computed based on the i-th sample randomly sampled from the experience playback pool:

$$y_i=r\left(s_i,a_i\right)+\gamma Q^{\prime }\left(s_{i+1},{\mu }^{\prime }\left(s_{i+1}\left|{\theta }^{{\mu }^{\prime }}\right.\right)\left|{\theta }^{Q^{\prime }}\right.\right)$$

(30)

where θ^Q′ and θ^μ′ are the target critic and actor network parameters, respectively.

The training objective of the critic network is to make the online network Q-value approximate to the target Q-value, and the critic network is updated by minimizing the loss function through gradient descent:

$$Loss={\displaystyle \frac{1}{N}}{{\displaystyle \sum _i\left(y_i-Q\left(s_i,\left.a_i\right|{\theta }^Q\right)\right)}}^2$$

(31)

where θ^Q is the online critic network parameter and N is the number of samples.

The actor network maximizes the Q-value evaluated by the critic network through gradient ascent:

$${\nabla }_{{\theta }^{\mu }}J\approx {\displaystyle \frac{1}{N}}{\sum }_i\nabla {}_{a}Q\left(s,\left.a\right|{\theta }^Q\right){|}_{s=s_i,a=\mu \left(s,i\right)}\nabla {}_{{\theta }^{\mu }}\mu \left(s|{\theta }^{\mu }\right){|}_{s_i}$$

(32)

where ▽_θμJ is the gradient of the objective function J with respect to the parameter θ^μ and θ^μ is the online actor network parameter.

The parameters are progressively synchronized with the target network parameters through soft updates:

$$\left\{\begin{array}{l}{\theta }^{Q^{\prime }}\leftarrow \mathit{\tau }{\theta }^Q+\left(1-\mathit{\tau }{\theta }^{Q^{\prime }}\right)\\ {\theta }^{{\mu }^{\prime }}\leftarrow \mathit{\tau }{\theta }^{\mu }+\left(1-\mathit{\tau }{\theta }^{{\mu }^{\prime }}\right)\end{array}\right.$$

(33)

where τ is the soft update factor.

4.3.3. Design of Energy—Saving Control Strategies

The action of the DDPG output and the torque compensation amount of the fuzzy control output need to be transferred to the whole machine model through the coupling calculation, and the specific calculation formula is as follows:

$$T_{actu}(t)=T_{DDPG}(t)+\alpha (t)T_{Fuzzy}(t)$$

(34)

where α(t) is the weighting factor of the torque correction quantity and satisfies the formula:

$$\alpha (t)={\displaystyle \frac{1}{1+k(e_v(t)+e_g(t))}}$$

(35)

where k is the weighting coefficient, taken as 0.01.

In summary, for the problem of high fuel consumption and poor fuel economy of hybrid tractor under complex working conditions, this paper proposes an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control. The specific principle is shown in Figure 8.

Figure 8 mainly includes the DDPG-based energy—saving control strategy module, torque compensation module, and torque calculation module. The torque compensation module contains the working condition prediction module and fuzzy control module. At the moment t, the working condition information (v_(t),F_g(t)) is inputted into the working condition prediction module, the working condition information (v_(t+1),F_g(t+1)) of the next moment is generated according to the exponential smoothing method, and the working condition error (e_v,e_g) is calculated at the same time, and the fuzzy control module outputs the torque correction amount T_fuzzy(t + 1) according to the error information through fuzzification, rule-based reasoning, and defuzzification. The energy—saving control strategy module of the DDPG generates the benchmark diesel torque T_DDPG(t + 1) based on the state space and the next moment’s working condition information, and then the torque calculation module calculates the actual torque according to Equations (34) and (35), and inputs it into the hybrid tractor model.

5. Analysis of Results

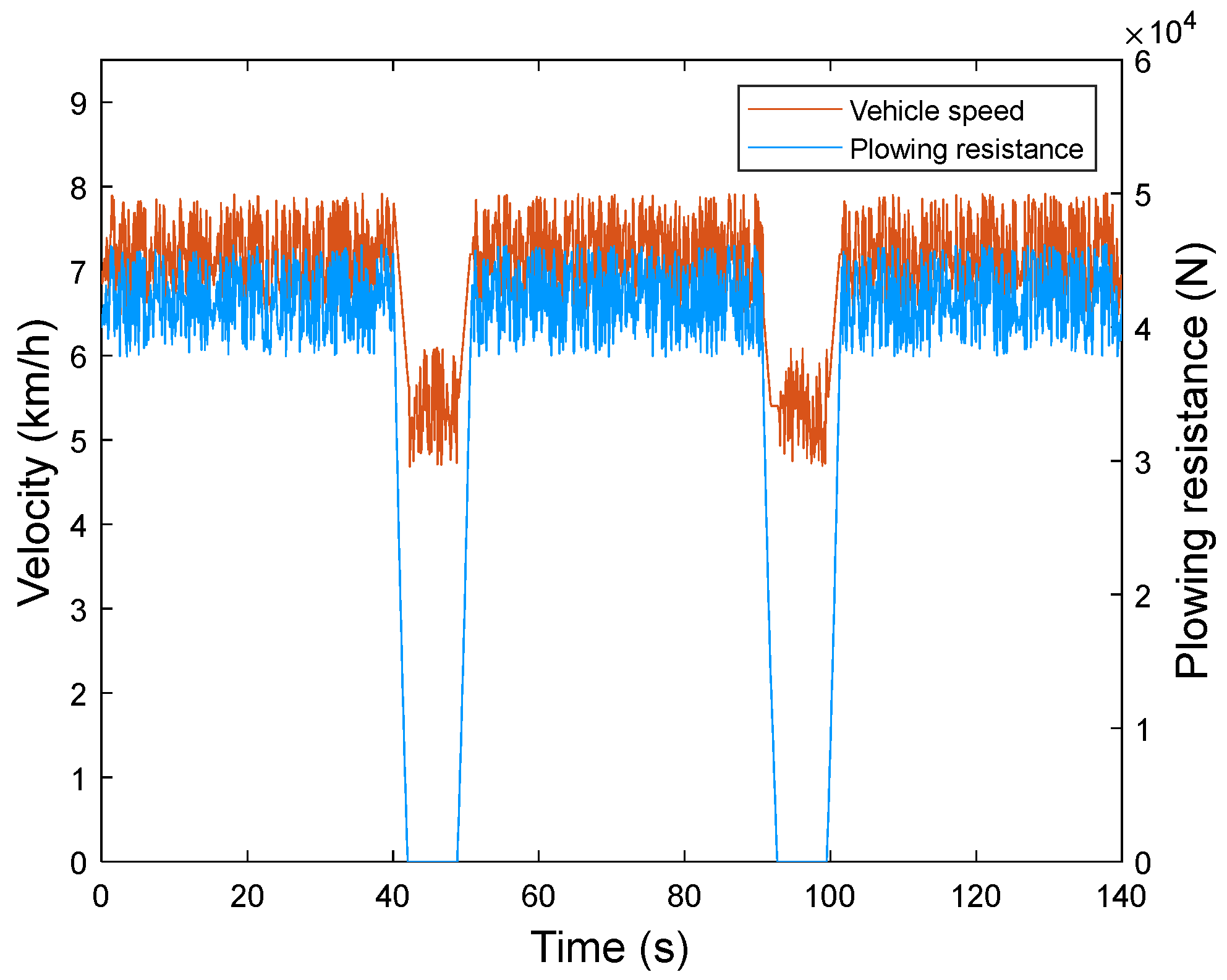
In this study, the control strategy based on power-following is used as the comparison strategy, and the test verification is carried out based on the MATLAB 2024b (Primary Developer: MathWorks; Location: Natick, MA, USA) simulation platform. The plowing condition is selected as the simulation condition of the hybrid tractor. Under a standard 140 s plowing cycle, the following content is analyzed within this cycle. Before the simulation, the data are initialized, the parameters of the hybrid tractor and the measured condition information are imported into the system, and the step size of the simulation is set to 0.1 s. Additionally, the State of Charge (SOC) initial value is set to 0.9, the vehicle speed initial value is set to 7.2 km/h, and the plowing resistance initial value is set to 42,000 N.

Figure 9 represents the hybrid tractor plowing operation condition. In the plowing operation of the hybrid tractor (0–40 s, 50–90 s, and 100–140 s), the velocity is approximately between 6 and 8 km/h to ensure that the soil is fully tilled, and the plowing resistance is approximately between 38 and 45 kN. In the turn-around operation (40–50 s and 90–100 s), the velocity is gradually reduced to between 5 and 6 km/h, and the tractor does not carry out the plowing operation.

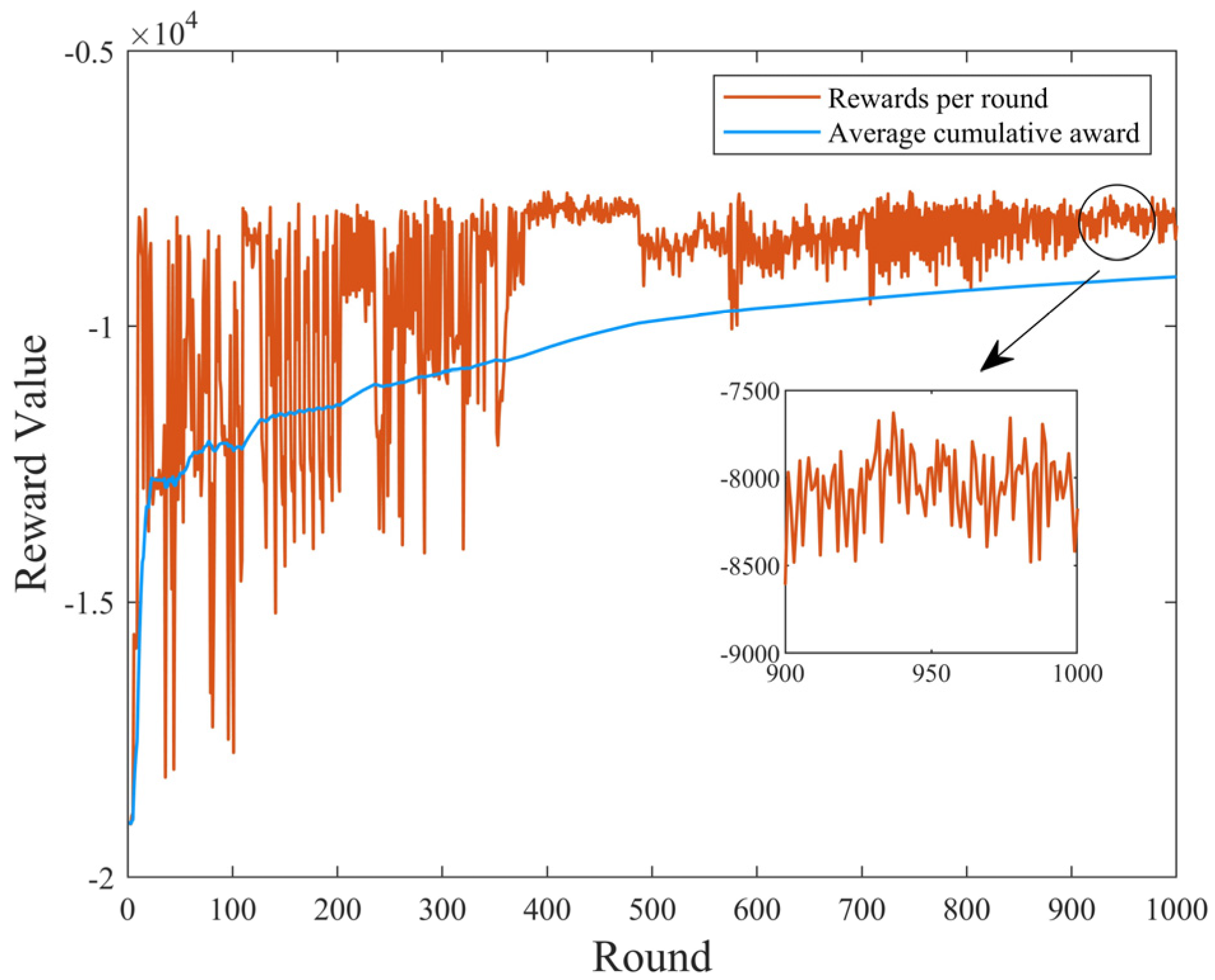
Figure 10 represents the training progress of DDPG agent for the hybrid tractor energy—saving strategy. Rewards per round expresses the cumulative weighted reward value of the round, while the average cumulative reward expresses the average reward value of all rounds for a certain amount of time. The training data shows that the training begins to converge after 400 rounds, and converges rapidly after 500–900 rounds with ups and downs. Rewards per round finally converges to around −8000. The training results show that the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control can achieve strategy convergence, and finally reach a steady state in the study of energy—saving control of hybrid tractor.

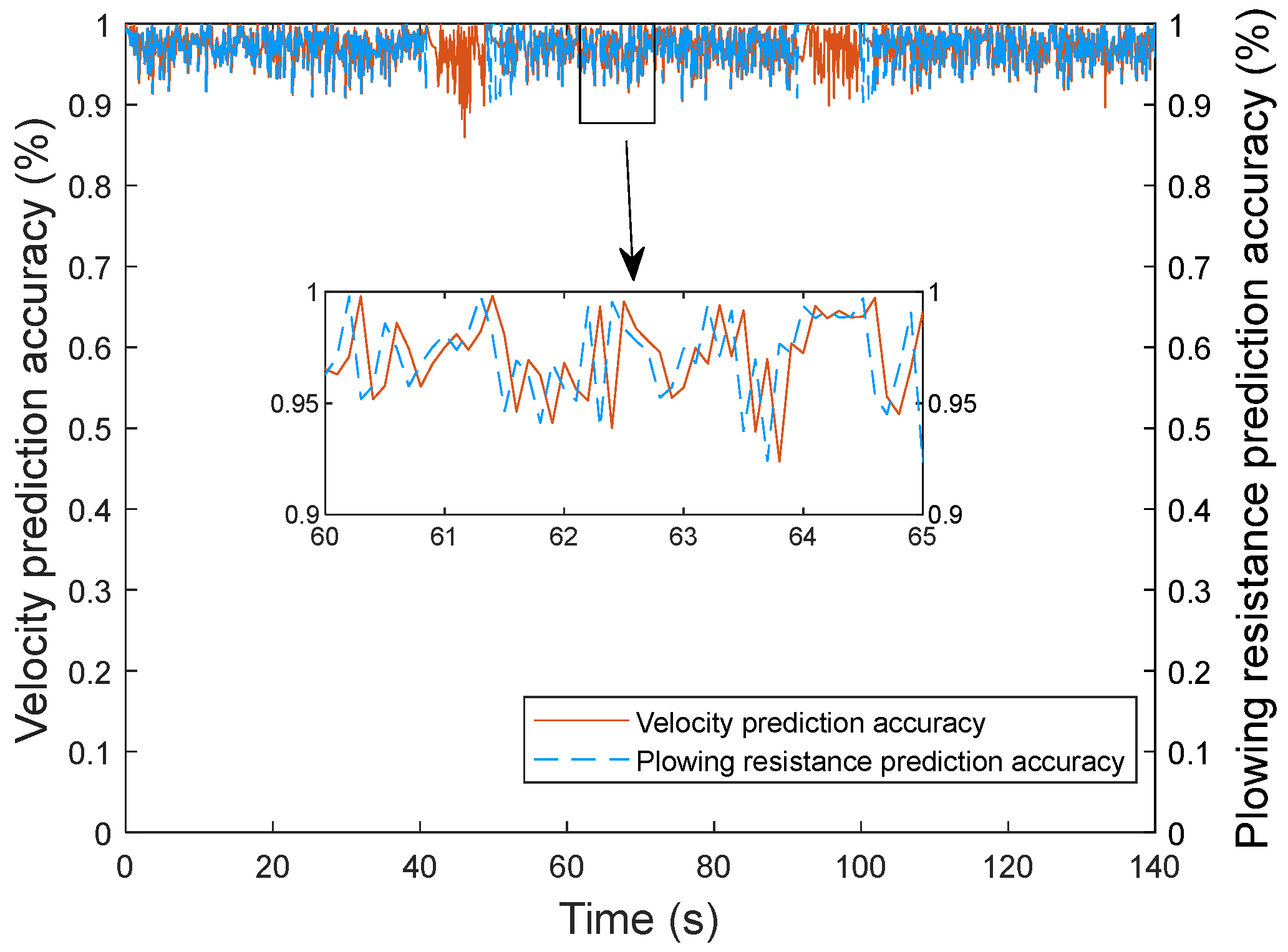
Figure 11 shows the prediction accuracy of the working condition prediction model based on the adaptive cubic exponential smoothing method. As can be seen from Figure 11, during the hybrid tractor plowing operation, the average value of plowing operation velocity prediction accuracy is about 97%, and the average value of plowing resistance prediction accuracy is about 96.8%. Additionally, the working condition prediction model has a high prediction accuracy of plowing operation velocity and resistance, which can effectively support the operation control process. However, when the hybrid tractor makes a U-turn, due to the gradual reduction in plowing operation velocity, the change amplitude is large, resulting in a significant decrease in the prediction accuracy of plowing operation velocity, which is due to the relatively poor prediction effect of the adaptive cubic exponential method on the linear mutation data. However, the error is within the permissible range.

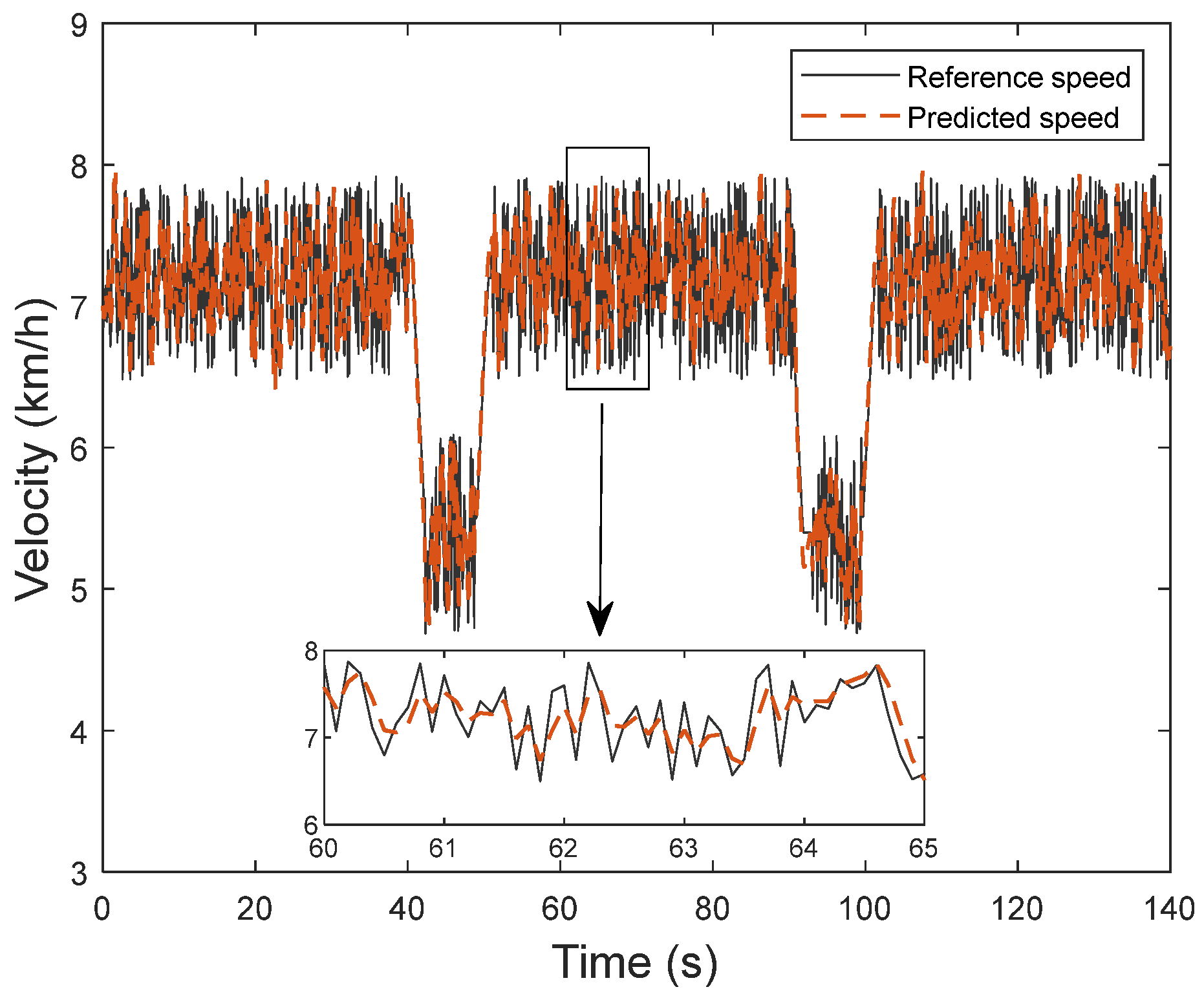
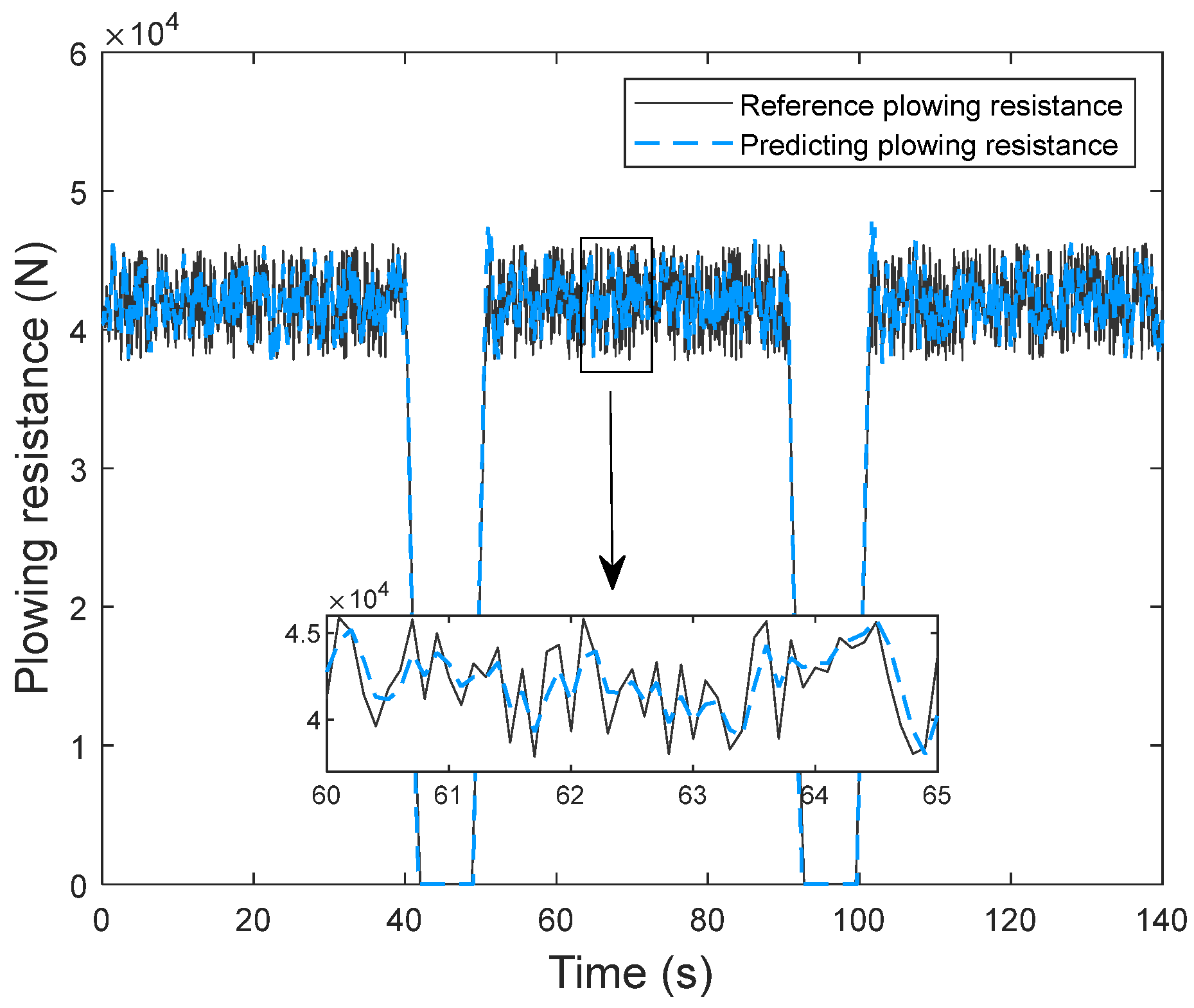
Figure 12 and Figure 13 show the comparison of plowing operation velocity and plowing resistance prediction results under the operating condition prediction model. Because the plowing operation velocity and plowing resistance varied greatly in the simulation time 60–65 s, this study conducted an independent analysis for this time period, and in this region, the maximum deviation of plowing operation velocity prediction was 0.23 km/h, the minimum deviation was less than 0.02 km/h, and the average value of the overall prediction accuracy was about 96.5%. The maximum deviation of plowing resistance prediction is 2500 N, the minimum deviation is less than 300 N, and the average value of the overall prediction accuracy is about 96.3%. It can be seen that although the overall prediction accuracy of the working condition prediction model in 60–65 s is slightly smaller than the average prediction accuracy, it can still maintain high prediction accuracy, which verifies the adaptability and effectiveness of the model in complex dynamic working conditions.

In order to verify the effectiveness of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control, the fuel economy analysis is conducted below. In addition, due to the large fluctuation of the whole diesel demand power in the simulation time 20–25 s, this study conducts an independent analysis for this time period.

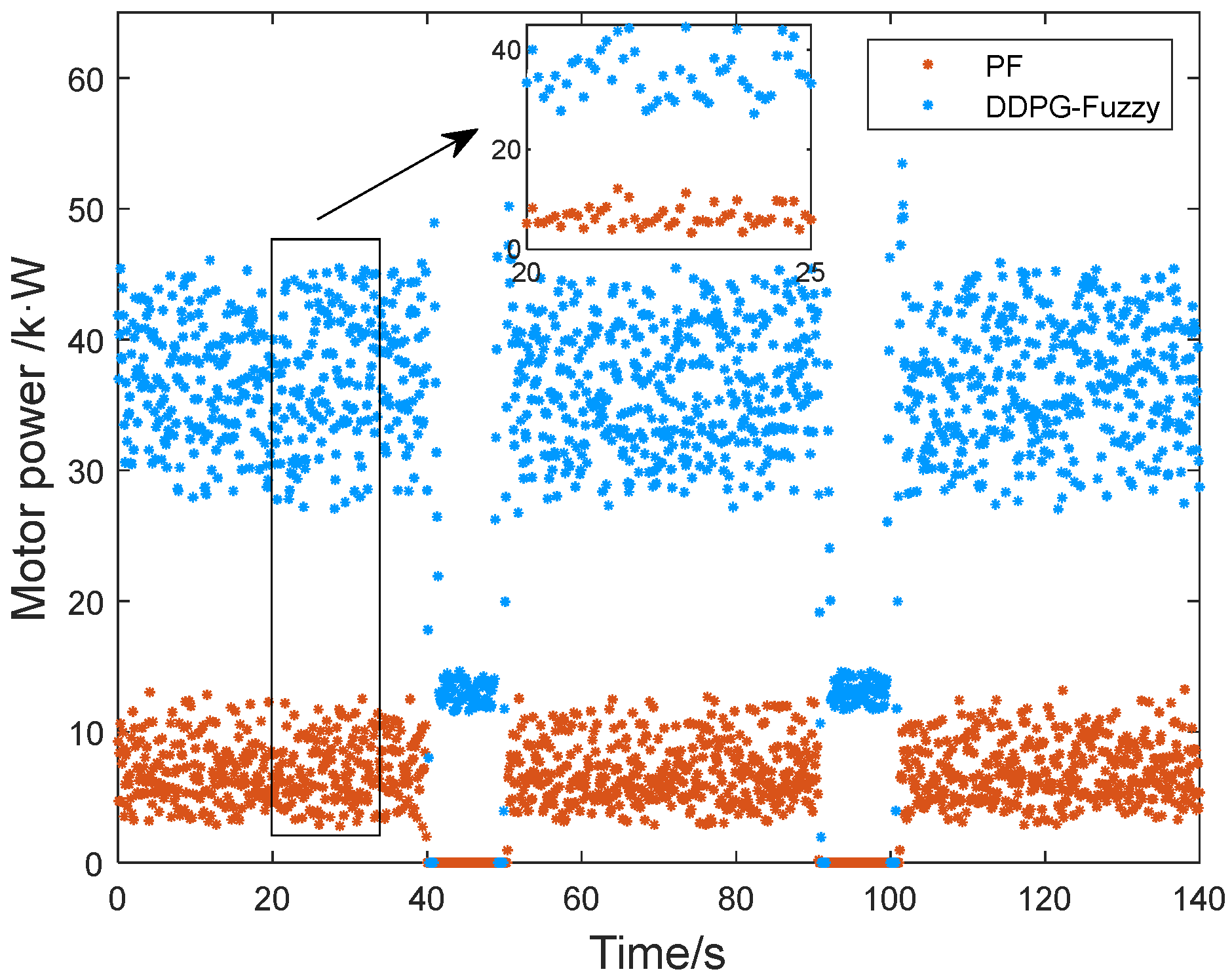
From Figure 14, Figure 15 and Figure 16, it can be seen that the power demand of the whole machine is around 120 kW during the plowing operations of the hybrid tractor. The energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control has a more concentrated diesel power of about 83–94 kW, and the motor power works at 30–45 kW, while the diesel power of the comparative strategy fluctuates greatly at about 100–118 kW, and the motor works only at 4–14 kW, which is not a reasonable distribution of power for the diesel and the motor. When turning around a hybrid tractor, the whole machine demand power is around 15 kW. With the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control, the diesel deactivates under low-load conditions, preventing fuel wastage, while the motor operates at around 15 kW. Meanwhile, the diesel works in the inefficient zone of around 15 kW in the comparative strategy and the motor does not work, which leads to a decrease in fuel economy.

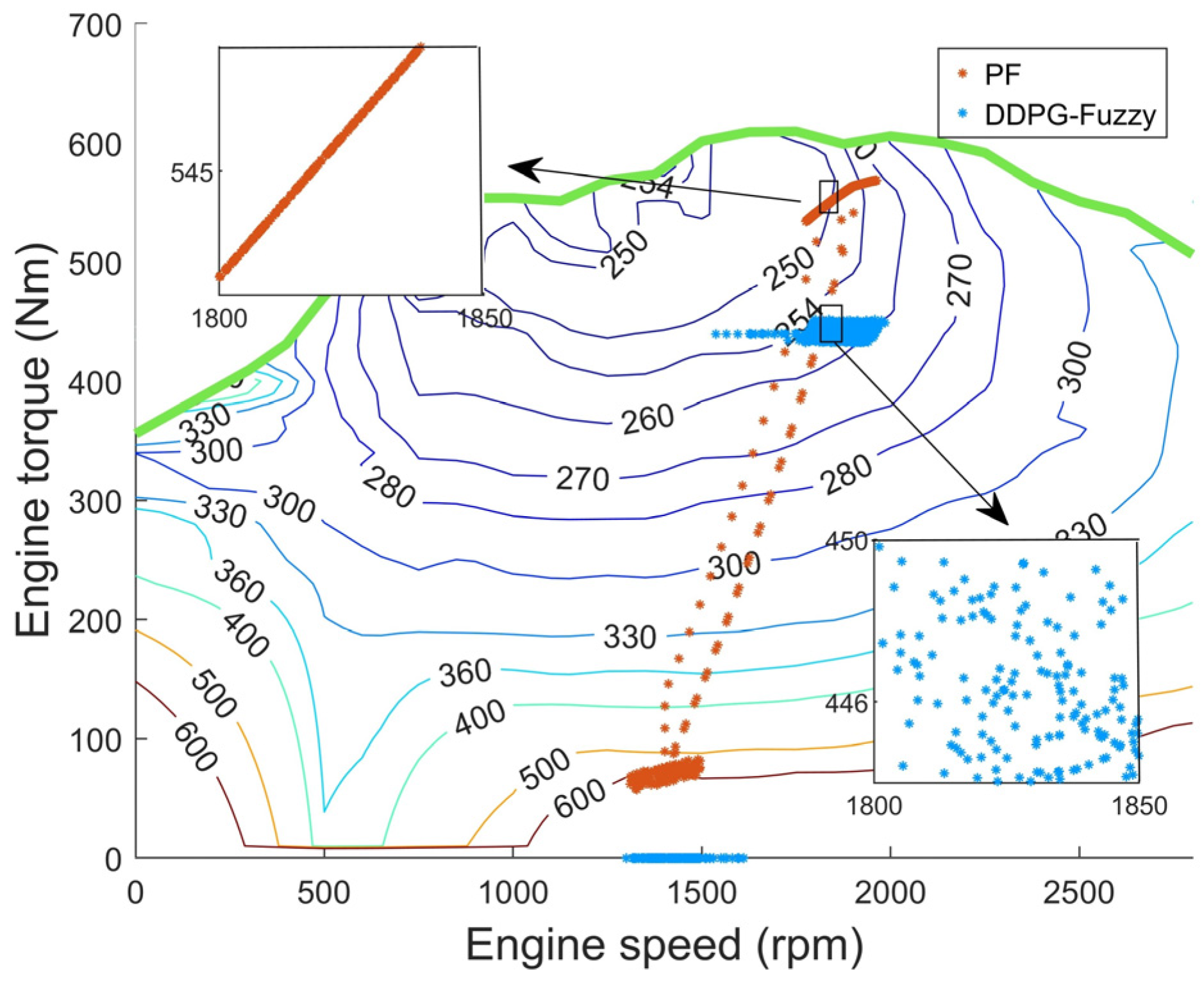
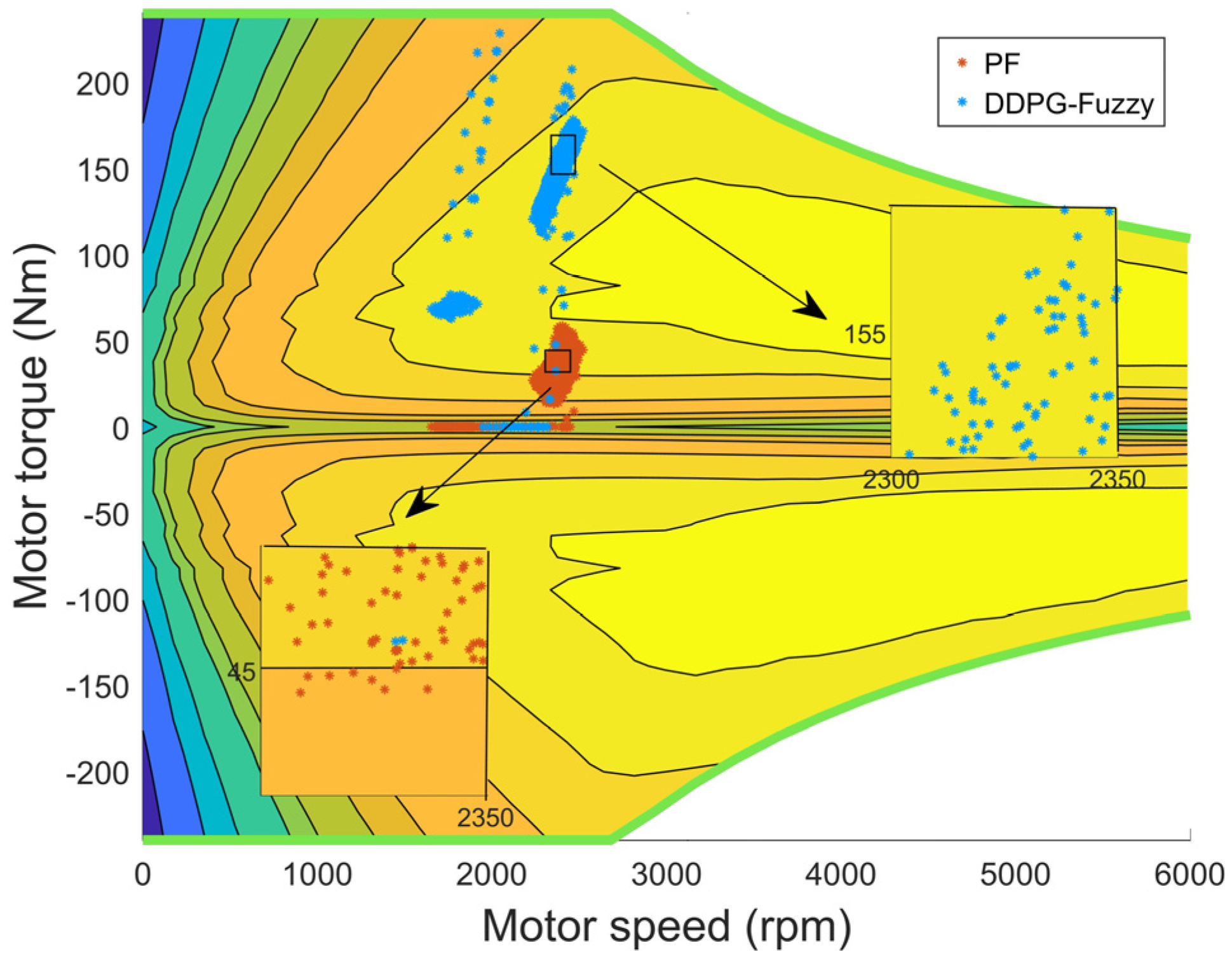
The working point diagrams of the diesel and the motor for the two control strategies under plowing operation conditions are shown in Figure 17 and Figure 18.

As can be seen from Figure 17 and Figure 18, during the hybrid tractor plowing operation, although the diesel operating points under both strategies are in the region of 250~260 g/(kW-h), the diesel torque of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control is smaller, while the motor operating points are concentrated in the high-efficiency region of 0.89~0.93. Meanwhile, the motor operating point of the comparison strategy is concentrated in the range of 0.86~0.90, which reflects that the proposed strategy in this study can effectively distribute the power of the diesel and the motor. In the hybrid tractor turnaround condition of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control, the diesel does not work, and the motor torque is concentrated in the high-efficiency region of 0.90~0.92, which gives full play to the advantages of the motor drive. In the contrasting strategy, the diesel working points are in the lower-efficiency region, and the motor does not work, which results in the irrational power distribution of the system.

Under the complex operating conditions in the simulation time period of 20–25 s, the average power of the diesel of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control is 86 kW, the average fuel consumption rate is 255 g/(kW∙h), the average power of the motor is 36 kW, and the average efficiency is 0.92; the average power of the diesel of the comparison strategy is 110.4 kW, the average fuel consumption rate is 252 g/(kW∙h), with an average motor power of 10.6 kW and an average efficiency of 0.88; the diesel of the comparison strategy has an average power of 110.4 kW and an average fuel consumption rate of 0.88. Although the fuel consumption rate of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control is higher than that of the comparison strategy, the diesel power is lower through the reasonable torque allocation, while the motor works in the high-efficiency zone. Meanwhile, the comparison strategy has irrational diesel torque allocation to the motor, which results in the motor working in the inefficient interval and the motor efficiency decreases. Comparison results show that the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control achieves better power distribution and improves fuel economy while hardly enhancing the fuel consumption rate.

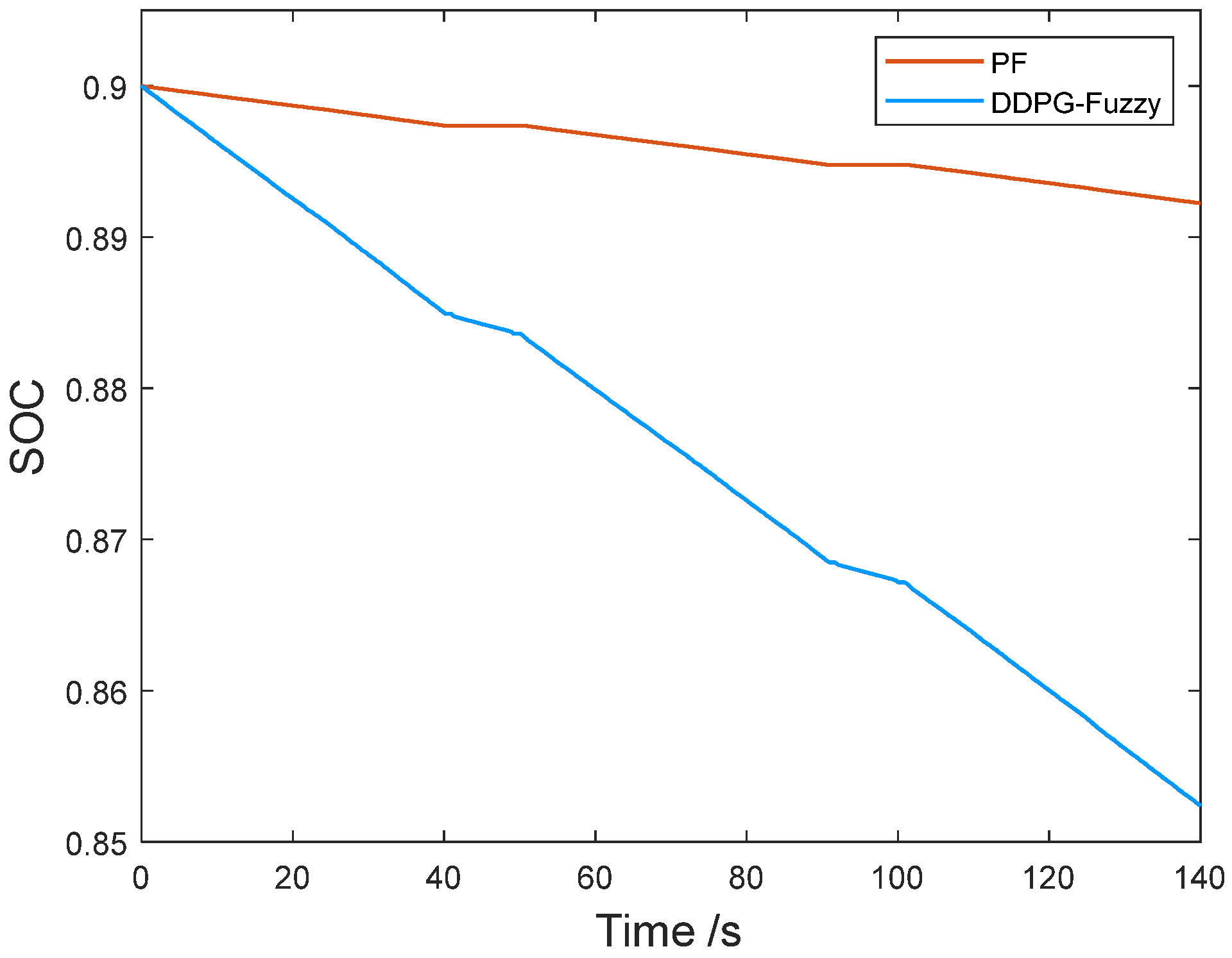
As can be seen from Figure 19, both control strategies maintain the State of Charge (SOC) of the power battery in a reasonable interval during the plowing operation and turnaround condition of the hybrid tractor; however, there is almost no significant decrease in the SOC of the comparison strategy, indicating that it fails to effectively utilize the advantages of the motor drive. Conversely, the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control maintains the SOC within a reasonable range while reducing it by 4.4%, thereby achieving an effective distribution of power between the diesel and the motor.

Figure 20 represents the comparison of equivalent fuel consumption under two control strategies for hybrid tractor plowing operations. As can be seen from the figure, the equivalent fuel consumption of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control is 1.061 L; the equivalent fuel consumption of the comparison strategy is 1.175 L. Compared with the comparison strategy, the equivalent fuel consumption of the energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control is reduced by 9.7%.

In summary, during the hybrid tractor plowing operation, the average value of the prediction accuracy of the working condition prediction model for plowing operation velocity is about 97%, and the average value of the prediction accuracy for plowing resistance is about 96.8% (as shown in

Table 3. Operating condition prediction results.

Index	Predictive Accuracy
Plowing operation velocity	97%
Plowing resistance	96.8%

), which is a high prediction accuracy. The energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control can optimize the power allocation between the diesel and the motor according to the plowing operation conditions, so that both of them always work in the high efficiency area, and the equivalent fuel consumption is reduced by 9.7%, and the SOC of the battery is reduced by 4.4% compared with the comparative strategy (as shown in

Table 4. Comparison of equivalent fuel consumption and SOC and average motor efficiency under different energy—saving strategies.

Control Strategy	The Equivalent Fuel Consumption	SOC	Average Motor Efficiency
DDPG-Fuzzy	1.061	0.8524	0.91
PF	1.175	0.8922	0.89

). In contrast, the power-following control strategy only distributes power based on preset rules, which cannot ensure that the diesel and motor work efficiently at the same time, and lacks the ability to adaptively regulate the plowing working conditions.

6. Conclusions

To greatly reduce fuel consumption and improve fuel economy of hybrid tractor under complex working conditions, this paper proposes an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control, and the results of the study show that the control strategy makes the diesel and the motor always work in the high-efficiency interval, which effectively reduces the energy consumption of the hybrid tractor in the process of plowing operation. The conclusions of this study are as follows:

(a)

Aiming at the problem of decreasing prediction accuracy and insufficient adaptability of plowing resistance and plowing operation velocity caused by the change in complex working conditions in the plowing operation of hybrid tractor, a working condition prediction model based on the adaptive cubic exponential smoothing method is constructed. Under a standard 140 s plowing cycle, the results show that the working condition prediction model achieves mean prediction accuracies of 97% in plowing velocity and 96.8% in plowing resistance, which can effectively track the expected value.

(b)

To significantly reduce fuel consumption and improve fuel economy in hybrid tractor under complex working conditions, this paper proposes an energy—saving strategy for hybrid tractor based on working condition prediction and DDPG-Fuzzy control. Under a standard 140 s plowing cycle, the results show that the proposed strategy in this study reduces the equivalent fuel consumption by 9.7% under the plowing condition than the power-following strategy, and reduces the SOC by 4.4% while ensuring that the SOC is at a reasonable range. In addition, it can optimize the power distribution between the diesel and the motor according to the working conditions, and improve the energy utilization of the whole machine.

The energy—saving control strategy for hybrid tractor proposed in this study is mainly designed for plowing conditions, and although the fuel economy is improved by this strategy, there are three limitations: Firstly, it does not take into account the differences in the conditions of rotary plowing, planting and other multi-operating scenarios. Specifically, the strategy can be extended to these scenarios by retraining or fine-tuning the DDPG model with task-specific driving data (e.g., torque demand patterns, speed profiles, and energy flow variations under transport or rotary tillage conditions) to align the reward function with the unique operational objectives of each task. Secondly, it only takes fuel economy as a single optimization objective, and does not take into account the multi-objective optimization such as the battery life degradation. Thirdly, this study validated its static and dynamic characteristics based on a high-precision simulation platform (such as MATLAB 2024b (Primary Developer: MathWorks; Location: Natick, MA, USA)), but due to seasonal constraints on field trials and prototype development cycles, real-vehicle testing has not yet been conducted. This limitation will be supplemented by subsequent research through collaborative testing sites to further evaluate the reliability of the model in real working environments. Therefore, follow-up research will conduct systematic analyses under various operating conditions, combine field test data, and use multi-objective optimization algorithms to jointly optimize key indicators of fuel economy and battery life.