Electrify the Field: Designing and Optimizing Electric Tractor Drivetrains with Real-World Cycles
Abstract
1. Introduction
2. State of the Art
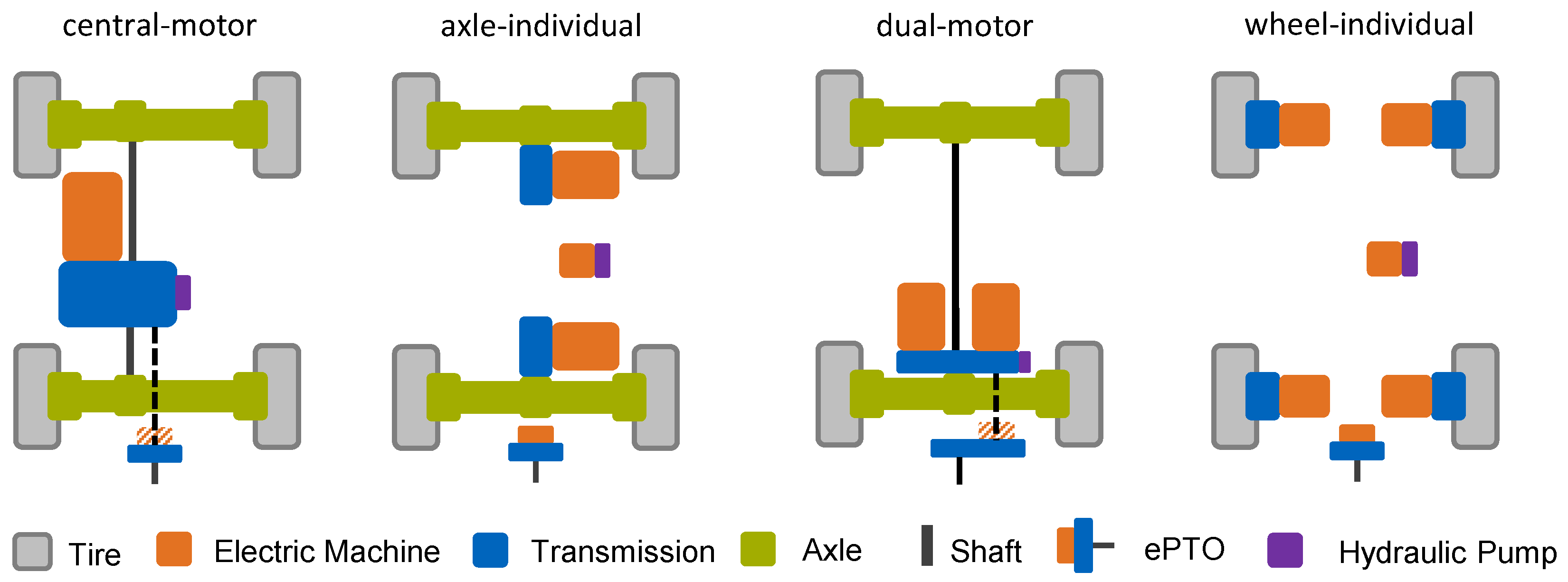
2.1. Drivetrain Topology
2.2. Optimization of Drivetrains
- (i)
- Integrate real-world load cycles across various operations suitable to electric tractors to enable comparisons, performance benchmarking and applicability for farmers.
- (ii)
- Develop a system-level design strategy that considers the interdependencies between load, topology, and drivetrain components to ensure that the entire system achieves optimal efficiency and performance.
- (iii)
- Execute longitudinal dynamic simulations to quantify energy consumption and efficiency on each mission profile.
3. Materials and Methods
3.1. Application of Real-World Cycles
- SPN 190, “engine speed”, which reports the rotational speed of the engine’s crankshaft, denoted as .
- SPN 544, “engine reference torque,” which reports the maximum torque the engine can deliver under its current conditions, denoted as .
- SPN 513, “actual engine percent torque”, which reports the engine’s current torque as a percentage of the reference torque (SPN 544), denoted as .
- ISOBUS 1859, “ground-based machine speed”, which reports the tractor’s speed over the ground as measured by a sensor such as radar or GPS, representing its true forward velocity without the influence of wheel slip, denoted as and in the simulation as .
- ISOBUS 1879, “rear draft”, which reports the apparent horizontal force applied to the rear hitch by the implement, denoted as .
- ISOBUS 1862, “wheel-based machine speed”, which reports the speed of a machine as calculated from the measured wheel or tail-shaft speed, denoted as .
- ISOBUS 1860, “ground-based machine distance”, which reports the distance travelled.
- SPN 1883, “rear PTO output shaft speed”, which reports the rotational speed of the rear power take-off (PTO) shaft, denoted as .
- ISOBUS 1877, “rear hitch in-work indication”, indicating if the rear hitch is in work position.
- SPN 580, “altitude”, which reports the tractor’s current altitude above sea level, typically measured using GPS.
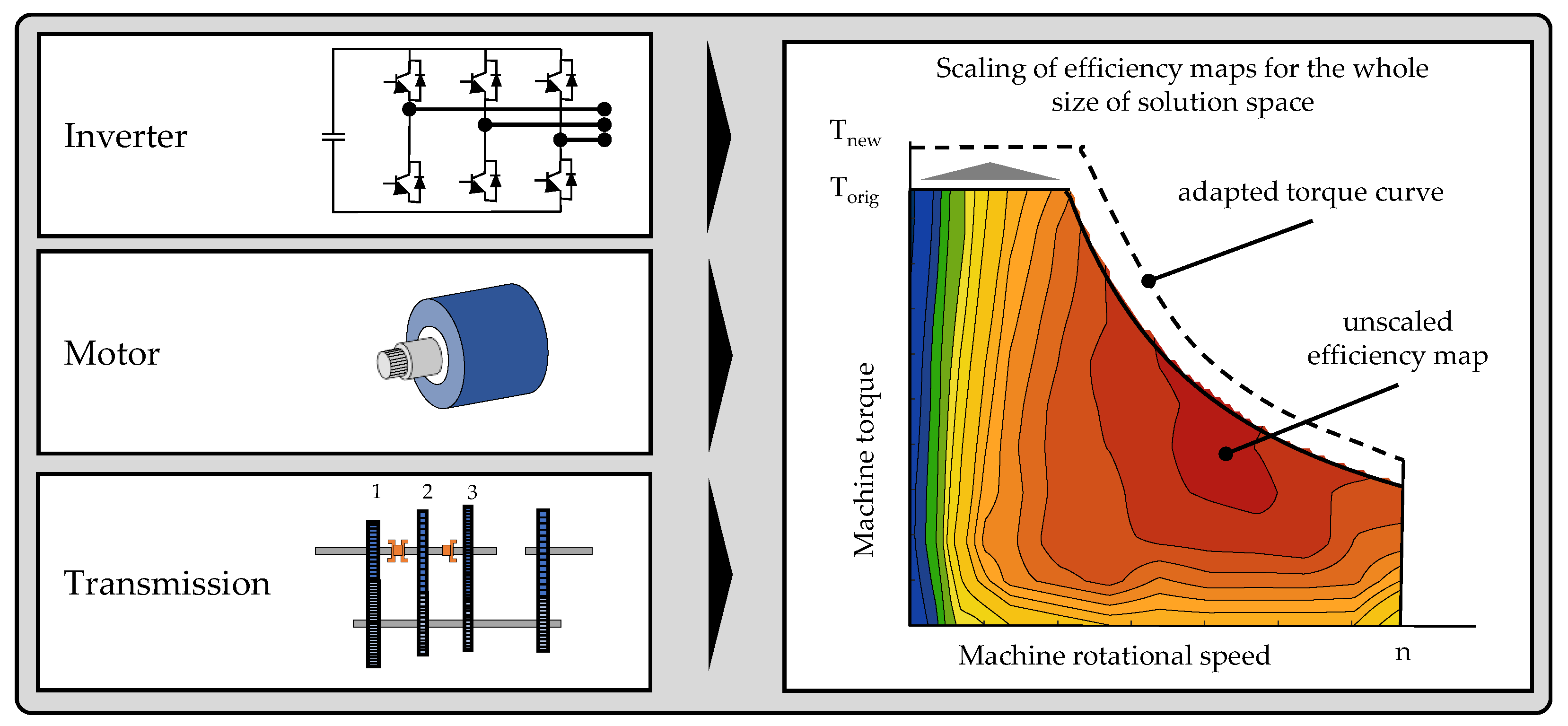
3.2. Drivetrain Solution Space
3.3. Optimization
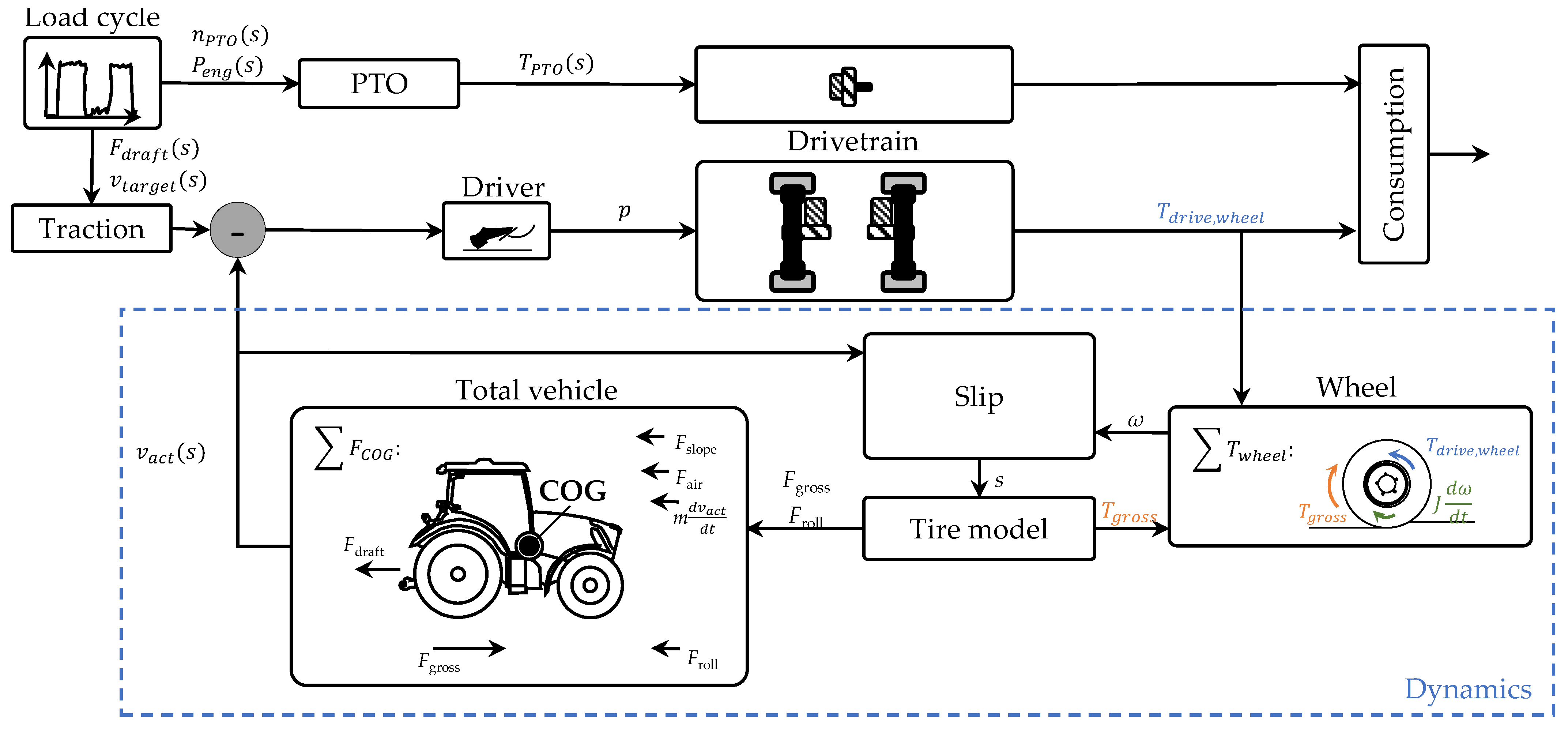
3.4. Forward Longitudinal Simulation
3.4.1. Driver and Drivetrain
3.4.2. Dynamics
3.4.3. Power Take-Off (PTO)
4. Results
4.1. Working Cycle Characteristics
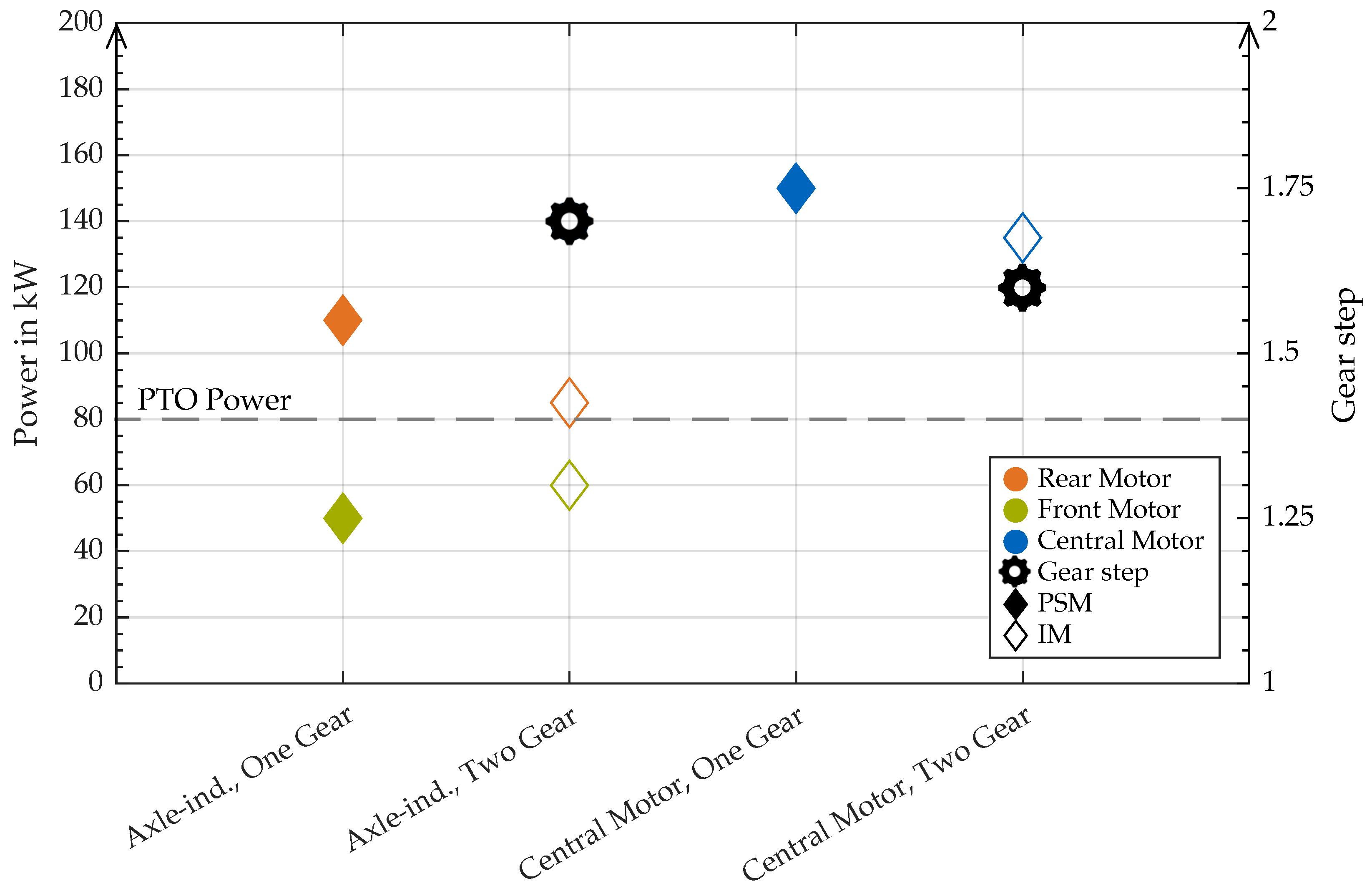
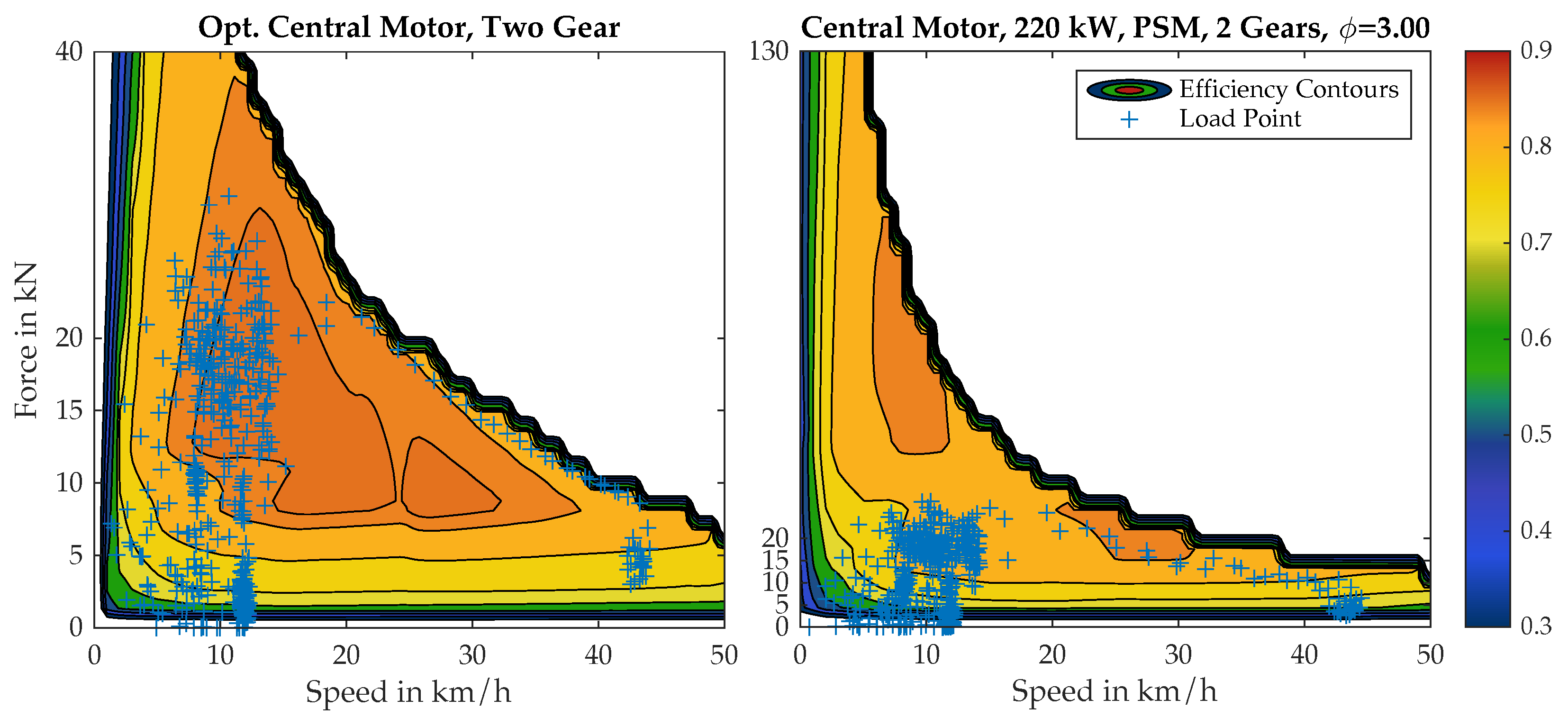
4.2. Optimized Drivetrain
4.3. Productivity of Optimized Drivetrain
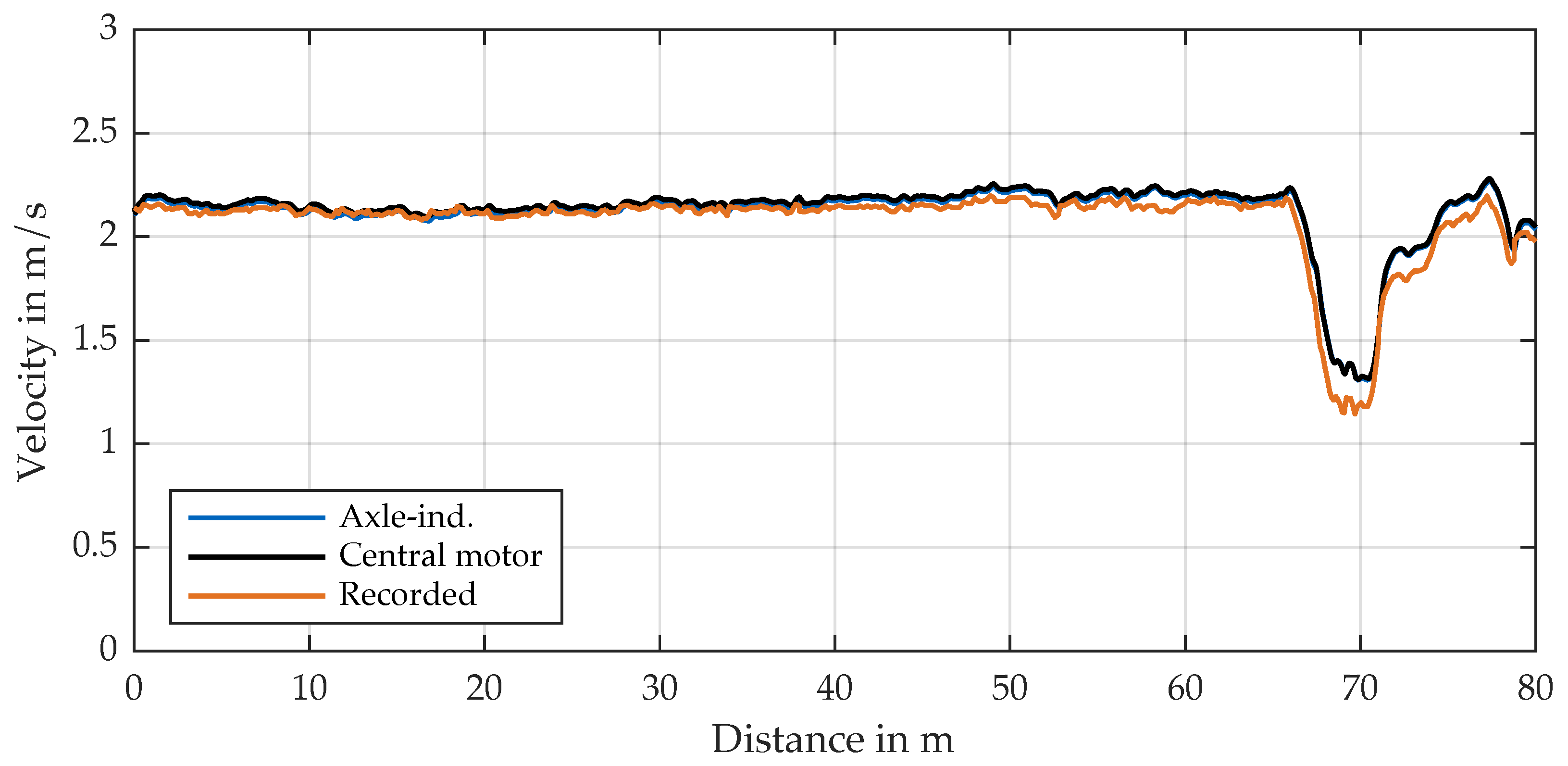
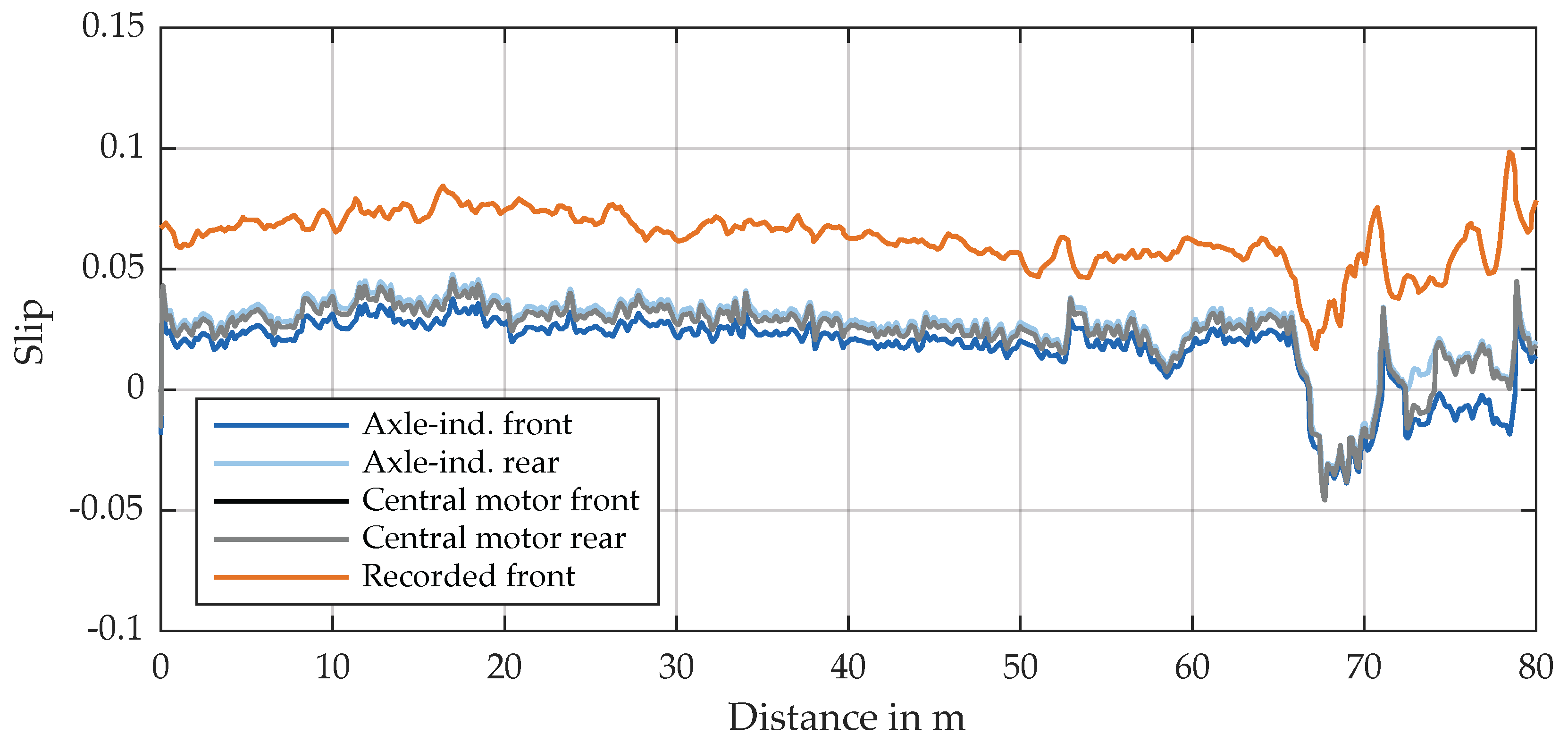
4.4. Potential and Plausibility of the Design Method
5. Discussion
5.1. Performance of Optimized Topology
5.2. Limitations of the Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PTO | power take-off |
| PSM | permanent synchronous magnetic motor |
| IM | induction motor |
| ASABE | American Society of Agricultural and Biological Engineers |
| SAE | Society of Automotive Engineers |
| PSO | particle swarm optimization |
| CI | cone index |
| ED | energy demand |
Appendix A
| Symbol | Parameter | Category | Value |
|---|---|---|---|
| m | mass of tractor | vehicle | 6380 kg |
| nominal mass on front axle | vehicle | 2320 kg | |
| nominal weight on rear axle | vehicle | 4060 kg | |
| wheelbase | vehicle | 2.42 m | |
| RW distance to COG | vehicle | m | |
| FW distance to COG | vehicle | m | |
| height of COG | vehicle | 0.5 m | |
| height of force attack | vehicle | 0.5 m | |
| FW lead | vehicle | 0% | |
| b | tire width unloaded | rear tire 650/60 R38 | 677 mm |
| front tire 540/65 R24 | 532 mm | ||
| d | tire diameter unloaded | rear tire 650/60 R38 | 1735 mm |
| front tire 540/65 R24 | 1312 mm | ||
| vertical tire deflection under load | rear tire 650/60 R38 | 118.5 mm | |
| front tire 540/65 R24 | 83.0 mm | ||
| h | tire section height | rear tire 650/60 R38 | 406.2 mm |
| front tire 540/65 R24 | 345.8 mm | ||
| tire weight | rear tire 650/60 R38 | 266 kg | |
| front tire 540/65 R24 | 171 kg | ||
| Drivetrain efficiency | recorded tractor | 0.85 | |
| PTO efficiency | recorded tractor | 0.95 | |
| drag coefficient | drag force | 0.9 [55] | |
| air density | drag force | 1.2 kg/m3 | |
| A | frontal area | drag force | 5.6 m2 |
| gradient from load cycle | slope force | - |
| Implement | Width | Mass | Rolling Resistance Coef. |
|---|---|---|---|
| Disc Harrow | 3 m | - | - |
| Fertilizer | 25 m | - | - |
| Seeder | 3 m | - | - |
| Mower | 8.3 m | - | - |
| Trailer | - | 10.6 t | 0.1 |
| Symbol | Parameter | Value |
|---|---|---|
| efficiency differential | 0.97 | |
| efficiency final drive | 0.98 | |
| efficiency transfer case | 0.96 | |
| ratio differential | 4 | |
| ratio final drive | 7 | |
| ratio transfer case |
| Parameter | Value |
|---|---|
| Swarm Size | 200 |
| Max. Iterations | 20 |
| Inertia Range | [0.7, 1.1] |
| Social Adjustment Weight | 0.2 |
| Self Adjustment Weight | 0.5 |
| Function Tolerance | 1 |
| Parameter | Value |
|---|---|
| Solver | Runge-Kutta |
| Time step | 0.001 |
| minimum velocity | 0.1 m s−1 |
| max. velocity gear one | 15 km h−1 |
| Avg. Throttle Position in % | Axle-Ind., One Gear | Axle-Ind., Two Gear | Central Motor, One Gear | Central Motor, Two Gear |
|---|---|---|---|---|
| Disc Harrow | 66.07 | 56.46 | 65.87 | 49.36 |
| Fertilizing | 14.67 | 13.18 | 14.78 | 11.97 |
| Mowing | 12.19 | 10.12 | 11.97 | 9.24 |
| Seeding | 33.99 | 27.46 | 34.38 | 24.83 |
| Transport | 64.39 | 66.64 | 63.86 | 66.91 |
References
- Maja, M.M.; Ayano, S.F. The Impact of Population Growth on Natural Resources and Farmers’ Capacity to Adapt to Climate Change in Low-Income Countries. Earth Syst. Environ. 2021, 5, 271–283. [Google Scholar] [CrossRef]
- Statista. India—Diesel Consumption Volume in Agriculture Industry 2020; Statista: Munich, Germany, 2020. [Google Scholar]
- Olkkonen, V.; Lind, A.; Rosenberg, E.; Kvalbein, L. Electrification of the agricultural sector in Norway in an effort to phase out fossil fuel consumption. Energy 2023, 276, 127543. [Google Scholar] [CrossRef]
- Mrema, G.C.; Kienzle, J.; Rome, J.J. Current Status and Future Prospects of Agricultural Mechanization in Sub-Saharan Africa [SSA]. AMA Agric. Mech. Asia Afr. Lat. Am. 2018, 49, 13–30. [Google Scholar]
- Lagnelöv, O.; Dhillon, S.; Larsson, G.; Nilsson, D.; Larsolle, A.; Hansson, P.A. Cost analysis of autonomous battery electric field tractors in agriculture. Biosyst. Eng. 2021, 204, 358–376. [Google Scholar] [CrossRef]
- Beligoj, M.; Scolaro, E.; Alberti, L.; Renzi, M.; Mattetti, M. Feasibility Evaluation of Hybrid Electric Agricultural Tractors Based on Life Cycle Cost Analysis. IEEE Access 2022, 10, 28853–28867. [Google Scholar] [CrossRef]
- Kivekäs, K.; Lajunen, A. Effect of Soil Properties and Powertrain Configuration on the Energy Consumption of Wheeled Electric Agricultural Robots. Energies 2024, 17, 966. [Google Scholar] [CrossRef]
- Beltrami, D.; Iora, P.; Tribioli, L.; Uberti, S. Electrification of Compact Off-Highway Vehicles—Overview of the Current State of the Art and Trends. Energies 2021, 14, 5565. [Google Scholar] [CrossRef]
- Graeub, B.E.; Chappell, M.J.; Wittman, H.; Ledermann, S.; Kerr, R.B.; Gemmill-Herren, B. The State of Family Farms in the World. World Dev. 2016, 87, 1–15. [Google Scholar] [CrossRef]
- AGCO Fendt. Fendt e100 Vario—Der E-Standardtraktor. 2025. Available online: https://www.fendt.com/de/landmaschinen/e-traktoren/fendt-e100vario (accessed on 17 February 2025).
- Böhrnsen, A. Neuer 100-kW-Elektro-Traktor von Tadus. Profi Online. 29 September 2023. Available online: https://www.profi.de/aktuell/aktuelle-meldungen/neuer-100-kw-elektro-traktor-von-tadus-31143.html (accessed on 17 February 2025).
- Rigitrac Traktorenbau. Rigitrac SKE 40 Electric. 2023. Available online: https://www.rigitrac.ch/produkte-1/rigitrac-ske-40-electric/ (accessed on 17 February 2025).
- Monarch Tractor. World’s First Electric Autonomous Tractor | Monarch Tractor. 2025. Available online: https://www.monarchtractor.com/ (accessed on 17 February 2025).
- Deere & Company. John Deere Stellt Neue Autonome Maschinen und Technologien auf der CES 2025. 2025. Available online: https://www.deere.de/de/unser-unternehmen/news-und-medien/pressemeldungen/2025/john-deere-stellt-neue-autonome-maschinen-und-technologien-auf-der-ces-2025-vor.html (accessed on 17 February 2025).
- Götz, K.; Pizzinini, C.; Strauss, J.; Tennakoon, S.; Menelaos, M.; Booysen, T.; Lienkamp, M. Conception of an electric tractor for farming in sub-Saharan Africa. In Proceedings of the 7th E-Mobility Power System Integration Symposium (EMOB 2023), Copenhagen, Denmark, 25 September 2023; pp. 221–227. [Google Scholar] [CrossRef]
- Serrao, L. Driving the electric transformation—The evolution of off-highway powertrain. In Powertrain Systems in Mobile Machines 2022; VDI Verlag: Ludwigsburg, Germany, 2022; pp. 135–150. [Google Scholar] [CrossRef]
- Felden, M.; Butterling, P.; Jeck, P.; Eckstein, L.; Hameyer, K. Electric vehicle drive trains: From the specification sheet to the drive-train concept. In Proceedings of the 2010 14th International Power Electronics and Motion Control Conference (EPE/PEMC 2010), Ohrid, Macedonia, 6–8 September 2010. [Google Scholar] [CrossRef]
- Pesce, T.; Lienkamp, M. Definition And Optimization of the Drive Train Topology for Electric Vehicles. World Electr. Veh. J. 2012, 5, 24–35. [Google Scholar] [CrossRef]
- Baek, S.Y.; Kim, Y.S.; Kim, W.S.; Baek, S.M.; Kim, Y.J. Development and Verification of a Simulation Model for 120 kW Class Electric AWD (All-Wheel-Drive) Tractor during Driving Operation. Energies 2020, 13, 2422. [Google Scholar] [CrossRef]
- Baek, S.Y.; Baek, S.M.; Jeon, H.H.; Kim, W.S.; Kim, Y.S.; Sim, T.Y.; Choi, K.H.; Hong, S.J.; Kim, H.; Kim, Y.J. Traction Performance Evaluation of the Electric All-Wheel-Drive Tractor. Sensors 2022, 22, 785. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.; Lu, Z. A Novel 10-Parameter Motor Efficiency Model Based on I-SA and Its Comparative Application of Energy Utilization Efficiency in Different Driving Modes for Electric Tractor. Agriculture 2022, 12, 362. [Google Scholar] [CrossRef]
- Li, T.; Xie, B.; Li, Z.; Li, J. Design and Optimization of a Dual-Input Coupling Powertrain System: A Case Study for Electric Tractors. Appl. Sci. 2020, 10, 1608. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, B.; Du, Y.; Mao, E. Powertrain parameter matching and optimal design of dual-motor driven electric tractor. Int. J. Agric. Biol. Eng. 2019, 12, 33–41. [Google Scholar] [CrossRef]
- van Dingenen, J.; Faggiani, G.; Serrao, L. Evolution of transmission technology for electric off-highway machines. In Powertrain Systems in Mobile Machines 2024; VDI-Berichte, VDI Verlag GmbH: Düsseldorf, Germany, 2024; pp. 79–94. [Google Scholar] [CrossRef]
- Machado, F.; Kollmeyer, P.; Barroso, D.; Emadi, A. Multi-Speed Gearboxes for Battery Electric Vehicles: Current Status and Future Trends. IEEE Open J. Veh. Technol. 2021, 2, 419–435. [Google Scholar] [CrossRef]
- Kampker, A.; Heimes, H.H.; Schmitt, F.; Backes, T.; Betz, M.; Hadzovic, T. Design of an Electric Drive Axle for Heavy Duty Commercial Vehicles in the Long-Haul Application Under Consideration of Energy Consumption. In Proceedings of the 2022 12th International Electric Drives Production Conference (EDPC), Regensburg, Germany, 29–30 November 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Gözen, E.; Çevirgen, M.S.; Özgül, E. Transmission speed and ratio optimization for heavy-duty electric truck. Heliyon 2022, 8, e10028. [Google Scholar] [CrossRef] [PubMed]
- Domingues-Olavarria, G.; Marquez-Fernandez, F.J.; Fyhr, P.; Reinap, A.; Andersson, M.; Alakula, M. Optimization of Electric Powertrains Based on Scalable Cost and Performance Models. IEEE Trans. Ind. Appl. 2019, 55, 751–764. [Google Scholar] [CrossRef]
- Eghtessad, M.; Meier, T.; Rinderknecht, S.; Küçükay, F. Antriebsstrangoptimierung von Elektrofahrzeugen. ATZ—Automob. Z. 2015, 117, 78–85. [Google Scholar] [CrossRef]
- Schönknecht, A.; Babik, A.; Rill, V. Electric Powertrain System Design of BEV and HEV Applying a Multi Objective Optimization Methodology. Transp. Res. Procedia 2016, 14, 3611–3620. [Google Scholar] [CrossRef]
- Verbruggen, F.J.R.; Silvas, E.; Hofman, T. Electric Powertrain Topology Analysis and Design for Heavy-Duty Trucks. Energies 2020, 13, 2434. [Google Scholar] [CrossRef]
- Fries, M.; Lehmeyer, M.; Lienkamp, M. Multi-criterion optimization of heavy-duty powertrain design for the evaluation of transport efficiency and costs. In Proceedings of the IEEE ITSC 2017, Yokohama, Japan, 16–19 October 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, B.; Xu, M.; Yang, L. Study on the economic and environmental benefits of different EV powertrain topologies. Energy Convers. Manag. 2014, 86, 916–926. [Google Scholar] [CrossRef]
- Lajunen, A. Comparison of Different Powertrain Configurations for Electric City Bus. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Pathak, A.; Sethuraman, G.; Krapf, S.; Ongel, A.; Lienkamp, M. Exploration of Optimal Powertrain Design Using Realistic Load Profiles. World Electr. Veh. J. 2019, 10, 56. [Google Scholar] [CrossRef]
- Götz, K.; Kusuma, A.; Dörfler, A.; Lienkamp, M. Agricultural load cycles: Tractor mission profiles from recorded GNSS and CAN bus data. Data Brief 2025, 60, 111494. [Google Scholar] [CrossRef] [PubMed]
- Lajunen, A.; Kivekäs, K.; Freyermuth, V.; Vijayagopal, R.; Kim, N. Simulation of Alternative Powertrains in Agricultural Tractors. In Proceedings of the 36th International Electric Vehicle Symposium and Exhibition (EVS36), Sacramento, CA, USA, 11–14 June 2023; pp. 1–11. [Google Scholar]
- Regazzi, N.; Maraldi, M.; Molari, G. A theoretical study of the parameters affecting the power delivery efficiency of an agricultural tractor. Biosyst. Eng. 2019, 186, 214–227. [Google Scholar] [CrossRef]
- Lajunen, A. Simulation of energy efficiency and performance of electrified powertrains in agricultural tractors. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference (VPPC), Merced, CA, USA, 1–4 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Lagnelöv, O.; Larsson, G.; Nilsson, D.; Larsolle, A.; Hansson, P.A. Performance comparison of charging systems for autonomous electric field tractors using dynamic simulation. Biosyst. Eng. 2020, 194, 121–137. [Google Scholar] [CrossRef]
- American Society of Agricultural and Biological Engineers. Agricultural Machinery Management Data; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2011; p. 1. [Google Scholar] [CrossRef]
- Renius, K.T. Fundamentals of Tractor Design; Springer: Cham, Germany, 2020. [Google Scholar]
- Götz, K. Agricultural Load Cycles: Tractor Mission Profiles From Recorded Gnss and Can Bus Data. Zenodo 2025. [Google Scholar] [CrossRef]
- Chang, F.; Ilina, O.; Hegazi, O.; Voss, L.; Lienkamp, M. Adopting MOSFET multilevel inverters to improve the partial load efficiency of electric vehicles. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.13. [Google Scholar] [CrossRef]
- Wassiliadis, N.; Steinsträter, M.; Schreiber, M.; Rosner, P.; Nicoletti, L.; Schmid, F.; Ank, M.; Teichert, O.; Wildfeuer, L.; Schneider, J.; et al. Quantifying the state of the art of electric powertrains in battery electric vehicles: Range, efficiency, and lifetime from component to system level of the Volkswagen ID.3. eTransportation 2022, 12, 100167. [Google Scholar] [CrossRef]
- Goss, J. Performance Analysis of Electric Motor Technologies for an Electric Vehicle Powertrain. 2019. Available online: https://www.semanticscholar.org/paper/Performance-Analysis-of-Electric-Motor-Technologies/c547b9dc18ae70ab987c3903796b5d958c7e9840 (accessed on 9 August 2025).
- Luque, P.; Mántaras, D.A.; Roces, J.; Castejón, L.; Malón, H.; Valladares, D. Optimization of the powertrain of electric vehicles for a given route. Transp. Res. Procedia 2021, 58, 246–253. [Google Scholar] [CrossRef]
- Hegazy, O.; van Mierlo, J. Particle Swarm Optimization for optimal powertrain component sizing and design of fuel cell hybrid electric vehicle. In Proceedings of the 2010 12th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 20–22 May 2010; pp. 601–609. [Google Scholar] [CrossRef]
- Zoz, F.; Grisso, R. Traction and tractor performance. In SAE Distinguished Lecture # 27, Agricultural; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- MacAdam, C.C. An Optimal Preview Control for Linear Systems. J. Dyn. Syst. Meas. Control 1980, 102, 188–190. [Google Scholar] [CrossRef]
- Brixius, W.W. Traction Prediction Equations for Bias Ply Tires. In ASAE Paper 87-1622; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1987; p. 8. [Google Scholar]
- Mattetti, M.; Annesi, G.; Intrevado, F.P.; Alberti, L. Investigating the efficiency of hybrid architectures for agricultural tractors using real-world farming data. Appl. Energy 2025, 377, 124499. [Google Scholar] [CrossRef]
- Saetti, M.; Mattetti, M.; Varani, M.; Lenzini, N.; Molari, G. On the power demands of accessories on an agricultural tractor. Biosyst. Eng. 2021, 206, 109–122. [Google Scholar] [CrossRef]
- Angelucci, L.; Varani, M.; Pinet, F.; Martin, V.; Vertua, A.; Molari, G.; Mattetti, M. The role of tyres and soil conditions in enhancing the efficiency of agricultural tractors. Soil Tillage Res. 2025, 251, 106570. [Google Scholar] [CrossRef]
- Reif, K.; Dietsche, K.H. Bosch Automotive Handbook, 9th ed.; John Wiley & Sons Ltd.: New York, NY, USA, 2014. [Google Scholar]

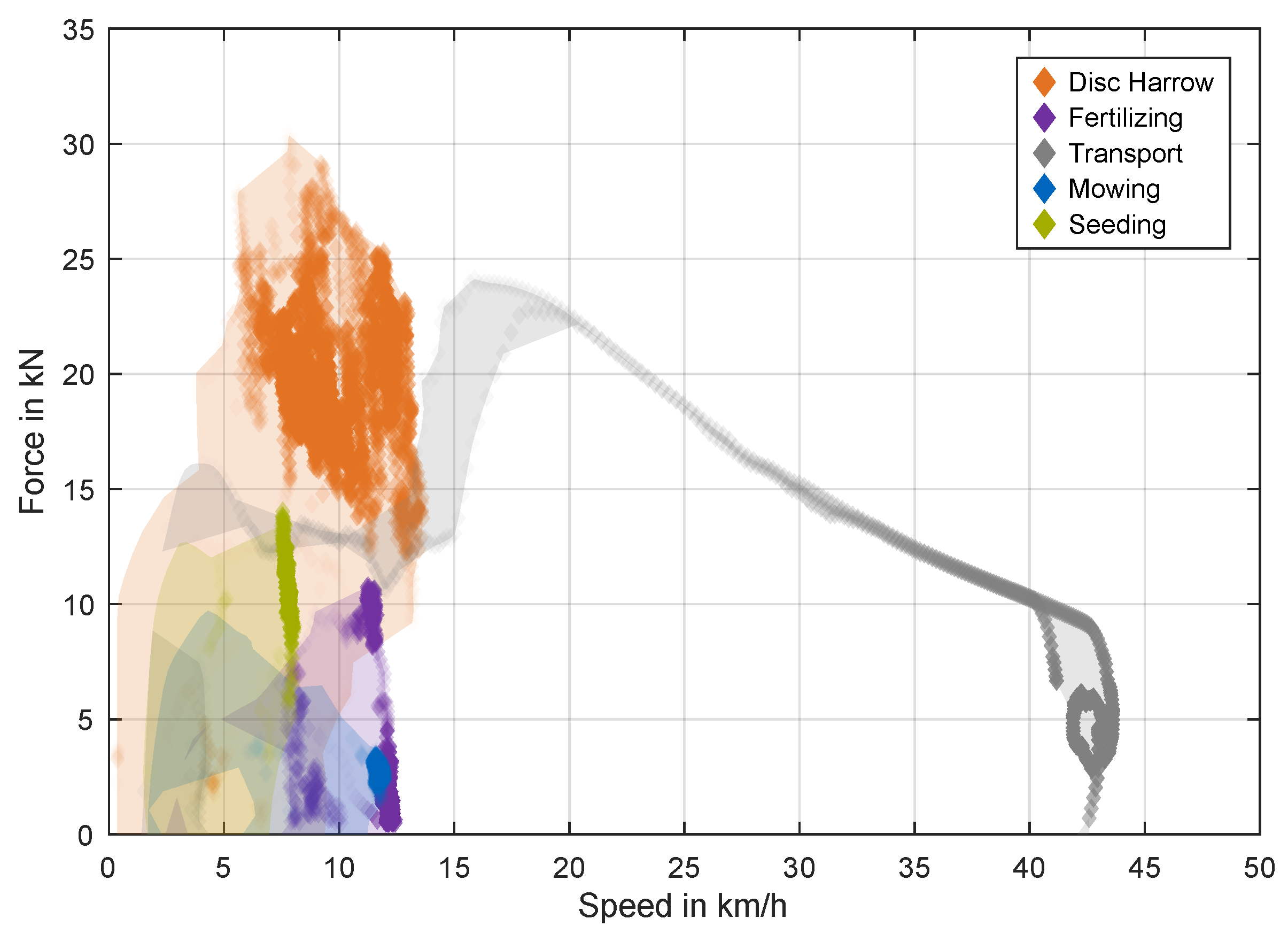


| Work Type | Time Share | Traveled Distance | Average Speed | Implement Width | Cone Index CI | |
|---|---|---|---|---|---|---|
 | Tillage | 45% | 638 m | 9.9 km/h | 3 m | 900 kPa |
 | Fertilizing | 12% | 319 m | 9.5 km/h | 15 m | 700 kPa |
 | Seed drill combination | 10% | 97 m | 6.8 km/h | 3 m | 450 kPa |
 | Mowing | 15% | 272 m | 10.1 km/h | 8.3 m | 1200 kPa |
 | Transport | 18% | 711 m | 28.7 km/h | 13 t | 1800 kPa |
| Topology | Component | Component Characteristic | Number of Variants | |
|---|---|---|---|---|
| axle-individual | central motor | Inverter type | IGBT | 1 |
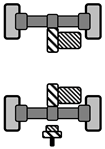 | 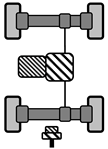 | Machine type | PSM, IM | 2 |
| Transmission—number of gears | 1, 2 | 2 | ||
| Power rear axle | 50–150 kW in steps of 5 | 315 | ||
| Power front axle | 30–100 kW in steps of 5 | |||
| Power CM | 70–220 kW in steps of 5 | 31 | ||
| Gear step | 1.0–3.0 in steps of 0.1 | 21 | ||
| Variable | Axle-Ind., One Gear | Axle-Ind., Two Gear | Central Motor, One Gear | Central Motor, Two Gear |
|---|---|---|---|---|
| 0.579 | 0.582 | 0.571 | 0.574 | |
| 0.700 | 0.700 | 0.700 | 0.700 | |
| 0.827 | 0.833 | 0.816 | 0.820 | |
| Energy Demand in kW h ha−1 | ||||
| Disc Harrow | 26.61 | 26.66 | 27.18 | 26.92 |
| Fertilizing | 0.53 | 0.53 | 0.54 | 0.55 |
| Mowing | 4.04 | 4.00 | 4.06 | 4.07 |
| Seeding | 30.30 | 29.67 | 30.54 | 29.92 |
| Transport | 2.87 | 2.88 | 2.90 | 2.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Götz, K.; Pointner, M.; Mayr, L.; Mailhammer, S.; Lienkamp, M. Electrify the Field: Designing and Optimizing Electric Tractor Drivetrains with Real-World Cycles. World Electr. Veh. J. 2025, 16, 463. https://doi.org/10.3390/wevj16080463
Götz K, Pointner M, Mayr L, Mailhammer S, Lienkamp M. Electrify the Field: Designing and Optimizing Electric Tractor Drivetrains with Real-World Cycles. World Electric Vehicle Journal. 2025; 16(8):463. https://doi.org/10.3390/wevj16080463
Chicago/Turabian StyleGötz, Korbinian, Markus Pointner, Lukas Mayr, Simon Mailhammer, and Markus Lienkamp. 2025. "Electrify the Field: Designing and Optimizing Electric Tractor Drivetrains with Real-World Cycles" World Electric Vehicle Journal 16, no. 8: 463. https://doi.org/10.3390/wevj16080463
APA StyleGötz, K., Pointner, M., Mayr, L., Mailhammer, S., & Lienkamp, M. (2025). Electrify the Field: Designing and Optimizing Electric Tractor Drivetrains with Real-World Cycles. World Electric Vehicle Journal, 16(8), 463. https://doi.org/10.3390/wevj16080463






