Multi-Lane Congestion Control Model for Intelligent Connected Vehicles Integrating Optimal Traffic Flow Difference Information in V2X Environment
Abstract
1. Introduction
2. Models
- (1)
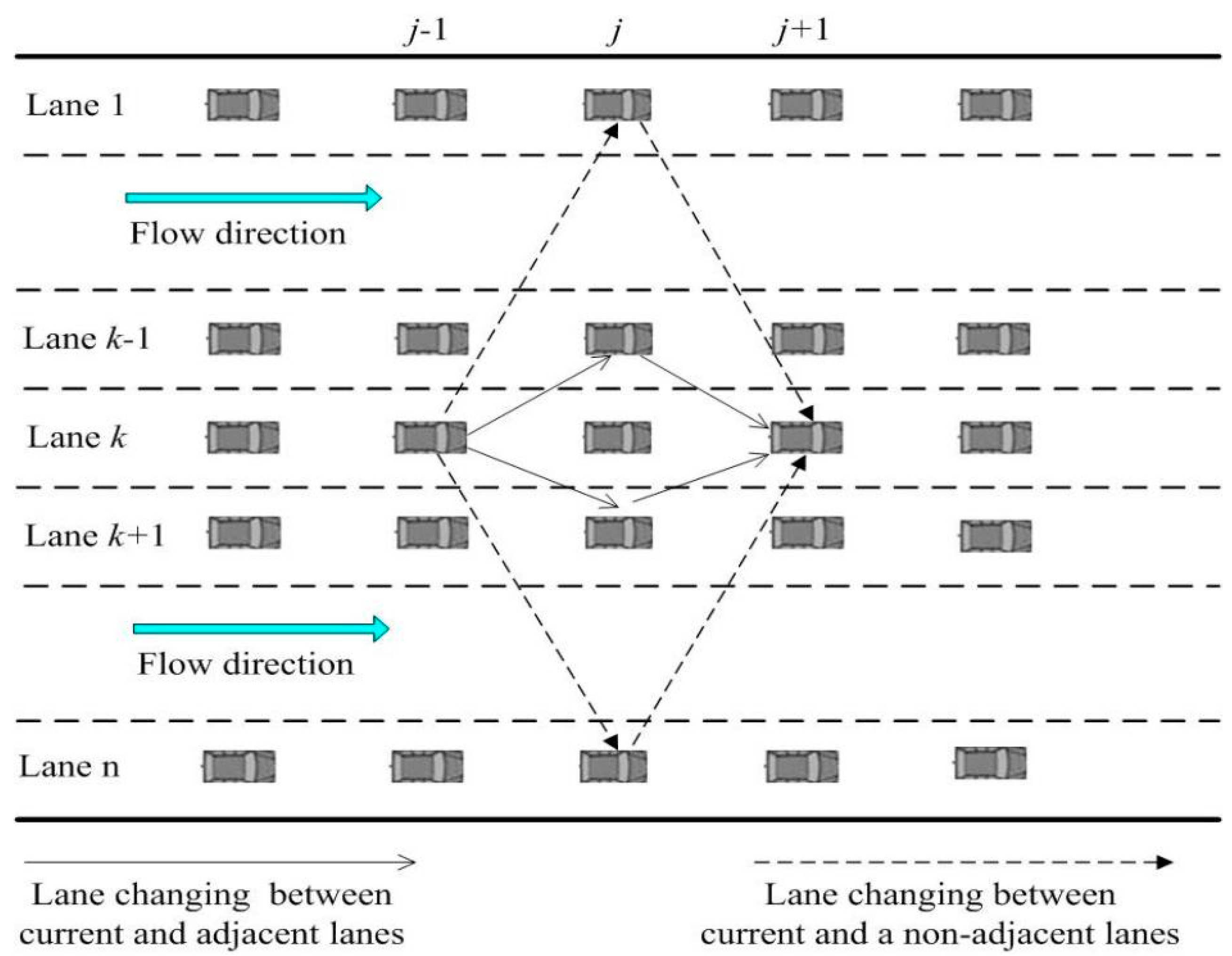
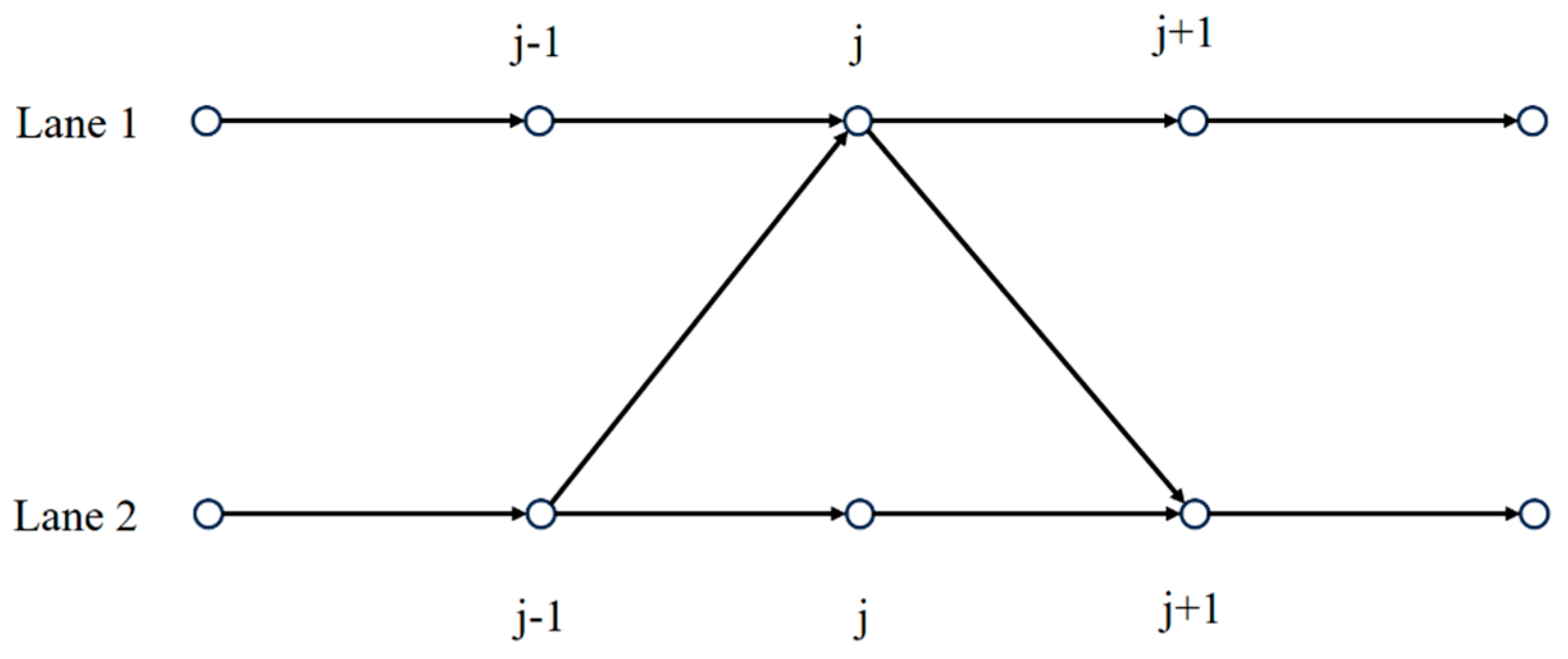
- For , the total number of vehicles in the -th lane remains unchanged, and this conservation is only disrupted when lane-changing occurs.
- (2)
- The variable represents the traffic density at position of the -th lane. If holds, where m ∈ [1, n] and , vehicles may change from to lane with lane-changing rate .
- (3)
- When holds, where m ∈ [1, n] and , vehicles are likely to change from lane to lane , with the lane-changing rate being .
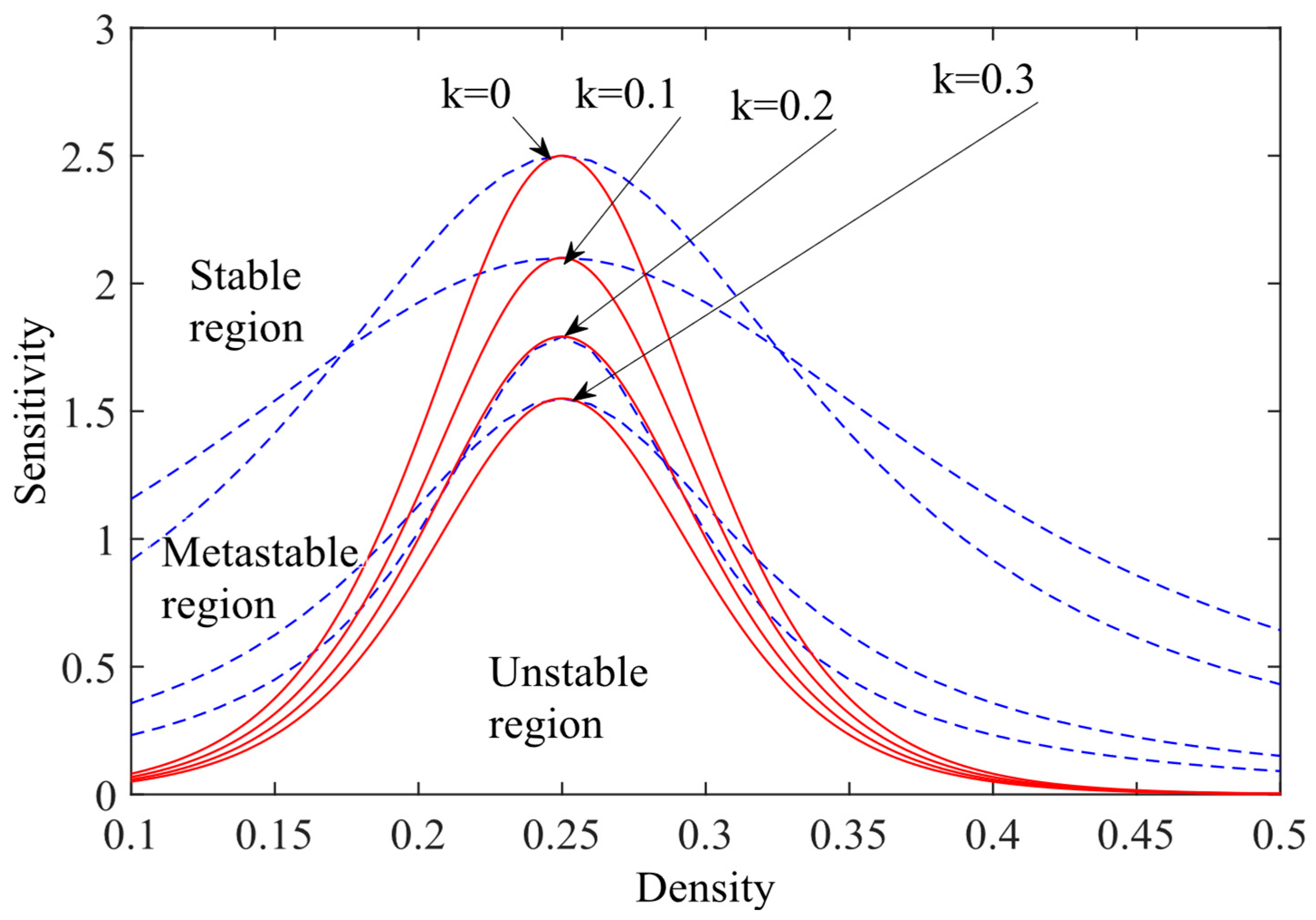
3. Linear Stability Analysis
4. Nonlinear Stability Analysis
5. Numerical Simulation
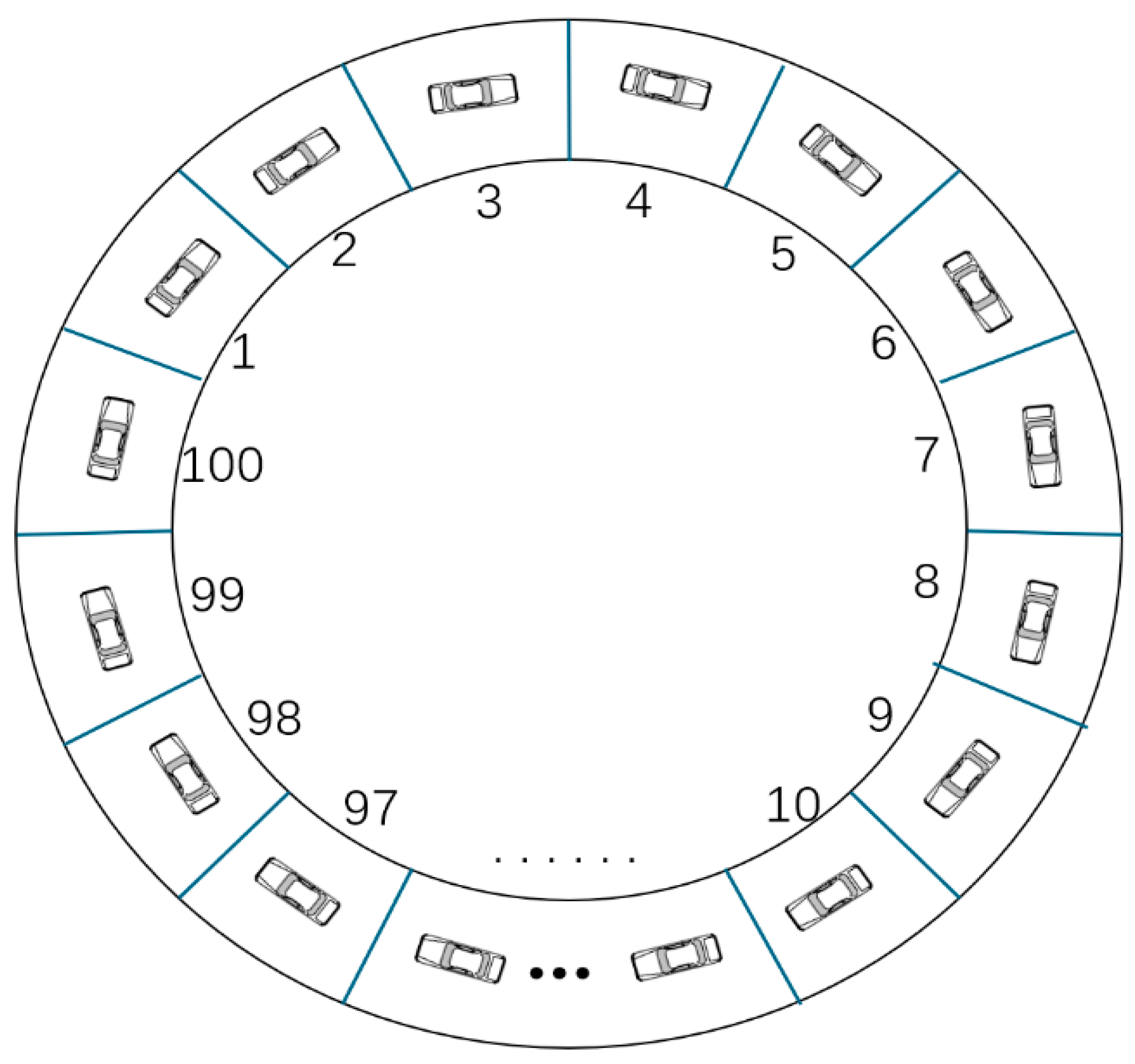
5.1. Experimental Design
5.2. Results Analysis and Discussion
5.2.1. Analysis of the Density Wave Evolution
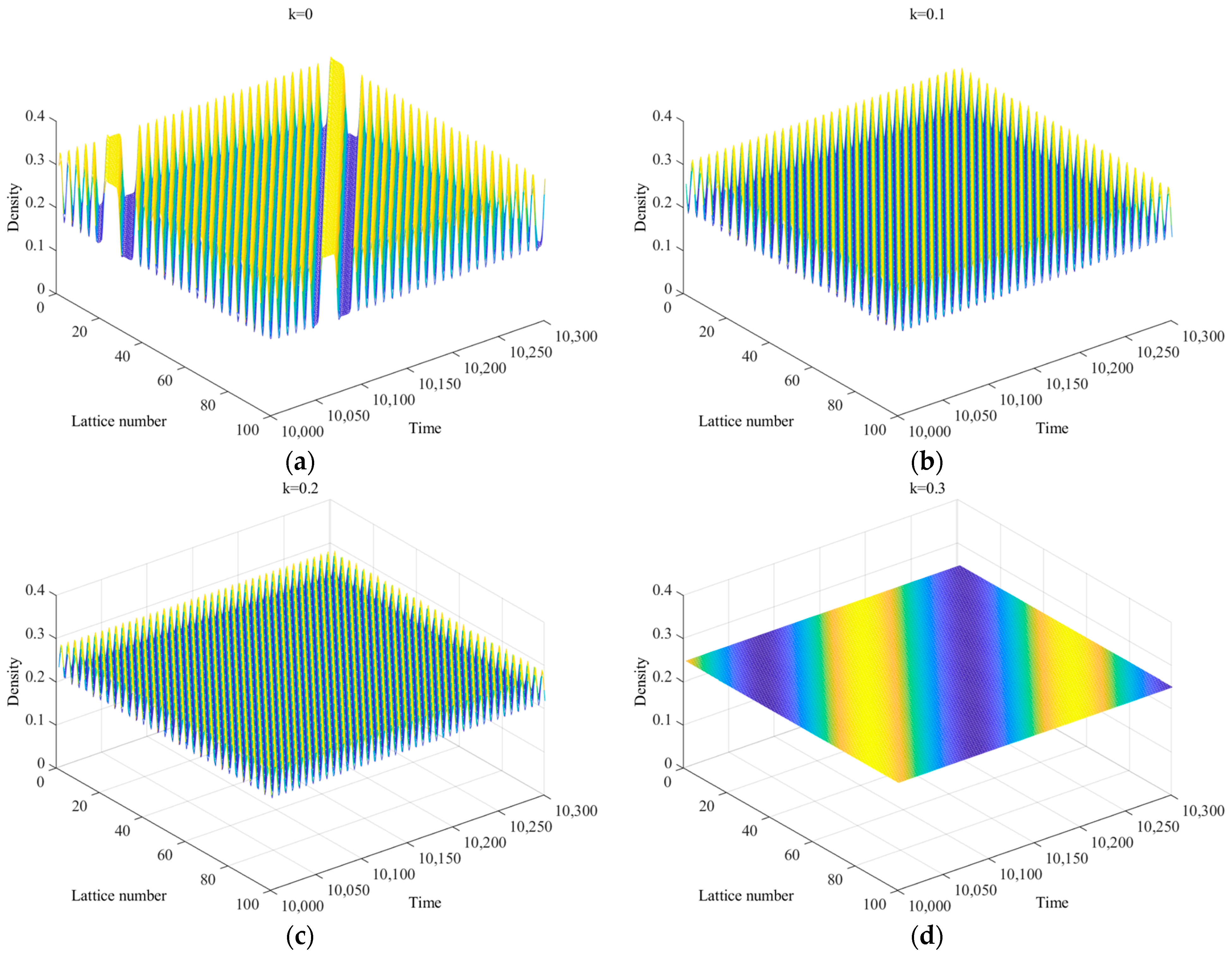

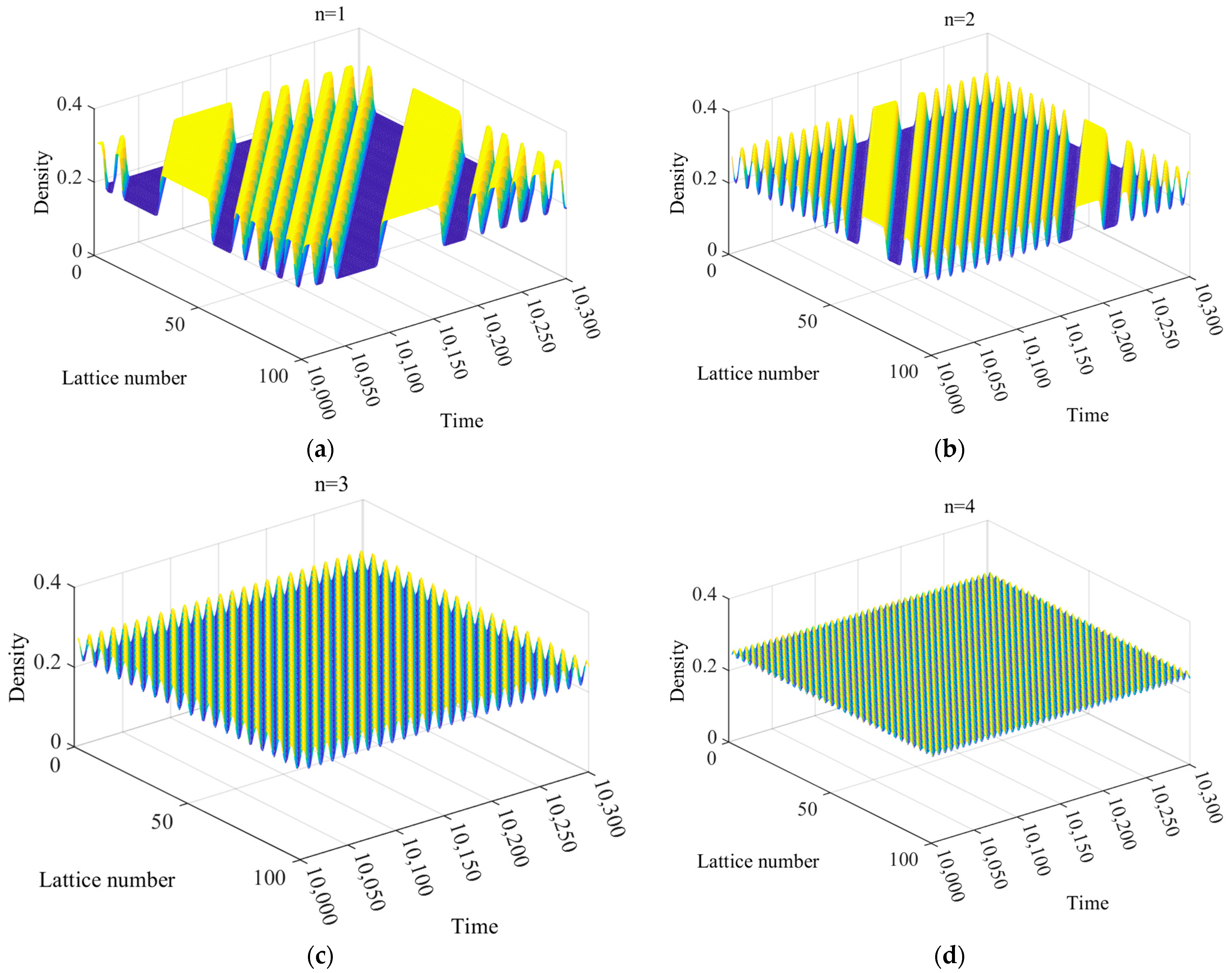
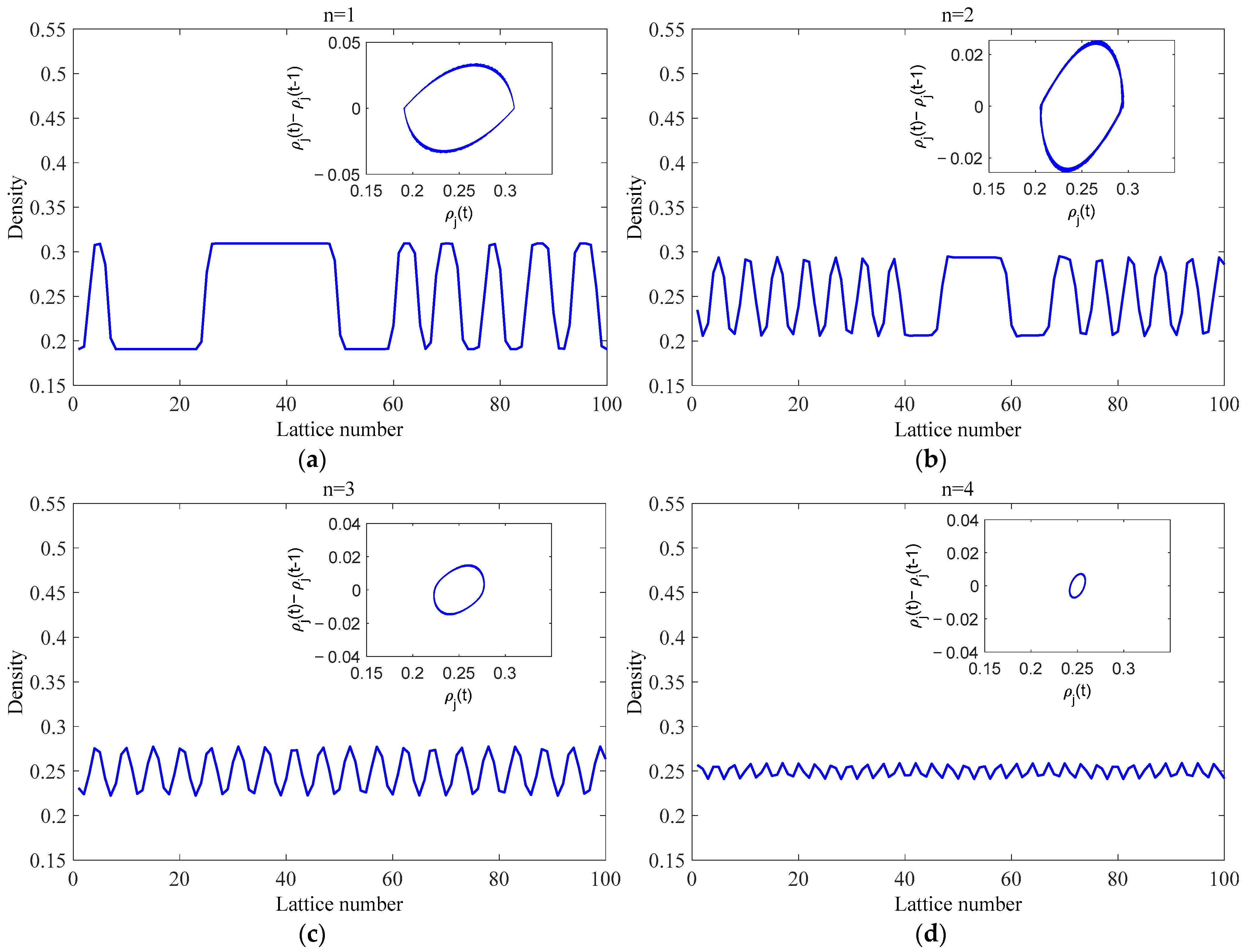
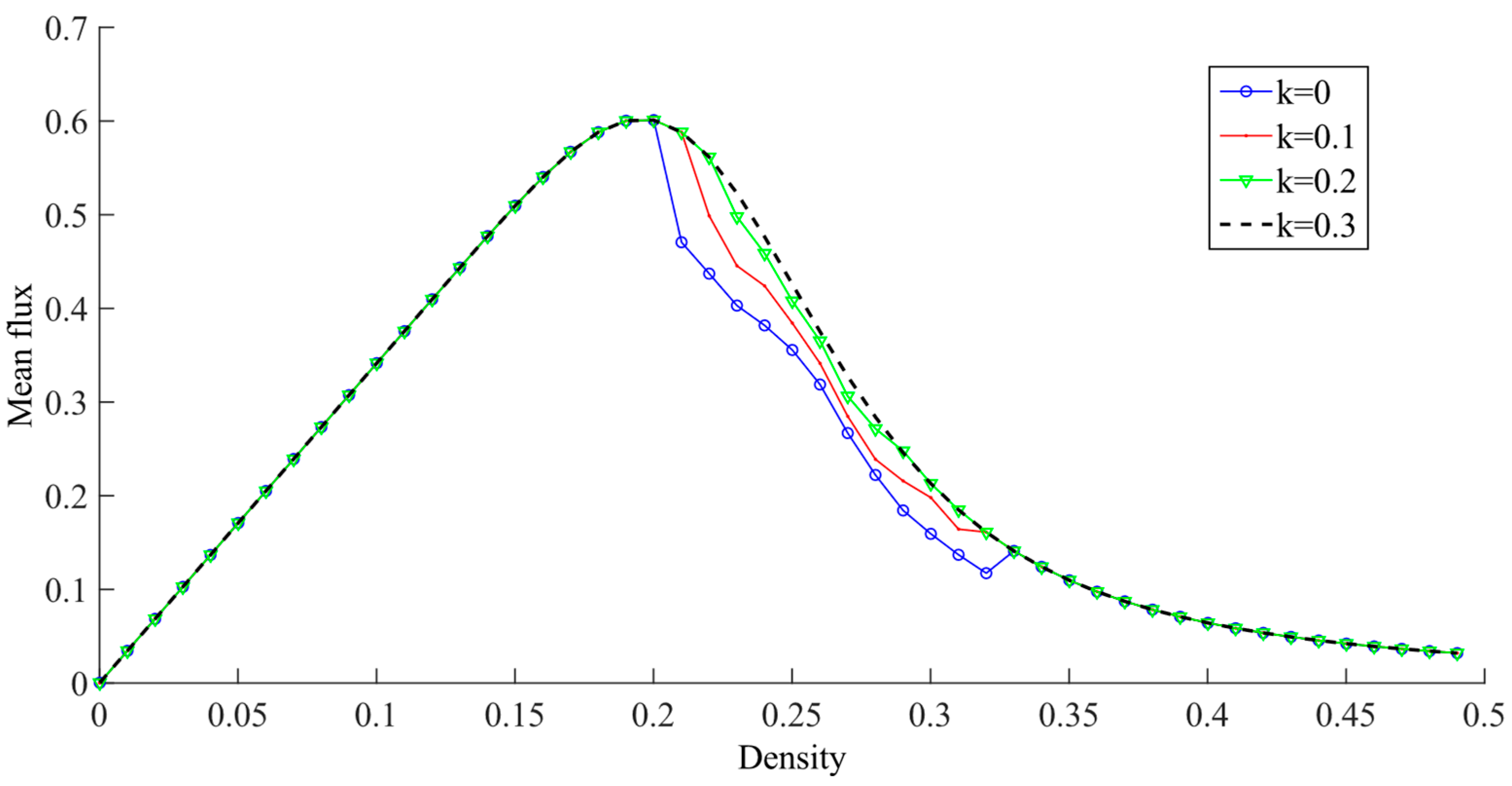
5.2.2. Analysis of Traffic Flow Optimization
6. Conclusions
- (1)
- Its robustness and other performance metrics have not yet been validated using field data or public datasets. Future work will collect field data to refine parameters for engineering applications.
- (2)
- The model does not account for driver-type differences in real-world traffic nor the traffic flow characteristics of asymmetric lane-changing scenarios. To address this issue, we will extend the model by drawing on the modeling approach for different types of driver behavior patterns in Ref. [33] to enhance its applicability. Regarding asymmetric lane-changing, we will adopt the lane-changing modeling framework from recent multi-lane literature [28] and simulate asymmetric lane-changing patterns by setting different parameter conditions.
- (3)
- The model is only applicable to multi-lane segment scenarios. In the future, efforts can be made to extend it to urban-scale environments that include intersections and various types of disturbances.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.Y.; Tang, W.; Feng, W.M.; Liu, Z.; Huang, C.X. An Extended Car-Following Model Considering Lateral Gap and Optimal Velocity of the Preceding Vehicle. Sustainability 2024, 16, 5983. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Ge, H.X.; Cheng, R.J. A car-following model considering the effect of electronic throttle opening angle over the curved road. Phys. A 2019, 534, 122377. [Google Scholar] [CrossRef]
- Liu, K.Y.; Feng, T.J. Heterogeneous traffic flow cellular automata model mixed with intelligent controlled vehicles. Phys. A 2023, 632, 129316. [Google Scholar] [CrossRef]
- Fukui, M.; Ishibashi, Y. Traffic flow in 1d cellular automaton model including cars moving with high speed. J. Phys. Soc. Jpn. 1996, 65, 1868–1870. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W.T. A continuous traffic flow model considering predictive headway variation and preceding vehicle’s taillight effect. Phys. A 2021, 584, 126364. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, Q.S.; Zhu, Z.J. A new continuum model for traffic flow and numerical tests. Transp. Res. B 2002, 36, 405–419. [Google Scholar] [CrossRef]
- Nagatani, T. Modified KdV equation for jamming transition in the continuum models of traffic. Phys. A 1998, 261, 599–607. [Google Scholar] [CrossRef]
- Nagatani, T. Jamming transitions and the modified Korteweg–de Vries equation in a two-lane traffic flow. Phys. A 1999, 265, 297–310. [Google Scholar] [CrossRef]
- Kaur, D.; Sharma, S. A new two-lane lattice model by considering predictive effect in traffic flow. Phys. A 2020, 539, 122913. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, R.J.; Ge, H.X. Analysis of a novel lattice hydrodynamic model considering predictive effect and flow integral. Phys. A 2019, 527, 121425. [Google Scholar] [CrossRef]
- Peng, G.H.; Kuang, H.; Qing, L. A new lattice model of traffic flow considering driver’s anticipation effect of the traffic interruption probability. Phys. A 2018, 507, 374–380. [Google Scholar] [CrossRef]
- Redhu, P.; Siwach, V. An extended lattice model accounting for traffic jerk. Phys. A 2018, 492, 1473–1480. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, R.J.; Ge, H.X. An extended two-lane lattice hydrodynamic model for traffic flow on curved road with passing. Phys. A 2019, 533, 121915. [Google Scholar] [CrossRef]
- Jin, Y.D.; Zhou, J.; Shi, Z.K.; Zhang, H.L.; Zhang, C.P. Lattice hydrodynamic model for traffic flow on curved road with passing. Nonlinear Dyn. 2017, 89, 107–124. [Google Scholar] [CrossRef]
- Peng, G.H.; Kuang, H.; Zhao, H.; Li, Q. Nonlinear analysis of a new lattice hydrodynamic model with the consideration of honk effect on flux for two-lane highway. Phys. A 2019, 515, 93–101. [Google Scholar] [CrossRef]
- Peng, G.H.; Kuang, H.; Bai, K.Z. The impact of the individual difference on traffic flow under honk environment in lattice hydrodynamic model. Phys. A 2019, 526, 120772. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Ge, H.X. An improved lattice hydrodynamic model accounting for the effect of “backward looking” and flow integral. Phys. A 2019, 513, 438–446. [Google Scholar] [CrossRef]
- Ge, H.X.; Cheng, R.J. The “backward looking” effect in the lattice hydrodynamic model. Phys. A 2008, 387, 6952–6958. [Google Scholar] [CrossRef]
- Qi, X.Y.; Ge, H.X.; Cheng, R.J. Analysis of a novel lattice hydrodynamic model considering density integral and “backward looking” effect. Phys. A 2019, 525, 714–723. [Google Scholar] [CrossRef]
- Verma, M.; Gupta, A.K.; Sharma, S. Phase transitions in a multi-phase lattice hydrodynamic area occupancy model in mixed disorder traffic considering connected and human-driven vehicles. Phys. A 2025, 658, 130264. [Google Scholar] [CrossRef]
- Dangi, R.; Redhu, P. Analyzing the impact of nearby information of vehicles on a car-following model in a V2X communication with passing. Int. J. Non-Linear Mech. 2025, 175, 105113. [Google Scholar] [CrossRef]
- Peng, G.H.; Jia, T.T.; Zhao, H.Z.; Tan, H.L. Phase transitions in dual-lane traffic model based on the continuous historical evolution message effect under V2X environment. Chin. J. Phys. 2025, 95, 422–432. [Google Scholar] [CrossRef]
- Mehta, S.; Mehra, M.; Redhu, P. Analysis of optimal velocity deviation with reaction time up to second order in a lattice hydrodynamic model with V2X communication. Int. J. Non-Linear Mech. 2025, 170, 104985. [Google Scholar] [CrossRef]
- Kang, Y.R.; Tian, C. Study on the multi-lane lattice model for highways based on a novel lane-changing mechanism. Heliyon 2024, 10, e33262. [Google Scholar] [CrossRef] [PubMed]
- Madaan, N.; Sharma, S. A lattice model accounting for multi-lane traffic system. Phys. A 2021, 564, 125446. [Google Scholar] [CrossRef]
- Madaan, N.; Sharma, S. Delayed-feedback control in multi-lane traffic system. Phys. A 2022, 599, 127393. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W.T.; Xiao, Y.P. The jamming transition of multi-lane lattice hydrodynamic model with passing effect. Chaos Solitons Fractals 2023, 171, 113515. [Google Scholar] [CrossRef]
- Xiao, Y.P.; Wu, W.T.; Zhai, C.; Zhai, M.; Zhang, J.Y. Analysis of empirical lane-changing rate effect on multi-lane traffic on curved roads. Chin. J. Phys. 2025, 95, 260–274. [Google Scholar] [CrossRef]
- Yang, S.H.; Li, C.G.; Tang, X.L.; Tian, C. Effect of optimal estimation of flux difference information on the lattice traffic flow model. Phys. A 2016, 463, 394–399. [Google Scholar] [CrossRef]
- Peng, G.H.; Yang, S.H.; Xia, D.X.; Li, X.Q. A novel lattice hydrodynamic model considering the optimal estimation of flux difference effect on two-lane highway. Phys. A. 2018, 506, 929–937. [Google Scholar] [CrossRef]
- Tian, C.; Yang, S.; Kang, Y. A Novel Two—Lane Lattice Model Considering the Synergistic Effects of Drivers’ Smooth Driving and Aggressive Lane—Changing Behaviors. Symmetry 2024, 16, 1430. [Google Scholar] [CrossRef]
- Ge, H.X.; Cheng, R.J.; Dai, S.Q. KdV and kink-antikink solitons in car-following models. Phys. A 2005, 357, 466–476. [Google Scholar] [CrossRef]
- Sharma, S. Lattice hydrodynamic modeling of two-lane traffic flow with timid and aggressive driving behavior. Phys. A 2015, 421, 401–411. [Google Scholar] [CrossRef]


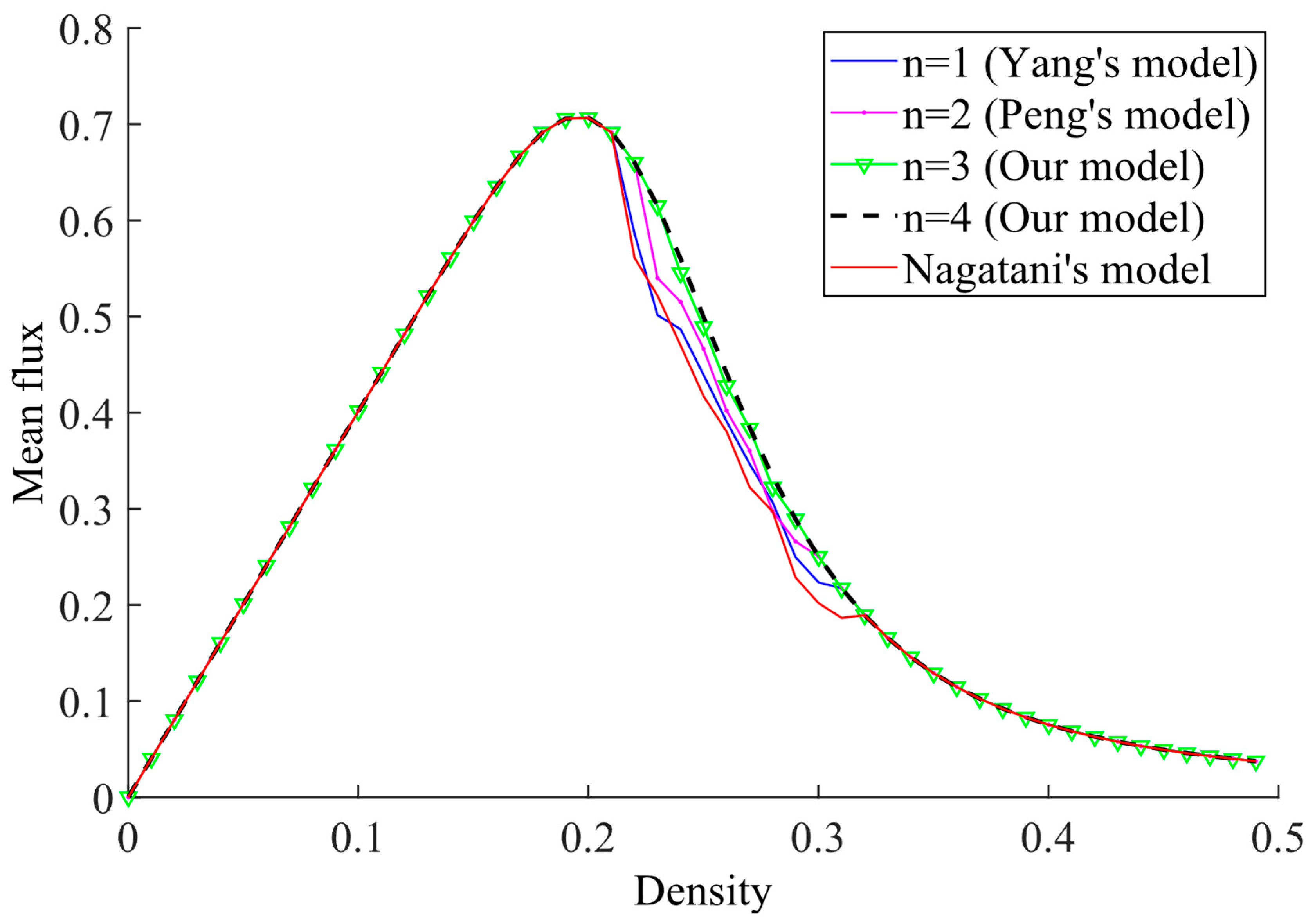
| 1 | |||||
|---|---|---|---|---|---|
| Our model | ac | 2.5620 | 2.3081 | 2.1000 | 1.9263 |
| MS multi-lane lattice model | ac | 3 | 2.7273 | 2.5000 | 2.3077 |
| Notation | Definition | Unit |
|---|---|---|
| N | The total number of road segments in the simulation system. | - |
| j | The index of a roadway segment. | - |
| a | Driver’s sensitivity. | s−1 |
| t | Time variable. | s |
| Delay time in driver’s reaction, . | s | |
| The overall average density of the multi-lane system. | veh/km | |
| Critical density. | veh/km | |
| The lane-changing coefficient. | - | |
| Number of lanes in multi-lane systems. | - | |
| k | The response coefficient associated with the OEFDI effect. | s−1 |
| V | Optimized velocity function. | km/h |
| The average velocity at time t on the -th segment in the multi-lane system. | km/h | |
| The average density at time t on the -th segment in the multi-lane system. | veh/km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Tian, C.; Yang, S. Multi-Lane Congestion Control Model for Intelligent Connected Vehicles Integrating Optimal Traffic Flow Difference Information in V2X Environment. World Electr. Veh. J. 2025, 16, 457. https://doi.org/10.3390/wevj16080457
Zhou L, Tian C, Yang S. Multi-Lane Congestion Control Model for Intelligent Connected Vehicles Integrating Optimal Traffic Flow Difference Information in V2X Environment. World Electric Vehicle Journal. 2025; 16(8):457. https://doi.org/10.3390/wevj16080457
Chicago/Turabian StyleZhou, Li, Chuan Tian, and Shuhong Yang. 2025. "Multi-Lane Congestion Control Model for Intelligent Connected Vehicles Integrating Optimal Traffic Flow Difference Information in V2X Environment" World Electric Vehicle Journal 16, no. 8: 457. https://doi.org/10.3390/wevj16080457
APA StyleZhou, L., Tian, C., & Yang, S. (2025). Multi-Lane Congestion Control Model for Intelligent Connected Vehicles Integrating Optimal Traffic Flow Difference Information in V2X Environment. World Electric Vehicle Journal, 16(8), 457. https://doi.org/10.3390/wevj16080457





