The Speed of Shared Autonomous Vehicles Is Critical to Their Demand Potential
Abstract
1. Introduction
- We present an ex post validation of the simulation predictions presented by Schlenther et al. [13] against the reality. The validation reveals the importance of having precise details of DRT service parameters, such as vehicle speed and fleet size. This part features the report of some of the key findings of one of Germany’s lighthouse research in autonomous driving.
- We build on [13] by reviewing fundamental assumptions and improving them by calibrating the AMoD service with (now) existing real demand data.
- We present a detailed sensitivity analysis of further adjustments to the configuration of the AMoD service with regard to future demand potentials, including sensitivities to the expansion of the service area, fleet, and operating times, as well as increased AV speed.
2. State of Research
- An ex post validation of demand forecasts based on simulation, as presented in Section 3; and
- An assessment of the demand sensitivity to specific configuration parameters of an AMoD system in a small town.
2.1. Literature on the Ex Post Validation of Travel Demand Predictions
while specific specific forecast inputs, such as projected demand sensitivities, explained less than half of the gap. Among the recommendations for improving forecast accuracy are the performance of sensitivity studies on underlying variables and the acknowledgment of uncertainty in ridership forecasts. The present study takes up these points by conducting an analysis of the sensitivity of demand to assumptions about the operating pattern of a DRT service or, more specifically, the positioning of idle vehicles.Overly optimistic assumptions about the frequency and speed of service […] made the largest contribution to the over-estimation of their future ridership levels([26], p. viii),
2.2. Literature on the Configuration and Operation of DRT and Implications for Demand
- The first MATSim extension is described by Ruch et al. [39] and is related to [34]. It is used by Sieber et al. [6], who investigate the replacement of four conventional rail lines by DRT in a rural area in Switzerland and conclude that with self-driving cars, travel times and operational costs can be reduced in three of those cases. Sieber et al. [6] predefine the demand for each of the areas and regard multiple operational strategies, similarly to Ruch et al. [39].
- The second extension is described in a study that simulated real-world taxicab demand in Berlin [40]. This extension, called DRT, was further extended to reflect rebalancing, and multiple strategies were investigated with static demand in Berlin [41] and the rural region of Vulkaneifel in Germany [42], as well as with demand reaction in Berlin [4]. The DRT extension of MATSim was also used to investigate the replacement of all car trips in Berlin by DRT [43], as well as for the present study. In a similar domain as [6], Lu et al. [1] investigate the replacement of school buses by DRT in one of the least populated areas in Germany under various operation strategies and find potential for substantial reductions in operational costs, while DRT could serve additional purposes.
- Kuhlen et al. [47] present a spatial regression model for the prediction of DRT demand based on origin–destination relations. Their model represents an improvement compared to Zwick and Axhausen [48], who use spatial regression on a zonal level with regard to sensitivity to service area size. However, the predictions are not backed by physical simulations and are therefore not sensitive to changes in operation strategies such as rebalancing or stop network design, and Kuhlen et al. [47] state limitations regarding transferability to other areas.
- Vosooghi et al. [49] use MATSim with user-specific taste variations to simulate multiple DRT fleet sizes and vehicle capacities in the metropolitan area of Rouen, France. The authors also compare the operational pooling scheme against serving single requests and conclude that all of the variables influence the system’s performance. In another study, Vosooghi et al. [50] assess the impacts of charging infrastructure on operations.
- Diallo et al. [51] compare three scenarios for the deployment of AVs as private vehicles or as part of a DRT system with and without ridepooling for case studies in Montréal, Canada, and Lyon, France. The authors conclude that AVs can account for significant transport-mode shares, with most of the modal shift coming from private cars, PT, and walking trips.
- Hörl et al. [52] perform dynamic a demand estimation experiment for a hypothetical large-scale AMoD service in Paris, France, using agent-based simulation. The authors formulate research questions regarding the usage of DRT in a stop-based system and as a feeder to PT, which are both addressed in the present study.
- Schlenther et al. [53] recently described a transport model for Hamburg, Germany, that includes mode-choice calibration based on real-world MOIA data and apply it to investigate various DRT pricing strategies for integration with PT.
- Agriesti et al. [54] present another framework that integrates a behavioral model with mesoscopic traffic assignment including car-following behavior to assess demand reactions to large-scale AMoD operations, focusing on fleets that are constrained either in size or in driving style. The authors apply the framework to a case study of Tallinn, Estonia. The authors also provide an extensive overview of the existing literature.
3. Ex Post Validation of Demand Predictions for the KelRide Project
“assume[d] that the AV service is generally perceived similarly as the conventional KEXI and we apply the same marginal utility () parameters retrieved from the conventional KEXI calibration […]. This assumption can be justified by the fact that the overall nature of the two transport services is essentially the same, while operational differences, such as vehicle speed, service areas, travel times and wait times, are explicitly modeled. In reality, public perception of the autonomous service might necessitate adjustments to the parameters, as the population of Kelheim, for example, might be particularly biased or open-minded toward autonomous vehicles. The later stages of the project will reveal the actual demand response to the service and enable calibration.”([13], p. 9).
- The average vehicle speed was significantly lower than 18 km/h, which was assumed in [13] based on the manufacturer’s specifications. Reasons included frequent emergency braking due to other vehicles and pedestrians getting close to the AVs, protruding tree branches, and loss of connectivity to the control center. During some tests, the average vehicle speed was around 9 km/h with passengers on board. As the initial service area was rather small (circa 0.37 km2), the total travel time, including the wait time for pickup, often was not competitive with the time of walking (for non-handicapped persons).
- Following Römer et al. [56], who present findings from 17 other AMoD pilot projects in Germany and state that vehicle speed is crucial for the acceptance of the technology and needs to further improve in the future, vehicle speed is declared to be a variable for sensitivity analyses (see Section 5).
- Despite the fact that two AVs plus an additional AV as a backup were planned to be regularly available, only one vehicle could be supplied on some days. Reasons included unavailability of the technical operators and of the vehicles due to maintenance or technical issues (According to the current legal restrictions, technical operators still need to be on board of the AVs, which concerns SAE Level 3 [57]). For the final project stage beginning in 2024, data on the actual supply was available and was used to recalibrate the model for the present study (see Section 4.2). The fleet size was expanded prior to that stage, leading to higher vehicle availability.
- During the final project stage in 2024, a qualitative empirical yet unpublished study revealed that the public perception of AVs is dominated by the car–driver perspective (which is plausible, given the car mode share of 59%). AVs are primarily seen as traffic obstructions in this context. It was pointed out that the prevailing negative opinion of autonomous KEXIs discourages people from using the vehicles.
- Further reported burdens were difficulties in the booking process, as well as the fact that the AMoD service, in contrast to the conventional service, is not connected to the train Station in Saal an der Donau, the adjacent town to the east of Kelheim [13], which reduces the number of use cases, particularly for people commuting to other cities by train.
4. Methodology
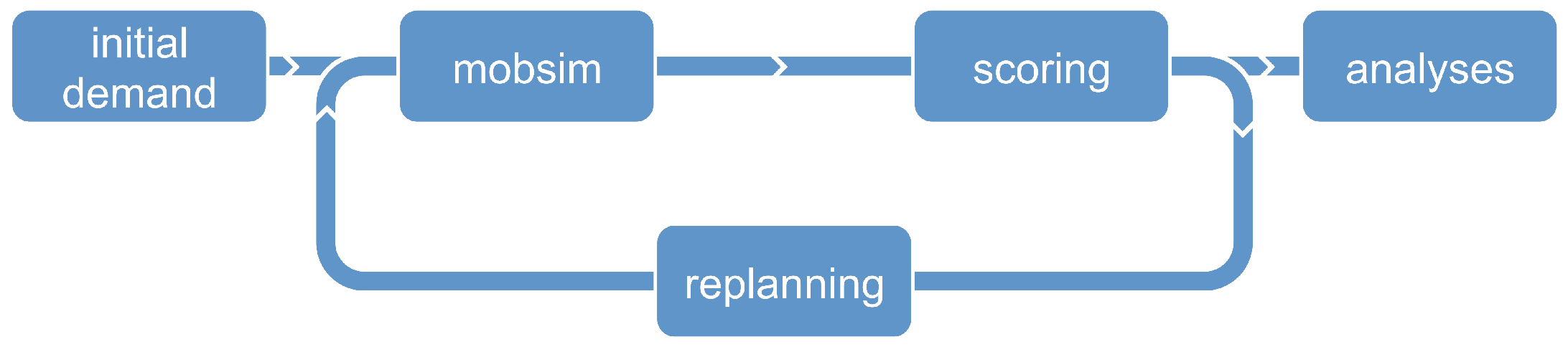
4.1. MATSim
4.2. Recalibration of the MATSim Kelheim Scenario
4.3. Rebalancing
5. Case Study Motivation and Parameter Variation
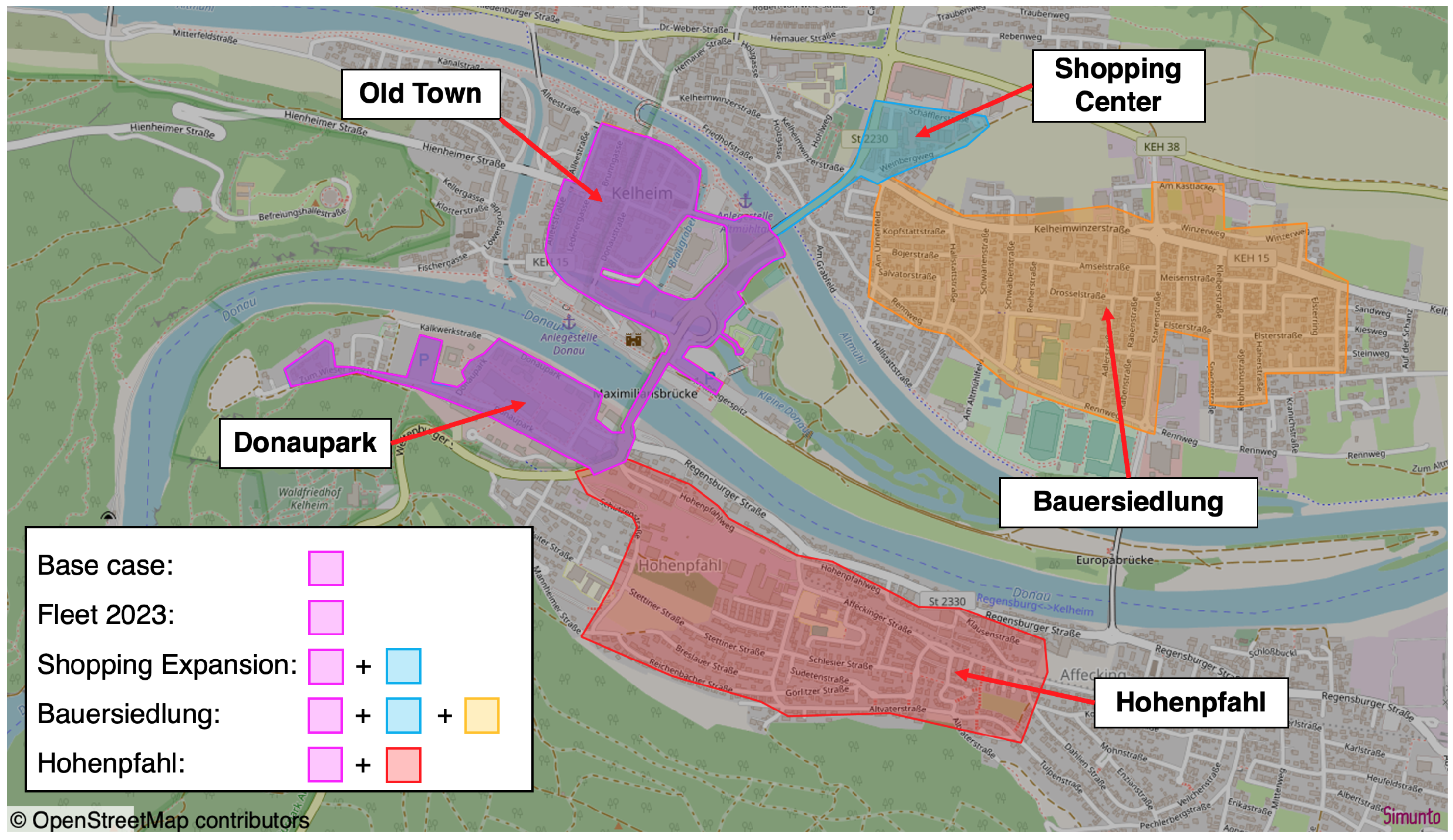
- AMoD Service Area: An extension of the 2024 AV KEXI service area, which is illustrated by the black dots in Figure 3 and hereafter referred to as Area 2024, to the entire existing MoD stop network from the conventional KEXI. The latter case covers all stops shown in Figure 3 and is referred to as Area All-City.
- Fleet Size: Increases in the fleet size from the 2 AVs in the base case to 5, 8, 10, 20, 50, and 100 vehicles.
- Operating Times: An increase in the operating times from 9 am to 4 pm in the base case to a full day’s operation (referred to as ‘all-day’).
- AV Speed: Increases in the effective speed from 12 km/h in the base case to 18 km/h and 30 km/h.
6. Results
6.1. The Relationship Between Service Configuration and Demand
- With increasing fleet size, the number of passengers initially increases superlinearly but eventually saturates.
- Passenger numbers increase superlinearly with vehicle speed—more strongly at small fleet sizes and less pronounced but still superlinear at larger fleet sizes.
- The number of passengers grows approximately linearly with the service area, provided that fleet size is sufficiently large.
- Extending operating times from 9 a.m.–4 p.m. to full-day operation increases passenger numbers by a factor of two to four.
6.2. The Relationship Between Service Configuration and Fleet Efficiency
6.3. The Relationship Between Waiting-Point Location and Wait Time and Demand
7. Discussion and Outlook
7.1. Discussion and Interpretation of the Results
7.2. Limitations
7.3. Transferability
7.4. Outlook
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMoD | Autonomous Mobility on Demand |
| ASC | Alternative-specific constant |
| AV | Autonomous vehicle |
| CO2 | Carbon dioxide |
| DRT | Demand-responsive transport |
| FTA | Federal Transit Administration of the United States |
| KEXI | Landkreis Kelheim Express Individuell |
| MATSim | A framework for Multi-Agent Transport Simulation, see www.matsim.org |
| MoD | Mobility on Demand |
| PT | Public transport |
| PvA | Predicted versus Actual |
Appendix A. DRT Insertion Cost Calculation
- The additional total vehicle travel time induced by the insertion;
- The total violation of the wait time constraint, if any (Specifically, for each second that the pickup is delayed beyond , the total insertion cost is increased by one second);
- The total violation of the travel time constraint, if any (Specifically, for each second that the drop-off is delayed beyond , the total insertion cost is increased by ten seconds).
Appendix B. Changing the Modal Split of the Base Model
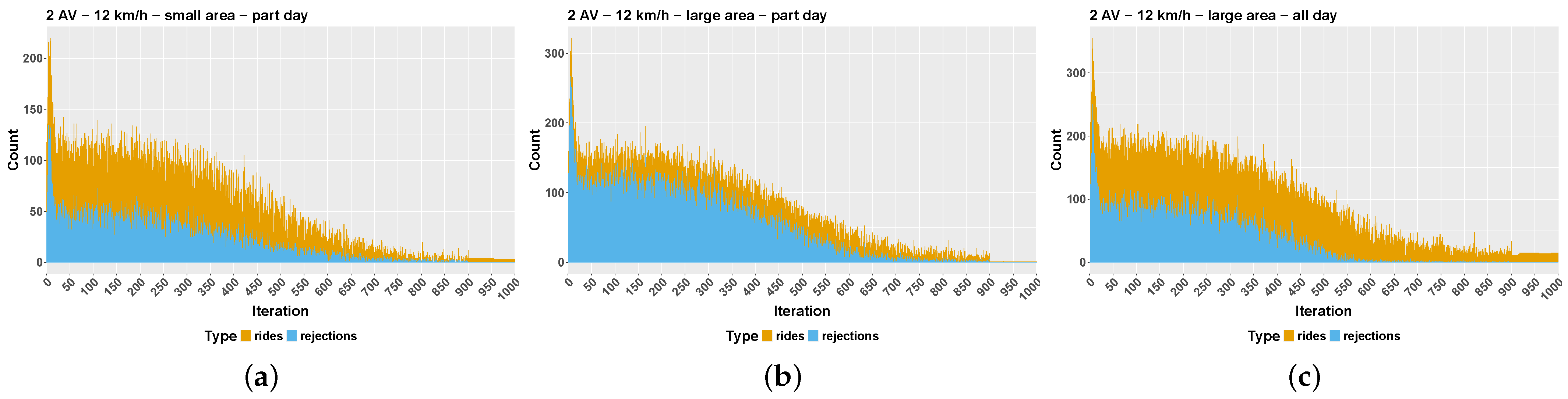
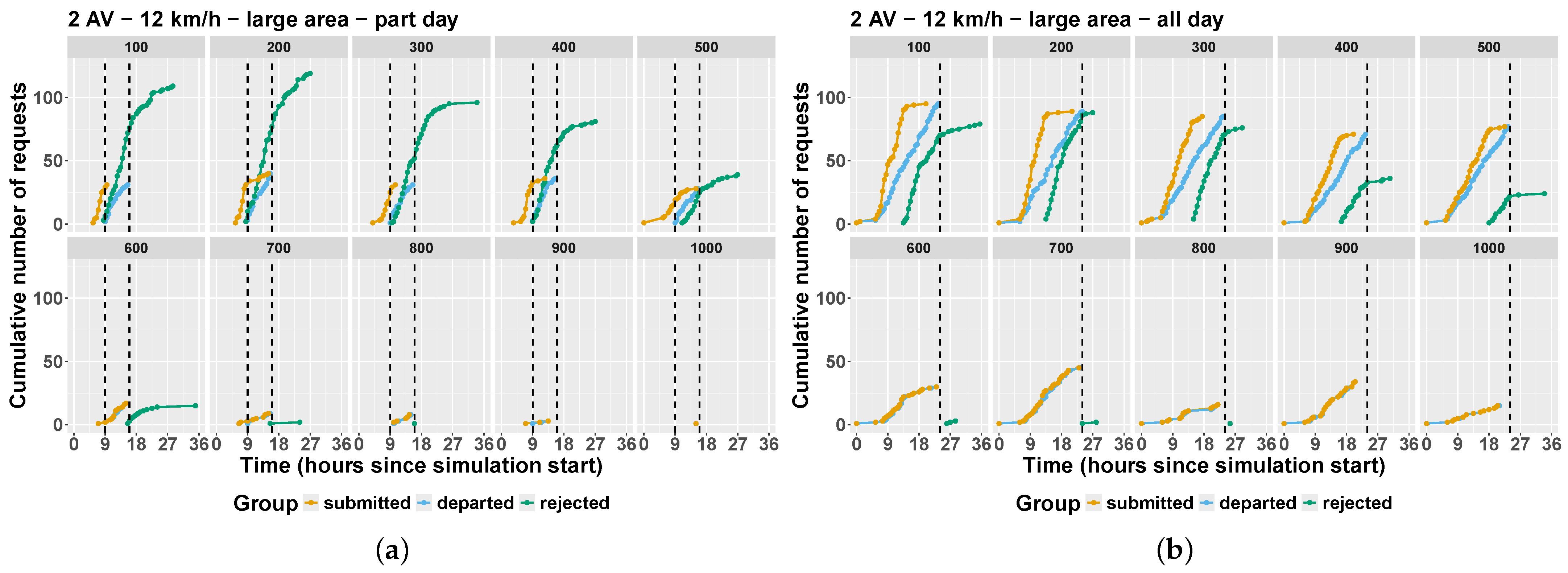
Appendix C. Investigating the Simulation of Two AVs in the Larger Area All-City
References
- Lu, C.; Maciejewski, M.; Wu, H.; Nagel, K. Demand-responsive transport for students in rural areas: A case study in Vulkaneifel, Germany. Transp. Res. Part A Policy Pract. 2023, 178, 103837. [Google Scholar] [CrossRef]
- Qiao, S.; Yeh, A.G.O. Mobility-on-demand public transport toward spatial justice: Shared mobility or Mobility as a Service. Transp. Res. Part D Transp. Environ. 2023, 123, 103916. [Google Scholar] [CrossRef]
- Wang, C.; Quddus, M.; Enoch, M.; Ryley, T.; Davison, L. Multilevel modelling of Demand Responsive Transport (DRT) trips in Greater Manchester based on area-wide socio-economic data. Transportation 2014, 41, 589–610. [Google Scholar] [CrossRef]
- Schlenther, T.; Leich, G.; Maciejewski, M.; Nagel, K. Addressing Spatial Service Provision Equity for Pooled Ride-Hailing Services through Rebalancing. IET Intell. Transp. Syst. 2023, 17, 547–556. [Google Scholar] [CrossRef]
- Liu, J.; Kockelman, K.M.; Boesch, P.M.; Ciari, F. Tracking a system of shared autonomous vehicles across the Austin, Texas network using agent-based simulation. Transportation 2017, 44, 1261–1278. [Google Scholar] [CrossRef]
- Sieber, L.; Ruch, C.; Hörl, S.; Axhausen, K.; Frazzoli, E. Improved public transportation in rural areas with self-driving cars: A study on the operation of Swiss train lines. Transp. Res. Part A Policy Pract. 2020, 134, 35–51. [Google Scholar] [CrossRef]
- Bösch, P.M.; Becker, F.; Becker, H.; Axhausen, K.W. Cost-based analysis of autonomous mobility services. Transp. Policy 2018, 64, 76–91. [Google Scholar] [CrossRef]
- Hörl, S.; Ruch, C.; Becker, F.; Frazzoli, E.; Axhausen, K. Fleet operational policies for automated mobility: A simulation assessment for Zurich. Transp. Res. Part C Emerg. Technol. 2019, 102, 20–31. [Google Scholar] [CrossRef]
- Winter, K.; Cats, O.; Correia, G.; van Arem, B. Performance analysis and fleet requirements of automated demand-responsive transport systems as an urban public transport service. Int. J. Transp. Sci. Technol. 2018, 7, 151–167. [Google Scholar] [CrossRef]
- Fagnant, D.J.; Kockelman, K.M. Dynamic Ride-Sharing and Fleet Sizing for a System of Shared Autonomous Vehicles in Austin, Texas. Transportation 2016, 45, 143–158. [Google Scholar] [CrossRef]
- Bundesministerium für Verkehr. Gesetz Zum Autonomen Fahren Tritt in Kraft. 2021. Available online: https://www.bmv.de/SharedDocs/DE/Artikel/DG/gesetz-zum-autonomen-fahren.html (accessed on 19 May 2025).
- Landkreis Kelheim. KelRide—Weather-Proof Smart Shuttle. 2022. Available online: https://kelride.com/en/ (accessed on 30 December 2024).
- Schlenther, T.; Lu, C.; Meinhardt, S.; Rakow, C.; Nagel, K. Autonomous mobility-on-demand in a rural area: Calibration, simulation and projection based on real-world data. Case Stud. Transp. Policy 2025, 20, 101418. [Google Scholar] [CrossRef]
- Landkreis Kelheim. Europas Größtes Zusammenhängendes Betriebsgebiet für Hochautomatisierte Shuttles Startet in Kelheim. 2024. Available online: https://kelride.com/europas-groesstes-zusammenhaengendes-betriebsgebiet-fuer-hochautomatisierte-shuttles-startet-in-kelheim/ (accessed on 30 December 2024).
- Choi, J.; Maisel, J.L. Assessing the Implementation of On-Demand Transportation Services for People with Disabilities. Transp. Res. Rec. 2022, 2676, 437–449. [Google Scholar] [CrossRef]
- Westervelt, M.; Schank, J.; Huang, E. Partnerships with technology-enabled mobility companies: Lessons learned. Transp. Res. Rec. 2017, 2649, 106–112. [Google Scholar] [CrossRef]
- Shaheen, S.; Cohen, A.; Yelchuru, B.; Sarkhili, S.; Hamilton, B.A. Mobility on Demand Operational Concept Report; Technical Report FHWA-JPO-18-611; U.S. Department of Transportation, Intelligent Transportation Systems Joint Program Office: Washington, DC, USA, 2017.
- Saberi, M.; Rashidi, T.H.; Ghasri, M.; Ewe, K. A complex network methodology for travel demand model evaluation and validation. Netw. Spat. Econ. 2018, 18, 1051–1073. [Google Scholar] [CrossRef]
- Yasmin, F.; Morency, C.; Roorda, M.J. Macro-, meso-, and micro-level validation of an activity-based travel demand model. Transp. Transp. Sci. 2016, 13, 222–249. [Google Scholar] [CrossRef]
- Khan, N.A.; Shahrier, H.; Habib, M.A. Validation of an activity-based travel demand modeling system. Transp. Lett. 2021, 14, 1004–1018. [Google Scholar] [CrossRef]
- Flyvbjerg, B.; Skamris Holm, M.K.; Buhl, S.L. How (in)accurate are demand forecasts in public works projects? J. Am. Plan. Assoc. 2005, 71, 131–146. [Google Scholar] [CrossRef]
- Flyvbjerg, B.; Holm, M.; Buhl, S. Cost Underestimation in Public Works Projects: Error or Lie; Aalborg Universitetsforlag: Aalborg, Denmark, 2004. [Google Scholar]
- Flyvbjerg, B. Measuring inaccuracy in travel demand forecasting: Methodological considerations regarding ramp up and sampling. Transp. Res. Part A Policy Pract. 2005, 39, 522–530. [Google Scholar] [CrossRef]
- Berechman, J. Inaccuracies in Cost and Demand Forecasts. In The Infrastructure We Ride On: Decision Making in Transportation Investment; Springer: Berlin/Heidelberg, Germany, 2018; pp. 51–80. [Google Scholar]
- Nicolaisen, M.S.; Driscoll, P.A. Ex-post evaluations of demand forecast accuracy: A literature review. Transp. Rev. 2014, 34, 540–557. [Google Scholar] [CrossRef]
- Pickrell, D.H. Urban Rail Transit Projects: Forecast Versus Actual Ridership and Costs [October 1989]; Technical Report UMTA-MA-08-9021-89-1; United States Urban Mass Transit Administration, Department of Transportation, Federal Transit Administration: Washington, DC, USA, 1989. [CrossRef]
- Pickrell, D.H. Urban Rail Transit Projects: Forecast Versus Actual Ridership and Costs [October 1990]; Technical Report DOT-T-91-04; United States Urban Mass Transit Administration, Department of Transportation, Federal Transit Administration: Washington, DC, USA, 1990. [CrossRef]
- Federal Transit Administration. Predicted Versus Actual Impacts of Capital Investment Grants Projects—2020. Capital Cost and Ridership; Technical Report; United States Office of Planning and Environment, US Department of Transportation, Federal Transit Administration: Washington, DC, USA, 2020.
- GAO. Capital Investment Grants Program—Cost Predictions Have Improved, but the Pandemic Complicates Assessing Ridership Predictions; Technical Report GAO-23-105479; United States Government Accountability Office: Washington, DC, USA, 2023.
- Espinoza-Molina, F.E.; Valladolid, J.D.; Bautista, P.B.; Quinde, E.; Villa Uvidia, R.; Vazquez Salazar, J.S.; Miranda, G.J.A. Backcasting analysis of autonomous vehicle implementation: A systematic review. World Electr. Veh. J. 2024, 15, 393. [Google Scholar] [CrossRef]
- Fagnant, D.J.; Kockelman, K.M. The travel and environmental implications of shared autonomous vehicles, using agent-based model scenarios. Transp. Res. Part C Emerg. Technol. 2014, 40, 1–13. [Google Scholar] [CrossRef]
- Fagnant, D.J.; Kockelman, K.M.; Bansal, P. Operations of shared autonomous vehicle fleet for Austin, Texas, market. Transp. Res. Rec. J. Transp. Res. Board 2016, 2563, 98–106. [Google Scholar] [CrossRef]
- Waymo LLC. Autnomous Ride-Hailing in Austin, Texas—Waymo. 2025. Available online: https://waymo.com/waymo-one-austin/ (accessed on 20 February 2025).
- Alonso-Mora, J.; Samaranayake, S.; Wallar, A.; Frazzoli, E.; Rus, D. On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment. Proc. Natl. Acad. Sci. USA 2017, 114, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Dandl, F.; Hyland, M.; Bogenberger, K.; Mahmassani, H.S. Evaluating the impact of spatio-temporal demand forecast aggregation on the operational performance of shared autonomous mobility fleets. Transportation 2019, 46, 1975–1996. [Google Scholar] [CrossRef]
- Liu, Y.; Bansal, P.; Daziano, R.; Samaranayake, S. A framework to integrate mode choice in the design of mobility-on-demand systems. Transp. Res. Part C Emerg. Technol. 2019, 105, 648–665. [Google Scholar] [CrossRef]
- Engelhardt, R. Autonomous Ride-Pooling-Services in Urban Environments: Operational Strategies and Simulation. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2024. [Google Scholar]
- Maciejewski, M. Dynamic Transport Services. In The Multi-Agent Transport Simulation MATSim; Ubiquity: London, UK, 2016; Chapter 23. [Google Scholar]
- Ruch, C.; Lu, C.; Sieber, L.; Frazzoli, E. Quantifying the efficiency of ride sharing. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5811–5816. [Google Scholar] [CrossRef]
- Bischoff, J.; Maciejewski, M.; Nagel, K. City-wide shared taxis: A simulation study in Berlin. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar] [CrossRef]
- Bischoff, J.; Maciejewski, M. Proactive empty vehicle rebalancing for Demand Responsive Transport services. Procedia Comput. Sci. 2020, 170, 739–744. [Google Scholar] [CrossRef]
- Lu, C.; Maciejewski, M.; Nagel, K. Effective Operation of Demand-Responsive Transport (DRT): Implementation and Evaluation of Various Rebalancing Strategies. In Proceedings of the 27th ITS World Congress, Hamburg, Germany, 11–15 October 2021. [Google Scholar]
- Bischoff, J.; Maciejewski, M. Simulation of city-wide replacement of private cars with autonomous taxis in Berlin. Procedia Comput. Sci. 2016, 83, 237–244. [Google Scholar] [CrossRef]
- Zwick, F.; Axhausen, K.W. Analysis of Ridepooling Strategies with MATSim; Technical Report; ETH Zurich: Zurich, Switzerland, 2020. [Google Scholar] [CrossRef]
- MOIA GmbH. Revolutionize Mobility. MOIA. 2025. Available online: https://www.moia.io/en (accessed on 20 February 2025).
- Zwick, F.; Kuehnel, N.; Moeckel, R.; Axhausen, K.W. Ride-pooling efficiency in large, medium-sized and small towns -simulation assessment in the Munich metropolitan region. Procedia Comput. Sci. 2021, 184, 662–667. [Google Scholar] [CrossRef]
- Kuhlen, T.E.; Kuehnel, N.; Zwick, F.; Rabemananjara, S. Spatial Demand Prediction of On-Demand Ride-Pooling Based on Origin-Destination-Regressions; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar] [CrossRef]
- Zwick, F.; Axhausen, K.W. Ride-pooling demand prediction: A spatiotemporal assessment in Germany. J. Transp. Geogr. 2022, 100, 103307. [Google Scholar] [CrossRef]
- Vosooghi, R.; Puchinger, J.; Jankovic, M.; Vouillon, A. Shared autonomous vehicle simulation and service design. Transp. Res. Part C Emerg. Technol. 2019, 107, 15–33. [Google Scholar] [CrossRef]
- Vosooghi, R.; Puchinger, J.; Bischoff, J.; Jankovic, M.; Vouillon, A. Shared autonomous electric vehicle service performance: Assessing the impact of charging infrastructure. Transp. Res. Part D Transp. Environ. 2020, 81, 102283. [Google Scholar] [CrossRef]
- Diallo, A.O.; Moliner, M.; Manout, O.; Ciari, F. Implications of Three Autonomous Mobility Scenarios: A Comparison Between Lyon, France and Montreal, Canada; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Hörl, S.; Balac, M.; Axhausen, K. Dynamic demand estimation for an AMoD system in Paris. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 260–266. [Google Scholar] [CrossRef]
- Schlenther, T.; Volotskiy, T.; Leich, G.; Zwick, F.; Kuehnel, N.; Smirnov, J.; Nagel, K. Ridepooling and Public Transit—How Pricing Schemes Reveal the Trade-off Between Intermodality and On-Demand Efficiency; Preprint; TU Berlin, Transport Systems Planning and Transport Telematics: Berlin, Germany, 2025. [Google Scholar]
- Agriesti, S.; Roncoli, C.; Nahmias-Biran, B.H. A simulation-based framework for quantifying potential demand loss due to operational constraints in automated mobility services. Transp. Res. Part A Policy Pract. 2025, 192, 104372. [Google Scholar] [CrossRef]
- Liu, J.; Jones, S.; Adanu, E.K. Challenging human driver taxis with shared autonomous vehicles: A case study of Chicago. Transp. Lett. 2019, 12, 701–705. [Google Scholar] [CrossRef]
- Römer, J.; Goldbach, C.; Sickmann, J.; Pitz, T. Autonome Shuttle-Busse im ÖPNV. Erkenntnisse aus 17 Pilotprojekten in Deutschland. Z. Verkehrswissenschaft 2023, 93, 18–29. [Google Scholar]
- Society of Automotive Engineers (SAE). SAE Levels of Driving Automation™ Refined for Clarity and International Audience. 2021. Available online: https://www.sae.org/blog/sae-j3016-update (accessed on 28 March 2025).
- Horni, A.; Nagel, K.; Axhausen, K.W. (Eds.) The Multi-Agent Transport Simulation MATSim; Ubiquity: London, UK, 2016. [Google Scholar] [CrossRef]
- Schlenther, T.; Lu, C.; Rakow, C.; Meinhardt, S.; Nagel, K. The MATSim Open Kelheim Scenario. 2024. Available online: https://zenodo.org/records/13132756 (accessed on 1 July 2024).
- Neumann, A.; Balmer, M. Mobility Pattern Recognition (MPR) und Anonymisierung von Mobilfunkdaten; V1.0.; White Paper; Senozon Deutschland GmbH: Berlin, Germany; Senozon AG: Zurich, Switzerland, 2020. [Google Scholar]
- Zwick, F.; Kuehnel, N.; Hörl, S. Shifts in perspective: Operational aspects in (non-)autonomous ride-pooling simulations. Transp. Res. Part A Policy Pract. 2022, 165, 300–320. [Google Scholar] [CrossRef]
- Lu, C.; Kühnel, N. To Wait or to Cruise: The Trade-Off Between Waiting Time and Detours for Service Efficiency in Ride-Pooling Systems; Technical University Berlin: Berlin, Germany, 2024. [Google Scholar] [CrossRef]
- Nagel, K.; Kickhöfer, B.; Horni, A.; Charypar, D. A Closer Look at Scoring. In The Multi-Agent Transport Simulation MATSim; Ubiquity: London, UK, 2016; Chapter 3. [Google Scholar]
- OpenStreetMap. 2025. Available online: https://www.openstreetmap.org (accessed on 28 February 2025).
- Eisele, P.; Wasel, J. Application Scenarios for Autonomous Transportation; Whitepaper; P3 Group GmbH: Stuttgart, Germany, 2025; Available online: https://www.p3-group.com/en/p3-updates/application-scenarios-for-autonomous-driving/ (accessed on 23 June 2025).
- Steck, F.; Kolarova, V.; Bahamonde-Birke, F.; Trommer, S.; Lenz, B. How Autonomous Driving May Affect the Value of Travel Time Savings for Commuting. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 11–20. [Google Scholar] [CrossRef]
- Winter, K.; Cats, O.; Correia, G.H.d.A.; van Arem, B. Designing an automated demand-responsive transport system: Fleet size and performance analysis for a campus–train station service. Transp. Res. Rec. J. Transp. Res. Board 2016, 2542, 75–83. [Google Scholar] [CrossRef]
- Lu, C.; Schlenther, T.; Meinhardt, S.; Nagel, K. Quantifying the Benefits of Pre-Booking in Demand-Responsive Systems Based on Real-World Scenarios; Preprint; TU Berlin, Transport Systems Planning and Transport Telematics: Berlin, Germany, 2023. [Google Scholar]
- Meinhardt, S.; Paltra, S.; Schlenther, T.; Nagel, K. Researching the impact of extreme weather events on an On-Demand Transport service—A case study. In Proceedings of the 17th International Conference on Travel Behaviour Research, Vienna, Austria, 14–18 July 2024. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- infas.; DLR.; IVT.; infas 360. Mobilität in Deutschland—MiD Regionalbericht Freistaat Bayern. resreport, infas, DLR, IVT and infas 360, 2019. Available online: https://www.stmb.bayern.de/assets/stmi/vum/handlungsfelder/42_mid2017_regionalbericht_bayern.pdf (accessed on 1 July 2024).


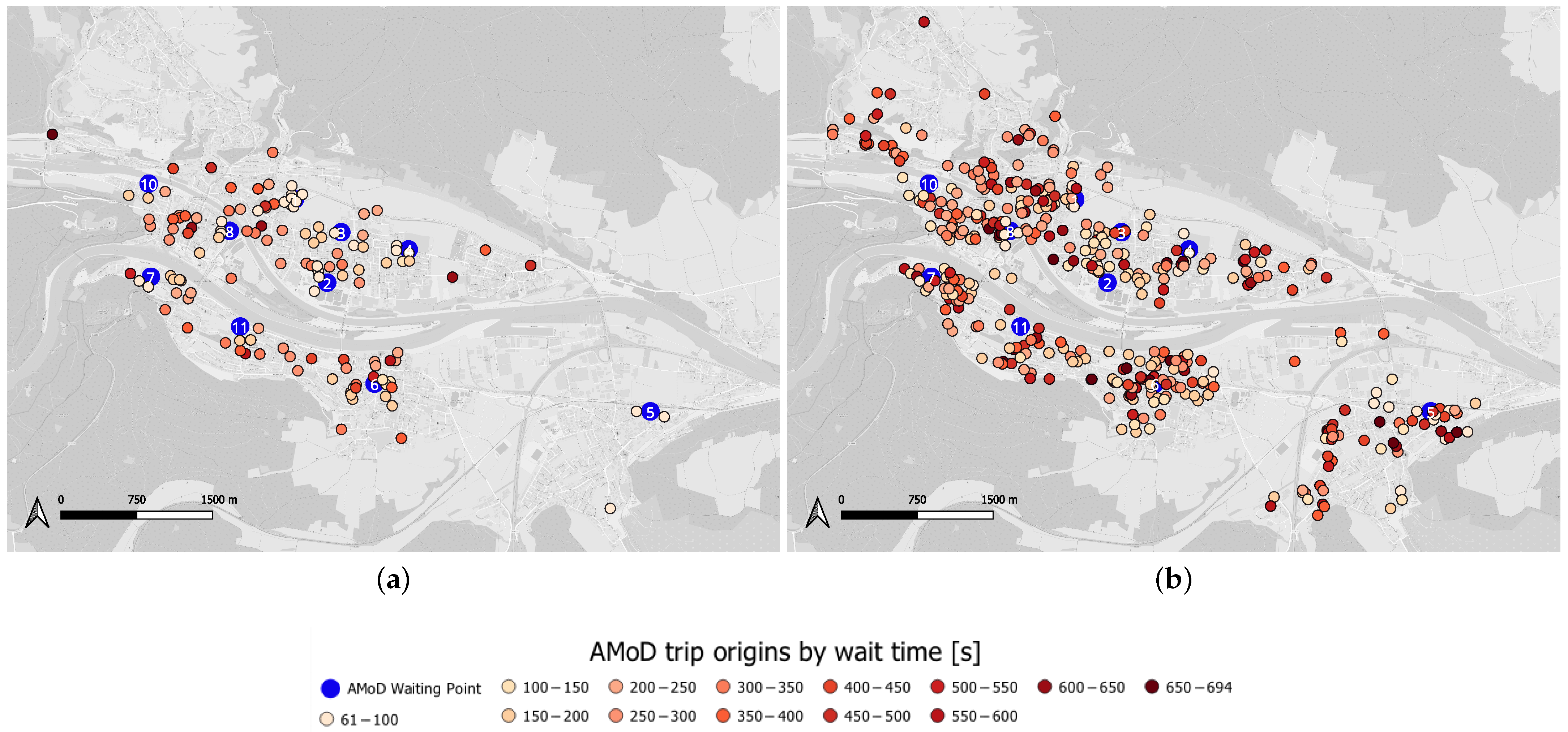

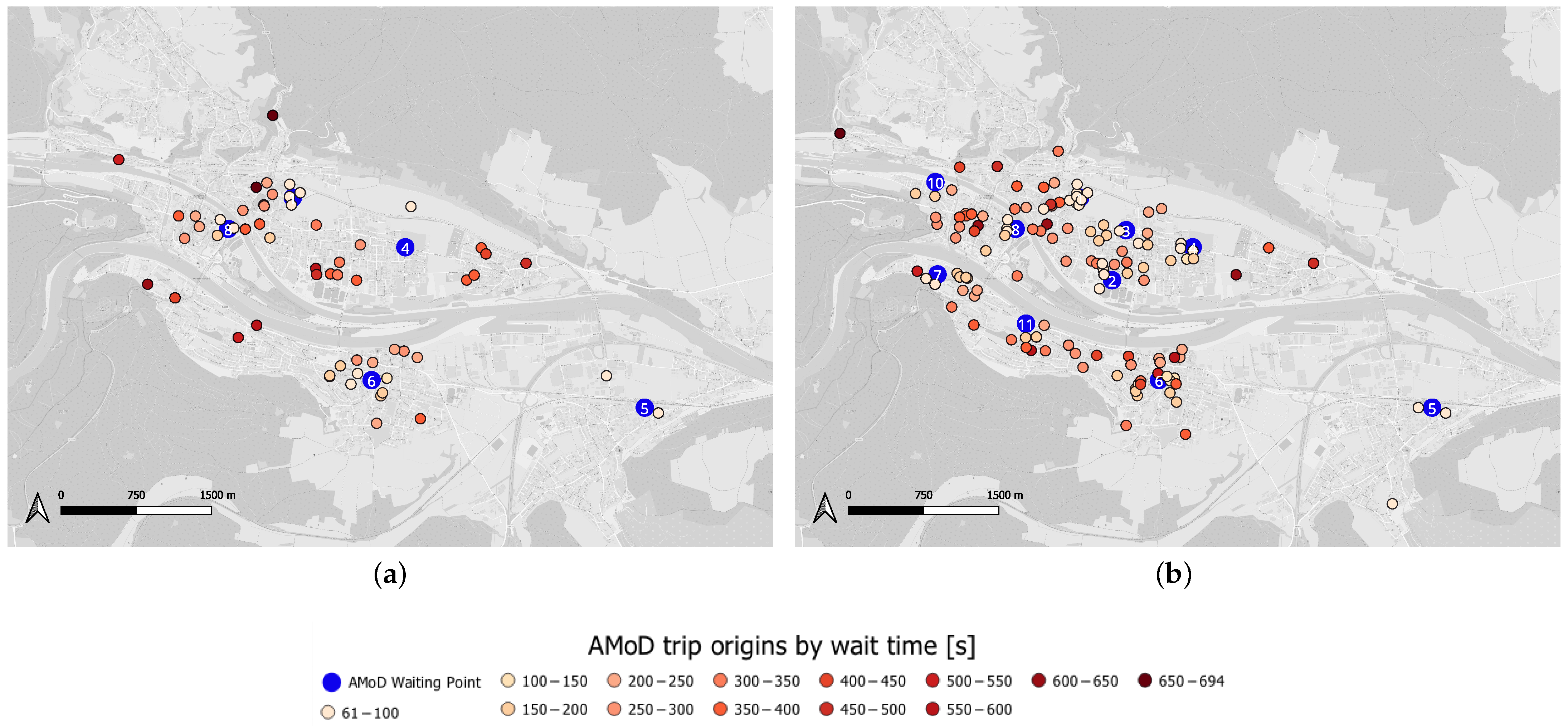

| Fleet Size | Waiting Points Area 2024 | Waiting Points Area All-City |
|---|---|---|
| 2 | 2, 7 | 5, 8 |
| 5 | 2, 7, 1, 3, 8 | 5, 8, 1, 4, 6 |
| ≥8 | 2, 7, 1, 3, 8, 4, 9, 10 | 5, 8, 1, 4, 6, 2, 10, 11 |
| ≥10 | 2, 7, 1, 3, 8, 4, 9, 10, 1, 9 | 5, 8, 1, 4, 6, 2, 10, 11, 3, 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlenther, T.; Nagel, K. The Speed of Shared Autonomous Vehicles Is Critical to Their Demand Potential. World Electr. Veh. J. 2025, 16, 447. https://doi.org/10.3390/wevj16080447
Schlenther T, Nagel K. The Speed of Shared Autonomous Vehicles Is Critical to Their Demand Potential. World Electric Vehicle Journal. 2025; 16(8):447. https://doi.org/10.3390/wevj16080447
Chicago/Turabian StyleSchlenther, Tilmann, and Kai Nagel. 2025. "The Speed of Shared Autonomous Vehicles Is Critical to Their Demand Potential" World Electric Vehicle Journal 16, no. 8: 447. https://doi.org/10.3390/wevj16080447
APA StyleSchlenther, T., & Nagel, K. (2025). The Speed of Shared Autonomous Vehicles Is Critical to Their Demand Potential. World Electric Vehicle Journal, 16(8), 447. https://doi.org/10.3390/wevj16080447







