The Impact of Renewable Generation Variability on Volatility and Negative Electricity Prices: Implications for the Grid Integration of EVs

Abstract

The introduction of Renewable Energy Sources (RESs) into the electricity grid is changing the price dynamics of the electricity market and creating room for flexibility on the consumption side. This paper investigates different aspects of the interaction between the RES share, electricity spot prices, and electric vehicle (EV) charging strategies. Based on empirical data from Germany, France, and the Czech Republic for the period 2015–2025, four research hypotheses are tested using correlation and regression analysis, cost simulations, and classification algorithms. The results confirm a negative correlation between the RES share and electricity prices, as well as the effectiveness of smart charging in reducing costs. At the same time, it is shown that the occurrence of negative prices is significantly affected by a high RES share. The correlation analysis further suggests that higher production from RESs increases the potential for price optimisation through smart charging. The findings have implications for policymaking aimed at flexible consumption and efficient RES integration.

1. Introduction

In recent years, electromobility has experienced dynamic growth, reflecting global efforts to decarbonise transport and reduce greenhouse gas emissions. The promotion of electric vehicles (EVs) in the European Union, as well as in other regions, is accompanied by a number of challenges related to their integration into the electricity grid. The most prominent of these is the impact of EV charging on both local and system loads in the distribution network, which can become a significant factor affecting the quality of supply and the stability of operation.

In parallel, the share of renewable energy sources (RESs), in particular photovoltaic and wind power plants, which are characterised by a high degree of variability and low predictability, is increasing. These characteristics lead to more frequent occurrences of market imbalances, which in practice are also reflected in negative electricity prices at certain times of the day. Such price fluctuations arise mainly at times of low demand and high RES generation and represent a significant challenge and opportunity for active market participants.

In this context, the concept of smart charging is gaining importance, which allows the EV charging process to be adapted to the current situation in the electricity market. Different forms of time-flexible charging can mitigate load peaks, increase RES availability, and reduce costs for end-users. However, research to date often relies on simulation scenarios, assumed input conditions, or complex optimisation algorithms, the application of which, in practice, is limited by data availability and the need for specialised software.

While the scientific literature [1,2,3,4] provides a number of models that show the potential of smart charging under ideal conditions, there is a lack of practice-oriented analyses based on historical data from the real market. There is also a lack of work that demonstrates that even using commonly available tools (e.g., Microsoft Excel and custom macros in VBA), the underlying relationships between RES generation, spot price development, and EV charging optimisation can be effectively quantified.

The aim of this paper is to analyse the relationships between electricity market prices, renewable generation, and the potential of smart charging strategies, using analytical tools developed in VBA in the Microsoft Excel environment. This research is based on historical data, focusing on the identification of statistically significant correlations, occurrences of negative prices, and the simulation of potential savings through time optimisation of charging. The results can be beneficial for DSOs and flexibility aggregators, as well as researchers looking for images of electricity market behaviour. This research primarily adopts the perspective of the individual electric vehicle user, aiming to minimise charging costs by responding to price signals in the day-ahead electricity market. At the same time, we acknowledge that aggregated charging behaviour can have broader implications for market dynamics and grid flexibility. These system-level aspects are addressed in the discussion, although the core analytical focus remains on the economic outcomes from the end-user perspective.

2. The Current Status of the Issue

The global expansion of electromobility raises new challenges for distribution networks. According to [5], uncoordinated EV charging—dumb charging—combined with a high penetration of renewables can cause localised congestion in distribution infrastructure, reduced voltage quality, and degraded grid limits. Conversely, an extensive analysis [6] elaborates that smart charging allows EVs to act as a flexible element of grids, where charging adapts to available capacity and price signals, leading to load smoothing, cost reduction, and support for renewables. In addition, there is a methodological overview in [7] that systematically summarises centralised, decentralised, and hybrid charging strategies, including pricing algorithms and grid and service management for necessary flexibility. The findings confirm that smart charging management can reduce daily peaks and financial costs for EV users.

At the same time as the development of RESs, the incidence of negative electricity prices is increasing. In [8], the author points out the increasing frequency of negative hours in Germany due to an excess of wind and solar generation capacity. Moreover, in other papers, an analysis of the impact of RESs on the European Day Ahead market has been carried out, showing that symptoms such as negative prices, their frequency and duration are strongly correlated with the high penetration of renewables. Research has also shown that RES growth not only promotes more frequent occurrence of negative prices, but also significantly increases price volatility, motivating the need for flexible consumer behaviour, including smart charging and V2G [9,10,11,12,13,14,15].

The recent literature has also increasingly discussed the potential of EVs as a distributed element of flexibility, particularly in the environment of developing markets for aggregated services (e.g., FCR, aFRR). Several EU countries (e.g., Germany, the Netherlands) are already piloting schemes where EVs provide regulatory services through smart charging and V2G. However, these schemes require a high level of coordination, digitisation, and trust between users and operators. In [10], the importance of Distribution Service Operators (DSOs) as key players in the integration of EVs into local flexibility markets is highlighted as another dimension to be analysed in the future [16,17,18,19,20].

While there is strong theoretical and simulated evidence for the possibility of smart charging, there is a lack of extensive empirical analysis based on historical data from market prices, RES generation, and real-world EV charging behaviour. This gap leads to a limited ability to quantify the real benefits of smart charging in the specific economic and technical contexts of distribution networks [17,20,21,22,23].

The author of [24] demonstrates the practical applicability of a PV-driven smart charging system in an urban environment, thereby confirming the importance of local production–consumption matching in preventing energy surpluses and negative electricity prices. Recent studies have also explored hybrid approaches that combine unidirectional smart charging with bidirectional energy exchange through Vehicle-to-Grid (V2G) systems. In [25], it is demonstrated that intelligent control of EV charging and discharging within a Hybrid Energy Storage System (HESS) can enhance system stability and reduce operational costs. Their findings support the growing consensus that V2G-enabled smart charging represents not only a cost-saving tool for users but also a potential grid-balancing mechanism in the context of high RES penetration. In addition to unidirectional smart charging, recent developments increasingly emphasise Vehicle-to-Grid (V2G) technologies, which enable bidirectional power flow between EVs and the grid. These systems allow electric vehicles to not only consume but also inject electricity back into the grid, supporting services such as frequency regulation, peak shaving, and congestion management. For example, Ref. [25] demonstrates how V2G-enabled smart charging improves the performance of Hybrid Energy Storage Systems (HESSs) in balancing variable renewable generation and reducing system costs. Several European countries (e.g., Germany, the Netherlands) are already piloting V2G-based regulatory service models in which aggregated EV fleets participate in balancing markets [24,25].

Based on the above, it is clear that the development of electromobility and its integration impact on the distribution network presents a multidimensional challenge, especially in the context of the increasing incidence of negative electricity prices due to the high variability of renewable energy sources. Although the high share of renewables is a key driver of negative electricity prices, market design features also play a crucial role. These include minimum bid price thresholds (e.g., −500 EUR/MWh in EPEX spot markets), limited cross-border transmission capacity, and insufficient real-time export flexibility. As highlighted in ENTSO-E, negative prices often arise when high RES generation coincides with structural limitations in market responsiveness. Thus, the phenomenon is not purely a function of supply but also of institutional and infrastructural constraints, which must be accounted for in future flexibility policies. Although several scholarly contributions confirm the technical and economic effectiveness of smart charging strategies, there is a lack of a coherent view that supports these findings with quantitative analysis based on historical market data. This paper, therefore, aims to fill this gap through an in-house analysis that focuses on identifying the relationships between electricity market prices, RES generation volumes, and EV charging time profiles in order to assess the potential of smart charging as a tool for grid flexibility and cost reduction. Based on the literature analysed and the identified research gap, the following hypotheses were established (

Table 1. Formulation of research hypotheses and proposed analytical methods.

Hypothesis	Formulation	Independent Variable	Dependent Variable	Testing Method
H1	There is a negative correlation between the RES share and spot prices.	Share of RES production (%)	Spot price (EUR)	Pearson correlation
H2	Negative prices are more common during high RES production.	Production from RESs (MWh)	Frequency of negative prices	Logistic regression
H3	Smart charging reduces costs compared to dumb charging.	Type of charging strategy	Charging costs (EUR)	Pairwise comparison/simulation
H4	A higher share of RESs leads to a larger difference between fixed and smart charging costs (∆C).	Share of RES production (%)	Difference ∆C (EUR)	Pearson correlation

), which are the subject of this paper. Their aim is to investigate the relationships between the generation profile of renewable energy sources, the evolution of electricity spot prices, and opportunities for the optimised charging of electric vehicles under conditions of price volatility [13,19,26].

3. Data and Analytical Methods Used

This section describes the input data and analytical approaches used to investigate the relationships between renewable electricity generation, electricity market prices, and the potential for the optimised charging of electric vehicles using simple algorithms implemented in Microsoft Excel. The chosen methodology reflects the desire to create fully transparent and replicable calculations based on publicly available data, without the need for advanced programming or external modelling platforms.

The analysis is based on historical data obtained from Energy-Charts.com, which offers visualised data on electricity generation, consumption, and prices. The data is processed on the basis of primary data from the ENTSO-E Transparency Platform, which guarantees its credibility and consistency within the framework of the pan-European standard for energy data transparency. Specifically, the following data types have been analysed:

−

Hourly generation from RESs (wind, solar, etc.),

−

Hourly spot prices on the Day-Ahead Market,

The period of analysis covers the years 2015 to 2025, which includes years of significant price fluctuations and increasing penetration of renewables. The chosen period of 2015 to 2025 covers major changes in the European electricity sector, including the increase in generation from RESs, the implementation of new market rules, and the increased incidence of price volatility. The methodology is based on the hypotheses formulated in the previous section, where each hypothesis was analysed as a separate relationship between two or more variables derived from the available data. All analyses were performed using built-in MS Excel functions and custom scripts created in VBA. Missing or incomplete records were identified and excluded from the analysis. Days with less than 24 h records were automatically flagged as incomplete, but were included in the statistical calculations. The analytical techniques used included the calculation of correlation coefficients, comparison of event occurrences (e.g., negative prices), simulations of costs under different charging strategies, and simple logic rule tests (rule-based detection). Each calculation was tested on a representative sample of data, and then validated by visual inspection of the outputs. All calculations respect the hourly granularity of the data, with aggregation to daily averages. Hypothesis H1 was tested using the Pearson correlation; H2 using contingency analysis and binary sorting; H3 using cost simulation under different charging time profiles; and H4 also using correlation.

3.1. Testing Hypothesis H1: Correlation Between RES Share and Electricity Price

Hypothesis H1 assumes that a higher share of electricity generation from renewable energy sources, in particular wind and solar power plants, leads to a decrease in wholesale electricity spot prices. To test it, the relationship between the hourly share of generation from RES and the corresponding hourly electricity price on the Day-Ahead Market was analysed. The Pearson correlation coefficient, which measures the strength and direction of the linear relationship between two sets of data, was used to quantify the relationship between the two variables. The calculation was performed according to the following relationship:

$$r ={\displaystyle \frac{\sum \left(X_i-\overline{X}\right)(Y_i-\overline{Y})}{\sqrt{\sum {(X_i-\overline{X})}^2}\sqrt{\sum {(Y_i-\overline{Y})}^2}}}$$

(1)

where x_i represents the fraction of RESs in hour i, y_i is the corresponding electricity spot price, $\overline{X}\overline{Y}$ are the arithmetic averages of the given variables, and n denotes the number of hours in the analysed dataset. The analysis was performed at the hourly data level, thus maintaining high temporal granularity. In this way, it is possible to account for short-term fluctuations in production from RESs and their immediate impact on market prices. This analysis results in a correlation coefficient value that allows for the determination of whether there is a statistically significant negative relationship between the RES share and the electricity price. This result will be further interpreted in the following section, which is devoted to the presentation and discussion of the obtained results.

3.2. Testing Hypothesis H2: The Occurrence of Negative Prices Depending on the Level of RESs

The second hypothesis aims to test the assumption that a high share of electricity generation from renewable sources increases the probability of negative electricity prices in the daily market. This phenomenon is increasingly common, especially in states with high wind and solar penetration, where there is a short-term surplus of electricity during low demand. The analysis was based on the classification of all hours in the period under review into two categories according to the level of RES share, namely 0–10%, 10–20%, and so on. For each of these coupes, the number of hours with a negative electricity price was then recorded. The contingency data thus obtained allow for testing the independence of negative price occurrences at the RES level using the Pearson chi-square test X². The chi-square test was calculated according to the following standard formula:

$$X^2={\sum }_{i=1}^r{\sum }_{j=1}^C {\displaystyle \frac{{\left({\mathrm{Q}}_{ij}-E_{ij}\right)}^2}{E_{ij}}}$$

(2)

where Q_ij is the observed value in cell i, j is the contingency table, and E_ij is the expected value under the independence hypothesis. Four values were used in the calculation: the number of negative and non-negative hours for low and high RESs. The test then evaluated whether the difference between the two groups is statistically significant, or whether a high proportion of RESs systematically increases the incidence of negative prices. These outputs will be presented in the next section, along with an interpretation of the results.

3.3. Testing Hypothesis H3: Impact of Smart Charging on Average Charging Costs

Hypothesis H3 assumes that smart charging of electric vehicles, which responds to price signals in the daily market, leads to a reduction in the average cost of charging compared to conventional charging over a fixed time interval. This hypothesis builds on findings from the literature that electricity consumption flexibility can be used both to optimise costs and to reduce the load on the distribution network during peak hours.

To test the hypothesis, two models of EV user behaviour were simulated:

• Fixed Charging Mode—the electric vehicle is charged at the same time every day, e.g., from 17:00 to 21:00, regardless of price trends.
• Smart Charging Mode—the vehicle is charged at the cheapest four-hour interval of the day, identified from hourly spot prices.

For each day in the analysis period, the average cost of charging in both modes was calculated. The calculations are based on the assumption that the EV needs 4 h of charging per day, with the smart algorithm aiming to minimise the cost. The difference in cost between the two modes was expressed as:

$$∆C=P_{fix}-P_{smart}$$

(3)

where P_fix is the average electricity price at a fixed charging time (e.g., 17:00–21:00) and P_smart is the average of the cheapest four consecutive hours of the day. The calculations were performed in Microsoft Excel, with the identification of the cheapest time period implemented using a sliding window and comparing the totals within the 21 possible four-hour intervals within each day. The output of this analysis is the distribution of the daily cost difference, as well as the average monthly savings when switching to smart charging. The results obtained not only allow for quantifying the economic benefits of smart charging, but also show the degree of variability in the benefits, depending on the volatility of electricity market prices.

To quantify the difference between conventional (fixed-timed) and smart (price-optimised) charging, a calculation of the daily average electricity price in both modes was created. The calculations were based on hourly spot prices for each day during the analysis period.

Fixed charging mode implies charging every day at the same four-hour interval (17:00–21:00), regardless of price. The average price per day was calculated as:

$$P_{fix,d}={\displaystyle \frac{1}{4}}{\sum }_{h=17}^{20}{Price}_{h,d}$$

(4)

where P_fix,d is the average price of electricity on a given day, d, under fixed mode and Price_ℎ,d is the price of electricity in hours ℎ during day d. The indices h = 17 to 20 denote the time interval from 17:00 to 21:00.

In the case of smart charging, the cheapest continuous four-hour period was identified for each day. For this purpose, a sliding window algorithm was applied, which analysed all 21 possible four-hour periods during each day. The calculation was defined as follows:

$$P_{smart,d}={min}_{h=0}^{20}\left({\displaystyle \frac{1}{4}}\right){\sum }_{i=0}^3{C}_{h+1,d}$$

(5)

where P_smart,d is the average price of electricity during the cheapest four-hour interval of day d, ℎ is the start of the time window that moves from hour 0 (0:00) to hour 20 (20:00). i is the shift within the window width (0 to 3) and C_h+1,d are the individual prices within the selected section.

Days have 24 h. If we want to find a continuous four-hour interval, we have to start at the 20th hour at the latest, because then we still have 20, 21, 22, and 23 (4 h). Therefore, we tested all possible “beginnings” of a 4 h interval, as follows:

h = 0—interval 00:00–04:00

h = 1—interval 01:00–05:00

…

h = 20—interval 20:00–24:00

Thus, there are 21 of these possibilities. For each “window” starting at hour h, we added the prices of four consecutive hours, e.g., if h = 5, we added C_5,d, C_6,d, C_7,d, and C_8,d. We then divide this value by ¼ because we wanted to calculate the average price.

The difference between fixed and smart charging was calculated for each day as:

$$∆C=P_{fix,d}-P_{smart,d}$$

(6)

where ΔC is the daily cost difference between the fixed and smart mode.

The average monthly and annual savings were then derived from the daily differences thus obtained. The results were also analysed in terms of their distribution (e.g., by histogram), allowing for the estimation of the occurrence of extreme advantages or disadvantages in smart charging. This methodology forms the basis for further analysis in the Results section, where the potential economic benefits of smart charging in different countries and time periods are assessed.

Relations (4) to (6) are valid if the charging analysis is performed for 4 h of charging. Similarly, this would also be true for a change in the number of hours of charging.

3.4. Testing Hypothesis H4: The Effect of the RES Share on the Cost Difference (∆C)

Hypothesis H4 assumes that a higher share of electricity generation from renewable energy sources (RESs) increases the potential for cost optimisation through smart charging. This assumption is based on an economic and physical reality: when there is a high share of solar and wind generation in the system, spot prices fall, their extremes occur more frequently, and the price differentials between hours widen. This creates a space that smart charging can exploit to minimise costs compared to fixed (inflexible) charging.

Correlation analysis was used to test the hypothesis between the following variables:

−

Independent variable: daily share of RESs in total electricity generation (%);

−

Dependent variable: daily difference ∆C between fixed and smart charging costs (in EUR/MWh);

−

Range of charging lengths: 2, 3, 4, 5, and 6 h per day.

The analysis was carried out separately for each country (Germany, France, and the Czech Republic) and for each year in the period 2015–2025, as well as for the whole period in total. This resulted in a set of correlation matrices that quantify the relationship between RESs and ∆C in each scenario. The correlation coefficient was calculated using the Pearson correlation method.

In addition to the relationship between RESs and ∆C, the correlations between each ∆C at different charging times were also analysed. This additional analysis served to verify the consistency of ∆C between different strategies—that is, the extent to which the results depend on the specific number of charging hours chosen. The high correlation between the two may indicate the robustness of the model to this choice.

The aim of this analysis was to answer the question of whether the assumption “The more RESs in the system, the more room for savings through smart charging” is valid. The results obtained are presented in detail in the Results section for H4 and interpreted in the context of each country separately.

4. Comparative Analysis

In order to extend the validity of the results and to take into account the different characteristics of the national electricity systems, the analysis was extended by comparing three countries with different resource mixes and market behaviour. The selection of countries was guided by the desire to capture contrasting approaches to renewable energy development and their impact on pricing.

Germany is a country with a high penetration of renewables, especially wind and solar, and at the same time, frequent negative electricity prices. The high price volatility makes Germany a good case for testing hypotheses about the impact of RESs and the effectiveness of smart charging.

France’s dominance in nuclear power has given it a more stable production profile and less dependence on short-term flexibility. It serves as a contrasting case, with a lower probability of extreme price fluctuations.

The Czech Republic represents a country with a gradually increasing share of RESs and an electricity system undergoing transformation. Due to its location in Central Europe and moderate price volatility, it serves as a transitional case between Germany and France.

The inclusion of these three countries creates room for testing hypotheses in different contexts and also opens up the possibility of a comparative evaluation that will contribute to the formulation of more generalizable conclusions.

Hypothesis H1.

The correlation between the RES share and the electricity price.

The objective of this part of the analysis is to quantitatively test the assumption that a higher share of renewables in the electricity system leads to lower spot electricity prices in the daily market. Thus, Hypothesis H1 assumes that there is a negative linear correlation between the RES share and the electricity price in a given hour.

The calculations do not consider the absolute amount of generation from wind and solar resources (e.g., in megawatt hours), but their share of total hourly generation, which takes into account the current demand and system context. This approach is methodologically sounder, as it eliminates seasonal and volume biases that could arise when analysing disproportionate or incomparable electricity volumes between different time periods or countries.

The proportion of RESs in each hour was calculated using the following formula:

$${Ratio}_{RES}={\displaystyle \frac{P_{RES}}{P_T}}$$

(7)

where P_RES is renewable energy generation, P_W is wind generation, and P_T is total electricity generation. Based on this proportion, a pair of values, Ratio_RES and Day Ahead price, was constructed for each hour in the period 2015–2025. For each calendar year, the hourly Pearson correlation between these two variables was then calculated using the standard correlation coefficient (1).

The results (Figure 1 and

Table 2. Table of annual correlation between RES share and electricity price for Germany, France, Czech Republic during years 2015–2025.

Year	GE	FR	CZ
2015	−0.83	−0.21	−0.27
2016	−0.79	−0.65	−0.35
2017	−0.83	−0.51	−0.32
2018	−0.72	−0.70	−0.39
2019	−0.82	−0.56	−0.51
2020	−0.85	−0.65	−0.60
2021	−0.51	−0.53	−0.56
2022	−0.65	−0.28	−0.09
2023	−0.88	−0.63	−0.56
2024	−0.70	−0.72	−0.62
2025	−0.88	−0.71	−0.79

) of the correlation analysis between the hourly share of generation from renewable energy sources and the spot price of electricity in the period 2015 to 2025 confirm a consistent negative linear dependence in all the countries analysed—Germany, France, and the Czech Republic. The calculations were carried out separately for each year, thus taking into account the dynamics of the energy mix evolution over time.

Germany (GE), as the country with the highest penetration of RESs, observed the most significant negative correlation coefficients throughout the period. The values ranged from −0.51 (in 2021) to −0.88 (2023 and 2025), indicating a consistently strong negative relationship between the RES share and price. This trend reflects a strong market response to high volumes of nearly cost-free generation from wind and solar, which often leads to prices falling into negative territory.

In France (FR), where nuclear power dominates, the correlations are also mostly negative, but less pronounced. The weakest correlation was in 2015 (r = −0.21), while in 2018 and 2025, they were already around −0.70. This suggests that even in a system with a stable base, the gradual integration of the RES can affect price dynamics, albeit less directly and with more inertia than in the case of Germany.

In the Czech Republic (CZ), the correlation values were initially weaker (e.g., −0.27 in 2015), but have strengthened with the increasing integration of renewables. From 2020 onwards, correlations dropped below −0.50, reaching −0.79 in 2025, the strongest negative correlation in the whole decade. This development confirms that as the RES share also increases in Central European systems, conditions for greater price sensitivity to renewable generation emerge.

A graphical representation of the evolution of the correlation coefficients is presented in Figure 1. It is clear that, despite short-term fluctuations (e.g., 2022), there is an amplifying trend of a negative relationship between the RES share and electricity price in the long term in almost all countries. These results confirm the validity of hypothesis H1 and also highlight the importance of adaptive consumer behaviour and market mechanisms in an environment with increasing renewable generation dynamics. The bar chart clearly shows the persistent presence of a negative relationship in all three countries, with Germany consistently showing the strongest negative relationship throughout the period. France and the Czech Republic show more variability from year to year, which may be due to the different stability of production and the structure of the resource mix. Temporary weakening of the correlation is visible in 2022–2023, which may be related to exceptional market events (e.g., energy crisis, instability in supply). Despite these fluctuations, the long-term trend confirms the increasing influence of RESs on pricing across Central Europe.

Table 1 shows the values of the Pearson correlation coefficient between the hourly RES share and the spot electricity price on the daily market, calculated separately for each calendar year in the period 2015 to 2025 and for the three countries analysed: Germany (GE), France (FR), and the Czech Republic (CZ). Negative correlation values document an inverse relationship between the share of renewables and price, while more significant negative values indicate a higher price sensitivity to a change in the RES share. The strongest negative correlation was observed in Germany, where r-values during the period under review were below −0.85 in some years. In contrast, in the Czech Republic, the trend of an amplifying correlation was particularly pronounced after 2020.

Hypothesis H2.

The occurrence of negative prices depending on the level of RESs.

The aim of this section is to test hypothesis H2, according to which a higher share of electricity generated from renewable sources correlates with a higher incidence of negative spot prices in the daily market. The theoretical basis for this hypothesis is based on the well-known mechanisms of the merit-order effect, which causes resources with higher marginal costs to be driven out of the market during periods of high generation from wind or solar resources. When demand becomes saturated with low-cost generation from RECs, a situation can arise where the remaining demand is met exclusively by near-zero-cost resources, which, combined with low system flexibility, can result in negative price signals. Aggregated hourly data was used to empirically test this hypothesis, as follows:

−

The share of RES production in total consumption;

−

The spot price of electricity (Day-Ahead Price).

The data covers the period 2015–2025 and has been analysed for three countries, Germany (DE), France (FR), and the Czech Republic (CZ), which differ in terms of RES penetration rates, generation structure, and regulatory frameworks. For each country, the hourly data were divided into intervals of RES share of 10% (0–10%, 10–20%, and up to 90–100%). Within each interval, the frequency of occurrence of negative prices was then calculated. This approach allows for capturing the non-linear behaviour of the market while providing an intuitive visual overview of which RES share ranges are most likely to have negative prices.

The results can then be interpreted in terms of:

−

The economic consequences of high RES production;

−

System flexibility and market response;

−

Cross-country differences in price sensitivity to RES generation.

The analysis of Hypothesis H2, which focuses on the association between the occurrence of negative electricity prices and the share of renewables in total generation, yielded clear and consistent patterns both within and across country comparisons. The results were analysed on the basis of histograms in which hourly values were divided according to the RES share into 10% intervals (0–10%, 10–20%, …, 90–100%). Within each interval, the proportion of hours with a negative electricity market price (Day Ahead Price < 0 EUR/MWh) was detected. Detailed tables of the results are presented in Appendix A.

In the case of Germany, the results clearly show an increasing probability of negative prices with a higher share of RESs. For intervals below 50%, negative prices are practically non-existent. However, their incidence starts to increase sharply for RESs above 60%, with the share of negative prices in the 70–80% category reaching more than 40% in several years, and in the 80–90% category reaching almost 100% (e.g., 2019). A cumulative analysis over the entire 2015–2025 period shows that the highest proportion of negative prices (34.76%) occurred in hours with an RESs share between 80–90%, which contrasts sharply with the zero occurrence of negative prices for RESs shares below 40%. These results clearly support Hypothesis H2.

In France, the incidence of negative prices is generally very low, being practically insignificant until 2019. It is only in recent years (2020–2025) that higher proportions of negative prices are starting to be recorded, with a higher share of RESs. For example, in 2025, the share of negative prices reaches 21.42% at RES shares of 30–40%, and as high as 37.66% at RES shares of 40–50%. However, these figures remain isolated and appear only in very small numbers of hours. Overall, France confirms that, although the increasing share of RESs may create the preconditions for negative prices, their occurrence is likely to be dampened by the different structure of the electricity system and the flexibility of demand or exports. Aggregate data for the period 2015–2025 show that only when the RES share is above 30% does the share of negative prices approach or exceed 5%.

For the Czech Republic, the results are in a sense between Germany and France, although closer to France. In years with a low RES share, negative prices are rare, but at a share of 30–40% they are already more frequent in some years (e.g., 18.96% in aggregate over the whole period). The increase in the share of negative prices is particularly pronounced for RESs in the 40–60% range, reaching up to 57.14% (40–50%) and 73.33% (50–60%) in the aggregate data. Given that the Czech electricity system has a lower share of RESs than Germany, these figures suggest that even with lower network load, negative prices can occur if there is insufficient flexibility in generation regulation or export possibilities.

These results support Hypothesis H2 in the sense that the occurrence of negative prices is strongly associated with a high share of RESs. However, the magnitude of this phenomenon varies considerably between countries, highlighting the importance of national market structures and the technical flexibility of energy systems. The results of Hypothesis H2 clearly confirm that a higher share of RESs in the generation mix significantly increases the probability of negative spot prices, especially in countries with high renewable penetration and limited system flexibility. However, it is important to recognise that the occurrence of negative prices is not solely a function of renewable output. Market design elements, such as minimum bid price thresholds, limited cross-border transmission capacity, and a lack of responsive demand-side flexibility, also play a critical role in amplifying price inversions. For example, in Germany, even with high RES production, negative prices often arise only when export options are constrained or when the system is saturated with inflexible base-load generation. Similarly, in France and the Czech Republic, structural differences in market configuration and interconnection levels help explain why negative prices are less frequent or more contained, despite growing RES shares. These findings suggest that while the correlation between RESs and negative prices is statistically strong, a complete understanding of the phenomenon requires integrating market architecture and regulatory conditions into the analysis. Future research could, therefore, benefit from including variables related to grid congestion, bidding rules, or export dynamics to further refine the causal framework underlying price volatility and market imbalance. It is important to recognise that price formation within the integrated electricity market is not determined solely by local imbalances between generation and demand. Network constraints also play a critical role and are explicitly captured in flow-based market models using Power Transfer Distribution Factors (PTDFs). These matrices quantify how cross-zonal commercial exchanges affect loading on individual transmission elements and, in turn, determine the available cross-border capacities. As a result, even if there is a renewable generation surplus in one bidding zone, negative prices may not occur in neighbouring countries due to limited transmission capacity and congestion risks defined by the PTDF structure.

Hypothesis H3.

Impact of smart charging on average charging costs.

The development of electromobility is driving a growing demand for efficient and cost-optimised electric vehicle (EV) charging. From a consumer perspective, charging represents a significant item of total operating costs, and it is the price volatility in the electricity spot market that creates scope for cost reduction through the optimisation of the timing of off-take. In this context, the concept of ‘smart’ charging is increasingly being promoted, which responds flexibly to current price and network signals and makes targeted use of periods of low electricity prices—for example, at night or during high RESs on the grid.

The object of testing hypothesis H3 is to quantify the difference in the average price of electricity that would be consumed for EV charging in two contrasting scenarios:

−

Dumb charging represents a rigid, time-fixed charging profile that does not take into account price signals (e.g., regular charging from 17:00 to 20:00),

−

Smart charging implies flexible charging management that targets the three hourly intervals with the lowest spot electricity price each day.

In both cases, the same daily volume of energy needed to recharge the vehicle is considered, allowing direct cost comparability without being affected by the overall consumption range. The calculations are based on historical hourly prices from the Day-Ahead market and assume ideal conditions in terms of charging availability and user (or automated system) responsiveness.

The aim of this analysis is to identify whether smart charging leads to a statistically significant reduction in the average price per kWh compared to traditional fixed charging, and to observe how this difference evolves over time and between countries with different market and production profiles. The results will be presented in the form of clear tables, graphs, and their scientific interpretation.

4.1. Monthly Cost Savings (∆C)—Heatmap 2015–2025

To test hypothesis H3, an analysis of the monthly cost savings of charging electric vehicles using a smart charging algorithm compared to a conventional fixed charging mode was performed. As a baseline scenario, the fixed mode was chosen between 17:00 and 21:00, with a daily charging requirement of 4 h. For each day in the period 2015–2025, a cost difference ∆C was calculated, defined as the difference between the average price in a given fixed interval and the lowest possible average price in any four-hour window of that day. Subsequently, these daily values were aggregated into monthly totals to produce a cumulative monthly savings metric. The results are visualised in the form of heatmaps, where each row represents a month (1–12) and each column represents the corresponding calendar year (2015–2025). The intensity of the colour represents the amount of monthly savings, allowing for the identification of time periods with the highest potential for cost reduction through a smart charging strategy. The heatmaps prepared in this way were created separately for each of the countries studied—Germany (

Table 3. Heatmap of the cumulative ∆C value for Germany during the years 2015–2025 in EUR/MWh.

	2015	2016	2017	2018	2019	2020	2021	2022	2023	2024	2025
1	557.23	525.72	661.86	535.79	348.26	224.63	90.39	556.1	166.52	68.18	297.08
2	633.03	460.85	490.45	252.91	196.59	177.43	102.91	577.71	312.38	82.11	335.56
3	697.6	402.95	422.27	422.63	361.04	342.18	322.68	1531.53	397.08	495.21	1794.85
4	565.64	313.62	533.72	493.73	347.46	517.55	501.4	1087.75	857.71	1032.1	2424.68
5	400.04	531.24	511.46	509.97	402.84	365.88	852.3	1611.68	1451.12	1613.68	2895.61
6	425.42	376.11	493.94	406.32	569.48	315.94	430.86	1500.67	1057.84	2041.84
7	546.96	344.72	456.04	398.86	276.11	474.97	519.2	3160.37	1515.97	1721.73
8	520.46	446.37	465.51	570.82	418.05	304.21	438.13	2701.54	848.13	1914.73
9	598.49	484.13	487.45	577.46	305.23	287.19	444.25	1111.74	764.65	1234.12
10	622.35	452.91	732.06	537.97	251.95	246.32	674.03	706.59	542.8	399.61
11	637.01	414.9	394.67	119.84	152.96	79.21	317.52	113.14	121.85	308.89
12	584.33	582.29	512.46	478.17	329.07	167.13	495	64.94	98.27	235.62

Note: Cell background colours represent the monthly cost savings (∆C) in EUR/MWh. Green denotes low savings, yellow to orange medium savings, and red high savings.

), France (

Table 4. Heatmap of the cumulative ∆C value for France during the years 2015–2025 in EUR/MWh.

	2015	2016	2017	2018	2019	2020	2021	2022	2023	2024	2025
1	526.26	709.4	1175.67	780.85	801.52	554.38	864.58	2624.43	2260.65	1242.13	2042.56
2	551.59	518.47	650.3	575.83	485.81	465.37	736.38	2052.15	1420.12	976.26	1495.92
3	592.03	383.92	499.93	652.63	507.89	474.59	744.65	3047.96	1675.27	1162.58	2105.87
4	438.64	253.41	302.57	478.37	380.92	285.97	602.94	1888.85	1456.63	781.18	1603.16
5	365	343.06	399.17	532.01	401.12	297.89	951.94	1806.97	1446.29	787.98	1070.36
6	449.4	373.42	395.68	522.93	490.7	370.54	815.8	2601.32	1446.12	1200.4
7	544.48	323.01	354.7	464.74	436.39	445.03	983.74	4931.12	1404.97	1595
8	456.18	419.27	404.88	593.14	429.3	560.07	1293.08	5704.28	1545.64	1778.59
9	582.16	579.06	524.96	744.86	611.24	838.58	1822.35	5682	2121.37	1720.49
10	669.86	919.66	873.8	944.48	766.5	702.15	3156.34	3469.33	2393.46	1879.4
11	799.76	2101.57	1170.72	1114.61	692.36	671.34	2870.14	3388.6	1925.36	1717.96
12	737.94	854.63	957.06	866.48	747.14	937.12	3607.73	4128.83	1279.53	2081.92

Note: Cell background colours represent the monthly cost savings (∆C) in EUR/MWh. Green denotes low savings, yellow to orange medium savings, and red high savings.

), and the Czech Republic (

Table 5. Heatmap of the cumulative ∆C value for the Czech Republic during the years 2015–2025 in EUR/MWh.

	2015	2016	2017	2018	2019	2020	2021	2022	2023	2024	2025
1	691.86	570.8	706.07	459.77	266.71	120.7	100.29	295.54	98.49	63.62	366.12
2	623.5	512.18	494.56	240.07	173.29	170.09	104.99	421.62	223.8	102.59	378.87
3	651.35	414.72	439.63	394.01	306.17	230.88	100.36	1259.51	316.07	445	1726.26
4	481.38	310.6	463.05	480.85	262.07	271.19	242.34	862.44	553.11	1014.23	2387.41
5	397.11	436.77	489.86	464.72	386.53	294.31	459.45	1032.84	1027.54	1606.89	2610.54
6	421.43	483.15	478.62	405.57	479.72	242.95	370.26	1108.46	957.94	1405.54
7	523.54	372.98	526.11	394	281.81	285.55	332.52	2569.35	639.57	1282.98
8	556	407.83	494.14	548.07	303.63	243.62	300.66	1662.48	818.97	1622.86
9	636.47	536.94	512.82	559.95	254.75	203.73	358.72	739.52	709.58	1090.74
10	658.83	699.33	716.24	529.71	207.29	202.41	458.2	463.71	410.69	428.69
11	664.31	436.92	404.82	173.77	124.46	62.05	222.39	50.96	113.29	478.24
12	580.01	482.83	467.16	402.6	217.48	104.03	326.39	77.21	92.03	372.67

Note: Cell background colours represent the monthly cost savings (∆C) in EUR/MWh. Green denotes low savings, yellow to orange medium savings, and red high savings.

)—and provide a comprehensive picture of the temporal and spatial variability of smart charging efficiency.

Based on simulations of the cost difference between fixed charging (17:00–21:00) and smart charging, heatmaps for Germany, France, and the Czech Republic for the period 2015–2025 have been produced. These maps visualise the monthly sum of the daily cost difference (∆C), with each cell representing the cumulative cost saving for a specific month of a given year, expressed in EUR/MWh.

The results for Germany show a stable and consistent benefit of smart charging across the entire period under review. Savings average between EUR 300 and EUR 600/month until 2020, with the exception of slightly lower values in 2020 and 2021, which may reflect reduced price volatility during the COVID-19 pandemic. However, a sharp increase in savings is observed from 2022 onwards, with monthly ∆C values reaching as high as EUR 2000–2900 in some months in 2023 and 2024, indicating extreme price volatility during this period. Such developments confirm that the potential of smart charging grows with increasing price dynamics.

In the case of France, there is significantly higher year-to-year variability. The most significant savings are concentrated in the period 2022–2024, when monthly ∆C values in the summer and autumn months (e.g., July to October) often exceed EUR 4000, and in extreme cases, up to EUR 5700. This evolution is in line with the significant price fluctuations on the French market, mainly due to the nuclear generation crisis and the increased reliance on imports during 2022–2023. In contrast, the period 2015–2019 shows savings of a lower order (EUR 300–800), suggesting that the smart charging effect is more pronounced in times of market turbulence.

For the Czech Republic, the results are consistent, but on average slightly lower than for the previous countries. Until 2020, monthly savings are mostly in the EUR 300–600 range, with a slight increase after 2021. A significant increase in ∆C occurs especially in 2023–2024, where monthly savings reach up to EUR 2600 (e.g., May 2025), which correlates with increasing penetration of renewables and increased price volatility. Although the Czech market is smaller and less volatile, the benefits of smart charging are still evident here, especially during periods of high load or regional price fluctuations.

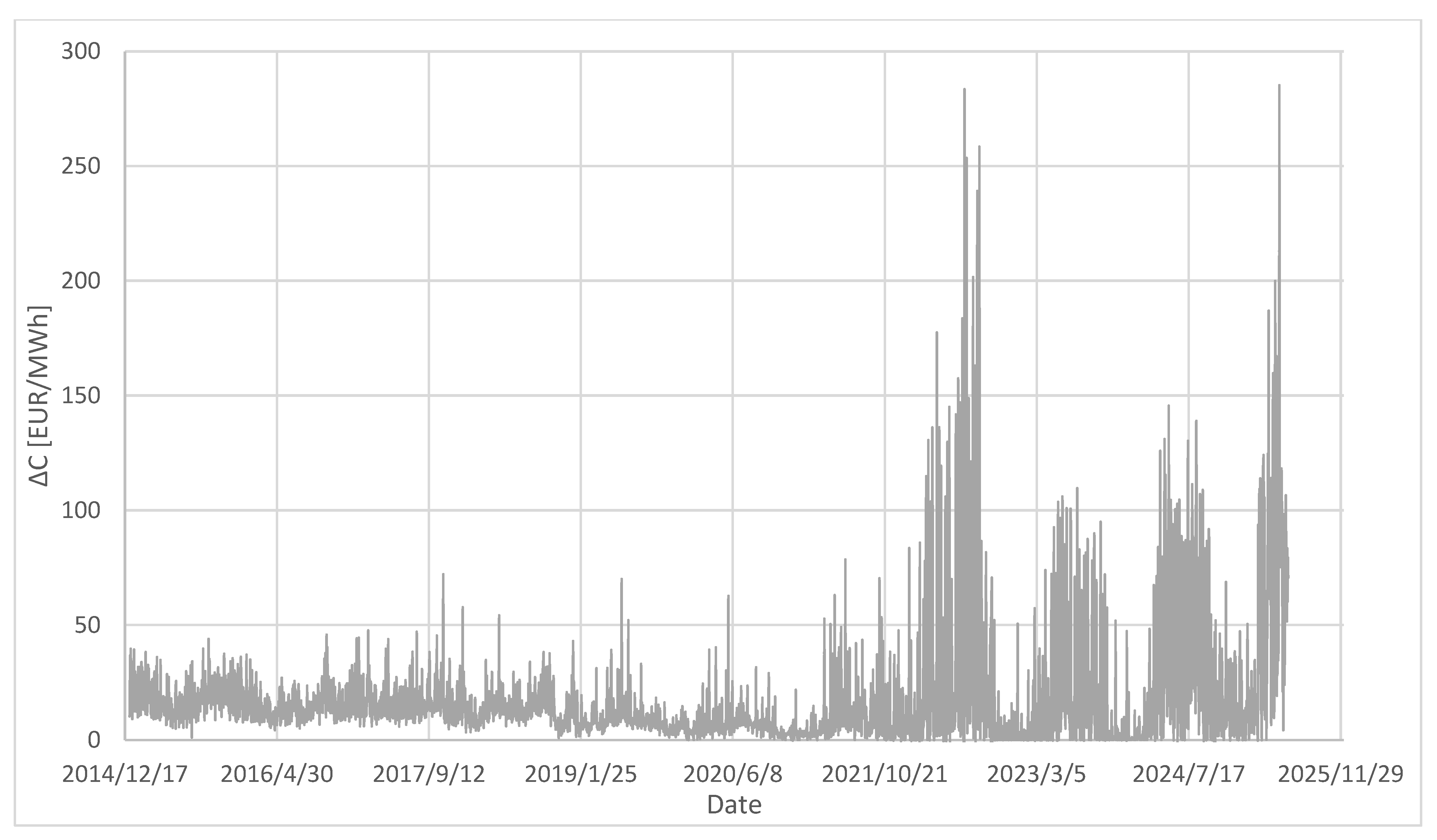
4.2. The Evolution of the Daily Saving ∆C over Time (2015–2025)

To better understand the dynamics of the impact of smart charging on daily costs, the differences between fixed and smart charging were calculated for each day of the analysis period. The resulting daily ∆C values (in EUR/MWh) are visualised over time through a trio of graphs, each corresponding to one country under study—Germany (Figure 2), France (Figure 3), and the Czech Republic (Figure 4).

Germany—Figure 2

The evolution of ∆C in Germany shows relatively stable values between 2015–2019, with slight fluctuations mainly related to price seasonality. From 2020 onwards, there is a gradual increase in variability and in the value of the ∆C itself, culminating in 2022 and 2023—periods of high electricity prices. In these years, extreme savings peaks of more than 60 EUR/MWh are visible. This trend shows the growing economic potential of the smart charging approach at a time of increasing price volatility.

France—Figure 3

French data show even higher volatility than German data. Between 2017 and 2021–2023, significant daily savings, often in excess of EUR 50/MWh, repeatedly appear. Particularly high values were recorded during 2022, which corresponds to the energy crisis and the reduced availability of nuclear generation. These developments suggest that charging flexibility can be a key tool for households and fleet operators to reduce costs in the face of market shocks.

Czech Republic—Figure 4

In the Czech Republic, the daily differences between fixed and smart charging are generally lower than in the previous two countries. However, the development is similar—stable and lower ∆C in 2015–2019, a gradual increase in variability after 2020, and clear price peaks in 2022 and 2023. Although absolute savings are smaller on average, the increasing benefit of smart charging management is also confirmed here with increasing price volatility.

4.3. The Effect of Charging Duration on the Amount of ∆C Saving

To assess the impact of charging duration on the cost difference (∆C) between fixed and smart charging, an analysis was performed for a range of 2 to 6 h of charging per day. For each country (Germany, France, and the Czech Republic), aggregated heatmaps were created, capturing the ∆C for each month over the period 2015–2025. Smart charging was always optimised to select the cheapest hourly intervals corresponding to a fixed charging duration. The results show a clear trend: as the charging length increases, the total monthly saving (∆C) increases in most cases. This phenomenon is due to the fact that for longer intervals, the smart charging algorithm has a wider choice of prices and can select the cheapest hourly blocks more efficiently. In particular, the highest ∆Cs were obtained at the 6 h charging interval, while the lowest differences were observed at the 2 h interval.

At the same time, there were significant differences between countries. France showed the highest monthly savings at all intervals, reflecting greater price volatility and differences between peak and off-peak hours. Germany showed a more stable increase in ∆C with increasing charging duration, while the Czech Republic showed lower but still consistent savings, especially after 2020.

An important insight also emerges from the comparison between years: in years with extreme price fluctuations (e.g., 2022–2023), the differences between fixed and smart charging were most pronounced, confirming the benefit of dynamic strategies in times of market uncertainty.

These findings support hypothesis H3 that the expansion of flexible smart charging can lead to significant savings, especially if the user is able to adjust the time range of charging to the current price conditions.

In the next part of this research, hypothesis H3, the dependency between the length of the daily charging interval and the amount of potential savings brought about by intelligent (smart) charging of electric vehicles compared to fixed charging, was analysed. The aim was to investigate how the cost difference between the two modes varied with the amount of time flexibility the user had.

The simulation was carried out for five scenarios:

−

2 h of charging (e.g., 17:00–19:00),

−

3 h (17:00–20:00),

−

4 h (17:00–21:00),

−

5 h (17:00–22:00),

−

6 h (17:00–23:00).

In each case, the fixed mode assumed that the user charges the vehicle daily at a fixed interval. In contrast, in smart mode, the cheapest continuous period of time with a corresponding length was identified individually for each day, using the sliding window principle. Thus, for each day, the smart algorithm selected the time window that minimised the average price for the desired number of hours. The daily cost difference was calculated according to Formula (6).

The obtained daily ∆C values were subsequently:

−

Aggregated into monthly totals and visualised in the form of heatmaps;

−

Averaged over the whole period 2015–2025 from the values for different charging times (2 h to 6 h).

Since displaying all ∆C traces for each day and all charging regimes at once would be graphically opaque, an alternative form of visualisation was chosen. For each state, the average value of daily ∆C was calculated separately for each scenario (2 to 6 h). The result was a single waveform (Figure 5) for each state, which captures the trend of the relationship between the length of charging and the amount of economic benefit of the smart mode. The three waveforms were then plotted in a common graph, allowing for direct comparison between countries.

This analysis provides a comprehensive view of how the amount of flexibility provided (in hours) affects the cost difference between traditional and cost-optimised charging.

In order to complement the previous analysis, the average daily value of the cost difference ∆C (in EUR/MWh) over time was processed separately for Germany (GE), France (FR), and the Czech Republic (CZ). The graph in Figure 5 shows the individual time series for each country over the period 2015 to 2025. Each point represents the average of the daily ∆C values across all the tested charging lengths (2 to 6 h), thus suppressing excessive variability and making the overall trends stand out more clearly.

This analysis confirms significant volatility over the period under review. The most significant increases in ∆C are observed during the energy crisis in 2022 and 2023, which is consistent with the extreme increase in electricity prices in spot markets. It is during this period that smart charging achieves the greatest relative advantage over fixed mode.

A comparison between countries shows that:

−

France (FR) had the highest ∆C values at the time of the crisis, with peaks exceeding EUR 300/MWh, indicating a high potential for savings in smart charging. However, fluctuations are relatively frequent and dispersed.

−

The Czech Republic (CZ) shows a similar trend to France, albeit with lower peaks. The trend is smoother and less extreme.

−

Germany (GE) has the most stable pattern with relatively lower ∆C values over most of the period under study. Nevertheless, more pronounced fluctuations are observed in 2022–2023, which correspond to turbulent market conditions.

In the period before 2021, differences between modes were, on average, low and relatively stable, suggesting lower price volatility and less benefit from smart charging optimisation. From 2021 onwards, however, there is a rapid increase in the contribution of smart algorithms due to extreme market fluctuations.

In conclusion, this graph confirms the ability of smart charging to respond flexibly to price signals in the market, and also highlights an important insight: the more volatile the market, the greater the economic difference between fixed and smart modes can be achieved.

To assess the impact of charging duration on the cost difference (∆C) between fixed and smart charging, an analysis was performed for a range of 2 to 6 h per day. Summary heatmaps were created for each country (Germany, France, and the Czech Republic), capturing the ∆C for each month over the period 2015–2025, which can be seen in Appendix B. Smart charging was always optimised to select the cheapest hourly intervals corresponding to a fixed charging duration.

The heatmap visualisations for Germany clearly show that the cost savings from smart charging (∆C) increase systematically with increasing charging duration. This relationship is consistent across the entire analysis period (2015–2025), although the degree varies depending on market conditions and price volatility in specific years.

From the heatmap results, it can be observed that the highest ∆C values for Germany were between 2015 and 2017. On the other hand, between 2018 and 2021, the ∆C parameter reached its lowest values. For France, however, the situation is different. The highest ∆C values were observed between 2022 and 2025, and partly in the second half of 2021. This is true for all charging periods. From the results, it can be observed that the highest ∆C values were reached in the first years of the period under study, and the ∆C values gradually decrease.

The heatmaps of France show that from 2015 to 2025, ∆C values increased steadily. While in 2015, the ∆C values were in the order of hundreds of EUR/MWh, later, higher values in the order of thousands started to appear.

In the case of the Czech Republic, the situation is slightly different. The highest ∆C values were reached in 2022, 2024, and 2025. The ∆C values first decreased over the period under consideration and started to increase again after 2021.

The results of the analysis clearly demonstrate that extending the charging interval significantly increases the potential cost savings when switching from fixed to smart charging. In all the countries analysed—Germany, France, and the Czech Republic—a positive correlation between the length of daily charging and the value of the cost difference ∆C was identified. This correlation is a consequence of the wider optimisation possibilities for longer intervals, which smart charging makes efficient use of.

However, the dynamics of the ∆C vary considerably across countries and time periods, highlighting the importance of specific market conditions. For Germany in particular, the highest ∆C values were recorded in the early years of the analysis period (2015–2017), reflecting the price volatility and opportunities for price arbitrage at the time. In contrast, the years 2018 to 2021 were characterised by lower levels of savings, which may be a consequence of a more stable price profile in the market. In France, an inverse trajectory was identified—the value of the ∆C increased systematically during the period under review, with the highest savings recorded between 2022 and 2025. This trend suggests a gradual increase in price volatility in later years, creating favourable conditions for smart charging to operate effectively. In the case of the Czech Republic, the development has been non-linear. After an initial decline in savings in 2015–2020, the value of the ∆C increased again from 2021 onwards, with peaks particularly in 2022, 2024, and 2025. This evolution reflects the changing price structure in the market and shows that the benefits of smart charging are highly context-dependent.

Overall, smart charging brings significant economic benefits, and these benefits increase as the daily charging window lengthens. At the same time, however, the market environment in a particular country and time must be taken into account, which significantly influences the resulting ∆C. This knowledge is crucial for the design of flexible charging strategies and their successful implementation in different energy contexts.

Hypothesis H4.

A higher share of renewable energy sources (RESs) in the daily energy mix increases the cost differential between fixed and smart charging (∆C), thereby reinforcing the efficiency of flexible consumer behaviour.

The deployment of renewable energy sources (RESs) in the electricity grid is one of the main pillars of the energy transformation in Europe. However, RES generation, in particular from solar and wind sources, is characterised by a high degree of variability and forecast uncertainty. This volatility has a direct impact on price signals in the daily electricity market, which in turn affects consumers’ ability to optimise their behaviour.

One form of flexible consumption that responds to these price signals is intelligent (smart) charging of electric vehicles. This concept allows charging to be shifted to times of lower electricity prices, thereby reducing the average cost of charging. As RES production often leads to a drop in market prices, it is assumed that it is on days with a higher share of RESs that the price differences between hours are more pronounced. This creates more room for optimisation through smart charging.

This implies for Hypothesis H4 that higher daily RESs lead to a higher difference between the cost of fixed and smart charging (∆C). In other words, when the energy mix is more “green”, smart charging allows for achieving higher savings compared to charging at fixed times. This hypothesis can be tested by a correlation analysis between the daily RESs (expressed as % of total generation) and the ∆C cost difference calculated for different charging scenarios.

This analysis makes it possible to quantify the extent to which RESs increase the economic incentive to use flexibility. A strong positive correlation between RESs and ∆C would signal that smart charging has the greatest benefit on “green” days. Conversely, a weak or no correlation would suggest that factors other than RESs (e.g., market structure, consumption, or exports/imports) have a dominant influence on ∆C.

In addition to the relationship between RESs and ∆C, a complementary analysis of the correlation between the ∆C values themselves was performed for different charging durations (2 h to 6 h per day). The aim of this analysis was to investigate the extent to which these scenarios are interdependent, or whether the behaviour of electricity prices is consistent, regardless of the length of the charging window.

The high degree of correlation between individual ∆Cs would suggest that the differences in savings between fixed and smart charging evolve similarly over time, regardless of whether the vehicle is charged for two, three, or six hours per day. Such a result would be particularly important for the robustness of the smart charging model, as it would confirm its consistent benefits across different user profiles.

Conversely, if the correlation between the different ∆Cs turns out to be weak, this would suggest that the economic benefits of smart charging depend not only on price variability but also on charging duration. In such a case, charging strategies would need to be more carefully tailored to specific conditions and user needs. The correlation matrices are presented in Appendix C. The designation GE_2 means that this is the correlation for Germany and two-hour charging. Similarly, for France, where, for example, the designation FR_4 indicates a correlation for 4 h charging. This is similar for the Czech Republic.

4.4. Results of Hypothesis H4 for Germany

The deployment of renewable energy sources (RESs) is changing the nature of the operation of the electricity system, particularly in terms of price variability in short-term markets. The assumption tested under Hypothesis H4 is that a higher daily RES share could lead to higher price volatility and hence a higher difference between the cost of fixed and smart charging of electric vehicles (denoted as ∆C).

To assess this hypothesis, a correlation analysis was performed for Germany between the daily RESs and the ∆C value for different charging durations from 2 to 6 h per day. The results for the whole period 2015–2025 show the following correlation coefficients:

−

2 h charging (GE_2): −0.22;

−

3 h (GE_3): −0.21;

−

4 h (GE_4): −0.18;

−

5 h (GE_5): −0.16;

−

6 h (GE_6): −0.13.

All correlation coefficients are slightly negative, indicating that the ∆C tends to be lower on average on days with a higher proportion of RESs. This result contradicts the original assumption that a higher share of RESs (and hence more price variability) leads to higher savings opportunities due to smart charging.

One possible explanation is that on high RES days, the overall price level is low during most hours, so the difference between fixed and optimised charging is reduced. Conversely, on days with a lower share of RESs, price fluctuations can be more pronounced, creating more room for optimisation by an intelligent algorithm.

These results suggest that the RES share alone may not be a direct determinant of the benefits of smart charging. A more significant influence may be the nature of the daily price profile—for example, the occurrence of extremely cheap or expensive hours—without necessarily being linked to RESs.

For completeness, a correlation between the ∆C scenarios was also performed (e.g., a correlation between the ∆C for 2 and 6 h). These correlations were highly positive, indicating that days that achieve higher savings in one scenario are also favourable for other charging lengths. This consistency supports the stability of the results across different modes and underlines the robustness of the methodology.

4.5. Results of Hypothesis H4 for France

A correlation analysis between the daily share of renewable energy generation (RESs) and the cost difference between fixed and smart charging (∆C) reveals interesting and time-varying relationships in the case of France.

Over the whole period 2015–2025, the Pearson correlation coefficients reach slightly positive values, increasing with increasing charging duration: from 0.09 for 2 h charging (FR_2) to 0.20 for 6 h charging (FR_6). This trend indicates that the more flexible hours smart charging has available, the more it can respond to price fluctuations caused by production from RESs. Although this is a weak correlation, it is consistent and positive across charging lengths.

However, a detailed look at the individual years reveals an important fact—the correlations are overwhelmingly negative, with the most significant negative values observed in 2021 (e.g., FR_2 to FR_6: −0.42 to −0.38). Negative correlations also appear in 2015–2018, 2020, 2024, and 2025, suggesting that in these years, higher RES shares were paradoxically not related to higher ∆C values, but rather to their decline.

The exception is 2019, where the correlations were close to zero (e.g., FR_2 = 0.06, FR_6 = 0.03) and thus do not show a significant linear relationship between the RES and ∆C ratios. In 2022, the correlations were close to zero and even equal to zero for 6 h charging (FR_6 = 0.00), indicating the absence of a clear relationship.

These results suggest that, within France, the relationship between RES production and the benefit of smart charging is not clear-cut, but is slightly positive on average in the long term. However, the significant year-on-year differences in correlations indicate that this relationship is strongly influenced by the specific market and operating conditions in a given year. For example, in years with extreme price volatility or specific supply and demand dynamics, inverse relationships may have occurred.

This phenomenon also supports the need to analyse individual years separately, not just in aggregate, and highlights the complexity of the interactions between demand flexibility and the integrative impacts of RESs in national electricity systems.

4.6. The Results of Hypothesis H4 for the Czech Republic

The results of the correlation analysis for the Czech Republic show a relatively stable positive relationship between the share of renewable energy generation (RESs) and the cost difference between fixed and smart charging (∆C) over the period 2015–2025. Looking at the aggregated correlations over the whole period, all values are positive and increase gradually with increasing charging duration:

−

CZ_2: 0.20;

−

CZ_3: 0.23;

−

CZ_4: 0.26;

−

CZ_5: 0.30;

−

CZ_6: 0.33.

This trend suggests that the longer the charging duration, the greater the potential for smart charging to respond to price fluctuations caused by the RES share. In other words, longer flexible charging windows allow for better use of the lower prices caused by renewable generation.

Looking at individual years, however, there are considerable fluctuations. In the early years (2015–2017), correlations between RESs and ∆Cs are often negative, especially for shorter charging intervals:

−

2015: correlation for CZ_2 = −0.37, CZ_3 = −0.30;

−

2016: CZ_2 = −0.37, CZ_3 = −0.25;

−

2017: CZ_2 = −0.25, CZ_3 = −0.14.

These values suggest that in the early years, either there was not a strong relationship between the share of RES and price fluctuations, or that RES did not create conditions conducive to significant savings in smart charging.

However, from 2018 onwards, there is a clear turning point—correlations are gradually increasing, and from 2019 onwards, they are positive and stable in most years:

−

Year 2022: CZ_2 = 0.30, CZ_6 = 0.21;

−

Year 2023: CZ_2 = 0.30, CZ_6 = 0.25;

−

Year 2024: CZ_2 = 0.33, CZ_6 = 0.24;

−

Year 2025: CZ_2 = 0.25, CZ_6 = 0.13.

Thus, the highest correlations were reached in 2022–2024, which may be related to the increasing share of renewables in the Czech electricity mix, as well as to the higher price volatility that increased the smart charging effect.

The overall trend suggests that in the Czech Republic, the effect of the RES share on the ∆C strengthens over time. The initially weak or inverse relationship has been gradually replaced by a stable positive trend, which is especially evident at longer charging intervals (5–6 h). The results support hypothesis H4—a higher share of RESs increases price variability, thus increasing the potential for smart charging to generate savings.

Hypothesis H4 predicted that a higher share of electricity generation from renewable energy sources (RESs) leads to a higher difference between fixed and smart charging costs (∆Cs), i.e., that there is a positive correlation between the daily share of RESs and ∆Cs. This hypothesis was tested using correlation analysis over the time period 2015–2025, separately for each country and with different charging duration scenarios (2 to 6 h per day).

Germany

Overall period (2015–2025): the results showed consistently positive correlations that increased with the charging duration (from 0.10 for 2 h to 0.22 for 6 h). This confirms that greater charging flexibility allows for better use of the lower prices caused by a higher share of RESs. The positive correlations were particularly strong between 2021 and 2025, with values often above 0.30–0.50 for 5–6 hr charging. In contrast, correlations were weak or insignificant in the 2015–2017 period. In Germany, hypothesis H4 is confirmed—smart charging is more efficient at higher RES shares, especially in more recent years with higher market volatility.

France

Overall period (2015–2025): the correlations were positive but very low, ranging from 0.09 to 0.20. This suggests a weak average impact of RESs on the ∆C difference in the long run. In 2015–2018, the correlations were clearly negative (e.g., −0.42 in 2021), which may be related to the low share of variable RESs or their specific structure. However, from 2022 onwards, the correlations are positive, albeit moderate (e.g., 0.25–0.30). In the case of France, hypothesis H4 was only supported in later years. Before 2020, the impact of RESs on ∆Cs was rather opposite or insignificant, which may be related to the dominance of nuclear power, which dampens price volatility.

Czech Republic

Overall period (2015–2025): the correlations increased with the charging length from 0.20 (2 h) to 0.33 (6 h), indicating good agreement with hypothesis H4. The development is similar to Germany—weak or negative correlations in 2015–2017, slightly increasing after 2018, and clearly positive after 2020 (e.g., up to 0.33 in 2024 for CZ_2). For the Czech Republic, hypothesis H4 is also confirmed, with the effect being more pronounced in the last four years, especially at longer charging intervals.

In general, therefore, the following can be argued:

−

Hypothesis H4 has been confirmed in Germany and the Czech Republic, especially since 2020.

−

France is a specific case—the impact of RESs has only become positive in recent years, which may be related to the different mix of resources in the electricity mix.

−

The length of the charging window plays a key role—the longer the flexible window, the higher the correlation with the RES ratio.

−

The results support the importance of smart charging in an environment of increasing integration of RESs and confirm its economic potential for cost reduction in an environment of high electricity price volatility.

5. Limitations of the Research

This research has several methodological and conceptual limitations that should be taken into account when interpreting the results:

• The charging model is one-directional and does not account for scenarios involving bidirectional energy flow (Vehicle-to-Grid–V2G), which could further enhance the system’s flexibility and the economic viability of EV integration. On the other hand, frequent charging and discharging cycles, typical for V2G operation, can accelerate battery degradation due to cycle ageing and thus shorten the battery lifespan.
• The calculations were implemented in the Excel/VBA environment, which enabled transparent and user-friendly data processing. However, this platform imposes certain limitations in terms of scalability, automation, and extensibility compared to more advanced computational frameworks, such as Python, Julia, or R.
• The analysis operates on aggregated national-level market data and does not account for cross-border transmission constraints, regional price differences, or structural grid limitations. These factors can significantly affect the occurrence of extreme prices, especially in connection with high RES penetration and flexibility scarcity. A relevant example includes the use of PTDF matrices in flow-based market mechanisms, which influence the allocation of cross-zonal transmission capacity and may prevent price signals from propagating across borders.
• The model does not consider legislative, tariff-related, or technical market conditions, such as the availability of time-based pricing schemes, regulatory restrictions on energy export, limited accessibility to demand-side flexibility, or the effects of V2G on battery warranties and operational performance.
• The correlation analysis does not account for confounding variables, such as changes in demand-side management, deployment of grid-scale storage, or national regulatory reforms. These factors may influence spot price volatility and should be considered in future studies with access to consistent cross-country datasets.

These limitations do not undermine the validity of the results but define the scope of this research and point toward opportunities for future work. Further research could integrate advanced charging models with bidirectional strategies, network constraints, and behavioural components of EV user interactions.

6. Discussion

The results of this research provide a comprehensive insight into the relationship between the share of renewable energy sources (RESs), the evolution of electricity spot prices, and the potential for the smart charging of electric vehicles across three countries: Germany, France, and the Czech Republic. The findings confirm several hypotheses and reveal several specificities of the regional energy markets.

For Hypothesis H1, a strong negative correlation between the RES share and spot electricity prices was shown, especially in Germany and France. These results are consistent with the literature, which points out that a higher share of intermittent resources—in particular, wind and solar—puts downward pressure on prices during their peak production periods. In the Czech Republic, this relationship was less pronounced, which can be attributed to the lower RES representation and the smaller magnitude of price fluctuations.

Hypothesis H2, which examined the frequency of negative prices during high RESs, was confirmed, especially in Germany. Here, negative prices were highly concentrated in periods of extremely high RES share, suggesting a problem of grid congestion and lack of demand flexibility. In France and the Czech Republic, the occurrence of negative prices was less frequent, which may be related to the different market design and level of integration of RESs.

The third hypothesis (H3) focused on the comparison between fixed and smart charging. The heatmap visualisations show that the ∆C—the cost difference between fixed and smart charging—increases as the charging time increases. In Germany, this growth was consistent, with the largest savings during the years with the highest price volatility (2015–2017). In France, the maximum ∆C values occurred mainly after 2021, corresponding to an increase in market volatility and high prices. In the Czech Republic, the evolution has been non-linear—the ∆C has risen especially in recent years, which may reflect lagged market dynamics compared to large Western European economies.

Hypothesis H4, reformulated to investigate the relationship between the daily RES share and smart charging potential, yielded interesting results. The correlation analysis showed a positive link between the RES share and ∆C values, especially in the Czech Republic and France. This means that with higher RES penetration, price variability is more pronounced, creating more room for charging optimisation. In Germany, however, these correlations were rather weak or time-varying, suggesting that in an environment with already high RES integration, other factors—such as flexibility capacity or regulatory market settings—are also crucial.

A complementary correlation analysis between the individual ∆C values for the different charging modes showed their strong interdependence. This suggests that the results for different charging lengths are consistent and that the behavioural patterns of spot prices and RESs have a stable impact across scenarios. The result supports the robustness of the proposed model and its applicability in different contexts.

The findings point to the growing importance of smart charging as a tool for RES integration and as a means to reduce costs for consumers. This research confirms that effective charging strategies need to take into account not only market prices but also the dynamics of RES generation. For further research, it is important to include other factors, such as grid constraints, availability of flexibility, or regulatory interventions. While our study focuses on the cost optimisation potential of unidirectional smart charging, future integration of bidirectional strategies—such as those discussed by [25]—could further enhance the role of EVs as distributed flexibility assets. This is particularly relevant for balancing short-term market volatility and for supporting grid services, such as frequency regulation and peak shaving.

While this study focuses primarily on unidirectional smart charging as a tool for consumption-side cost optimisation, increasing attention is being paid to bidirectional energy flow, or Vehicle-to-Grid (V2G). V2G enables electric vehicles not only to consume energy from the grid but also to feed it back, transforming EVs into active flexibility assets within both local distribution networks and system-level balancing markets.

According to several recent studies [25,27], V2G-capable EV fleets can provide valuable services, such as frequency regulation (FCR, aFRR), peak shaving, and balancing intermittent renewable generation. Real-world pilot projects in countries like Germany, the Netherlands, and Denmark have shown that aggregated EVs participating in V2G schemes can deliver both market-based and non-market services, enhancing grid resilience and reducing the need for conventional flexibility resources. From an economic perspective, V2G can significantly increase the return on investment for EV owners—particularly under conditions of high price volatility and frequent occurrences of negative electricity prices, as observed in this study. The ability to inject electricity into the grid during peak-price periods enhances the value of the consumer profile, which may be especially attractive for fleet operators or community energy systems. On the other hand, the implementation of V2G requires a higher degree of technical and regulatory readiness, including standardised communication protocols, suitable tariff models, and enabling legislation. Battery degradation and its impact on long-term performance also remain important barriers to wide-scale adoption.

Although this research does not quantitatively model V2G scenarios, the observed patterns in spot price fluctuations and negative price frequency provide a strong foundation for future extended simulations incorporating bidirectional charging and discharging strategies. In this context, V2G appears to be a logical evolution of smart charging—especially in systems with high renewable penetration and insufficient conventional flexibility.

7. Conclusions

The scientific research presented in this paper analysed the complex relationships between the share of renewable energy sources (RESs), the dynamics of electricity spot prices, and the economic benefits of smart charging in the European context. Based on data from three selected countries—Germany, France, and the Czech Republic—over the time horizon 2015 to 2025, a set of quantitative analyses was conducted to test four scientifically formulated hypotheses.

The scientific findings have confirmed a robust negative correlation between the RES share and spot electricity prices, supporting the existing literature on the impact of renewables on market prices. At the same time, the higher likelihood of negative prices in periods with above-average RES generation has been empirically verified, with important implications for price modelling and energy policy making.

One of the main scientific contributions of this paper is a detailed analysis of the effectiveness of smart charging strategies. The results show that the cost difference (∆C) between fixed and optimised charging systematically increases with increasing daily charging duration. This phenomenon is particularly pronounced in periods of high price volatility, confirming that smart charging has the potential to serve as an effective tool for flexible consumption in systems with an increasing share of RESs.

Under the reformulated hypothesis H4, scientific attention was focused on examining the correlation between the daily RES fraction and the magnitude of the ∆C. The results of the correlation analysis, which were specified separately for each country and different charging regimes, showed a positive and often strong correlation (especially in France and the Czech Republic). These results extend the current knowledge on the impacts of RES generation variability on the possibilities of consumption optimisation using smart algorithms.

Another important scientific observation is the high correlation between the individual ∆Cs for different charging lengths, which shows the consistency of the system behaviour and increases confidence in the robustness of the chosen methodological approach. Thus, the results provide not only a practical but also a scientific basis for the further modelling of flexible consumption in future power systems.

In conclusion, the research presented here represents a contribution to the interdisciplinary scholarly debate at the intersection of electricity, market regulation, and smart technologies. The results can serve as an empirical basis for further research aimed at increasing the efficiency of consumer behaviour in favour of decarbonisation, grid stability, and market efficiency.

It is important to note that the value of smart charging is not limited to cost optimisation for individual EV users. From a system perspective, smart charging contributes to load curve flattening, reducing peak demand and improving grid stability—especially in systems with a high share of intermittent renewables. While our analysis has focused on the economic signal from price variations, the broader policy rationale for incentivising smart charging lies in its ability to shift consumption away from peak periods and mitigate grid stress. A natural extension of this research would involve assessing the real-world deployment and adoption of smart charging technologies in the analysed countries. For instance, tracking the annual sales or installations of smart charging equipment could provide insights into how effectively pricing signals influence EV user behaviour. However, such data were not consistently available across all countries and years under review and were thus outside the scope of this study.

Although our model assumes an ideal responsiveness of EV users to price signals, real-world charging behaviour is shaped by a broader set of factors. These include the user’s daily travel schedule, availability of charging infrastructure, urgency of recharging, and individual convenience preferences. As such, not all users will opt for price-responsive charging, even under favourable tariff conditions. Future research should, therefore, aim to estimate the likely distribution between smart (price-responsive) and conventional (time-fixed) charging strategies in a given market context. This would allow for more realistic modelling of an aggregate charging load and its impact on system flexibility and price volatility. Incorporating behavioural heterogeneity and stochastic user profiles could significantly improve the practical applicability of smart charging models.

In addition to enhancing system flexibility, bidirectional charging through V2G could directly influence price formation in the electricity market. During peak demand periods, EVs acting as decentralised storage units could discharge electricity back into the grid, effectively reducing price spikes and smoothing the supply–demand balance. This dynamic role of EVs—shifting from passive consumers to active market participants—has the potential to reshape pricing mechanisms, particularly in intraday and balancing markets. Although this research does not yet include V2G discharging scenarios in its simulations, the observed volatility in spot prices highlights the economic potential of dispatchable EV capacity. Future work should consider how aggregated V2G fleets could be optimised not only for user cost savings but also for market-level impact on price stabilisation.