Dynamic Reconfiguration for Energy Management in EV and RES-Based Grids Using IWOA

Abstract

Effective energy management is vital for enhancing reliability, reducing operational costs, and supporting the increasing penetration of electric vehicles (EVs) and renewable energy sources (RESs) in distribution networks. This study presents a dynamic reconfiguration strategy for distribution feeders that integrates EV charging stations (EVCSs), RESs, and capacitors. The goal is to minimize both Energy Not Supplied (ENS) and operational costs, particularly under varying demand conditions caused by EV charging in grid-to-vehicle (G2V) and vehicle-to-grid (V2G) modes. To improve optimization accuracy and avoid local optima, an improved Whale Optimization Algorithm (IWOA) is employed, featuring a mutation mechanism based on Lévy flight. The model also incorporates uncertainties in electricity prices and consumer demand, as well as a demand response (DR) program, to enhance practical applicability. Simulation studies on a 95-bus test system show that the proposed approach reduces ENS by 16% and 20% in the absence and presence of distributed generation (DG) and EVCSs, respectively. Additionally, the operational cost is significantly reduced compared to existing methods. Overall, the proposed framework offers a scalable and intelligent solution for smart grid integration and distribution network modernization.

1. Introduction

1.1. Motivation

Modern power systems are evolving rapidly due to the widespread adoption of electric vehicles (EVs) and the integration of renewable energy sources [1]. While these advancements promote a more sustainable energy future, they introduce significant challenges in the management and operation of distribution networks. The uncertain nature of EV charging demand and the variability of renewable energy output can lead to voltage instability, increased power losses, and imbalanced load distribution [1]. These dynamic and complex issues are further exacerbated by the uncertainty inherent in key power system parameters, particularly in distribution networks. Traditional network management techniques often fall short in addressing these multifaceted problems effectively. Addressing the uncertainties in load demand, renewable generation, and other critical variables requires innovative approaches that enable dynamic adaptation to evolving network conditions. By employing advanced optimization techniques and leveraging dynamic reconfiguration of distribution feeders, it is possible to achieve new levels of operational efficiency and reliability.

This research aims to develop a robust and scalable framework for energy management, addressing the challenges posed by uncertainty in power system parameters. Using an enhanced Whale Optimization Algorithm tailored to handle the discrete and variable nature of distribution networks, this work provides a practical solution to improve system performance. The proposed approach ensures that distribution networks remain resilient and efficient, even under fluctuating demands and uncertain operating conditions, paving the way for smarter and more sustainable power systems.

1.2. Literature Review

The concept of dynamic reconfiguration in distribution networks (DNR) has attracted growing interest as an effective strategy to enhance energy efficiency, reduce power losses, and improve system reliability. This literature review highlights recent studies that utilize evolutionary and metaheuristic algorithms for optimal DNR. Special attention is paid to configurations involving electric vehicles (EVs), distributed generation (DG) units, and dynamic load conditions, all of which reflect emerging challenges in modern power systems.

In [2], a state-of-the-art metaheuristic approach is proposed to address DNR and optimal DG placement. The technique aims to minimize energy losses and improve voltage stability, particularly under variable load conditions and renewable energy integration. In [3], a Fractal Search Algorithm (SFS) is introduced for DNR optimization, emphasizing improvements in network reliability and flexibility. This method effectively lowers energy losses while enhancing response capabilities. In [4], the Coyote Optimization Algorithm (COA) is applied to solve both DNR and DG allocation problems. Inspired by the pack-hunting behavior of coyotes, this method improves voltage regulation and reduces losses. In [5], an equilibrium-based algorithm is utilized to manage DNR under dynamic load profiles, successfully enhancing resource distribution and network efficiency. In [6], a multi-objective fuzzy optimization model integrates DSTATCOMs and DERs into the network. It simultaneously targets loss reduction, voltage profile improvement, and operational cost minimization, offering a comprehensive power system planning solution. In [7], the Electric Eel Optimization Algorithm handles DNR with integrated DG units. It shows adaptability to load and generation fluctuations, supporting system stability. In [8], the Tabu Search Algorithm is used for DNR, with a focus on minimizing switching costs and improving operational efficiency, particularly when incorporating DGs. In [9], the study examines joint DG placement and DNR, with a focus on maintaining network flexibility under varying load levels. In [10], the integration of parallel capacitors in smart networks is explored to enhance voltage stability and reduce reactive power losses through optimized DNR. In [11], a Differential Evolution Algorithm is employed to plan STATCOM placement in radial networks, aiming to minimize planning costs under diverse load conditions. In [12], a flexible simulated annealing technique is applied for optimal DG and capacitor allocation, reducing energy losses and improving network performance. In [13], a hybrid APSO and GWO-PSO algorithm is proposed for simultaneous planning of solar units and DSTATCOMs in DNR, improving voltage profiles and loss metrics. In [14], an enhanced Sine-Cosine Algorithm (SCA) is developed for integrated DNR and DG placement, aiming to improve voltage quality and loss minimization. In [15], the configuration of distributed wind turbines and DSTATCOMs is optimized to improve voltage recovery at sensitive nodes, thus increasing network resilience. In [16], a novel metaheuristic optimization method is applied to DNR and DG planning, delivering better voltage regulation and energy efficiency. In [17], a parallel simulated annealing approach is implemented for DNR with DG units to reduce power losses and enhance overall performance. In [18], the study focuses on line reconfiguration in smart grids for active loss minimization, while evaluating the influence of EVs on network operation. In [19], a hybrid simulated annealing and spanning tree algorithm is employed for DNR and reactive power compensation, significantly improving system efficiency. In [20], DNR in radial systems is optimized with integrated DGs, highlighting improvements in losses and system robustness under various operational conditions. In [21], a multi-objective dynamic reconfiguration framework using the LDBAS algorithm is introduced. This method considers DGs and EVs simultaneously, optimizing losses, voltage quality, and operational costs.

1.3. Challenges and Contributions

A review of the existing studies indicates that most have not simultaneously accounted for the combined effects of distributed generation units, capacitors, and EVs in addressing the optimization challenges of network reconfiguration. Additionally, when modeling the impact of electric vehicles, these studies typically consider either G2V or V2G interactions, failing to address the combined influence of both modes on the network. Furthermore, the majority of research has primarily focused on traditional objective functions, such as power losses, operational costs, and voltage deviation, while placing less emphasis on objectives related to the reliability and security of the distribution network. The inclusion of uncertainty parameters, which significantly increases the complexity of the optimization process, has also been largely overlooked. Most studies that do consider uncertainties often limit their scope to a single factor, such as demand or electricity prices, rather than addressing multiple uncertainty parameters simultaneously. This limitation reduces the accuracy and robustness of the proposed solutions under real-world conditions, leaving the complexity induced by uncertainties insufficiently addressed. Regarding multi-objective optimization, the majority of research favors weighted-sum methods due to their simplicity and widespread applicability. However, these methods have drawbacks, including the need for precise weight selection and their limited ability to identify the entire Pareto-optimal front. Conversely, more advanced approaches based on fuzzy logic and Pareto optimality—which better capture the trade-offs between conflicting objectives and provide a diverse set of optimal solutions—are less commonly employed. This limited use stems from computational complexity and modeling challenges, but expanding the application of these sophisticated techniques can enhance the comprehensiveness and accuracy of optimization outcomes and offer more flexible decision-making options. Based on the identified gaps in the literature, this study aims to achieve the following research objectives:

• To develop a dynamic mathematical model for distribution network reconfiguration that enables optimal energy management in the presence of Electric Vehicle Charging Stations (EVCSs), Renewable Energy Sources (RESs), and capacitors. The model incorporates both Vehicle-to-Grid (V2G) and Grid-to-Vehicle (G2V) operational modes of electric vehicles.
• To design and implement an improved Whale Optimization Algorithm (IWOA) to solve the Dynamic Network Reconfiguration (DNR) problem with the dual objectives of minimizing Energy Not Supplied (ENS) and operational costs. The enhanced algorithm addresses the local optima problem commonly encountered in the standard WOA.
• To establish a multi-objective optimization framework using a fuzzy-based Pareto approach to balance ENS and operational cost objectives. The objective function includes comprehensive operational costs, covering the expenses related to purchasing both active and reactive power from all relevant equipment and sources within the network.
• To propose a realistic uncertainty modeling approach based on generation/reduction techniques to represent stochastic parameters such as electricity prices and customer demand. This approach enables network operators to identify optimal operating conditions under uncertainty, improving the robustness of decision-making in real-world power systems.

This is how the rest of the paper is structured. Section 2 presents the problem formulation including objectives, constraints, uncertainty modeling, and DR formulation. Section 3 introduces IWO and how it is used in network reconfiguration. Section 4 discusses the simulation results on the 95-bus system. Conclusions are given in Section 5.

2. Problem Formulation

2.1. Objective Functions

This study’s objective goals include operational cost and ENS minimization [22].

• Operational cost

The operation cost can be calculated as follows:

$$\begin{gathered} f_3\left(X\right)={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{DG}}({{\mathrm{P}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}_{\mathrm{D}\mathrm{G},\mathrm{i}}}^h\times {P_{\mathrm{D}\mathrm{G},\mathrm{i}}}^h)+{\sum }_{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{S}\mathrm{u}\mathrm{b}}}{{(\mathrm{P}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}_{\mathrm{S}\mathrm{u}\mathrm{b},\mathrm{k}}}^h\times {P_{\mathrm{S}\mathrm{u}\mathrm{b},\mathrm{k}}}^h)+\dots \\ \sum _{j=1}^{N_{Sw}} {Price}_{Sw,j}\times \left|{{SW}_j}^h-{{SW}_j}^{h-1}\right|+{Cost}_{EVCS}+{Cost}_{Cap} \end{gathered}$$

(1)

$${Cost}_{EVCS}={\sum }_{r=1}^{N_{ES}}{{Price}_{EVCS,r}}^h\times {P_{EVCS,r}}^h$$

(2)

$${Cost}_{Cap}=\sum _{l=1}^{N_{Cap}}{{Price}_{Cap,l}}^h\times {Q_{Cap,l}}^h$$

(3)

The first term in the goal function shown in (1) deals with the electricity costs generated by DGs. The costs of purchasing power from sub-stations come in second, and switching costs come in third. The cost of purchasing active and reactive power from the electric vehicle station and capacitor is introduced in terms 4 and 5 of Equation (1), respectively.

• Energy not supplied

Following is how the ENS [21] is formulated:

$${ENS}_i=P_i\sum _{i,j\in V, i\ne j}(U_{i,j}+U_{i,j}^{\prime })$$

(4)

2.2. Optimization Constraints

Let us now discuss the limits of the optimization problem under discussion [22]. The network limit associated with being radial is computed using the following formula:

$$N_{branch}=N_{Bus}-N_{source}$$

(5)

The following formulas can be used to calculate the constraint of load flow [22] equations:

$$P_j=\sum _{i=1}^{N_{Bus}}{V}_i{V}_j{Y}_{ij}\mathit{cos}\left({\mathrm{\theta }}_{ij}-{\delta }_i+{\delta }_j\right)+{\alpha }_{PDG}{P}_{DG}$$

(6)

$$Q_j=\sum _{i=1}^{N_{Bus}}{V}_i{V}_j{Y}_{ij}sin({\mathrm{\theta }}_{ij}-{\delta }_i+{\delta }_j)$$

(7)

The following explanation explains the node’s voltage [23] limitation:

$$V_{min}\le V_i\le V_{max}$$

(8)

The feeder current constraint [23] is described as follows:

$$\left|I_{f,i}\right|\le I_{f,i}^{Max} i=1,2,\dots {, N}_{feeder}$$

(9)

The limitations pertaining to the generation capacity of DG units [24] are as follows:

$$0\le \sum _{i=1}^P{P}_{DG}\le \sum P_{Load}$$

(10)

$$2\le L_{DG}\le N_{DG}$$

(11)

The following is a definition of the state of balance between generation and consumption [24]:

$$P_{DG} + P_{Grid}= P_{Load}+ P_{EVCS}$$

(12)

The switching restriction [24] can be formulated as follows:

$$\left|S_i-S_{0i}\right|\le N_{Switch} , i=1,2,\dots {,N}_{Switch}$$

(13)

The limitation related to the capacitors [23] is as follows:

$$Q_{min}\le Q_l\le Q_{max}$$

(14)

The restrictions related to EVCSs [1] are described below.

$$P_{EVCS}=\sum _{c=1}^{N_c}{P}_{EVCS}^c$$

(15)

If it is assumed that Nev EV is at the EVCS c, we have

$$P_{EVCS}^c=\left\{p_{EV}^1, \dots ,p_{EV}^v,\dots ,p_{EV}^{N_v}\right\}$$

(16)

According to the 2009 National Household Travel Survey (NHTS), EV arrival time could be represented by the following normal probability distribution function [25,26]:

$$F_t^{arr}={\displaystyle \frac{1}{{\sigma }_{rr\sqrt{2\pi }}}} e^{{\displaystyle \raisebox{1ex}{$-(t-{\mu }_{rr})$}\!\left/ \!\raisebox{-1ex}{$2{{\sigma }_{rr}}^2$}\right.}} 0\le t\le 24$$

(17)

Therefore, the power consumption of each EVCS is calculated based on the probability of each EV arriving at each EVCS and the number of hours spent at the EVCS for charging or discharging.

2.3. Uncertainty Modeling

In actuality, all projections have errors because of measurement or sampling errors as well as uncertainty in all data and variables. Consequently, it is necessary to analyze the power system in an uncertain setting. To move variables from a deterministic environment to a random one in this new space, a strong tool is needed. There is additional unpredictability in the load variable in a restructured setting. This research models load-related uncertainty as a normal distribution function [27].

Scenario Generation and Reduction Strategy

Initial load scenarios are created in order to model uncertainty. A specific number of scenarios with the greatest chance of occurring are chosen after the occurrence of each scenario has been calculated. The probabilities of the occurrence of the chosen scenarios are then normalized so that the probability of the sum of the chosen scenarios equals one [28].

2.4. Demand Response Formulation

The US Department of Energy (DOE) defines demand response (DR) as changes to end-user customers’ typical consumption patterns in response to fluctuations in electricity prices over time, or incentive payments meant to promote lower electricity use during times of high wholesale market prices or when system reliability is at risk. This definition divides DR into two groups: incentive-based DR and time-based rates. Price elasticity of demand is a phrase used in the context of DR. The price-sensitivity of demand is the definition of elasticity [29].

$$E={\displaystyle \frac{{\rho }_0}{d_0}}\times {\displaystyle \frac{\partial d}{\partial d}}$$

(18)

Equation (19) provides the following description of the price elasticity of the ith period relative to the jth period (E(i, j)):

$$E(i,j)={\displaystyle \frac{{\rho }_0\left(j\right)}{d_0\left(i\right)}}\times {\displaystyle \frac{\partial d\left(i\right)}{\partial d\left(j\right)}}$$

(19)

Some loads, such as lighting loads, cannot fluctuate from one period to the next and are only ever on or off. For a certain amount of time, these loads are therefore sensitive; this sensitivity is referred to as “self-elasticity,” and it is always negative. Process loads are one example of a consumption that can be shifted from peak to off-peak or low times. This kind of behavior is known as multi-period sensitivity, and it is quantified by “cross elasticity,” which is consistently positive [29].

$$\left[\begin{array}{c}∆p\left(1\right)\\ ⋮\\ ∆p\left(j\right)\\ ⋮\\ ∆p\left(T\right)\end{array}\right]=\left[\begin{array}{c}\begin{array}{ccc}E\left(\mathrm{1,1}\right)& \cdots & E(1,i)\end{array}\begin{array}{cc}\cdots & E(1,T)\end{array}\\ .\\ .\\ \begin{array}{ccc}E(j,1)& \cdots & E(j,i)\end{array}\begin{array}{cc}\cdots & E(j,T)\end{array}\\ .\\ .\\ \begin{array}{ccc}E\left(\mathrm{1,1}\right)& \cdots & E(T,i)\end{array}\begin{array}{cc}\cdots & E(T,T)\end{array}\end{array}\right]\times \left[\begin{array}{c}∆\rho \left(1\right)\\ ⋮\\ ∆\rho \left(j\right)\\ ⋮\\ ∆\rho \left(T\right)\end{array}\right]$$

(20)

The following is the definition of the modified load at hour j on the day after the application of the DR:

$$p_{DR}\left(j\right)=p(j)\times \left\{1+\sum _{j=1}^{T}E\left(i,j\right)·{\displaystyle \frac{\left[p\left(j\right)-p_0\left(i\right)+A\left(i\right)+pen\left(i\right)\right]}{p_0\left(i\right)}}\right\}$$

(21)

3. Solution Method

This section provides a brief description of the multi-objective strategy, IWO algorithm, which takes into account the continuity of objective functions, derivatives, and integral operators, as opposed to mathematical methods that rely on beginning conditions.

3.1. Multi-Objective Strategy

The following is a mathematical definition of a multi-objective optimization problem with inequality and equality constraints present:

$$\begin{gathered} Min f_i\left(X\right)={\left[f_1\left(X\right),f_2\left(X\right),\dots f_n\left(X\right)\right]}^T \\ {g}_i\left(X\right) \le 0,h_j\left(x\right) =0 \end{gathered}$$

(22)

The Pareto-optimal solution concept replaces the optimal solution concept in multi-objective optimization [28]. When both requirements are met, X₂ dominates the solution X₁:

$$\forall i\in \left\{1,2,\dots N_{obj}\right\}, f_i\left(X_1\right)\le f_i\left(X_2\right)$$

(23)

$$\exists j\in \left\{1,2,\dots N_{obj}\right\},{ f}_j\left(X_1\right)<f_j\left(X_2\right)$$

(24)

During the optimization process, any Pareto solutions found are stored in an external memory called the repository. The optimization algorithm’s speed may decrease as the number of Pareto solutions increases. To avoid the heavy computational load, a fuzzy clustering approach is employed [28]. Accordingly, each objective function’s fuzzy membership function is as follows:

$${\phi }_{f_i}\left(X\right)=\left\{\begin{array}{c}1 f_i\left(X\right)\le f_i^{min}\\ 0 { f}_i\left(X\right)\ge f_i^{max}\\ {\displaystyle \frac{f_i^{max}-f_i\left(X\right)}{f_i^{max}-f_i^{min}}} f_i^{min} \le f_i\left(X\right)\le f_i^{max}\end{array}\right.$$

(25)

Based on (26), we sort the non-dominated solutions in the repository to identify the optimal compromise solution.

$${\tau }_j={\displaystyle \frac{\sum _{i=1}^n{\beta }_i\times {\phi }_{f_i}\left(X_j\right)}{{\sum }_{j=1}^m{\sum }_{i=1}^n{\beta }_i\times {\phi }_{f_i}\left(X_j\right)}}$$

(26)

3.2. Improved WOA

Based on the communal hunting behavior of humpback whales, the Whale Optimization Algorithm (WOA) is a metaheuristic optimization technique inspired by nature [30,31]. It looks for the best answers by imitating the whales’ special bubble-net hunting technique.

Important Mechanisms in WOA:

1. 

Encircling Prey:

WOA use the following method to update whale locations in the search space with respect to the prey, assuming that the current best solution represents the prey:

$$X\left(t+1\right)=X^{*}\left(t\right)-A.D$$

(27)

2. 

Bubble-Net Method of Attack:

This behavior is simulated using two methods:

Shrinking Encircling Mechanism: This method refines the search region by gradually lowering the A value.

Spiral Updating Mechanism: This mechanism simulates the helix-like movement of whales around their prey by generating a logarithmic spiral.

The following is used to update the positions:

$$X\left(t+1\right)=X^{/}·e^{bl}·\mathit{cos}\left(2\pi l\right)+X\left(t\right)$$

(28)

3. 

Phase of Exploration:

When the probability p leads to exploration rather than exploitation, whales randomly scan the space to avoid local optima [30,31]. This is accomplished by choosing solutions at random rather than depending only on the best one.

In this study, Levy flight is utilized as a complementary mechanism in the WOA to enhance the algorithm’s exploration capability and prevent it from getting trapped in local optima. This mechanism, by generating long and sudden random jumps, increases population diversity and efficiency in large search spaces. Additionally, it improves the exploitation of optimal points and provides an effective solution for complex problems with uncertainty. The explanation of the Levy distribution-based mutation in the improved WOA (IWOA) is as follows:

Levy Flight is a random search strategy that combines short and big steps with jumps that follow a heavy-tailed distribution. This jump method enhances search space exploration and keeps optimization algorithms from being stuck in local optima. The following is a mathematical representation of the Levy Flight mutation:

$$X_{new}=X_{current}+\alpha ·Levy \left(\mathsf{\lambda }\right)$$

(29)

Levy(λ) is a sample from the Levy distribution, defined as

$$Levy \left(\lambda \right)~{\left|x\right|}^{-\lambda }$$

(30)

The intensity of large leaps is controlled by the value λ in this formula. The IWO can more efficiently search the search space by avoiding local optima and identifying better optimal spots by implementing Levy Flight. The pseudocode for this method is shown in the Figure 1 below.

4. Simulation Results

In this section, after introducing the test system, simulation results in two scenarios are presented and analyzed.

4.1. Case Study

It should be mentioned that a 95-node test system was introduced in this section to evaluate the suggested method for solving the considered optimization problem. The 95-node test system under study is shown in Figure 2 [32]. Three 1000 kW diesel generators (DGs) are located at buses #6, #6, #25, and #50; four 100 kVAr capacitors are installed at buses #10, #20, #34, #70; additionally, four EVCSs 250 kWh are located on buses #31, #45, #57, and #78. The capacity of each EVCS is four electric vehicles (EVs). It is also assumed that 75% of the EVs’ capacity will be used for G2V capability and the remaining 25% for V2G capability. The average hourly predicted load profile in the test network before and after the DRP implementation is shown in Figure 3. The MATLAB 2016b environment is used for all simulations. The IWOA method, the enhanced gravitational search algorithm (ESGA) [22], and the imperialist competitive algorithm (ICA) [22] are used to solve the suggested optimization issue in order to compare and validate the outcomes. The initial population and number of iterations for the proposed method are 400 and 100, respectively. The cost of the substation is USD 0.04 per kWh, while the costs for DGs and EVCSs are USD 0.043, USD 0.041, and USD 0.040 for heavy, middle, and base loads, respectively. The cost for capacitor units is USD 0.02 per unit, and the switching cost is USD 0.041 for each switch operation. The simulation results are shown in two scenarios below:

4.2. Scenario 1

In both single-objective and multi-objective frameworks, the DNR problem is resolved in this scenario when DG units, capacitors, and EVCSs are present. The optimization problem in this scenario has been solved without taking into account the impact of demand response and uncertainty.

Table 1. Best obtained results by the proposed IWO method.

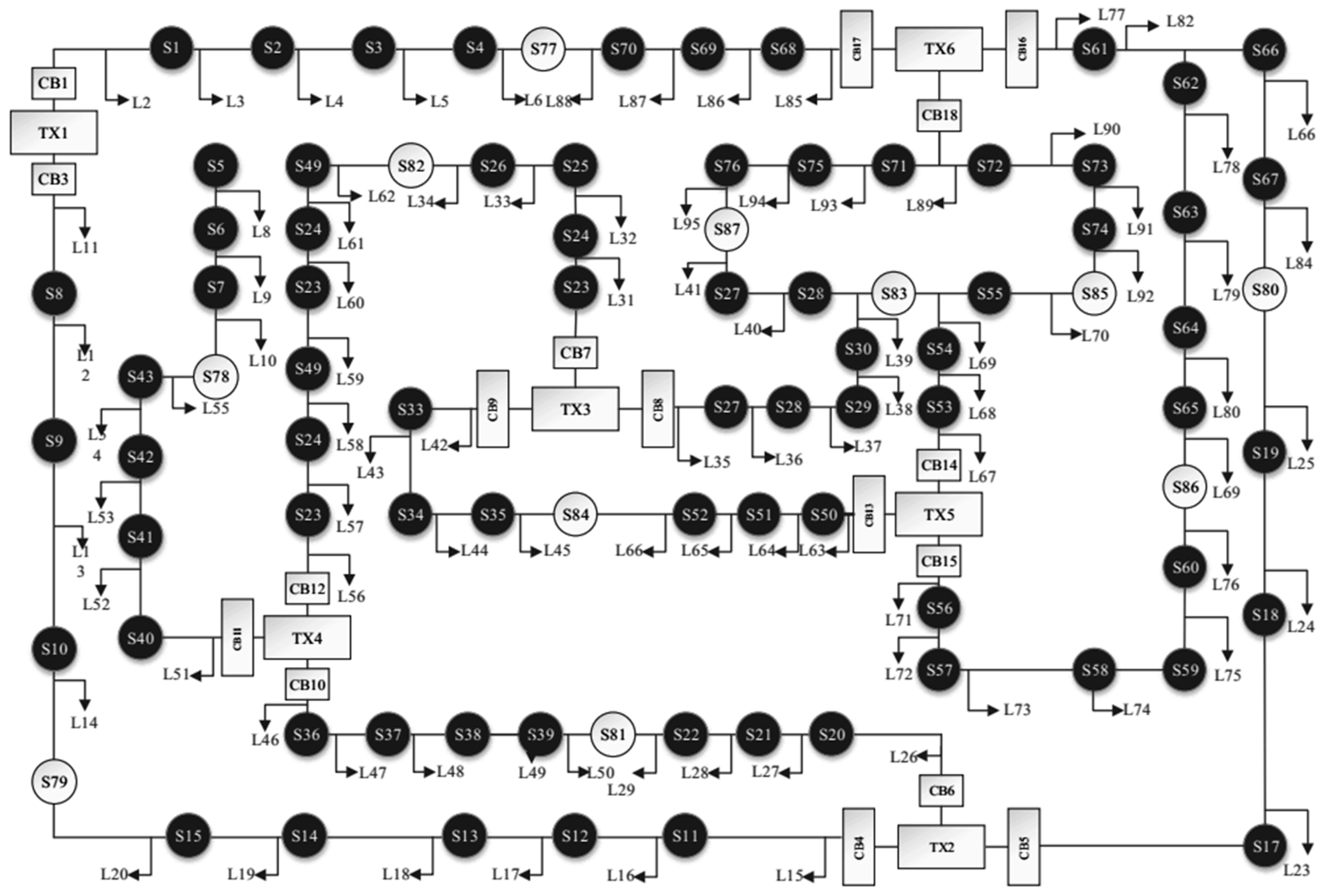
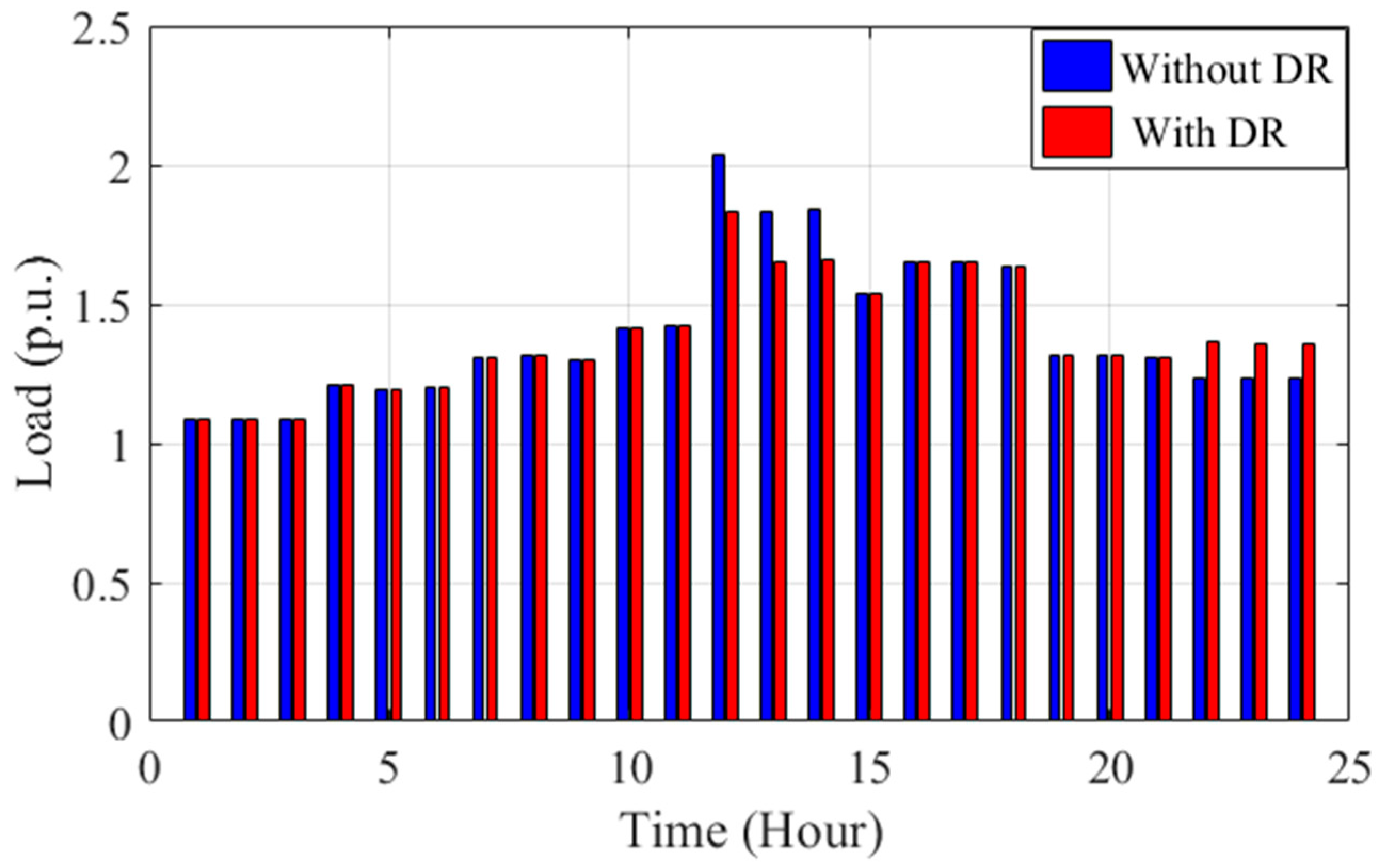
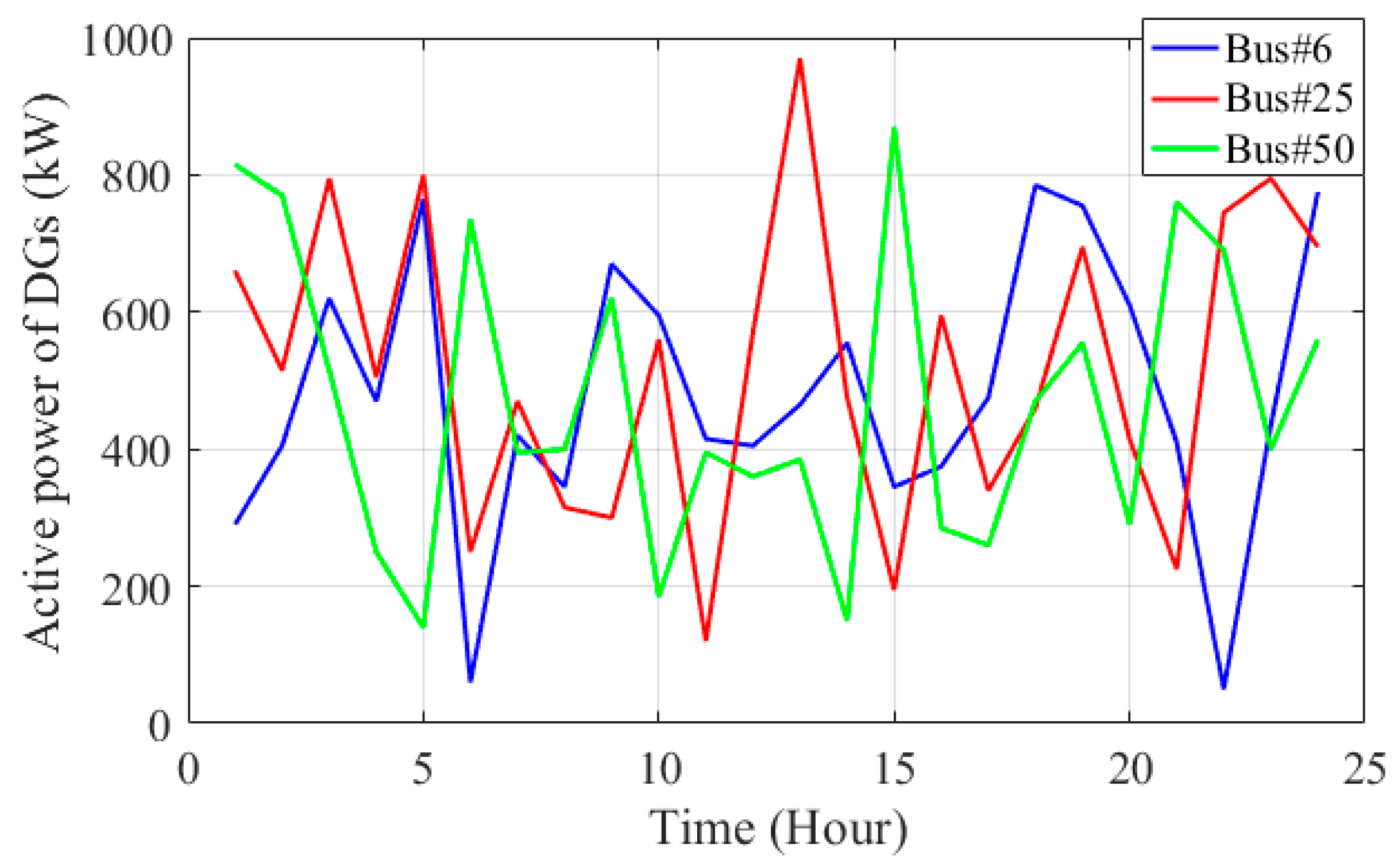
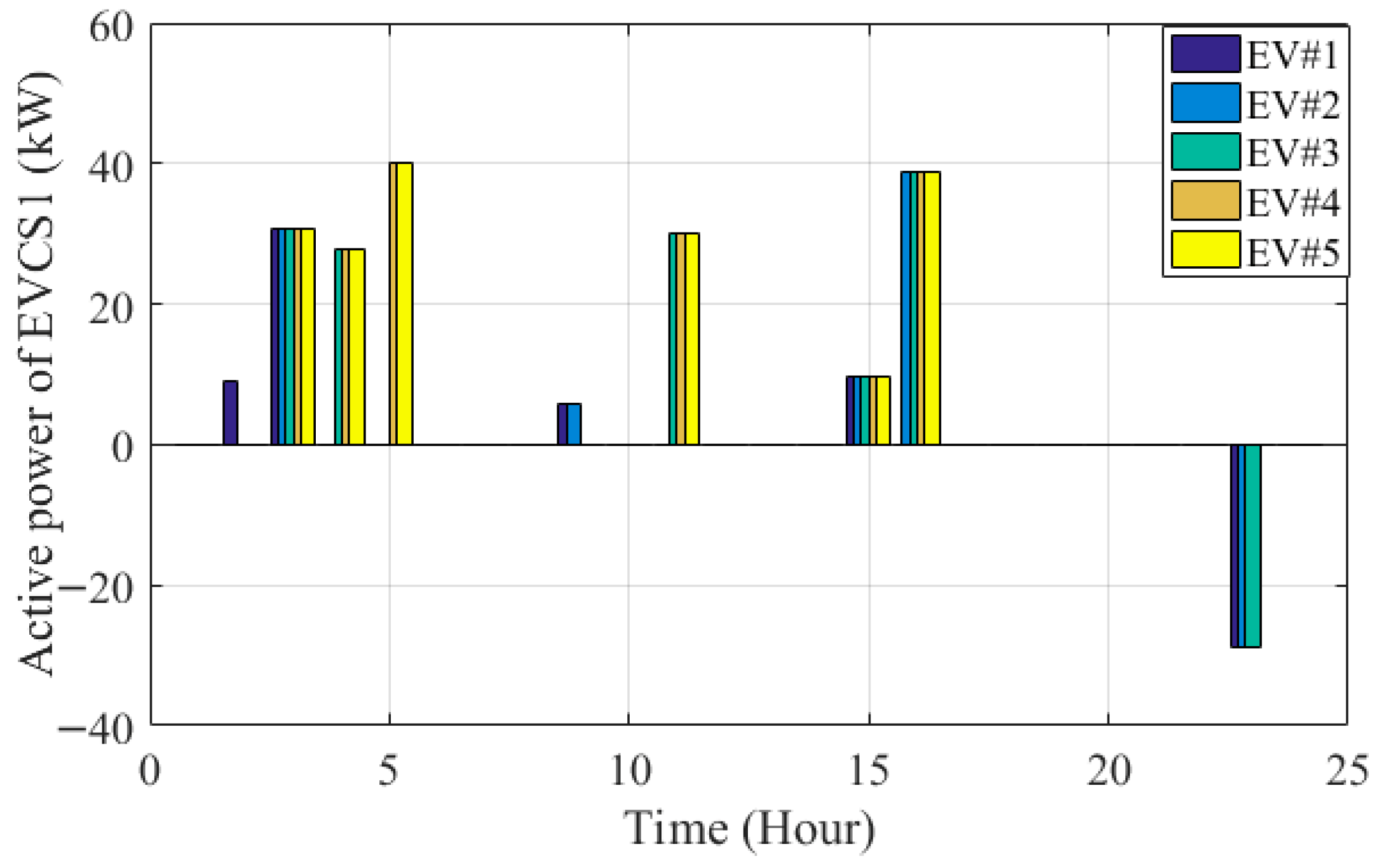
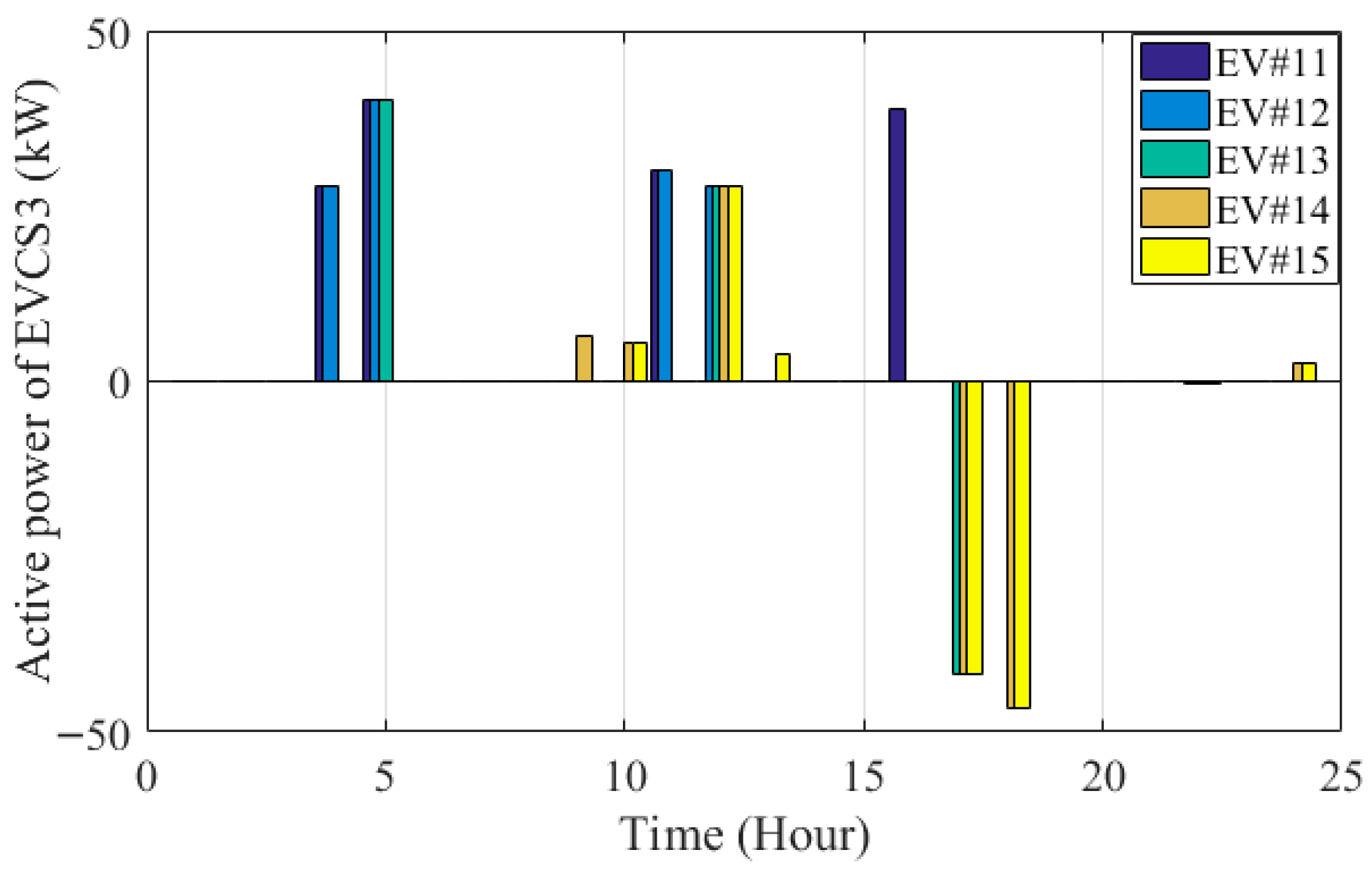
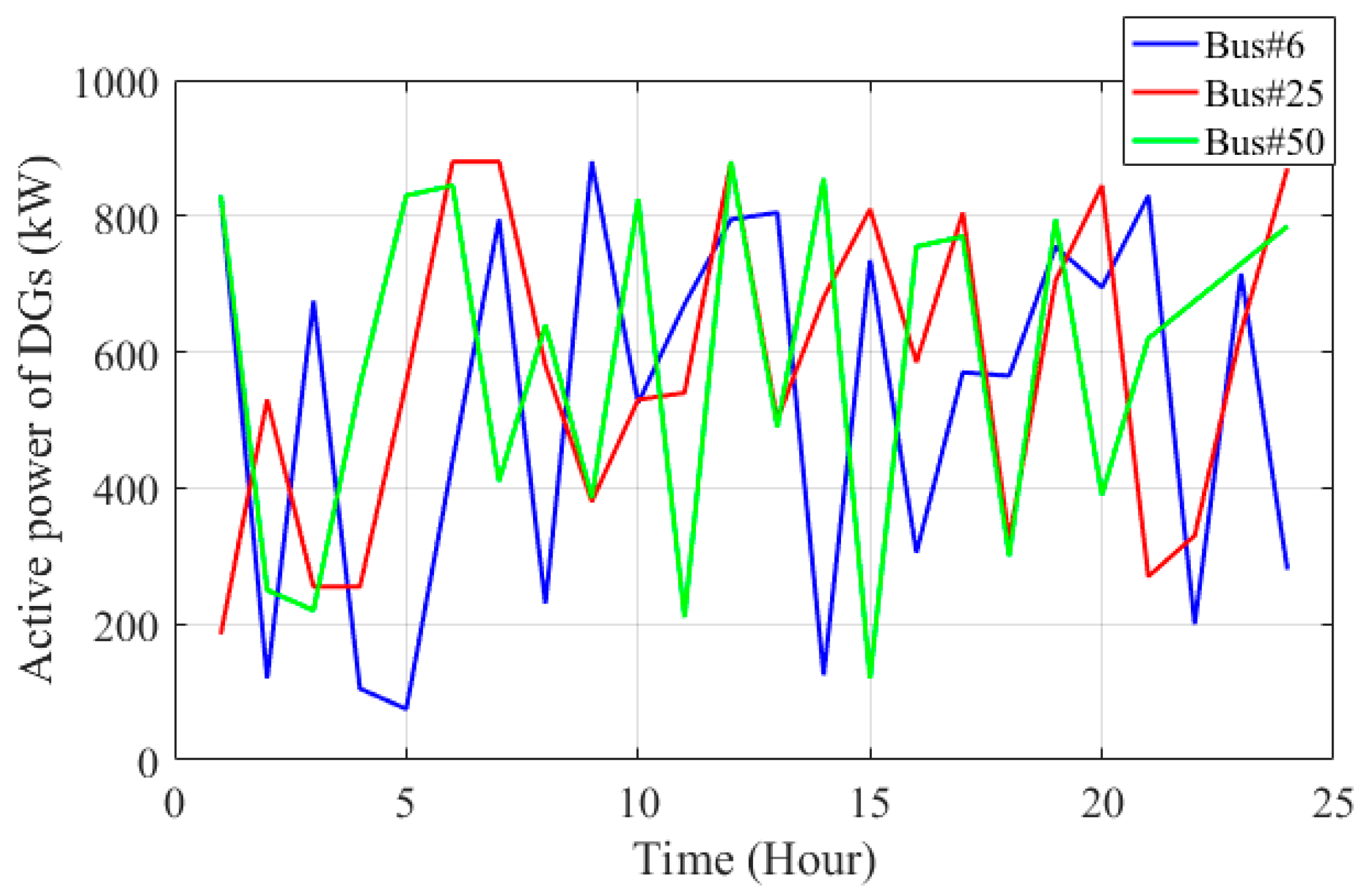
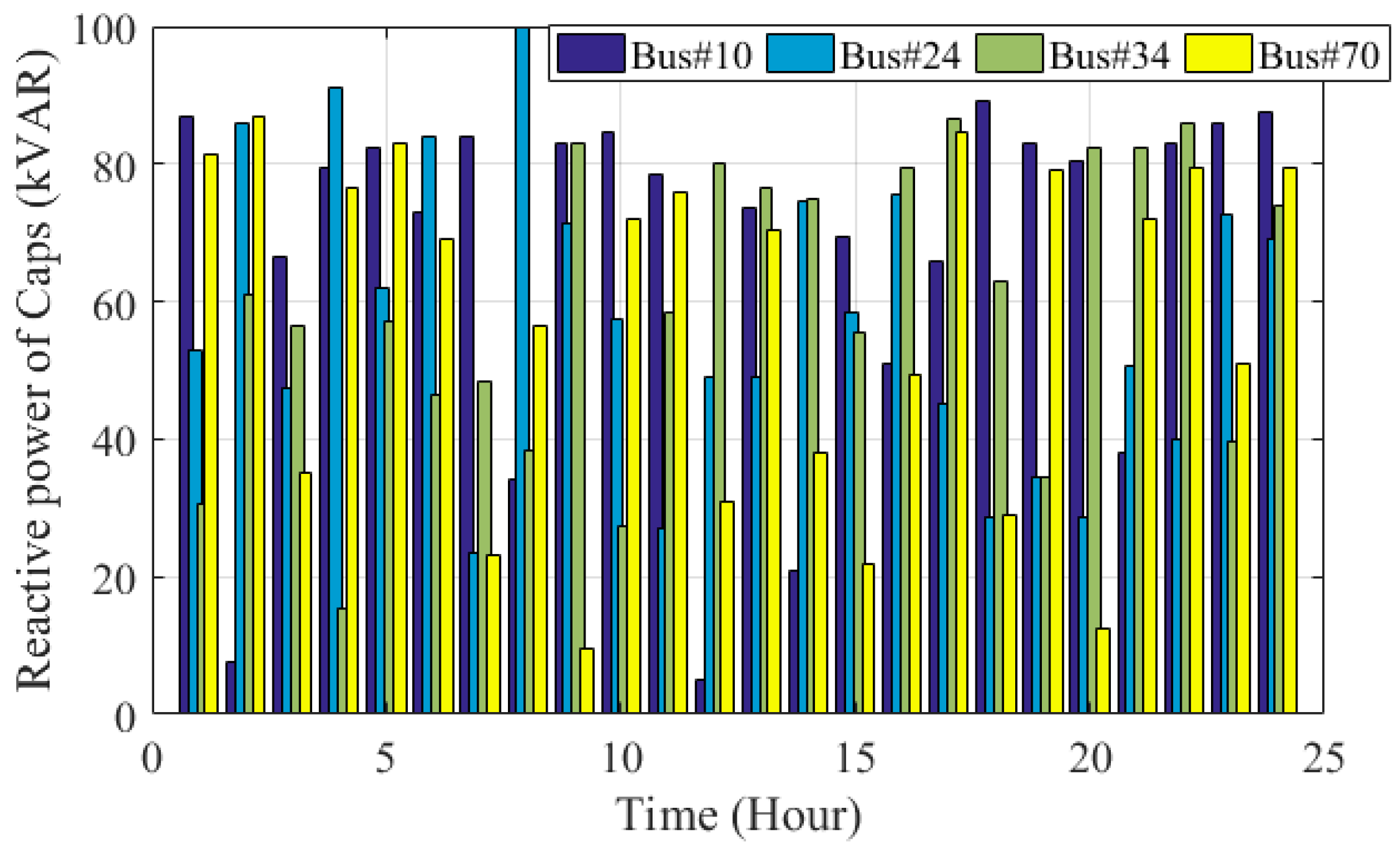
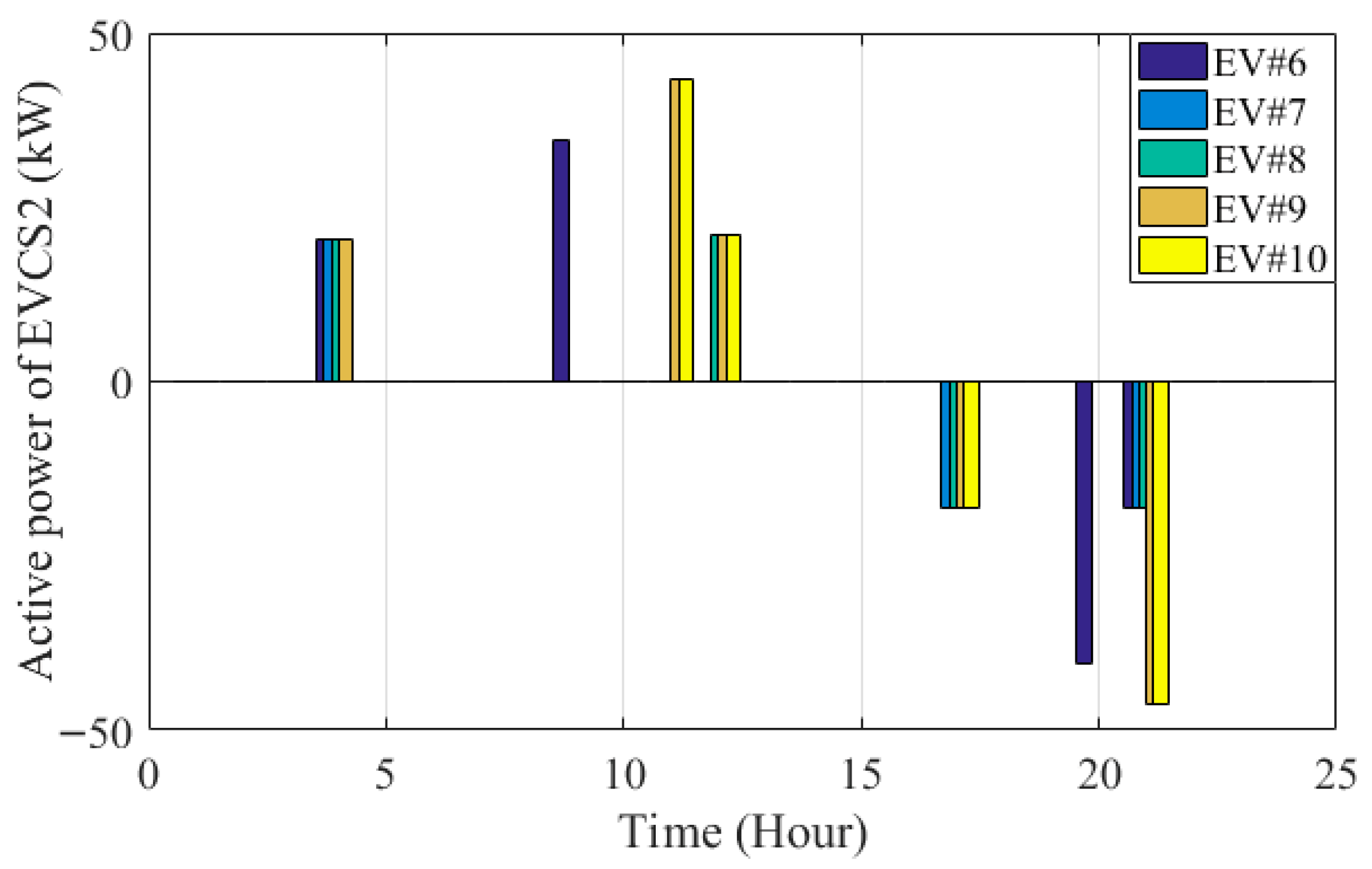
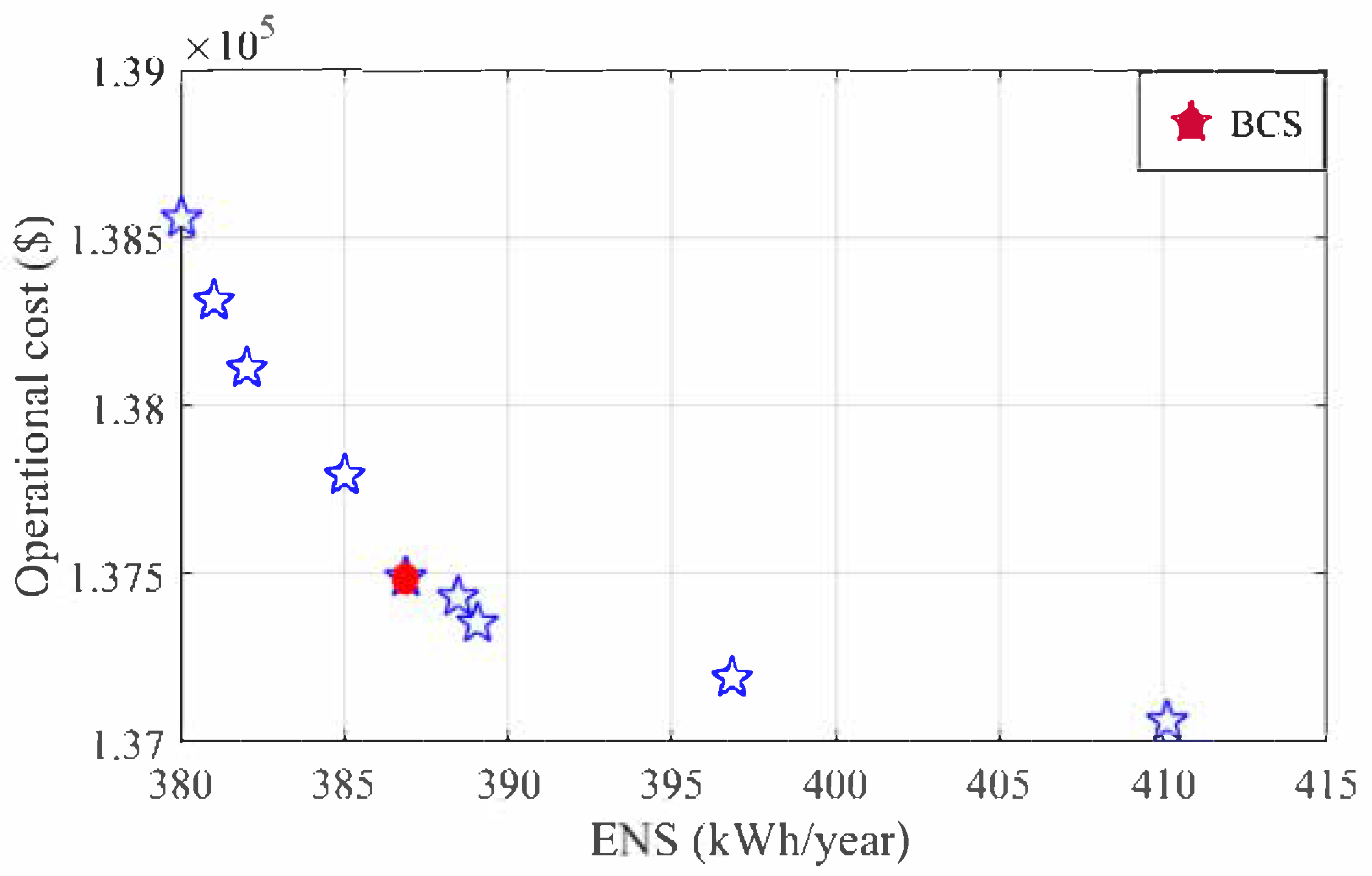
Case Studies	ENS (kWh/Year)	Operational Cost (USD)
ENS optimization	381.25	137,858.25
Operational cost optimization	485.21	136,535.23
Two-objective optimization (BCS)	386.25	137,453.25

displays the outcomes of this case as determined by the suggested approach. The single-objective optimization results for the operating cost and ENS functions are shown in

Table 2. Obtained results by different methods for ENS optimization.

Algorithms	Best Solution	Mean Value	Worst Solution	Standard Deviation	CPU Time (s)
ESGA	396.43	406.25	421.20	9.38	82
ICA	390.35	395.15	406.31	6.2	96
IWO	381.25	386.24	396.15	4.51	88

and

Table 3. Obtained results by different methods for operational cost optimization.

Algorithms	Best Solution	Mean Value	Worst Solution	Standard Deviation	CPU Time (s)
ESGA	136,620.56	136,667.52	136,725.42	33.36	64
ICA	136,599.23	136,641.15	136,695.56	31.35	78
IWO	136,535.23	136,575.23	136,620.52	29.59	69

so that the outcomes of the suggested approach can be compared to those of alternative optimization techniques. Table 2 and Table 3 present the findings from 30 different tests. The optimal configuration of switches, the output power of DG units, capacitors, and the charge/discharge status of two EVCSs for ENS optimization are presented in

Table 4. List of open switches obtained for ENS optimization.

Hour	Open Switches
	Sw1	Sw2	Sw3	Sw4	Sw5	Sw6	Sw7	Sw8	Sw9	Sw10	Sw11
1	4	41	15	39	25	52	66	86	55	76	28
2	4	40	13	22	82	50	66	60	74	75	83
3	77	40	12	22	48	52	66	65	85	87	27
4	70	43	15	20	26	33	19	60	74	71	27
5	68	40	15	22	49	52	19	86	54	76	30
6	1	43	79	37	48	35	17	65	55	87	29
7	3	7	79	38	25	52	67	58	55	87	30
8	3	43	15	39	49	52	19	86	55	32	30
9	3	78	15	36	82	52	19	60	72	76	83
10	4	43	8	81	49	50	67	65	55	71	30
11	70	43	8	39	46	34	66	65	55	76	28
12	4	43	15	22	26	84	19	60	74	87	30
13	70	43	15	39	44	35	19	65	55	76	28
14	4	41	15	39	49	84	67	65	55	71	30
15	4	5	79	20	82	52	67	64	74	76	83
16	3	40	13	22	49	50	66	58	55	75	83
17	2	43	15	38	49	52	67	65	55	32	83
18	4	43	15	39	82	52	19	65	74	75	30
19	3	42	9	38	49	52	80	65	74	32	28
20	3	5	12	22	25	35	67	65	72	76	30
21	4	7	79	37	48	35	19	64	55	87	83
22	70	7	15	38	45	34	67	60	74	75	30
23	70	40	15	39	26	35	66	65	55	87	83
24	4	43	10	38	23	52	66	65	74	75	30

and Figure 4, Figure 5, Figure 6 and Figure 7 respectively. The output of the first and third EVCS is shown in this section. Electric vehicle charging and discharging at the charging station are shown by positive and negative numbers in Figure 6 and Figure 7.

The final row of Table 1 shows that the optimal objective function values obtained from the compromise solution exhibit a greater deviation from those of the single-objective optimizations. This is expected, as multi-objective optimization seeks a balanced trade-off between conflicting objectives, rather than optimizing each independently. As seen in Table 3 and Table 4, the proposed IWO algorithm demonstrates superior performance compared to other methods, particularly in reducing both ENS and operating costs. Specifically, Table 3 shows that the ENS achieved by the IWO algorithm improves upon the best solution of the competing methods by 4.6%, which is a noteworthy enhancement in terms of network reliability. Furthermore, the proposed method achieves an USD 88 reduction in total operating cost relative to the alternatives, contributing to more economical operation of the distribution network.

It is evident from Table 4 and Figure 4, Figure 5, Figure 6 and Figure 7 that the radial topology of the distribution network remains consistently preserved throughout the 24 h simulation period. Among the DG units, the one located at bus 6 demonstrates the highest power output of 815 kW at 1:00 AM, while the DG at bus 50 records the lowest output of only 50 kW at 10:00 PM. Regarding reactive power support, the capacitors at bus 20 and bus 70 show the maximum and minimum reactive power generation, producing 88 kVAr at 2:00 PM and 5 kVAr at 10:00 PM, respectively. This variation highlights the dynamic nature of reactive power compensation based on the network’s operational needs. In terms of EV charging behavior, the third and first EVs connected to the EVCS at bus 31 record the highest and lowest total energy intake over 24 h, amounting to 176.5 kW and 26 kW, respectively. Additionally, at the EVCS located at bus 57, the 14th EV achieves the highest net charging amount of 35.5 kW, while the 12th EV exhibits the highest net discharging (vehicle-to-grid contribution), amounting to −45.5 kW over the same time horizon.

4.3. Scenario 2

The DNR issue in the presence of DG units, capacitors, and EVCSs has been resolved in this scenario, just like in the last one. In contrast to the last scenario, both single-objective and multi-objective optimization now take into account the effects of uncertainty and the DR program.

Table 5. Best obtained results by the proposed IWO method without uncertainty.

Case Studies	ENS (kWh/Year)	Operational Cost (USD)
ENS optimization	367.45	137,545.25
Operational cost optimization	453.21	136,215.23
Two-objective optimization (BCS)	373.25	137,196.19

shows the outcomes of single-objective and two-objective optimization taking only the DR program into consideration. While

Table 6. Best obtained results by the proposed IWO method with uncertainty.

Case Studies	ENS (kWh/Year)	Operational Cost (USD)
ENS optimization	374.15	138,256.16
Operational cost optimization	473.16	136,273.19
Two-objective optimization (BCS)	379.25	137,379.56

shows the results of optimization taking into account both the DR program and uncertainty,. In order to meet DR program, 4% of the demand has been reduced from during peak hours (12:00 PM–14:00 PM) and shifting it to off-peak hours (10:00 AM–12:00 PM).

The optimal configuration of switches, the output power of DG units, capacitors, and the charge/discharge status of two EVCSs for two-objective optimization without uncertainty are presented in

Table 7. List of open switches obtained for two-objective optimization.

Hour	Opened Switches
	Sw1	Sw2	Sw3	Sw4	Sw5	Sw6	Sw7	Sw8	Sw9	Sw10	Sw11
1	77	7	14	81	82	84	19	56	55	75	30
2	68	40	9	81	26	33	66	63	55	75	30
3	4	40	15	81	23	84	80	64	55	76	28
4	70	78	14	37	23	84	67	64	85	87	30
5	4	40	14	22	26	50	67	64	55	32	30
6	68	78	15	39	49	35	19	65	85	75	30
7	68	7	15	22	26	35	67	64	55	32	30
8	70	78	9	36	24	50	67	63	55	32	28
9	4	7	10	37	26	84	19	62	55	76	30
10	4	7	15	39	26	52	19	60	55	32	30
11	4	78	10	37	44	84	19	58	72	32	30
12	4	6	14	37	82	84	67	65	85	76	83
13	70	7	15	22	82	35	67	58	55	32	29
14	4	78	15	39	26	84	19	64	85	32	27
15	4	78	15	22	26	35	16	64	55	75	30
16	4	6	15	37	82	33	67	64	72	87	29
17	1	5	15	36	82	35	67	59	85	32	30
18	68	78	14	36	26	34	67	65	72	32	83
19	4	5	15	39	45	84	67	64	85	71	30
20	70	43	79	37	26	50	67	56	74	76	27
21	70	5	15	39	49	50	67	60	55	76	83
22	70	7	15	81	82	35	19	63	74	32	83
23	4	78	79	22	26	84	67	64	55	75	27
24	70	78	14	22	49	50	19	64	85	76	30

and Figure 8, Figure 9, Figure 10 and Figure 11, respectively.

According to Table 7, the radial topology of the distribution network is preserved across all time intervals in this scenario, similar to the previous case. This consistency indicates that the applied control strategy and power flow coordination mechanisms successfully maintain the desired operational structure of the network under varying load and generation conditions throughout the day.

A comparison between scenarios one and two indicates that incorporating the DR program has improved reliability. For instance, the ENS has decreased by approximately 5% compared to the first scenario, which is directly related to enhanced reliability. Additionally, a noticeable reduction in operational cost is observed when incorporating the DR program in the second scenario. The operational cost in scenarios one and two are USD 136,535.23 and USD 136,215.23, respectively.

A comparison between Table 5 and Table 6 reveals that incorporating uncertainty into the optimization framework leads to a deterioration in the objective function values. For example, the ENS increases from 367.45 kWh/year in the deterministic case to 375.5 kWh/year when uncertainty is considered. This degradation stems from the fact that, under uncertainty, the optimization model adopts more conservative and risk-averse strategies to preserve system stability and reliability across a range of possible scenarios. Such an approach inherently restricts the feasible solution space by introducing additional constraints and robustness requirements. As a result, the optimization process may forgo more cost-effective or lower-ENS solutions that would only be valid under ideal or precisely known conditions. Furthermore, accounting for uncertainty often necessitates the deployment of supplementary resources—such as increased energy storage capacity or more resilient network configurations—which, in turn, elevate operational costs and reduce the overall optimality of the solution compared to the deterministic case.

As illustrated in Figure 8, Figure 9, Figure 10 and Figure 11, the distributed generation (DG) units at buses 6 and 25 recorded the lowest and highest power outputs between 5:00 and 6:00 AM, generating 75 kW and 880 kW, respectively. This variation highlights the influence of location-specific factors and demand profiles on DG unit performance during early morning hours. In terms of reactive power compensation, the capacitor unit at bus 10 exhibited both the lowest and highest values, generating 5 kVAr at 12:00 PM and 89 kVAr at 6:00 PM, respectively. This reflects the system’s dynamic reactive power requirements during midday and early evening, potentially driven by fluctuating load patterns and voltage regulation needs. Regarding EV activity, the seventh and ninth EVs at the EVCS installed at bus 45 registered the highest net charging and discharging amounts over the 24 h period, with energy transfers of 20.15 kW and −15 kW, respectively. Additionally, at the EVCS located at bus 78, the 16th EV achieved the highest total charging amount of 109.5 kW, while the 19th EV recorded the lowest, at 53.5 kW. These differences underscore the diversity in user behavior and mobility patterns, which significantly affect the overall impact of EVs on network loading and energy exchange.

4.4. Analysis of Pareto-Optimal Solutions

This study’s evaluation of the DNR problem as a multi-objective optimization problem is one of its primary objectives. Getting the non-dominated options is the first stage in creating the Pareto front, from which the system operator can select the solution that best suits his or her needs. In situations 1 and 2, the two-dimensional Pareto-optimal fronts produced by the suggested IWO method are displayed in Figure 12 and Figure 13, respectively. The red star in Figure 12 and Figure 13 represents the BCS that was achieved by applying Equation (26). It is important to note that operator preferences determine which BCSs are acquired.

All of the generated Pareto-optimal solutions, as depicted in Figure 12 and Figure 13, are non-dominated, which confirms the effectiveness of the proposed algorithm in addressing the complexities of the multi-objective DNR problem. An additional noteworthy observation is the shape and distribution of the Pareto fronts. The solutions are well spread across the objective space and include the extreme points corresponding to single-objective optimization outcomes. This indicates that the algorithm is capable of capturing a diverse set of trade-off solutions, allowing decision-makers to select from a wide range of feasible operating conditions based on their preferred objective prioritization.

5. Conclusions

This paper presents an effective methodology for addressing the DNR with the aim of energy management in the presence of EVCSs, DGs, and capacitors. Operational expenses and ENS are two of the main goals of the optimization problem, which is composed as a sophisticated multi-objective and nonlinear model. The WOA, which is renowned for its capacity to identify the best answers for complicated and multi-objective problems, has been used to tackle this challenging issue. The results show how these factors significantly affect system performance by combining sophisticated optimization approaches and comparing scenarios with and without demand response and uncertainty.

The main findings of this paper are summarized as follows:

• The proposed approach effectively optimizes energy management in distribution networks with EV charging stations, distributed generation (DGs), and capacitors through dynamic network reconfiguration.
• The Whale Optimization Algorithm (WOA) successfully solves the complex multi-objective optimization problem by minimizing both operational costs and Energy Not Supplied (ENS). Compared to existing methods, the proposed algorithm achieves superior results by reducing total operating costs and improving system dependability.
• Incorporating demand response (DR) programs enhances system reliability and significantly reduces Energy Not Supplied (ENS), even under uncertain operating conditions. By enabling flexible load adjustments and peak shaving, DR contributes to better load balancing and improved voltage profiles across the network, which is especially beneficial in scenarios with high variability in demand or renewable generation.
• Although uncertainties necessitate more conservative decision-making to ensure system robustness, demand response mechanisms help mitigate their negative impacts on overall system performance. DR acts as a distributed and responsive resource that provides operational flexibility, allowing the system to maintain acceptable performance levels despite fluctuations in load profiles, renewable output, or market prices.

Limitations and Practical Challenges:

This study assumes certain patterns for EV arrivals and simplified models for DR implementation, which may not fully capture real-world complexities. Furthermore, practical deployment of the proposed algorithm requires consideration of hardware limitations and real-time adaptability within smart grid infrastructures. Computational demands and communication delays can affect implementation feasibility and should be addressed in future work.

Future Research Directions:

Future research can focus on developing adaptive dynamic reconfiguration methods that not only address the variability and intermittency of renewable energy sources through short-term forecasting but also integrate system protection considerations. Ensuring coordination between feeder switching actions and protection constraints is crucial to maintain system reliability and avoid unintended outages during reconfiguration. In addition, investigating the impact of communication delays, data loss, and cyber-physical threats on the reliability of dynamic reconfiguration is essential. Creating robust and secure control systems will enhance the resilience of distribution networks. Machine learning approaches, especially deep reinforcement learning, offer promising tools to predict grid conditions and automate feeder reconfiguration based on real-time data, reducing the need for manual rule-setting. Moreover, the practical implementation of the proposed methodology in real smart grid environments requires addressing challenges such as hardware requirements for real-time data acquisition and control, computational limitations of edge devices, and the adaptability of the algorithm for real-time operation. Finally, testing these strategies in hardware-in-the-loop (HIL) environments or with practical operational data can validate their effectiveness and facilitate their implementation in real-world distribution systems with electric vehicles and renewable energy.