From Simulation to Implementation: A Systems Model for Electric Bus Fleet Deployment in Metropolitan Areas

Abstract

Urban bus fleets worldwide face urgent decarbonization requirements, with Germany targeting net-zero emissions by 2050. Current electrification research often addresses individual components—energy consumption, scheduling, or charging infrastructure—in isolation, lacking integrated frameworks that capture complex system interactions. This study presents “eflips-X”, a modular, open-source simulation framework that integrates energy consumption modeling, battery-aware block building, depot–block assignment, terminus charger placement, depot operations simulation, and smart charging optimization within a unified workflow. The framework employs empirical energy models, graph-based scheduling algorithms, and integer linear programming for depot assignment and smart charging. Applied to Berlin’s bus network—Germany’s largest—three scenarios were evaluated: maintaining existing blocks with electrification, exclusive depot charging, and small batteries with extensive terminus charging. Electric fleets need 2.1–7.1% additional vehicles compared to diesel operations, with hybrid depot-terminus charging strategies minimizing this increase. Smart charging reduces peak power demand by 49.8% on average, while different charging strategies yield distinct trade-offs between infrastructure requirements, fleet size, and operational efficiency. The framework enables systematic evaluation of electrification pathways, supporting evidence-based planning for zero-emission public transport transitions.

1. Introduction

Worldwide, city bus fleets must achieve radical emissions reductions. In Germany, the current emissions of 93 g of CO₂-equivalent per passenger kilometer [1] need to be reduced to net-zero by 2050 [2]. While 8.5% of German buses were electric in 2022, this transition faces critical implementation challenges: Limited charging infrastructure, grid capacity constraints, and cost-effectiveness requirements demand systematic planning.

Electrifying bus networks necessitates solving interconnected technical and operational challenges. Current research remains fragmented: Existing models either focus on isolated aspects or propose non-reusable integrated models with limited scope. No unified framework exists that combines all necessary steps for bus electrification. Our work aims to fill this gap, creating a unified, extensible simulation framework and implementing the core parts. In this work, based on extensive literature review and discussions with bus operators in Munich and Berlin, we focus on the following core elements:

• Energy Consumption Simulation Identifying the energy consumption of a given trip. This part serves as a building block for subsequent steps.
• Block Building Finding sequences of trips (subsequently called “blocks”, also called “vehicle schedules” in other literature) that minimize the total cost while respecting the limited battery capacity.
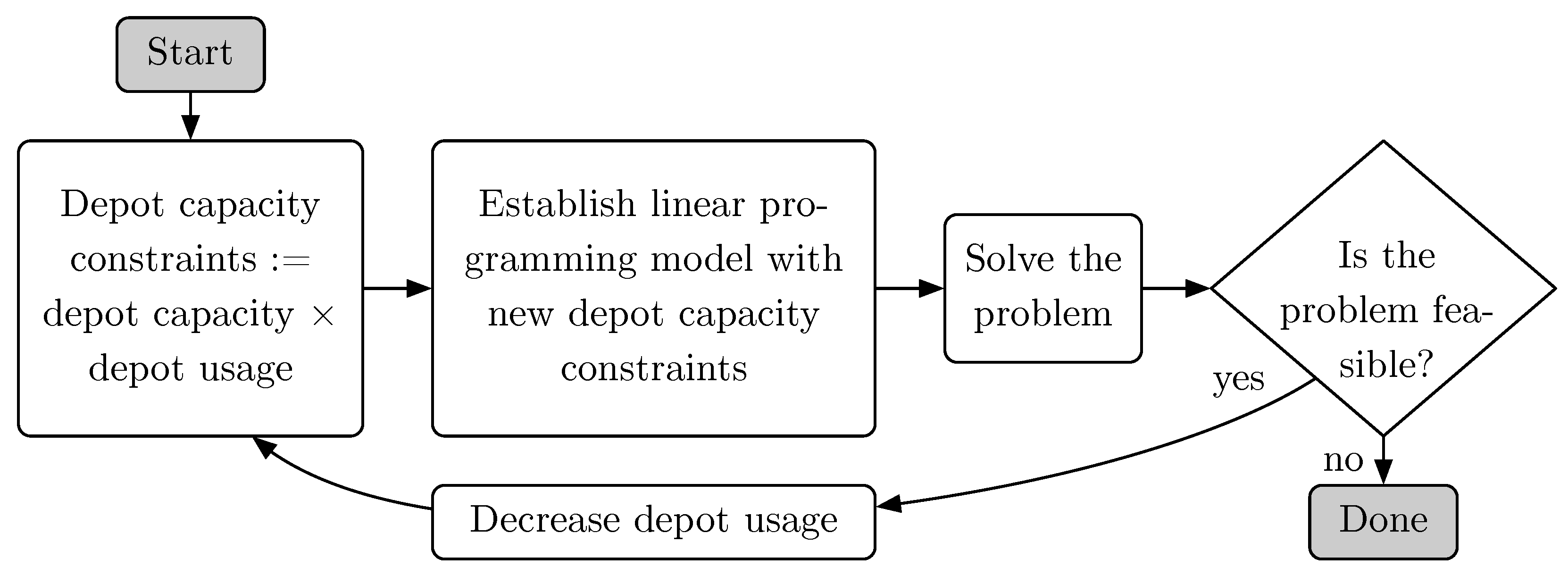
• Depot–Block Assignment Choosing which blocks depart from which depot, respecting limited physical and electrical depot capacities.
• Terminus Charger Placement Choosing a useful, preferably optimal, set of terminus stations to electrify.
• Depot Simulation Identifying the number of in-depot charging stations and vehicles required.

1.1. Battery-Electric Bus Deployment and Charging Technologies

After unsuccessful attempts in the late 19th century ([3], p. 8) and in the 1970s ([4], p. 170), battery-powered city buses—enabled by lithium-ion batteries—are now being deployed in large numbers. They are now the overwhelming majority of new zero-tailpipe-emission buses, with fuel cell vehicles not available at competitive prices.

China plays a pivotal role in the worldwide deployment of battery-electric city buses. Early policy support for electrification led to 90% of global electric bus sales occurring there in 2020, though this share decreased to 60% by 2023 as the Chinese market approaches saturation—with 74.1% of buses being electric in 2024 [5]—and international demand picks up ([6], p. 61). However, these early deployments utilized immature technology not supported by detailed planning, leading to additional vehicle needs ranging from 50% to 100% [7]. If governments are not willing to invest as much into bus electrification, more efficient paths must be found.

For battery-electric buses in Germany, three charging technologies are utilized [8]:

• Depot Charging The buses are driven until their batteries are depleted, then return to the depot to recharge. While this technology needs no changes to the schedule or infrastructure outside the depot—which is already owned by the bus operator—using it on lines with high service frequency and long service days requires excessively large and expensive batteries or incurs an additional vehicle demand if one diesel bus has to be replaced by multiple electric ones.
• Opportunity/Terminus Charging Opportunity charging refers to the provision of charging infrastructure at the stations of a bus line. If charging infrastructure is only installed at the termini, it is called “terminus charging”. The power of the charging infrastructure and in-vehicle charging systems is calculated so that the already existing breaks at the end of each trip can be used to recharge the energy consumed during the preceding trip. The charger usually connects to the vehicle automatically, for example, by mounting the contacts on an overhead pantograph.
• In-Motion Charging Buses can be recharged while driving. A large-scale implementation would add overhead wires to the parts of the network shared by most bus lines, with branches served under battery power. While this solution is technologically elegant—with “zero” time dedicated for charging—the need for large-scale infrastructure along a significant part of the bus system makes this technology politically and financially difficult to implement.

In-motion charging is not widely used, with only three networks remaining in Germany. The opportunity charging systems are less widely deployed, but rapidly increasing in importance, especially in dense cities and highly developed countries. This work will therefore focus on depot charging and opportunity charging in its electrification scenarios.

1.2. Scientific Contribution of the Publication

This publication presents the first fully integrated, open-source simulation framework for battery-electric bus fleets. Extensive previous research has either focused on individual aspects of the problem or conducted coarse-grained integrated analyses. While fine-grained, integrated solutions exist in the commercial domain [9], they are not accessible to the research community.

The modular, open-source approach allows for flexible comparisons between different bus networks and algorithms. Existing works often vary in both methodology and datasets, making direct comparison difficult. In contrast, our framework enables researchers to interchange datasets or algorithms and compare results under consistent conditions.

While some parts, such as energy consumption (Section 2.1), terminus electrification (Section 2.4), and smart charging (Section 2.6) match the state of the art, our work on block building (Section 2.2) and depot–block assignment (Section 2.3) extends the existing algorithms. This allows for the integration of new constraints and enhances the realism of the simulations.

1.3. Structure of This Study

This study is structured as follows: In Section 1.4, a literature review is conducted, structured along the core parts mentioned above, also investigating existing integrated models in Section 1.4.7. In Section 2, an integrated, modular approach is presented and its steps detailed. Section 3 applies this approach to the largest bus network in Germany, in the city of Berlin. Finally, in Section 4, the implications and potential future research avenues are discussed, with a summary provided in Section 5.

1.4. Literature Review

The literature review employed a two-phase approach: an initial exploratory phase that mapped the foundational components of a systems-level framework for bus electrification planning, followed by detailed investigation of current methodologies and innovations within each identified component.

Outside of this publication’s scope is the electric power grid, where the effects of a large number of buses charging simultaneously are investigated. This has been investigated by other researchers for the cities of Hamburg [10], Berlin [11], and Belleville [12].

Also not considered in this work are analyses of results according to total cost of ownership (TCO) [13], environmental impact [14], or both [15].

1.4.1. Energy Consumption Simulation

The energy consumption of electric buses is mainly composed of the traction energy needed to keep the bus moving and the auxiliary energy, which is dominated by the heating, ventilation, and air conditioning (HVAC) system.

The traction energy can be calculated using a physics-based model, if the driving profile and vehicle parameters are known [16,17]. Similarly, the HVAC energy consumption can be estimated using a physics-based model [18].

If the exact driving cycle or vehicle specifications are not known, empirical models derived from real-world data are used [19]. In order to predict the energy consumption of a bus based on a different vehicle, a mathematical model must be created. These models vary greatly in complexity, from simple but transparent regression models [20] to approaches based on neural networks [21].

1.4.2. Block Building

The underlying optimization problem is called the “electric vehicle scheduling problem” and has been proven to be NP-hard, meaning that for large networks, finding an optimal solution quickly imposes implausibly high computational demands [22]. For this reason, most authors focus on developing heuristics for parts of the problem, focusing on charging station placement under a fixed schedule and timetable [23], on schedule and charging station optimization for a fixed timetable [13], or on temporal charging optimization with the other parameters fixed [24].

The work of Reuer et al. [25] (building on Lenstra and Kan [26]) explores the theoretical considerations for optimal scheduling of electric buses, showing that a heuristic approach can be used to calculate an upper bound of the number of vehicles, while a time-space network (TSN) can be used to calculate the exact solution. The review paper of Perumal et al. [27] presents a comprehensive overview of the work on electric city buses in the field of operations research.

Of special interest to us is the approach of Wang et al. [28], who showed that by modeling core parts of the vehicle scheduling problem as the “minimum path cover on directed acyclic graphs”, it can be solved in polynomial time, thereby finding usable solutions for large bus networks. However, the method is unable to create time- and distance-limited schedules, which are required due to limited battery capacities (when not recharging outside of the depot) and periodic cleaning and maintenance requirements.

1.4.3. Depot–Block Assignment

To reduce operational costs in bus networks, minimizing non-revenue “deadhead mileage”—empty trips between depots and route termini—is critical. Each block begins and ends with an empty deadhead trip: the first from a depot to the terminus and the last back to a depot. Assigning blocks to depots located near their termini shortens these empty trips, lowering costs. However, depot capacity limits must be respected to avoid overcrowding.

In some literature, this optimization challenge is termed as the bus-to-depot allocation problem, where buses are assumed to be already assigned to specific blocks. With this information, the number of buses required at each depot becomes straightforward to calculate. Mathirajan et al. [29] have shown that linear programming can effectively solve this problem under certain constraints, ensuring depots are allocated optimally to minimize deadhead distances while adhering to operational limits.

Kontou et al. [30] reviewed different methods minimizing the deadhead cost and proposed their own method using a genetic algorithm, where the balance between depot occupancy and the operational cost per depot are also part of the optimization objective. A study by Mahadikar et al. [31] proposed an algorithm using linear programming, where the assignment of block and depots is determined under the assumption that each bus operates a single block. In Djiba et al. [32], the assignment between blocks and depots is solved knowing the initial distribution of buses in all depots.

However, the depot–block assignment problem, without any knowledge of the buses or the fleet, is not yet studied to our best knowledge.

1.4.4. Terminus Charger Placement

Terminus charger placement involves deciding which terminus stations will be electrified. While some publications, such as Wang et al. [33], plan the placement of charging equipment at intermediate stops (“opportunity charging”), most real-world implementations solely electrify termini.

Xylia et al. [34] developed an initial placement optimization model that overlooked charging time constraints, later refining it with temporal considerations [35]. Tzamakos et al. [36] extended this approach by incorporating charger queuing dynamics.

Wu et al. [23] show that by optimizing the placement of charging stations within the network, costs can be reduced by more than 50%. Rather than placing charging stations at all termini, they have some buses travel to another line’s terminus to charge. The costs caused by this extra travel (in time, energy, and additional vehicle need) are considered in their algorithm as well, leading to a solution that balances a minimal number of chargers with the minimum acceptable extra travel.

Several authors formulate mixed-integer linear programs (MILPs) that account for cost-related parameters, including charger placement [37,38,39]. However, scaling these models to large networks poses computational challenges. Stumpe et al. [40] show that solution times become impractical when incorporating all cost factors, while Wang et al. [33] assert the problem’s NP-hardness. Notably, they observe that the relative difference in result quality between an optimal solution and a simple greedy algorithm diminishes as the network grows more complex.

1.4.5. Depot Simulation

Simulating vehicle behavior and charging profiles in depots allows fleet composition, power grid impact, and depot capacity to be assessed, which are key indicators for evaluating an electrification strategy.

Table 1. Sub-topics regarded in studies of depot simulation.

	Lauth [41]	Giuntoli et al. [42]	Guanetti et al. [43]	Eskander et al. [44]	Jahic [45]
Year	2021	2022	2023	2023	2024
Depot Process Simulation	×	×	×
Vehicle-to-Slot Assignment	×		×
Vehicle-to-Block Assignment	×		×	×	×
Depot Layout Design	×			×
Multi-depot					×

× the study investigates the corresponding topic.

summarizes recent studies of depot simulation which focus on at least one of these perspectives.

Depot process simulation integrates additional processes beyond charging, such as cleaning, shunting, and preconditioning. Limited research includes auxiliary depot processes in depot simulation. In Giuntoli et al. [42], arrival delay, energy consumption, and cleaning duration were generated using predefined probability distributions, which impact the final results.

Vehicle-to-slot assignment decides where a bus should park and can potentially influence the vehicle-to-block assignments if certain slots are not always accessible. Vehicles are then dispatched to blocks, and using dispatch strategies other than simple first-in-first-out, can potentially reduce fleet size. This problem is rarely integrated in most of the simulation frameworks.

Depot layout design ensures a geometrically feasible arrangement for the fleet while potentially minimizing space requirements. The method proposed by Eskander et al. [44] constrains the number of buses based on the length and width of a given depot, assuming the buses are parked in an aligned manner. Minimizing area demand is also an objective in some of their studied cases.

Several studies integrate multiple perspectives to create realistic depot profiles. Lauth [41] developed a simulation-based software integrating all the aforementioned sub-topics. In this work, the line parking areas are used in the depot layout design where not all slots are accessible at all times, affecting both vehicle-to-slot and vehicle-to-block assignments. Fleet size is determined after simulation, and a feasible depot layout is subsequently generated using a genetic algorithm. Guanetti et al. [43] aimed to maximize the total mileage of an e-bus fleet when integrating it into a traditional bus fleet. They developed a simulation framework incorporating accurate energy consumption prediction, vehicle-to-block assignment, charging scheduling, and vehicle-to-slot assignment, while integrating trajectory calculation for autonomous driving. The results demonstrated the state of charge (SoC) of vehicles during driving, charging preparation, and charging. In a recently published dissertation by Jahic [45], various aspects in large-scale depot operation are investigated. The simulation and optimization of charging scheduling, preconditioning, and vehicle dispatch enables further analyses on depot profiling, including the impact from temperature, day of the week, and other flexibilities. Among all reviewed studies, only Jahic [45] profiles multiple depots and performs comparative and clustering analyses.

1.4.6. Smart Charging

Charging scheduling determines the time of charging of each bus, and is thus essential for assessing the power demand and charging infrastructure. In addition to simple approaches, such as first-in-first-out scheduling and constant-power charging, smart charging—also known as managed or controlled charging—optimizes charging schedules or charging curves to reduce peak loads or energy cost. Zhou et al. [46] comprehensively reviewed various approaches of smart charging using conductive charging. They revealed the objectives of depot charging scheduling mainly focused on minimizing peak load and minimizing energy cost, and which can be solved with heuristic algorithms or solvers. Jahic et al. [10] modeled charging scheduling similarly to the job scheduling problem and solved it with both greedy and heuristic algorithms. Their case study, conducted on a large-scale depot in Hamburg, showed that a peak load reduction of 27.1% was achieved in winter with preconditioning (turning on the heating while the bus is still connected to the power grid). Verbrugge et al. [24] accomplished the real-time charging scheduling by genetic algorithm with the purpose of minimizing charging cost. The result shows a maximum 9.4% reduction in charging cost within the grid limit. Casella et al. [47] use a periodic discrete event approach and model the charging scheduling problem as a nonlinear optimization problem, aiming to minimize the total cost of energy, with optional objectives of minimizing peak load and dissatisfaction of demand response requests. Brinkel et al. [48] concluded that considering the day-ahead market, the charging cost can be further reduced by at least 6% compared to peak-shaving.

According to Zhou et al. [46], smart charging is also applicable in opportunity charging, sometimes also combined with bus-to-trip assignment. While controlling the charging schedule and power is a common approach for smart charging, technologies such as Vehicle-to-Grid (V2G) and Vehice-to-Everything (V2X) can also be used for minizing peak load or energy cost, though Deb et al. [49] note that V2G and V2X technologies are not as mature as simple on/off control or variable unidirectional charging.

1.4.7. Synthesis of Current Research

Most existing works focus on specific parts of the bus network electrification problem, while only limited studies integrate more than one of the sub-problems mentioned in Section 1.4, as presented in

Table 2. Research on integrated bus network electrification.

	Rogge et al. [50]	Berthold [51]	Topić et al. [52]	He et al. [53]	Foda et al. [54]	Zeng et al. [55]	Guanetti et al. [43]	Jahic [45]
Year	2018	2019	2020	2022	2023	2023	2023	2024
Energy Consumption Simulation	×	×	×		×		×	×
Block Building	×					×
Depot–Block Assignment
Terminus Charger Placement	×	×		×	×	×
Depot Simulation		×	(×)	(×)	(×)		×	×

× the study investigates the corresponding topic. (×) Charging at depots and termini is planned jointly.

.

Among the reviewed works, Jahic [45], Guanetti et al. [43], and Topić et al. [52] incorporate detailed energy consumption simulations to support charging scheduling in depots. While Jahic [45] and Guanetti et al. [43] focus exclusively on overnight depot charging, Topić et al. [52] extends the scheduling to include both depots and terminus stations using a uniform method.

Another line of research investigates the joint planning of terminus charger placement and charging scheduling across depots and termini, as seen in He et al. [53] and Foda et al. [54], with the latter also integrating high-resolution consumption simulations. Berthold [51] has developed a comprehensive methodology also including depot simulation, yet his work focuses on a single bus line.

Block building is addressed in combination with terminus charger placement by Rogge et al. [50] and Zeng et al. [55]. However, to the best of our knowledge, no existing study has yet incorporated depot–block assignment into a holistic electric bus network planning framework.

This reveals a gap in the comprehensive integration of sub-problems within a single framework, which is crucial for advancing electric bus network planning.

2. Modular Simulation Framework “eflips-X”

As discussed in Section 1.4, electrifying a bus network consists of multiple technological and strategic dimensions, each of which may have a significant impact on the total system cost and robustness. As such, a complete system simulation—showing the results of certain strategic choices and allowing them to be evaluated and optimized—is very useful in designing the network, allowing operators to rapidly iterate on their designs. The existing models each provide very good or optimal solutions for parts of this design process; however, a fully integrated model is currently not available.

Therefore, this work presents a fully integrated model, simulating the complete conversion from diesel to an electric bus system and allowing the comparison (and later, optimization) of different electrification strategies. The integrated simulation model consists of several sequential steps that interact through a well-defined data flow, as illustrated in Figure 1. The process begins with the import of an existing diesel network timetable. Taking vehicle parameters such as electric range into account, Block Building generates passenger trip sequences based on scheduling rules. These sequences then undergo Depot-Block Assignment, where blocks are allocated to specific depots while considering depot capacities and locations. The Terminus Charger Placement step follows, determining which terminus stations should be equipped with charging infrastructure. With extremely high energy consumption and short breaks at termini, the energy recharged there may not be sufficient for the coming trip. If this is the case, the break times at the relevant termini must be extended and the process repeated from the Block Building step. Once all data are prepared, the central Simulation is run and the results can be analyzed.

The central Simulation is shown in detail in Figure 2. It starts with an initial Out-of-Depot Simulation to obtain the behavior outside of the depot. The depot simulation then simulates depot processes, such as charging and cleaning, and crucially creates the block sequences followed by vehicles throughout the multi-day simulation periods. The Out-of-Depot Simulation is then run again to obtain vehicle behavior over the multi-day simulation period. Finally, smart charging can be simulated to minimize peak depot power.

The framework is designed on two levels: abstract and implementation. Abstractly, the “eflips-X” framework proposes a simulation flow and a unified data model that specifies all relevant data required for electrification planning, ensuring seamless integration. On the implementation level, we provide a reference implementation of this data model (named eflips-model [56]) and reference code for each simulation step, enabling modular development and reproducibility. All code is available under the GNU Affero General Public License [57].

The formal design of the data model is complete, with an Entity-Relationship model and corresponding UML class structure that unambiguously describes the attributes and relationships required at each simulation stage. While the data structure is well defined, a formal machine-readable representation of the process does not yet exist and remains a subject for future work. Such formalization would further enhance interoperability and enable more automated workflows across the electrification planning process.

2.1. Energy Consumption Simulation

Energy consumption simulation (with the input and output data shown in

Table 3. Inputs and outputs of the energy consumption simulation.

Input	Output
Energy consumption model for each vehicle type	Energy consumption for each trip
Time-distance profiles for each trip	Battery discharge for each trip
Terminus charger locations if any	Battery recharge at each terminus

) serves as a fundamental cornerstone of the integrated model, influencing multiple steps throughout the process. This component provides essential inputs for battery-aware block building and determining the necessity and placement of terminus chargers.

As discussed in Section 1.4.1, multiple approaches exist to estimate a vehicle’s energy consumption.

When planning an electric bus system, the highest energy consumption that can be reasonably assumed to occur must be used. While energy consumption—and correspondingly, charging durations—will be lower most of the time, the system must be able to deal with the most difficult day without collapsing.

The demand for both heating and cooling, along with the efficiency of HVAC systems, fluctuate significantly with outdoor temperature variations. In western Europe, for example, cold weather can reduce the operational range of these systems by up to 50% [8]. However, whether the highest energy consumption occurs on the warmest or coldest days—and the magnitude of this consumption—depends on local climate conditions and the internal temperature set points.

Taking these issues into account, a generic workflow for energy consumption estimation looks as follows:

• Establish an energy consumption model for the vehicles. Prioritize utilizing actual operational data from comparable systems if available; alternatively, adopt empirical models.
• Identify extreme temperature thresholds expected in the region. These can be derived from historical meteorological records, local engineering standards, or regulatory requirements.
• Run simulations to estimate energy consumption for representative routes under both maximum and minimum temperature scenarios, incorporating HVAC performance impacts at these extremes.
• Design the system based on the critical temperature (either peak heat or severe cold) that induces the greatest energy demand.

The eflips-model package [56] provides a framework for simulating electric bus energy consumption using multi-dimensional lookup tables parameterized by speed, gradient, ambient temperature, and vehicle loading. This implementation includes a configurable lookup table generator derived from the methodology of Ji et al. [20]. The architecture supports modular extensions, allowing third-party energy models to be integrated via standardized interfaces.

2.2. Block Building

The “Electric Vehicle Scheduling Problem” describes the creation of a feasible sequence of trips (known as a “block”) which also approximates or achieves one or more optimization goals. The primary feasibility criterion is not exceeding the vehicle’s battery capacity, with a maximum duration (after which cleaning is needed) also required. The optimization goal is to minimize the time buses are not in revenue service. Non-revenue time is composed of “deadhead time”, driving before the first and after the last trip, and “break time”, standing in between trips. Deadhead time can be minimized by creating the longest possible blocks, thereby reducing its relative impact.

In our approach, with the input and output data shown in

Table 4. Inputs and outputs of the block building stage.

Input	Output
Timetable of all trips	Blocks for all passenger trips (not including depot trips)
Battery discharge for each trip
Maximum waiting times at termini

, block building is performed for passenger trips only at first—minimizing the total amount blocks—and deadhead trips are minimized using the depot–block allocation in Section 2.3.

2.2.1. Solution Algorithm

Problem Formulation

Figure 3 and Figure 4 show a simple bus network with only six trips on two lines, with one shared terminus. At each terminus, an arriving bus can either return to the depot or take one of the subsequent trips departing from this terminus. The resulting set of choices can be represented as a directed acyclic graph. Wang et al. [28] proved that this graph is a directed acyclic graph of this graph—the proof can be summed up as “buses can only take subsequent trips (they cannot travel backwards in time), so there can be no cycles”.

The schedule construction problem can now be expressed as the task of finding a path cover for the graph, in which each trip is visited (assigned a vehicle), while primarily minimizing the number of paths (vehicles) and secondarily minimizing the total dwell time at the termini.

The result in Figure 3 shows a solution with three blocks and a total waiting time of 20 min. While this solution has a low waiting time, it is not the best solution, as one with two vehicles exists, which is shown in Figure 4. This solution has a total waiting time of 40 min, but requires only two vehicles. Once deadhead trips are taken into account, the solution from Figure 4 can be assumed to be superior.

Solution—Non-Battery-Aware

The solution to this problem starts by creating a bipartite graph, then finding either the maximum matching or minimum weight full matching. The maximum matching approach is based on the approach of Özçelik [58] and also used by Wang et al. [28]. The minimum weight full matching approach is a novel addition.

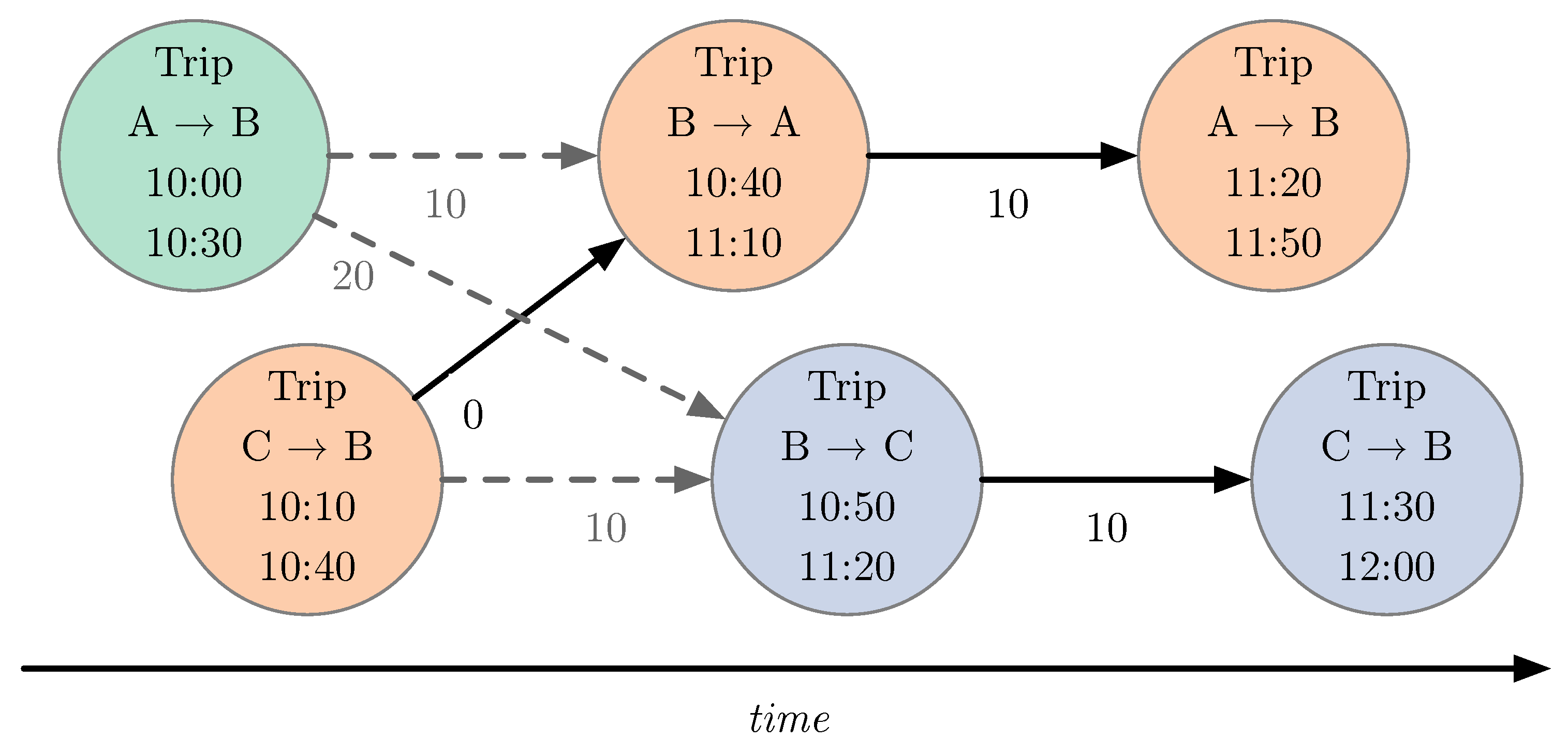
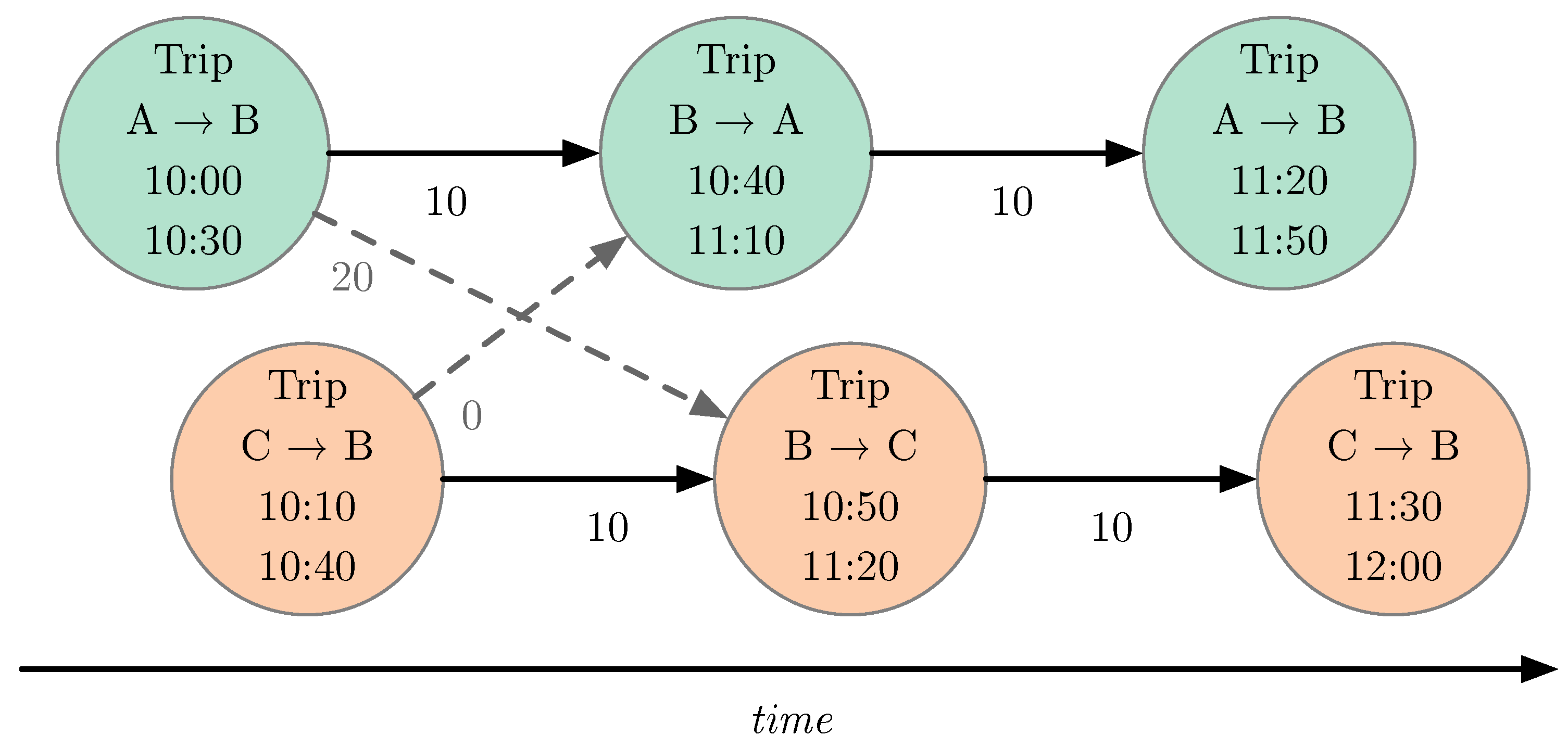
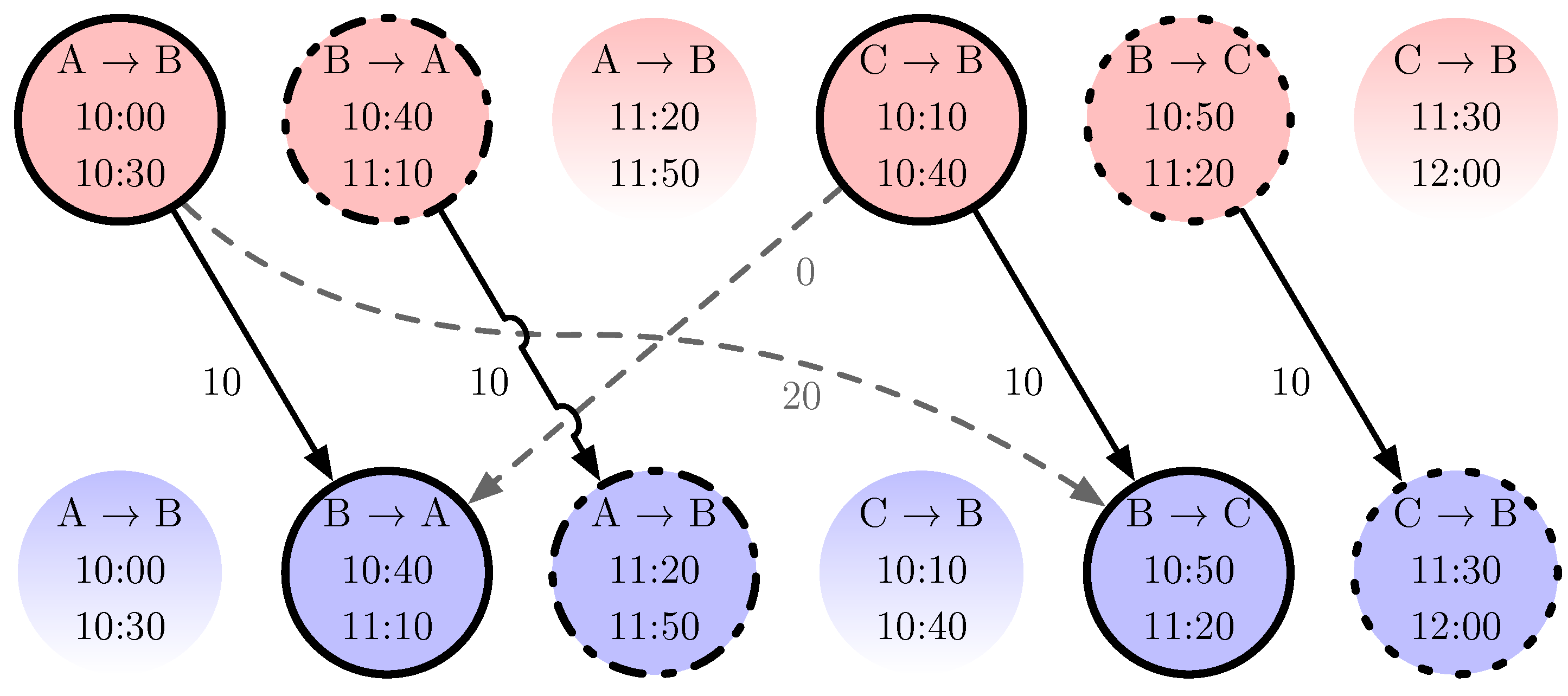
Figure 5 shows the bipartite graph created from the directed acyclic graph of the example bus network. Each node is split in two, with one set of nodes only having outgoing edges, the other set of nodes only having incoming edges. The nodes with only outgoing edges are shown in red, the ones with only incoming edges are shown in blue. It can be seen that some nodes have no outgoing or incoming edges. These are the nodes at which a block must start or end.

Using this transformation to the bipartite graph, the problem changes from the minimum path cover (minimum number of blocks) with the lowest total edge weight (minimizing waiting times) to the maximum matching (minimum number of blocks) and minimum weight matching (minimizing wait times).

Figure 5 also shows that there are three distinct connected sets of nodes, of which two are composed of only two nodes. In a realistically sized problem, there are many such sets, ranging from two nodes to hundreds of nodes. Some of these sets have a full matching, some do not. For those that have a full matching, the Kuhn–Munkres algorithm [59] can be used to find the minimum weight full matching, the solution with the lowest total wait time. For those sets which do not have a full matching, the Hopcroft–Karp algorithm [60] is used to find one—but not necessarily the best—maximum matching.

The runtime of the Kuhn–Munkres algorithm is bounded by $\mathcal{O}\left({\left|\mathrm{vertices}\right|}^3\right)$, whereas the Hopcroft–Karp algorithm has a runtime bounded by $\mathcal{O}\left(\left|\mathrm{edges}\right|\left|\sqrt{\mathrm{vertices}}\right|\right)$. Since most of the subgraphs have full matchings, the overall runtime performance is bounded by $\mathcal{O}\left({\left|\mathrm{vertices}\right|}^3\right)$.

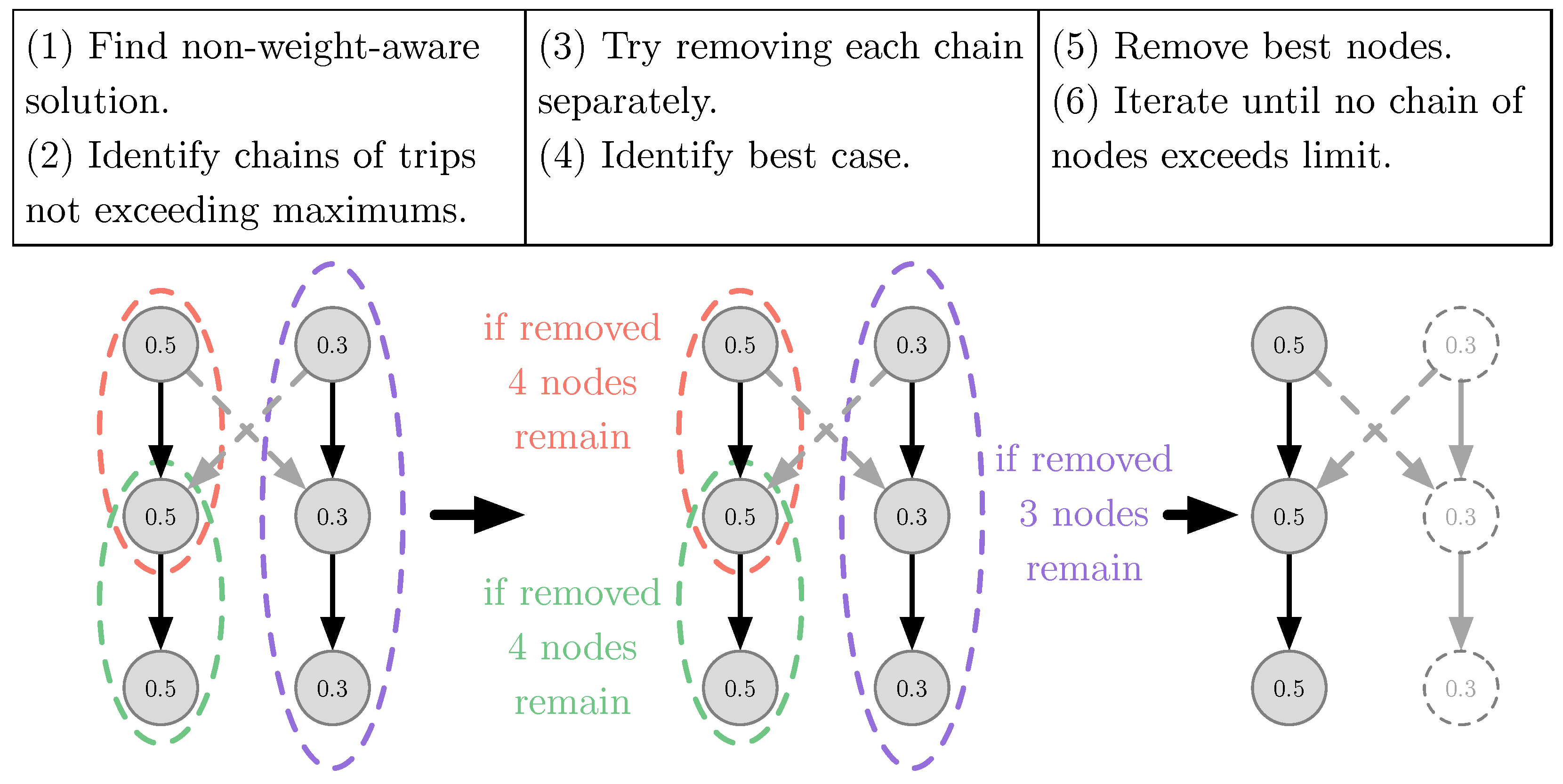
Respecting Battery Capacity

The algorithms presented in the previous section generate the fewest possible blocks without respecting battery capacity or a maximum schedule duration. In the next step, chains of trips that are of an allowable length are iteratively removed. For each chain exceeding the maximum allowed length, the longest still-allowable chain from the start and end is identified. Each possible schedule is then removed, and the number of blocks after re-running the planning algorithm on the remaining set of trips is noted. Finally, the schedule leading to the lowest total number of blocks is permanently removed. This process is continued iteratively until all blocks fall within the capacity constraints. Figure 6 demonstrates this process.

Implementation

The scheduling algorithm was implemented in Rust with Python bindings in the eflips-schedule-rust package [61]. By combining a compiled language and multiprocessing for the “evaluate candidates for removal” step, the runtime for the BVG dataset is 5 h.

2.3. Depot–Block Assignment

Each block generated in Section 2.2 must be assigned to exactly one depot by adding deadhead trips from the depot to the block’s first station and from the block’s last station to the depot. The assignment between blocks and depots should minimize the non-revenue deadhead mileage while considering the capacity and supported vehicle types of each depot. In this work, we choose the integer linear programming (ILP) to solve this problem (using the input and output data shown in

Table 5. Inputs and outputs of the depot–block assignment stage.

Input	Output
Blocks for all passenger trips	Blocks including depot trips
Locations of all depots
Capacities of all depots, by vehicle type

), since it is used in most of the literature for solving the similar bus–depot-allocation problem and the feasibility is guaranteed under the constraints [29].

2.3.1. Problem Setting

To formulate this problem as an ILP, we introduce sets for blocks, depots, vehicle types, and time slots. Time slots are generated by dividing the total simulation duration into intervals, where each interval equals the duration of the shortest block. The set of time slots is used to indicate the occupation of blocks over time.

Table 6. Notation of the model.

Sets
I	Set of blocks	i
J	Set of depots	j
T	Set of vehicle types	t
S	Set of time slots	s
Parameters
$c_{ij}$	Deadhead mileage if block i is assigned to the depot j	km
$v_{it}$	1 if vehicle type t is assigned to block i, otherwise 0
$o_{si}$	1 if time slot s and block i overlap, otherwise 0
$N_j$	Capacity of depot j in the unit of 12-m bus
$f_{tj}$	Size factor of vehicle type t for each depot j
Decision variables
$x_{ij}$	1 if block i is assigned to depot j, otherwise 0

displays all the sets, parameters, and decision variables constructing the linear programming model. The capacity of each depot is represented in terms of the equivalent number of 12 m buses it can accommodate. For vehicle types other than 12 m buses, a size factor $f_{tj}$ is introduced to reflect the relative space occupied by each bus type compared to a 12 m bus in depot j. For example, the size factor of an 18 m bus is $18/12=1.5$. If a depot does not support a certain vehicle type, the factor is set to the total capacity of this depot.

With these aforementioned notations, the problem can be described using the following equations:

$$\mathrm{minimize}\sum _{j\in J}\sum _{i\in I}{c}_{ij}{x}_{ij}$$

(1)

subject to:

$$\sum _{i\in I}{x}_{ij}=1,\forall j$$

(2)

$$\sum _{t\in T}{f}_{jt}(\sum _{i\in I}{o}_{si}{v}_{it}{x}_{ij})\le N_j,\forall s,j$$

(3)

Equation (1) describes the objective: minimizing the total deadhead kilometers. Constraint (2) ensures that each block can be assigned to one single depot. Constraint (3) limits the number of vehicles that can be en route at the same time for a given depot. Specifically, the sum of active vehicles per time slot, measured in equivalent 12 m buses, must not exceed the depot’s capacity. This provides a rapid evaluation of the required fleet size, assuming that the maximum number of simultaneously operating vehicles determines the total vehicle demand.

The depot–block assignment package is implemented in the eflips-opt package [62]. The ILP is modeled using the Pyomo framework [63] and solved with the Gurobi solver [64].

2.3.2. Iterative Workflow

To ensure balanced utilization across depots and prevent the optimization algorithm from concentrating vehicles in a single depot, we adjust depot capacities through an iterative scaling process. Initially, each depot’s capacity is set to its maximum value. However, if these capacities are too large relative to the required vehicle allocation, the optimization might disproportionately assign vehicles to a few depots. To address this, we proportionally scale down all depot capacities by the same percentage in each iteration, preserving their original size ratios. This process is shown in Figure 7.

2.4. Terminus Charger Placement

Terminus station electrification refers to the placement of charging infrastructure not only at the depot, but also at selected terminus stations, where the buses recharge the batteries during short breaks between trips.

In this work, we implement a charging simulation that accounts for congestion and dead time, combined with a greedy algorithm for terminus station selection. The inputs and outputs of our algorithm can be seen in

Table 7. Inputs and outputs of the Terminus Charger Placement.

Input	Output
Blocks including depot trips	Terminus charger locations
Battery discharge for each trip	Charging port counts for each location
(Optional) Denylist of termini that must not be electrified
(Optional) Pre-Existing list of all termini that are already electrified
This stage is optional, it can also be skipped

. The greedy approach was chosen over an optimization model to obtain quick results even for large-scale scenarios, and based on findings from Wang et al. [33], which demonstrated that the performance gap between optimal and greedy strategies becomes smaller for large scenarios.

2.4.1. Terminus Charging Simulation

Terminus Charging is simulated after the blocks and the depot assignment are known, but before the depot simulation takes place (as the energy needed in the depot depends on how much was charged outside). Terminus charging takes place when the following conditions are met:

• The vehicle is capable of terminus charging.
• The block the vehicle is operating requires terminus charging.
• The station the vehicle is currently operating has terminus charging equipment.

Terminus charging is simulated without regard to the state of charge of the vehicle. First, the time required to fully charge the vehicle is determined based on its battery capacity and charger power output. The calculated duration also accounts for the time taken to connect and disconnect from the charging station. If the duration of the charging break at the terminus is shorter than the time needed for a full charge, the bus will charge for the entire available period of the charging break. If a full charge is feasible within the break, the simulation selects time slots to minimize concurrent charging (e.g., staggering buses to avoid simultaneous demand).

While this approach creates adequate results in practice, some improvements could still be made. Considering the battery state of charge would lead to buses skipping charging events when they are not needed, thereby increasing total efficiency since the deadtime to connect and disconnect from the charger will be reduced. Additionally, for reasons described in Section 3.4, a rigid 10 min break is used whenever a charging event could take place, even if the time needed for charging might be shorter than those 10 min.

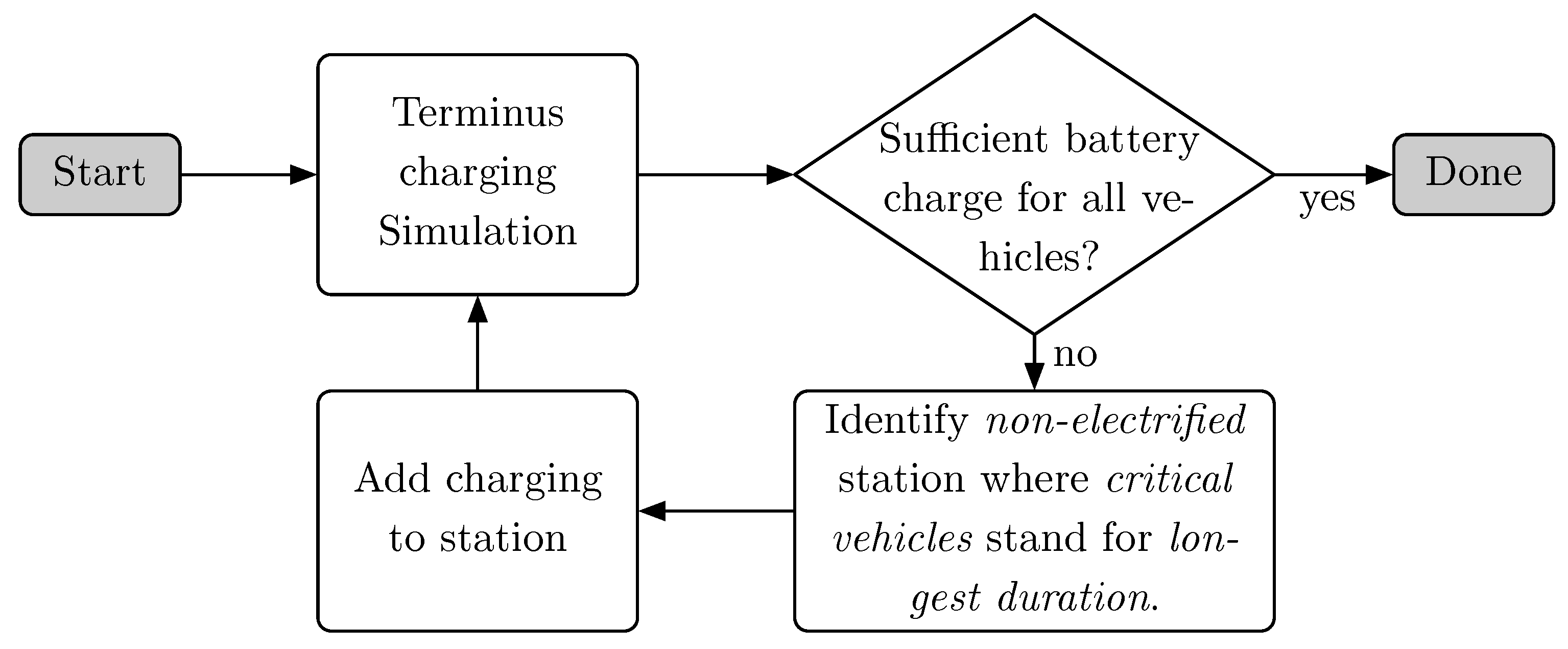
2.4.2. Greedy Algorithm

The algorithm for choosing which stations to electrify is shown in Figure 8. It uses the total time spent at the station by vehicles requiring charging as its heuristic. After an initial consumption simulation without terminus charging to find all the blocks which need terminus charging (e.g., those returning to the depot with a negative state of charge), terminus charging is continuously added until no block reaches the depot with a negative state of charge.

2.4.3. Implementation

The terminus charging simulation is implemented as part of the “driving energy consumption” estimation in the eflips-depot package [65]. For the greedy charging simulation, a throwaway implementation was created due to the simplicity of the algorithm.

2.5. Depot Simulation

In the previous sections, all processes of the vehicles outside of the depot have been simulated. Until this point, each block was simulated individually, with the sequence of blocks traveled by each vehicle on different days being of no importance.

This section focuses on simulating in-depot processes, using the inputs shown in

Table 8. Inputs and outputs of the depot simulation.

Input	Output
Depot data location, electric power and layout	Depot behavior used capacity, vehicle counts, energy consumption
Depot processes including shunting and cleaning	Vehicle behavior total vehicle count and multi-day block sequences
Blocks including depot trips	Charging flexibility vehicles plugged in but not charging
Battery discharge for each trip, taking into account terminus charging

to create the outputs shown in the same table. By modeling the sequential assignment of blocks to vehicles, we estimate the minimum fleet size required for operations. After completing a block, a bus returns to the depot for charging and servicing, remaining parked until its next scheduled block. Integrating depot dynamics, such as vehicle parking, dispatch protocols, and charging logistics, using the framework developed by Lauth [41], enables a realistic assessment of depot profiles. Specifically, we analyze depot capacity requirements and vehicle counts. Grid load implications, refined through post-processing with a smart charging strategy (Section 2.6), will be detailed later.

2.5.1. Depot Activities

When a vehicle enters a depot, processes presented in Figure 9 will be performed in order. If any area is fully occupied (or if all shunting drivers are assigned), the bus must wait for a vacancy in the area of the previous process.

In this case study, all areas are assumed to be “direct”, with each parking spot being accessible at all times. In the simulation framework “line” areas, simulating vehicles parking behind each other and potentially blocking each other are also implemented. The amount of charging spaces is set to be sufficient for all vehicles, based on the assumption that the creation of more charging places is much cheaper than purchasing additional vehicles to cover shortfalls caused by congestion. The simulation framework is also capable of simulating a space-constrained depot, where significant congestion might take place.

We used the “First” strategy in the model of Lauth [41] for parking and dispatch. Under this strategy, a bus is assigned to the first vacant charging slot and dispatched following a first-in-first-out method. For a successful dispatch, the following criteria must be met: the vehicle type matches the block requirement (double-decker, single-decker, or articulated bus), the vehicle has sufficient energy for the entire block, and it is not engaged in an uninterruptible process (e.g., cleaning or shunting).

In the depot simulation, blocks are linked into block sequences that are traveled by a single vehicle, with vehicles often traveling on different lines on different days, as the total time spent charging and driving does not sum up to 24 h. The vehicle count is then calculated from the total number of block sequences, each of which needs one vehicle.

2.5.2. Implementation

The depot simulation is implemented in the eflips-depot package [65].

2.6. Smart Charging

A naive charging strategy has each vehicle charged with full power as soon as it arrives at its charging station in the depot. However, this behavior will lead to the power demand and battery degradation being larger than it needs to. In a depot charging scenario, there usually exists significant temporal flexibility, as the charging power needed for the battery to be sufficiently full is much lower than the full power the charger can provide. This flexibility can be utilized in multiple ways:

• Improve Battery Longevity Charge each vehicle continuously with the minimum power required for the battery to be full.
• Peak-Shaving Balance different vehicles’ charging power in order to minimize depot-level peak power and allow a smaller grid connection.
• Price-Following Charge vehicles with a price-based charging strategy, trying to charge more in periods of low electricity prices.
• GHG Minimization Similar to a price following strategy, charging can be shifted to times where the greenhouse gas emissions are low.

The peak-shaving, price-following, and GHG minimization strategies could also be combined with bidirectional charging technology to increase the leverage by also allowing some buses to discharge their battery back into the local (peak-shaving) or national (price-following and GHG minimization) grid.

Our simulation framework allows the addition of various smart charging strategies in the post-processing stage, utilizing the existing “naive” charging times and the known departure time to provide flexibility information to the smart charging simulation.

2.7. Integer Linear Program for Peak Shaving

In this work, a peak-shaving algorithm was implemented as an Integer Linear Program (ILP), with the input and output data shown in

Table 9. Inputs and outputs of our smart charging implementation.

Input	Output
Charging flexibility vehicles plugged in but not charging	Time-power profiles for each vehicle
Maximum power for each vehicle
This stage is optional, it can also be skipped.

.

The ILP operates on a set of charging events V and timesteps T:

$$\begin{array}{ccc}\hfill V& =\{1,2,\dots ,|V\left|\right\}\hfill & \hfill \mathrm{Set}\mathrm{of}\mathrm{charging}\mathrm{events}\end{array}$$

(4)

$$\begin{array}{ccc}\hfill T& =\{1,2,\dots ,|T\left|\right\}\hfill & \hfill \mathrm{Set}\mathrm{of}\mathrm{timesteps}\end{array}$$

(5)

For each charging event at a depot, we calculate the total available time and required energy $e_v$ (shown in Equation (9)), subtracting a five-minute buffer before departure. Time is discretized into five-minute intervals. Vehicle presence $V{T}_{present}$ is represented as a binary variable (shown in Equation (6)), while charging power is constrained to integer multiples of 10 kW (Equation (17)), between zero and the maximum allowable power $r_v$ (Equation (8)).

$$\begin{array}{cc}\hfill V{T}_{present}& =\left\{\right(v,t)\in V\times T\mid \mathrm{charging}\mathrm{event}v\mathrm{is}\mathrm{present}\mathrm{at}\mathrm{timestep}t\}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill T_{active}& =\{t\in T\mid \exists v\in V:(v,t)\in V{T}_{present}\}\hfill \end{array}$$

(7)

The parameters for each vehicle are:

$$\begin{array}{ccc}\hfill r_v& =\mathrm{Quantized}\mathrm{maximum}\mathrm{charging}\mathrm{power}\mathrm{for}\mathrm{charging}\mathrm{event}v\hfill & \hfill \forall v\in V\end{array}$$

(8)

$$\begin{array}{ccc}\hfill e_v& =\mathrm{Total}\mathrm{energy}\mathrm{required}\mathrm{by}\mathrm{charging}\mathrm{event}v\hfill & \hfill \forall v\in V\end{array}$$

(9)

Quantizing the charging power simplifies both computation and practical implementation, as charging equipment need only adjust power levels at fixed intervals to predetermined values, rather than following arbitrary power curves. The auxiliary set $T_{active}$ (Equation (7)) reduces the problem size significantly by allowing the optimizer to skip all the timesteps where no vehicles are present at the charging station (Equation (15)).

The decision variables are:

$$\begin{array}{ccc}\hfill x_{v,t}& =\mathrm{Quantized}\mathrm{energy}\mathrm{for}\mathrm{charging}\mathrm{event}v\mathrm{at}\mathrm{timestep}t\hfill & \hfill \forall (v,t)\in V{T}_{present}\end{array}$$

(10)

$$\begin{array}{cc}\hfill P& =\mathrm{Peak}\mathrm{total}\mathrm{quantized}\mathrm{energy}\mathrm{across}\mathrm{all}\mathrm{timesteps}\hfill \end{array}$$

(11)

Here, $x_{v,t}$ represents the core scheduling decision—when and at what power to charge each vehicle. The auxiliary variable P simplifies the peak power minimization objective through the following relationship:

$$\begin{array}{c}\hfill P_t=\sum _{v:(v,t)\in V{T}_{present}}{x}_{v,t}\forall t\in T_{active}\end{array}$$

(12)

The constraints ensure feasible charging schedules:

$$\begin{array}{cccc}{x}_{v,t}\hfill & \le r_v\hfill & \forall (v,t)\in V{T}_{present}\hfill & (\mathrm{Charging}\mathrm{rate}\mathrm{limit})\hfill \end{array}$$

(13)

$$\begin{array}{cccc}\sum _{t:(v,t)\in V{T}_{present}}{x}_{v,t}\hfill & =e_v\hfill & \forall v\in V\hfill & (\mathrm{Energy}\mathrm{requirement})\hfill \end{array}$$

(14)

$$\begin{array}{cccc}{P}_t\hfill & \le P\hfill & \forall t\in T_{active}\hfill & (\mathrm{Peak}\mathrm{power}\mathrm{definition})\hfill \end{array}$$

(15)

The optimization objective is:

$$\begin{array}{c}\hfill \mathrm{minimize}P\end{array}$$

(16)

subject to the domain constraints:

$$\begin{array}{ccc}\hfill x_{v,t}& \in {\mathbb{Z}}_0^{+}\hfill & \hfill \forall (v,t)\in V{T}_{present}\end{array}$$

(17)

$$\begin{array}{c}P\in {\mathbb{Z}}_0^{+}\hfill \end{array}$$

(18)

This peak-shaving program is implemented in the eflips-opt package [62]. We implemented this ILP using the Pyomo framework [63] and solved it with either GLPK [66] or Gurobi [64].

3. The “One-Week Berlin” Case Study

“Berliner Verkehrsbetriebe AöR” (BVG) is the largest bus operator in Germany, with 1510 buses driving 93.1 million revenue kilometers per year [67,68]. BVG has been tasked with transitioning to 100% non-fossil drivetrains by 2030 [69]. This transition will be effected by switching to battery-electric buses, with a mixture of depot and terminus charging.

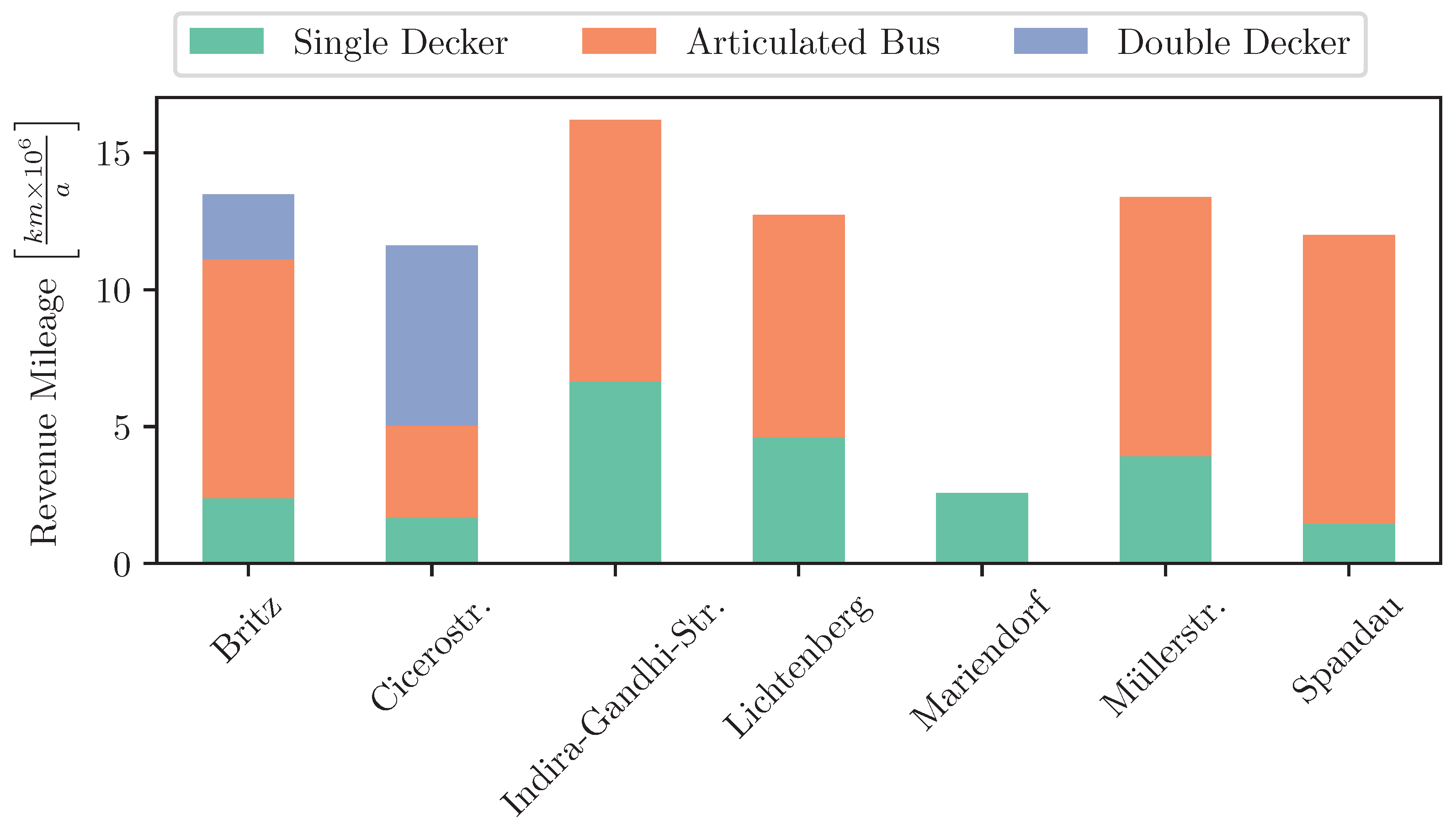
Currently BVG operates six depots and one parking area (where no cleaning is performed) throughout Berlin. The fleet is composed of single deckers, articulated buses, and double deckers. Figure 10 shows the mileage distribution over the different depots and bus types. BVG’s electrification strategy consists of electrifying the existing depots in multiple construction stages and building three additional depots.

The routes operated by BVG are diverse, with extremely dense and high-frequency urban services, but also higher-speed and lower-frequency suburban services in the outskirts of Berlin. Its high operational complexity and large fleet size makes Berlin a challenging test case for developing electrification strategies.

BVG has provided us with the complete schedules and blocks for a representative week of operations, for which electrification strategies will be developed.

3.1. Considered Electrification Strategies

In this work, three different electrification scenarios will be explored, which were developed together with BVG. They were developed to explore the outer boundaries and extremes of possible solutions, laying the groundwork for later, more realistic planning. These scenarios serve to map the breadth of the solution space and identify the constraints and trade-offs inherent in different approaches to electrifying transportation systems.

Specifically, the three scenarios are as follows:

• Existing Blocks Unchanged (EBU) This scenario maintains the blocks, showing the effects of electrification within those fixed constraints.
• Depot Charging Only (DCO) This scenario investigates the implications of not electrifying any terminus stations, relying exclusively on depot charging.
• Small Batteries and Termini (SBT) This scenario explores the limits of what can be achieved with severely constrained battery capacities and extensive terminus charging.

Table 10. Differences in parameters for the electrification strategies.

	Existing Blocks Unchanged	Depot Only Charging	Small Batteries and Termini
Abbreviation	EBU	DCO	SBTD
electrified trips	100%	100%	100%
blocks	same as diesel	sized for battery	minimum count
terminus electrification	where necessary	none	where necessary
battery size	large	large	medium
terminus charger power	450 kW	—	300 kW
depot charger power	120 kW	120 kW	120 kW

concisely shows the differences between the scenarios. These scenarios are purposefully designed to be non-optimal or unrealistic in order to better understand the full range of possibilities and challenges. The insights gained from analyzing these extreme cases can then inform the development of more detailed, nuanced, and practical electrification strategies in future work. The primary focus of this paper is on the methodological approach to constructing and evaluating such boundary scenarios, rather than the specific scenarios themselves.

3.2. Vehicle Parameters

Based on market research, three vehicle types were identified for our electric bus fleet. The simulation environment supports the evaluation of alternative bus configurations beyond these selected types. For all bus types two scenarios are investigated: one set of technical parameters is used for the scenarios “Existing Blocks Unchanged” and “Depot Charging Only”, and another set of parameters—representing the effects of the smaller batteries—is used in the “Small Batteries and Termini” scenario.

Table 11. Technical parameters of the buses.

	Scenario	Single Decker	Articulated Bus	Double Decker	Unit
OEM		Ebusco	Solaris	Alexander Dennis
Model		3.0 12 [70]	Urbino 18 Electric [71]	Enviro500EV [72]
usable energy	DCO, EBU	500	640	472	kWh
	SBT	250	320	320	kWh
curb weight	DCO, EBU	12	19	19	t
	SBT	9.95	17	18	t
passengers	–	70	100	112	–

shows the key technical characteristics of the vehicles.

3.3. Energy Consumption Simulation

For the BVG case study, a look-up table directly based on measurements is used for the articulated bus, where such data are available, and for the other two bus types, the empirical model developed by Ji et al. [20] is adapted.

3.3.1. Look-Up Table for Articulated Buses

For articulated buses, an empirical approach based on real-world measurements is used. Over the course of the “E-MetroBus” research project, 798,502 km of driving data were recorded over a period of two years. These data were then segmented, with each segment containing 1 km of driving data. The segments were binned according to average speed in the segment and outside temperature. For each bin, the median energy consumption was calculated. The results are shown in Figure 11a.

3.3.2. Empirical Regression Model

For the single decker and double decker buses, the regression model of Ji et al. [20] was adapted to generate look-up tables in the same format as our empirical measurements and scaled to match our measurements. In this model, the vehicle weight, and therefore the passenger weight, plays an important role. For this publication, the average number of passengers of 17.6 was taken from the German public transport statistics [73] and multiplied with the passenger weight of 68 kg [74], leading to a payload of 1.2 t. For cities with large differences in load factor coupled with significant inclines, our framework allows for payload masses varying for each trip, increasing the accuracy of the energy consumption estimation. The results of this consumption model for an articulated bus are shown in Figure 11b.

3.3.3. Impact of Ambient Temperature

For defining the coldest day, the design temperature for building heating systems according to the national standard DIN/TS 12831-1 [75] was used, being −12 °C throughout the day. For the warmest day, the warmest measured within the last 30 years was used (29.6 °C daily average, own analysis based on meteoblue [76] data). The bars on the left in Figure 12 show the energy consumption for the three vehicle types during these extreme days. It can be seen that the cold day has the highest energy consumption.

Consequently, the winter temperature according to DIN/TS 12831-1 is used to derive the maximum energy consumption, for which the schedules and charging systems will be designed.

The right graph in Figure 12 shows how energy consumption varies seasonally.

3.4. Block Building

The algorithm was applied to the BVG dataset. The “Existing Blocks Unchanged” scenario was not changed and will be used as reference. For the “Small Batteries and Termini” scenario, no battery capacity limit was set (as the buses will be recharged at terminus stations), and the minimum break time at charging stations was set to 10 min. For the “Depot Charging Only” scenario, the maximum battery depletion was set to 90% to allow a reserve for the “depot → first station” and “last station → depot” deadhead trips.

The most important criteria for the quality of blocks are their total number and the block efficiency, which is defined as $\eta ={\displaystyle \frac{\mathrm{time}\mathrm{in}\mathrm{revenue}\mathrm{service}}{\mathrm{total}\mathrm{block}\mathrm{duration}}}$.

Table 12. Block building results for the scenarios. All values represent outcomes for a single week of operations.

Scenario	Number of Blocks	Mean Block Distance	Duration of Longest Block	Block Efficiency $\mathit{\eta }$	Passenger Trips on Same Line
Unit	–	km	hours	–	–
Existing Blocks Unchanged	8498	198	26	73.4%	96.1%
Depot Charging Only	8794	193	32	74.2%	70.0%
Small Batteries and Termini	8203	206	44	71.2%	68.9%

shows the efficiency and other results. It can be seen that our blocks roughly match the efficiency of BVG’s current blocks (used in the “Existing Blocks Unchanged” scenario). The efficiency is slightly higher for the “Depot Charging Only” scenario and slightly lower for the “Small Batteries and Termini” scenario. This is due to the optimizer optimizing for the minimum number of blocks first, then for efficiency. It can also be seen that the results come at the expense of buses taking fewer trips on the same line during their shift, thereby increasing driver workload. Additionally, our algorithm constructs longer-duration blocks.

3.5. Depot–Block Assignment

The depot–block assignment process is essential across all scenarios for the BVG case study. Even the “Existing Blocks Unchanged” scenario, which reflects current operational blocks, requires reassignment due to infrastructure changes: BVG is phasing out the Mariendorf parking space and introducing two new depots. For the “Depot Charging Only” and “Small Batteries and Termini” scenarios, depot assignment is necessary, as the results of the block building are only passenger trips; deadhead trips to/from depots must still be incorporated. Thus, all scenarios involve solving the depot–block assignment problem to align vehicle deployments with the updated depot network.

Blocks generated in Section 3.4 are used as the input blocks. The vehicle–type–block assignment and the depot capacities were provided by the bus operator (BVG). The deadhead kilometers are obtained using OpenRouteService [77] with the “driving-car” profile, which calculates the route between two coordinates for a normal car. However, the “driving-car” profile does not consider the limitation of vehicle length or height—it might generate a route not accessible to buses. This difference is assumed to be insignificant.

In Figure 13, the change in depot allocation for the “Existing Blocks Unchanged” scenario can be seen. Most existing depots see their total vehicle kilometers reduced by shifting some blocks to new depots, with the exception of Cicerostraße, where due to an advantageous position and remaining capacity, the number of blocks increases.

Table 13. Results of depot–block-assignment. All values represent outcomes for a single week of operations.

	Deadhead Miledage
Unit	km
Diesel Schedule (baseline)	110,665
Existing Blocks Unchanged	102,878
Depot Charging Only	123,319
Small Batteries and Termini	170,453

shows the results of the three different scenarios, with the addition of BVG’s current schedule as a baseline. It can be seen that our “Existing Blocks Unchanged” scenario improves on the baseline, whereas the other two scenarios, by optimizing for the minimum number of blocks, accept a larger deadhead mileage. In the “Small Batteries and Termini” Scenario, with its very long blocks and many line changes (see Table 12), the effect of buses ending and starting their service days in different parts of the city is especially pronounced.

3.6. Terminus Charger Placement

For the “Depot Charging Only” scenario, no terminus charging was used. In the “Existing Blocks Unchanged” scenario, 33% of all vehicle kilometer traveled were on blocks that needed terminus charging. For the “Small Batteries and Termini” scenario, this value increased to 95%. The number of needed electrified termini, however, increased less, from 44 to 64. The largest electrified terminus, the “Hertzallee” hub in central Berlin, needs either eight charging points with a peak power of 3.15 MW (scenario “Existing Blocks Unchanged”) or 20 charging points, with a peak power of 5.4 MW (“Small Batteries and Termini”) to satisfy the demand of the simultaneously charging vehicles.

Initially, the “Existing Blocks Unchanged” scenario was configured with a 300 kW charging power, while the “Small Batteries and Termini” scenario did not incorporate additional charging breaks. However, analysis revealed that under these settings—with the worst-case energy consumption—the energy lost during operation surpassed the amount replenished during charging breaks. For this reason, the charging power for the “Existing Blocks Unchanged” scenario was increased to 450 kW, and based on the observed battery depletion, a minimum 10 min turnaround time was introduced for the “Small Batteries and Termini” scenario whenever charging was required.

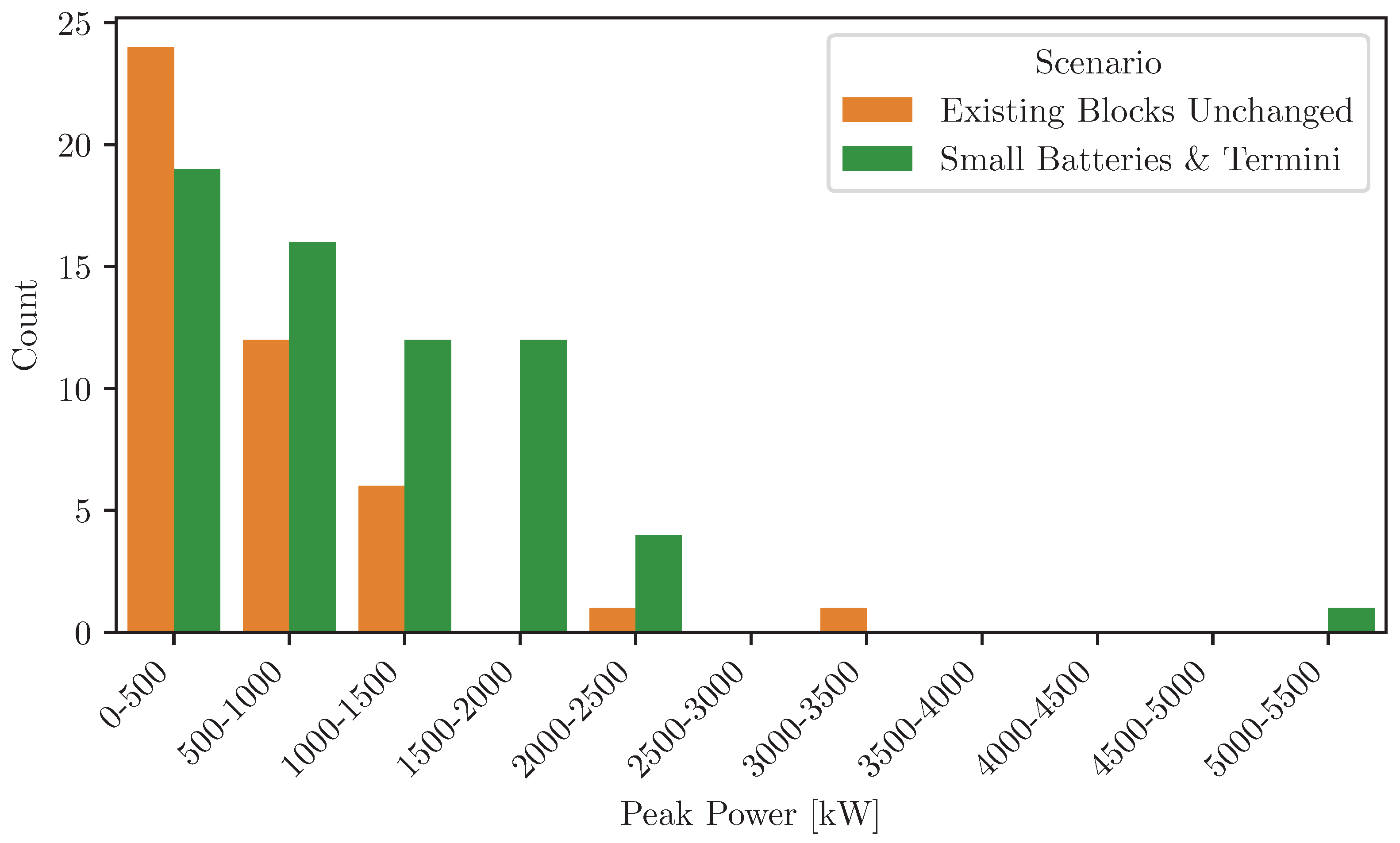
Figure 14 shows the distribution of the peak electric power demand at each terminus. It can be seen how most termini are visited by few vehicles simultaneously, with some seeing a higher number of simultaneously charging vehicles. Additionally, it can be seen how both the power and the amount of electrified termini needed is much higher for the “Small Batteries and Termini” scenario.

3.7. Depot Simulation and Vehicle Count Estimation

This section presents key outcomes of the depot process simulation, determining the minimum operational fleet size required under different electrification scenarios.

Table 14. Vehicle counts and depot capacities of the scenarios.

Scenario	Vehicle Type	Vehicles	Chargers	Additional Vehicles for Electrification
Existing Blocks Unchanged	single decker	346	337	1.2%
	articulated bus	730	706	2.9%
	double decker	132	127	0.0%
	total	1208	1170	2.1%
Depot Charging Only	single decker	370	360	7.6%
	articulated bus	760	730	6.7%
	double decker	143	138	7.7%
	total	1273	1228	7.1%
Small Batteries and Termini	single decker	360	350	5.0%
	articulated bus	721	694	1.7%
	double decker	141	136	6.4%
	total	1222	1180	3.2%

shows the number of vehicles needed to cover each scenario. It can be seen that the results are broadly similar, with the “Existing Blocks Unchanged” scenario needing the fewest vehicles, followed by the “Small Batteries and Termini” scenario, which places a lot of charging processes outside of the depot, minimizing the charging time and allowing a high vehicle utilization. The “Depot Charging Only” scenario needs the most vehicles; however, in this scenario, no terminus chargers whatsoever are required. It must be noted that our simulation calculates the number of operational vehicles. To find the number of vehicles to purchase, this number must be divided by the operational availability coefficient, a number below 1 indicating which fraction of vehicles are available for dispatch, as opposed to being in scheduled or unscheduled maintenance.

In addition to the three electric scenarios, a “diesel reference” scenario was simulated by using the simulation framework on the “Existing Blocks Unchanged” scenario and setting the energy consumption to a fixed value of 0 ${\displaystyle \raisebox{1ex}{$\mathrm{kWh}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{km}$}\right.}$. This “diesel reference” is used to estimate the additional vehicles needed for electrification. The additional vehicle need is due to the charging breaks, which mean that an electric vehicle will take a longer time to be available for its next block after arriving at the depot. The percentage of additional vehicles needed ranges from 2.1% in the “Existing Blocks Unchanged” scenario to 7.1% in the “Depot Charging Only” scenario, where no terminus charging takes place and charging time at the depot is the longest.

Figure 15 shows the number of vehicles in the largest depot, “Indira-Gandhi-Straße”, for the “Existing Blocks Unchanged” scenario. It can be seen how the peak occupancy of the depot is reached late at night, and cleaning mostly happens throughout the night hours. With 20 parallel cleaning areas, the waiting time is minimal. If fewer cleaning areas were used, waiting time would go up and it might be advisable to also install charging equipment in the waiting area.

3.8. Smart Charging

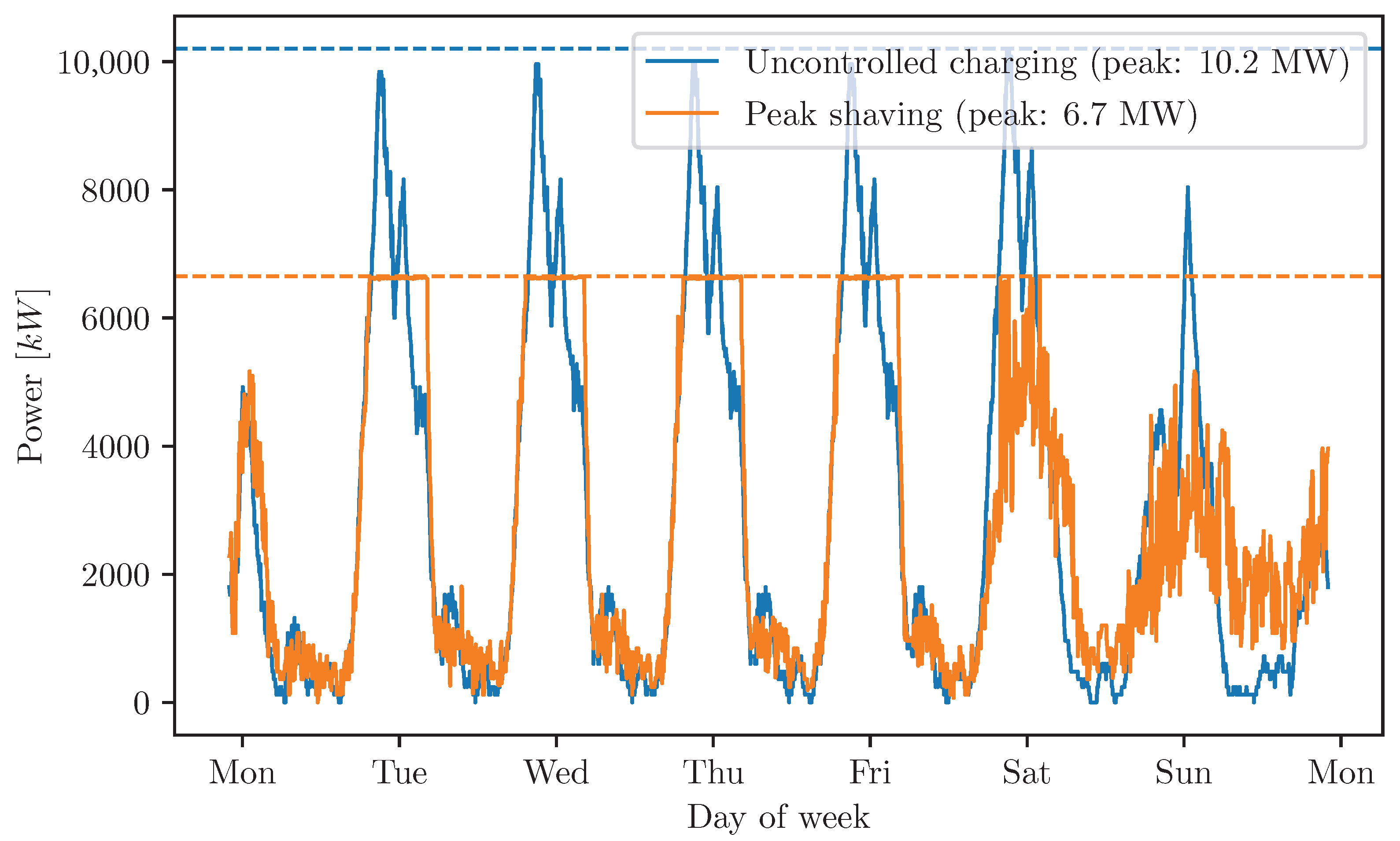
This section presents outcomes of the peak-shaving strategy formulated as an integer linear program. Figure 16 shows the power demand for an example depot with naive charging and peak shaving. It can be seen that with peak shaving, the power demand gets capped and moved to later times, as some buses delay their charging if there is flexibility. Over all depots and scenarios, the peak power reductions range from 0.85 MW to 4.42 MW, with an average peak power reduction of 49.82%.

Figure 17 shows the peak power and therefore the required power grid capacity at each depot. It can be seen that the “Depot Charging Only” scenario requires the highest grid capacity, with the “Existing Blocks Unchanged” not being much lower, even though 44 terminus stations have also been electrified. The “Small Batteries and Termini” scenario, where the smaller batteries force much more of the charging to take place at the termini, has significantly reduced grid power demands in the depot.

The current peak-shaving strategy does not reflect different energy prices throughout the day or a varying maximum power, with, e.g., the grid power available to a bus depot being limited in the peak hours of residential electricity use. However, such constraints can easily be added to the presented linear program.

4. Discussion and Outlook

The fully integrated bus network electrification framework presented in this paper enables comprehensive system-level electrification planning through its modular architecture. By simulating energy consumption, block building, depot assignment, terminus charger placement, depot operations, and smart charging within a single coherent workflow, this approach bridges multiple domains that have previously been treated in isolation. An example of the capabilities of this model is the feedback mechanism, where insufficient charging breaks can trigger rescheduling, representing an important connection between the energy consumption and scheduling components.

A direct quantitative comparison between our results and prior research can only be carried out partially, since we provide the first publicly available high-fidelity study of electrifying a complete large city bus network. While previous studies by Rogge et al. [50] and Jahic [45] have addressed aspects of network electrification, they either focused on partial networks or excluded key elements like terminus charging. The holistic approach—incorporating both depot and terminus charging strategies along with realistic operational constraints—distinguishes it from the existing literature.

The integrated nature of our framework also enables exploration of the complex interactions between subsystems. For example, our results demonstrate how charging infrastructure placement decisions directly influence fleet size requirements, an interdependency that is hard to show in separate approaches. Similarly, the simulations reveal how block building strategies affect both deadhead mileage and energy consumption patterns, ultimately impacting infrastructure planning decisions.

4.1. Key Findings and Implications

4.1.1. Energy Consumption and Temperature Effects

The energy consumption simulation results show that, for Berlin, extremely cold days are critical for the overall system design. Based on our real-world measurements, we found an approximately 50% higher overall consumption on the coldest day compared to the warmest day. This finding emphasizes the importance of designing systems for worst-case conditions to ensure operational reliability, particularly in regions with significant seasonal temperature variations. Reliance on average consumption profiles would lead to substantial operational disruptions during extreme weather.

4.1.2. Block Building and Scheduling

Our scheduling algorithms yielded different results across the three scenarios. The “Depot Charging Only” scenario demonstrated slightly higher scheduling efficiency (74.2%) compared to the diesel reference, but at the cost of increased deadhead mileage. Conversely, the “Small Batteries and Termini” scenario showed reduced efficiency (71.2%) at greatly reduced depot electric power and battery size. These results indicate that there is no “one size fits all” solution to designing electric bus systems, with the technology choices depending on the local technical and socioeconomic factors.

4.1.3. Depot–Block Assignment

The Depot–Block Assignment results revealed that optimizing for minimum block count can lead to increased deadhead mileage, particularly evident in the “Small Batteries and Termini” scenario where deadhead kilometers increased by 54% compared to the diesel baseline. This finding underscores that optimization objectives must be carefully selected to balance operational efficiency with environmental and economic considerations. While minimizing vehicle count is often the primary objective, the associated increase in non-revenue kilometers can partially offset the emissions benefits of electrification.

4.1.4. Terminus Charger Placement

The Terminus Charger Placement analysis demonstrated significant differences between scenarios, with the “Small Batteries and Termini” scenario requiring 64 electrified termini compared to 44 in the “Existing Blocks Unchanged” scenario. The peak power distribution across terminus stations revealed that most require relatively modest infrastructure (1–2 charging points), while a small number of hub stations demand substantial electrical capacity. This finding suggests that a differentiated approach to terminus electrification may be more cost-effective than uniform implementation across the network.

4.1.5. Vehicle Requirements and Depot Simulation

The Depot Simulation results indicate that electric bus fleets require a 2.1% to 7.1% increase in vehicle count compared to diesel operations, depending on the charging strategy employed. While this is a relatively modest increase, it also shows that a “1-for-1” electrification strategy is infeasible. The “Existing Blocks Unchanged” scenario demonstrated that with optimized terminus charging, the additional vehicle requirement can be limited to just 2.1%, suggesting that well-designed hybrid charging strategies can minimize capital expenditure on vehicles.

4.1.6. Smart Charging

The peak-shaving strategy implementation achieved an average 49.8% reduction in peak power demand across scenarios, with absolute reductions of up to 4.42 MW at individual depots. This substantial decrease in required grid connection capacity represents a significant cost-saving opportunity. The results also highlight the considerable differences in grid capacity requirements between scenarios, with the “Small Batteries and Termini” approach demonstrating significantly reduced depot power demands by shifting the charging load to termini.

4.2. Practical Implications

Our results have several important practical implications for transit operators pursuing bus fleet electrification:

• Hybrid charging approaches offer greater flexibility The comparison between exclusive depot charging and hybrid depot-terminus charging strategies demonstrates that hybrid approaches can provide more favorable outcomes across multiple metrics, including fleet size and depot power requirements.
• Temperature effects demand robust planning The significant impact of temperature on energy consumption emphasizes the need for worst-case design parameters rather than average conditions when planning infrastructure and scheduling.
• Smart charging provides substantial benefits The dramatic reduction in peak power demand achieved through smart charging control suggests that smart charging systems should be considered as essential infrastructure rather than optional enhancements.
• Scheduling optimization objectives matter The results demonstrate that different optimization objectives (minimizing vehicles versus minimizing deadhead mileage) can lead to substantially different outcomes. Transit agencies must carefully define their priorities when implementing electrification strategies.

The modular nature of our framework allows transit operators to incorporate their specific constraints and preferences while exploring the full range of electrification options, rather than being restricted to predetermined approaches. This flexibility is particularly valuable given the diverse operational contexts of different transit agencies.

4.3. Outlook

The integrated simulation framework presented in this work provides a foundation for comprehensive bus electrification planning. However, future extensions and research directions could further enhance its practical impact and policy relevance.

Economic evaluation represents a natural next step. By incorporating total cost of ownership (TCO) calculations or net present value (NPV) analysis as post-processing modules, the framework could provide financial metrics alongside operational results. When combined with life-cycle assessment (LCA), this would enable calculation of cost-effectiveness metrics, such as “money spent per tonne of CO₂ avoided”, allowing policymakers to compare bus electrification investments with other decarbonization options. These economic and environmental assessments will be implemented as additional analysis steps using the simulation outputs, without modifying the core framework. This is going to be presented in an upcoming paper.

Integration with power grid simulation would enable more sophisticated planning. Using a co-simulation approach, the charging profiles generated by our framework could feed into grid impact assessments. Furthermore, day-ahead planning could be employed to reduce energy costs [78]. The resulting grid constraints and costs could then be incorporated back into the scheduling, terminus electrification, depot simulation, and smart charging modules. This iterative process would support the development of electrification strategies that minimize grid infrastructure requirements.

To broaden accessibility beyond the research community, work is underway to develop a graphical user interface. This will enable transit planners and operators without programming expertise to utilize the framework for their electrification planning needs.

5. Summary and Conclusions

This paper has presented a fully integrated simulation framework for bus network electrification planning and demonstrated its application to Berlin’s bus system. The framework addresses the multidisciplinary nature of electrification by incorporating energy consumption simulation, block building, depot–block assignment, terminus station electrification, depot simulation, and smart charging within a coherent workflow. By implementing this approach as a modular, open-source system, we enable other researchers and operators to carry out a comprehensive evaluation of electrification strategies that consider the complex interactions between technological, operational, and economic factors.

The Berlin case study examined three distinct electrification approaches: maintaining existing blocks with electrification (“Existing Blocks Unchanged”), exclusive depot charging (“Depot Charging Only”), and smaller batteries with extensive terminus charging (“Small Batteries and Termini”). Through these scenarios, we explored the boundaries of possible solutions rather than attempting to identify a single optimal strategy. The energy consumption simulation revealed that Berlin’s coldest days represent the critical design point, with heating requirements significantly increasing energy demand. Our block-building algorithm achieved block efficiencies comparable to the existing diesel operations (71.2–74.2% versus 73.4%), though with different patterns of line changes and deadhead mileage. The depot–block assignment optimization demonstrated that our approach could reduce deadhead kilometers in some scenarios while increasing them in others, depending on the primary optimization objective. The scenarios and results of the block building and depot–block assignment are summarized in

Table 15. Summary of block building results, Refer to Table 11 for the exact battery capacity values.

Scenario	Battery Capacity	Block Building Goal	Number of Blocks	Block Efficiency	Deadhead Mileage
Existing Blocks Unchanged	large	–	8498	73.4%	102,878 km
Depot Charging Only	large	all depot charging	8794	74.2%	123,319 km
Small Batteries and Termini	small	minimum block count	8203	71.2%	170,453 km

.

For terminus charging infrastructure, we found that between 44 and 64 terminus stations required electrification, with overall power demands ranging from 300 kW (peak) at most locations to over 5 MW (peak) at some central hubs. Our depot simulation determined that electric buses would require 2.1–7.1% more vehicles than the equivalent diesel fleet, with the hybrid charging approach (“Existing Blocks Unchanged”) showing the smallest increase. Finally, the smart charging implementation achieved an average 49.8% reduction in peak power demand across all depots, dramatically reducing required grid connection capacity. The vehicle counts, charger counts, and required grid connections are summarized in

Table 16. Summary of vehicle counts and peak powers.

Scenario	Electrified Termini	Depot Chargers	Vehicle Count	Additional Vehicles Rel. to Diesel	Depot Peak Power	Terminus Peak Power
Existing Blocks Unchanged	44	1170	1208	2,1%	6.7 MW	3.2 MW
Depot Charging Only	–	1228	1273	7,1%	7.6 MW	–
Small Batteries and Termini	64	1180	1222	3,2%	1.3 MW	5.4 MW

.

As transit agencies worldwide accelerate their transition to zero-emission fleets, comprehensive planning frameworks that address the full complexity of electrification will become increasingly valuable. The approach presented in this paper provides a foundation for such planning efforts, enabling the systematic evaluation of electrification strategies across multiple scenarios and constraints.