Three-Dimensional Unmanned Aerial Vehicle Path Planning in Simulated Rugged Mountainous Terrain Using Improved Enhanced Snake Optimizer (IESO)
Abstract
1. Introduction
2. Methodologies: Improved Enhanced Snake Optimizer (IESO) Algorithm and Simulation Design
2.1. Fundamental Principles of Snake Optimizer (SO)
2.2. Enhanced Snake Optimizer (ESO)
2.3. Improved Enhanced Snake Optimizer (IESO)
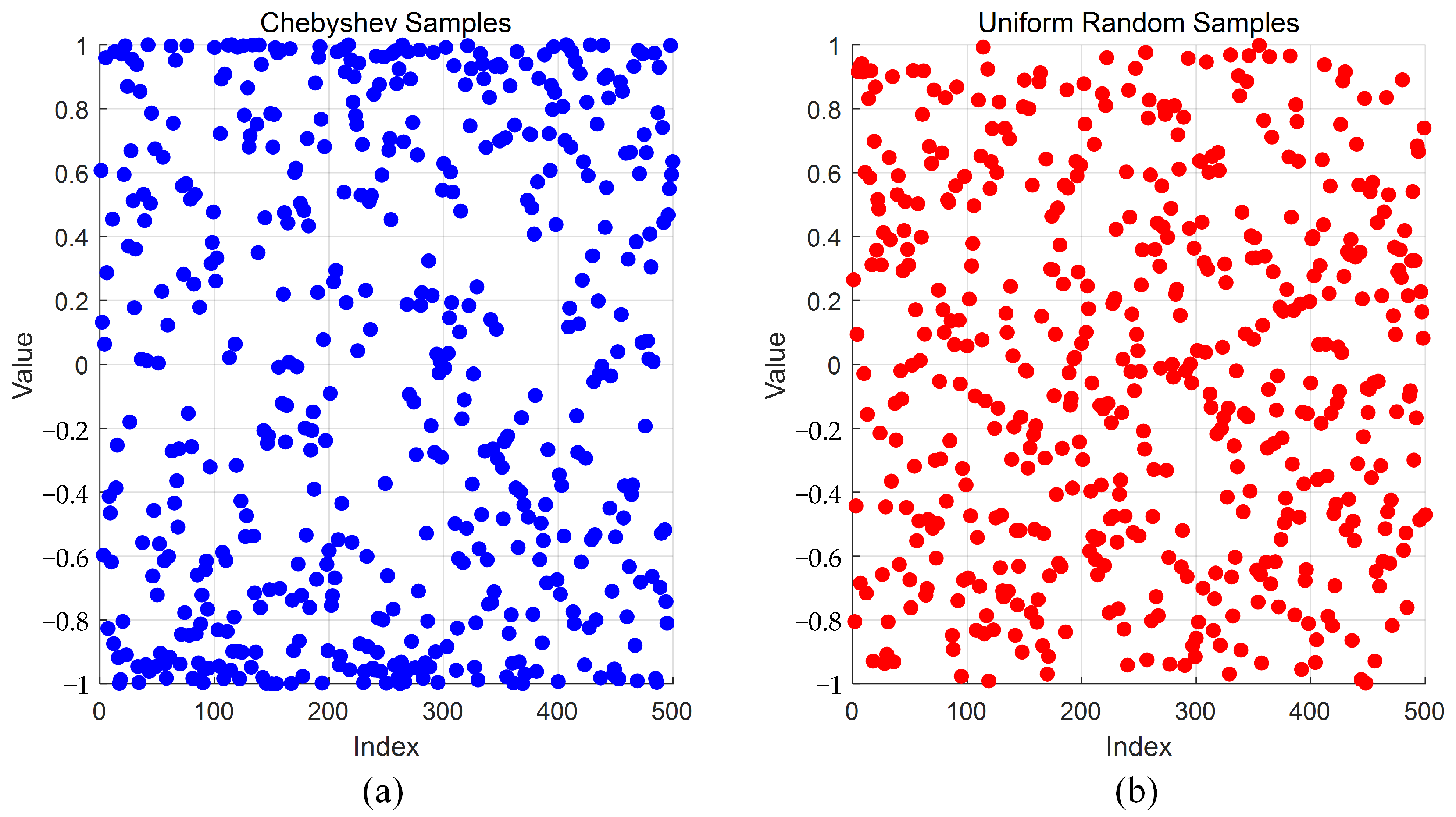
2.3.1. Chebyshev Population Initialization
2.3.2. Non-Monotone Temperature Factor
2.3.3. Dynamic-Boundary-Based Opposition Learning (DBOL)
2.4. Simulation Experiments Design and the Evaluation Criteria
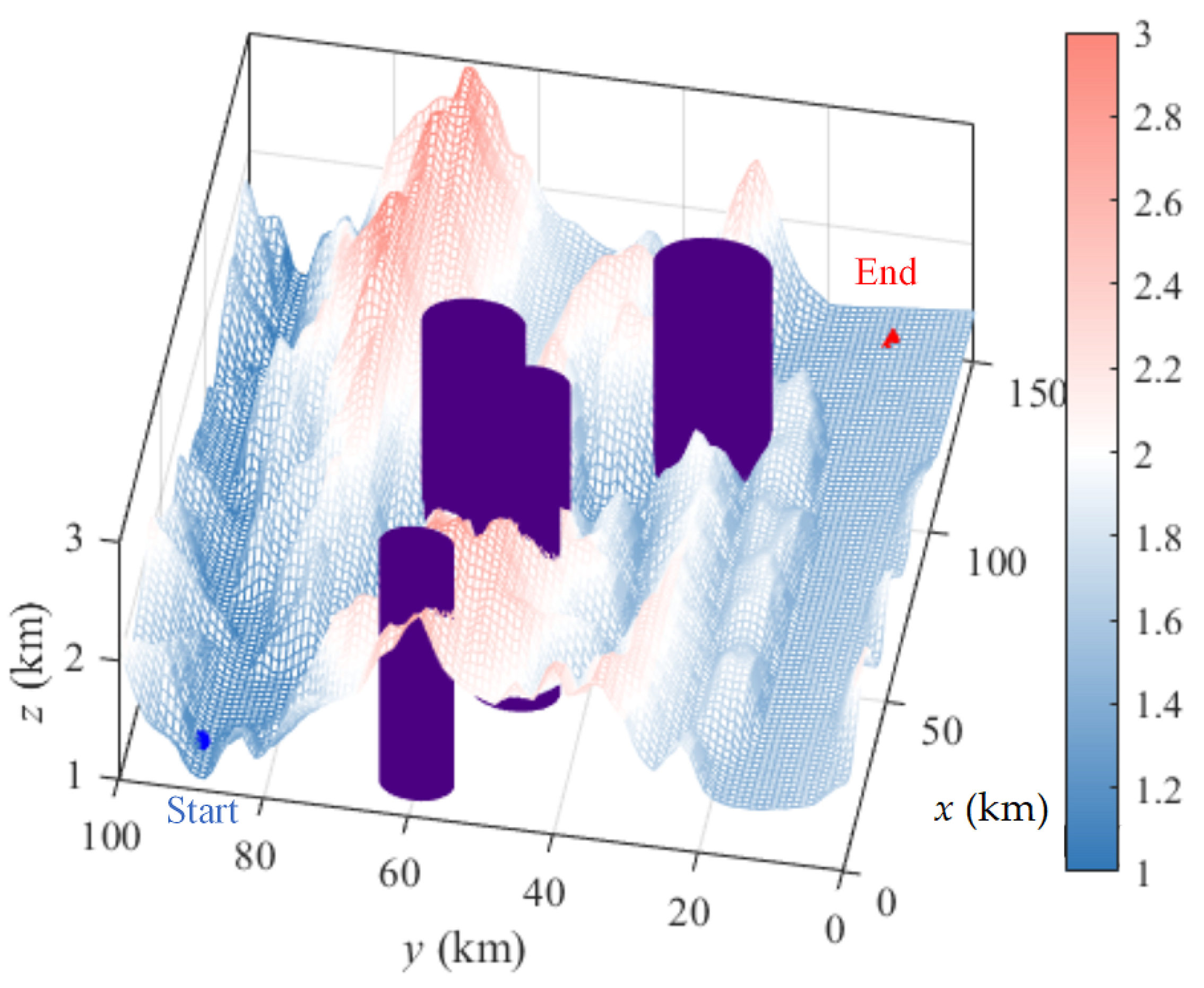
2.4.1. Simulated Experiment
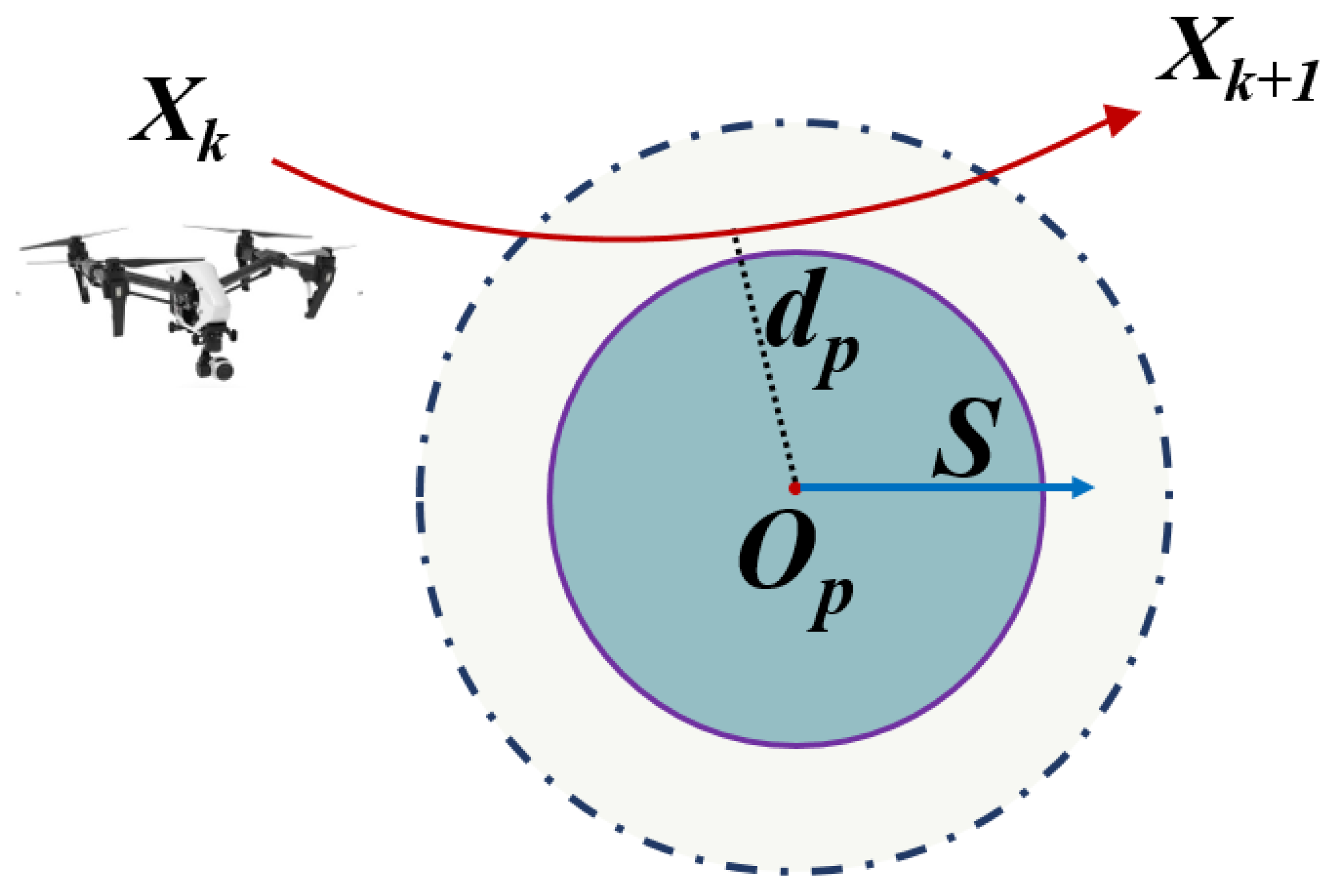
2.4.2. Evaluation Criteria
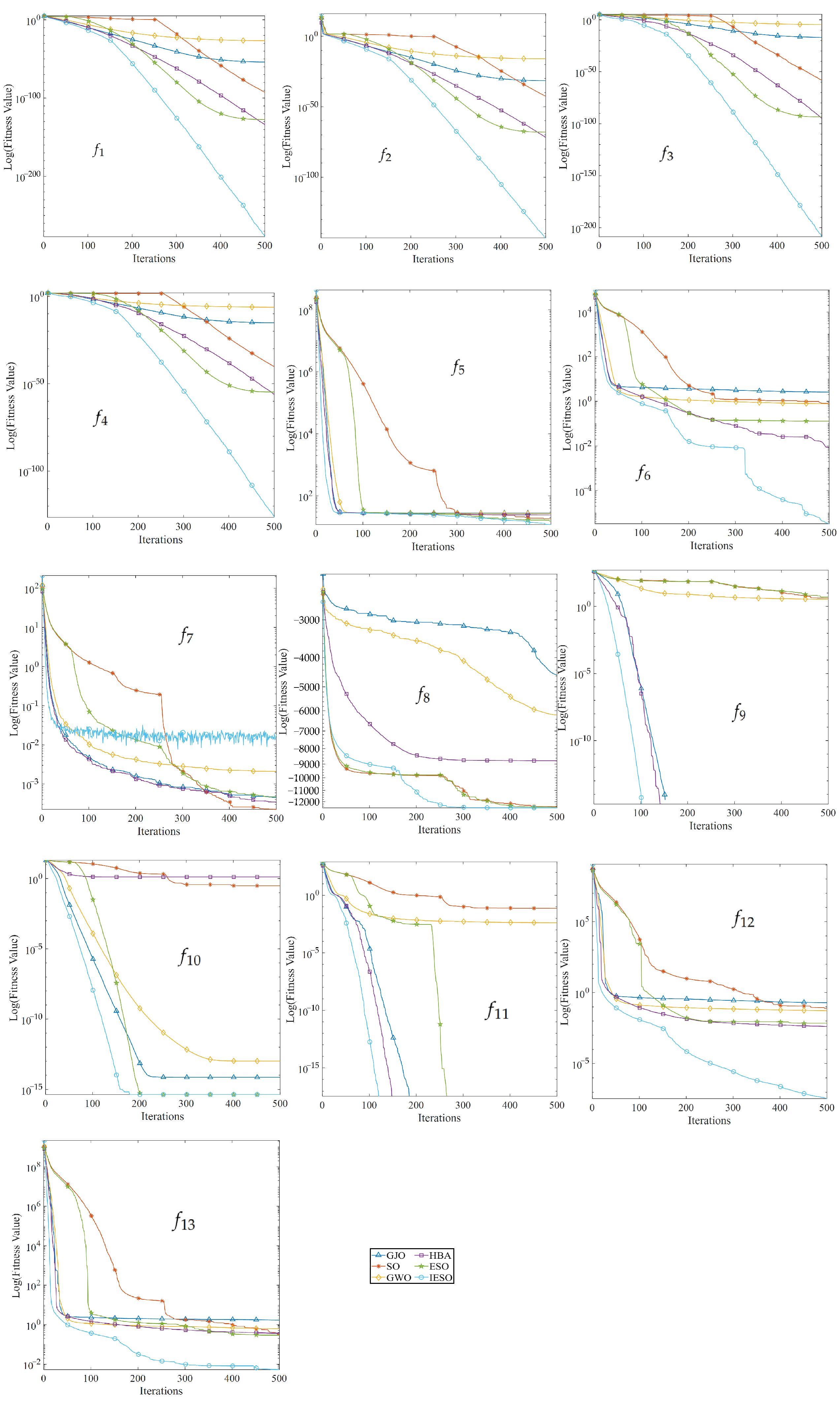
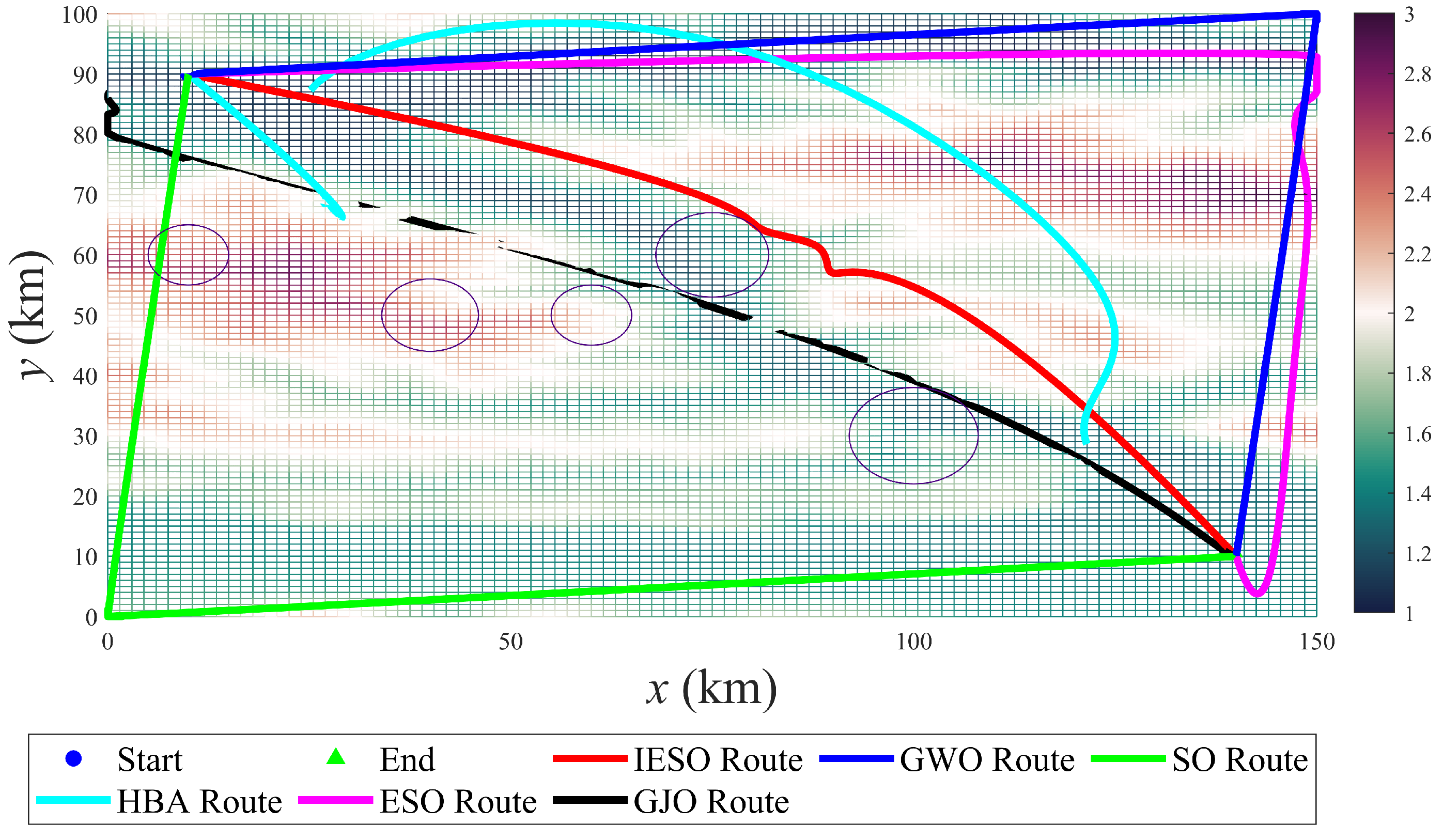
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DBOL | dynamic-boundary-based opposition learning |
| DOL | dynamic opposition learning |
| ESO | Enhanced Snake Optimizer |
| GJO | Golden Jackal Optimization |
| GWO | Grey Wolf Optimizer |
| HBA | Honey Badger Algorithm |
| MA | meta-heuristic algorithm |
| SO | Snake Optimizer |
| IESO | Improved Enhanced Snake Optimizer |
| OBL | opposition-based learning |
| UAV | unmanned aerial vehicle |
References
- Zhang, W.; Li, J.; Yu, W.; Ding, P.; Wang, J.; Zhang, X. Algorithm for UAV path planning in high obstacle density environments: RFA-star. Front. Plant Sci. 2024, 15, 1391628. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.; Djahel, S.; Welsh, K. Path-Planning for Unmanned Aerial Vehicles with Environment Complexity Considerations: A Survey. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Yahia, H.S.; Mohammed, A.S. Path Planning Optimization in Unmanned Aerial Vehicles Using Metaheuristic Algorithms: A systematic review. Environ. Monit. Assess. 2023, 195, 30. [Google Scholar] [CrossRef]
- Li, D.; Yin, W.; Wong, W.E.; Jian, M.; Chau, M. Quality-oriented Hybrid Path Planning Based on A* and Q-learning for Unmanned Aerial Vehicle. IEEE Access 2021, 10, 7664–7674. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An Improved Artificial Potential Field Method for Path Planning and Formation Control of the Multi-UAV Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1129–1133. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Li, R.; Chen, H.; Chu, K. Trajectory Planning for UAV Navigation in Dynamic Environments with Matrix Alignment Dijkstra. Appl. Soft Comput. 2022, 26, 12599–12610. [Google Scholar] [CrossRef]
- Prasad, N.L.; Ramkumar, B. 3-D Deployment and Trajectory Planning for Relay Based UAV Assisted Cooperative Communication for Emergency Scenarios Using Dijkstra’s Algorithm. IEEE Trans. Veh. Technol. 2022, 72, 5049–5063. [Google Scholar] [CrossRef]
- Flores-Caballero, G.; Rodríguez-Molina, A.; Aldape-Pérez, M.; Villarreal-Cervantes, M.G. Optimized Path-Planning in Continuous Spaces for Unmanned Aerial Vehicles Using Meta-Heuristics. IEEE Access 2020, 8, 176774–176788. [Google Scholar] [CrossRef]
- Lin, H.; Liu, T. Research on path planning method of driverless vehicle based on improved A* algorithm. J. Hunan Univ. Arts Sci. 2021, 33, 17–20. [Google Scholar]
- He, Y.; Hou, T.; Wang, M. A new method for unmanned aerial vehicle path planning in complex environments. Sci. Rep. 2024, 14, 9257. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; He, C.; Zhao, Y.; Wu, X. Efficient Trajectory Planning for UAVs Using Hierarchical Optimization. IEEE Access 2021, 9, 60668–60681. [Google Scholar] [CrossRef]
- Chen, J.C.; Ling, F.Y.; Zhang, Y.; You, T.; Liu, Y.F.; Du, X.Y. Coverage Path Planning of Heterogeneous Unmanned Aerial Vehicles Based on Ant Colony System. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Fu, J.; Sun, G.; Liu, J.; Yao, W.; Wu, L. On Hierarchical Multi-UAV Dubins Traveling Salesman Problem Paths in a Complex Obstacle Environment. IEEE Trans. Cybern. 2024, 4, 3265926. [Google Scholar] [CrossRef]
- Fu, J.; Yao, W.; Sun, G.; Ma, Z.; Dong, B.; Ding, J. Multirobot Cooperative Path Optimization Approach for Multiobjective Coverage in a Congestion Risk Environment. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1816–1827. [Google Scholar] [CrossRef]
- Zhao, F.; Li, D.; Wang, Z.; Mao, J.; Wang, N. Autonomous localized path planning algorithm for UAVs based on TD3 strategy. Sci. Rep. 2024, 14, 763. [Google Scholar] [CrossRef]
- Luo, J.; Tian, Y.; Wang, Z. Research on Unmanned Aerial Vehicle Path Planning. Drone 2024, 8, 51. [Google Scholar] [CrossRef]
- Wang, H.; Pan, W. Research on UAV Path Planning Algorithms. IOP Conf. Ser. Earth Environ. Sci. 2021, 693, 012120. [Google Scholar] [CrossRef]
- Debnath, D.; Vanegas, F.; Sandino, J.; Hawary, A.F.; Gonzalez, F. A Review of UAV Path-Planning Algorithms and Obstacle Avoidance Methods for Remote Sensing Applications. Remote Sens. 2024, 16, 4019. [Google Scholar] [CrossRef]
- Yao, L.; Yuan, P.; Tsai, C.Y.; Zhang, T.; Lu, Y.; Ding, S. ESO: An Enhanced Snake Optimizer for Real-world Engineering Problems. Expert Syst. Appl. 2023, 230, 120594. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A Novel Meta-heuristic Optimization Algorithm. Expert Syst. Appl. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden Jackal Optimization: A Novel Nature-inspired Optimizer for Engineering Applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Qi, D.; Chan, W.H.; Zain, A.M.; Junaidi, A.; Yang, H. An improved algorithm based on snake optimizer. Proc. Comput. Sci. 2023, 1, 0017. [Google Scholar] [CrossRef]
- Mai, C.; Zhang, L.; Hu, X. An adaptive snake optimization algorithm incorporating Subtraction-Average-Based Optimizer for photovoltaic cell parameter identification. Heliyon 2024, 10, 15. [Google Scholar] [CrossRef]
- Zheng, W.; Ai, Y.; Zhang, W. Improved Snake Optimizer Using Sobol Sequential Nonlinear Factors and Different Learning Strategies and Its Applications. Mathematics 2024, 12, 1708. [Google Scholar] [CrossRef]
- Li, S.; Tang, Z. An Enhanced Snake Optimizer Algorithm for Feature Selection. In Proceedings of the 2023 8th International Conference on Big Data and Computing, Shenzhen, China, 26–28 May 2023; pp. 81–86. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, H.; Wei, J.; Yi, J.; Liu, J.; Li, M. ISO: An improved snake optimizer with multi-strategy enhancement for engineering optimization. Expert Syst. Appl. 2025, 281, 127660. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, G.; Kong, M.; Zhang, T.; Wang, D. CGJO: A novel complex-valued encoding golden jackal optimization. Sci. Rep. 2024, 14, 19577. [Google Scholar] [CrossRef] [PubMed]
- Hassan, I.H.; Abdullahi, M.; Isuwa, J.; Yusuf, S.A.; Aliyu, I.T. A comprehensive survey of honey badger optimization algorithm and meta-analysis of its variants and applications. Frankl. Open 2024, 8, 100141. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, Z.; Li, W.; Li, K. An Enhanced Grey Wolf Optimizer with Elite Inheritance and Balance Search Mechanisms. arXiv 2024. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Yang, J.; Zhang, D. Integrate the original face image and its mirror image for face recognition. Neurocomputing 2014, 131, 191–199. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 131, pp. 695–701. [Google Scholar] [CrossRef]
- Wu, T.Y.; Li, H.; Chu, S.C. CPPE: An Improved Phasmatodea Population Evolution Algorithm with Chaotic Maps. Mathematics 2023, 11, 1977. [Google Scholar] [CrossRef]
- Wang, C.; Jiao, S.; Li, Y.; Zhang, Q. Capacity Optimization of a Hybrid Energy Storage System Considering Wind-Solar Reliability Evaluation Based on A Novel Multi-strategy Snake Optimization Algorithm. Expert Syst. Appl. 2023, 231, 120602. [Google Scholar] [CrossRef]




| Num. | Name | Formula | Range | |
|---|---|---|---|---|
| Sphere is Function | [−100,100] | 0 | ||
| Schwefel’s Problem 2.22 | [−10,10] | 0 | ||
| Schwefel’s Problem 1.2 | [−100,100] | 0 | ||
| Schwefel’s Problem 2.21 | [−100,100] | 0 | ||
| Generalized Rosenbrock’s Function | [−30,30] | 0 | ||
| Step Function | [−100,100] | 0 | ||
| Quartic Function | [−1.28,1.28] | 0 | ||
| Generalized Schwefel’s Problem 2.26 | [−500,500] | −2094 | ||
| Generalized Rastrigin’s Function | [−10,10] | 0 | ||
| Ackley’s Function | [−10,10] | 0 | ||
| Generalized Griewank’s Function | [−10,10] | 0 | ||
| Generalized Penalized Function 1 | [−10,10] | 0 | ||
| Generalized Penalized Function 2 | [−10,10] | 0 |
| Algorithms | Parameters |
|---|---|
| IESO | |
| ESO | |
| SO | |
| GJO | |
| HBA | |
| GWO |
| Num. | GJO | SO | GWO | HBA | ESO | IESO |
|---|---|---|---|---|---|---|
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| ()/= | ()/= | ()/+ | ()/= | ()/= | () | |
| ()/+ | ()/+ | ()/+ | ()/= | ()/= | () | |
| ()/= | ()/= | ()/= | ()/= | ()/= | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/= | () | |
| ()/+ | ()/+ | ()/+ | ()/+ | ()/+ | () | |
| Wilcoxon Test Summary | 12/1/0 | 10/3/0 | 12/1/0 | 9/4/0 | 8/5/0 | Wilcoxon |
| Algorithms | Best | Average | Worst | Standard | Difference |
|---|---|---|---|---|---|
| IESO | 78.944 | 78.990 | 80.332 | 0.253 | - |
| ESO | 120.260 | 120.260 | 120.260 | +34.32 | |
| SO | 123.640 | 123.76 | 123.760 | 0.022 | +36.17 |
| GJO | 89.466 | 89.466 | 89.466 | +11.71 | |
| HBA | 113.730 | 113.730 | 113.730 | +30.54 | |
| GWO | 123.760 | 123.870 | 123.87 | +36.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhang, K.; Xiong, Q.; Chen, X. Three-Dimensional Unmanned Aerial Vehicle Path Planning in Simulated Rugged Mountainous Terrain Using Improved Enhanced Snake Optimizer (IESO). World Electr. Veh. J. 2025, 16, 295. https://doi.org/10.3390/wevj16060295
Li W, Zhang K, Xiong Q, Chen X. Three-Dimensional Unmanned Aerial Vehicle Path Planning in Simulated Rugged Mountainous Terrain Using Improved Enhanced Snake Optimizer (IESO). World Electric Vehicle Journal. 2025; 16(6):295. https://doi.org/10.3390/wevj16060295
Chicago/Turabian StyleLi, Wuke, Kongwen Zhang, Qi Xiong, and Xiaoxiao Chen. 2025. "Three-Dimensional Unmanned Aerial Vehicle Path Planning in Simulated Rugged Mountainous Terrain Using Improved Enhanced Snake Optimizer (IESO)" World Electric Vehicle Journal 16, no. 6: 295. https://doi.org/10.3390/wevj16060295
APA StyleLi, W., Zhang, K., Xiong, Q., & Chen, X. (2025). Three-Dimensional Unmanned Aerial Vehicle Path Planning in Simulated Rugged Mountainous Terrain Using Improved Enhanced Snake Optimizer (IESO). World Electric Vehicle Journal, 16(6), 295. https://doi.org/10.3390/wevj16060295







