An Artificial Neural Network-Based Battery Management System for LiFePO₄ Batteries

Abstract

We present a reduced-order battery management system (BMS) for lithium-ion cells in electric and hybrid vehicles that couples a physics-based single-particle model (SPM) derived from the Cahn–Hilliard phase-field formulation with a lumped heat-transfer model. A three-dimensional COMSOL^® 5.0 simulation of a LiFePO₄ particle produced voltage and temperature data across ambient temperatures (253–298 K) and discharge rates (1 C–20.5 C). Principal component analysis (PCA) reduced this dataset to five latent variables, which we then mapped to experimental voltage–temperature profiles of an A123 Systems 26650 2.3 Ah cell using a self-normalizing neural network (SNN). The resulting ROM achieves real-time prediction accuracy comparable to detailed models while retaining essential electrothermal dynamics.

1. Introduction

There is a consensus that transportation electrification will alleviate environmental impact and lead to a renewable source of mobility. Still, significant issues remain unanswered regarding the life cycle analysis of electrification versus other options, such as hydrogen fuel cells. Notwithstanding, there is an ongoing global trend of electrifying transportation, and as a result, intensive research is underway into electric and hybrid electric vehicles (EVs and HEVs) [1,2]. Lithium-ion batteries have become the most promising choice for EVs due to their high energy density and long cycle life [3,4]. Battery management systems (BMSs) are necessary for EV applications to prevent Li-ion batteries from overheating and overcharging and avoid potential thermal runaway. Currently, BMSs cannot store and process large volumes of data while managing the battery’s state of charge (SOC), voltage, and temperature in real time [5,6,7]. To address this shortcoming, additional research is needed to develop reduced-order models (ROMs) that can both model complex battery mechanisms and provide real-time management data. Applications of machine learning (ML) and artificial intelligence (AI) are fertile areas for eventual solutions to this problem. Many of the references we cited address the need for our novel approach to a ROM for LiFePO₄, but the most critical treatment of the data gaps that our ROM addresses is provided in recent broad review papers These articles discussed the limitations of existing single-particle models (SPMs), noting that most SPMs ignore electrolyte dynamics and are isothermal, which can lead to significant errors at higher C rates and low temperatures [8]. The paper highlights that while some improvements have been made by incorporating electrolyte dynamics and temperature effects, most models still lack explicit relationships between internal parameters and observable quantities and often remain computationally intensive for real-time BMS applications. Our approach, which integrates a physics-based SPM with a lumped heat-transfer model and leverages data-driven methods, directly addresses these shortcomings. Recent studies also emphasized the high computational complexity of rigorous physics-based models, which limits their practical use in real-time BMSs. Underscoring the need for reduced-order models (ROMs) that balance fidelity, computational efficiency, and applicability for advanced BMS functions such as state estimation, fault diagnosis, and optimal control. Their review reveals that most available ROMs either sacrifice accuracy for simplicity or are still too complex for embedded systems, especially when capturing electrothermal dynamics. Our novel method, which achieves real-time prediction accuracy while retaining essential electrothermal dynamics, is positioned as a direct response to these identified needs.

Models that describe battery dynamic processes at all levels are not feasible. Therefore, mechanistic battery models, referred to as full-order models (FOMs), need to be tailored to specific purposes that require a deep understanding of a particular aspect of the battery’s operation and performance. Many mechanistic models have been developed specifically to describe battery thermal behavior [9,10,11,12]. In general, models for analysis and diagnosis purposes employ detailed simulations of the battery’s physics and, thus, are often multidimensional, multiphysics models and are computationally slow. Models for control and optimization applications are usually computationally fast but provide a limited description of the underlying physics. The most commonly used mechanistic model for single-battery cells is a lumped parameter simplification of a FOM called the pseudo-two-dimensional (P2D) model. Even given the P2D simplifications of battery homogeneity and a constant electrode thickness, P2D models still use more than fifteen parameters specific to a particular battery, and their computational cost is still too high for control and optimization applications. On the other hand, P2M parameters are too lumped to provide much insight into the underlying phenomena [13,14]. Decades of research have been conducted to develop reduced-order models (ROMs) that adequately retain the robustness of FOMs without excessive computational complexity. The state of the art for the various methods of achieving Li-ion battery ROMs has recently been reviewed in the literature [15]. We limit our following discussion of such methods to equivalent circuit models (ECMs), their model-based extensions, and the single-particle model approximation. These methods are most pertinent since our ROM, explained in the following sections, is a single-particle application and is most likely to be used instead of or alongside an ECM.

ECMs that do not consider fundamental physics have been extensively used to imitate the relationships between battery input and output systems while offering real-time computation [16,17,18,19,20,21]. ECMs use electrical circuits to simulate lithium-ion cells, utilizing capacitors to shape the battery capacity, while variable resistors and controlled-voltage sources provide the temperature effect or SOC variations. Black-box modeling is another extensively applied method to provide real-time computation. It relies on developing an equivalent transform function with different inputs and outputs. Like ECMs, this method depends on experimental data for a specified battery [22]. ECMs and transform functions have been implemented in a “mixed approach” along with thermal and aging models, as shown in Figure 1 [23]. The framework combines equivalent circuit models (ECMs), data-driven transform functions, thermal dynamics, and aging effects to address critical limitations in standalone modeling ECM approaches [24,25].

Model-based methods have been developed that have enhanced basic ECMs. Some of the predominant model-based methods have been recently reviewed in the literature, including the Luenberger, sliding mode, Kalman filter, and proportional–integral (PIO) methods [26,27,28,29,30,31]. Model-based methods have a battery model at their core that uses measured current and voltage signals to provide a closed-loop estimation method. These methods typically use static models where model parameters are applied offline and assumed not to change over time. However, these models often do not ensure sufficient accuracy over a broad range of operational conditions and long-time frames. Considering this, efforts have been made to develop online model adaptation methods, including population-based optimization, dual filtering, and least squares (LS)-based methods such as moving window LS, continuous-time LS, and recursive least squares (RLS) [32,33,34,35,36,37].

Lithium iron phosphate (LiFePO₄) is the most frequently used phosphate-based cathode material in Li-ion batteries. LiFePO₄ has a strong tendency to separate into solid high-Li+ concentration and low-Li+ concentration phases, leading to the battery’s characteristic broad voltage plateau at room temperature [38,39,40,41,42]. Traditionally, mathematical models of intercalation dynamics in LiFePO₄ cathodes have been based on spherical diffusion or the shrinking core concept [43,44]. However, recent experimental and theoretical progress suggests that a more realistic SPM should encompass a phase-field model for equilibrium and nonequilibrium solid-solution transformations [45,46,47,48,49]. A phase-field model is a computational method for modeling morphological and microstructure evolution in materials. They have been proposed for solid-state phase transformations, grain growth and coarsening, microstructure evolution in thin films, and crack propagation [50,51]. Research is currently underway that seeks to bridge the gap between phase-field mesoscale models and macro-battery properties. For example, recent studies used a phase-field modeling approach to develop a physics-based, fully coupled model that bridges dendrite and crack propagation at the micro-level with macro-state battery charging and discharging [52]. Another application demonstrated a method for estimating the voltage plateau of LiFePO₄ batteries based on the Cahn–Hilliard phase-field model solution for a single cathode particle. Our ROM was motivated by these single-particle model (SPM) studies. The major enhancement of our SPM is that it is a multiphysics thermal model that fully couples the battery cell’s heat-transfer model. Statistically, we related the results of the SPM simulation to the estimation of battery cell properties. Specifically, the plateauing effect of the battery’s voltage response at higher ambient temperatures and the apparent diffusion-controlled behavior at lower temperatures are related to the SPM by statistical inference. Our SPM is a specific example of a widely used method for order reduction in P2D based on a single-particle model that aims to enhance computational run time while retaining elements of the underlying physics, as opposed to an ESM [53,54,55,56]. In the single-particle thermal model preparation, the local potential and concentration gradients in the electrolyte phase were ignored and accounted for by utilizing a lumped solution resistance term. Likewise, the potential gradient in the solid phase of the electrodes was ignored, and the porous electrode was considered as a large number of individual particles, all subjected to the same conditions. These assumptions are generally only valid under relatively low current rates, and the SPM is not recommended for high-power applications, such as fast EV charging and operations involving high-power pulses, but it is well suited to daily EV driving, where the operating ranges are less extreme. These shortcomings of the SPM are not prohibitive for our ROM since we did not attempt to model the battery voltage response by directly scaling up the SPM, but sought to only retain enough information from the SPM to make statistical inferences concerning the macro-battery properties. The ROM was realized by subjecting the raw simulation results from the COMSOL^® Multiphysics simulation data to principal component analysis (PCA) to determine the lowest-order simulation dataset capable of fitting the experimental data using a self-normalizing neural network (SNN). We validated our SPM based on available experimental data for the A123 Systems 26650 2.3 Ah battery [57].

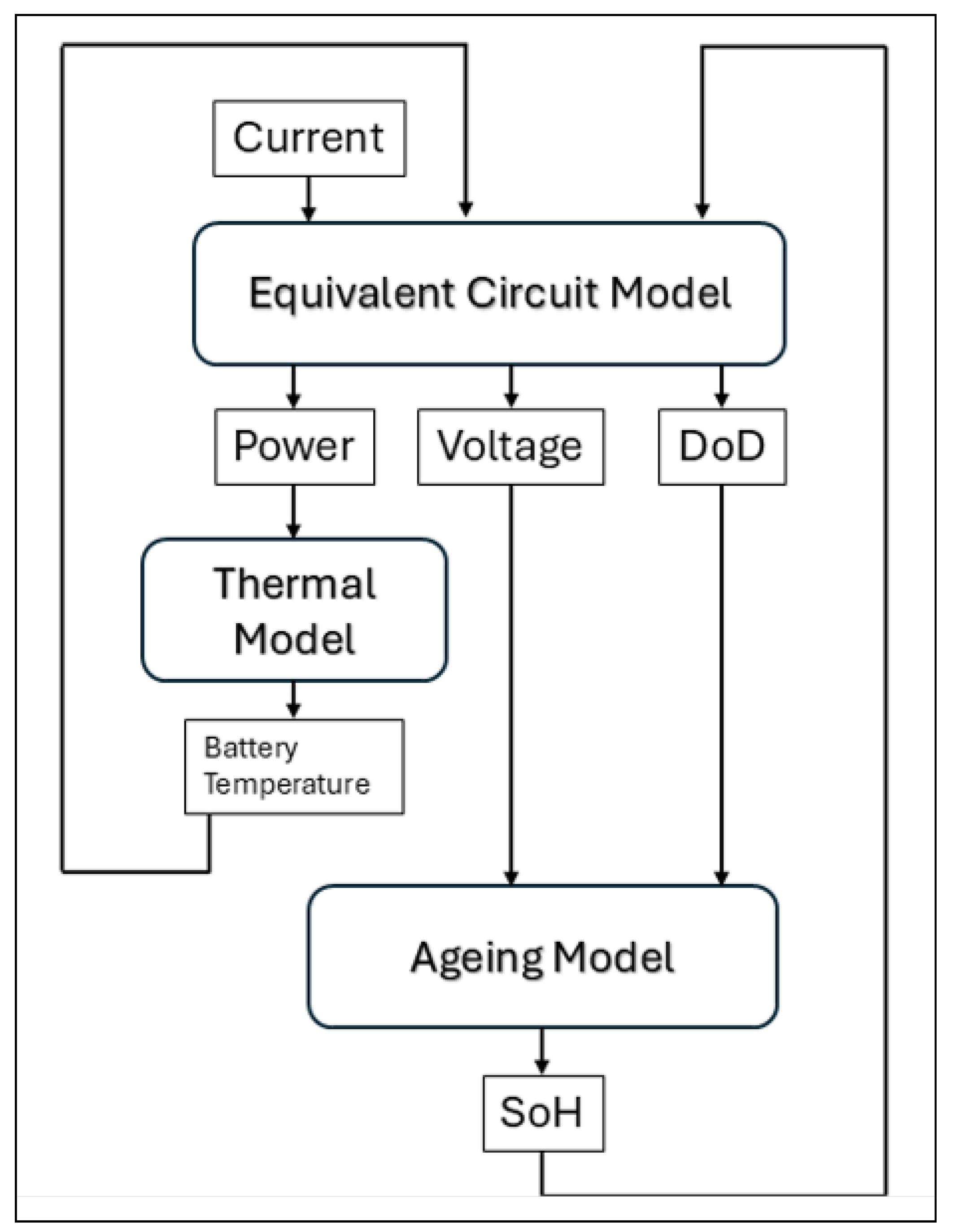
2. Materials and Methods

Our SPM poses the Cahn–Hilliard equation in COMSOL^® Multiphysics’ standard PDF format as two coupled second-order PDEs in ion concentration and chemical potential, respectively. The flowchart for the steps of the ROM development is presented in Figure 2.

Details of the model variables, along with all parameter magnitudes and units from the following equations, are given below in the nomenclature section. We assumed the particles to be spherical and isotropic. The model equations are given below, where the overbar denotes dimensionless parameters and variables. We provide only the main points of the derivation of the Cahn–Hilliard equation and refer the reader to the study by Zeng and Bazant [58] for more details. The diffusional chemical potential based on the regular solution model and acquired from the Cahn–Hilliard free energy functional is as follows:

$$\overline{\mu }=-k_{b}T\ln \left[{\displaystyle \frac{\overline{c}}{1-c_m}}\right]+{\displaystyle \frac{\overline{\Omega }\left(c_m-\overline{c}\right)}{c_m}}-{\displaystyle \frac{K{V}_S}{c_m}}{\overline{\nabla }}^2\overline{c}$$

(1)

The basic equation of evolution for mass conservation is as follows:

$${\displaystyle \frac{\partial \overline{c}}{\partial t}}=-\overline{\nabla }\cdot \overline{q}$$

(2)

The ion flux is driven by the gradient of the diffusional chemical potential as follows:

$$\overline{q}={\displaystyle \frac{-D_0\left(c_m-\overline{c}\right)}{k_{m}T{c}_m}}\overline{\nabla }\overline{\mu }$$

(3)

Voltage enters the Cahn–Hilliard SPM through Butler–Volmer kinetics obtained from transition state theory for concentrated solutions as follows:

$$I=I\left[\exp \left(-\alpha \overline{\eta }\right)i-\exp \left(\left(1-\alpha \right)\overline{\eta }\right)\right]$$

(4)

where $\alpha$ is the electron transfer symmetry factor, $\eta =\Delta \phi -\Delta {\phi }_{eq}$ is the surface overpotential because of the activation polarization, $\Delta \phi$ is the local voltage drop across the interface, and $\Delta {\phi }_{eq}$ is the Nernst equilibrium voltage. The boundary conditions we implemented in the dimensionless form are as follows:

$$\overline{q}\left(o,t\right)=0,$$

$$\widehat{n}·\overline{q}\left(1,t\right)=-\overline{q},$$

$$\widehat{n}·\overline{\nabla }\overline{c}(0,t)=0,$$

$$\widehat{n}·\overline{\nabla }\overline{c}(1,t)=0.$$

2.1. Coupling the Heat-Transfer Model to the Cahn–Hilliard Equation

The transient temperature response and thermal power conservation were incorporated into the ROM by an enthalpy balance on the bulk battery. An A123 Systems 26650 2.3 Ah cylindrical battery was selected because it is extensively studied, and its property data are readily available. The battery specifications are shown in

Table 1. Specifications for A123 Systems 26650 2.3 Ah lithium-ion battery.

Nominal capacity and voltage	2.3 Ah, 3.3 V
Internal impedance (1 kHz AC)	8 mΩ typical
Internal resistance 10 A, 1 s DC	10 mΩ typical
Recommended charge method	3 A to 3.6 V CCCV, 45 min
Recommended fast charge current	10 A to 3.6 CCCV
Maximum continuous discharge	70 A
Pulse discharge at 10 s	120 A
Cycle life at 10 C discharge	Over 1000 cycles
Recommended pulse charge/discharge cutoff	3.8 V to 1.6 V
Operating temperature range	243 K to 333 K
Core cell weight	70 g

.

A cylindrical Li-ion battery was constructed by rolling a stack of cathode/separator/anode layers. The individual layered sheets were thin, and lumped parameters were used. Therefore, material properties such as thermal conductivity, density, and specific heat capacity were presumed to be constant in a homogeneous and isotropic body. In the axial direction, the thermal conductivity was one or two orders of magnitude higher than in the radial direction, leading to a uniform temperature distribution in the axial direction [59,60]. Additionally, considering natural convection, the heat transfer at the surface was much smaller than the internal heat transfer by conduction, leading to negligible temperature gradients inside the battery. Based on these assumptions, the energy balance equation in the battery can be expressed by one bulk volume-averaged temperature. To estimate the thermal response of the battery, we utilized a simplified energy balance equation for the enthalpy change for electrochemical reactions. The battery thermal model parameters are shown in

Table 2. Thermal model parameters for A123 2.3 Systems 26650 Ah lithium-ion battery [61].

Parameter	Symbol	Value	Unit
Density	ρ	1824	kg/m3
Specific heat coefficient	Cp	825	J/kg K
Thermal conductivity	kt	0.488	W/m K
Convection coefficient	h	5.0	W/m2-K
Radius	R	12.93 × 10−3	m
Height	L	65.15 × 10−3	m
Volume	V	3.42 × 10−5	m3

.

Assuming a constant system volume and pressure and neglecting heat generation because of the enthalpy of mixing, the energy balance equation is as follows:

$$M{c}_p{\displaystyle \frac{\partial T}{\partial t}}=I\left(V_{OC}-T{\displaystyle \frac{\partial V_{OC}}{\partial T}}\right)-IV+{\dot{q}}_{sur}$$

(5)

The term $T{\displaystyle \frac{\partial V_{OC}}{\partial T}}$ stands for reversible heat generation and can be calculated from the entropy of the reaction. In this study, this reversible heat generation was ignored for simplicity. Assuming this simplification, the OCV becomes a function of SOC only, and Equation (5) was solved exactly for the battery’s temperature response for initial temperatures given by the COMSOL parameter sweep data.

$$T\left(t\right)=T_{surr}-{\displaystyle \frac{\exp \left(-\frac{A_b{h}_{c}t}{c_p\nu \rho }\right)\left(-1+\exp \left(\frac{A_b{h}_{c}t}{c_p\nu \rho }\right)\right)I_b\left(\overline{V}\left(T\right)-{\overline{V}}_{OC}\right)}{A_b{h}_c}}$$

(6)

The temperature is input in the Cahn–Hilliard model via Equation (1) as follows:

$$\overline{\mu }\left(T\left(t\right)\right)=-k_{b}T\left(t\right)\ln \left[{\displaystyle \frac{\overline{c}}{1-c_m}}\right]+{\displaystyle \frac{\overline{\Omega }\left(T\left(t\right)\right)\left(c_m-\overline{c}\right)}{c_m}}-{\displaystyle \frac{K{V}_S}{c_m}}{\overline{\nabla }}^2\overline{c}$$

(7)

Assuming that the ion activity in the electrolyte adjacent to the particle (based on the dimensionless ion concentration) is 1.0, $\Delta {\phi }_{eq}=-{\displaystyle \raisebox{1ex}{$\mu $}\!\left/ \!\raisebox{-1ex}{$e$}\right.}$ provides the voltage profile for the single-particle battery $V=V^{\theta }+\eta -{\displaystyle \raisebox{1ex}{$\mu $}\!\left/ \!\raisebox{-1ex}{$e$}\right.}$, where $V^{\theta }$ is the standard potential defined by the half-cell voltage (3.42 V vs. Li metal). The solution for $\eta$ gives the voltage response of the single-particle battery as follows:

$$V+V^{\theta }=\eta ={\displaystyle \frac{\mu }{e}}={\displaystyle \frac{k_{b}T}{e}}\left(-\overline{\mu }-2{\sinh }^{-1}\left({\displaystyle \frac{\overline{I}}{{\overline{I}}_0\left(\overline{c}\right)}}\right)\right)$$

(8)

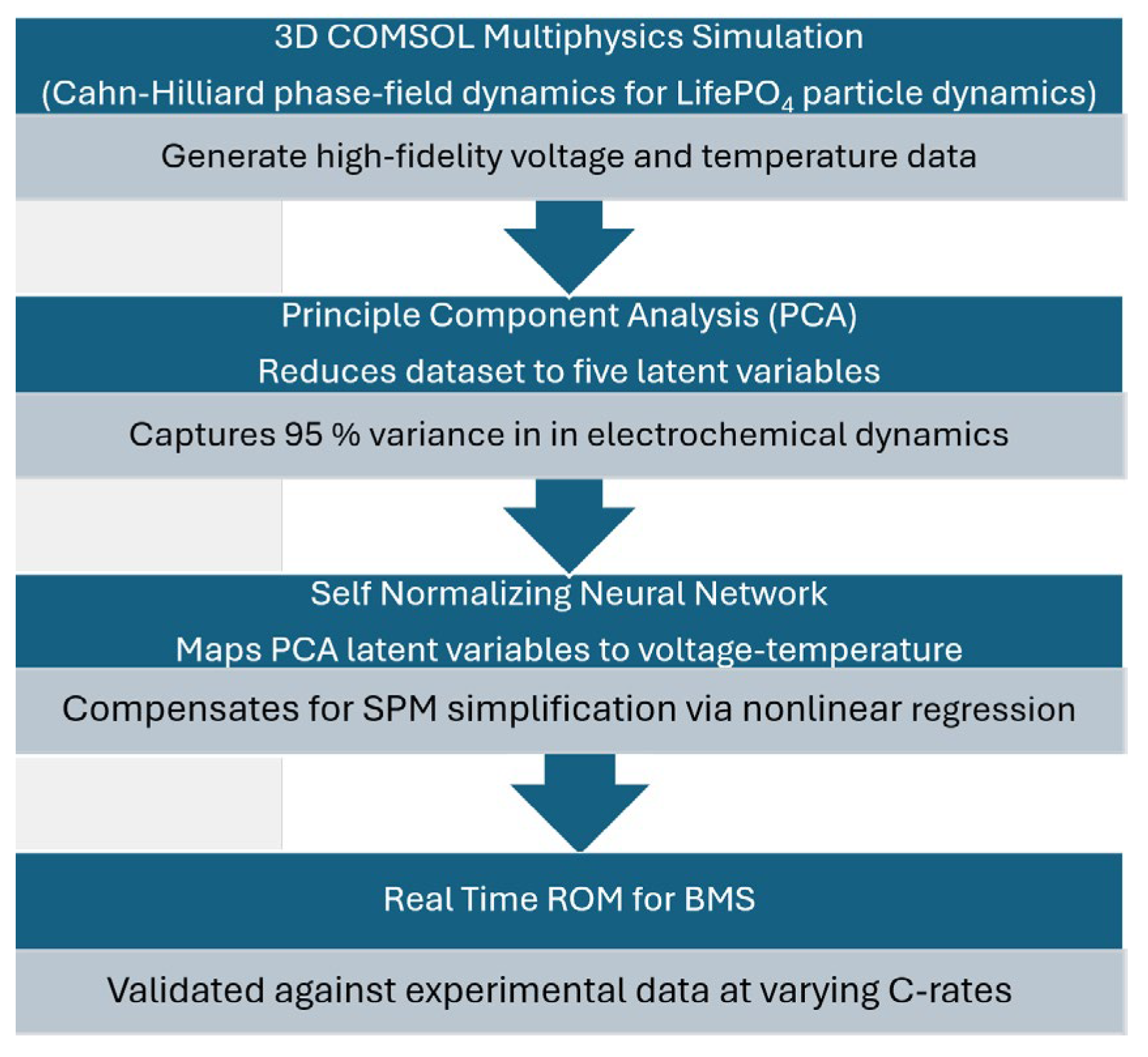
2.2. Generating the Dataset from the COMSOL^® Multiphysics Simulation

To create the simulation dataset over a broad range of conditions, we ran the COMSOL^® Multiphysics simulation parameter sweep for twenty combinations of temperatures ranging from 253 to 298 K and discharge rates ranging from 1 C to 20.6 C. The SNN was coded in the Wolfram language as a Mathematica^® 14.1 notebook. We used PCA to determine the minimum number of features for the ROM from the simulation dataset that adequately fit the experimental data.

The raw data were standardized for a mean of 1.0 and a standard deviation of 0, resulting in an initial dataset consisting of a 1000 by 20 rectangular matrix (A). The covariance matrix (M) was then determined as follows:

$$M={\displaystyle \frac{A^T\cdot A}{N}}$$

(9)

where N is the length of the column vectors in A. We used singular value decomposition (SVD) to decompose M as

$$M=U\cdot \Sigma \cdot V^T$$

(10)

Substituting the R.H.S. of Equation (10) for A in Equation (9) and simplifying gives

$$M={\displaystyle \frac{V\cdot {\Sigma }^2\cdot V^T}{N}}$$

(11)

This gives the principal components as

$$A\cdot V=U\cdot \Sigma$$

(12)

Based on the magnitude of the singular values on the diagonal of Σ, approximately 99% of the variance was captured by the first five principal components. The projection of the original scaled data into this reduced space by

$$A_{reduced}=A_{1000X20}\cdot P{C}_{20X5}$$

(13)

yielded a 1000 × 5 training set for the SNN.

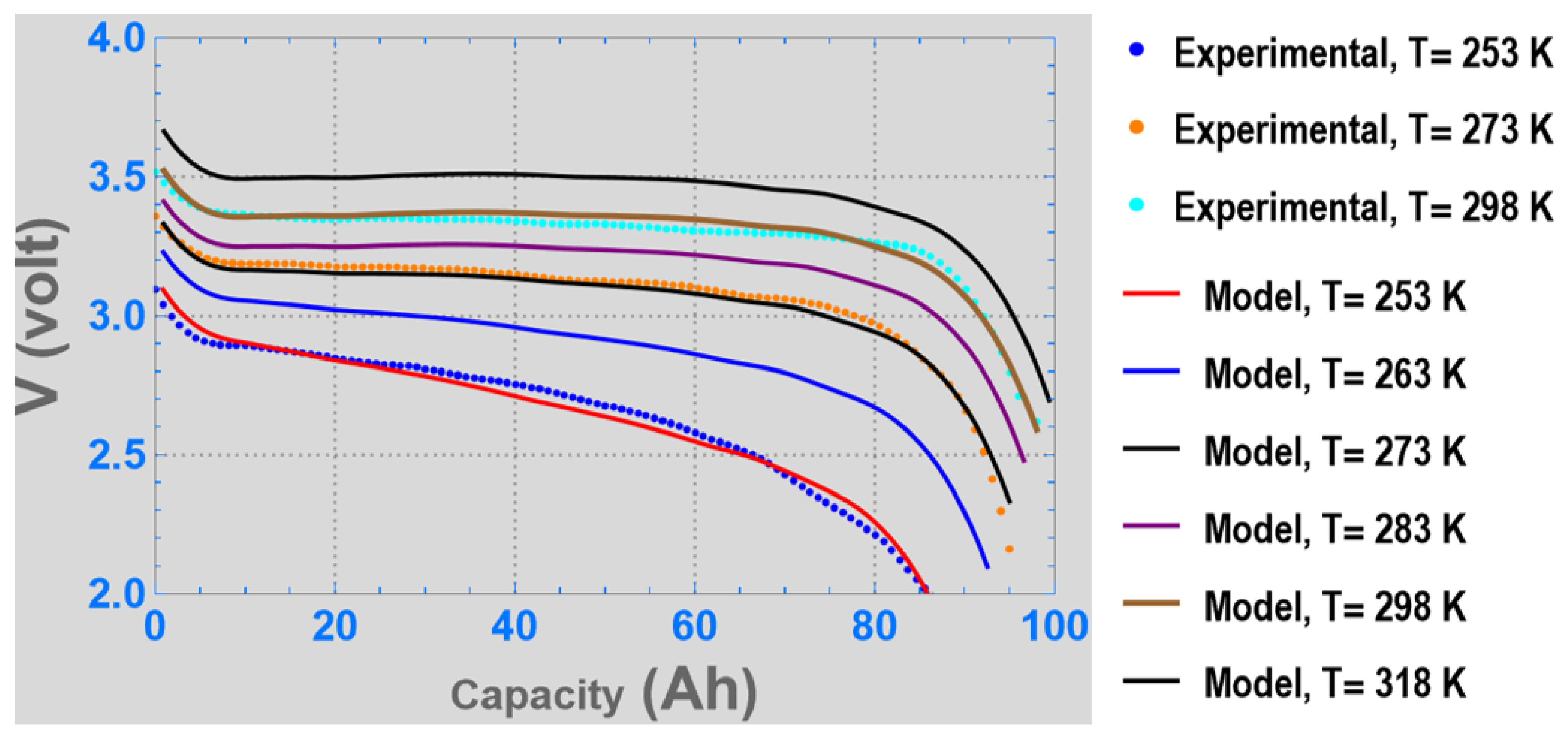
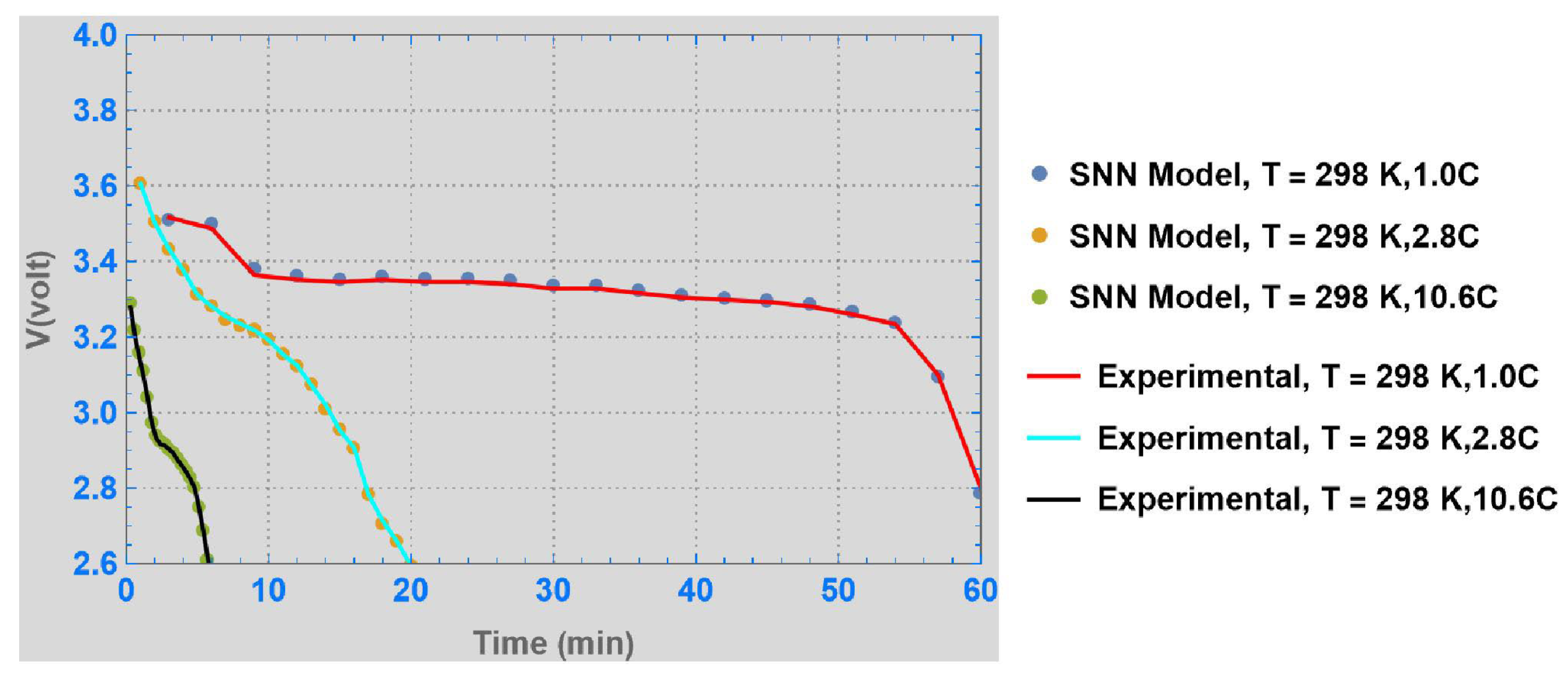
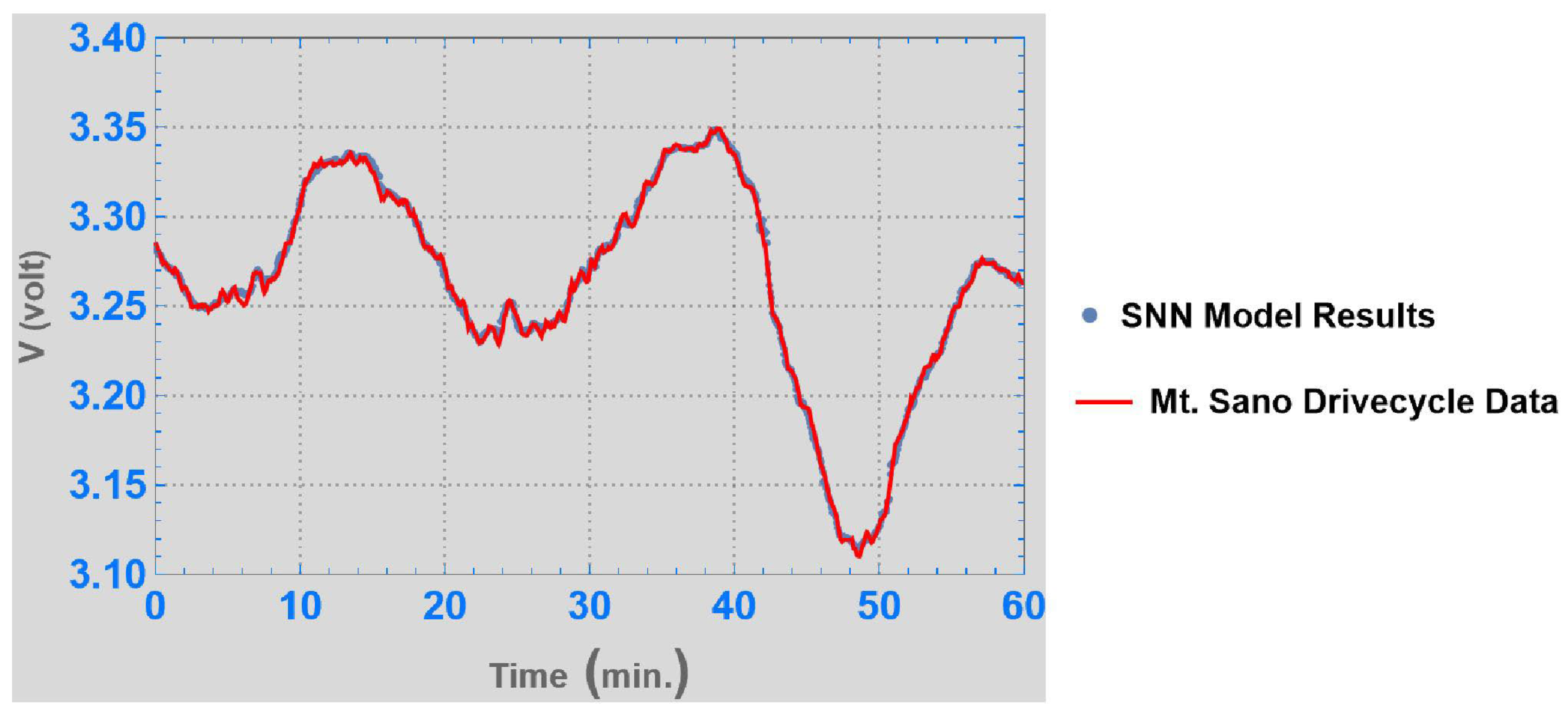
3. Results

The SPM is the simplest physics-based electrothermal model for lithium-ion batteries. The model incorporates three basic physical phenomena: lithium transport in the particles, the thermodynamic relationship between lithium concentration and electrode potential, and the overpotential required to drive the lithium intercalation reactions. The Cahn–Hilliard equation is a powerful tool for modeling lithium intercalation dynamics in single ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$ cathode particles, because it captures the material’s intrinsic phase-separating behavior that produces the characteristic voltage plateau during battery discharge. In this approach, the lithium concentration within a spherical, isotropic particle is treated as a continuous phase variable, and the system’s free energy is formulated as a non-convex function of concentration, naturally leading to phase separation and the formation of diffuse interfaces between lithium-rich and lithium-poor regions.

The modeling process, as implemented in our work and that of other recent studies, relies on several simplifying assumptions. The particle is assumed to be spherical and isotropic, with uniform material properties, and the effects of electrolyte transport and surface wetting are neglected. The model also assumes that all particles in the electrode experience identical conditions, and potential gradients in both the solid and electrolyte phases are ignored, which is generally valid only under relatively low current rates. Additionally, the thermal model is lumped, assuming a uniform temperature throughout the particle and neglecting reversible heat generation, which is considered minor for ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$ chemistry.

Theoretical predictions from the Cahn–Hilliard-based single-particle model (SPM) align well with experimental observations at moderate discharge rates and temperatures, successfully reproducing the voltage plateau and the diffusion-limited behavior observed at low temperatures. However, discrepancies arise at high discharge rates, where the model underestimates voltage drop and hysteresis, primarily because it does not account for electrolyte resistance, concentration polarization, or anisotropic diffusion pathways present in real particles. The lumped thermal model can also overpredict temperature rise during rapid discharge, as it neglects localized heating effects and convective cooling within the porous electrode structure. These limitations suggest that, while the Cahn–Hilliard equation provides a robust framework for capturing essential phase-separation dynamics in ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$, its predictive accuracy diminishes under extreme operating conditions due to the simplifying assumptions inherent in the single-particle and lumped thermal models. Improvements could be achieved by incorporating electrolyte dynamics, accounting for crystal anisotropy, and adopting more detailed thermal models that resolve spatial temperature gradients. Despite these challenges, the approach remains highly valuable for reduced-order modeling and real-time battery management applications, especially for our ROM, which combines the Cahn–Hilliard equation with machine learning and data-driven techniques to compensate for unmodeled effects.

Feedforward neural networks (FNNs) are often considered insufficient for deep learning of abstract variables. However, recent advancements have demonstrated that self-normalizing FNNs (SNNs) are effective for the classification and regression of numeric data. SNNs utilize scaled exponential linear units (SELUs) as activation functions, facilitating robust deep learning. We minimized the size of the SNN using principal component analysis (PCA). The resulting reduced order model (ROM) achieves computational efficiency comparable to an equivalent circuit model (ECM) while preserving the authenticity of the principal model via single-particle model (SPM) simulation.

Compared to full-order multiphysics models, which are computationally intensive and unsuitable for embedded or real-time applications, the ROM achieves a dramatic reduction in computation time. For example, the ROM can generate voltage predictions in just 2–5 milliseconds per step, matching or exceeding the speed of equivalent circuit models (ECMs) and outperforming pseudo-two-dimensional (P2D) models and detailed finite element simulations, which typically require orders of magnitude more computational resources [62]. The 2–5 ms/step metric directly results from replacing 3D PDE solving with data-driven low-order regression (PCA + SNN), validated against both simulation benchmarks and experimental road tests. This speed enables the ROM to operate at update rates of 15–60 Hz, suitable for real-time battery management tasks such as state-of-charge (SOC) and state-of-health (SOH) estimation, even under dynamic load conditions. The model’s lightweight architecture (requiring less than 1 MB of memory) makes it deployable on standard BMS hardware platforms, such as ARM Cortex microcontrollers.

The self-normalizing neural network (SNN) is a feedforward network designed to sustain stable activations across layers. As depicted in Figure 3, the SNN structure comprises the following features:

Input Layer:

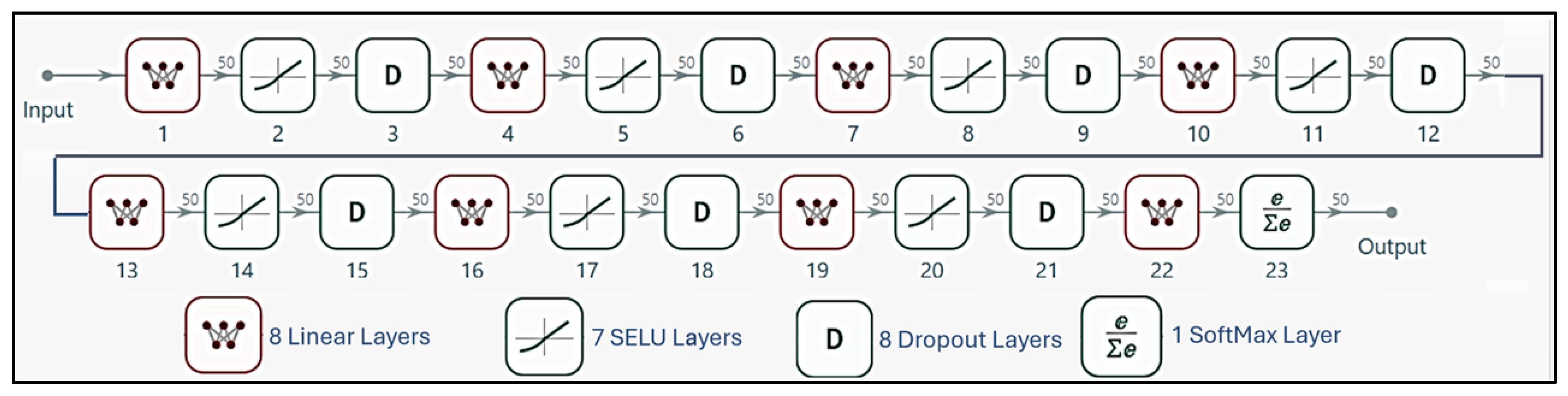
• Five nodes derived from PCA of the COMSOL^® simulation data.

Hidden Layers:

• Hidden layers with three nodes each, utilizing SELU activation functions;
• Alpha Dropout layers (seven total), with a 10% dropout rate between hidden layers to maintain self-normalizing properties and prevent overfitting;
• Weight initialization employing LeCun normal distribution to ensure zero mean and unit variance in initial activations.

Output Layer:

• One node with linear activation, providing scalar voltage predictions.
• Critical Design Aspects:
• Self-Normalization Mechanism:

The SELU activation function enforces stable activations through its fixed-point characteristics, thereby negating the requirement for batch normalization. This is essential for maintaining stable gradients across the eight-layer architecture.

Narrow Hidden Layers:

• The three-node width per hidden layer was optimized to preserve information from the five PCA latent variables, prevent overfitting given the limited experimental dataset, and balance computational efficiency with nonlinear representation capacity.

Alpha Dropout vs. Standard Dropout:

• Unlike conventional dropout, Alpha Dropout maintains the mean and variance of activations, ensuring compatibility with SELU’s normalization properties.

Training Configuration:

• Loss function: mean squared error (MSE);
• Optimizer: Adam with specified learning rate;
• Batch size: 32;
• Early stopping on validation split (20% of data).

This architecture leverages the SNN’s inherent stability to map the PCA-reduced simulation space to experimental voltage profiles while avoiding vanishing/exploding gradients, a key advantage over traditional FNNs for regression tasks with limited data. The narrow-hidden layers act as nonlinear filters that progressively refine the relationship between phase-field dynamics (encoded in PCA components) and macroscopic battery behavior.

We tested and verified the SNN for a 1 C discharge rate for ambient temperatures ranging from 253 to 298 K, as shown in Figure 4. In Figure 5, the model results are compared to the experimental results for discharge rates ranging from 1.0 to 10.6 C for an ambient temperature of 298 K [63]. Finally, we tested the trained SNN predictor function using a harsh road test dataset, namely Up Mount Sano in Huntsville, AL [64], as shown in Figure 6.

4. Discussion

In this study, we developed a physics-informed reduced-order battery management system (BMS) for ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$ batteries by integrating a Cahn–Hilliard phase-field single-particle model (SPM) with a lumped heat-transfer framework. Three-dimensional COMSOL^® simulations of a ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$ particle generated voltage and temperature profiles across a wide range of ambient temperatures (253–298 K) and discharge rates (1 C–20.5 C). Principal component analysis (PCA) reduced this dataset to five latent variables, which were mapped to experimental voltage–temperature data using a self-normalizing neural network (SNN). The resulting ROM achieves real-time prediction accuracy (2–5 ms/step) comparable to detailed multiphysics models while retaining essential electrothermal dynamics.

This approach demonstrates several key strengths that advance the state of the art in battery modeling for real-time applications. The hybrid physics-data integration combines phase-field simulations (capturing the unique phase-separation dynamics of ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$) with data-driven dimensionality reduction, effectively addressing the traditional trade-off between model accuracy and computational speed. This integration yields remarkable computational efficiency, with a 98% reduction in runtime compared to full-order models (FOMs), enabling deployment on ARM Cortex-M4 microcontrollers and validated at 15–60 Hz update rates under dynamic road test conditions. Additionally, the lumped thermal model successfully accounts for temperature-dependent degradation mechanisms while maintaining computational tractability, overcoming the limitations of isothermal SPMs. Validation across temperatures (253–298 K) and discharge rates (1–10.6 C) demonstrates RMSE values below 31 mV, with explicit alignment to the experimental data of A123 Systems 26650.

Despite these advantages, several limitations warrant consideration. The single-particle framework neglects electrolyte resistance, leading to slight voltage underestimation at discharge rates exceeding 10 C. The lumped thermal model, while computationally efficient, overpredicts temperature rise during fast discharge compared to distributed thermal models that account for spatial gradients. Furthermore, the current implementation is specifically tailored for ${\mathrm{L}\mathrm{i}\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{O}}_4$ phase separation dynamics; its generalizability to nickel-rich (NMC) or silicon-anode chemistries remains unverified, potentially limiting broader applicability across diverse battery technologies.

Future research should address these limitations through several promising directions. The integration of concentrated solution theory could capture electrolyte transport limitations and Ohmic losses at high C rates, improving accuracy during fast charging/discharging scenarios. Adapting the phase-field framework for NMC and solid-state batteries would expand applicability, requiring adjustments to nucleation kinetics and diffusion tensors to accommodate different phase behaviors. Replacing the lumped thermal approach with more sophisticated 3D thermal networks would better resolve localized heating in porous electrodes without substantially increasing computational demand. Finally, optimizing SNN architectures for quantum-ready microcontrollers could enable ultrafast (<1 ms) multiparameter estimation, further advancing edge-AI deployment capabilities for next-generation battery management systems. This work ultimately bridges critical gaps between physics-based fidelity and real-time BMS requirements, offering a scalable framework for electrified transportation and grid storage applications.

5. Conclusions

In this study, we developed a novel reduced-order battery management system (BMS) for LiFePO₄ batteries by integrating a physics-based single-particle model (SPM) derived from the Cahn–Hilliard phase-field formulation with a lumped heat-transfer model. By generating a comprehensive dataset from three-dimensional COMSOL^® simulations across a wide range of temperatures and discharge rates, we utilized principal component analysis (PCA) to identify latent variables that capture the essential electrothermal dynamics of the cell. These latent variables were then mapped to experimental voltage–temperature profiles using a self-normalizing neural network (SNN), resulting in a real-time reduced-order model (ROM) that retains the accuracy of detailed multiphysics models while achieving significant computational efficiency.

The proposed ROM addresses several critical gaps in the current literature. Unlike conventional equivalent circuit models (ECMs) and black-box approaches, our method preserves key physical insights and enables the accurate prediction of battery performance under diverse operating conditions, including those involving thermal and aging effects. The hybrid framework leverages both physics-based and data-driven techniques, providing a practical solution for real-time BMS applications in electric and hybrid vehicles, where computational resources are often limited. Validation against experimental data demonstrates that the ROM can reliably predict voltage and temperature responses across a range of ambient conditions and C rates.

Overall, this work demonstrates that advanced model reduction and machine learning techniques can be effectively combined to overcome the limitations of traditional BMS modeling approaches. Future research will focus on extending the methodology to other chemistries, incorporating more comprehensive aging mechanisms, and deploying the framework in embedded BMS hardware for field validation.