Integrating Metaheuristics and Machine Learning for Enhanced Vehicle Routing: A Comparative Study of Hyperheuristic and VAE-Based Approaches
Abstract
1. Introduction
1.1. Motivation
1.2. Contributions
1.3. Paper Structure
2. Related Works
2.1. Hyperheuristics-Based Approaches
2.2. Machine Learning-Based Approaches
2.3. State-of-the-Art Techniques: A Summary
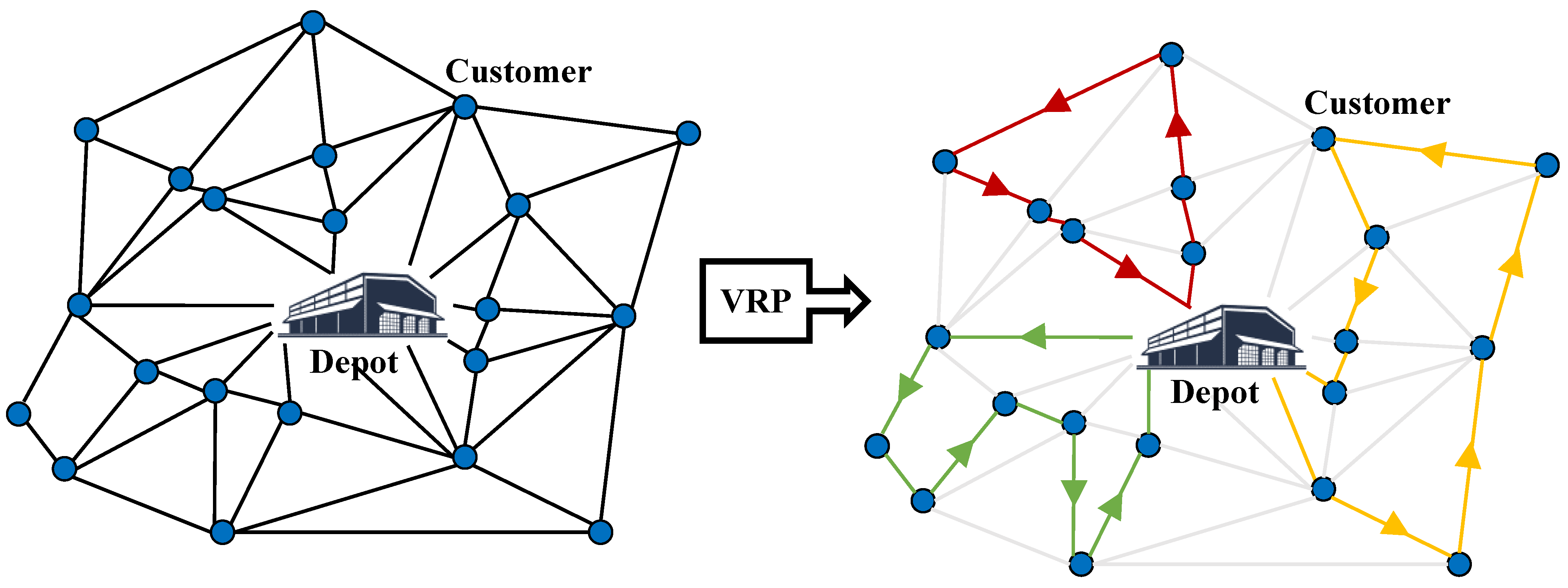
3. Problem Statement
3.1. Problem Reformulation
- Each route starts and ends at the depot.
- Each customer is visited exactly once by a single vehicle.
- The total demand served by each vehicle does not exceed its capacity Q.
- The total cost C of the routes is minimized, where C is typically a function of the total distance traveled or the total time taken.
- Customers with higher priorities are served earlier or within stricter time windows, ensuring preferential treatment without significantly increasing total operational costs.
3.2. Challenges and Computational Complexity
- Prioritized customers must be served earlier in a manner that does not violate vehicle capacity constraints.
- Prioritization can disrupt the efficient clustering of customers, leading to increased travel distances.
- The interplay between cost minimization and prioritization adds a multi-objective aspect to the problem.
3.3. Research Focus and Methodological Approach
- A Metaheuristic-Based Hyperheuristic Framework that dynamically selects and adapts low-level heuristics using Simulated Annealing (SA) and Ant Colony Optimization (ACO), improving search efficiency and balancing solution quality.
- A Variational Autoencoder (VAE)-Based Hyperheuristic, leveraging deep learning techniques to generate and refine heuristics based on learned representations of historical routing data, enhancing adaptability and solution generalization.
- Assess the effectiveness of both approaches in handling customer prioritization constraints.
- Compare their ability to optimize solution quality, computational efficiency, and scalability.
- Provide insights into the potential for integrating metaheuristic strategies with deep learning-based heuristic generation.
4. Mathematical Formulation
4.1. Sets and Indices
- : Set of all vertices, where 0 represents the depot and represent customers.
- E: Set of all edges representing possible routes between vertices.
- : Set of available vehicles.
4.2. Parameters
- : Cost of traveling from vertex i to vertex j.
- : Demand of customer i.
- Q: Maximum capacity of each vehicle.
- : Priority level of customer i (higher values indicate higher priority).
- and : Earliest and latest time windows for customer i.
- : Service time at customer i.
- : Travel time from node i to node j.
- M: A large constant used for constraint enforcement.
4.3. Decision Variables
- : Binary variable; 1 if vehicle k travels from vertex i to vertex j, 0 otherwise.
- : Binary variable; 1 if customer i is served, 0 otherwise.
- : Time when service starts at customer i.
- : Load of vehicle k when leaving customer i.
4.4. Objective Function
- The first term represents the total travel cost.
- The second term incentivizes the servicing of high-priority customers.
- is a weighting parameter to balance cost minimization and priority fulfillment.
4.5. Constraints
4.5.1. Routing Constraints
- Each customer must be visited exactly once by a single vehicle:
- Each vehicle must start and end at the depot:
4.5.2. Flow Conservation Constraints
- Vehicles must enter and leave each customer exactly once:
4.5.3. Capacity Constraints
- The total demand assigned to each vehicle must not exceed its capacity:
- The load of a vehicle is updated after serving a customer:
- Vehicle load must remain within valid limits:
4.5.4. Time Window Constraints
- Vehicles must arrive within the allowed time window:
- Ensuring sequential servicing while accounting for travel and service time:
4.5.5. Prioritization Constraints
- To ensure service order based on customer priority, a hard constraint is imposed such that higher-priority customers are served earlier than lower-priority ones. This is mathematically formulated aswhere and represent the service start times at customers i and j, respectively, and and denote their priority levels.
4.6. Discussion of Model Complexity
- Balancing cost efficiency with priority satisfaction, leading to a multi-objective trade-off.
- Dynamic route adjustments, as priority constraints may override standard distance-based optimization.
- Increased computational complexity since the problem now involves additional ordering constraints for prioritization.
5. Hyperheuristic
- Heuristic Selection: Choosing and applying predefined low-level heuristics based on specific selection criteria.
- Heuristic Generation: Constructing new heuristics through learning mechanisms, often using machine learning techniques.
- Online learning: Adjusting heuristic selection strategies dynamically based on real-time feedback from the optimization process.
- Offline learning: Learning heuristic selection patterns from historical data and applying them to new problem instances.
5.1. Low-Level Heuristics for VRP-PC
- Constructive heuristics: Used to build the initial solutions.
- Improvement heuristics: Used to refine the existing solutions.
- Perturbation heuristics: Used to introduce controlled randomness and escape the local optima.
5.1.1. Constructive Heuristics
- CH1: Priority-Based Customer Insertion: This heuristic constructs routes by iteratively inserting the highest-priority customer into the position that minimizes incremental travel cost while respecting vehicle capacity and time window constraints:
- CH2: Clustered Nearest Neighbor: Customers are grouped into clusters based on geographic proximity and priority level. Each cluster is served by a single vehicle, prioritizing high-priority customers:
5.1.2. Improvement Heuristics
- IMP1: Priority-Based Route Optimization: This heuristic reorders customers within each route to prioritize higher-priority customers while minimizing increased travel distance:
- IMP2: Capacity-Constrained Customer Relocation: Customers are relocated between routes to balance load while reducing travel costs:
5.1.3. Perturbation Heuristics
- PRT1: Random Customer Swap: Two customers from different routes are randomly swapped, provided no constraints are violated:
- PRT2: Route Reversal: A segment of a route is reversed if it reduces overall cost:
5.2. Heuristic Selection Methods
- Random selection: Selects heuristics randomly without performance evaluation.
- Greedy selection: Selects the heuristic that provides the best immediate improvement.
- Peckish selection: A compromise between greedy and random selection, where heuristics are selected probabilistically based on performance.
- Choice function selection: Assigns scores to heuristics based on performance history.
- Reinforcement learning-based selection: Utilizes machine learning to adapt heuristic selection over time.
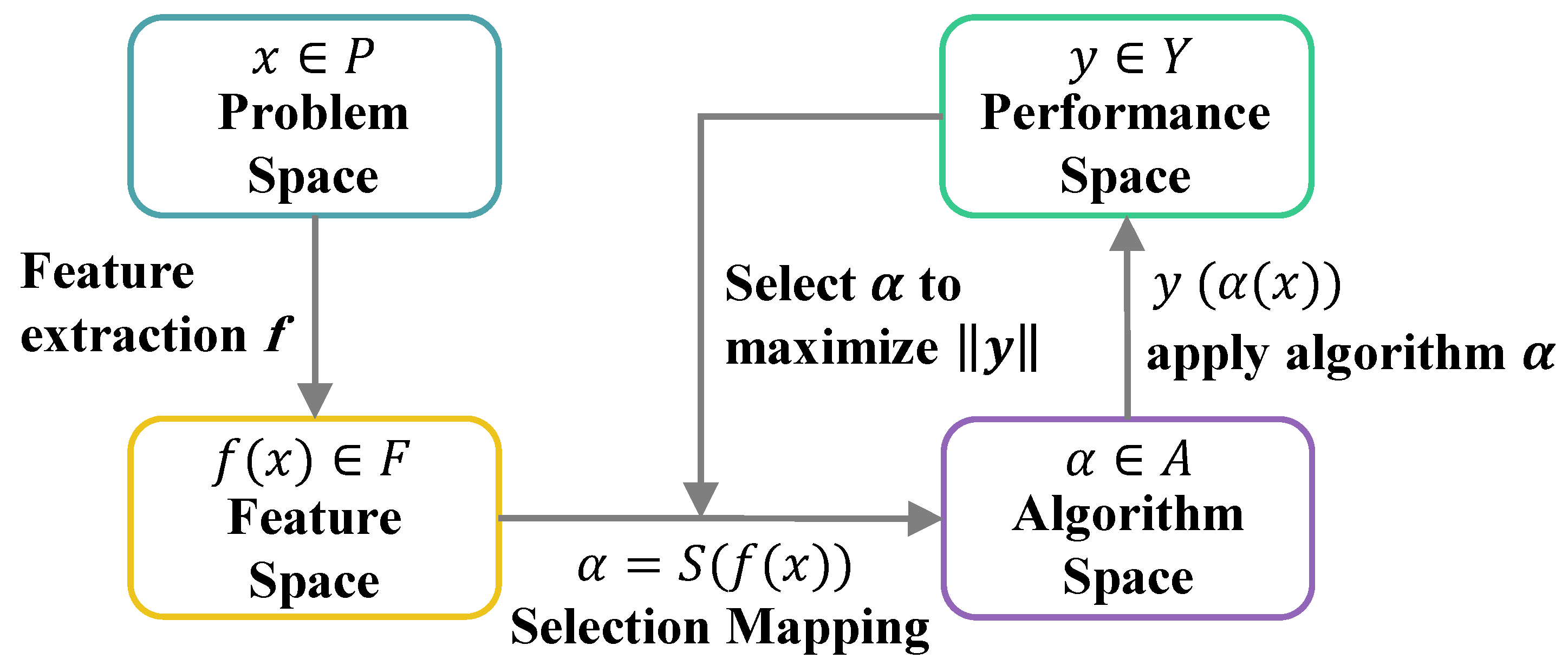
5.3. VAE-Based Hyperheuristic and Its Implementation
- (i)
- Input Representation: Historical heuristic sequences are encoded as binary vectors, where each bit represents the application of a specific low-level heuristic. Each sequence captures the order of heuristic applications used to solve a specific VRP-PC instance.
- (ii)
- VAE Architecture: The encoder is a 3-layer feedforward neural network with ReLU activation, compressing heuristic sequences into a latent vector . The latent dimension d was experimentally set to 32. The decoder mirrors the encoder and reconstructs heuristic sequences from z, optimized to minimize binary cross-entropy and Kullback–Leibler divergence.
- (iii)
- Training Details: The model is trained offline using 1000 historical solutions from Al Amir VRP-PC instances. We used the Adam optimizer with a learning rate of 0.001 and batch size of 64 over 100 epochs. The training dataset was split 80/20 for training/validation. Reconstruction accuracy stabilized at 96%, and the model generalizes well to unseen instances.
5.4. Move Acceptance Criteria
- Deterministic strategies: Always accept improved solutions (e.g., Only Improvements, Improving, and Equal).
- Non-deterministic strategies: Accept worsening solutions probabilistically (e.g., Simulated Annealing and Great Deluge).
- -
- is the difference between the new and current objective function values.
- -
- T is a temperature parameter that gradually decreases.
- -
- is a random number between 0 and 1.
5.5. Termination Criteria
- A global time limit: milliseconds.
- Non-improving iterations limit: The algorithm stops if consecutive iterations fail to improve the solution.
6. Experimental Results
6.1. Test Instances
6.2. Experimental Setup
- Processor: Intel Core i7, 3.4 GHz (Intel Corporation, Santa Clara, CA, USA);
- RAM: 16 GB;
- Operating System: Windows 10 (Microsoft Corporation, Redmond, WA, USA);
- Implementation: Custom-developed optimization framework in Python v3.10.11.
6.3. Scalability and Robustness Evaluation
6.4. Evaluation Metrics
- Total Travel Cost (): Measures the total distance traveled by the fleet:
- Priority Satisfaction (): Percentage of high-priority customers serviced within the expected timeframe:
- Computational Time (): Measures the total execution time in seconds:
6.5. Heuristic-Based Hyperheuristics
- Constructive heuristics: CH1 (Priority-Based Customer Insertion), CH2 (Clustered Nearest Neighbor);
- Improvement heuristics: IMP1 (Route Optimization), IMP2 (Customer Relocation).
- Random Selection: Randomly selects heuristics at each iteration.
- Greedy Based: Selects the best-performing heuristic based on immediate improvement.
- Peckish: A probabilistic greedy approach that incorporates performance history.
- Choice Function: Assigns scores to heuristics and selects the highest-scoring one.
- Simulated Annealing Based: Uses Simulated Annealing to balance exploitation and exploration.
- Ant Colony Optimization Based: Uses pheromone trails to guide heuristic selection.
6.6. Results and Analysis
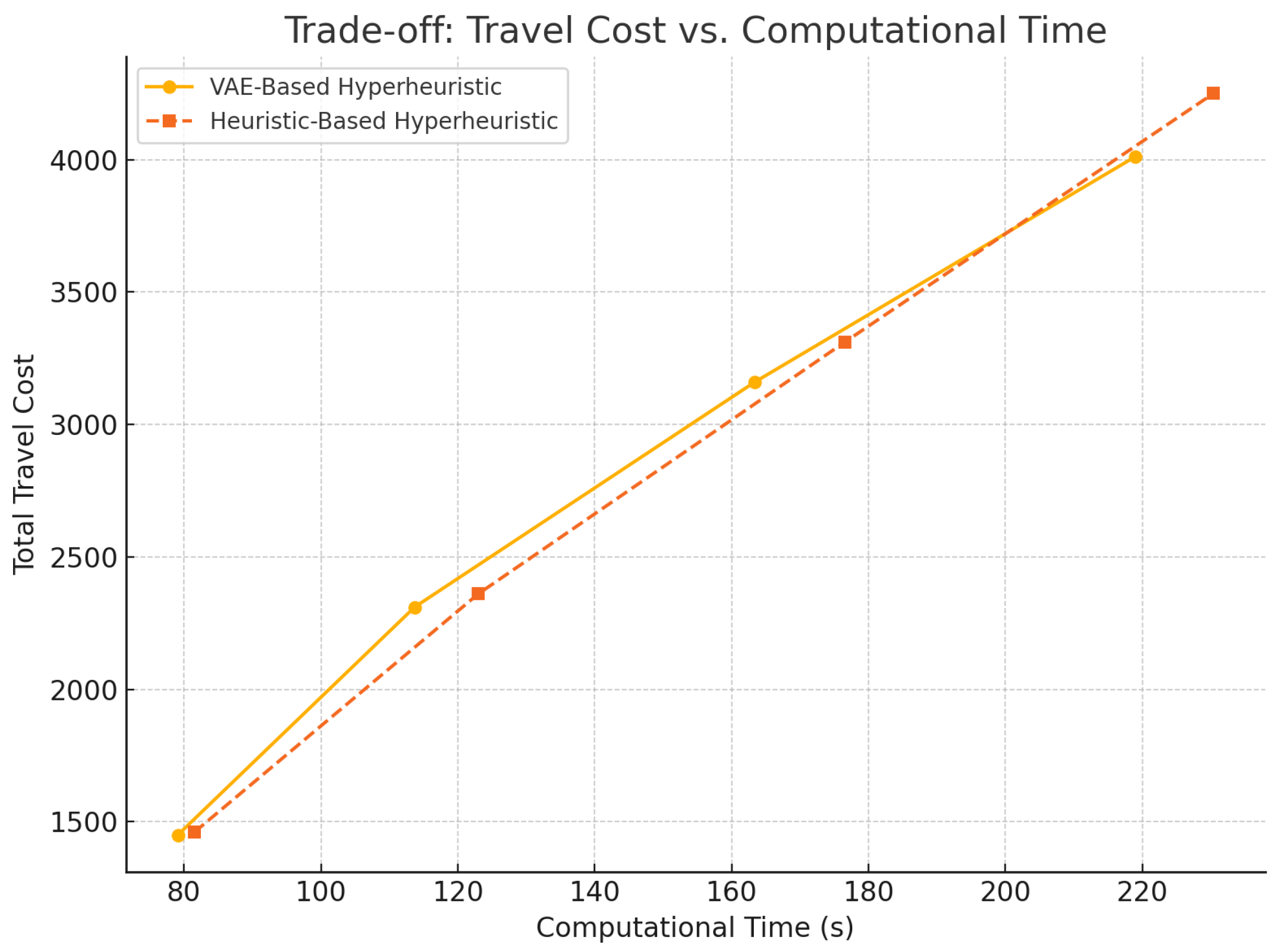
- Cost Efficiency: The VAE-based hyperheuristic consistently achieved lower travel costs compared to heuristic-based methods across all test instances, saving an average of 5–8% on total travel cost.
- Priority Satisfaction: The VAE approach prioritized high-priority customers more effectively, ensuring that over 95% of high-priority deliveries were met within the expected timeframe.
- Computational Efficiency: While the VAE model required slightly higher computational time (5–8% increase in execution time for larger instances), its improved routing efficiency outweighs this drawback.
| Instance | VAE () | VAE () | Best Heuristic () | Best Heuristic () | Priority Satisfaction (%) |
|---|---|---|---|---|---|
| Instance 1 | 750.4 | 40.2 s | 760.3 | 42.8 s | 98.5% |
| Instance 10 | 1450.2 | 79.1 s | 1460.4 | 81.5 s | 97.9% |
| Instance 20 | 2310.7 | 113.7 s | 2360.7 | 123.0 s | 96.4% |
| Instance 30 | 3160.7 | 163.4 s | 3310.7 | 176.5 s | 94.7% |
| Instance 40 | 4010.5 | 218.9 s | 4250.4 | 230.4 s | 92.3% |
6.7. Generalization to Other VRP Variants
- Charging station availability can be encoded as additional constraints in route feasibility.
- The VAE latent space can be trained on energy consumption patterns, considering battery degradation and recharging profiles.
- Time windows can incorporate charging durations to avoid infeasible scheduling.
6.8. Hyperparameter Sensitivity Analysis
- Latent dimension: Tested values from 8 to 64. Best performance was achieved between 16 and 32; below 16, the model underfit, and above 32, no significant improvements were observed.
- Learning rate: Varied from 0.0005 to 0.01. An optimal range was found between 0.001 and 0.005. Too low a rate led to slow convergence, while a too high rate destabilized the training.
- Batch size: Ranged from 32 to 256. Batch sizes between 64 and 128 yielded the best balance between convergence speed and generalization.
6.9. Further Discussion of Results
- Dynamic Adaptability: Unlike heuristic-based methods, the VAE model learns and generates heuristics tailored to each test instance.
- Cost Reduction: The VAE-based approach consistently outperformed heuristic methods by reducing total travel costs.
- Scalability: The VAE model generalized well to larger problem instances, proving effective even at 400+ customers.
7. Conclusions
- The metaheuristic-based hyperheuristic framework, utilizing Simulated Annealing (SA) and Ant Colony Optimization (ACO), efficiently navigates large solution spaces by dynamically selecting heuristics.
- The Variational Autoencoder (VAE)-based hyperheuristic, leveraging deep learning, autonomously learns and generates heuristic strategies, providing better generalization and adaptability across diverse operational conditions.
7.1. Key Findings
- Efficiency in Routing Optimization: Both approaches significantly reduced total travel costs and improved computational efficiency, with the VAE-based model demonstrating superior adaptability to new problem instances.
- Improved Priority Satisfaction: The VAE-based hyperheuristic prioritized high-importance customers more effectively, ensuring faster and more reliable deliveries.
- Scalability and Generalization: The VAE-based approach exhibited strong generalization, effectively handling larger instances and offering insights into potential real-world applications in logistics.
7.2. Future Research Directions
- Hybrid models: Combining metaheuristics with deep learning frameworks for enhanced adaptability.
- Online learning mechanisms: integrating online learning mechanisms to allow the VAE model to dynamically update its heuristic generation process based on real-time feedback from newly encountered problem instances.
- Real-time VRP adaptations: Incorporating dynamic data streams to adjust routes in real-time.
- Application in other domains: Extending the VAE-based hyperheuristic to supply chain optimization, warehouse management, and drone delivery systems.
7.3. Real-Time Deployment Considerations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kanj, H.; Kulaglic, A.; Aly, W.H.F.; Al-Tarawneh, M.A.; Safi, K.; Kanj, S.; Flaus, J.M. Agent-based risk analysis model for road transportation of dangerous goods. Results Eng. 2025, 25, 103944. [Google Scholar] [CrossRef]
- Danach, K.; El Dirani, A.; Rkein, H. Revolutionizing Supply Chain Management with AI: A Path to Efficiency and Sustainability. IEEE Access 2024, 12, 188245–188255. [Google Scholar] [CrossRef]
- Harb, H.; Jaoude, C.A.; Makhoul, A. An energy-efficient data prediction and processing approach for the internet of things and sensing based applications. Peer-to-Peer Netw. Appl. 2020, 13, 780–795. [Google Scholar] [CrossRef]
- Eido, W.M.; Ibrahim, I.M. Ant Colony Optimization (ACO) for Traveling Salesman Problem: A Review. Asian J. Res. Comput. Sci. 2025, 18, 20–45. [Google Scholar] [CrossRef]
- Tarhini, A.; Danach, K.; Harfouche, A. Swarm intelligence-based hyper-heuristic for the vehicle routing problem with prioritized customers. Ann. Oper. Res. 2022, 308, 549–570. [Google Scholar] [CrossRef]
- Harb, H.; Makhoul, A. Energy-efficient scheduling strategies for minimizing big data collection in cluster-based sensor networks. Peer-to-Peer Netw. Appl. 2019, 12, 620–634. [Google Scholar] [CrossRef]
- Frey, C.M.; Jungwirth, A.; Frey, M.; Kolisch, R. The vehicle routing problem with time windows and flexible delivery locations. Eur. J. Oper. Res. 2023, 308, 1142–1159. [Google Scholar] [CrossRef]
- Wu, Y.; Zeng, B. Dynamic parcel pick-up routing problem with prioritized customers and constrained capacity via lower-bound-based rollout approach. Comput. Oper. Res. 2023, 154, 106176. [Google Scholar] [CrossRef]
- Bi, J.; Ma, Y.; Zhou, J.; Song, W.; Cao, Z.; Wu, Y.; Zhang, J. Learning to handle complex constraints for vehicle routing problems. Adv. Neural Inf. Process. Syst. 2024, 37, 93479–93509. [Google Scholar]
- Zhao, J.; Liu, Y.; Zhang, J.; Zhang, J.; Huang, Y.; Yu, L.; Xie, B. An exact method for vehicle routing problem with backhaul discounts in urban express delivery network. Clean. Logist. Supply Chain. 2024, 11, 100157. [Google Scholar] [CrossRef]
- Garside, A.K.; Erlinda, L.; Amallynda, I. Solving heterogeneous fleet vehicle routing problem with clarke wright saving heuristic and genetic algorithm. AIP Conf. Proc. 2024, 2927, 050002. [Google Scholar]
- Liu, J.; Tong, L.; Xia, X. A genetic algorithm for vehicle routing problems with time windows based on cluster of geographic positions and time windows. Appl. Soft Comput. 2025, 169, 112593. [Google Scholar] [CrossRef]
- Elatar, S.; Abouelmehdi, K.; Riffi, M.E. The vehicle routing problem in the last decade: Variants, taxonomy and metaheuristics. Procedia Comput. Sci. 2023, 220, 398–404. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, M.; Yang, J.; Shi, Y.; Middendorf, M. A hybrid swarm intelligence algorithm for vehicle routing problem with time windows. IEEE Access 2020, 8, 93882–93893. [Google Scholar] [CrossRef]
- Doan, T.T.; Bostel, N.; Hà, M.H. The vehicle routing problem with relaxed priority rules. EURO J. Transp. Logist. 2021, 10, 100039. [Google Scholar] [CrossRef]
- Abdirad, M.; Krishnan, K.; Gupta, D. A two-stage metaheuristic algorithm for the dynamic vehicle routing problem in Industry 4.0 approach. J. Manag. Anal. 2021, 8, 69–83. [Google Scholar] [CrossRef]
- İlhan, İ. An improved simulated annealing algorithm with crossover operator for capacitated vehicle routing problem. Swarm Evol. Comput. 2021, 64, 100911. [Google Scholar] [CrossRef]
- Jia, Y.H.; Mei, Y.; Zhang, M. A bilevel ant colony optimization algorithm for capacitated electric vehicle routing problem. IEEE Trans. Cybern. 2021, 52, 10855–10868. [Google Scholar] [CrossRef]
- Li, C.; Wei, X.; Wang, J.; Wang, S.; Zhang, S. A review of reinforcement learning based hyper-heuristics. PeerJ Comput. Sci. 2024, 10, e2141. [Google Scholar] [CrossRef]
- Tyasnurita, R.; Özcan, E.; Drake, J.H.; Asta, S. Constructing selection hyper-heuristics for open vehicle routing with time delay neural networks using multiple experts. Knowl.-Based Syst. 2024, 295, 111731. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Z.; Huang, M.; Guo, X.; Qi, L. Multi-Objective Integrated Energy-Efficient Scheduling of Distributed Flexible Job Shop and Vehicle Routing by Knowledge-and-Learning-Based Hyper-Heuristics. IEEE Trans. Emerg. Top. Comput. Intell. 2025; early access. [Google Scholar]
- Danach, K.; Gelareh, S.; Monemi, R.N. The capacitated single-allocation p-hub location routing problem: A Lagrangian relaxation and a hyper-heuristic approach. EURO J. Transp. Logist. 2019, 8, 597–631. [Google Scholar] [CrossRef]
- Bogyrbayeva, A.; Meraliyev, M.; Mustakhov, T.; Dauletbayev, B. Machine learning to solve vehicle routing problems: A survey. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4754–4772. [Google Scholar] [CrossRef]
- Shahbazian, R.; Pugliese, L.D.P.; Guerriero, F.; Macrina, G. Integrating Machine Learning Into Vehicle Routing Problem: Methods and Applications. IEEE Access 2024, 12, 93087–93115. [Google Scholar] [CrossRef]
- Stamadianos, T.; Taxidou, A.; Marinaki, M.; Marinakis, Y. Swarm intelligence and nature inspired algorithms for solving vehicle routing problems: A survey. Oper. Res. 2024, 24, 47. [Google Scholar] [CrossRef]
- Ji, X.F.; Pan, J.S.; Chu, S.C.; Hu, P.; Chai, Q.W.; Zhang, P. Adaptive cat swarm optimization algorithm and its applications in vehicle routing problems. Math. Probl. Eng. 2020, 2020, 1291526. [Google Scholar] [CrossRef]
- Kang, H.Y.; Lee, A.H. A genetic-based approach for vehicle routing problem with fuzzy alpha-cut constraints. Soft Comput. 2025, 29, 1169–1189. [Google Scholar] [CrossRef]
- Vu, N.G.H.; Tang, Y.; Lim, R.; Wang, G.G. Hybrid Metaheuristic Vehicle Routing Problem for Security Dispatch Operations. arXiv 2025, arXiv:2503.01121. [Google Scholar]
- Campuzano, G.; Lalla-Ruiz, E.; Mes, M. The two-tier multi-depot vehicle routing problem with robot stations and time windows. Eng. Appl. Artif. Intell. 2025, 147, 110258. [Google Scholar] [CrossRef]
- Tadaros, M.; Migdalas, A.; Quttineh, N.H.; Larsson, T. Evaluating metaheuristic solution quality for a hierarchical vehicle routing problem by strong lower bounding. Oper. Res. Perspect. 2025, 14, 100332. [Google Scholar] [CrossRef]
- Muriyatmoko, D.; Djunaidy, A.; Muklason, A. Heuristics and metaheuristics for solving capacitated vehicle routing problem: An algorithm comparison. Procedia Comput. Sci. 2024, 234, 494–501. [Google Scholar] [CrossRef]
- Prakash, R.; Pushkar, S. Green vehicle routing problem: Metaheuristic solution with time window. Expert Syst. 2024, 41, e13007. [Google Scholar] [CrossRef]
- Jasim, A.N.; Fourati, L.C. Guided genetic algorithm for solving capacitated vehicle routing problem with unmanned-aerial-vehicles. IEEE Access 2024, 12, 106333–106358. [Google Scholar] [CrossRef]
- Rahmanifar, G.; Mohammadi, M.; Sherafat, A.; Hajiaghaei-Keshteli, M.; Fusco, G.; Colombaroni, C. Heuristic approaches to address vehicle routing problem in the Iot-based waste management system. Expert Syst. Appl. 2023, 220, 119708. [Google Scholar] [CrossRef]
- Sarbijan, M.S.; Behnamian, J. A mathematical model and metaheuristic approach to solve the real-time feeder vehicle routing problem. Comput. Ind. Eng. 2023, 185, 109684. [Google Scholar] [CrossRef]
- Kumari, M.; De, P.K.; Chaudhuri, K.; Narang, P. Utilizing a hybrid metaheuristic algorithm to solve capacitated vehicle routing problem. Results Control Optim. 2023, 13, 100292. [Google Scholar] [CrossRef]
- Fu, R.; Bi, Y.; Han, G.; Zhang, X.; Liu, L.; Zhao, L.; Hu, B. MAGVA: An open-set fault diagnosis model based on multi-hop attentive graph variational autoencoder for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14873–14889. [Google Scholar] [CrossRef]
- Xie, L.; Guo, T.; Chang, J.; Wan, C.; Hu, X.; Yang, Y.; Ou, C. A novel model for ship trajectory anomaly detection based on Gaussian mixture variational autoencoder. IEEE Trans. Veh. Technol. 2023, 72, 13826–13835. [Google Scholar] [CrossRef]
- Fellek, G.; Farid, A.; Gebreyesus, G.; Fujimura, S.; Yoshie, O. Graph transformer with reinforcement learning for vehicle routing problem. IEEE Trans. Electr. Electron. Eng. 2023, 18, 701–713. [Google Scholar] [CrossRef]
- Aslan Yıldız, Ö.; Sarıçiçek, İ.; Yazıcı, A. A Reinforcement Learning-Based Solution for the Capacitated Electric Vehicle Routing Problem from the Last-Mile Delivery Perspective. Appl. Sci. 2025, 15, 1068. [Google Scholar] [CrossRef]
- Bogyrbayeva, A.; Dauletbayev, B.; Meraliyev, M. Reinforcement Learning for Efficient Drone-Assisted Vehicle Routing. Appl. Sci. 2025, 15, 2007. [Google Scholar] [CrossRef]
- Yang, B.; Ren, T.; Yu, H.; Chen, J.; Wang, Y. An evolutionary algorithm driving by dimensionality reduction operator and knowledge model for the electric vehicle routing problem with flexible charging strategy. Swarm Evol. Comput. 2025, 92, 101814. [Google Scholar] [CrossRef]
- Luo, J.; Li, C. An efficient encoder-decoder network for the capacitated vehicle routing problem. Expert Syst. Appl. 2025, 278, 127311. [Google Scholar] [CrossRef]
- Hua, C.; Berto, F.; Son, J.; Kang, S.; Kwon, C.; Park, J. CAMP: Collaborative Attention Model with Profiles for Vehicle Routing Problems. arXiv 2025, arXiv:2501.02977. [Google Scholar]
- Pan, Y.; Liu, R.; Chen, Y.; Cao, Z.; Lin, F. Hierarchical Learning-based Graph Partition for Large-scale Vehicle Routing Problems. arXiv 2025, arXiv:2502.08340. [Google Scholar]
- Wang, C.; Cao, Z.; Wu, Y.; Teng, L.; Wu, G. Deep reinforcement learning for solving vehicle routing problems with backhauls. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 4779–4793. [Google Scholar] [CrossRef]
- Zong, Z.; Tong, X.; Zheng, M.; Li, Y. Reinforcement learning for solving multiple vehicle routing problem with time window. ACM Trans. Intell. Syst. Technol. 2024, 15, 1–19. [Google Scholar] [CrossRef]
- Pan, W.; Liu, S.Q. Deep reinforcement learning for the dynamic and uncertain vehicle routing problem. Appl. Intell. 2023, 53, 405–422. [Google Scholar] [CrossRef]
- Jiang, Y.; Cao, Z.; Wu, Y.; Song, W.; Zhang, J. Ensemble-based deep reinforcement learning for vehicle routing problems under distribution shift. Adv. Neural Inf. Process. Syst. 2023, 36, 53112–53125. [Google Scholar]
- Danach, K. Reinforcement Learning for Dynamic Vehicle Routing Problem: A Case Study with Real-World Scenarios. Int. J. Commun. Netw. Inf. Secur. 2024, 16, 580–589. [Google Scholar]
- Denzinger, J.; Scholz, S. Using Teamwork for the Distribution of Approximately Solving the Traveling Salesman Problem with Genetic Algorithms; Technische Universität Kaiserslautern, Fachbereich Informatik: Kaiserslautern, Germany, 1997. [Google Scholar]
- Cowling, P.; Kendall, G.; Soubeiga, E. A hyperheuristic approach to scheduling a sales summit. In Proceedings of the International Conference on the Practice and Theory of Automated Timetabling; Springer: Berlin/Heidelberg, Germany, 2000; pp. 176–190. [Google Scholar]
- Kallestad, J.; Hasibi, R.; Hemmati, A.; Sörensen, K. A general deep reinforcement learning hyperheuristic framework for solving combinatorial optimization problems. Eur. J. Oper. Res. 2023, 309, 446–468. [Google Scholar] [CrossRef]

| Methods [Ref.] | Year | Approach | |
|---|---|---|---|
| Hyperheuristics | Machine Learning | ||
| DRL [48] | 2023 | X | |
| Ensemble-based DRL [49] | 2023 | X | |
| Two-Echelon WMS, IoT [34] | 2023 | X | |
| RTFVRP, DIWPSO [35] | 2023 | X | |
| GA-RR [36] | 2023 | X | |
| Variational Autoencoder [37] | 2023 | X | |
| Variational Autoencoder [38] | 2023 | X | |
| EEMHA [39] | 2023 | X | |
| Swarm Intelligence, Adaptive Learning [25] | 2024 | X | |
| Path Cheapest Arc, Path Most Constrained Arc, Savings, Christofides, Greedy Descent, Guided Local Search, Simulated Annealing, Tabu Search [31] | 2024 | X | |
| GVRP-TW [32] | 2024 | X | |
| UAV, GGA [33] | 2024 | X | |
| DRL [46] | 2024 | X | |
| VRPTW [47] | 2024 | X | |
| FMOLP, IGA [27] | 2025 | X | |
| ALNS, TA, TS [28] | 2025 | X | |
| 2T-MDVRP-RS-TW, MILP, MS-ILS-CR [29] | 2025 | X | |
| Two Column Generation-based Formulations [30] | 2025 | X | |
| Q-learning [40] | 2025 | X | |
| Markov Decision Process, Reinforcement Learning [41] | 2025 | X | |
| EVRP-FCS [42] | 2025 | X | |
| RGCMA [43] | 2025 | X | |
| CAMP [44] | 2025 | X | |
| HLGP [45] | 2025 | X | |
| Instance | Customers | Priority Levels | Vehicle Capacity |
|---|---|---|---|
| Instance 1–10 | 50–140 | 1 to 5 | 1000 |
| Instance 11–20 | 150–240 | 1 to 5 | 1000 |
| Instance 21–30 | 250–340 | 1 to 5 | 1000 |
| Instance 31–40 | 350–440 | 1 to 5 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danach, K.; Saker, L.; Harb, H. Integrating Metaheuristics and Machine Learning for Enhanced Vehicle Routing: A Comparative Study of Hyperheuristic and VAE-Based Approaches. World Electr. Veh. J. 2025, 16, 258. https://doi.org/10.3390/wevj16050258
Danach K, Saker L, Harb H. Integrating Metaheuristics and Machine Learning for Enhanced Vehicle Routing: A Comparative Study of Hyperheuristic and VAE-Based Approaches. World Electric Vehicle Journal. 2025; 16(5):258. https://doi.org/10.3390/wevj16050258
Chicago/Turabian StyleDanach, Kassem, Louai Saker, and Hassan Harb. 2025. "Integrating Metaheuristics and Machine Learning for Enhanced Vehicle Routing: A Comparative Study of Hyperheuristic and VAE-Based Approaches" World Electric Vehicle Journal 16, no. 5: 258. https://doi.org/10.3390/wevj16050258
APA StyleDanach, K., Saker, L., & Harb, H. (2025). Integrating Metaheuristics and Machine Learning for Enhanced Vehicle Routing: A Comparative Study of Hyperheuristic and VAE-Based Approaches. World Electric Vehicle Journal, 16(5), 258. https://doi.org/10.3390/wevj16050258







