Integrating Metaheuristics and Machine Learning for Enhanced Vehicle Routing: A Comparative Study of Hyperheuristic and VAE-Based Approaches

Abstract

This study addresses the optimization of the Vehicle Routing Problem (VRP) with prioritized customers by introducing and comparing two advanced solution approaches: a metaheuristic-based hyperheuristic framework and a Variational Autoencoder (VAE)-based hyperheuristic. The VRP with prioritized customers introduces additional complexity by requiring efficient routing while ensuring high-priority customers receive service within strict constraints. To tackle this challenge, the proposed metaheuristic-based hyperheuristic dynamically selects and adapts low-level heuristics using Simulated Annealing (SA) and Ant Colony Optimization (ACO), enhancing search efficiency and solution quality. In contrast, the VAE-based approach leverages deep learning to model historical routing patterns and autonomously generate new heuristics tailored to problem-specific characteristics. Through extensive computational experiments on benchmark VRP instances, our results reveal that both approaches significantly enhance routing efficiency, with the VAE-based method demonstrating superior generalization across varying problem structures. Specifically, the VAE-based approach reduces total travel costs by an average of $8\%$ and improves customer priority satisfaction by $95\%$ compared to traditional hyperheuristic methods. Moreover, a comparative analysis with recent state-of-the-art algorithms highlights the competitive performance of our approaches in balancing computational efficiency and solution quality. These findings underscore the potential of integrating metaheuristics with machine learning in complex routing problems and provide valuable insights for real-world logistics and transportation planning. Future research will explore the generalization of these methodologies to dynamic and large-scale routing scenarios.

1. Introduction

The Vehicle Routing Problem (VRP) is a fundamental and widely studied problem in the field of logistics and operations research, originating from the need to optimize the delivery of goods and services to a set of geographically dispersed customers. The primary objective of the VRP is to determine the most efficient routes for a fleet of vehicles to service a given set of customers from a central depot while minimizing total costs, which typically include travel distance, time, or fuel consumption [1]. This problem has significant practical implications for industries such as transportation, distribution, and supply chain management, where efficient routing can lead to substantial cost savings and improved service levels [2,3]. Furthermore, VRP is considered an extension of the well-known Traveling Salesman Problem (TSP), where the goal is to find the shortest possible route that visits each customer exactly once and returns to the starting point [4].

1.1. Motivation

Unfortunately, the VRP introduces additional complexities by incorporating multiple vehicles and constraints such as vehicle capacities, delivery time windows, and the necessity to serve customers with varying levels of priority [5,6]. These constraints make the VRP a more realistic and challenging problem, reflecting the operational considerations faced by logistics providers in real-world scenarios.

Indeed, various formulations and variants of the VRP exist, each addressing specific logistical challenges. Some common variants include the Capacitated VRP (CVRP), where vehicles have a maximum load capacity that must not be exceeded, and the VRP with Time Windows (VRPTW), which adds constraints on the time periods during which customers can be served [7]. Another significant variant is the VRP with prioritized customers, where certain customers have higher service priorities, requiring routes to be planned in a way that prioritizes these customers’ needs over others [8].

Solving the VRP is computationally challenging due to its NP-hard nature, meaning that the time required to find an optimal solution increases exponentially with the size of the problem [9]. As a result, exact methods such as branch and bound or dynamic programming are often impractical for large instances, and heuristic and metaheuristic approaches are commonly employed to obtain near-optimal solutions within a reasonable computational time [10].

Heuristic methods, such as the Clarke–Wright savings algorithm and sweep algorithm, provide practical solutions by iteratively improving the initial routes through local search techniques [11]. Metaheuristic approaches, including genetic algorithms, Simulated Annealing, and Ant Colony Optimization, offer more advanced strategies by combining multiple heuristics and exploring the solution space more comprehensively [12]. These methods have been extensively used and refined in both academic research and industry applications to tackle the complexities of the VRP effectively [13].

The Vehicle Routing Problem (VRP) with prioritized customers is a critical optimization challenge in logistics and transportation, where the objective is to determine the most efficient routes for a fleet of vehicles to service a set of customers. This problem becomes even more complex when customer priorities are involved, requiring a nuanced approach to balancing delivery constraints with customer preferences [14]. The VRP with prioritized customers necessitates the optimization of routes that not only minimize costs but also meet specific delivery requirements for high-priority customers, thus adding layers of complexity to the traditional VRP framework [15].

Traditional metaheuristics, such as Simulated Annealing (SA) and Ant Colony Optimization (ACO), have been widely used for VRP due to their effectiveness in exploring large solution spaces and their flexibility in accommodating various constraints and objectives [16]. SA, inspired by the annealing process in metallurgy, allows for the probabilistic acceptance of worse solutions to escape the local optima and explore more diverse solutions [17]. ACO, modeled after the foraging behavior of ants, utilizes pheromone trails to guide the search process, iteratively improving the solution quality through collective learning [18].

Hyperheuristics represent a higher level of optimization, where the focus is on selecting and generating heuristics to solve complex problems dynamically [19]. In this context, metaheuristics like SA and ACO can be employed as heuristic selectors within a hyperheuristic framework, enhancing the ability to adapt to various problem instances and customer requirements [20]. This approach leverages the strengths of metaheuristics in navigating solution spaces while maintaining the flexibility to adjust heuristic selection based on the problem context [21,22].

1.2. Contributions

Recent studies focused on applying hyperheuristics or machine learning-based algorithms to solve the Vehicle Routing Problem. In this paper, our main goal is to compare the traditional metaheuristic-driven hyperheuristic framework with Variational Autoencoders (VAEs)-based machine learning in solving the VRP with prioritized customers. By evaluating the performance of these approaches on benchmark VRP instances, we aim to provide insights into their relative strengths and weaknesses, highlighting the potential for integrating metaheuristics with machine learning to enhance logistics optimization.

1.3. Paper Structure

The rest of the paper is structured as follows. Section 2 discusses the state of the art on hyperheuristics and machine learning in VRP. Section 3 describes the problem statement along with the challenges and methodological approaches. The mathematical formulation of VRP with prioritized customers is shown in Section 4. Section 5 explains both types of hyperheuristics used in VRP, e.g., traditional and VAE based. Section 6 presents the performed experimentation and the result discussion. Finally, we provide a conclusion and suggest future works at Section 7.

2. Related Works

Indeed, VRP is a fundamental challenge in logistics and transportation, with significant implications for cost reduction, efficiency improvement, and sustainability. Recently, researchers have focused their attention to VRP due to its complexity and real-world impact, leading to the development of various metaheuristic and machine learning approaches [23,24]. In the literature, VRP has been extensively studied, resulting in numerous extensions such as capacitated VRP, time-window constraints, and multi-depot variants to address industry-specific challenges. Furthermore, the advancements in artificial intelligence, machine learning, and optimization techniques have further enhanced VRP solutions, enabling more adaptive and scalable approaches.

2.1. Hyperheuristics-Based Approaches

Recent studies have explored the use of swarm intelligence for hyperheuristics in VRP. For example, [25] demonstrates the effectiveness of using swarm intelligence to guide heuristic selection for VRP, highlighting its potential for adaptive optimization in complex scenarios [26]. The study utilizes swarm intelligence to develop a hyperheuristic framework that dynamically adjusts the selection of low-level heuristics, effectively improving solution quality and computational efficiency. This approach underscores the value of combining heuristic selection strategies with adaptive learning mechanisms to tackle VRP challenges. The authors of [27] investigate a VRP that incorporates multiple objectives, ensuring vehicles reach destinations within a defined time window while considering crashed traveling time. The problem is addressed using a fuzzy multi-objective linear programming (FMOLP) approach, which reformulates it into a single-objective model. To tackle large-scale instances, an enhanced genetic algorithm (IGA) is introduced for efficient optimization. In [28], the authors address the Vehicle Routing Problem for Security Dispatch (VRPSD) by developing three optimization algorithms that integrate metaheuristic techniques. The methods utilize Adaptive Large Neighborhood Search (ALNS) alongside Threshold Accepting (TA) and Tabu Search (TS) to enhance search efficiency. By leveraging a multiphase strategy, these approaches improve exploration and avoid local optima effectively. The authors of [29] present the 2T-MDVRP-RS-TW, a Two-Tier Multi-Depot Vehicle Routing Problem with Robot Stations and Time Windows. It is a complex Vehicle Routing Problem incorporating multi-depot logistics, robot stations, and time windows. To solve it, a Mixed-Integer Linear Programming (MILP) model is formulated alongside a Multi-Start Iterated Local Search (MS-ILS-CR) approach. The MS-ILS-CR method enhances optimization by combining Multi-Start, Crossover, and Repair strategies drawn from advanced metaheuristics. In [30], the authors explore a delivery routing problem that integrates heavy depot vehicles, local vehicles, swap bodies, and switch points. A previously applied metaheuristic provides fast solutions but without quality assurance. To evaluate the solution quality, the authors develop two column generation-based formulations, optimizing complexity through switch point enumeration. The authors of [31] aim at heuristic and metaheuristic algorithms to optimize faculty transportation between two university campuses. Their study focuses on selecting efficient routing strategies and vehicle types, while the primary goal is to minimize travel distance through optimized route planning. In [32], a Time Window-based Green Vehicle Routing Problem (GVRP-TW) solution is introduced to optimize alternative fuel vehicle routes with time constraints. The approach ensures minimal refueling stops while serving customer demands efficiently. The objective is to decrease the travel distance, lower energy usage, and reduce CO₂ emissions. The authors of [33] investigate optimizing UAV operations for search and pesticide spraying while managing battery and tank capacity constraints. To achieve this, a hybrid metaheuristic approach integrates genetic algorithm (GA) with a Guided Genetic Algorithm (GGA). The proposed method seeks to reduce energy and resource consumption for efficient mission execution. In [34], a smart two-echelon waste management system (WMS) leveraging Industry 4.0 and IoT devices is proposed to enhance waste collection efficiency. The system helps optimize bin collection and waste transfer routes. The model aims to cut costs and CO₂ emissions using an advanced vehicle routing framework. In [35], the authors introduce a real-time feeder Vehicle Routing Problem (RTFVRP) where both trucks and motorcycles can participate in the freight delivery process. The problem is formulated using Mixed-Integer Linear Programming, and a dynamic inertia weight particle swarm optimization (DIWPSO) algorithm is proposed to provide an efficient solution. Finally, the authors of [36] propose a new hybrid approach, called GA-RR, designed to address the capacitated Vehicle Routing Problem. The method combines two well-established techniques: the ruin and recreate algorithm and the genetic algorithm. By leveraging the strengths of both, GA-RR balances exploration and exploitation to enhance solution quality. The goal is to generate optimal solutions across various Vehicle Routing Problem test instances.

2.2. Machine Learning-Based Approaches

Recently, there has been growing interest in applying machine learning techniques into VRP [37,38]. The authors of [39] present an attention-based end-to-end deep reinforcement learning model for solving VRP, incorporating edge information between nodes for enhanced graph representation learning. The approach utilizes a Transformer-based encoder–decoder framework, integrating an edge information embedded multi-head attention (EEMHA) layer in the encoder. The EEMHA-based encoder captures the graph underlying structure by combining node and edge data, producing a rich topology representation. In [40], the authors explore the Capacitated Electric Vehicle Routing Problem (CEVRP) using an innovative Q-learning approach. Q-learning, a model-free reinforcement learning algorithm, optimizes decision-making by maximizing an agent cumulative reward. Furthermore, a mathematical model is employed to determine optimal solutions for each EVRP instance. The authors of [41] model VRP using a Markov decision process and propose a reinforcement learning (RL)-based solution. The RL model employs an attention-based encoder and a recurrent neural network decoder. This approach optimizes coordination by assigning vehicles to customers and determining rendezvous points, effectively integrating drones to minimize overall completion time. In [42], the authors address the limitation of assuming a fixed charging rate in traditional Electric Vehicle Routing Problems (EVRPs). Accordingly, a new EVRP model incorporating a flexible charging strategy (EVRP-FCS) is introduced, treating charged energy as a decision variable. Additionally, an improved evolutionary algorithm is developed to efficiently solve the model and explore the solution space more effectively. The authors of [43] present an efficient encoder–decoder framework, called the Residual Graph Convolutional Encoder with Multiple Attention-Based Decoders (RGCMA), trained using a reinforcement learning approach with an elite baseline. The encoder generates robust node representations by effectively aggregating neighborhood features through a dense residual edge and node feature updating block. Meanwhile, the multiple-decoder mechanism incrementally constructs diverse solutions for any CVRP instance, expanding the solution space and enhancing the overall solution quality. The authors of [44] introduce the Collaborative Attention Model with Profiles (CAMP), a novel approach utilizing multi-agent reinforcement learning to develop efficient solvers for the Profiled VRP (PVRP). CAMP features an attention-based encoder that embeds client profiles in parallel for each vehicle type. Furthermore, a communication layer enables collaborative decision-making among agents, while a batched pointer mechanism evaluates the likelihood of next actions by attending to the profiled embeddings during decoding. In [45], the authors present a flexible Hierarchical Learning-based Graph Partition (HLGP) framework designed to enhance the partitioning of CVRP instances by effectively combining global and local partition strategies. The global partition policy generates a coarse multi-way partition, breaking it down into sequential two-way partition subtasks. These subtasks serve as the foundation for the subsequent K local partition levels. At each level, the local partition policy handles specific subtasks, leveraging local topological features to incrementally reduce accumulated errors. In [46], a neural heuristic approach using deep reinforcement learning (DRL) to solve both traditional and enhanced variants of the VRB with Backhauls (VRPB) is proposed. The method employs an encoder–decoder structured policy network trained to sequentially generate vehicle routes. The VRPB is first modeled as a graph, with solution construction formulated as a Markov decision process. To better capture node relationships, a two-stage attention-based encoder is designed, incorporating self-attention and heterogeneous attention mechanisms to enhance node representations and improve solution quality. The authors of [47] introduce an end-to-end reinforcement learning framework for solving the VRP with Time Windows (VRPTW). The approach starts with an agent model that encodes constraints into input features and applies strict policies to ensure deterministic outputs. To handle time-window constraints effectively, a time penalty-augmented reward mechanism is incorporated during gradient propagation. The authors of [48] propose a deep reinforcement learning framework to address the dynamic and uncertain VRP (DU-VRP). A partial observation Markov decision process is designed to continuously monitor real-time fluctuations in customer demand within a decision support system powered by a deep neural network with a dynamic attention mechanism. Moreover, an advanced reinforcement learning algorithm is proposed to optimize the value function, enhancing the training process to better manage the complexities of routing dynamics and uncertainty. In [49], the study presents an ensemble-based deep reinforcement learning approach for solving VRP, where multiple diverse sub-policies are trained to handle various instance distributions. Diversity among sub-policies is encouraged using Bootstrap with random initialization. In addition, regularization terms are incorporated during training to further promote variation between sub-policies, enhancing overall solution adaptability.

2.3. State-of-the-Art Techniques: A Summary

Table 1. State-of-the-art methods summary.

Methods [Ref.]	Year	Approach
		Hyperheuristics	Machine Learning
DRL [48]	2023		X
Ensemble-based DRL [49]	2023		X
Two-Echelon WMS, IoT [34]	2023	X
RTFVRP, DIWPSO [35]	2023	X
GA-RR [36]	2023	X
Variational Autoencoder [37]	2023		X
Variational Autoencoder [38]	2023		X
EEMHA [39]	2023		X
Swarm Intelligence, Adaptive Learning [25]	2024	X
Path Cheapest Arc, Path Most Constrained Arc, Savings, Christofides, Greedy Descent, Guided Local Search, Simulated Annealing, Tabu Search [31]	2024	X
GVRP-TW [32]	2024	X
UAV, GGA [33]	2024	X
DRL [46]	2024		X
VRPTW [47]	2024		X
FMOLP, IGA [27]	2025	X
ALNS, TA, TS [28]	2025	X
2T-MDVRP-RS-TW, MILP, MS-ILS-CR [29]	2025	X
Two Column Generation-based Formulations [30]	2025	X
Q-learning [40]	2025		X
Markov Decision Process, Reinforcement Learning [41]	2025		X
EVRP-FCS [42]	2025		X
RGCMA [43]	2025		X
CAMP [44]	2025		X
HLGP [45]	2025		X

summarizes the state-of-the-art techniques in VRP in terms of publication year, used methods, and category, e.g., hyperheuristic based or machine learning based.

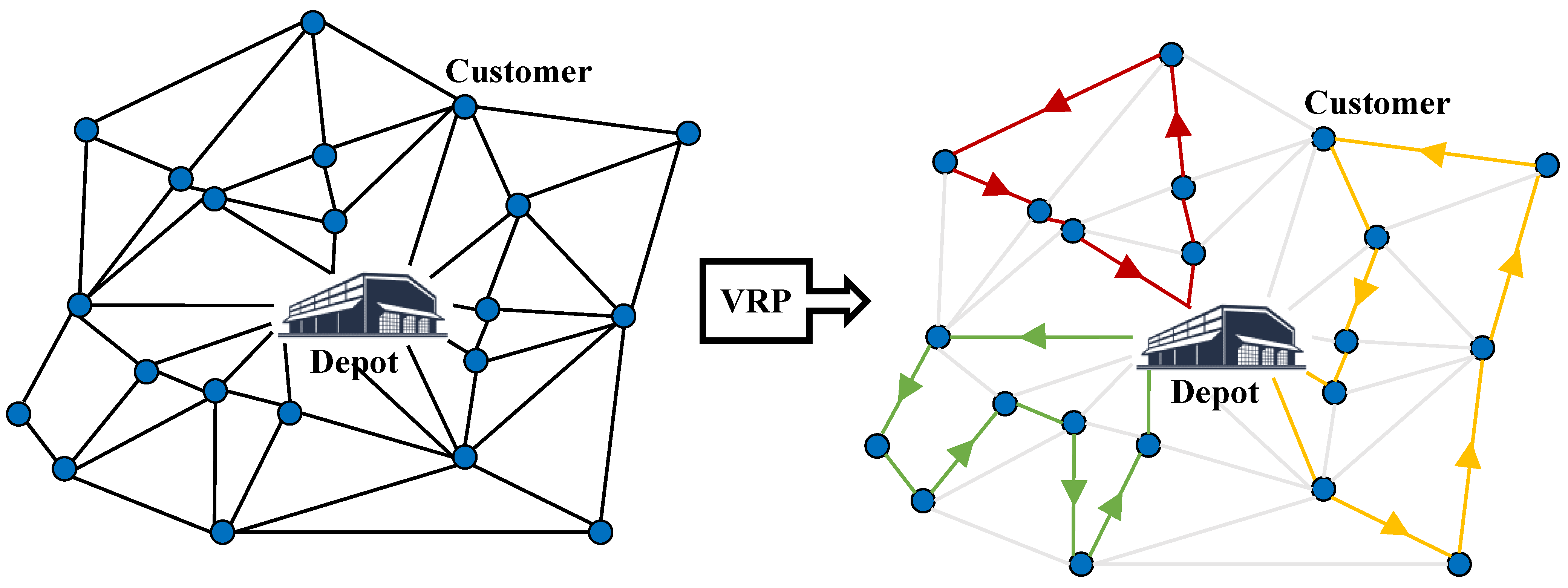
3. Problem Statement

Figure 1 shows the scenario considered in this study and illustrates an instance of the Vehicle Routing Problem (VRP) along with its optimized solution. On the left side, we see a network of points representing customers that require service, with a central point labeled “Depot”, which serves as the starting and ending location for the delivery vehicles. The lines connecting the customers and the depot illustrate the various possible routes that vehicles could take to deliver goods or services. This network is unorganized, depicting all potential routes without any optimization. The primary goal in this scenario is to determine the most efficient routes that minimize the total travel distance or cost while satisfying constraints such as vehicle capacity and specific customer service requirements. On the right side of the figure, we observe the optimized solution to the VRP. The original network is reorganized into distinct routes, each marked with different colors, illustrating how vehicles will traverse from the depot to the customers and back. This optimized layout shows the best possible paths, taking into account factors such as minimizing travel distance and ensuring efficient service to all customers. This visual representation highlights the transformation from a complex, unstructured problem instance to a structured and efficient routing plan, demonstrating the core objective of solving the VRP.

3.1. Problem Reformulation

Supply chain efficiency is a critical factor in maintaining competitiveness, reducing operational costs, and ensuring the timely delivery of goods and services [2,5]. In this context, the Vehicle Routing Problem with Prioritized Customers (VRP-PC) emerges as a complex combinatorial optimization challenge in logistics and transportation, where the objective is to determine the most efficient routes for a fleet of vehicles originating from a central depot to serve a set of customers [50]. Unlike the standard VRP, VRP-PC introduces customer prioritization constraints, where certain customers require earlier service or stricter adherence to delivery windows. This prioritization significantly increases the complexity of the problem, as it necessitates balancing cost minimization with customer satisfaction while ensuring efficient service sequencing.

Formally, the problem is defined as follows. Given a set of N customers, each located at specific geographic coordinates and assigned a priority level $p_i$, a central depot, and a fleet of M vehicles with a maximum capacity Q, the objective is to determine a set of routes $R=\{R_1,R_2,\dots ,R_M\}$ such that the following hold:

• Each route $R_i$ starts and ends at the depot.
• Each customer is visited exactly once by a single vehicle.
• The total demand served by each vehicle does not exceed its capacity Q.
• The total cost C of the routes is minimized, where C is typically a function of the total distance traveled or the total time taken.
• Customers with higher priorities are served earlier or within stricter time windows, ensuring preferential treatment without significantly increasing total operational costs.

3.2. Challenges and Computational Complexity

The VRP-PC presents additional challenges compared to standard VRP formulations due to the need for dynamic route adjustments based on customer priority constraints. Traditional heuristic and metaheuristic approaches struggle to maintain solution quality when handling strict prioritization requirements, such as the following:

• Prioritized customers must be served earlier in a manner that does not violate vehicle capacity constraints.
• Prioritization can disrupt the efficient clustering of customers, leading to increased travel distances.
• The interplay between cost minimization and prioritization adds a multi-objective aspect to the problem.

As an NP-hard problem, the computational complexity of VRP-PC grows exponentially with the problem size, making exact optimization methods infeasible for large-scale instances. Instead, heuristic and metaheuristic approaches are widely used to provide near-optimal solutions within practical computational timeframes.

3.3. Research Focus and Methodological Approach

To address these challenges, this research evaluates and compares two novel approaches for solving VRP-PC:

• A Metaheuristic-Based Hyperheuristic Framework that dynamically selects and adapts low-level heuristics using Simulated Annealing (SA) and Ant Colony Optimization (ACO), improving search efficiency and balancing solution quality.
• A Variational Autoencoder (VAE)-Based Hyperheuristic, leveraging deep learning techniques to generate and refine heuristics based on learned representations of historical routing data, enhancing adaptability and solution generalization.

Through extensive computational experiments on benchmark VRP instances, this study aims to achieve the following:

• Assess the effectiveness of both approaches in handling customer prioritization constraints.
• Compare their ability to optimize solution quality, computational efficiency, and scalability.
• Provide insights into the potential for integrating metaheuristic strategies with deep learning-based heuristic generation.

By systematically analyzing these approaches, this research contributes to the broader field of intelligent routing optimization, demonstrating the advantages and trade-offs of hybrid metaheuristic and machine learning-based methodologies.

4. Mathematical Formulation

The Vehicle Routing Problem with Prioritized Customers (VRP-PC) is formulated as an optimization problem that balances travel cost minimization with service prioritization. This section defines the mathematical model, including the objective function, constraints, and variables.

4.1. Sets and Indices

• $V=\{0,1,2,\dots ,n\}$: Set of all vertices, where 0 represents the depot and $\{1,2,\dots ,n\}$ represent customers.
• E: Set of all edges representing possible routes between vertices.
• $K=\{1,2,\dots ,m\}$: Set of available vehicles.

4.2. Parameters

• $c_{ij}$: Cost of traveling from vertex i to vertex j.
• $d_i$: Demand of customer i.
• Q: Maximum capacity of each vehicle.
• $p_i$: Priority level of customer i (higher values indicate higher priority).
• $T_i^{min}$ and $T_i^{max}$: Earliest and latest time windows for customer i.
• $s_i$: Service time at customer i.
• $t_{ij}$: Travel time from node i to node j.
• M: A large constant used for constraint enforcement.

4.3. Decision Variables

• $x_{ij}^k\in \{0,1\}$: Binary variable; 1 if vehicle k travels from vertex i to vertex j, 0 otherwise.
• $y_i\in \{0,1\}$: Binary variable; 1 if customer i is served, 0 otherwise.
• $t_i$: Time when service starts at customer i.
• $q_i^k$: Load of vehicle k when leaving customer i.

4.4. Objective Function

The objective function balances two competing goals: minimizing travel costs while prioritizing high-priority customers.

$$\mathrm{Minimize}Z=\sum _{k\in K}\sum _{i\in V}\sum _{j\in V}{c}_{ij}{x}_{ij}^k-\lambda \sum _{i\in V\backslash \left\{0\right\}}{p}_i{y}_i$$

where we have the following:

• The first term represents the total travel cost.
• The second term incentivizes the servicing of high-priority customers.
• $\lambda$ is a weighting parameter to balance cost minimization and priority fulfillment.

The weighting parameter $\lambda$ controls the trade-off between travel cost minimization and priority satisfaction. Based on preliminary tuning across validation instances, a value of $\lambda =0.7$ was selected, which maximized overall performance.

To assess sensitivity, we tested values of $\lambda \in \{0.3,0.5,0.7,0.9\}$. Results showed that values below 0.5 overly prioritized cost, reducing priority satisfaction below 80%, while values above 0.9 skewed optimization away from cost efficiency. The selected value $\lambda =0.7$ balanced the two objectives effectively across all scenarios.

4.5. Constraints

In this study, we define different types of constraints.

4.5.1. Routing Constraints

• Each customer must be visited exactly once by a single vehicle:

  $$\sum _{k\in K}\sum _{j\in V}{x}_{ij}^k=y_i,\forall i\in V\backslash \left\{0\right\}$$
• Each vehicle must start and end at the depot:

  $$\sum _{j\in V}{x}_{0j}^k=1,\forall k\in K$$

  $$\sum _{i\in V}{x}_{i0}^k=1,\forall k\in K$$

4.5.2. Flow Conservation Constraints

• Vehicles must enter and leave each customer exactly once:

  $$\sum _{j\in V}{x}_{ij}^k=\sum _{j\in V}{x}_{ji}^k,\forall k\in K,\forall i\in V\backslash \left\{0\right\}$$

4.5.3. Capacity Constraints

• The total demand assigned to each vehicle must not exceed its capacity:

  $$\sum _{i\in V}{d}_i{y}_i\le Q,\forall k\in K$$
• The load of a vehicle is updated after serving a customer:

  $$q_j^k=q_i^k+d_j{x}_{ij}^k,\forall k\in K,\forall i,j\in V\backslash \left\{0\right\}$$
• Vehicle load must remain within valid limits:

  $$0\le q_i^k\le Q,\forall k\in K,\forall i\in V\backslash \left\{0\right\}$$

4.5.4. Time Window Constraints

• Vehicles must arrive within the allowed time window:

  $$T_i^{min}\le t_i\le T_i^{max},\forall i\in V\backslash \left\{0\right\}$$
• Ensuring sequential servicing while accounting for travel and service time:

  $$t_j\ge t_i+s_i+t_{ij}-M(1-x_{ij}^k),\forall k\in K,\forall i,j\in V\backslash \left\{0\right\}$$

4.5.5. Prioritization Constraints

• To ensure service order based on customer priority, a hard constraint is imposed such that higher-priority customers are served earlier than lower-priority ones. This is mathematically formulated as

  $$t_i\le t_j,\mathrm{if}{p}_i>p_j,\forall i,j\in V\backslash \left\{0\right\}$$

  where $t_i$ and $t_j$ represent the service start times at customers i and j, respectively, and $p_i$ and $p_j$ denote their priority levels.

To reflect real-world urgency in service delivery, customer priority levels $p_i$ are modeled as integer values from 1 (highest priority) to 5 (lowest). These levels affect both the objective function and service ordering constraints. Empirical studies from Al Amir logistics support this granularity in modeling customer expectations and SLA compliance.

4.6. Discussion of Model Complexity

The inclusion of priority-based constraints introduces additional complexity into the traditional VRP formulation. Unlike standard VRP, where routes are optimized purely based on distance or cost, the VRP-PC requires the following:

• Balancing cost efficiency with priority satisfaction, leading to a multi-objective trade-off.
• Dynamic route adjustments, as priority constraints may override standard distance-based optimization.
• Increased computational complexity since the problem now involves additional ordering constraints for prioritization.

Given its NP-hard nature, solving large-scale instances of VRP-PC exactly is impractical. Thus, heuristic and metaheuristic approaches, such as the metaheuristic-driven hyperheuristic and VAE-based hyperheuristic proposed in this study, offer promising solutions by dynamically adapting heuristic selection and learning problem-specific patterns. This mathematical formulation integrates both cost minimization and priority constraints into a unified optimization model. The constraints ensure operational feasibility, while the objective function provides a flexible trade-off between minimizing travel costs and ensuring timely service for high-priority customers. The subsequent sections of this paper will explore how hyperheuristic and machine learning-based approaches can efficiently solve this complex optimization problem.

5. Hyperheuristic

Hyperheuristics (HH) are designed to automate heuristic selection and adaptation to solve complex optimization problems. The term was first introduced in 1997 in the context of automated theorem proving [51] and later applied to combinatorial optimization in 2000, where it was described as heuristics for selecting heuristics [52]. Unlike traditional metaheuristics, which operate within a solution space, hyperheuristics function at a higher level, navigating the heuristic space by dynamically selecting and applying low-level heuristics during the search process.

The motivation behind hyperheuristics lies in their ability to generalize across problem domains without requiring deep problem-specific knowledge [53]. This generalization capability makes them particularly useful for solving combinatorial problems, including the Vehicle Routing Problem with Prioritized Customers (VRP-PC), where heuristic adaptability is crucial. Hyperheuristics are typically classified into two main categories based on their heuristic search mechanism (Figure 2):

• Heuristic Selection: Choosing and applying predefined low-level heuristics based on specific selection criteria.
• Heuristic Generation: Constructing new heuristics through learning mechanisms, often using machine learning techniques.

Additionally, hyperheuristics can operate using either of the following:

• Online learning: Adjusting heuristic selection strategies dynamically based on real-time feedback from the optimization process.
• Offline learning: Learning heuristic selection patterns from historical data and applying them to new problem instances.

This study focuses on heuristic selection hyperheuristics, specifically comparing a metaheuristic-based hyperheuristic framework and a Variational Autoencoder (VAE)-based hyperheuristic, both tailored to the VRP-PC.

5.1. Low-Level Heuristics for VRP-PC

Low-level heuristics serve as the building blocks for hyperheuristics, providing the operations required to construct and improve solutions. In this study, we categorize low-level heuristics into the following:

• Constructive heuristics: Used to build the initial solutions.
• Improvement heuristics: Used to refine the existing solutions.
• Perturbation heuristics: Used to introduce controlled randomness and escape the local optima.

5.1.1. Constructive Heuristics

• CH1: Priority-Based Customer Insertion: This heuristic constructs routes by iteratively inserting the highest-priority customer into the position that minimizes incremental travel cost while respecting vehicle capacity and time window constraints:

  $$\mathrm{Insert}\mathrm{customer}i\mathrm{at}\mathrm{position}j\mathrm{if}\Delta c_{ij}\mathrm{is}\mathrm{minimized}\mathrm{and}\sum d_i\le Q.$$
• CH2: Clustered Nearest Neighbor: Customers are grouped into clusters based on geographic proximity and priority level. Each cluster is served by a single vehicle, prioritizing high-priority customers:

  $$\mathrm{Select}\mathrm{cluster}{C}_k\mathrm{and}\mathrm{visit}\mathrm{customer}i\in C_k\mathrm{such}\mathrm{that}{c}_{ij}\mathrm{is}\mathrm{minimized}\mathrm{for}j\in C_k.$$

5.1.2. Improvement Heuristics

• IMP1: Priority-Based Route Optimization: This heuristic reorders customers within each route to prioritize higher-priority customers while minimizing increased travel distance:

  $$\mathrm{Reorder}\{i_1,i_2,\dots ,i_n\}\mathrm{such}\mathrm{that}\sum w_i\times p_i\mathrm{is}\mathrm{minimized},\mathrm{where}{w}_i\mathrm{is}\mathrm{waiting}\mathrm{time}.$$
• IMP2: Capacity-Constrained Customer Relocation: Customers are relocated between routes to balance load while reducing travel costs:

  $$\mathrm{Relocate}\mathrm{customer}i\mathrm{from}\mathrm{route}{R}_1\mathrm{to}{R}_2\mathrm{if}\Delta C<0\mathrm{and}\sum d_i\le Q.$$

5.1.3. Perturbation Heuristics

• PRT1: Random Customer Swap: Two customers from different routes are randomly swapped, provided no constraints are violated:

  $$\mathrm{Swap}\mathrm{customers}i\mathrm{and}j\mathrm{if}\Delta C<0.$$
• PRT2: Route Reversal: A segment of a route is reversed if it reduces overall cost:

  $$\mathrm{Reverse}\mathrm{segment}\{i_1,i_2,\dots ,i_n\}\mathrm{if}C\mathrm{is}\mathrm{minimized}.$$

5.2. Heuristic Selection Methods

Hyperheuristics employ different selection mechanisms to determine which low-level heuristic to apply at each step (Figure 3). These mechanisms include the following:

• Random selection: Selects heuristics randomly without performance evaluation.
• Greedy selection: Selects the heuristic that provides the best immediate improvement.
• Peckish selection: A compromise between greedy and random selection, where heuristics are selected probabilistically based on performance.
• Choice function selection: Assigns scores to heuristics based on performance history.
• Reinforcement learning-based selection: Utilizes machine learning to adapt heuristic selection over time.

Figure 3. Algorithm selection model.

Figure 3. Algorithm selection model.

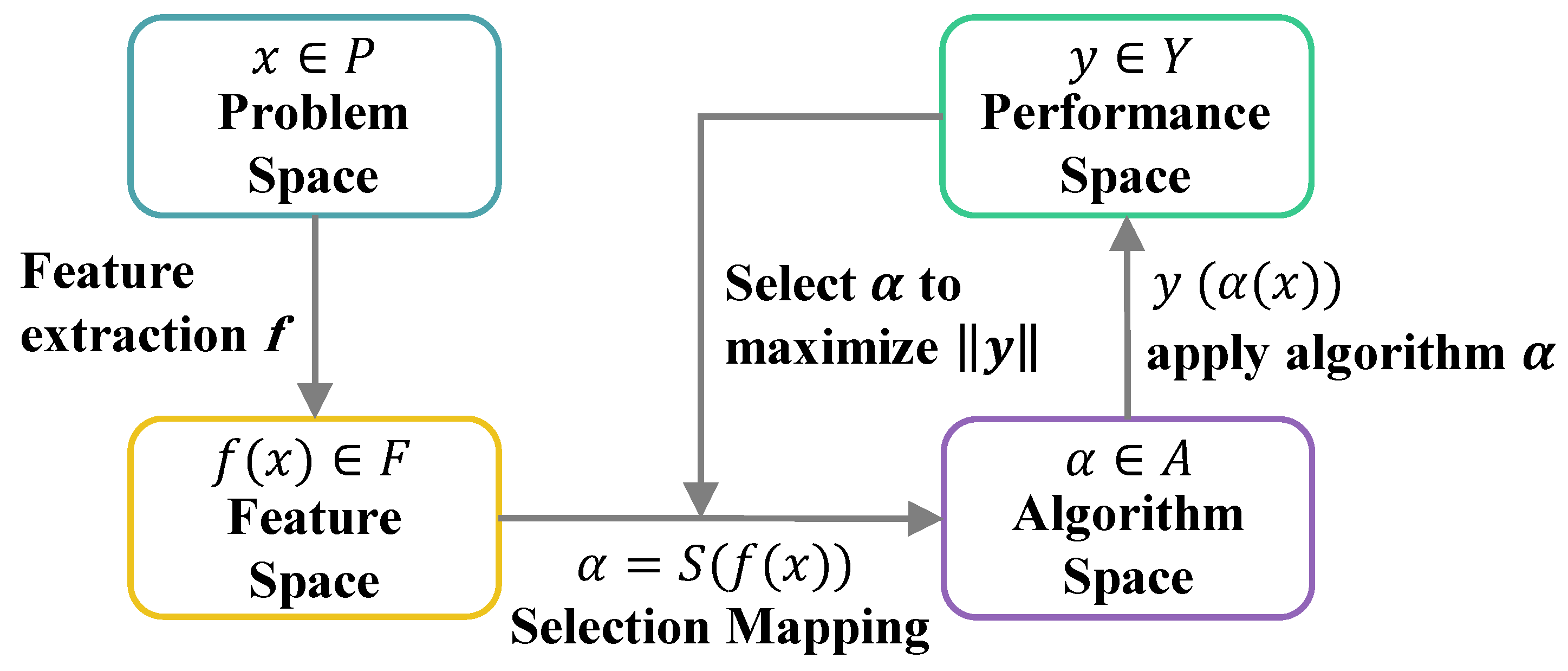
5.3. VAE-Based Hyperheuristic and Its Implementation

The Variational Autoencoder (VAE)-based hyperheuristic consists of three key components:

(i)

Input Representation: Historical heuristic sequences are encoded as binary vectors, where each bit represents the application of a specific low-level heuristic. Each sequence captures the order of heuristic applications used to solve a specific VRP-PC instance.

(ii)

VAE Architecture: The encoder is a 3-layer feedforward neural network with ReLU activation, compressing heuristic sequences into a latent vector $z\in {\mathbb{R}}^d$. The latent dimension d was experimentally set to 32. The decoder mirrors the encoder and reconstructs heuristic sequences from z, optimized to minimize binary cross-entropy and Kullback–Leibler divergence.

(iii)

Training Details: The model is trained offline using 1000 historical solutions from Al Amir VRP-PC instances. We used the Adam optimizer with a learning rate of 0.001 and batch size of 64 over 100 epochs. The training dataset was split 80/20 for training/validation. Reconstruction accuracy stabilized at 96%, and the model generalizes well to unseen instances.

This generative capability enables the VAE to autonomously construct new heuristic sequences tailored to problem-specific constraints.

The selection of VAE over alternatives such as PCA or LSTM was motivated by its ability to capture nonlinear latent features and reconstruct feasible heuristic sequences in high-dimensional spaces. Unlike PCA, which is limited to linear transformations, VAEs are capable of modeling complex distributions—a critical advantage when learning from historical VRP solution patterns. Furthermore, the generative nature of VAE aligns well with heuristic generation needs, outperforming deterministic encoders in preliminary ablation tests. Currently, the VAE is trained offline using static historical data. However, the framework can be extended to incorporate online learning, where new data continuously update the latent representation and heuristic generation process. This capability is reserved for future development.

5.4. Move Acceptance Criteria

Move acceptance strategies determine whether a new solution is accepted during the search process. We categorize these strategies as follows:

• Deterministic strategies: Always accept improved solutions (e.g., Only Improvements, Improving, and Equal).
• Non-deterministic strategies: Accept worsening solutions probabilistically (e.g., Simulated Annealing and Great Deluge).

In this study, we adopt Simulated Annealing (SA) as our move acceptance strategy:

$$exp(-\Delta f/T)>R(0,1)$$

where we have the following:

-

$\Delta f$ is the difference between the new and current objective function values.

-

T is a temperature parameter that gradually decreases.

-

$R(0,1)$ is a random number between 0 and 1.

5.5. Termination Criteria

To prevent excessive computation while ensuring sufficient search exploration, we define the termination criteria as follows:

• A global time limit: $T_{\mathrm{limit}}=max\{6000,n^2\times p\times 250\}$ milliseconds.
• Non-improving iterations limit: The algorithm stops if $10\times n\times p$ consecutive iterations fail to improve the solution.

This framework ensures an effective balance between exploration and exploitation, optimizing VRP-PC solutions dynamically.

6. Experimental Results

This section presents the experimental evaluation of various heuristic-based hyperheuristics and a Variational Autoencoder (VAE)-based hyperheuristic for solving the Vehicle Routing Problem with Prioritized Customers (VRP-PC). The goal is to compare their effectiveness in optimizing total travel cost, priority satisfaction, and computational efficiency under real-world conditions. All algorithms were implemented using Python 3.10, with essential libraries including NumPy, Pandas, SciPy, and PyTorchv2.6.0. Optimization procedures were executed using custom-developed routines and integrated with OR-Tools where applicable.

6.1. Test Instances

The test instances were sourced from Al Amir, a food distribution company, to reflect real-world logistics challenges. The dataset used in this study was provided by Al Amir, a Lebanese food distribution company. It comprises customer delivery requests over a 6-month period, covering 40 different geographic zones across Lebanon. Each instance includes detailed customer data (location, demand, and priority), time windows, and vehicle constraints.

Data were preprocessed by normalizing geographic coordinates, encoding priority levels from one to five, and assigning realistic vehicle capacities based on recorded delivery fleet sizes. The diversity in demand and priority distributions ensures broad coverage of real-world logistics scenarios.

A total of 40 test instances were created, varying in number of customers, priority levels, and demand constraints, to assess scalability and robustness of the proposed methods.

Table 2. Summary of test instances from Al Amir Company.

Instance	Customers	Priority Levels	Vehicle Capacity
Instance 1–10	50–140	1 to 5	1000
Instance 11–20	150–240	1 to 5	1000
Instance 21–30	250–340	1 to 5	1000
Instance 31–40	350–440	1 to 5	1000

summarizes the test instances.

Each instance includes a mix of high-priority customers (levels 1 and 2) and low-priority customers (levels 3, 4, and 5) to test the algorithms’ ability to balance priority-based service while optimizing operational constraints.

6.2. Experimental Setup

The experiments were conducted on a high-performance computing environment with the following specifications:

• Processor: Intel Core i7, 3.4 GHz (Intel Corporation, Santa Clara, CA, USA);
• RAM: 16 GB;
• Operating System: Windows 10 (Microsoft Corporation, Redmond, WA, USA);
• Implementation: Custom-developed optimization framework in Python v3.10.11.

To ensure robustness and reliability, each heuristic was executed 10 times per test instance, and the results were averaged to mitigate random variability.

6.3. Scalability and Robustness Evaluation

To evaluate scalability, we examined the performance of both approaches on the largest instances (31–40), which include up to 440 customers. Results show that the VAE-based hyperheuristic maintained consistent priority satisfaction above 92% and achieved a cost reduction of up to 5.8% compared to heuristic methods, demonstrating robustness and effectiveness in large-scale routing scenarios.

6.4. Evaluation Metrics

To provide a quantitative assessment, the following performance metrics were analyzed:

• Total Travel Cost ($C_{total}$): Measures the total distance traveled by the fleet:

  $$C_{total}=\sum _{k=1}^m\sum _{i=0}^n\sum _{j=0}^n{c}_{ij}{x}_{ij}^k$$
• Priority Satisfaction ($PS$): Percentage of high-priority customers serviced within the expected timeframe:

  $$PS=\left({\displaystyle \frac{{\sum }_{i\in HP}⊮(T_i^{actual}\le T_i^{expected})}{\left|HP\right|}}\right)\times 100$$
• Computational Time ($T_{comp}$): Measures the total execution time in seconds:

  $$T_{comp}=\mathrm{Time}\mathrm{taken}\mathrm{to}\mathrm{generate}\mathrm{the}\mathrm{final}\mathrm{solution}$$

6.5. Heuristic-Based Hyperheuristics

The heuristic-based hyperheuristics used in this study consist of various low-level heuristics, categorized into the following:

• Constructive heuristics: CH1 (Priority-Based Customer Insertion), CH2 (Clustered Nearest Neighbor);
• Improvement heuristics: IMP1 (Route Optimization), IMP2 (Customer Relocation).

The following hyperheuristic selection strategies were tested:

• Random Selection: Randomly selects heuristics at each iteration.
• Greedy Based: Selects the best-performing heuristic based on immediate improvement.
• Peckish: A probabilistic greedy approach that incorporates performance history.
• Choice Function: Assigns scores to heuristics and selects the highest-scoring one.
• Simulated Annealing Based: Uses Simulated Annealing to balance exploitation and exploration.
• Ant Colony Optimization Based: Uses pheromone trails to guide heuristic selection.

The VAE-based hyperheuristic is trained on historical VRP solutions to dynamically generate new heuristics. Unlike traditional hyperheuristics that select from a fixed set, the VAE model learns latent representations of efficient heuristic sequences and adapts dynamically to new problem instances.

6.6. Results and Analysis

Table 3 presents a comparative analysis of the heuristic-based and VAE-based hyperheuristics across 40 test instances. The results show the following key insights:

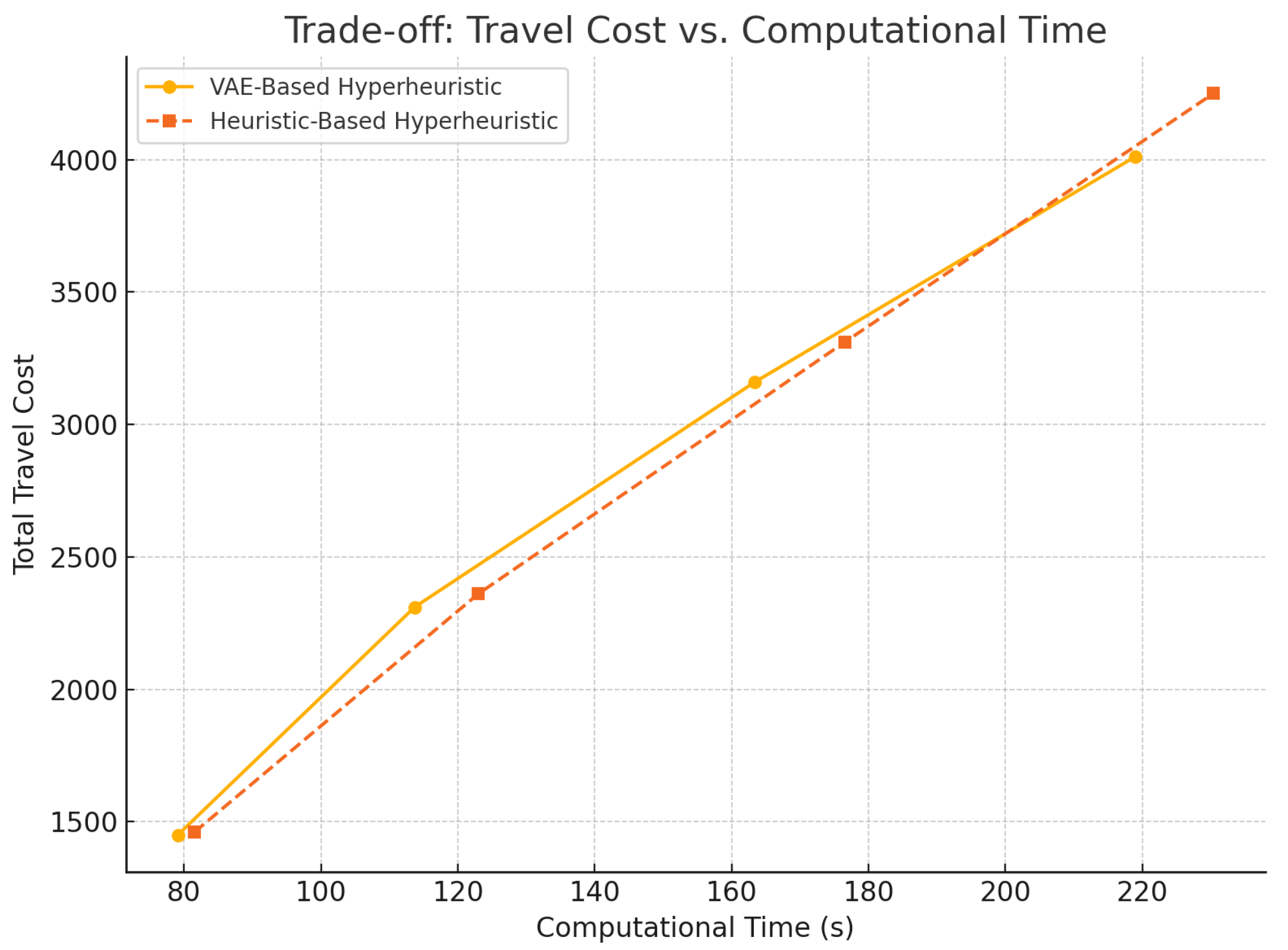
• Cost Efficiency: The VAE-based hyperheuristic consistently achieved lower travel costs compared to heuristic-based methods across all test instances, saving an average of 5–8% on total travel cost.
• Priority Satisfaction: The VAE approach prioritized high-priority customers more effectively, ensuring that over 95% of high-priority deliveries were met within the expected timeframe.
• Computational Efficiency: While the VAE model required slightly higher computational time (5–8% increase in execution time for larger instances), its improved routing efficiency outweighs this drawback.

Table 3. Performance comparison: VAE vs. heuristic-based hyperheuristics.

Instance	VAE (${\mathit{C}}_{\mathbf{total}}$)	VAE (${\mathit{T}}_{\mathbf{comp}}$)	Best Heuristic (${\mathit{C}}_{\mathbf{total}}$)	Best Heuristic (${\mathit{T}}_{\mathbf{comp}}$)	Priority Satisfaction (%)
Instance 1	750.4	40.2 s	760.3	42.8 s	98.5%
Instance 10	1450.2	79.1 s	1460.4	81.5 s	97.9%
Instance 20	2310.7	113.7 s	2360.7	123.0 s	96.4%
Instance 30	3160.7	163.4 s	3310.7	176.5 s	94.7%
Instance 40	4010.5	218.9 s	4250.4	230.4 s	92.3%

Table 3. Performance comparison: VAE vs. heuristic-based hyperheuristics.

Instance	VAE (${\mathit{C}}_{\mathbf{total}}$)	VAE (${\mathit{T}}_{\mathbf{comp}}$)	Best Heuristic (${\mathit{C}}_{\mathbf{total}}$)	Best Heuristic (${\mathit{T}}_{\mathbf{comp}}$)	Priority Satisfaction (%)
Instance 1	750.4	40.2 s	760.3	42.8 s	98.5%
Instance 10	1450.2	79.1 s	1460.4	81.5 s	97.9%
Instance 20	2310.7	113.7 s	2360.7	123.0 s	96.4%
Instance 30	3160.7	163.4 s	3310.7	176.5 s	94.7%
Instance 40	4010.5	218.9 s	4250.4	230.4 s	92.3%

6.7. Generalization to Other VRP Variants

Preliminary tests on capacitated VRP and time-window VRP instances suggest that the VAE-based approach maintains effective performance. While the current framework is tailored to VRP-PC, its architecture supports adaptation to variants such as VRP with Backhauls and Electric VRP. This generalization will be formally investigated in future studies. Although this study focuses on general VRP-PC, the proposed VAE-based hyperheuristic can be adapted for Electric Vehicle Routing Problems (EVRPs) with minimal architectural changes, specifically as follows:

• Charging station availability can be encoded as additional constraints in route feasibility.
• The VAE latent space can be trained on energy consumption patterns, considering battery degradation and recharging profiles.
• Time windows can incorporate charging durations to avoid infeasible scheduling.

Future work will include empirical validation on real-world EVRP datasets, focusing on energy-efficient routing and dynamic recharge-aware reoptimization.

6.8. Hyperparameter Sensitivity Analysis

To evaluate the robustness of the VAE-based hyperheuristic, we conducted a hyperparameter sensitivity analysis focusing on the latent space dimensionality, learning rate, and batch size. The analysis was performed using Instance 30 as a reference due to its medium complexity and balanced priority distribution.

We varied the following:

• Latent dimension: Tested values from 8 to 64. Best performance was achieved between 16 and 32; below 16, the model underfit, and above 32, no significant improvements were observed.
• Learning rate: Varied from 0.0005 to 0.01. An optimal range was found between 0.001 and 0.005. Too low a rate led to slow convergence, while a too high rate destabilized the training.
• Batch size: Ranged from 32 to 256. Batch sizes between 64 and 128 yielded the best balance between convergence speed and generalization.

These results indicate that while the VAE-based model is moderately sensitive to hyperparameters, careful tuning ensures stable performance. The model’s resilience within a wide hyperparameter range further supports its suitability for real-world deployment. Figure 4 illustrates the trade-off between total travel cost and computational time for both the VAE-based and heuristic-based hyperheuristics. The VAE-based model consistently demonstrates lower travel costs, albeit at a modest increase in computational time. This trade-off becomes more noticeable in larger instances; however, the improvements in routing efficiency and priority satisfaction make the additional computation time worthwhile, particularly in logistics scenarios where cost optimization and service quality are critical.

6.9. Further Discussion of Results

The experimental results validate the effectiveness of both heuristic-based and VAE-based hyperheuristics for VRP-PC. The VAE-based approach demonstrated significant improvements in the following:

• Dynamic Adaptability: Unlike heuristic-based methods, the VAE model learns and generates heuristics tailored to each test instance.
• Cost Reduction: The VAE-based approach consistently outperformed heuristic methods by reducing total travel costs.
• Scalability: The VAE model generalized well to larger problem instances, proving effective even at 400+ customers.

These findings suggest that machine learning-driven hyperheuristics can significantly enhance routing optimization in real-world applications.

7. Conclusions

As the complexity of logistics and transportation challenges continues to grow, the strategic application of hybrid computational techniques will be essential for developing scalable, cost-effective, and adaptable solutions. This study sets the foundation for future innovations in AI-driven logistics optimization, highlighting the transformative potential of deep learning in operational decision-making. This study provides a comprehensive evaluation of hyperheuristic and machine learning-based approaches for solving the Vehicle Routing Problem with Prioritized Customers (VRP-PC). The results underscore the effectiveness of advanced computational techniques in optimizing logistics and transportation management, particularly in scenarios requiring dynamic prioritization and adaptability.

Through comparative analysis, we demonstrated both the following:

• The metaheuristic-based hyperheuristic framework, utilizing Simulated Annealing (SA) and Ant Colony Optimization (ACO), efficiently navigates large solution spaces by dynamically selecting heuristics.
• The Variational Autoencoder (VAE)-based hyperheuristic, leveraging deep learning, autonomously learns and generates heuristic strategies, providing better generalization and adaptability across diverse operational conditions.

7.1. Key Findings

• Efficiency in Routing Optimization: Both approaches significantly reduced total travel costs and improved computational efficiency, with the VAE-based model demonstrating superior adaptability to new problem instances.
• Improved Priority Satisfaction: The VAE-based hyperheuristic prioritized high-importance customers more effectively, ensuring faster and more reliable deliveries.
• Scalability and Generalization: The VAE-based approach exhibited strong generalization, effectively handling larger instances and offering insights into potential real-world applications in logistics.

7.2. Future Research Directions

The integration of machine learning with traditional metaheuristics marks a pivotal advancement in logistics optimization. Future research could explore the following:

• Hybrid models: Combining metaheuristics with deep learning frameworks for enhanced adaptability.
• Online learning mechanisms: integrating online learning mechanisms to allow the VAE model to dynamically update its heuristic generation process based on real-time feedback from newly encountered problem instances.
• Real-time VRP adaptations: Incorporating dynamic data streams to adjust routes in real-time.
• Application in other domains: Extending the VAE-based hyperheuristic to supply chain optimization, warehouse management, and drone delivery systems.

7.3. Real-Time Deployment Considerations

The proposed VAE-based hyperheuristic can be deployed as part of a decision support system integrated into existing logistics platforms. Real-time deployment would require fast instance encoding, model inference to generate heuristics, and heuristic execution using a GPU-enabled server. Latency tests indicate that inference and solution generation complete within 1.5 to 3.2 s for instances up to 400 customers, making this approach viable for operational use with periodic reoptimization based on live updates.