A Block Controller with Integral Super-Twisting Algorithm for the Path Following of a Self-Driving Electric Vehicle Considering Actuator Dynamics
Abstract
1. Introduction
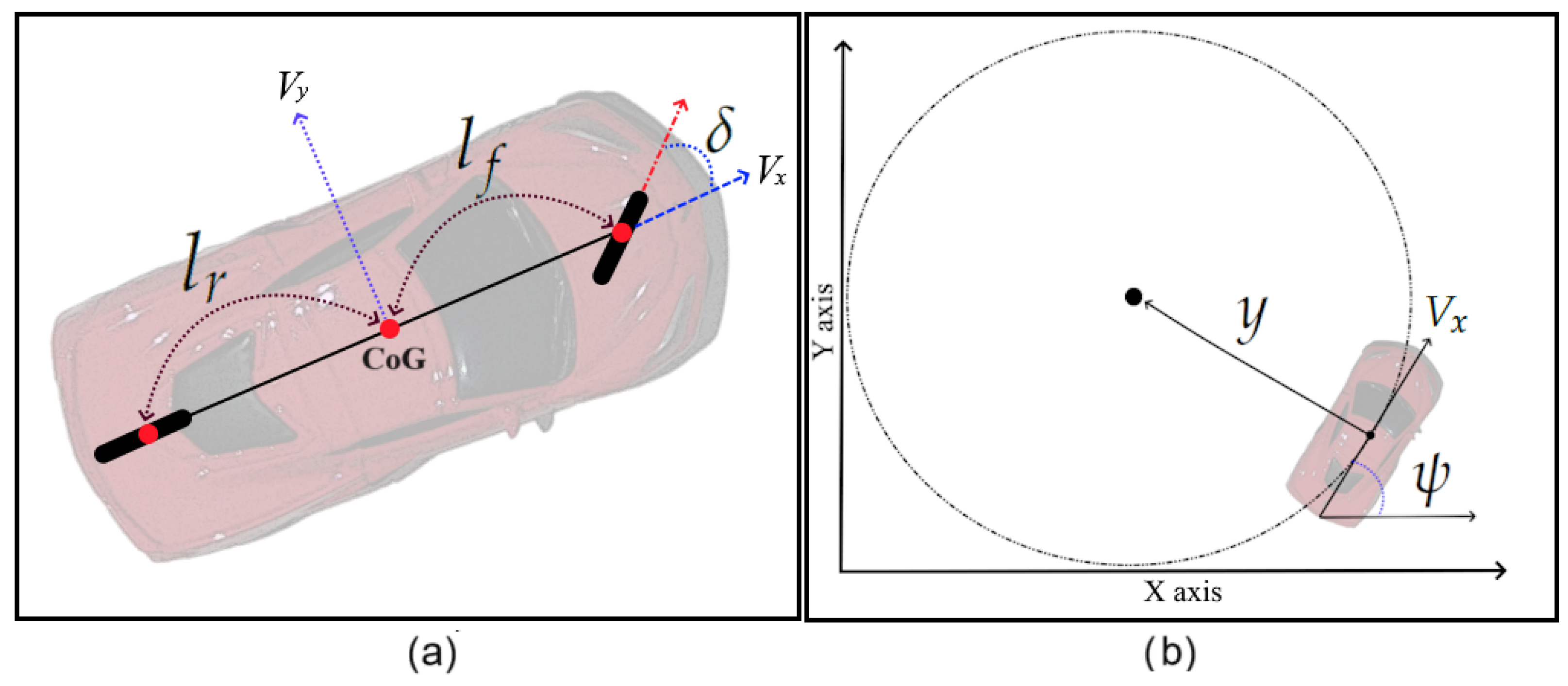
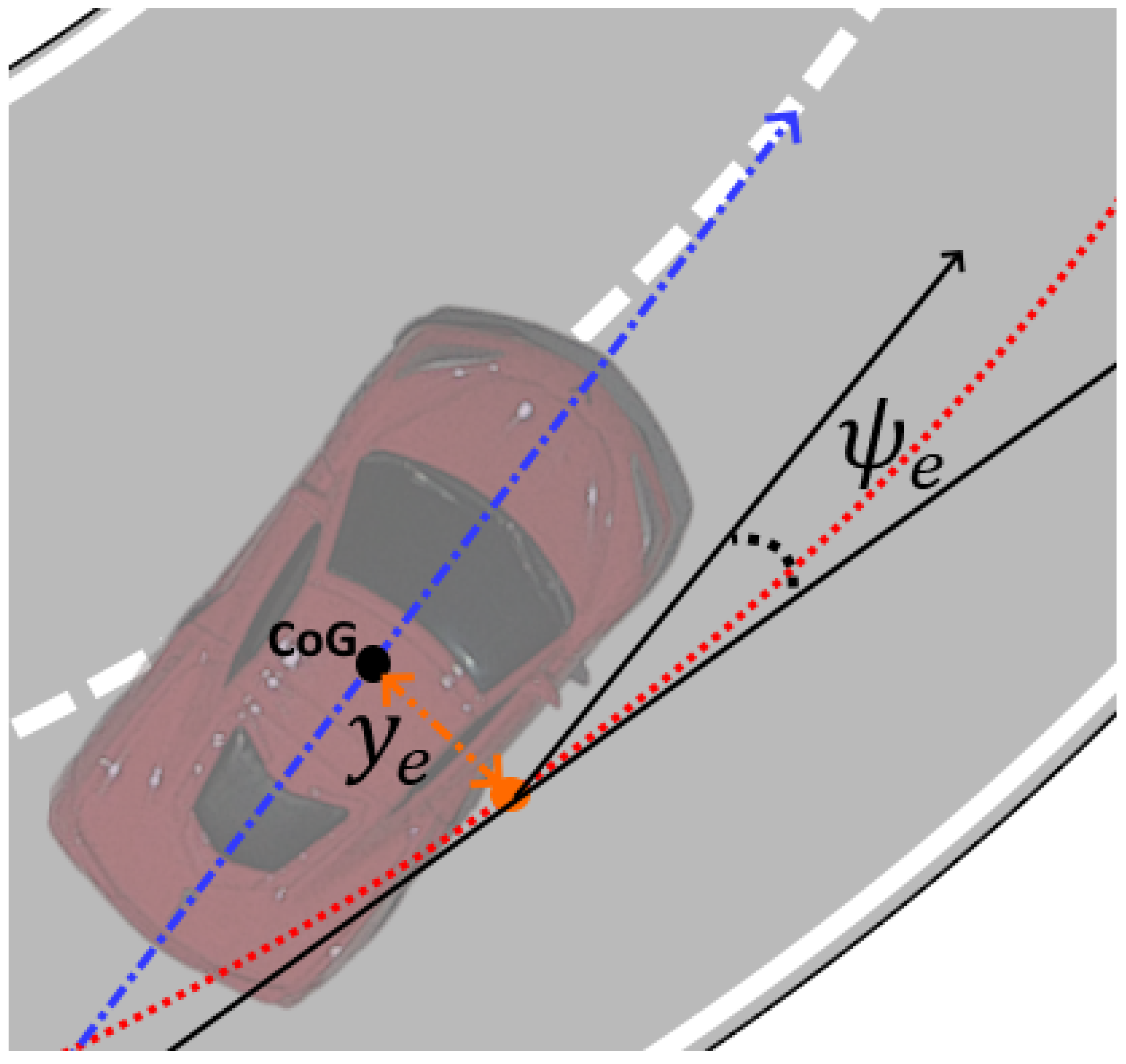
2. Path Following for a Self-Driving Automotive Vehicle
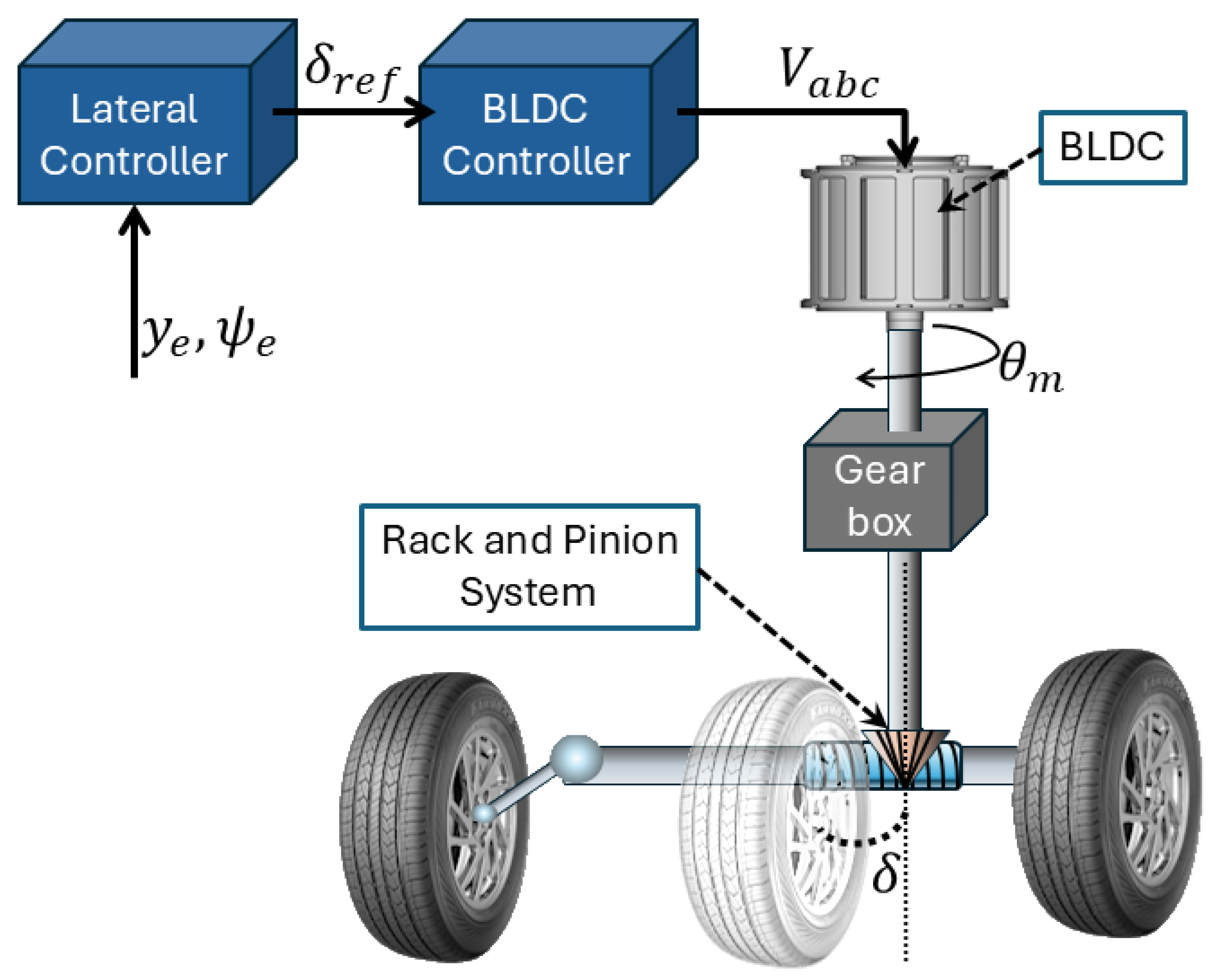
3. Overall Control Scheme
3.1. Lateral Sliding Mode Controller
3.2. Actuator Controller
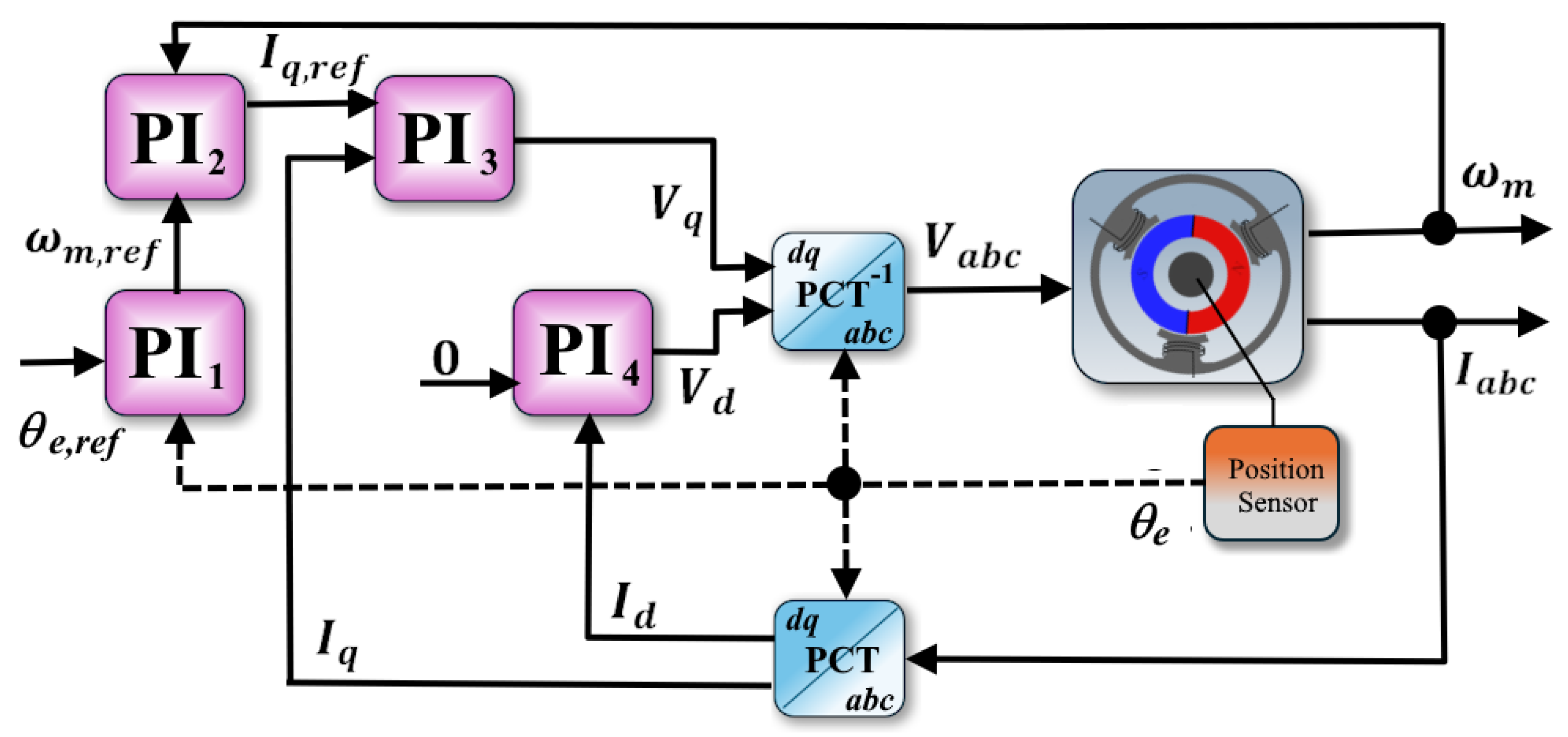
3.2.1. BLDC Motor Dynamics
3.2.2. Steering Rack System Model
3.2.3. Position Control Algorithm
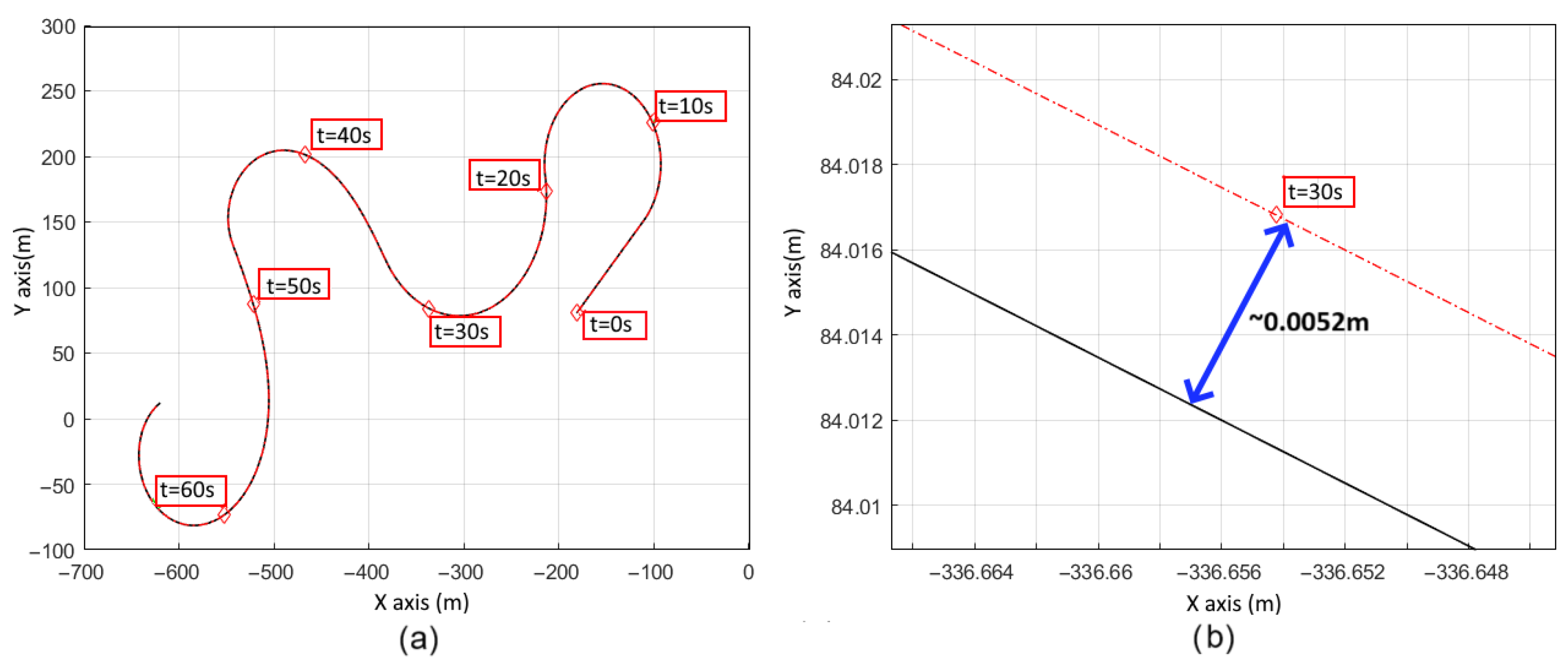
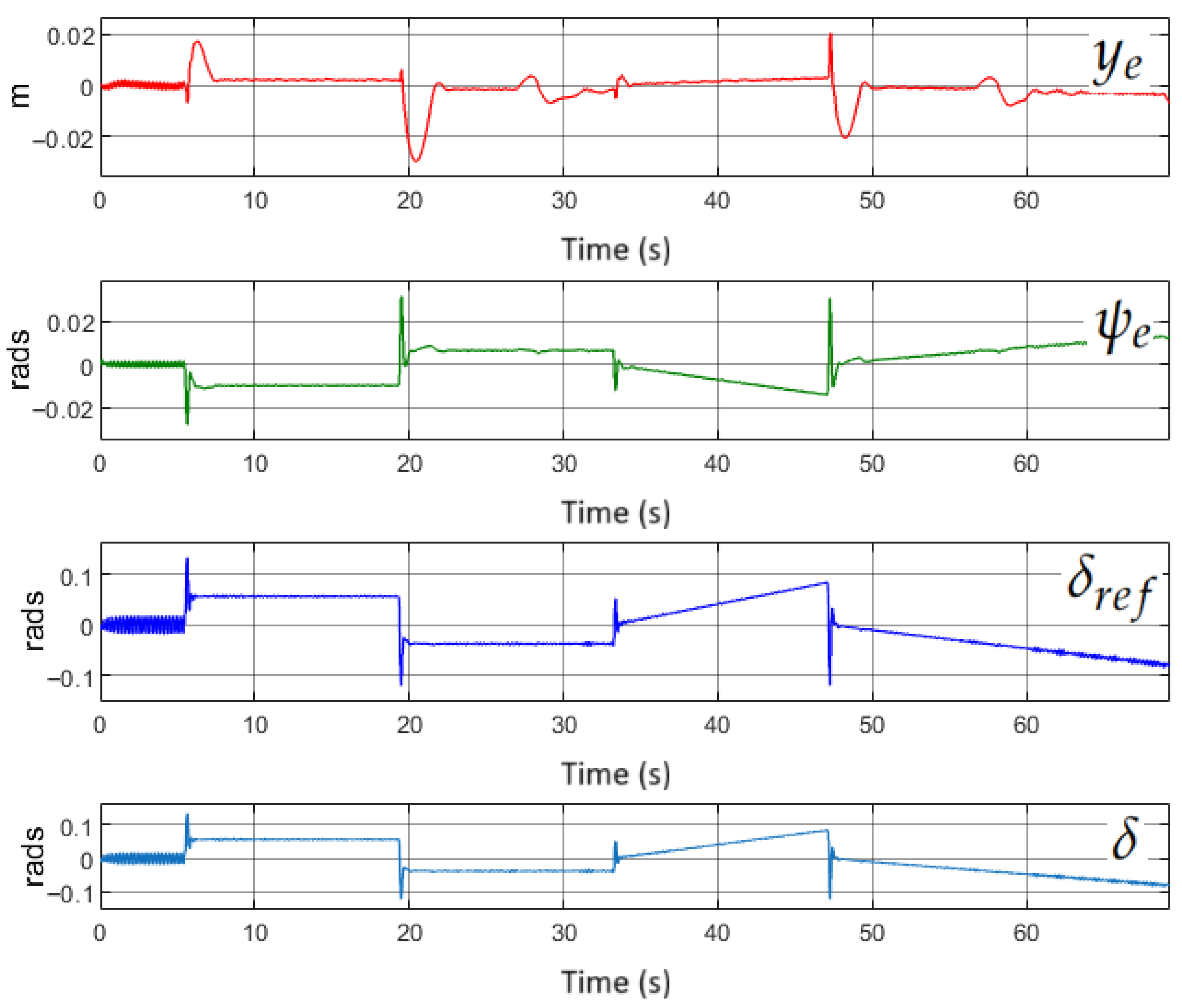
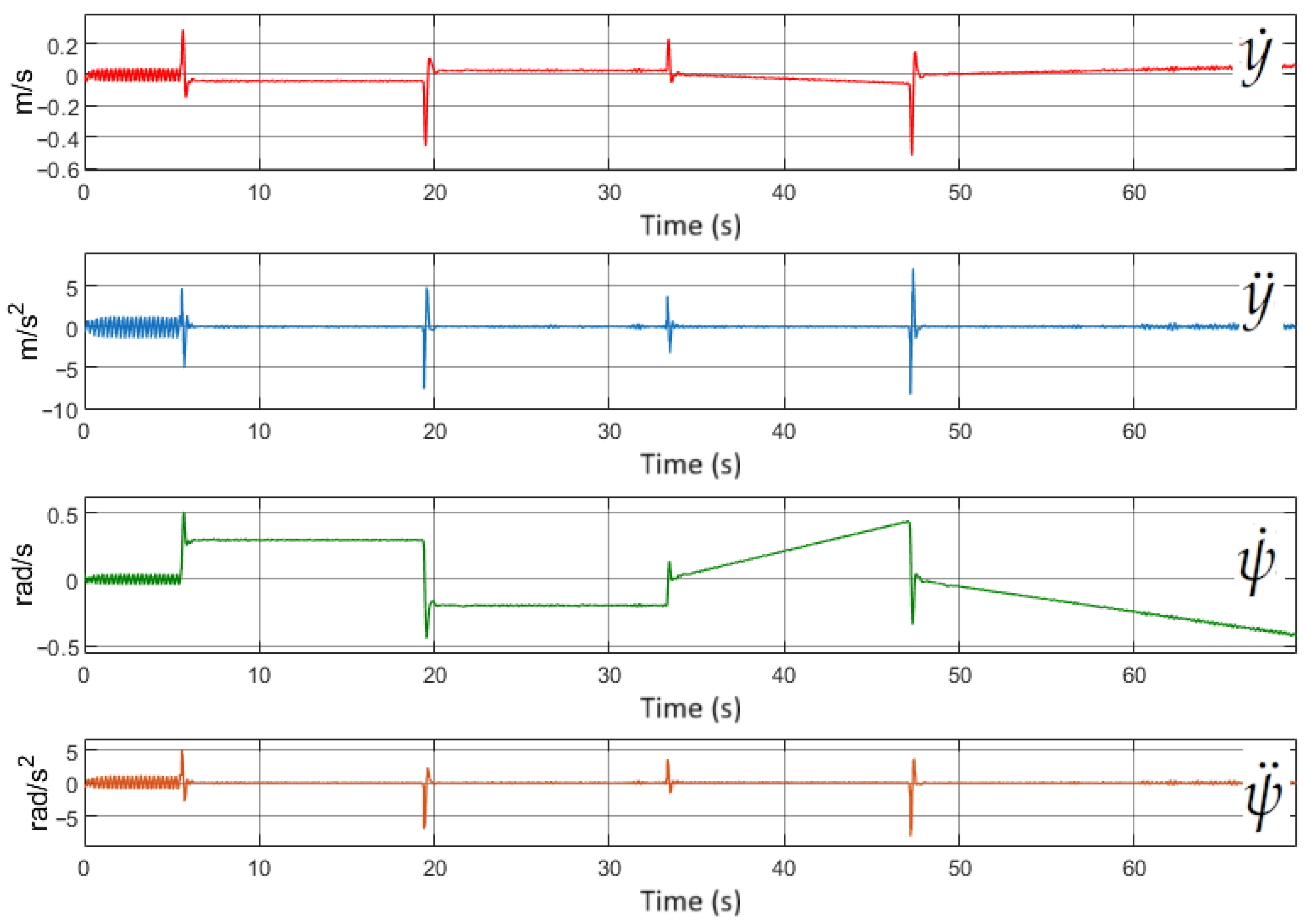
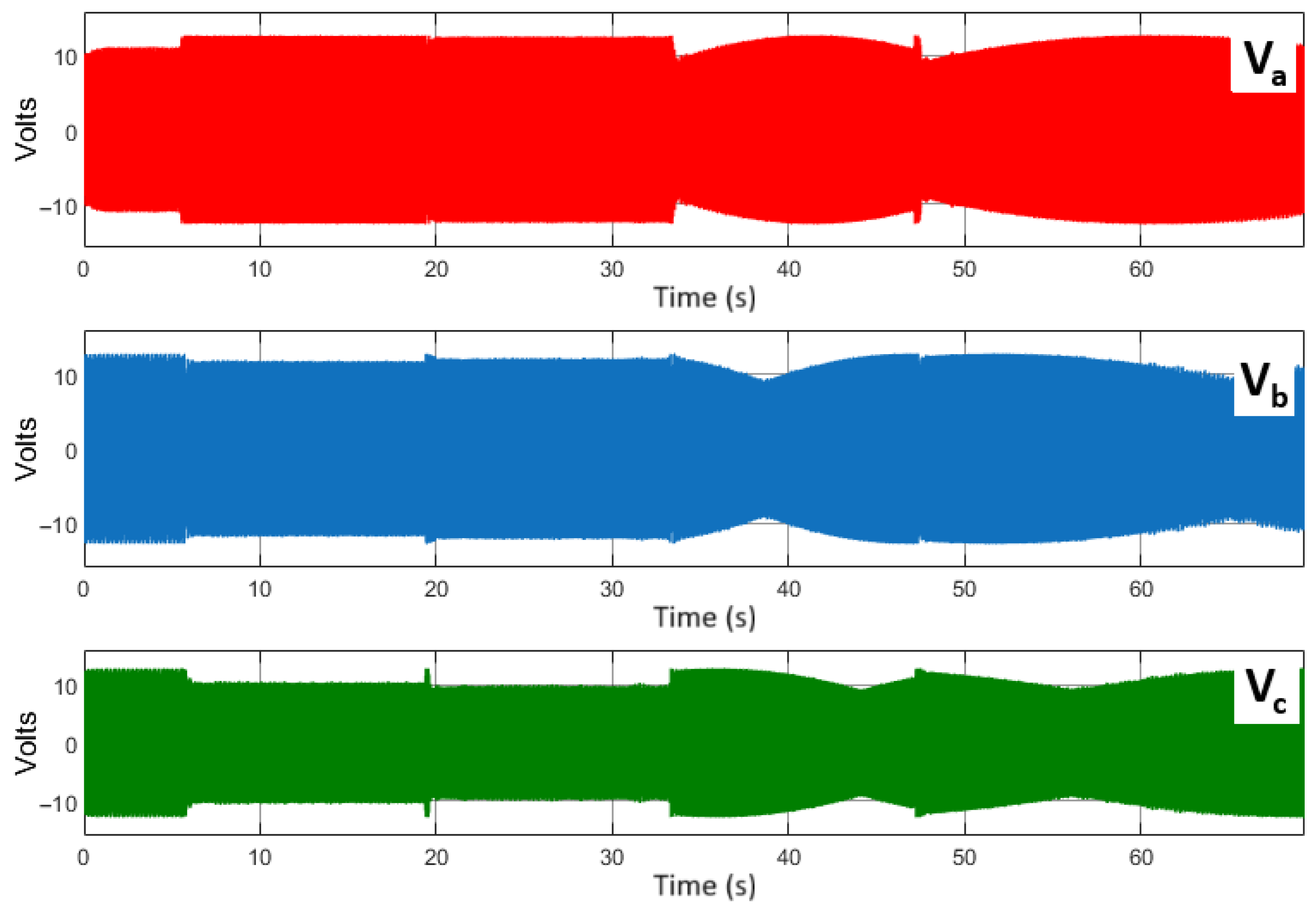
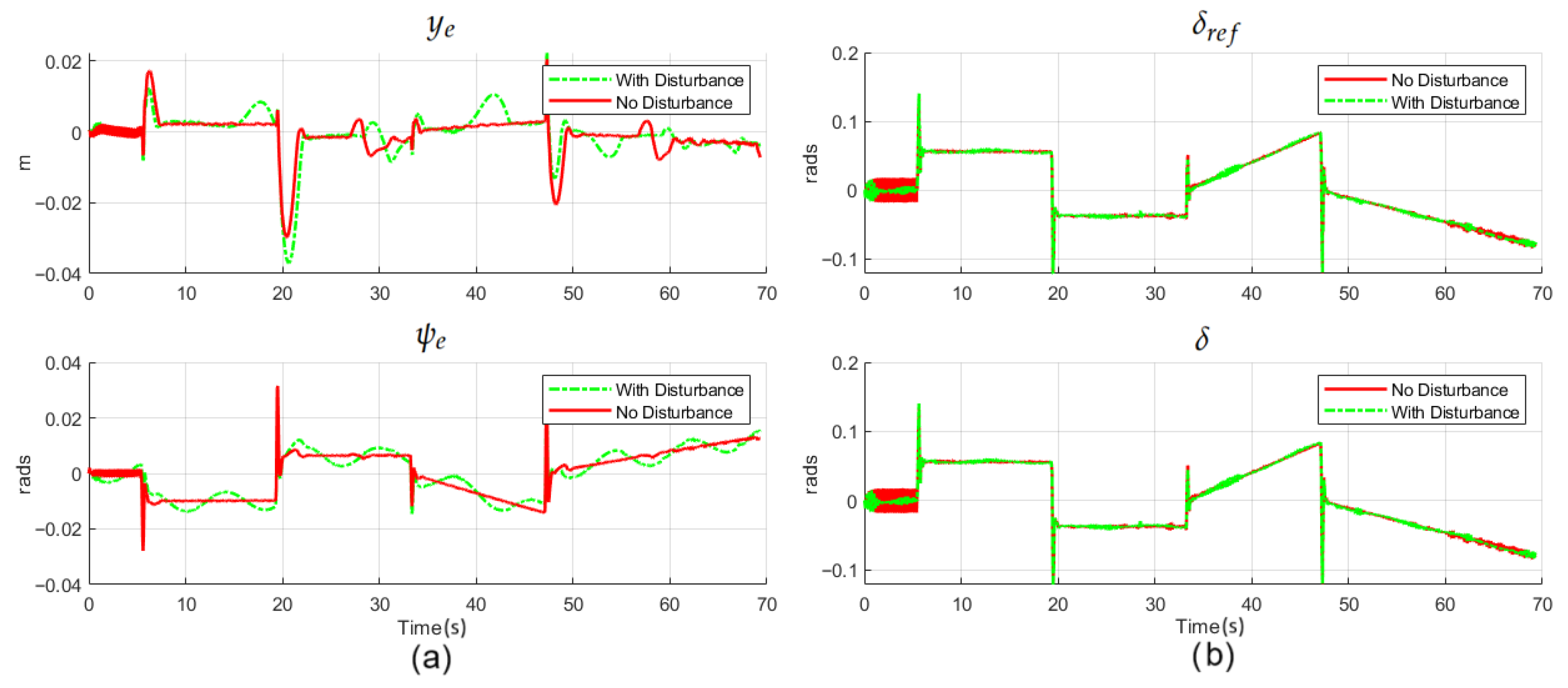
4. Simulation Results
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BLDC | Brushless Direct Current motor |
| FOC | Field-Oriented Control |
| SVPWM | Space Vector Pulse Width Modulation |
| PI | Proportional-Integral Control |
| MPC | Model Predictive Control |
| IMU | Inertial Measurement Unit |
| LIDAR | Light Detection and Ranging |
| SMC | Sliding Mode Control |
| ISM | Integral Sliding Mode |
| STA | Super-Twisting Algorithm |
| STSMC | Super-Twisting Sliding Mode Control |
| SAE | Society of Automotive Engineers |
| HOSM | High-Order Sliding Modes |
| LKAS | Lane Keeping Assist System |
| LDA | Lane Departure Avoidance |
| ELKS | Emergency Lane Keeping System |
References
- Paden, B.; Cap, M.; Yong, S.; Yershov, D.; Frazzoli, E.; Vázquez, D. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–35. [Google Scholar] [CrossRef]
- Velasco-Hernandez, G.; Yeong, D.J.; Barry, J.; Walsh, J. Autonomous Driving Architectures, Perception and Data Fusion: A Review. In Proceedings of the 2020 IEEE 16th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 3–5 September 2020; pp. 315–321. [Google Scholar] [CrossRef]
- Oh, K.; Seo, J. Development of a Sliding-Mode-Control-Based Path-Tracking Algorithm with Model-Free Adaptive Feedback Action for Autonomous Vehicles. Sensors 2023, 23, 405. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Huang, G.; Shi, K. Improved Adaptive Path Following Control System for Autonomous Vehicle in Different Velocities. IEEE Trans. Intel. Transp. Syst. 2020, 21, 3247–3256. [Google Scholar] [CrossRef]
- Liang, J.; Tian, Q.; Feng, J.; Pi, D.; Yin, G. A polytopic model-based robust predictive control scheme for path tracking of autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 9, 3928–3939. [Google Scholar] [CrossRef]
- Vu, T.M.; Moezzi, R.; Cyrus, J.; Hlava, J. Model Predictive Control for Autonomous Driving Vehicles. Electronics 2021, 10, 2593. [Google Scholar] [CrossRef]
- Xu, Z.; He, L.; Huang, C.; Zheng, X.; Li, S.; Shi, Q. A model-tuned predictive sliding control approach for steering angle following of full self-driving vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 7399–7409. [Google Scholar] [CrossRef]
- Fernandez, B.; Herrera, P.; Cerrada, J. A Simplified Optimal Path Following Controller for an Agricultural Skid-Steering Robot. IEEE Access 2019, 7, 95932–95940. [Google Scholar] [CrossRef]
- Guo, N.; Zhang, X.; Zou, Y.; Lenzo, B.; Zhang, T. A Computationally Efficient Path-Following Control Strategy of Autonomous Electric Vehicles With Yaw Motion Stabilization. IEEE Trans. Transp. Electrif. 2020, 6, 2. [Google Scholar] [CrossRef]
- Ritschel, R.; Schrödel, F.; Hädrich, J.; Jäkel, J. Nonlinear Model Predictive Path-Following Control for Highly Automated Driving. IFAC-PapersOnLine 2019, 52, 350–355. [Google Scholar] [CrossRef]
- Ultsch, J.; Mirwald, J.; Brembeck, J.; De Castro, R. Reinforcement Learning-based Path Following Control for a Vehicle with Variable Delay in the Drivetrain. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19–30 October 2020; pp. 532–539. [Google Scholar]
- Woo, J.; Yu, C.; Kim, N. Deep reinforcement learning-based controller for path following of an unmanned surface vehicle. Ocean Eng. 2019, 183, 155–166. [Google Scholar] [CrossRef]
- Ljungqvist, O.; Evestedt, N.; Axehill, D.; Cirillo, M.; Pettersson, H. A path planning and path-following control framework for a general 2-trailer with a car-like tractor. J. Field Robot. 2019, 36, 1345–1377. [Google Scholar] [CrossRef]
- Bacha, S.; Ayad, M.Y.; Aboubou, A.; Bahri, M.; Becherif, M. Modeling and Control Techniques for Autonomous Electric and Hybrid Vehicles Path following. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017; pp. 1–12. [Google Scholar]
- De Castro, R.; Tanelli, M.; Esteves, A.R.; Savaresi, S.M. Minimum-Time Path-Following for Highly Redundant Electric Vehicles. IEEE Trans. Control Syst. Technol. 2016, 24, 2. [Google Scholar] [CrossRef]
- Hossain, T.; Habibullah, H.; Islam, R. Steering and Speed Control System Design for Autonomous Vehicles by Developing an Optimal Hybrid Controller to Track Reference Trajectory. Machines 2022, 10, 420. [Google Scholar] [CrossRef]
- Maurya, P.; Morishita, H.M.; Pascoal, A.; Aguiar, A.P. A Path-Following Controller for Marine Vehicles Using a Two-Scale Inner-Outer Loop Approach. Sensors 2022, 22, 4293. [Google Scholar] [CrossRef]
- Dika, M.; Owayjan, M.; Achkar, R. Steering Control of Self-Driving Car Using Super-Twisting Sliding Mode Control. In Proceedings of the 2023 Fifth International Conference on Advances in Computational Tools for Engineering Applications (ACTEA), Zouk Mosbeh, Lebanon, 5–7 July 2023; pp. 190–196. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014; pp. 155–158. [Google Scholar]
- Takele, T.; Terefe, T.; Ma, S.S. Super Twisting Sliding Mode Controller for Trajectory Tracking Control of Autonomous Ground Vehicle System. In Proceedings of the International Conference on Advances of Science and Technology, Bahir Dar, Ethiopia, 4–6 November 2022; Springer Nature: Cham, Switzerland, 2022; pp. 272–289. [Google Scholar]
- Hakjoo, K.I.M.; Seok-Cheol, K.E.E. Neural Network Approach Super-Twisting Sliding Mode Control for Path-Tracking of Autonomous Vehicles. Electronics 2023, 12, 3635. [Google Scholar]
- Bei, S.; Hu, H.; Li, B.; Tian, J.; Tang, H.; Quan, Z.; Zhu, Y. Research on the Trajectory Tracking of Adaptive Second-Order Sliding Mode Control Based on Super-Twisting. World Electr. Veh. J. 2022, 13, 141. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Moreno, J.A.; Fridman, L. A survey on High-Order Sliding-Mode control design using Lyapunov functions. IFAC-PapersOnLine 2023, 56, 25–36. [Google Scholar] [CrossRef]
- Mondal, S.; Mitra, A.; Chattopadhyay, M. Mathematical modeling and simulation of brushless DC motor with ideal back emf for a precision speed control. In Proceedings of the 2015 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015; pp. 1–5. [Google Scholar]
- Pillay, P.; Krishnan, R. Modeling, simulation, and analysis of permanent-magnet motor drives. IEEE Trans. Ind. Appl. 1989, 25, 265–273. [Google Scholar] [CrossRef]
- Wu, X.; Xu, X.; Chen, L.; Cai, Y. Robust Control of Electric Power Steering System Based on Aligning Torque Model. In Proceedings of the 2024 IEEE 22nd International Conference on Industrial Informatics (INDIN), Beijing, China, 18–20 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Bose, B.K. Modern Power Electronics & AC Drives; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Bolton, W.C. Mechatronics: Electronic Control Systems in Mechanical and Electrical Engineering; Pearson Education: London, UK, 2018. [Google Scholar]
- Vehicle Dynamics and Controller Simulink Model. Available online: https://github.com/L-Arturo-Torres-Romero/VehicleModel/tree/master/VehicleModel (accessed on 24 October 2023).
- Torres-Romero, L. L-Arturo-Torres-Romero/VehicleModel: Conventional SMC for Lateral Dynamic 2. Zenodo 2024. Available online: https://zenodo.org/records/1054731 (accessed on 10 June 2025).
- Five Slippery Cars Enter a Wind Tunnel; One Slinks out a Winner. Available online: https://www.tesla.com/sites/default/files/blog_attachments/the-slipperiest-car-on-the-road.pdf (accessed on 10 June 2025).
- Torres-Romero, L.A.; Ruiz-Cruz, R.; González-Jiménez, L.E. Path-Following Sliding Mode Controller for an Electric Vehicle Considering Actuator Dynamics. Machines 2024, 12, 219. [Google Scholar] [CrossRef]
- CarSim: Mechanical Simulation. Available online: https://www.carsim.com/ (accessed on 27 November 2023).
- CARLA: Open-Source Simulator for Autonomous Driving Research. Available online: http://carla.org (accessed on 10 November 2023).



| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 1.58 m | b | ||
| 1.1 m | P | 8 | |
| m | 2238.93 kg | ||
| 4 (4:1 ratio) | |||
| g | 0.1 | ||
| 18 m/s | |||
| R | 0.08 Ω | ||
| J |
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| −15 | |||
| 1 | −75 | ||
| 1 | 40 | ||
| 1 | 80 | ||
| 1 | 30 | ||
| 50 | 0 | ||
| 2 | 4 |
| Variable | Maximum Value | Mean Value |
|---|---|---|
| (m) | 0.02976 | 0.00320 |
| (rads) | 0.03154 | 0.00716 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-Romero, L.A.; González-Jiménez, L.E. A Block Controller with Integral Super-Twisting Algorithm for the Path Following of a Self-Driving Electric Vehicle Considering Actuator Dynamics. World Electr. Veh. J. 2025, 16, 643. https://doi.org/10.3390/wevj16120643
Torres-Romero LA, González-Jiménez LE. A Block Controller with Integral Super-Twisting Algorithm for the Path Following of a Self-Driving Electric Vehicle Considering Actuator Dynamics. World Electric Vehicle Journal. 2025; 16(12):643. https://doi.org/10.3390/wevj16120643
Chicago/Turabian StyleTorres-Romero, Luis Arturo, and Luis Enrique González-Jiménez. 2025. "A Block Controller with Integral Super-Twisting Algorithm for the Path Following of a Self-Driving Electric Vehicle Considering Actuator Dynamics" World Electric Vehicle Journal 16, no. 12: 643. https://doi.org/10.3390/wevj16120643
APA StyleTorres-Romero, L. A., & González-Jiménez, L. E. (2025). A Block Controller with Integral Super-Twisting Algorithm for the Path Following of a Self-Driving Electric Vehicle Considering Actuator Dynamics. World Electric Vehicle Journal, 16(12), 643. https://doi.org/10.3390/wevj16120643







