Simulation and Experimental Validation of a 1D Cabin Thermal Model for Electric Trucks with Enhanced Insulation and Heating Panels
Abstract
1. Introduction
1.1. Previous Research in the Field
1.2. Current Study Novelty and Focus
- Integrated system-level modeling: The study introduces a 1D model that brings together multiple thermal measures, like insulation and heating panels. It offers a complete understanding of the system.
- Comfort measurement and validation: Linear comfort simulation is implemented within the 1D simulation, providing a robust assessment of passenger comfort.
- Electric Truck Focus: The study highlights the thermal aspects of electric truck cabins and fills a key gap in current research. An electric truck cabin with these types of measures was investigated and validated with real measurement data. The measurements made it possible to build an accurate 1D model and support further development.
- FMU compatibility: The model is ready to be exported as a FMU, making it easy to integrate into larger system simulations or real-time applications—an important step toward practical deployment.
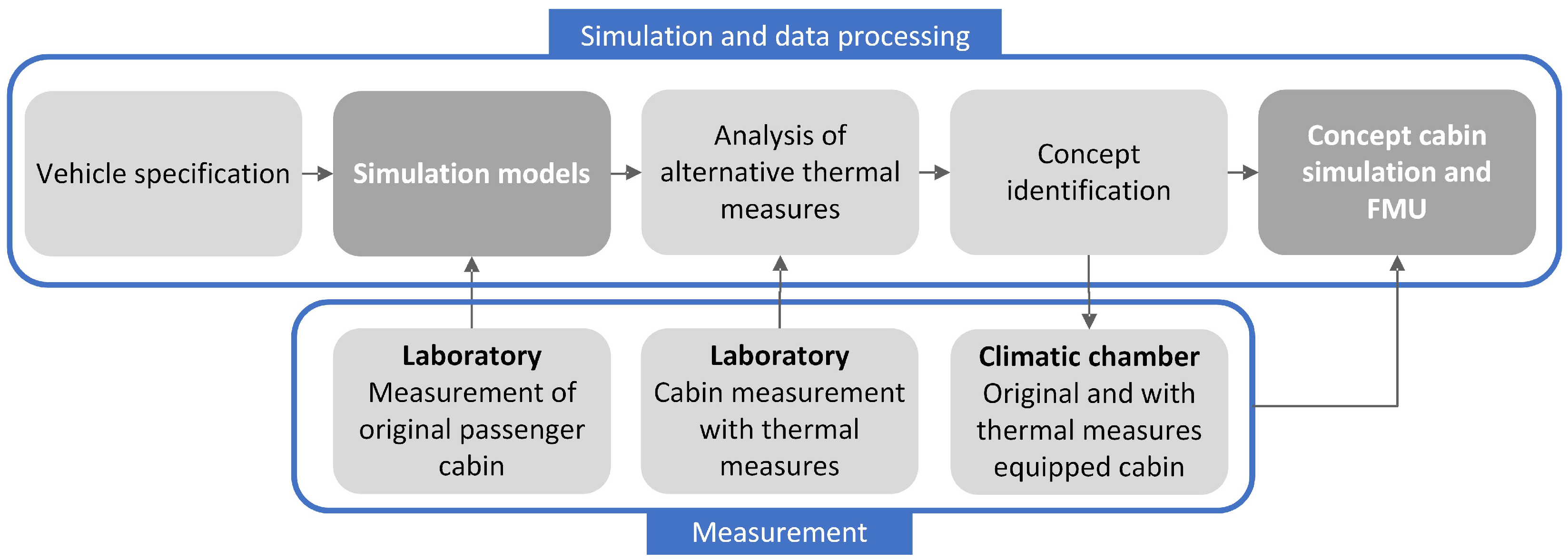
2. Physical Background
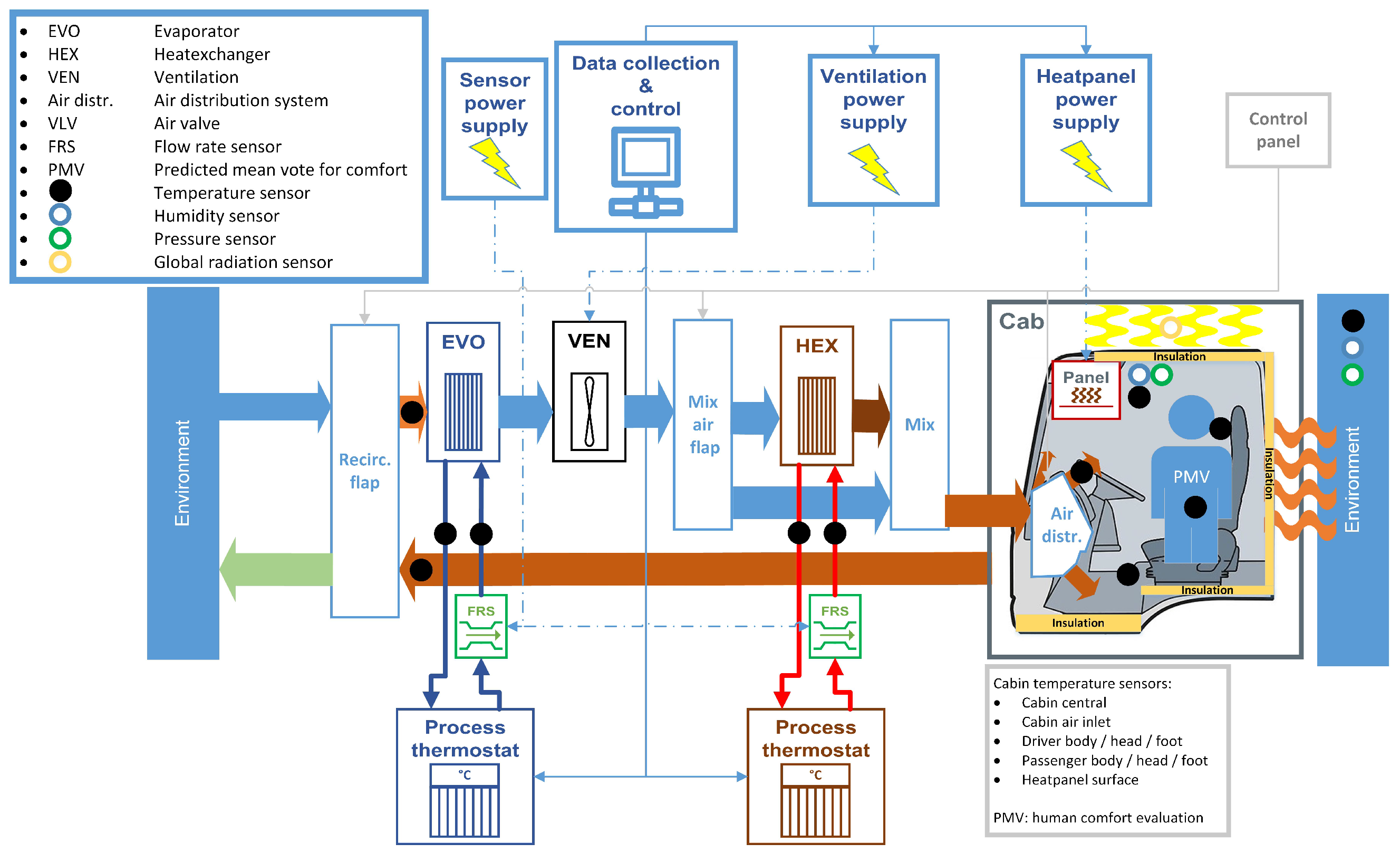
2.1. Measurement of the Prototype Cabin
- Laboratory measurements: The cabin was placed in a room-temperature environment and actively heated.
- Climatic chamber measurements: The cabin interior was held at room temperature while the external environment was cooled.
2.2. 1D Model
3. Results
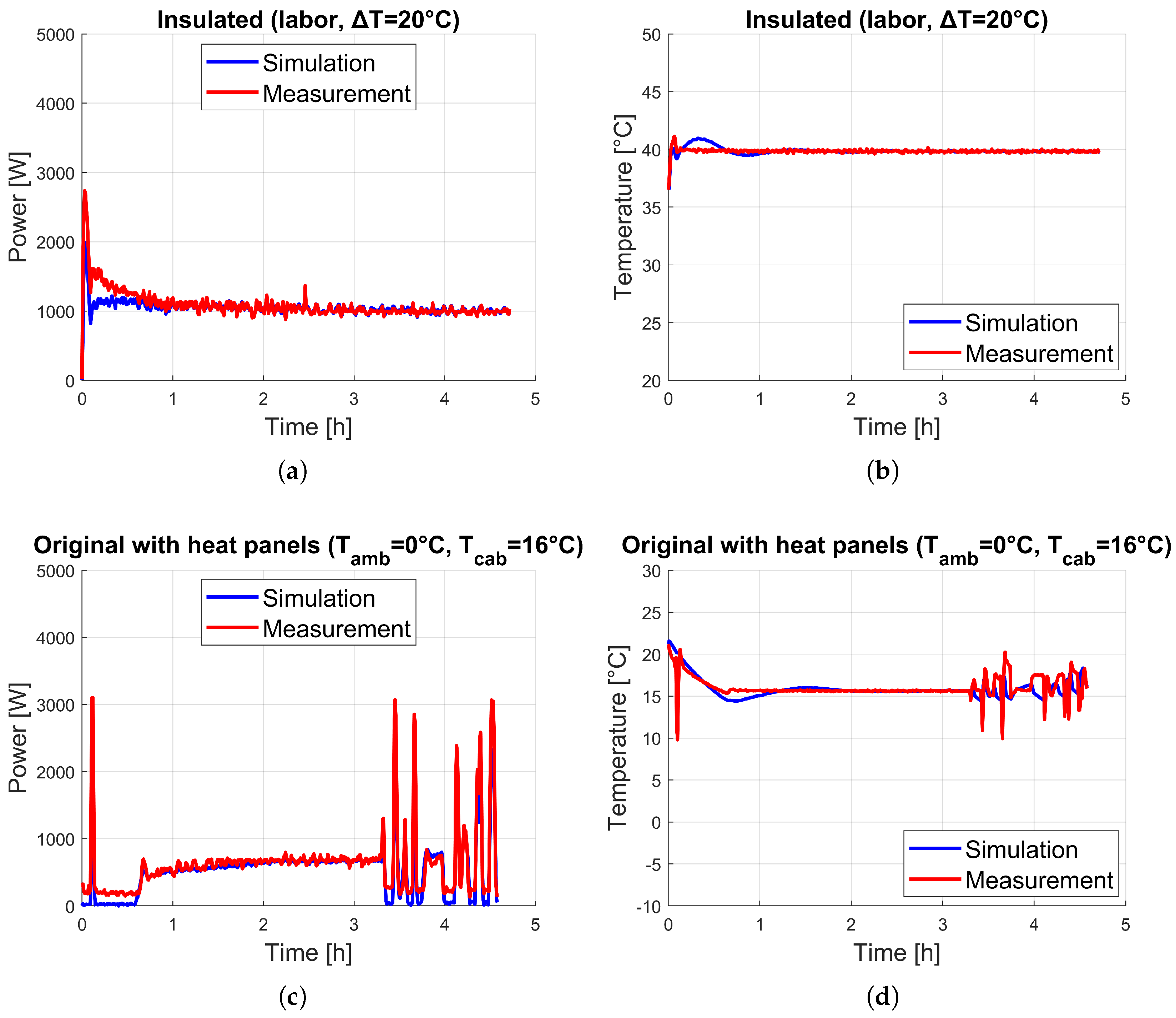
3.1. Model Validation
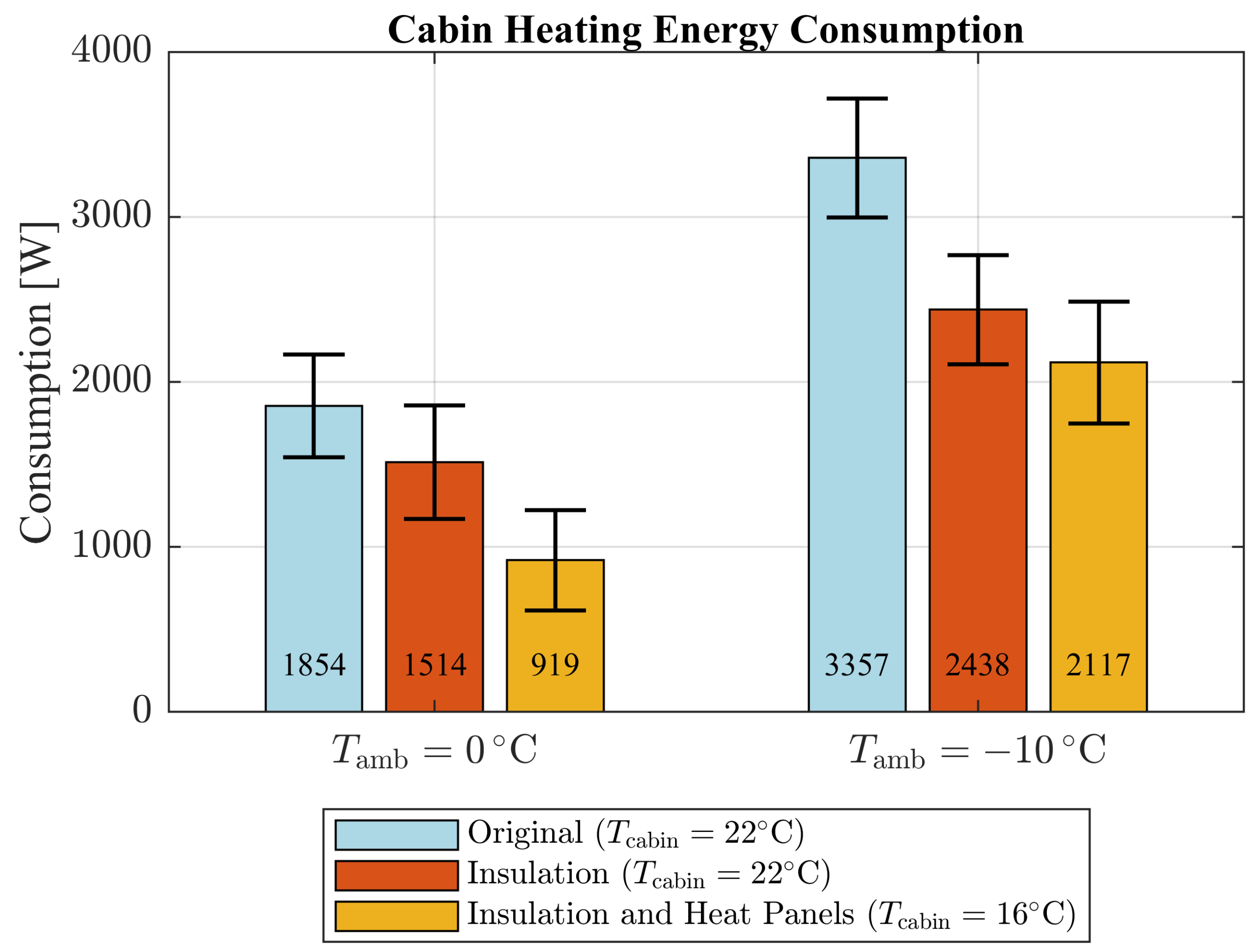
3.2. Evaluation of Thermal Measures
- Original cabin with 22 °C cabin air temperature,
- Cabin with additional insulation and 22 °C air temperature,
- Cabin with additional insulation and heating panels, with a lowered air temperature of 16 °C.
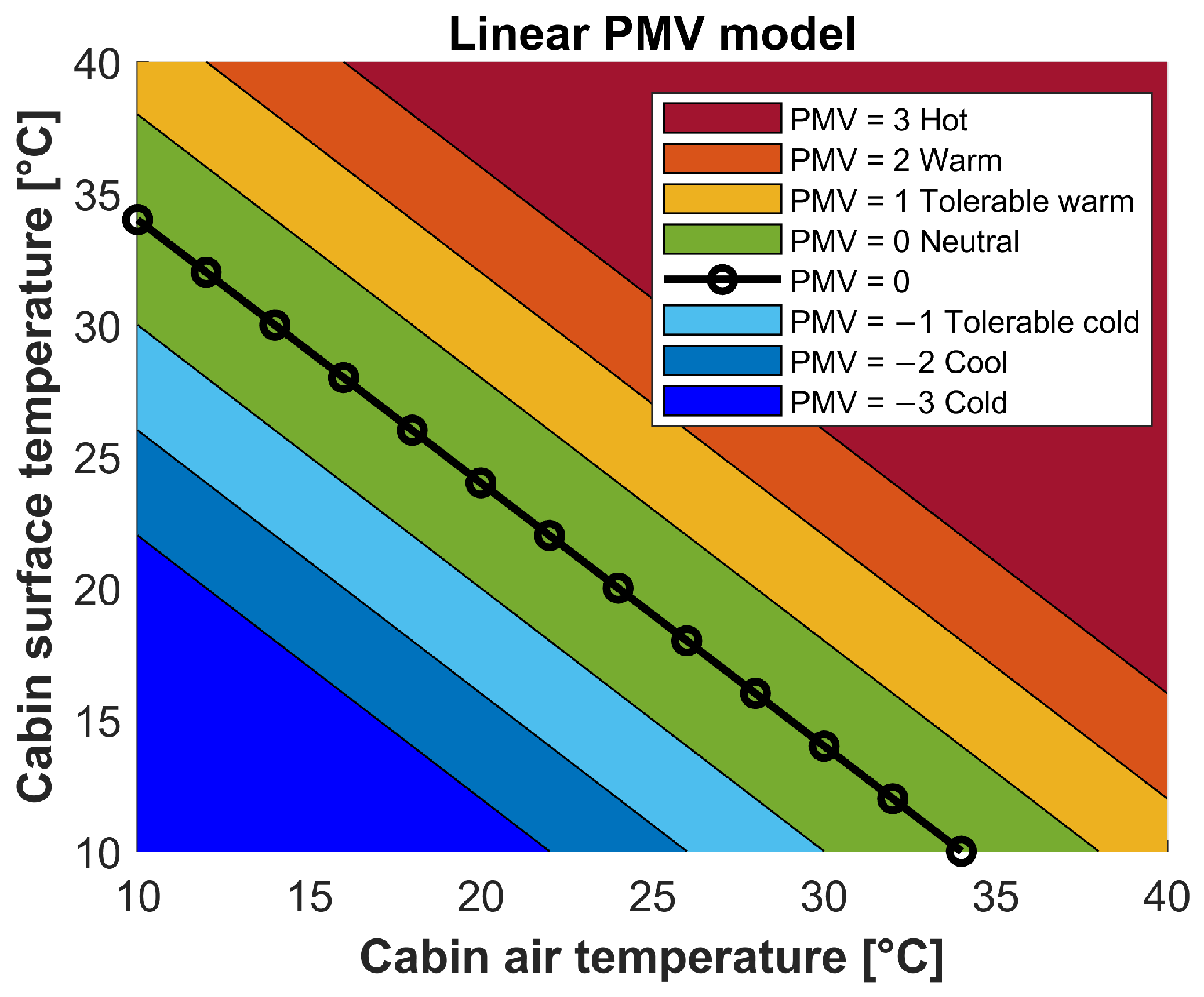
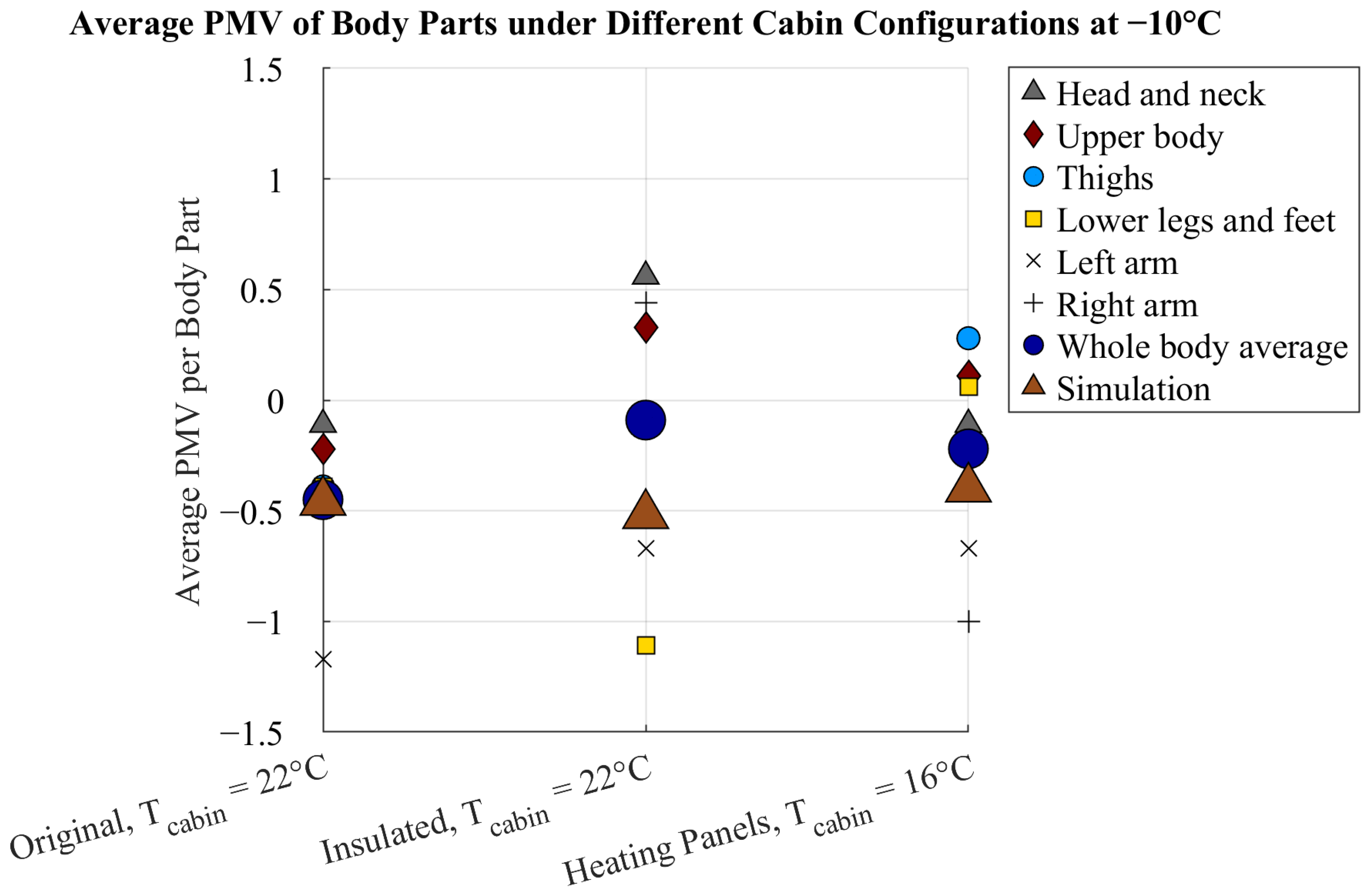
3.3. Comfort Analysis
3.4. Comparison of Laboratory and Climatic Chamber Measurements
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicle |
| BET | Battery Electric Truck |
| CAD | Computer-Aided Design |
| CFD | Computational Fluid Dynamics |
| CO2 | Carbon Dioxide |
| EU | European Union |
| FMU | Functional Mock-up Unit |
| HVAC | Heating, Ventilation, and Air Conditioning |
| HX | Heat Exchanger |
| LCOD | Levelized Cost of Driving |
| MPC | Model Predictive Control |
| OEM | Original Equipment Manufacturer |
| PID | Proportional-Integral-Derivative |
| PMV | Predicted Mean Vote |
| PTC | Positive Temperature Coefficient |
| Ref. | Reference |
| TCO | Total Cost of Ownership |
| 1D | One-Dimensional |
| 3D | Three-Dimensional |
References
- IEA. Global EV Outlook 2024; IEA: Paris, France, 2024; Available online: https://www.iea.org/reports/global-ev-outlook-2024 (accessed on 2 October 2025).
- European Union. The European Green Deal. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en (accessed on 2 October 2025).
- Samet, M.J.; Liimatainen, H.; Pihlatie, M.; van Vliet, O.P.R. Levelized Cost of Driving for Medium and Heavy-Duty Battery Electric Trucks. Appl. Energy 2024, 361, 122976. [Google Scholar] [CrossRef]
- Mu, Z.; Zhao, F.; Bai, F.; Liu, Z.; Hao, H. Evaluating Fuel Cell vs. Battery Electric Trucks: Economic Perspectives in Alignment with China’s Carbon Neutrality Target. Sustainability 2024, 16, 2427. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Mostofi, H. Technical and Business Aspects of Battery Electric Trucks—A Systematic Review. Future Transp. 2022, 2, 382–401. [Google Scholar] [CrossRef]
- Link, S.; Plötz, P. Technical Feasibility of Heavy-Duty Battery-Electric Trucks for Urban and Regional Delivery in Germany—A Real-World Case Study. World Electr. Veh. J. 2022, 13, 161. [Google Scholar] [CrossRef]
- Liimatainen, H.; van Vliet, O.; Aplyn, D. The Potential of Electric Trucks—An International Commodity-Level Analysis. Appl. Energy 2019, 236, 804–814. [Google Scholar] [CrossRef]
- Haiyan, Z.; Dawei, C.; Yu, L. Research on Key Influencing Factors of Endurance Mileage of Battery Electric Vehicle. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 235–239. [Google Scholar] [CrossRef]
- Li, X.; Wang, R. Towards Integrated Thermal Management Systems in Battery Electric Vehicles: A Review. eTransportation 2025, 24, 100396. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, Y.; Chen, A.; Chen, J.; Wu, Y.; Wang, X.; Fei, T. Review of Integrated Thermal Management System Research for Battery Electrical Vehicles. J. Energy Storage 2025, 106, 114662. [Google Scholar] [CrossRef]
- Guo, R.; Li, L.; Sun, Z.; Xue, X. An Integrated Thermal Management Strategy for Cabin and Battery Heating in Range-Extended Electric Vehicles under Low-Temperature Conditions. Appl. Therm. Eng. 2023, 228, 120502. [Google Scholar] [CrossRef]
- Schaut, S.; Sawodny, O. Thermal Management for the Cabin of a Battery Electric Vehicle Considering Passengers’ Comfort. IEEE Trans. Control Syst. Technol. 2020, 28, 1476–1492. [Google Scholar] [CrossRef]
- Dvorak, D.; Kardos, M.; Gellai, I.; Šimić, D. Experimental Performance Investigation of an Air–Air Heat Exchanger and Improved Insulation for Electric Truck Cabins. World Electr. Veh. J. 2025, 16, 129. [Google Scholar] [CrossRef]
- Liew, N.J.Y.; Suhaimi, M.F.B.; Ju, D.; Lee, H. Design and development of electric radiant heaters for local heating inside the cabin of electric vehicles. Appl. Therm. Eng. 2024, 256, 124087. [Google Scholar] [CrossRef]
- Frohner, A.; Dvorak, D.; Bäuml, T.; Simic, D. Novel heating concept for full electric vehicles. Electrotech. Inf. 2015, 132, 168–171. [Google Scholar] [CrossRef]
- Gellai, I.; Popovac, M.; Kardos, M.; Simic, D. Numerical Analysis of the Energy Efficiency Measures for Improving the Truck Cabin Thermal Performance. Eng. Model. Anal. Simul. 2025, 2, 2. [Google Scholar] [CrossRef]
- Cvok, I.; Ratković, I.; Deur, J. Multi-Objective Optimisation-Based Design of an Electric Vehicle Cabin Heating Control System for Improved Thermal Comfort and Driving Range. Energies 2021, 14, 1203. [Google Scholar] [CrossRef]
- Modelica Association. Modelica Standard Library. Available online: https://www.modelica.org/libraries (accessed on 20 August 2025).
- Electronic Temperature Instruments Ltd. Emissivity Table. Available online: https://thermometer.co.uk/img/documents/emissivity_table.pdf (accessed on 2 October 2025).
- TLK-Thermo GmbH. TIL Suite. Available online: https://www.tlk-thermo.com/de/software/til-suite (accessed on 20 August 2025).
- Henner, M.; Beddadi, Y.; Demory, B.; Zangeneh, M. Automotive blower design with inverse method applied on wheel and volute. In Proceedings of the Fan 2015, International Conference on Fan Noise, Technology and Numerical Methods, Lyon, France, 15–17 April 2015. [Google Scholar]
- Bedford, T. Environmental warmth and human comfort. Br. J. Appl. Phys. 1950, 1, 33–38. [Google Scholar] [CrossRef]
- Humphries, K.; Loiselle-Lapointe, A. A Comparison of Heat Pump and Resistive Heating Impacts on Battery Electric Vehicle Energy Consumption and Range in Cold Temperatures. In Proceedings of the 38th International Electric Vehicle Symposium and Exhibition (EVS38), Gothenburg, Sweden, 15–18 June 2025. [Google Scholar]
- Huang, Y.; Khajepour, A.; Bagheri, F.; Bahrami, M. Modeling and Optimal Energy-Saving Control of Automotive Air-Conditioning/Refrigeration Systems. Proc. IMechE Part D J. Automob. Eng. 2016, 230, 1419–1434. [Google Scholar] [CrossRef]




| Parameter | Value | Unit |
|---|---|---|
| Port cross-sectional area (non-circular) | m2 | |
| Port perimeter (non-circular) | m | |
| Louver pitch | m | |
| 2 | – | |
| Fin thickness | m | |
| 5 | – | |
| Heat exchanger height | 0.200 | m |
| Heat exchanger width | 0.300 | m |
| Heat exchanger depth | 0.030 | m |
| {9, 9} | – | |
| Port diameter | m | |
| Louver angle | 90 | ° |
| Tube thickness | m | |
| Louver length | m | |
| Fin pitch | m |
| Quantity | Value | Unit |
|---|---|---|
| Surface area of cabin | 12 | m2 |
| Volume of cabin | 2.4 | m3 |
| Heat capacity of cabin interior | 65,000 | J/K |
| Heat capacity of cabin walls | 21,000 | J/K |
| Heat capacity of air channels | 1040 | J/K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gellai, I.; Kardos, M.; Popovac, M.; Šimić, D. Simulation and Experimental Validation of a 1D Cabin Thermal Model for Electric Trucks with Enhanced Insulation and Heating Panels. World Electr. Veh. J. 2025, 16, 609. https://doi.org/10.3390/wevj16110609
Gellai I, Kardos M, Popovac M, Šimić D. Simulation and Experimental Validation of a 1D Cabin Thermal Model for Electric Trucks with Enhanced Insulation and Heating Panels. World Electric Vehicle Journal. 2025; 16(11):609. https://doi.org/10.3390/wevj16110609
Chicago/Turabian StyleGellai, Imre, Milán Kardos, Mirza Popovac, and Dragan Šimić. 2025. "Simulation and Experimental Validation of a 1D Cabin Thermal Model for Electric Trucks with Enhanced Insulation and Heating Panels" World Electric Vehicle Journal 16, no. 11: 609. https://doi.org/10.3390/wevj16110609
APA StyleGellai, I., Kardos, M., Popovac, M., & Šimić, D. (2025). Simulation and Experimental Validation of a 1D Cabin Thermal Model for Electric Trucks with Enhanced Insulation and Heating Panels. World Electric Vehicle Journal, 16(11), 609. https://doi.org/10.3390/wevj16110609









