Research on Path Planning Based on Multi-Dimensional Optimized RRT Algorithm
Abstract
1. Introduction
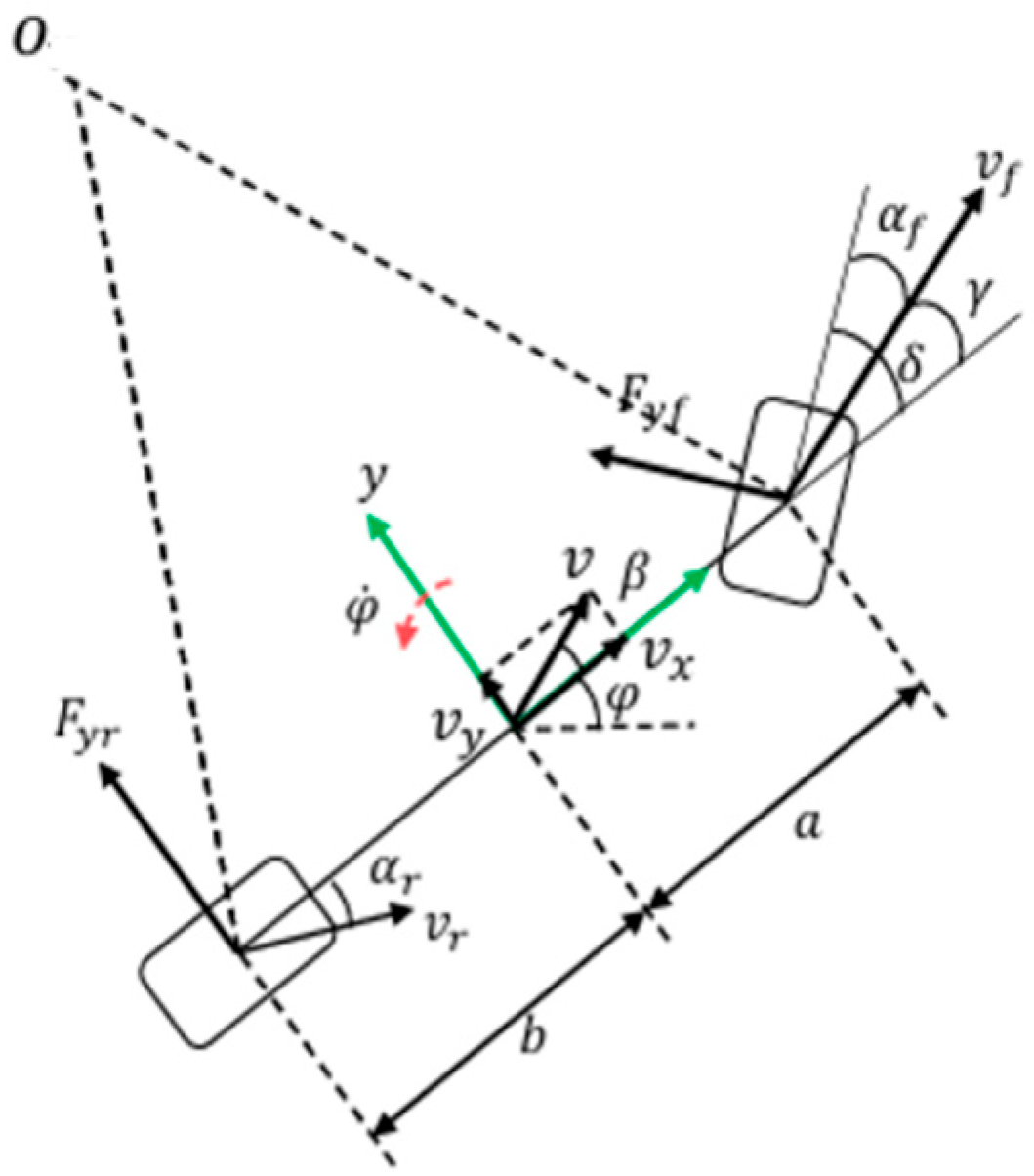
2. Vehicle Dynamics Model
2.1. Establishment of Vehicle Dynamics Model
- (1)
- It is assumed that the vehicle and the suspension are rigidly connected, and the suspension characteristics are not considered.
- (2)
- This paper holds that the vehicle cabin moves only within a plane parallel with the ground. The vehicle’s movement in the direction of the z-axis, as well as the pitch angle about the y-axis and the roll angle around the x-axis, are all equal to zero.
- (3)
- The roll acceleration is confined to within 0.4 g to secure that the tire cornering characteristics are situated in the linear region; (During simulation, the lateral acceleration is monitored in real time. If it exceeds 0.4 g (≈3.92 m/s2), the controller adjusts the front wheel steering angle to reduce lateral load transfer, ensuring roll acceleration stays within the linear range.)
- (4)
- Under the condition of small driving force, we ignore the ground tangential force on the tires and air resistance, as well as the modifications to tire behaviors induced by load fluctuations on the left and right wheels and the influence of tire aligning torque.
- (5)
- The vehicle is assumed to be simplified into a bicycle model, and the lateral load transfer is not considered.
- (6)
- When the vehicle speed is assumed to be constant, the vehicular system is equipped with just two degrees of freedom: lateral displacement and yaw.
2.2. Vehicle Dynamic Model Validation
3. Principle of Basic RRT Algorithm
- (1)
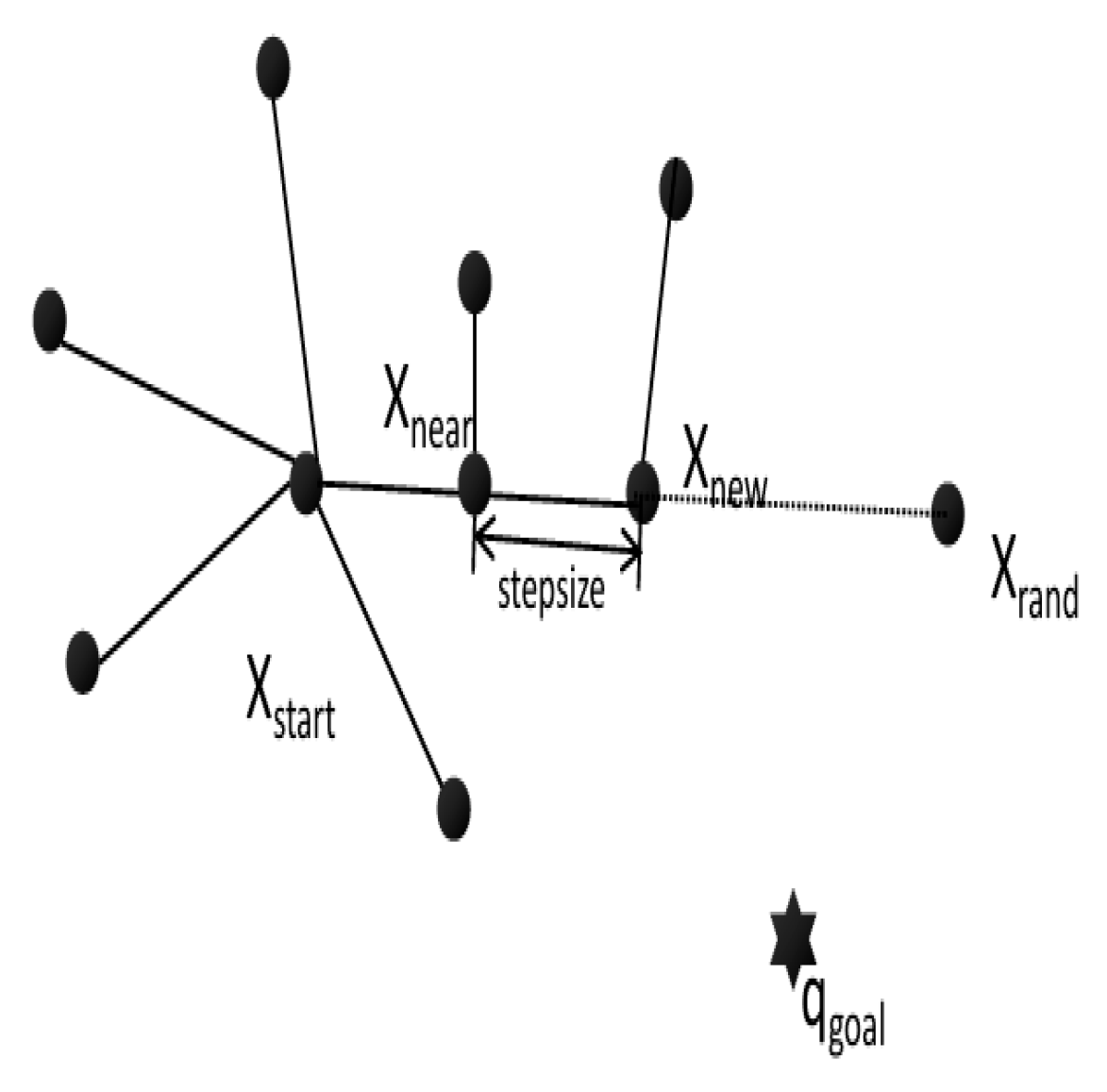
- In the initial setup phase, a random tree (Tree) is constructed, and the start point Xstart is set to be the root node of the tree. At this time, the tree structure contains only this single root node.
- (2)
- Perform random sampling in the map environment. A point Xrand is randomly generated in the environment through the Random Node function. Then, search for the node Xnear with the lowest cost among all the nodes within the random tree to this random point.
- (3)
- Produce a new node. First, define the step size as stepsize. By connecting nodes Xnear and Xrand, determine whether the line between them intersects with obstacles. In the event that no collision exists, a new node Xnew is generated from Xnear according to the step size Stepsize. Subsequently, check whether the line between Xnear and Xnew collides with obstacles. If no collision occurs, Xnew is inserted into the random tree to complete a tree expansion; if a collision occurs, this expansion is abandoned. Repeat steps 2 and 3.
- (4)
- Complete the planning. Once the target node Xgoal is included in the tree, the search process terminates. At this time, a shortest path is formed by connecting the line segment connecting the target point Xgoal and the starting point Xstart. Figure 3 shows the flow framework of the algorithm.
4. Multi-Dimensional Optimized RRT Algorithm
4.1. Target-Biased Random Sampling Strategy
4.2. New Node Expansion Method with Adaptive Step Size
4.3. Node Inflation
4.4. Removal of Redundant Nodes
4.5. Path Smoothing Processing
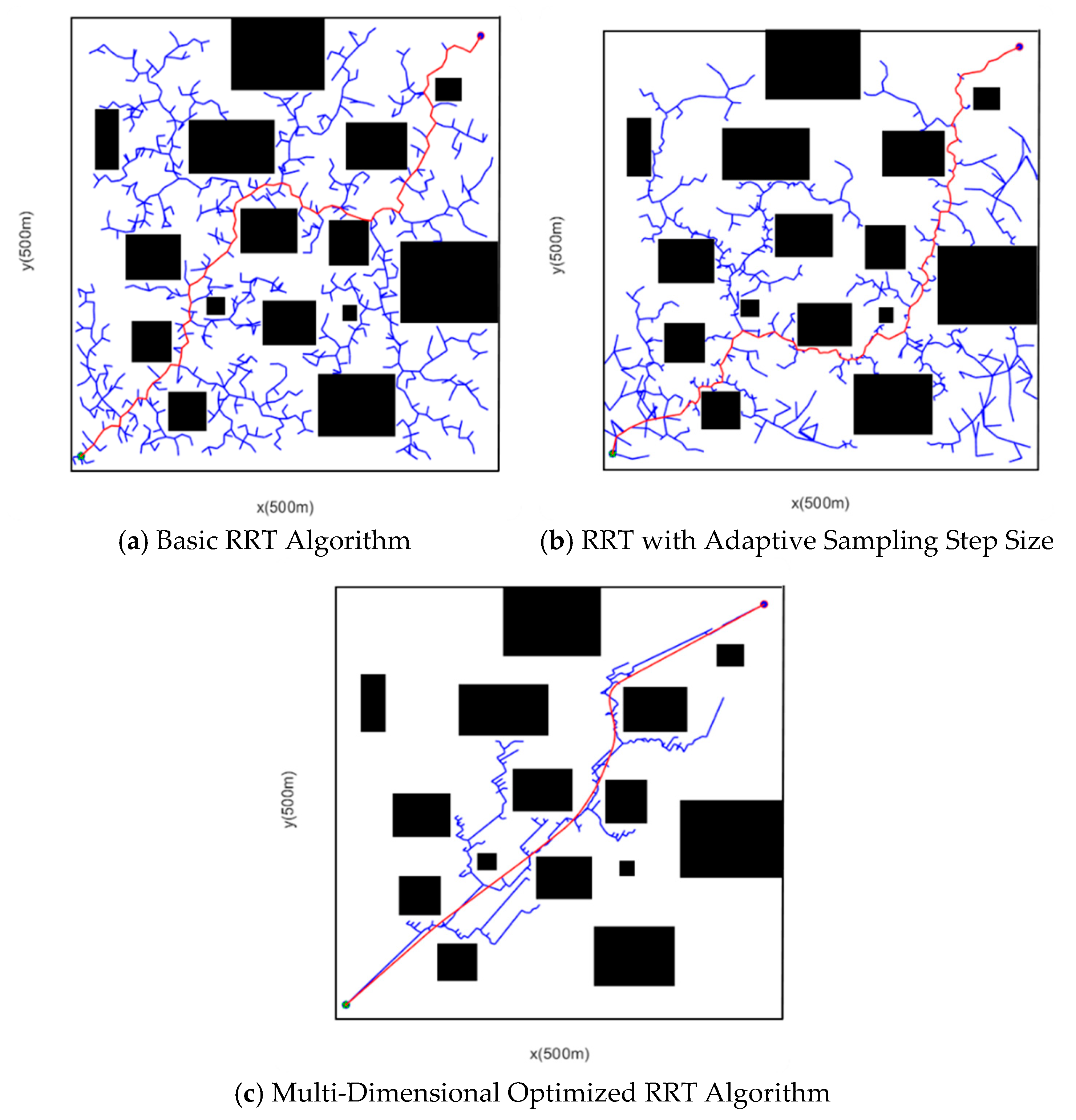
5. Simulation Analysis
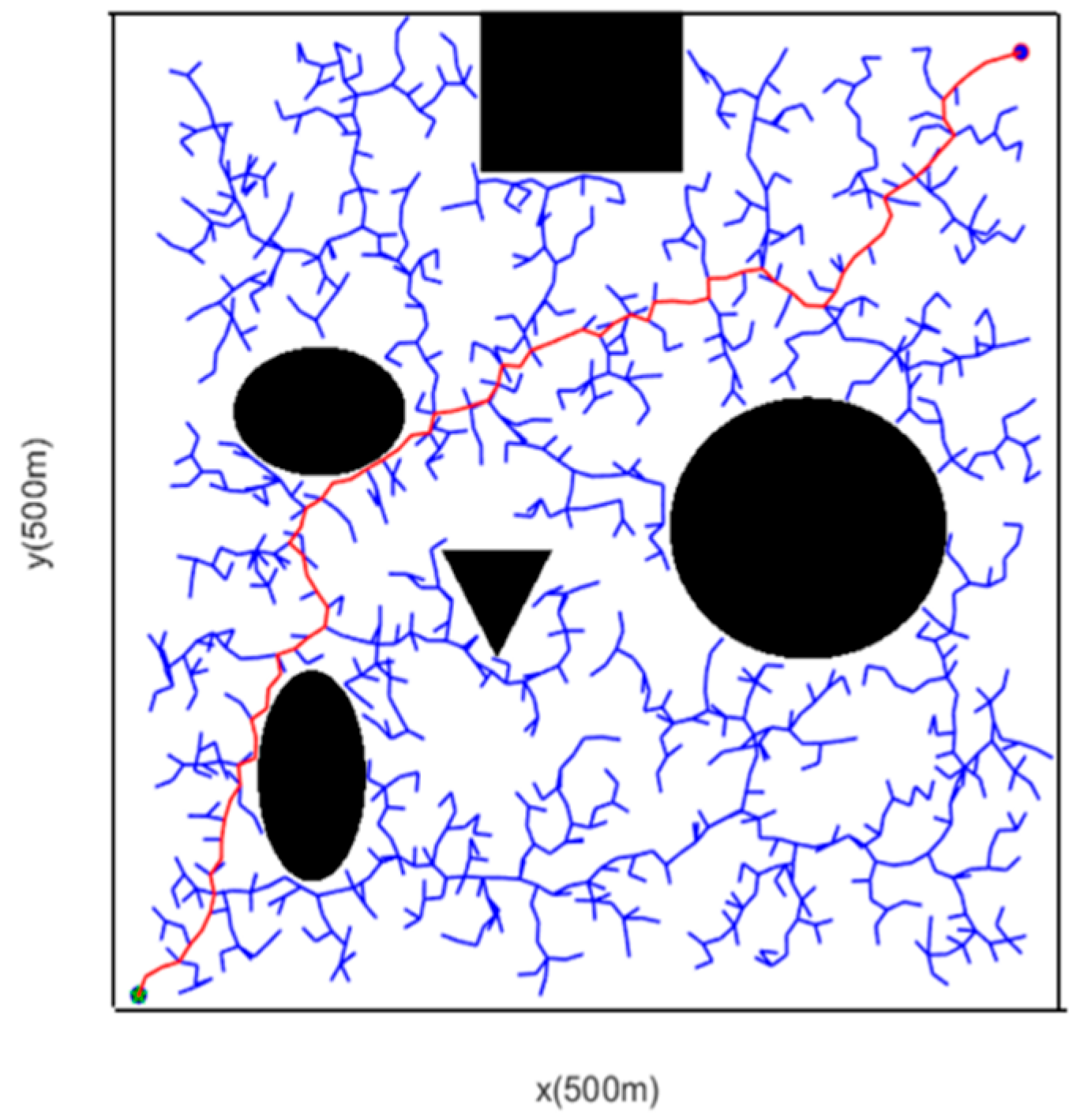
5.1. Simple Obstacle Scenario
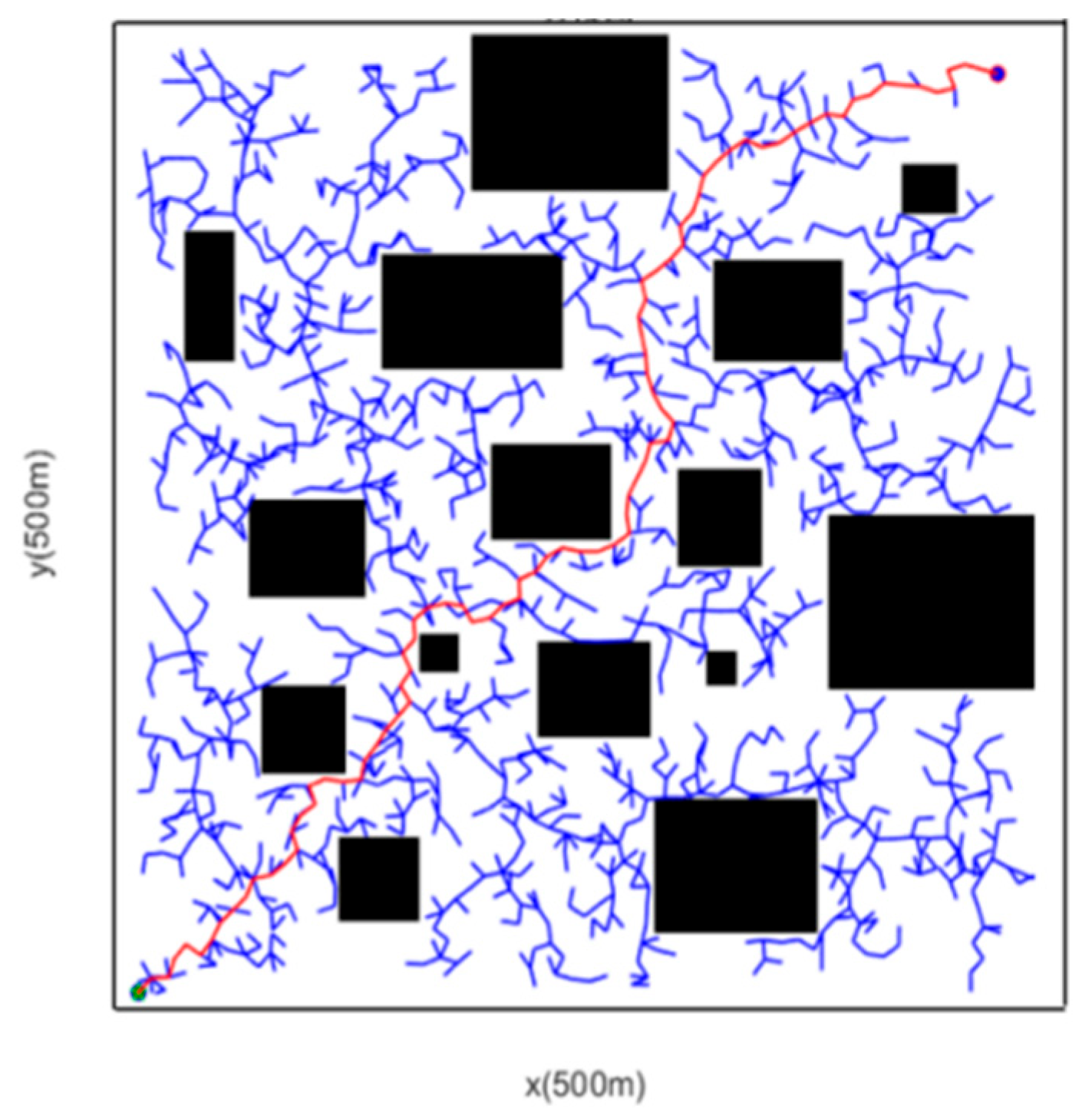
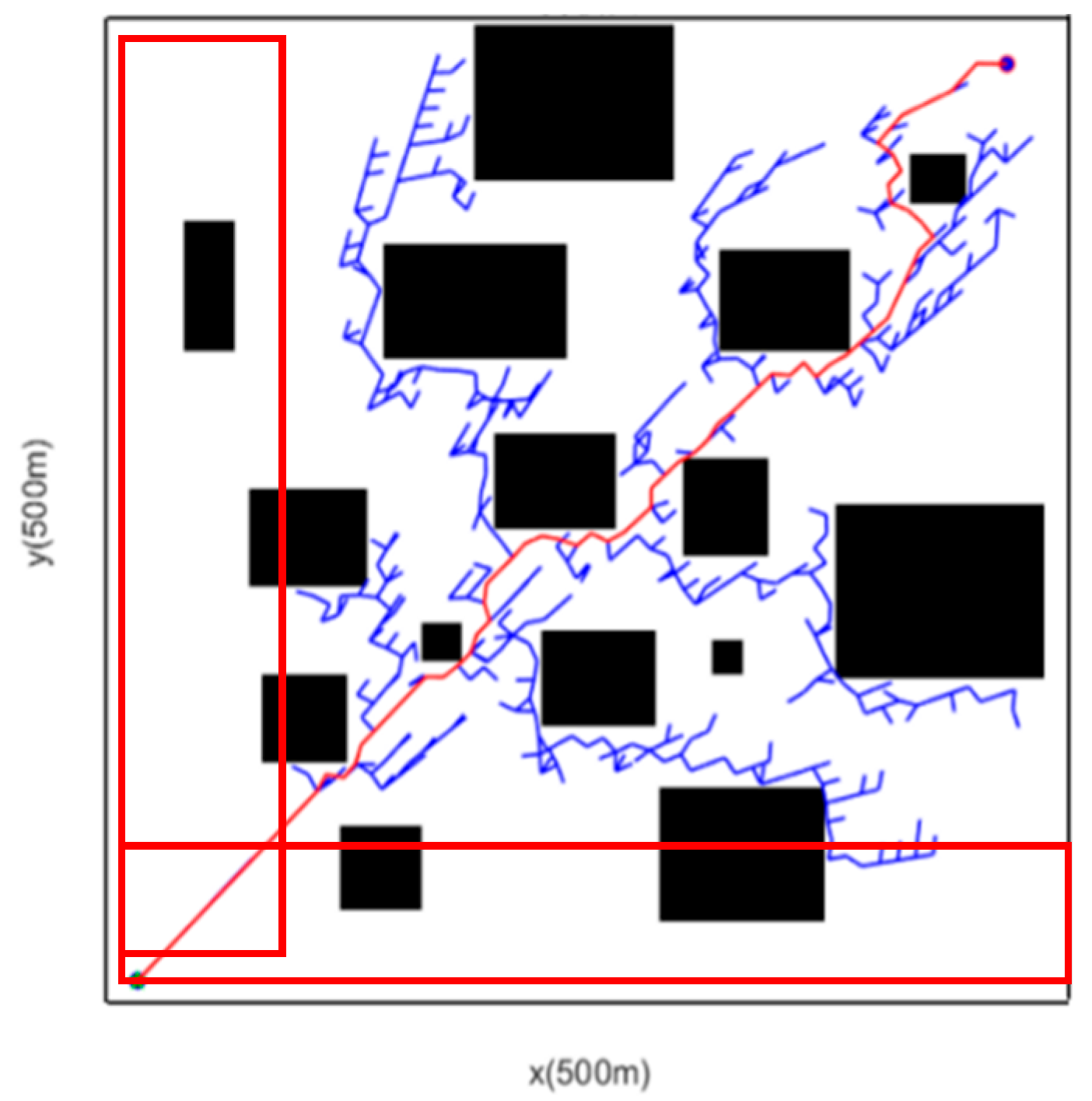
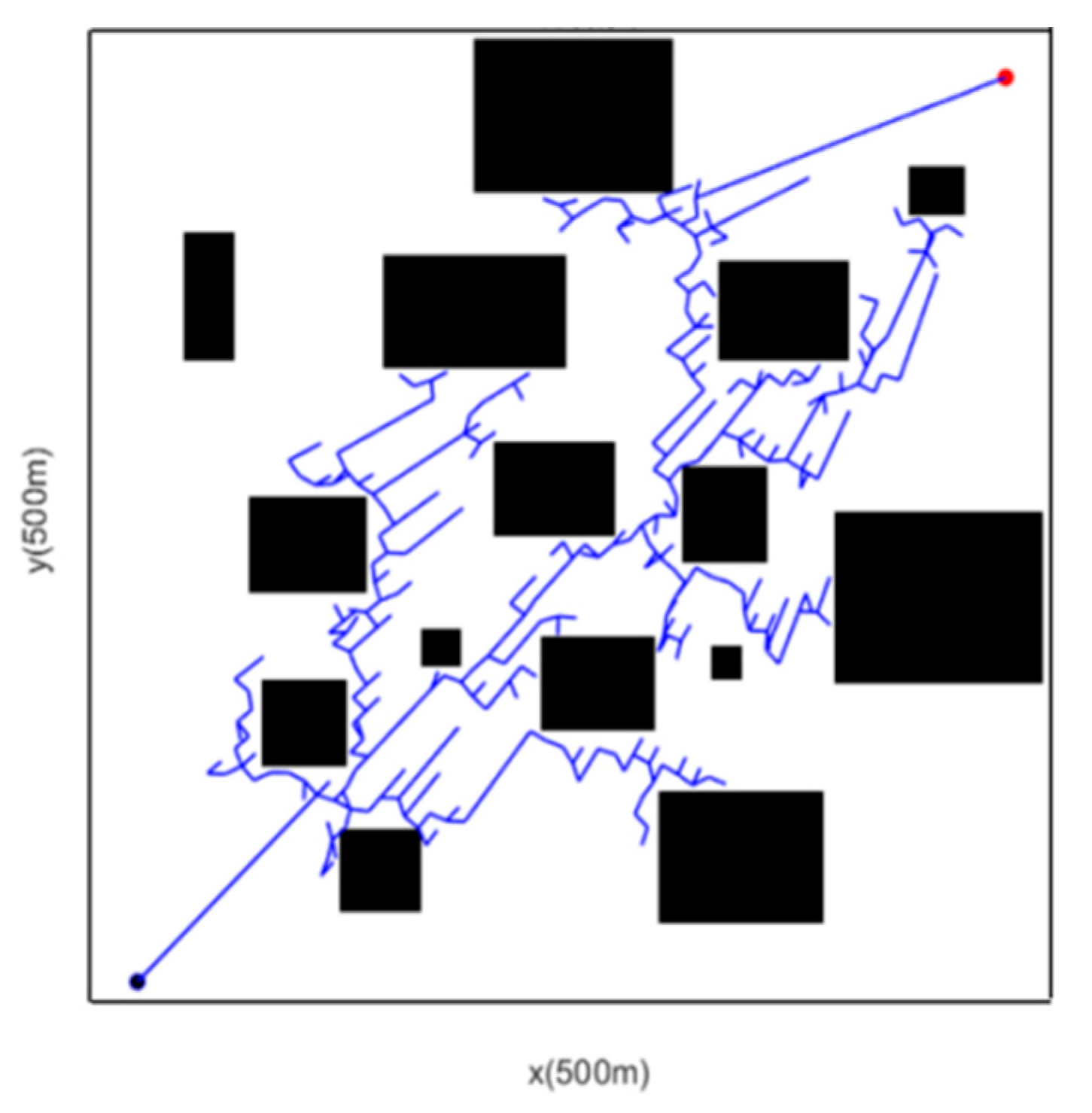
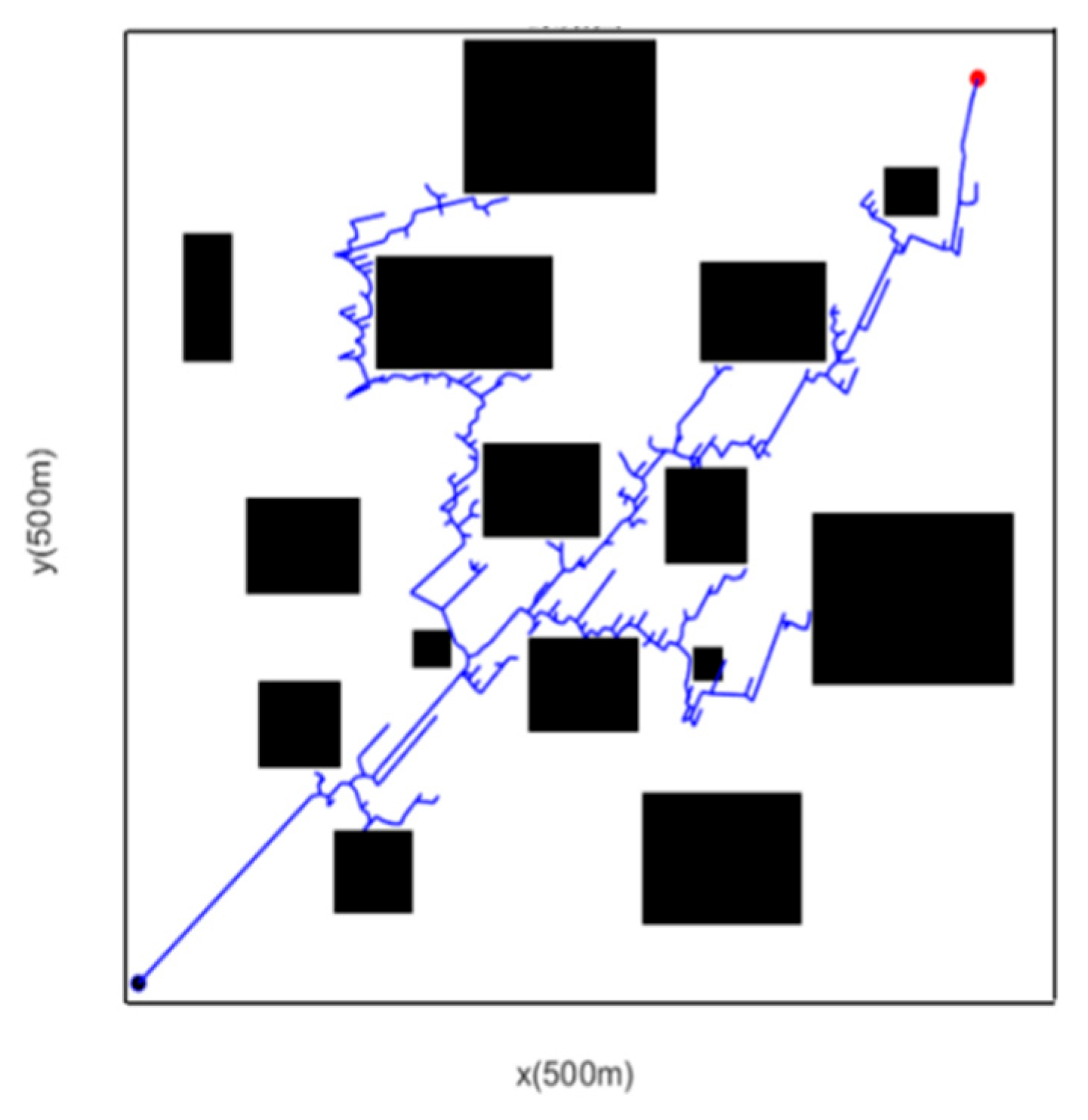
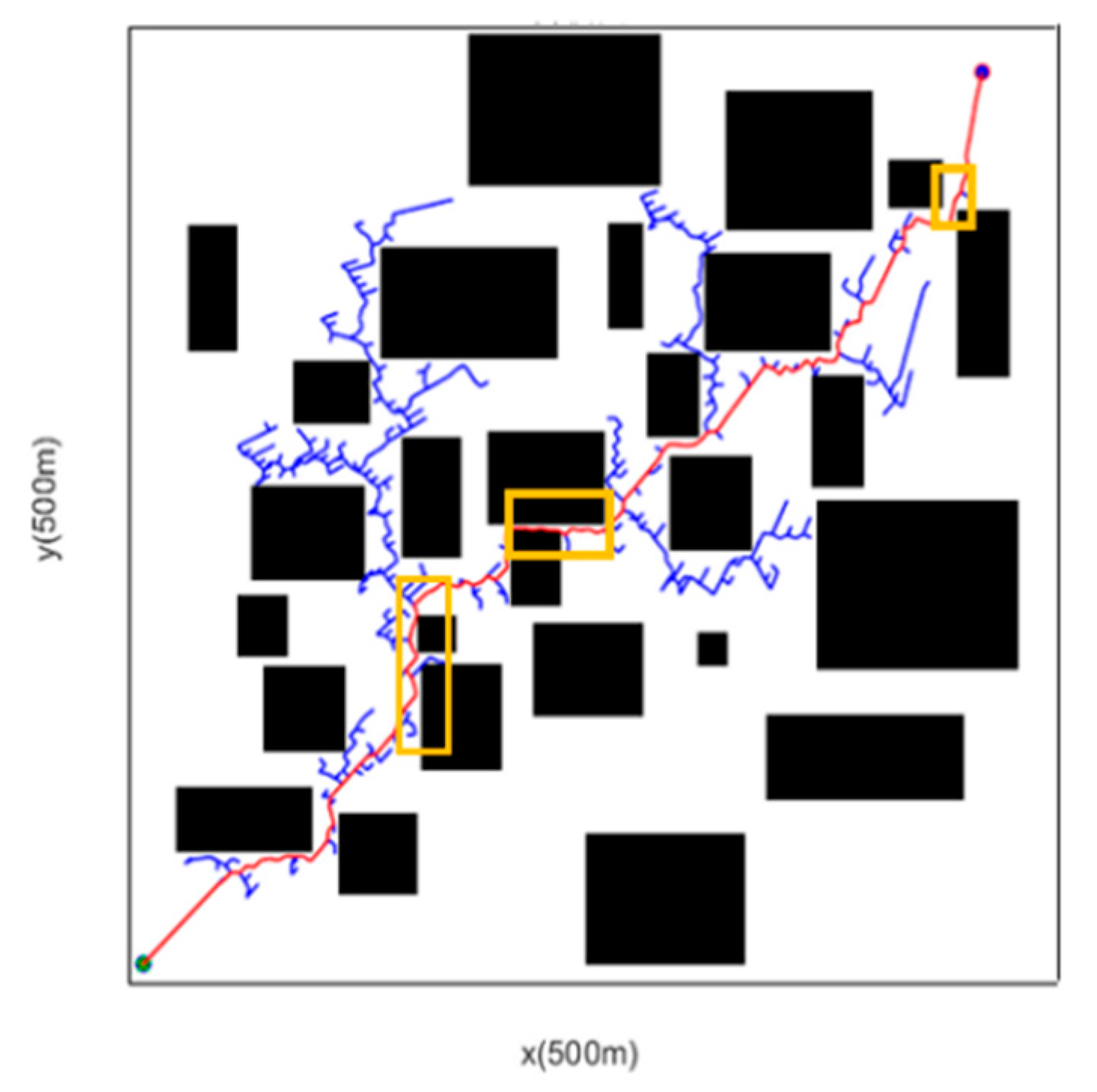
5.2. Complex Obstacle Scenario
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RRT | Rapidly Exploring Random Tree (RRT) |
References
- Wu, J.P.; Li, G.Z.; Zhao, S.; Huang, L. Autonomous driving simulation testing technology drives the intelligent leap of the automotive industry. J. Syst. Simul. 2025, 37, 1649–1664. [Google Scholar]
- Ganesan, S.; Thangamuthu, M.; Ramalingam, B.; Rayguru, M.M.; Tamilselvan, S.N. Accelerating RRT* convergence with novel nonuniform and uniform sampling approach. Sci. Rep. 2025, 15, 28342. [Google Scholar] [CrossRef]
- Pohan, M.A.R.; Trilaksono, B.R.; Santosa, S.P.; Rohman, A.S. Path planning using combined informed rapidly-exploring random tree star and particle swarm optimization algorithms. IEEE Access 2024, 12, 56582–56608. [Google Scholar] [CrossRef]
- Lin, Z.; Li, Y.F.; Zhang, Y.J. Trajectory planning of seven-degree-of-freedom redundant manipulator in narrow space. AIP Adv. 2024, 14, 12. [Google Scholar]
- Guo, S.; Gong, J.; Shen, H.; Yuan, L.; Wei, W.; Long, Y. DBVSB-P-RRT*: A path planning algorithm for mobile robot with high environmental adaptability and ultra-high speed planning. Expert Syst. Appl. 2025, 266, 126123. [Google Scholar] [CrossRef]
- Göktaş, A.G.; Sezer, S. A New Local Path Planning Approach by Synthesis of PRM and RRT* Algorithms for an Autonomous Mobile Robot. J. Control Autom. Electr. Syst. 2025, 36, 72–85. [Google Scholar] [CrossRef]
- Zhu, B.; Han, J.Y.; Zhao, J.; Liu, S.; Deng, W.W. A path planning method for intelligent vehicles based on RRT* algorithm improved by safety field. Automot. Eng. 2020, 42, 1145–1150, 1182. [Google Scholar]
- Arifi, A.; Jarray, R.; Bouallègue, S. Performance comparison of rapidly-exploring random tree algorithms for path planning of autonomous underwater vehicles in complex environments. Int. J. Intell. Robot. Appl. 2024, 9, 628–653. [Google Scholar] [CrossRef]
- Wang, Y.C.; Yang, M.Y.; Zhang, G.H. Research on path planning of automated guided vehicle based on improved A* algorithm. Fire Control Command. Control 2021, 46, 130–138, 144. [Google Scholar]
- Hu, Q.M.; Wang, J.G.; Zhang, X.J. Parallel parking path planning optimized by quintic polynomial. Comput. Eng. Appl. 2022, 58, 291–298. [Google Scholar]
- Zhong, H.; Cong, M.; Wang, M.; Du, Y.; Liu, D. HB-RRT: A path planning algorithm for mobile robots using Halton sequence-based rapidly-exploring random tree. Eng. Appl. Artif. Intell. 2024, 133, 108362. [Google Scholar] [CrossRef]
- Burzyński, W.; Stecz, W. Trajectory planning with multiplatform spacetime RRT. Appl. Intell. 2024, 54, 9524–9541. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Z.; Liu, J.; Liu, S. Research on APF-Bi-RRT algorithm of adaptive step strategy for robot path planning. Arab. J. Sci. Eng. 2024, 50, 14197–14210. [Google Scholar] [CrossRef]
- Tang, Z.; Ma, H.; Xue, B. Research on autonomous mobile robot path planning based on M-RRT algorithm. Inf. Technol. Control 2024, 53, 442–452. [Google Scholar] [CrossRef]
- Uwacu, D.; Yammanuru, A.; Nallamotu, K.; Chalasani, V.; Morales, M.; Amato, N.M. HAS-RRT: RRT-Based Motion Planning Using Topological Guidance. IEEE Robot. Autom. Lett. 2025, 10, 6223–6230. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, L. An improved Quick Informed-RRT* algorithm based on hybrid bidirectional search and adaptive adjustment strategies. Intell. Serv. Robot. 2024, 17, 847–870. [Google Scholar] [CrossRef]
- Li, N.; Han, S.I. Adaptive Bi-Directional RRT Algorithm for Three-Dimensional Path Planning of Unmanned Aerial Vehicles in Complex Environments. IEEE Access. 2025, 13, 23748–23767. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, Z.; Dong, C. A Path Planning Algorithm Based on Improved RRT Sampling Region. Comput. Mater. Contin. 2024, 80, 4303–4323. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, X.; Tang, L.; Wang, Y.; Peng, J.; Zou, J. RRT Autonomous Detection Algorithm Based on Multiple Pilot Point Bias Strategy and Karto SLAM Algorithm. Comput. Mater. Contin. 2024, 78, 2111–2136. [Google Scholar] [CrossRef]
- Wu, W.Q.; Kong, C.X.; Xiao, Z.M.; Huang, Q.P.; Yu, M.F.; Ren, Z.Y. Multi-Indicator Heuristic Evaluation-Based Rapidly Exploring Random Tree Algorithm for Robot Path Planning in Complex Environments. Machines 2025, 13, 274. [Google Scholar] [CrossRef]
- Jordan, M.; Perez, A. Optimal Bidirectional Rapidly-Exploring Random Trees; Computer Science and Artificial Intelligence Laboratory (CSAIL), Massachusetts Institute of Technology: Cambridge, MA, USA, 2013. [Google Scholar]
- Jeong, I.B.; Lee, S.J.; Kim, J.H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Huang, G.H.; Ma, Q.L. Research on Path Planning Algorithm of Autonomous Vehicles Based on Improved RRT Algorithm. Int. J. Intell. Transp. Syst. Res. 2022, 20, 170–180. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; TR 98-11; Computer Science Department, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Guan, T.; Han, Y.; Kong, M.; Wang, S.; Feng, D.; Yang, W. An improved artificial potential field with RRT star algorithm for autonomous vehicle path planning. Sci. Rep. 2025, 15, 16982. [Google Scholar] [CrossRef] [PubMed]
- Qi, E.; Zhang, T.; Zhao, L.; Han, F.; Ge, J.; Qi, Y.; Qi, Y. Research on robotic arm path planning method based on two-stage RRT* optimization algorithm. Eng. Res. Express 2025, 7, 035416. [Google Scholar] [CrossRef]
- Ziegler, J.; Stiller, C. Fast collision checking for intelligent vehicle motion planning. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium (IV), La Jolla, CA, USA, 21–24 June 2010; IEEE: San Diego, CA, USA, 2010; pp. 518–522. [Google Scholar]
- Huang, Y.; Jiang, W.; Xu, S. A multi strategy bidirectional RRT* algorithm for efficient mobile robot path planning. Sci. Rep. 2025, 15, 29501. [Google Scholar] [CrossRef]
- Qiao, Y.F.; Wang, H.X.; Zhou, S.W.; Yang, G.J. Research on path planning of unmanned vehicles based on improved RRT algorithm. Mach. Des. Manuf. 2023, 276–281+285. [Google Scholar] [CrossRef]
- Shao, L.; Liu, H.; Chen, C.; Du, D.; Li, J.; Liu, H. Path planning for mobile robots based on improved RRT algorithm. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020; IEEE: San Diego, CA, USA, 2020; pp. 1240–1244. [Google Scholar]
- Chen, Z.X.; Yang, Y.; Xu, X.R.; Rodic, A. Path planning of redundant series manipulators based on improved RRT algorithms. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 553–557. [Google Scholar]
- Mashayekhi, R.; Idris, M.Y.I.; Anisi, M.H.; Ahmedy, I.; Ali, I. Informed RRT*-Connect: An asymptotically optimal single-query path planning method. IEEE Access 2020, 8, 19842–19852. [Google Scholar] [CrossRef]






| Number of Sampling Points | Running Time (s) | Path Length (m) | |
|---|---|---|---|
| Before Optimization | 1404 | 28.4 | 873.3 |
| After Optimization | 371 | 3.6 | 796.9 |
| Number of Sampling Points | Running Time (s) | Path Length (m) | |
|---|---|---|---|
| Fixed Step Size | 904 | 12.0 | 831.8 |
| Dynamic Step Size | 797 | 9.6 | 783.4 |
| Algorithm | Number of Sampling Points | Running Time (s) | Path Length (m) |
|---|---|---|---|
| RRT | 949 | 15.7948 | 798.2348 |
| RRT with adaptive sampling step size | 622 | 6.4107 | 774.8383 |
| Multi-Dimensional Optimized RRT | 232 | 3.25258 | 673.8413 |
| Algorithm | Number of Sampling Points | Running Time (s) | Path Length (m) |
|---|---|---|---|
| RRT | 949 | 15.79 | 798.23 |
| Q-RRT* (Ref. [22]) | 723 | 11.56 | 738.45 |
| Multi-Dimensional Optimized RRT | 232 | 3.25 | 673.84 |
| Algorithm | Number of Sampling Points | Running Time (s) | Path Length (m) |
|---|---|---|---|
| RRT | 1010 | 26.8499 | 892.3703 |
| RRT with adaptive sampling step size | 933 | 23.1196 | 870.7378 |
| Multi-Dimensional Optimized RRT | 636 | 11.0702 | 699.6111 |
| Algorithm | Number of Sampling Points | Running Time (s) | Path Length (m) |
|---|---|---|---|
| RRT | 1010 | 26.85 | 892.37 |
| Q-RRT* (Ref. [22]) | 892 | 20.14 | 812.36 |
| Multi-Dimensional Optimized RRT | 636 | 11.07 | 699.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Pang, T.; Zhang, W.; Liao, W.; Du, T. Research on Path Planning Based on Multi-Dimensional Optimized RRT Algorithm. World Electr. Veh. J. 2025, 16, 605. https://doi.org/10.3390/wevj16110605
Wang J, Pang T, Zhang W, Liao W, Du T. Research on Path Planning Based on Multi-Dimensional Optimized RRT Algorithm. World Electric Vehicle Journal. 2025; 16(11):605. https://doi.org/10.3390/wevj16110605
Chicago/Turabian StyleWang, Jinbo, Tongjia Pang, Weihai Zhang, Wei Liao, and Tingwei Du. 2025. "Research on Path Planning Based on Multi-Dimensional Optimized RRT Algorithm" World Electric Vehicle Journal 16, no. 11: 605. https://doi.org/10.3390/wevj16110605
APA StyleWang, J., Pang, T., Zhang, W., Liao, W., & Du, T. (2025). Research on Path Planning Based on Multi-Dimensional Optimized RRT Algorithm. World Electric Vehicle Journal, 16(11), 605. https://doi.org/10.3390/wevj16110605






