Abstract
The rapid adoption of electric vehicles (EVs) requires efficient charging infrastructure planning. This study proposes a multi-objective optimization model for siting and capacity planning of EV charging stations, distinguishing between fast and slow chargers. The model integrates investment, dynamic electricity costs, and user experience, factoring in congestion-adjusted travel distances, time-of-use pricing, and queuing delays using an enhanced M/M/c approach. A comparison of algorithm reveals that the simulated annealing (SA) algorithm outperforms the genetic algorithm (GA) and ant colony optimization (ACO) in minimizing total costs. A case study in Changchun’s urban core demonstrates the model’s applicability, resulting in an optimal plan of 15 stations with 110 fast and 40 slow chargers, providing 11,544 kVA capacity at an annual cost of 38.2651 million yuan. Compared to traditional models that ignore charger types and simplify delays, the proposed model reduces total system costs by 4.31%, investment costs by 5.31%, and user costs by 3%, while easing delays in high-demand areas. This framework provides practical insights for urban planners and policymakers, helping balance investment and user satisfaction, and promoting sustainable EV mobility.
1. Introduction
The electrification of transportation is accelerating worldwide, driven by climate policies, technological advances, and consumer adoption of EVs. This transition brings new challenges for urban infrastructure systems, particularly the charging network, which must be planned to ensure adequate accessibility, service reliability, and economic feasibility. Poorly planned charging systems can lead to congestion, long waiting times, inefficient utilization of chargers, and unnecessary investment costs [1]. Therefore, developing intelligent planning frameworks for EV charging stations is critical for supporting sustainable urban mobility. Existing research on charging infrastructure has primarily focused on three areas: station siting, capacity design, and network operation. Many studies adopt traditional coverage models or other optimization methods to enhance accessibility. Others emphasize capacity sizing, typically estimating the number of chargers required to meet demand [2,3]. However, three important gaps remain. First, most models do not differentiate between fast and slow chargers, despite their very different impacts on both user convenience and grid operation. Second, user costs are often simplified, neglecting factors such as congestion-adjusted travel detours or queuing delays, which significantly influence service quality. Third, validation often relies on theoretical or stylized scenarios, limiting the practical value of results for policymakers and urban planners [4,5,6,7].
Regarding the layout and planning of EVs, different experts and scholars have conducted in-depth research from multiple perspectives and put forward their own insights and suggestions. MirHassani et al. [8] proposed two different flow-based requirements modeling concepts and conducted site selection based on this model. However, the user cost was not taken into consideration. Wiederer [9] mainly conducted in-depth research on the rational layout of charging facilities from the perspective of the urban traffic network. Research suggests that by optimizing the layout of charging facilities and enhancing the convenience of charging for EVs, the charging experience of users can be significantly improved, thereby increasing user satisfaction. However, the impact of construction costs and electricity costs was not considered. Moreover, there is no distinction between fast and slow types of charging piles. Jing et al. [10] took maximizing the traffic of EVs as the objective function and constructed a two-layer optimization model for the layout of EV charging stations. However, the impact of user-side costs was not considered. Bayram et al. [11] conducted an in-depth analysis of the charging load problem of EVs, studied the impact of different charging loads on the operation of the power grid, and constructed a stochastic model associated with the charging station network to achieve the optimal allocation of power resources. However, the impact of queuing time cost on the user side was not taken into consideration. Upchurch et al. [12] proposed a capacity-constrained interception and continuation charging model, specifically to study the site selection problem of charging stations for EVs. By using a specific case in the Arizona highway network, they verified the validity of the model and provided an operational theoretical basis for practical application. However, fewer practical factors were considered, such as queuing time and so on.
Liu H. [13] in combination with the node requirements and passing requirements, as well as the service radius, constructed a location model for the charging facilities of EVs, After comprehensively considering the influencing factors such as the future charging mode of EVs, the power of charging piles, users’ charging behavior habits and users’ site selection conditions. However, the impact of the real-time electricity price for charging on the user side was not taken into consideration. Yu J. C. [14] established a charging station site selection model and capacity determination model that included the annual investment cost of charging stations and the annual time cost of users. However, in the user queuing theory system, insufficient consideration has been given. Zhang H. C. [15], considering constraints such as the number of public charging stations, service scope and emergency mileage of EVs, constructed a location model for public charging facilities of EVs based on minimizing the generalized cost for investors and users, The candidate locations of public charging facilities were obtained by using the weighted K-Means clustering algorithm, and the optimal location scheme was determined by calculating the contour coefficient of the comparison and selection schemes. However, the proportion of fast and slow charging piles was not taken into consideration. When Cheng J. X. [16] was constructing the multi-objective programming model for EVs, she comprehensively considered the construction and operation costs of charging stations for operators, as well as the annual travel time cost during charging, the annual waiting time cost for charging, and the annual charging time and electricity price cost for new energy EV users. However, the real-time electricity price of the charging piles was not taken into consideration. While prior studies have considered investment and demand factors, few explicitly incorporate charger heterogeneity and queuing-based user costs, limiting their applicability to real-world urban contexts.
Overall, although many studies on the site selection and capacity determination of EV charging stations have been carried out at present, the impact of various factors in real life on them has not been fully considered. For instance, the electricity price of charging stations has not been fully considered. Currently, the electricity price of charging stations is not constant. Without considering the weight ratio of fast and slow charging within the charging station, from the perspective of the operator, setting up a combined mode of fast and slow charging in the charging station has many advantages compared to pure fast charging stations. To address these gaps, this study develops a multi-objective optimization framework that integrates investment and user costs into site selection and capacity planning. The framework introduces three major innovations. First, it explicitly distinguishes between fast and slow chargers and incorporates charger allocation ratios into the optimization process, thus improving the realism of infrastructure design. Second, it applies an enhanced M/M/c queuing model to estimate user waiting times and service delays, thereby advancing cost modeling beyond conventional approaches. Third, it validates the model through a real-world case study of Changchun’s urban core, using spatial demand data and benchmarking across three classical metaheuristic algorithms. The contributions of this study are both methodological and practical. Methodologically, it advances the literature by integrating charger type heterogeneity and queuing-based user costs into a unified framework. Practically, it offers a robust tool for urban planners and policymakers to balance infrastructure investment with service quality in the face of rapidly growing EV demand. By linking optimization modeling with real-world data and engineering constraints, the study provides actionable insights for the sustainable deployment of EV charging networks and contributes to the broader objectives of smart mobility and resilient urban infrastructure. These contributions not only advance methodological rigor but also provide actionable guidance for policymakers and urban planners in designing efficient and resilient EV charging networks.
2. Materials and Methods
2.1. Model Assumption Conditions and Flowchart
2.1.1. Model Assumption Conditions
Before designing the site selection model for EVs, it is necessary to set up hypothetical conditions. These hypothetical conditions can clarify the boundaries of the optimization objective and enhance the optimization effect. In real life, charging station location involves many complex factors, such as traffic flow, user charging behavior, and land use restrictions. Direct modeling would significantly increase the computational difficulty. Therefore, assumptions can reduce the number of variables and constraints, making the problem easier to solve. Without assumptions, the location model may become too large or unsolvable, making it difficult to obtain a feasible optimization solution. After the initial establishment of the model, simulation and verification are usually required to test the rationality of the site selection plan. If there are no assumptions, the test results may be difficult to analyze and even hard to identify problems. Therefore, the hypothetical conditions can provide benchmarks, making model validation more intuitive. Reasonable setting of assumption conditions is an indispensable step. It can simplify the calculation, improve the feasibility of the model, enhance the optimization effect, and ultimately help decision-makers make more scientific and reasonable site selection decisions. The hypothetical conditions set in this article are as follows:
- The actual traffic road network of the study area is abstracted into a network topology using ArcGIS software (https://www.arcgis.com/index.html), and the charging demand points within the study area are topologically processed to facilitate the site selection analysis and optimization of charging stations [17].
- The demand point and the construction site form a constant area. The daily demand at the demand points within the research area is uniform, and it is solely dependent on the population.
- The electricity consumption of EVs is directly proportional to their driving range. The energy consumption for the functionality use of EVs is negligible and can be ignored.
- The arrival rate of electric vehicle users follows the Poisson distribution and is only related to the conditions of the charging station itself and its surrounding environment.
- Users tend to choose charging stations that are nearer to their location, following the principle of proximity.
- Each waiting point operates as a queuing system with a fixed daily arrival rate. Each vehicle to be charged will not undergo secondary charging on the day of charging.
- Users choose fast or slow charging based on their needs (e.g., time constraints or free time), so they do not interfere with each other.
2.1.2. Optimization Framework Flowchart
The overall framework flowchart is shown in Figure 1.
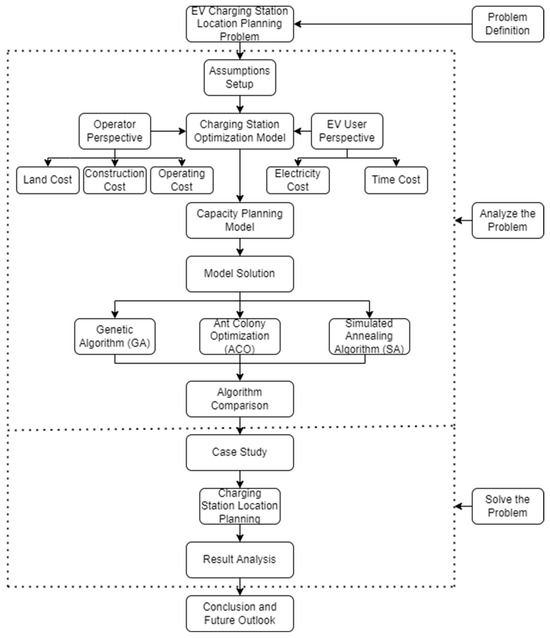
Figure 1.
Optimization process framework diagram.
2.2. Construction of the Optimal Site Selection and Capacity Determination Model for Charging Stations
2.2.1. Investment Cost Model Design
Unlike existing approaches, our framework explicitly integrates charger type allocation and queuing-based service modeling into the site selection and sizing optimization problem. The optimization model established in this study considers both the operator’s investment cost and user cost, with each having a weight of 50%.
The symbols explained and parameter settings are listed in Table 1.

Table 1.
Parameter Setting Table.
From the perspective of operators, the site selection model for EVs should consider the minimum investment cost. The investment cost of EV charging stations mainly includes land cost, station construction cost and operation cost. The land cost is related to the geographical location and land area of the charging station. The construction cost is related to the infrastructure cost of the charging station and the number of stations built. The operation cost is affected by factors such as workers’ wages, maintenance expenses, the number of charging stations and the years of operation. These costs are crucial for evaluating the economic feasibility of deploying EV charging stations. The reason for prioritizing investment cost is that it directly influences the financial sustainability of the charging network. Overinvestment may lead to excessive infrastructure development that does not correspond to actual demand, while underinvestment may result in insufficient coverage, leading to poor service quality. Therefore, considering investment costs ensures that the charging network is developed within reasonable financial constraints.
Cities that promote EVs are usually economically developed and have relatively tight land resources. Therefore, when building charging stations, land costs need to be given priority consideration. For operators, land is of utmost importance. Reasonable land prices will further encourage operators to establish charging stations, while the opposite will consume the demand of operators for building charging stations. Land prices are closely related to the region where they are located. Therefore, land prices need to be calculated based on the locations of different stations to be built. The calculation equation for land cost per unit area is Equation (1)
The construction cost mainly refers to the investment cost of charging piles and their supporting facilities, which is usually directly related to the number of charging piles. The construction cost comprehensively considers the setting of fast and slow charging in the charging station. Compared with pure fast charging stations, fast and slow charging mixed stations have many advantages:
- It can reduce costs. The combination of fast and slow charging can enhance the overall profitability through a differentiated pricing strategy.
- From the perspective of users of EVs, the combination of fast and slow charging can increase the utilization rate of charging stations, reduce queuing, fast charging is suitable for users who stay for a short time, and slow charging is suitable for users who park for a long time. By adopting the combination of fast and slow charging, it can meet the needs of different users, improve the service capacity of charging stations, and enhance the user experience.
- The combination of fast and slow charging can reduce the load impact on the power grid and optimize power dispatching.
The specific calculation equation for construction cost is Equation (2)
Operating costs mainly refer to labor expenses, wear and tear of supporting facilities, and daily maintenance costs, etc., and are usually directly proportional to construction costs. For operators, it is necessary to consider the usage wear and tear of charging piles, as well as the daily working hours of charging stations, which are measured in units of 365 days a year. The specific equation for calculating operating costs is Equation (3)
For operators, the construction of charging piles within EV charging stations involves a large amount of initial investment, such as equipment, construction, and power grid renovation, while the returns are gradually recovered over the long term. To assess whether an investment is worthwhile, future returns need to be converted to the current time point, and this requires the use of the discount rate [18]. The discount rate refers to the interest rate used when converting the value of future assets into present value, usually set as . The discount rate can be used to determine whether the payback period of an investment is reasonable, and a better investment plan can also be selected through the discount rate. The specific conversion rules are shown in Table 2.

Table 2.
Cash Flow Conversion Rules.
Suppose the normal operating years of the charging station are n, the total investment cost of the current year is T, and the average annual investment cost converted to the future is S. If the station starts operation in the first year after its completion, the conversion needs to be made from the first year in the future. From this, the equation can be obtained is Equation (4)
After organizing the equation, Equation (5) can be obtained:
If the annual operating cost remains unchanged and since its amount is relatively small, the impact of time on the operating cost can be ignored. However, the amounts of land cost and construction cost are large, so the influence of working years on them needs to be considered. Therefore, by integrating the discount rate equation into Equations (1) and (2), the objective function of the average annual total investment cost can be obtained as shown in Equation (6)
2.2.2. User Cost Model Design
From the above in this article, it can be known that the shortcomings of most existing location models are that they do not consider the needs of users of EVs. Moreover, in the current multi-objective function location models, most of them do not comprehensively consider the aspect of users of EVs, such as the real-time electricity price of each charging pile of EVs, the road tortuosity coefficient, etc. Because when users of EVs go to charging stations for charging, their travel routes may not be unobstructed. Therefore, they need to consider issues such as road congestion coefficient, as well as whether they need to wait in line after arriving at the charging station. These factors are critical for understanding the level of service that the charging network provides to users. The reason for including user cost as an optimization objective is to ensure that the network is not only economically feasible but also convenient for users. High user costs, such as long waiting times and excessive detour distances, can deter users from utilizing the charging stations, reducing the system’s effectiveness and efficiency. Therefore, minimizing user costs helps enhance user satisfaction and increases the utilization of the charging network. User costs mainly include two aspects: electricity costs and time costs.
For users of EVs charging, taking 365 days as the standard, a model was established to obtain the electricity cost for users as Equation (7)
In this paper, the user’s unit time cost is set to convert time into money for modeling, and the time cost of the user’s visit to the charging station can be obtained, as shown in Equation (8)
The time cost for users of EVs is ultimately the queuing time cost. If the site selection research is only conducted from the perspective of operators, the site selection result may require users to wait in line, which will greatly reduce users’ enthusiasm for using charging piles. Converted, it will lead to losses for operators. Therefore, the queuing time cost for users is extremely important. The queuing situation of users conforms to the M/M/c queuing model [19]. An optimal combination of fast and slow chargers can provide a balanced solution to queueing delays and service quality. By increasing the number of fast chargers in high-demand areas and strategically adding slow chargers, the charging station can maintain high service efficiency while avoiding long waiting times. For instance, during peak hours, fast chargers can handle the urgent demand, while slow chargers serve users who have more time to wait. Since the charging piles in the charging station are divided into fast and slow charging types, this model needs to be improved.
The improvement methods are as follows
- The total number of charging demands that a charging station can serve per unit time is Equation (9)
- 2.
- The average service capacity of public charging stations within a unit of time: Since this paper considers the proportion of fast and slow charging within the charging stations, it is necessary to fully discuss the fast and slow types. The service capacity of fast and slow charging can be obtained by dividing the number of slow charging and fast charging, respectively, by the charging time of slow charging and fast charging. The specific equation is shown in Equation (10)
- 3.
- Service intensity of charging piles: According to the above, the service intensity of charging piles also needs to be fully discussed in terms of speed. The specific equation is shown in Equation (11)
- 4.
- The total idle probability of the charging piles in the station to be built: Calculate the total idle probability of both fast and slow charging piles. Since and represent the total idle probabilities of slow and fast charging, respectively, the total idle probability of the charging station should be . The specific equation is shown as in Equations (12)–(14)
- 5.
- Average queuing waiting time for users: Multiply the queuing time cost of slow charging users by the slow charging weight and the queuing time cost of fast charging by the fast-charging weight, respectively, to obtain the total average queuing waiting time for users. The specific formulas are shown in Equations (15)–(17)
All the above formulas were calculated and modeled, and the objective function of the user’s queuing waiting time cost was obtained as shown in Equation (18)
The sum of the three costs of the user’s electricity cost, the time cost for the user to go to the charging station, and the queuing time cost for the user within the charging station is the objective function of the average annual user cost, as shown in Equation (19) specifically
After sorting, Equation (20) can be obtained
Based on the annual investment cost model and annual user cost model constructed above in this paper, this study aims to minimize (Min) the annual investment cost and annual user cost of the operator. Therefore, the equation of the dual-objective optimization model is shown in Equation (21)
2.2.3. Constant Volume Model Design
Based on the analysis of the existing site selection models mentioned above, it can be known that none of the existing site selection models have relevant research on capacity determination. This will lead to serious problems such as power grid overload, charging station overload, loss of control over operating costs, and traffic congestion. Adopting a reasonable capacity determination model can effectively improve the safety, economy and service quality of charging stations [20].
The fixed capacity model of the EV charging station designed in this paper comprehensively considers the simultaneous usage coefficient of the charging pile and the load rate of the charging pile. The specific capacity model of the EV charging station is shown in Equation (22)
2.3. Constraint Conditions of Site Selection and Volume Determination Model
In the site selection process of EV charging stations, multiple constraints need to be considered to ensure the feasibility, economy, service efficiency and long-term sustainability of the sites. If there are no reasonable constraints, the site selection results may lead to problems such as resource waste, poor user experience and low return on investment. The constraints set in this article are as follows
- ; When a website is built at point j, it is 1; when no website is built at point j, it is 0.
- ; The service range constraint of charging stations, where is the distance between two adjacent charging stations and is the service range of charging station j.
- ; Anxiety mileage limit, where represents the emergency charging mileage.
- ; The quantity constraint, as can be known from referring to the “Design Standard for Electric Vehicle Charging Stations” (GB/T50966-2024) [21], when the number of charging piles in a charging station is less than five, it cannot form a charging station.
- ; Meet the constraints of users’ charging demands.
- .5 h; The maximum tolerable queuing waiting time constraint for users.
- ; Constant volume model constraint conditions.
2.4. Model Parameter Setting
To make the model operable and reasonable in practical applications, it is necessary to precisely set each parameter in the model. Parameter setting not only relates to the actual effect of the model, but also largely determines the accuracy and feasibility of the optimization results. This process will provide the necessary numerical basis for the subsequent solution of the model and guarantee the stability and validity of the optimization results. The specific parameter Settings are shown in Table 3, and the unit price table of the relevant infrastructure is shown in Table 4.

Table 3.
Parameter setting table.

Table 4.
Unit Price Table for Infrastructure.
In the above table, determined by Yilaite Company, Changchun City, Jilin Province, China. according to the survey conducted by Yilaite Company in Changchun City, Jilin Province, China. this can be derived from the “Labor Law of the People’s Republic of China” and the “Changchun City Salary Level Report”. and determined based on the commonly available output power of fast and slow chargers in the market. determined through the Baidu Maps app, which shows that the road congestion coefficient in Changchun City is 1.723. determined based on the average power consumption per kilometer of new energy electric vehicles, with data obtained from the Dongchedi app. the average driving speed of new energy electric vehicles in urban areas in China is taken. and obtained by dividing the battery capacity of new energy electric vehicles by the charging power of different types of charging piles.
The data in the above table was obtained from a survey conducted by Yilaite Company in Changchun City, Jilin Province, China.
3. Results
3.1. Research Area Processing
Based on the site selection and volume determination optimization model and parameter calibration results established in the second part, this part is oriented towards the actual geospatial scenarios and constructs the computational experimental environment of the research area through multi-source data fusion and spatial discretization. Supported by the ArcGIS geographic information platform, the regional vector road network topology and the spatial distribution core density of the number of EVs are integrated to discreteize the continuous geographic space into candidate site grid units.
The research area of this paper is Changchun City, Jilin Province. As a new industry, the popularity and penetration rate of EVs are not particularly high. Moreover, EVs are mainly distributed in densely populated urban areas. Therefore, the main urban area of Changchun City, Jilin Province is selected as the research area. According to relevant data from the Ministry of Civil Affairs of the People’s Republic of China, the research area covers approximately 3219 square kilometers, mainly including five major districts: Nanguan District, Kuancheng District, Chaoyang District, Erdao District, and Lvyuan District. The research area is bordered by Xiaoxitun to the north, Yongchun Town to the south, Daling Town to the west, and Lianhua Mountain Overpass to the east. This area is displayed through the Google Maps, as shown in Figure 2.
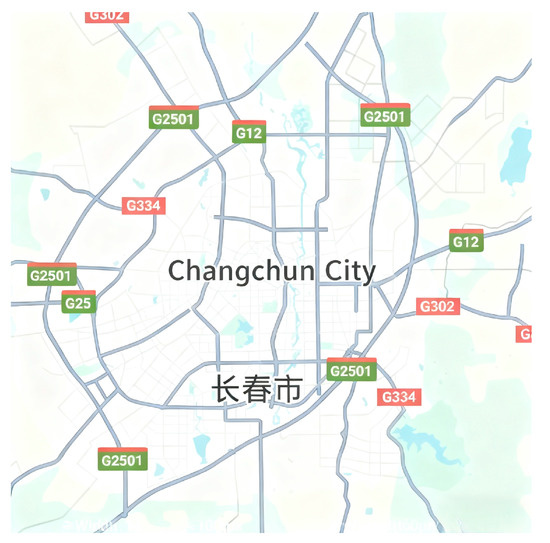
Figure 2.
Map of Research Area in Changchun City.
As can be seen from Figure 2, the map on the Google Maps alone cannot complete the true site selection and capacity determination of EVs. Therefore, vector map conversion and expansion processing need to be carried out on the above-mentioned Figure 2.
First, import the vector map into ArcMap to obtain the open-source road network SHP file. Set the extension rules in ArcCatalog and then edit it in ArcMap. Mainly use the functions such as breaking intersection lines and intersection line breakpoints in the extension editor to generate a new point layer [22], as shown in Figure 3.
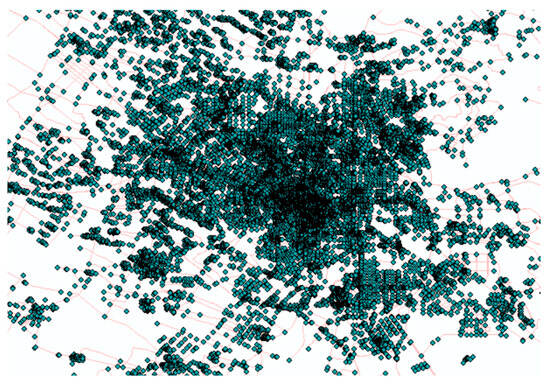
Figure 3.
Changchun City Point Layer.
Since there are too many points in point Figure 3, it is obviously impractical to take all the points in point Figure 3 as the sites to be built. Therefore, this point layer should be further processed. Use ArcToolbox in ArcGIS to process points that are too close and unreasonable paths. The specific operation diagram is shown in Figure 4.

Figure 4.
The schematic diagram of point layer processing. (a) Point merge diagram. (b) Route deletion diagram. (c) Interchange treatment diagram.
Point merging is mainly processed through attribute fields, topological relationships, and layer spatial relationships. When two or more points have the same or similar attributes, they can be merged through attribute field matching. When two points are “hanging points” and “intersection points” generated at the same position in a network node, they can be merged according to topological rules. Multiple nodes within the same road network range can be combined into a central point according to the road network boundary.
Path deletion is achieved by removing those paths in ArcGIS that do not meet the analysis requirements or network topology rules. Specifically, what is deleted are those redundant or invalid paths generated after point merging in the merged map. These paths may generate illogical or redundant lines after point merging, affecting the rationality of the data and the accuracy of subsequent analysis.
The basis for the processing of interchanges is the special structure of interchanges in the transportation network, which needs to be dealt with separately in map and network analysis. The processing of interchanges generally includes steps such as node merging, topology repair and path optimization. If the interchanges are retained as multiple discrete nodes, it will lead to multiple path misjudgments in the network and unnecessary “turning” logic between nodes. To enhance the consistency and analysis accuracy of the network dataset, its logic is merged into a central node. All entry and exit ramps or main lines are connected through this node to ensure the connectivity and rationality of traffic flow. At the same time, the network structure is simplified to facilitate subsequent path analysis and station layout.
To facilitate the subsequent site selection and capacity determination optimization of EV charging stations, K-Means clustering is used to aggregate the preprocessed point layers [23]. Firstly, the elbow analysis method is used to determine the number of clusters in K-means clustering. Since the longitude and latitude cannot calculate the exact distance between each point, The preprocessed point layers need to be transformed by using the ArcMap function in ArcGIS to convert the geographic coordinate system into the projected coordinate system [24]. This data should be exported from ArcGIS in the format of a text file. The file should be substituted into the elbow analysis method using Matlab software for simulation to obtain the optimal number of clusters. The specific operation schematic diagram is shown in Figure 5.
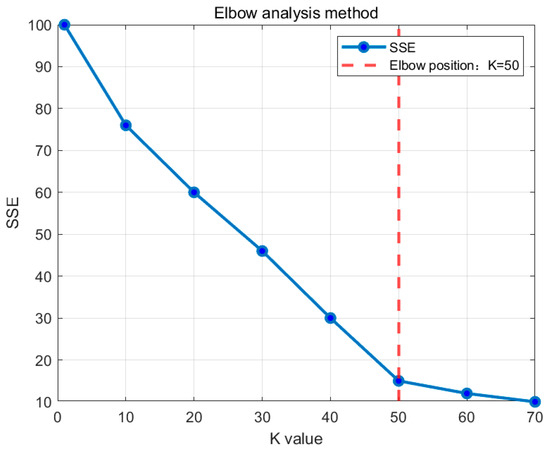
Figure 5.
Elbow Method Diagram.
It can be known from Figure 5 that the optimal number of clusters is K = 50. By using Matlab software to substitute the above text format file into the K-means algorithm for simulation, the point layer is aggregated into 50 points, The specific simulation results are shown in Figure 6.
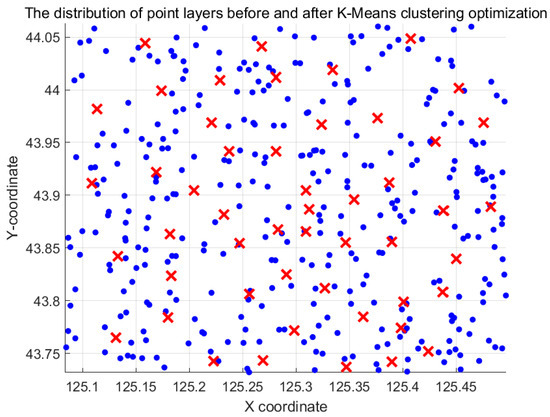
Figure 6.
K-Means Processing Diagram.
In Figure 6, the blue dots represent the points of the point layer, and the red crosses represent the points aggregated after K-Means processing. These 50 points are the sites to be built studied in this paper, also known as the demand points. The site selection and volume determination model designed in this paper can select whether to build a site and determine the volume within this range. By adopting the K-Means clustering method, the points within the point layer are evenly distributed, maximizing the coverage of the user demands of EVs in the research area. The total charging demand remains unchanged after clustering, while the number of demand points decreases, which greatly facilitates the site selection work in the later stage.
To highlight the specific location of the demand points, the vector map of Changchun City is presented as the background in ArcGIS, the red dots represent the demand points, as shown in Figure 7.
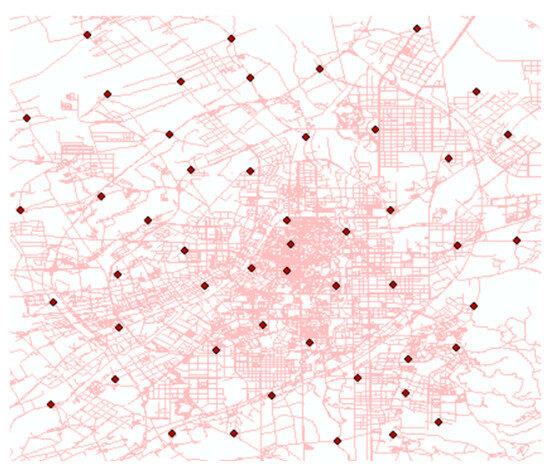
Figure 7.
Study Area Demand Point Map.
3.2. Calculation of Daily Charging Demand
After the research area is determined, the daily charging demand for EVs within the research area of Changchun City needs to be calculated. As the data on the number of EVs in use is not comprehensive and there is a lack of specific data on the number of EVs in use in each district of Changchun City, it is necessary to estimate the number of EVs in use in each district of Changchun City.
According to the “Annual Report on the Development of Transportation in Changchun City”, the total number of automobiles in each district can be known. The report rounded the total number of automobiles in each district to tens of thousands. Based on the new energy penetration rate of EVs in Changchun City and the total number of vehicles in each district, the estimated number of EVs in each district was obtained. The penetration rate of new energy in Changchun City was obtained by referring to the “Notice of the Ministry of Finance on the Proportion of Government Procurement of New Energy Vehicles” and the 2025 production capacity plan of Changchun City. The estimated number of EVs in each district of Changchun City is shown in Table 5.

Table 5.
Estimated Ownership Table of EVs in Each District.
The number of EVs in each district can be obtained from Table 5. Based on the number of EVs in each district, the daily charging demand is calculated. The daily charging demand of a certain district = (the number of EVs in the district/the total number of EVs in the city) × the total daily charging demand of the city [25]. The specific daily charging demand of each district is shown in Table 6.

Table 6.
Daily Charging Demand Table of EVs by District.
According to the seventh national census of China in 2020, the total population of Changchun City was 9,066,906. Meanwhile, the specific population figures of each district within the study area were obtained, as shown in Table 7.

Table 7.
Population Numbers of Each District in the Study Area.
Rank the contents of the above table, and we can obtain Table 8.

Table 8.
Population Level Ranking Table of Each District in the Study Area.
Based on the calculation of the daily charging demand for EVs and the ranking of population density levels in Changchun City, the daily charging demand for EVs in each district within the study area was allocated to the various stations to be built. The allocation principles strictly followed Table 6, the daily charging demand table for EVs in each district, and Table 8, the ranking table of population density levels in each district of the study area. By combining these two tables for analysis, the daily charging demand of each site to be built is obtained, as shown in Table 9.

Table 9.
Daily Charging Demand of Each Proposed Charging Station (vehicle).
3.3. Model Solution
With the rapid development of intelligent optimization algorithms, fusion algorithms have gradually become a popular choice for solving complex optimization problems. However, when solving the problem of site selection and capacity determination for EV charging stations in this paper, the classical GA, ACO and SA are selected. This choice is based on the following considerations:
- The theoretical basis and wide applicability of the algorithm.
- Model adaptability and problem complexity.
- Good algorithm comparability.
To effectively evaluate the performance of different site selection and volume determination schemes and algorithms, evaluation indicators need to be set. Through evaluation indicators, the optimization effect of the site selection and volume determination model can be comprehensively measured. This paper adopts a staged hybrid strategy. Firstly, the Pareto optimal solution set is generated through multi-objective optimization, and then the solution with the lowest total cost is selected as the optimal location scheme. The advantage of this method lies in that it cannot only retain the trade-off information of multi-objective optimization but also screen out a “compromise solution” through the total cost [26]. Selecting the lowest total cost as the evaluation index can measure the economic performance of the scheme. A lower total cost means a higher resource utilization efficiency and is a key goal of site selection and volume determination optimization.
3.3.1. Solution Steps of GA
The simulation environment processor in this paper is an Intel Core i5-7300HQ notebook computer with 8 GB of operating memory. The simulation is implemented by writing m files through Matlab 2019b software. For the solution of the above example data and the site selection model, the parameters of the GA are configured as follows: The population size is 5000, the maximum number of iterations is 200 times, the number of elite individuals retained is 50, the crossover probability and mutation probability are taken as 0.4 and 0.8, respectively, and the penalty value is 50,000,000 when the constraint conditions are not met [27]. According to the above GA Settings and parameter Settings, the steps of the GA are as follows:
- Parameter calibration. Calibrate the parameter values of the model according to the specific situation of the calculation example.
- Initialize the population. Generate a random initial population, with everyone representing a selection scheme of charging stations.
- Calculate the fitness. Calculate the fitness of everyone through the objective function and constraint conditions and consider the penalty term.
- Select the operation.
- Cross-operation.
- Mutation operation.
- Update the population.
- Stop Condition. Stop when the maximum number of iterations is reached or a solution that satisfies all constraints is found; otherwise, jump to the third step of the loop.
3.3.2. Solution Steps of ACO
For the solution of the above example data and the site selection model, the parameters of the ACO are configured as follows: the population size is 5000, the maximum number of iterations is 200 times, the pheromone volatilization factor is 0.8, the initial pheromone value is 1, the path selection probability is 0.7, and the penalty value when the constraint conditions are not met is 50,000,000 [28]. Based on the above ACO settings and parameter settings, the steps of the ACO are as follows:
- Initialize the parameters. Calibrate the parameter values of the model according to the specific situation of the calculation example.
- Initialize the population. Everyone (ant) represents a site selection plan for a charging station. The scheme is represented by binary vectors, where 1 indicates site selection and 0 indicates no site selection.
- Path Selection. Each ant determines the next charging station to choose based on the probability of path selection and updates the current path.
- Calculate the fitness.
- Local search. In each round of iteration, Ant will conduct a local search and optimize the current path by fine-tuning the path or choosing different charging station locations.
- Pheromone update.
- Termination Conditions. Determine whether the termination condition is met based on the preset number of iterations or the improvement of the path; otherwise, jump to the third step of the loop.
3.3.3. Solution Steps of the SA
For the solution of the above example data and the site selection model, the parameters of the SA are configured as follows: initial temperature 1000, temperature attenuation factor 0.95, maximum number of iterations 200 times, and maximum penalty value 50,000,000 [29]. According to the above settings of the SA and parameters, the steps of the SA are as follows:
- Initialize the parameters.
- Initial Solution. Randomly select several sites to build websites and satisfy the initial basic constraints.
- Perturbation generates new solutions.
- Acceptance criteria. If the new solution is better than the current one, that is, it has a lower cost, it is accepted directly. If it is worse, it is accepted with probability.
- Update the status.
- Termination Conditions. If the number of iterations reaches the upper limit or the temperature drops to the threshold, the algorithm will be terminated, and the current optimal website location and volumetric determination plan will be output.
3.4. Model Solution Result
Based on the steps of the above three algorithms, the solution results of the three algorithms can be obtained. The specific results are shown in Figure 8.

Figure 8.
The graphs of the solution results of the three algorithms. (a) GA solution result graph. (b) The solution result graph of ACO. (c) The solution result graph of the SA.
The Pareto optimal solution sets of the three algorithms are shown in Table 10.

Table 10.
Table of Pareto optimal solution sets for three algorithms.
According to the setting rules of the evaluation index, the number of charging stations in the site selection scheme is selected as 15 as the optimal site selection scheme of the GA. The number of charging stations in the site selection scheme is selected as 15 as the optimal site selection scheme of the ACO. The number of charging stations in the site selection scheme is selected as 15 as the optimal site selection scheme for the SA.
Three algorithms have obtained different results. Now, it is statistically analyzed which of the three algorithms has the lowest total cost. The costs of each of the optimal results of the three algorithms are shown in Table 11.

Table 11.
Cost Table of Optimal Simulation Results for Three Algorithms.
Figure 9 shows the iteration curves of the three algorithms:
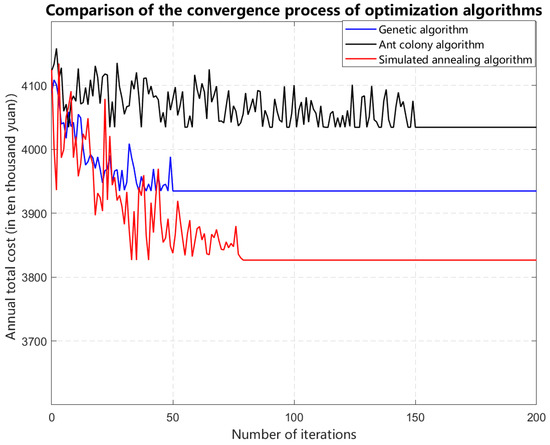
Figure 9.
Iteration Curves of Three Algorithms.
By comparing the above table data with the iterative curve graph, it can be known that the GA has the fastest solution speed, with approximately 50 iterations. The SA has approximately 80 iterations, and the ACO has approximately 150 iterations.
The performance of three optimization algorithms—SA, ACO, and GA—was compared by running each algorithm independently 20 times to observe their accuracy and stability. The results were analyzed in terms of the optimal solution and standard deviation obtained across multiple runs. The results are shown in Table 12.

Table 12.
Algorithm Performance Comparison Table.
The optimal solution obtained by the SA algorithm was 3826, with a standard deviation of 0.25, indicating that SA achieved stable and consistent results across all 20 runs. This low standard deviation reflects the algorithm’s ability to converge to a similar solution in each run, making it ideal for problems requiring high stability. The optimal solution for ACO was 3935, with a standard deviation of 0.6. While ACO demonstrated a higher optimal solution, the standard deviation was larger, reflecting greater variability in its performance across multiple runs. The optimal solution for GA was 3826, with a standard deviation of 0.4. GA’s performance lies between that of SA and ACO, with a moderate optimal solution and a middle-range standard deviation. This suggests that GA strikes a balance between exploration and exploitation, providing relatively stable results while maintaining competitive accuracy.
Based on the data content in Table 11, the total cost of the solution results of the ACO is the highest, while that of the SA is the lowest. By comparing the solution results of the three algorithms, in the GA solution results and the ACO solution results, the annual investment costs of the two algorithms are similar, but the user cost of the ACO is relatively high. To explore the reasons for this situation, Coordinate visualization was extracted using Matlab software. The specific visualization layout is shown in Figure 10.
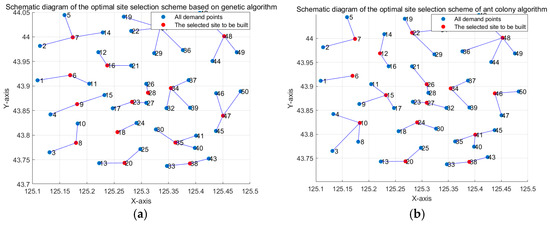
Figure 10.
The position map of the solution results of GA and ACO. (a) The location point graph of the result solved by the GA (b) The location point map of the solution result of the ACO.
As can be seen from Figure 10, the reason for the high user cost of the ACO is that although the solution results of both the ACO and the GA are 15 charging stations, the layout of the charging stations in the solution result of the ACO may not meet the best user experience, thus increasing the user cost and leading to an increase in the total cost.
The total cost of the solution result of the SA is the smallest, indicating that the result obtained by the SA can simultaneously meet the needs of both operators and users of EVs.
The superior performance of SA can be attributed to its ability to escape local optima. Unlike GA and ACO, which rely on population-based search mechanisms, SA utilizes a probabilistic approach based on temperature control. This allows SA to explore a broader search space in the initial stages and gradually refine the solution towards the global optimum as the temperature decreases. The annealing process in SA effectively balances exploration and exploitation, which is particularly beneficial for complex and multi-modal optimization problems, where GA and ACO may struggle with premature convergence to suboptimal solutions. While GA relies on genetic operators like crossover and mutation, it may suffer from convergence issues due to its tendency to converge prematurely, especially when the population diversity decreases. Similarly, ACO, which mimics the foraging behavior of ants, is highly effective in dynamic environments but can struggle with large-scale problems where the pheromone updating process becomes computationally expensive. The comparison results show that SA consistently achieves lower total costs, faster convergence, and better solution accuracy than both GA and ACO. These results indicate that SA is particularly well-suited for optimization problems involving complex, non-linear, and high-dimensional search spaces, such as the one addressed in this study.
Therefore, the solution result of this algorithm is the optimal result and serves as the optimal site selection scheme. After determining the optimal site selection scheme, the number of charging piles at each construction site in the optimal scheme of the SA was extracted, and the number of charging piles built within each construction site under the optimal scheme was obtained. The specific numbers are shown in Table 13.

Table 13.
Number of Charging Piles at Each Station in the Optimal Plan.
Extract the coordinates of the construction sites and the demand points served by the construction sites in the optimal site selection scheme and import them into Matlab to generate the schematic diagram of the optimal scheme. The schematic diagram of the optimal scheme is shown in Figure 11.
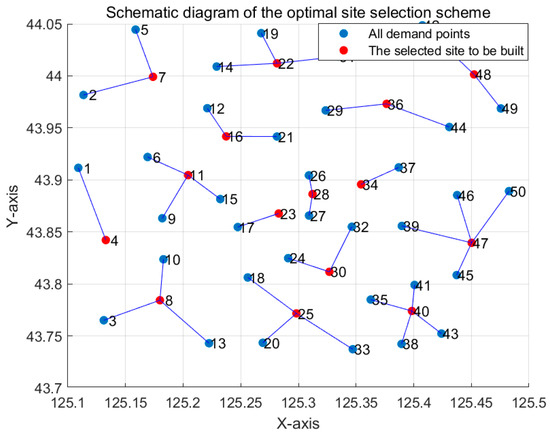
Figure 11.
Optimal Site Selection Scheme Diagram.
According to the volumetric model and combined with the number of charging piles built in each construction site in the optimal site selection scheme, it can be obtained that the total capacity in the optimal site selection scheme is 11,544 kVA.
4. Discussion
4.1. Selection of Other Models
According to the above chapters, it can be known that the solution result of the SA is the optimal solution. To further verify the universal applicability of the optimization model, several optimization models of other scholars are now selected for simulation comparison under the same conditions. A comprehensive evaluation and analysis of the optimal results are conducted to determine the optimal solution strategy of the optimization model constructed in this paper.
The multi-objective function location and volume determination model in the references of this paper is selected. The selected model is shown in Equations (23)–(25), and other models 1 are selected as follows [14]:
Its constraint conditions are:
- ; The service scope of the charging station covers all charging demand points.
- ; Anxiety mileage limit.
- ; The service capacity of charging stations is limited.
- ; The range of values for the number of charging piles within a charging station.
- ; When a website is built at point j, it is 1; when no website is built at point J, it is 0.
- Distance limit between charging stations.
Other models 2 are selected as follows [15]:
Its constraint conditions are:
- ; The quantity constraint of public charging piles.
- ; Emergency mileage limit for charging between charging demand points and public charging stations.
- ; Constraints on the number of public charging stations.
- ; The service capacity limitations of public charging stations.
- ; Full coverage of charging demand.
Other models 3 are selected as follows [16]:
Its constraint conditions are:
- ; The quantity configuration constraint of charging piles within the charging station.
- ; Service scope constraints of charging stations.
- ; Meet the constraints of users’ charging demands.
- ; All demand points are assigned corresponding charging station constraints.
- ; The demand point can only be charged at the corresponding charging station.
- ; When a website is built at point j, it is 1; when no website is built at point J, it is 0.
- ; The probability of going to a charging station to charge is 1 if it goes and 0 if it does not.
4.2. The Solution Results of Models 1–3
To ensure the fairness among model comparisons, the same dataset must be strictly used, and the consistency of parameters must be strictly guaranteed. Therefore, the parameter settings for Models 1–3 strictly use the same parameter data as in this paper. The comparison results adopt the same evaluation indicators. Since the above models 1–3 and the model designed in this paper are all multi-objective location models, the evaluation indicator is to select the solution with the lowest total cost in the Pareto optimal solution set as the optimal location scheme. Substitute all the data in this paper into the above models 1–3 and use the SA to solve the study area of the above multi-objective function location model 1–3. The simulation result Figure 12 of model 1–3 is obtained.
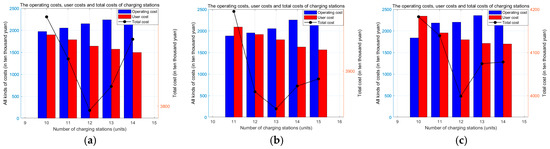
Figure 12.
The solution result graphs of Model 1–3. (a) Model 1 solution result graph. (b) Model 2 solution result graph. (c) Model 3 solution result graph.
The Pareto optimal solution sets of models 1–3 are shown in Table 14 as follows, the table includes operating costs, user costs, total costs, and the number of charging stations.

Table 14.
Pareto Optimal Solution Set Table for Models 1–3.
According to the setting rules of the evaluation index, the number of charging stations in the site selection scheme is selected as 12 as the optimal site selection scheme of Model 1. The number of charging stations in the site selection scheme is selected as 13 as the optimal site selection scheme of Model 2. The number of charging stations in the site selection scheme is selected as 12 as the optimal site selection scheme of Model 3.
4.3. The Comparison Results of the Optimal Schemes of the Optimization Model
According to the above simulation diagram, the cost table of the optimal results for models 1 to 3 can be obtained, as shown in Table 15. Table 15 contains the electricity prices of the optimal results of Models 1 to 3, such as investment cost, user cost and total cost. The optimal solution of this paper is also compared in Table 15.

Table 15.
Cost Table of Optimal Simulation Results for Model 13.
By comparing the solution results of the optimal scheme in this paper with those of the above three site selection models, it can be concluded that the total costs of Model 1 and Model 2 are slightly lower than those of the model designed in this paper, while the total cost of model 3 is higher than that of the model designed in this paper.
For Model 1–2, the solution result of the above model 1–2 shows that the number of charging stations is small, and the total cost is low. However, this is because the model ignores the electricity cost consumed by users when they go to the charging stations for charging and the electricity price cost. For the research on the site selection and capacity determination model of EV charging stations, the user’s electricity cost should be regarded as the core variable of the site selection and capacity determination model. Under the same conditions, the actual cost items such as the electricity cost consumed by users when they go to the charging station for charging and the electricity price cost can more comprehensively reflect the real cost. Although considering the user’s electricity cost makes the total cost of the model relatively high, this difference is of practical significance. The user’s electricity cost is an important factor affecting the overall cost, and the optimization model designed in this paper can provide a more realistic and feasible optimization scheme [30]. Therefore, considering the electricity cost of users, the site selection and capacity determination model designed in this paper is better.
For Model 3, the optimal result obtained by Model 3 is 12 charging stations. Although the number of stations in Model 3 is relatively small, their total cost is higher. This indicates that reducing the number of stations does not necessarily bring a cost advantage. The site selection model designed in this paper successfully optimizes the overall cost while ensuring a reasonable site distribution. Further analysis reveals that although the number of sites in Model 3 is less than that of the model designed in this paper, its total cost is higher. The main reason lies in the increase in user costs and annual investment costs. Although the number of stations built in Model 3 has decreased, users may need to travel longer distances, resulting in higher electricity costs and waiting time costs [31]. Moreover, fewer sites require higher power or more charging piles, resulting in increased construction and operation costs. Therefore, the model designed in this paper achieves a lower overall cost by optimizing the site distribution, controlling the number of established sites, and introducing a mixed construction of fast and slow charging sites.
In conclusion, the site selection and capacity determination model for EVs designed in this paper features economy, balance, adaptability, practical feasibility and system optimization. These characteristics collectively make the model designed in this paper superior to other models in the site selection problem of EV charging stations.
4.4. Sensitivity Analysis of the Optimization Model
In this study, we performed a sensitivity analysis to explore the impact of varying the weights assigned to investment costs and user costs. The optimization model tested three different weight combinations:
- Scenario 1: Investment costs 70%, user costs 30%
- Scenario 2: Investment costs 50%, user costs 50% (The original equal-weight setting)
- Scenario 3: Investment costs 30%, user costs 70%
The results of the sensitivity analysis are shown in Figure 13.
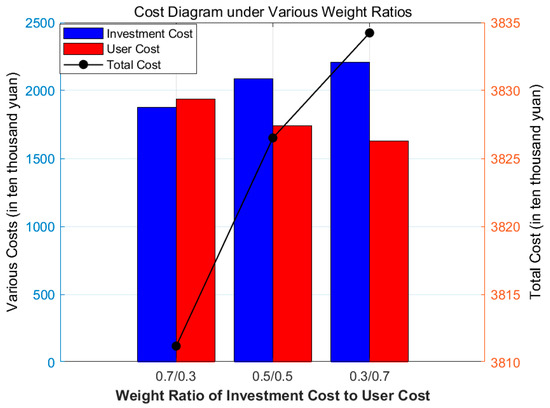
Figure 13.
Cost Diagrams under Three Different Weight Combinations.
Based on the above simulation diagrams, the sensitivity analysis cost table is shown in Table 16.

Table 16.
Cost Table of Optimal Simulation Results for Scenario 13.
The results show that when the weight of investment costs is higher (Scenario 1), the total cost is minimized by reducing the number of charging stations. However, this leads to higher user costs, such as increased waiting times and longer travel distances. Conversely, when user costs are prioritized (Scenario 3), the total number of charging stations increases, reducing user costs significantly, but investment costs rise accordingly. In Scenario 1, the total cost decreases by 0.4%, while the user cost increases by 11.2%. In Scenario 3, the user cost decreases by 6.5%, and the investment cost increases by 5.8%.
In contrast, Scenario 1 reduces the total cost by lowering investment costs but sacrifices user experience, leading to an increase in user costs, especially when the number of charging stations is reduced, resulting in longer wait times and greater travel distances. Scenario 2 lowers the total cost while maintaining relatively low user costs, reflecting a more balanced and reasonable optimization strategy. By configuring an appropriate number of charging stations, it effectively controls investment costs while ensuring minimal impact on user experience. In real-world applications, optimizing only investment costs at the expense of user experience may lead to long queues and inconvenient charging, affecting user willingness and charging station utilization. Scenario 2 is more aligned with urban planning and long-term sustainability, reducing excessive investment while ensuring service quality. Ignoring user costs in optimization may reduce initial investment but could lead to negative impacts in the long run, such as user loss and low station utilization. Scenario 2 achieves a reasonable total cost reduction (4.31%) while improving user experience, making it the ideal solution, especially for long-term sustainability in practical applications.
5. Conclusions
This paper proposes a comprehensive optimization framework for EV charging station planning that jointly addresses site selection, capacity sizing, and charger type configuration. By explicitly modeling the distinction between fast and slow chargers, the framework enables flexible allocation strategies that better capture the heterogeneity of user demand and grid impact. User costs are rigorously incorporated through a queuing-theoretic approach, which accounts for travel detours, dynamic electricity tariffs, and service delays specific to charger type.
The case study in Changchun demonstrates the practical relevance of the framework. The optimal results show:
- The optimal configuration of 15 charging stations, including 110 fast and 40 slow chargers with a total capacity of 11,544 kVA, minimized the total annual cost to 38.2651 million yuan.
- Compared with conventional baseline models, the proposed approach achieves up to 4.31% lower total system costs and over 5% lower investment costs, while also reducing user costs by about 3%.
- These improvements confirm the efficiency of explicitly accounting for charger heterogeneity and queuing effects in planning. Comparative benchmarking across three algorithms further verified the robustness of the optimization results.
However, the study is not without its limitations. The main limitations are as follows:
- The case study relies on theoretical data, and future research should validate the framework with real operational data from existing charging stations.
- Future work should consider more dynamic and uncertain factors, such as user behavior and issues like power outages or equipment failures in charging facilities.
Future Expansion:
- The integration of renewable energy into the optimization framework to reduce the environmental impact of EV charging.
- Vehicle-to-grid (V2G) technology could be incorporated to enable two-way energy flow between EVs and the grid, enhancing the resilience and efficiency of the energy system.
- Addressing demand uncertainty which can impact the performance and robustness of the charging network. Incorporating constraints related to grid capacity and transformer accessibility will provide a more realistic and practical model for EV charging station placement.
- The introduction of new algorithms, such as the PFA algorithm, could improve optimization.
These advancements would further enhance the alignment of EV infrastructure with the evolving objectives of smart mobility and sustainable energy systems.
Author Contributions
Conceptualization, H.W.; formal analysis, Z.W. and J.L.; funding acquisition, J.Z.; investigation, J.Z., X.L. and J.T.; methodology, Z.W.; software, H.W. and J.T.; supervision, J.Z.; validation, X.L.; visualization, H.W. and Z.W.; data curation, J.T.; writing—original draft, H.W. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by General Project of the “14th Five-Year Plan” for Educational Science in Jilin Province (2024)-“Topological Invariance of the Composition Elements of the Comprehensive Literacy of Excellent Primary and Secondary School Music Teachers in Jilin Province under the STEAM Background” (Project No. GH24563). Key Project of the Jilin Provincial Department of Education-“Structural Mechanism Study of the Jilin Province Student Aesthetic Education Evaluation Model Based on Kernel Functions” (Approval No. JJKH20231327SK). Jilin Provincial Philosophy and Social Science Planning Project-“Study on the Jilin Province Student Aesthetic Education Evaluation Model Based on Support Vector Machines” (Approval No. 2022B190).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Manoharan, Y.; Hosseini, S.E.; Butler, B.; Alzhahrani, H.; Senior, B.T.F.; Ashuri, T.; Krohn, J. Hydrogen fuel cell vehicles; current status and future prospect. Appl. Sci. 2019, 9, 2296. [Google Scholar] [CrossRef]
- Ma, P.; Zhang, S.; Zhou, B.; Shao, W.; Li, H.; Ma, T.; Guo, D. Research on Location Planning of Battery Swap Stations for Operating Electric Vehicles. World Electr. Veh. J. 2025, 16, 332. [Google Scholar] [CrossRef]
- Sun, L.; Yang, B. Optimal Planning of Electric Vehicle Charging Station Based on Spatio-Temporal Distribution Prediction of Charging Demand. Power Gener. Technol. 2024, 1–12. Available online: https://link.cnki.net/urlid/33.1405.TK.20240914.1014.002 (accessed on 20 September 2025).
- Hu, Y.; Yang, B.; Wu, P.; Wang, X.; Li, J.; Huang, Y.; Sang, Y. Optimal planning of electric-heating integrated energy system in low-carbon park with energy storage system. J. Energy Storage 2024, 99, 113327. [Google Scholar] [CrossRef]
- Alaee, P.; Shao, J.; Bemš, J.; Guerrero, J.M. Coordinated routing optimization and charging scheduling in a multiple-charging station system: A strategic bilevel multi-objective programming. Sustain. Energy Grids Netw. 2025, 42, 101659. [Google Scholar] [CrossRef]
- Shin, J.; Hwang, W.S.; Choi, H. Can hydrogen fuel vehicles be a sustainable alternative on vehicle market?: Comparison of electric and hydrogen fuel cell vehicles. Technol. Forecast. Soc. Change 2019, 143, 239–248. [Google Scholar] [CrossRef]
- Hu, W.; He, L.; Chen, J.; Yu, T.; Meng, L. A bi-layer optimization based schedule considering large-scale electric vehicles. Power Syst. Prot. Control 2016, 44, 22–28. [Google Scholar]
- MirHassani, S.A.; Ebrazi, R. A flexible reformulation of the refueling station location problem. Transp. Sci. 2013, 47, 617–628. [Google Scholar] [CrossRef]
- Initiative, C.C.; Wiederer, A.; Philip, R. Policy Options for Electric Vehicle Charging Infrastructure in C40 Cities; Harvard University: Cambridge, MA, USA, 2010. [Google Scholar]
- Jing, W.; An, K.; Ramezani, M.; Kim, I. Location design of electric vehicle charging facilities: A path-distance constrained stochastic user equilibrium approach. J. Adv. Transp. 2017, 2017, 4252946. [Google Scholar] [CrossRef]
- Bayram, I.S.; Michailidis, G.; Devetsikiotis, M.; Granelli, F. Electric power allocation in a network of fast charging stations. IEEE J. Sel. Areas Commun. 2013, 31, 1235–1246. [Google Scholar] [CrossRef]
- Upchurch, C.; Kuby, M.; Lim, S. A model for location of capacitated alternative-fuel stations. Geogr. Anal. 2009, 41, 85–106. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Leng, K.J. Considering service radius in the location problem of electric vehicle charging facilities. Comput. Integr. Manuf. Syst. 2020, 26, 2180–2189. [Google Scholar]
- Yu, J.C. Research and Application of Location and Capacity Determination For electric Vehicle Fast Charging Stations. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2019. [Google Scholar]
- Zhang, H.C. Research on Location Selection of Urban Electric Vehicle Public Charging Facilities Based on Demand Prediction. Ph.D. Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2024. [Google Scholar] [CrossRef]
- Cheng, J.X. Research on Location and Capacity Planning for Urban Electric Vehicle Charging Stations. Ph.D. Thesis, Shanghai Dianji University, Shanghai, China, 2023. [Google Scholar] [CrossRef]
- Lakshmikanthi, V.P.; Rao, M.D. Applications of QGIS and machine learning for road crash spot identification. Earth Sci. Inform. 2024, 17, 2331–2346. [Google Scholar]
- García-Gusano, D.; Espegren, K.; Lind, A.; Kirkengen, M. The role of the discount rates in energy systems optimisation models. Renew. Sustain. Energy Rev. 2016, 59, 56–72. [Google Scholar] [CrossRef]
- Meng, F.; Pei, W.; Zhang, Q.; Zhang, Y.; Ma, B.; Li, L. Research on the capacity of charging stations based on queuing theory and energy storage scheduling optimization sharing strategy. J. Energy Storage 2024, 96, 112673. [Google Scholar] [CrossRef]
- Ringlee, R.J.; Wood, A.J. Frequency and duration methods for power system reliability calculations: II-Demand model and capacity reserve model. IEEE Trans. Power Appar. Syst. 2007, PAS-88, 375–388. [Google Scholar] [CrossRef]
- GB/T 50966-2024; Electric Vehicle Charging Station Design Standard. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2024.
- Pucha-Cofrep, F.; Fries, A.; Cánovas-García, F.; Oñate-Valdivieso, F.; González-Jaramillo, V.; Pucha-Cofrep, D. Fundamentals of GIS: Applications with ArcGIS; Ediloja CIA Ltda: Loja, Ecuador, 2018. [Google Scholar]
- Abdullahi, M.R.; Lu, Q.C.; Hussain, A.; Tripura, S.; Xu, P.C.; Wang, S. Location optimization of EV charging stations: A custom K-means cluster algorithm approach. Energy Rep. 2024, 12, 5367–5382. [Google Scholar] [CrossRef]
- Wang, J. Location of Electric Vehicle Charging Station based on ArcGIS. Int. Core J. Eng. 2022, 8, 666–673. [Google Scholar]
- Csiszár, C. Demand calculation method for electric vehicle charging station locating and deployment. Period. Polytech. Civ. Eng. 2019, 63, 255–265. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Wang, H.; Liu, Z. A grey target-based multi-objective optimization framework for EV charging scheduling considering grid flexibility and user preferences. IEEE Trans. Sustain. Energy 2023, 1, 512–525. [Google Scholar]
- Zhou, G.; Zhu, Z.; Luo, S. Location optimization of electric vehicle charging stations: Based on cost model and genetic algorithm. Energy 2022, 247, 123437. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Ellinas, G.; Polycarpou, M. Ant colony optimization for the electric vehicle routing problem. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1234–1241. [Google Scholar]
- Türk, S.; Deveci, M.; Özcan, E.; Canıtez, F.; John, R. Interval type-2 fuzzy sets improved by Simulated Annealing for locating the electric charging stations. Inf. Sci. 2021, 547, 641–666. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Wang, Y.; Chen, R.; Xu, X. Bi-level programming model approach for electric vehicle charging stations considering user charging costs. Electr. Power Syst. Res. 2023, 214, 108889. [Google Scholar] [CrossRef]
- Li, J.; Sun, X.; Liu, Q.; Zheng, W.; Liu, H.; Stankovic, J.A. Planning electric vehicle charging stations based on user charging behavior. In Proceedings of the 2018 IEEE/ACM Third International Conference on Internet-of-Things Design and Implementation (IoTDI), Orlando, FL, USA, 17–20 April 2018; pp. 225–236. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).