Designing EV Charging Energy Hubs to Meet Flexibility Requirements in Smart Grids
Abstract
1. Introduction
- Proposes a novel mathematical optimization model designed to enhance the operational flexibility of EV charging stations by transforming them into EV charging energy hubs, focusing on the optimal sizing and operation of distributed energy resources (DERs), such as photovoltaic (PV) systems and battery energy storage systems (BESSs).
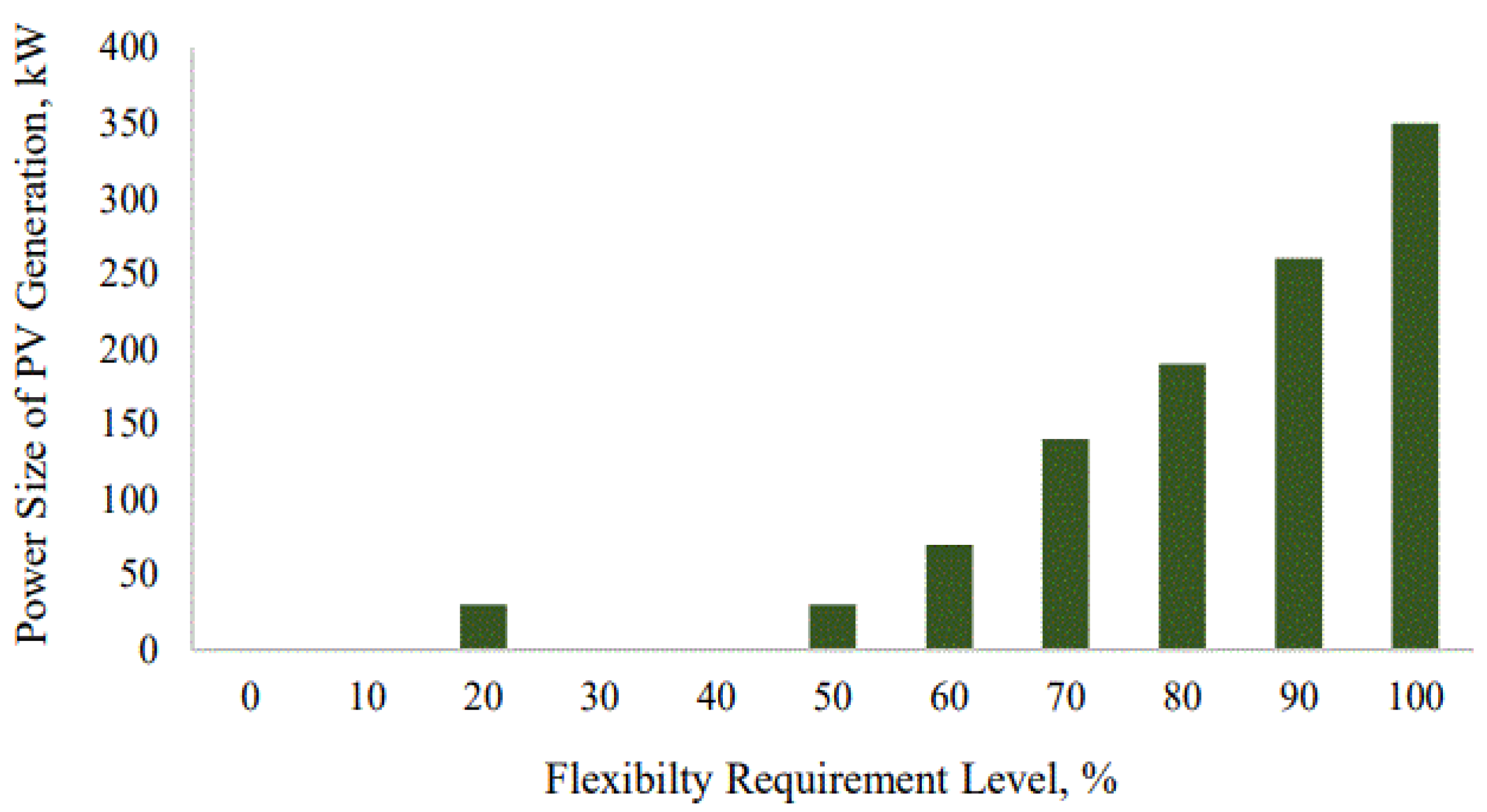
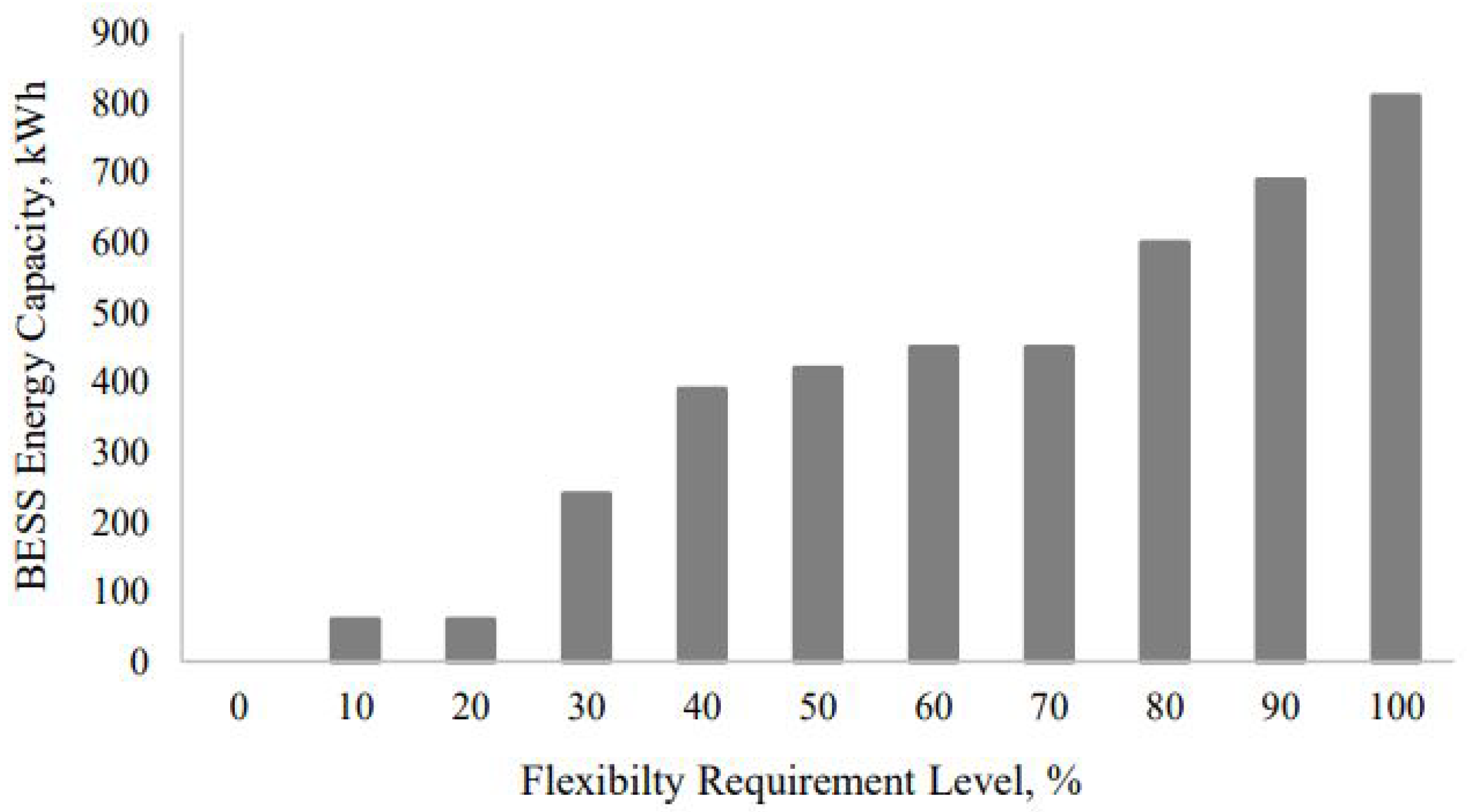
- Examines the effects of different levels of flexibility requirement on DER capacity needs and hence provides critical insights into the planning and design of future energy systems to support sustainable and resilient energy ecosystems.
- The proposed design of EV charging energy hubs enables operation with varying levels of grid independence, ranging from complete reliance on the grid (0%) to full autonomy (100%). This flexibility substantially decreases dependence on the central grid, representing a significant advancement toward achieving more sustainable and resilient energy systems.
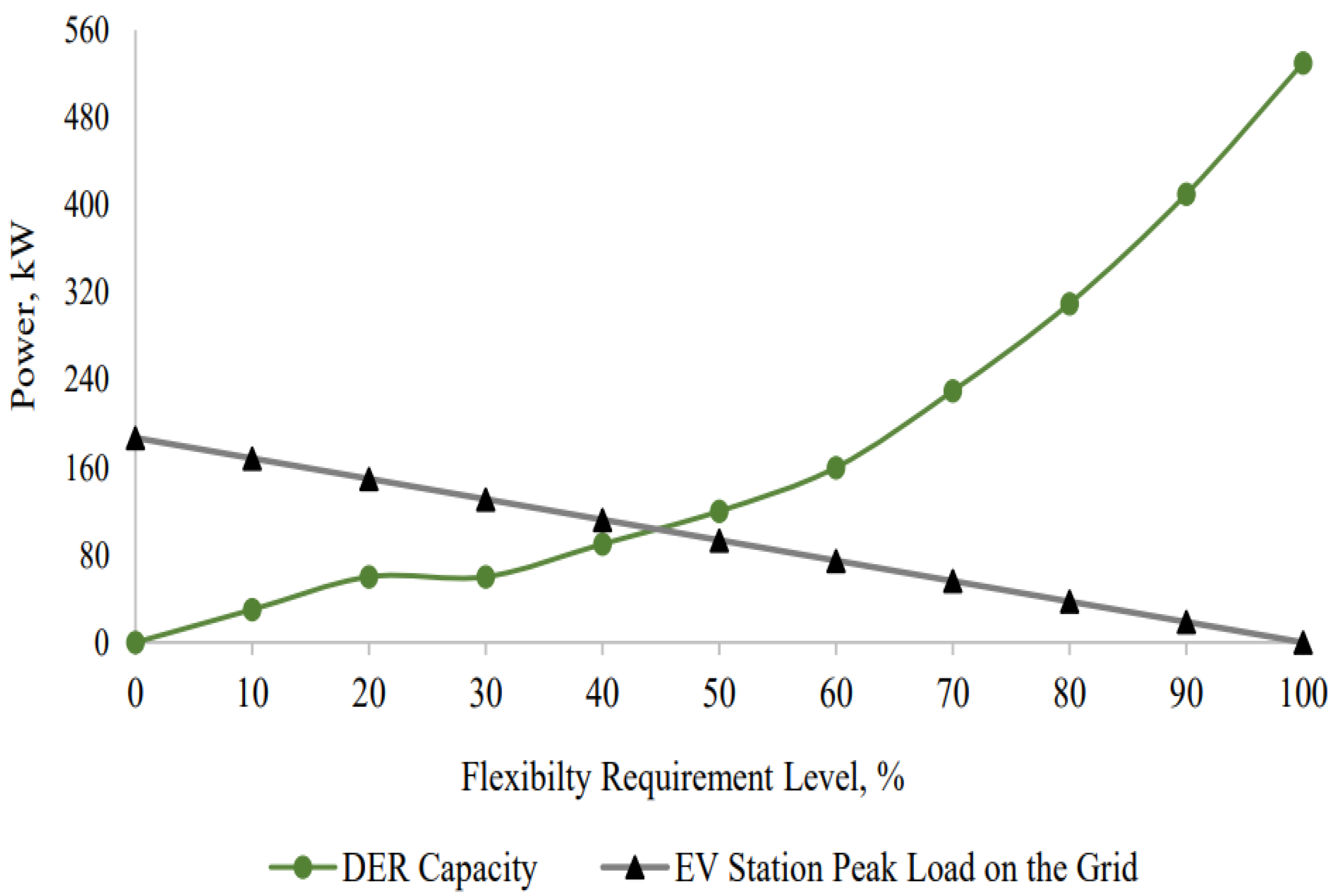
- Incorporating EV charging stations with varying levels of flexibility into distribution systems can effectively mitigate grid stress, enhance renewable energy utilization, and improve peak load management.
2. Proposed Mathematical Optimization Model
- The proposed model enables EV charging energy hubs to operate at different levels of grid reliance, from complete dependence to full autonomy (0% to 100% flexibility). This adaptability ensures that the hubs can respond dynamically to grid conditions, reducing stress and supporting stability in the distribution system.
- By optimizing the sizing and operation of PV systems and BESSs, the proposed model ensures efficient energy management. This allows the hubs to store surplus energy, utilize renewable sources, and shift loads away from peak periods, aligning with the demand for flexibility.
- The proposed model accounts for energy demands, load profiles, and grid conditions, enabling energy hubs to adjust operations based on real-time requirements. This adaptability enhances their ability to meet flexibility demands and support grid resilience.
- Objective Function: Minimize the capacity size of distributed energy resources associated with an EV charging station energy hub, such as PV generation and (BESSs) as given by:
- Demand–Supply Balance: Total generation should meet the demand at period h on a typical day, as follows:where .
Battery Energy Storage System Constraints
- Grid Dependency Constraint: The grid power contribution is capped at a predefined maximum, as follows:
- Energy-to-Power Ratio of BESS and Maximum Discharge Time: Each battery technology has a specific range of energy-to-power ratios and maximum discharge times. The range of the energy size for a specific power size is thus constrained as follows:
- Flexibility Requirements: The flexibility level, a core feature of the proposed model, governs peak load management.
- Peak Load Constraint: The following constraint ensures that the peak load is minimized, in conjunction with (1).
- Flexibility Provision Constraint: This constraint ensures that the peak grid load is reduced by a factor proportional to the flexibility . The higher the flexibility, the less energy the station draws from the grid during peak demand periods. It allows for flexibility in the system’s operation while ensuring that the energy hub remains within feasible limits based on the energy resources available (like PV and BESS).
3. Input Data and Simulation Results
3.1. Input Data
- It is posited that EVs maintain a battery state of charge within a 70% range, from 20% to 90%, to optimize battery usage and charging opportunities.
- EVs are expected to begin their daily operations fully charged from an overnight charge at home, eliminating the need for additional charging before commencing a trip. This situates fast charging as an ancillary option to home charging.
- The analysis focuses on data involving 850,000 trips and 150,000 vehicles culled from a broader NHTS dataset initially containing about 1,000,000 trips and 300,000 vehicles. The focus narrows to specific types of vehicles, excluding records with incomplete data to improve study precision.
- The research includes EVs categorized as EV20, EV40, and EV60, representing compact sedans equipped with batteries of 6.51 kWh, 10.4 kWh, and 15.6 kWh, respectively, capable of covering 20, 40, and 60 miles on a single charge.
- To optimize the study’s computational resources, vehicles that traverse less than 20 miles daily are omitted from the fast-charging demand analysis as their charging needs are minimal and do not substantially influence the demand calculations.
3.2. Results and Discussions
3.3. Impact of Flexibility Levels on DER Sizing and Capacity
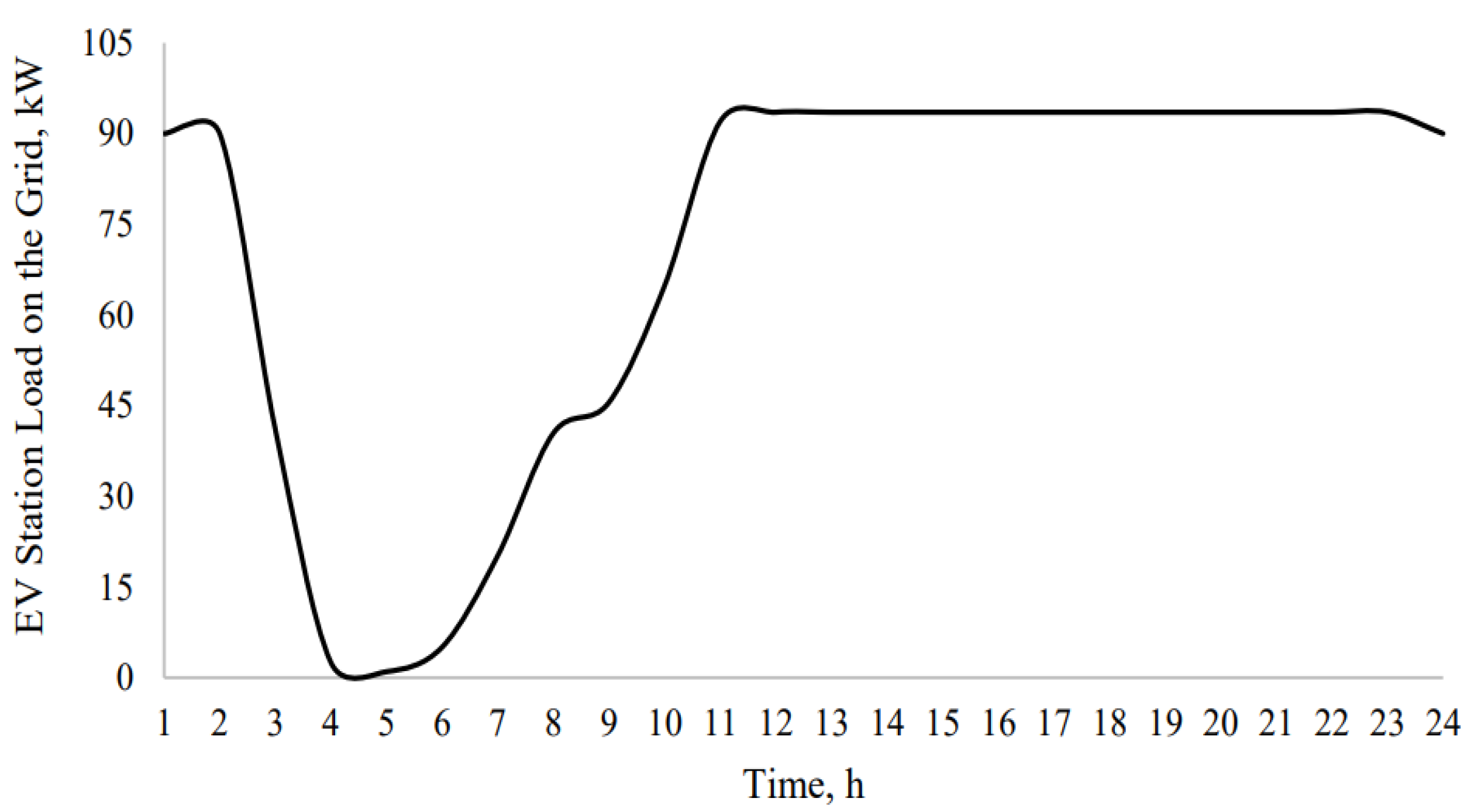
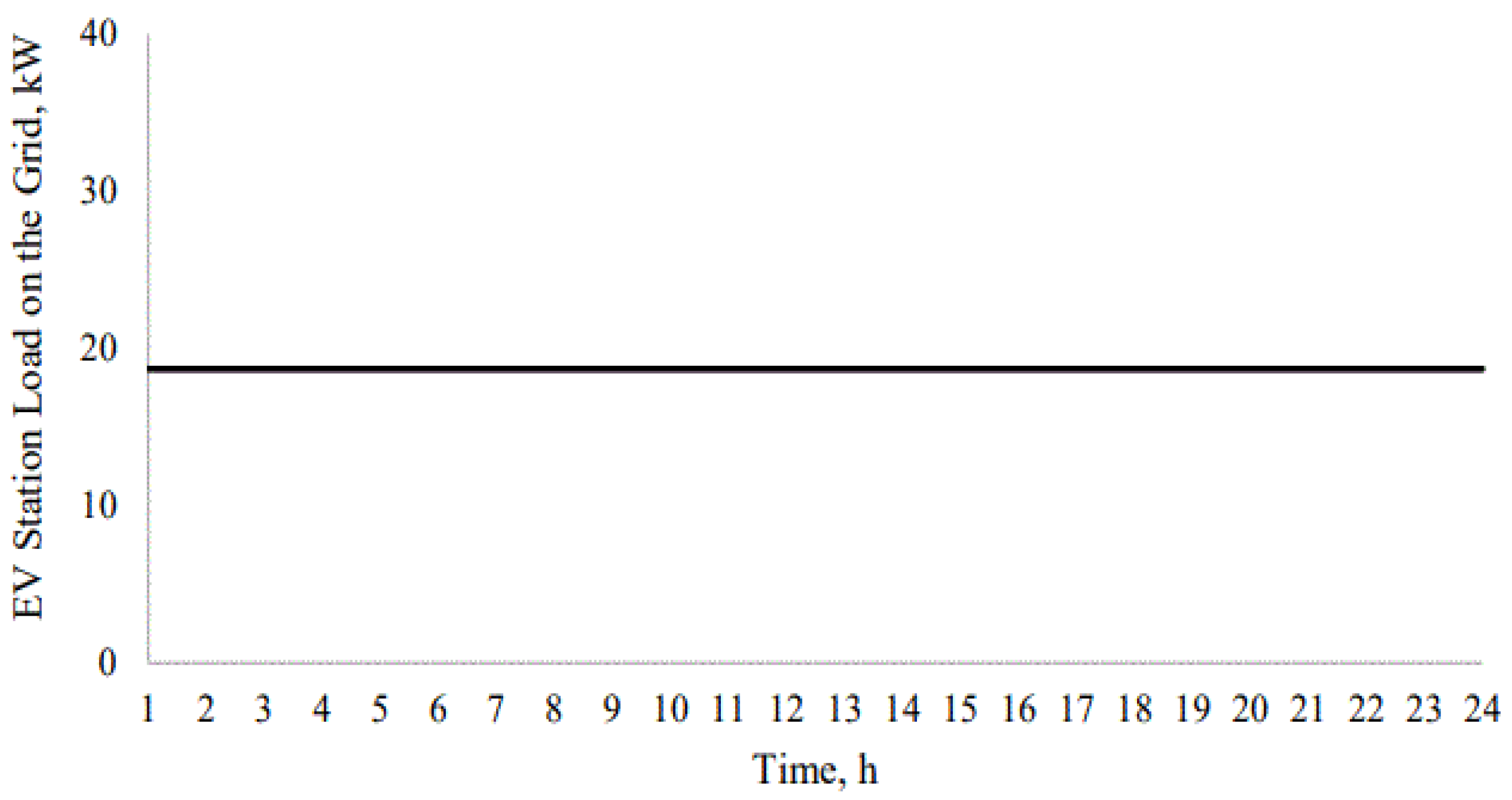
3.4. Load Profiles and Grid Implications Under Different Flexibility Scenarios
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saudi Vision 2030. Available online: https://www.vision2030.gov.sa/en (accessed on 10 April 2024).
- Alharbi, W.; Bhattacharya, K. Incentive design for flexibility provisions from residential energy hubs in smart grid. IEEE Trans. Smart Grid 2021, 12, 2113–2124. [Google Scholar] [CrossRef]
- Alharbi, W.; Bhattacharya, K. Electric Vehicle Charging Facility as a Smart Energy Microhub. IEEE Trans. Sustain. Energy 2017, 8, 616–628. [Google Scholar] [CrossRef]
- Habib, S.; Khan, M.M.; Abbas, F.; Numan, M.; Ali, Y.; Tang, H.; Yan, X. A framework for stochastic estimation of electric vehicle charging behavior for risk assessment of distribution networks. Front. Energy 2020, 14, 298–317. [Google Scholar] [CrossRef]
- Aboshady, F.M.; Pisica, I.; Axon, C.J. A stochastic model for estimating electric vehicle arrival at multi-charger forecourts. Energy Rep. 2022, 8, 11569–11578. [Google Scholar] [CrossRef]
- Faridimehr, S.; Venkatachalam, S.; Chinnam, R.B. A Stochastic Programming Approach for Electric Vehicle Charging Network Design. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1870–1882. [Google Scholar] [CrossRef]
- Tao, S.; Liao, K.; Xiao, X.; Wen, J.; Yang, Y.; Zhang, J. Charging demand for electric vehicle based on stochastic analysis of trip chain. IET Gener. Transm. Distrib. 2016, 10, 2689–2698. [Google Scholar] [CrossRef]
- Pashajavid, E.; Golkar, M.A. Charging of plug-in electric vehicles: Stochastic modelling of load demand within domestic grids. In Proceedings of the 20th Iranian Conference on Electrical Engineering (ICEE2012), Tehran, Iran, 15–17 May 2012; pp. 535–539. [Google Scholar] [CrossRef]
- Bi, X.; Chipperfield, A.; Tang, W.K. Coordinating Electric Vehicle Flow Distribution and Charger Allocation by Joint Optimization. IEEE Trans. Ind. Inform. 2021, 17, 8112–8121. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S.H. Optimal decentralized protocol for electric vehicle charging. IEEE Trans. Power Syst. 2013, 28, 940–951. [Google Scholar] [CrossRef]
- Hung, Y.C.; Lok, H.P.; Michailidis, G. Optimal routing for electric vehicle charging systems with stochastic demand: A heavy traffic approximation approach. Eur. J. Oper. Res. 2022, 299, 526–541. [Google Scholar] [CrossRef]
- Ivarsøy, E.; Torsæter, B.N.; Korpås, M. Stochastic Load Modeling of High-Power Electric Vehicle Charging—A Norwegian Case Study. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020. [Google Scholar]
- Irshad, U.B.; Rafique, S.; Town, G. Stochastic modelling of electric vehicle behaviour to estimate available energy storage in parking lots. IET Smart Grid 2020, 3, 760–767. [Google Scholar] [CrossRef]
- Yan, D.; Ma, C. Stochastic planning of electric vehicle charging station integrated with photovoltaic and battery systems. IET Gener. Transm. Distrib. 2020, 14, 4217–4224. [Google Scholar] [CrossRef]
- Gholinejad, H.R.; Adabi, J.; Marzband, M. Hierarchical energy management system for home-energy-hubs considering plug-in electric vehicles. IEEE Trans. Ind. Appl. 2022, 58, 5582–5592. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Dehghanian, P. Optimized probabilistic PHEVs demand management in the context of energy hubs. IEEE Trans. Power Deliv. 2014, 30, 996–1006. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Dehghanian, P.; Davoudi, M. Energy management of plug-in hybrid electric vehicles in renewable-based energy hubs. Sustain. Energy Grids Netw. 2022, 32, 100932. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cordiner, S.; Mulone, V.; Santarelli, M.; Lombardi, P.; Wenge, C.; Arendarski, B.; Komarnicki, P. Grid service potential from optimal sizing and scheduling the charging hub of a commercial Electric Vehicle fleet. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Haupt, L.; Schöpf, M.; Wederhake, L.; Weibelzahl, M. The influence of electric vehicle charging strategies on the sizing of electrical energy storage systems in charging hub microgrids. Appl. Energy 2020, 273, 115231. [Google Scholar] [CrossRef]
- Kazemi, B.; Kavousi-Fard, A.; Dabbaghjamanesh, M.; Karimi, M. IoT-enabled operation of multi energy hubs considering electric vehicles and demand response. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2668–2676. [Google Scholar] [CrossRef]
- George-Williams, H.; Wade, N.; Carpenter, R. A probabilistic framework for the techno-economic assessment of smart energy hubs for electric vehicle charging. Renew. Sustain. Energy Rev. 2022, 162, 112386. [Google Scholar] [CrossRef]
- Lin, H.; Liu, Y.; Sun, Q.; Xiong, R.; Li, H.; Wennersten, R. The impact of electric vehicle penetration and charging patterns on the management of energy hub—A multi-agent system simulation. Appl. Energy 2018, 230, 189–206. [Google Scholar] [CrossRef]
- Aslani, M.; Mashayekhi, M.; Hashemi-Dezaki, H.; Ketabi, A. Robust optimal operation of energy hub incorporating integrated thermal and electrical demand response programs under various electric vehicle charging modes. Appl. Energy 2022, 321, 119344. [Google Scholar] [CrossRef]
- Xylia, M.; Leduc, S.; Patrizio, P.; Kraxner, F.; Silveira, S. Locating charging infrastructure for electric buses in Stockholm. Transp. Res. Part C Emerg. Technol. 2017, 78, 183–200. [Google Scholar] [CrossRef]
- GAMS Development Corporation. General Algebraic Modeling System (GAMS), Software. Available online: https://http://www.gams.com (accessed on 4 May 2024).
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Power Eng. Rev. 1989, 9, 101–102. [Google Scholar] [CrossRef]
- Pinheiro, J.; Dornellas, C.; Schilling, M.T.; Melo, A.; Mello, J. Probing the new IEEE reliability test system (RTS-96): HL-II assessment. IEEE Trans. Power Syst. 1998, 13, 171–176. [Google Scholar] [CrossRef]
- U.S. Department of Transportation. National Household Travel Survey. Available online: http://nhts.ornl.gov (accessed on 5 April 2024).
- Alfraidi, W.; Shalaby, M.; Alaql, F. Modeling EV charging station loads considering on-road wireless charging capabilities. World Electr. Veh. J. 2023, 14, 313. [Google Scholar] [CrossRef]


| Flexibility Level (%) | Peak Load (kW) | Load Variability |
|---|---|---|
| 0 | 188 | High |
| 50 | 94 | Moderate |
| 90 | 19 | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfraidi, W.; Alaql, F.; AlMuhanna, K.; Farh, H.M.H.; Al-Shamma’a, A.A. Designing EV Charging Energy Hubs to Meet Flexibility Requirements in Smart Grids. World Electr. Veh. J. 2025, 16, 43. https://doi.org/10.3390/wevj16010043
Alfraidi W, Alaql F, AlMuhanna K, Farh HMH, Al-Shamma’a AA. Designing EV Charging Energy Hubs to Meet Flexibility Requirements in Smart Grids. World Electric Vehicle Journal. 2025; 16(1):43. https://doi.org/10.3390/wevj16010043
Chicago/Turabian StyleAlfraidi, Walied, Fahad Alaql, Khalid AlMuhanna, Hassan M. Hussein Farh, and Abdullrahman A. Al-Shamma’a. 2025. "Designing EV Charging Energy Hubs to Meet Flexibility Requirements in Smart Grids" World Electric Vehicle Journal 16, no. 1: 43. https://doi.org/10.3390/wevj16010043
APA StyleAlfraidi, W., Alaql, F., AlMuhanna, K., Farh, H. M. H., & Al-Shamma’a, A. A. (2025). Designing EV Charging Energy Hubs to Meet Flexibility Requirements in Smart Grids. World Electric Vehicle Journal, 16(1), 43. https://doi.org/10.3390/wevj16010043







