Multi-Cell Cooperative Resource Allocation and Performance Evaluation for Roadside-Assisted Automated Driving
Abstract
1. Introduction
- Proposal of a communication resource allocation framework based on a hierarchical MARL algorithm named multi-agent option-critic architecture for addressing the problem of resource allocation. The architecture has a hierarchical structure for the control of agents and the execution of their actions. Additionally, the option-critic architecture adopted will be more thoroughly introduced in the Related Work and Methodology Sections.
- Creation of a specialized reinforcement learning algorithm designed explicitly for the multi-agent option-critic framework. This algorithm centrally trains agent policies to facilitate collaboration and achieves the autonomous distributed allocation of communication resources.
- We performed several rounds of experiments, each tailored to specific communication demand patterns and environmental parameters. We then conducted thorough comparisons and analyses, considering both baseline methods and alternative approaches. Our observations revealed a noteworthy enhancement in system performance and its ability to adjust to diverse demand patterns when utilizing our algorithm.
2. Related Work
2.1. Hierarchical Reinforcement Learning and Option-Critic Framework
2.2. Resource Allocation for Vehicular Networks and MARL Solutions
3. System Model
3.1. System Architecture
3.2. Communication Links
3.3. Problem Formulation
4. Methodology
4.1. Observation Space, Action and Reward
- Local Channel Information (I): interference from non-local V2I links over the local V2I link (current time).
- Local Resource Block Allocation Matrix (): observations of the local resource block allocation matrix at time .
- Vector of Remaining Payload of All V2I Links (E): remaining payload sizes for all V2I links at the current time.
- Remaining Time (V): Remaining time for transmission.
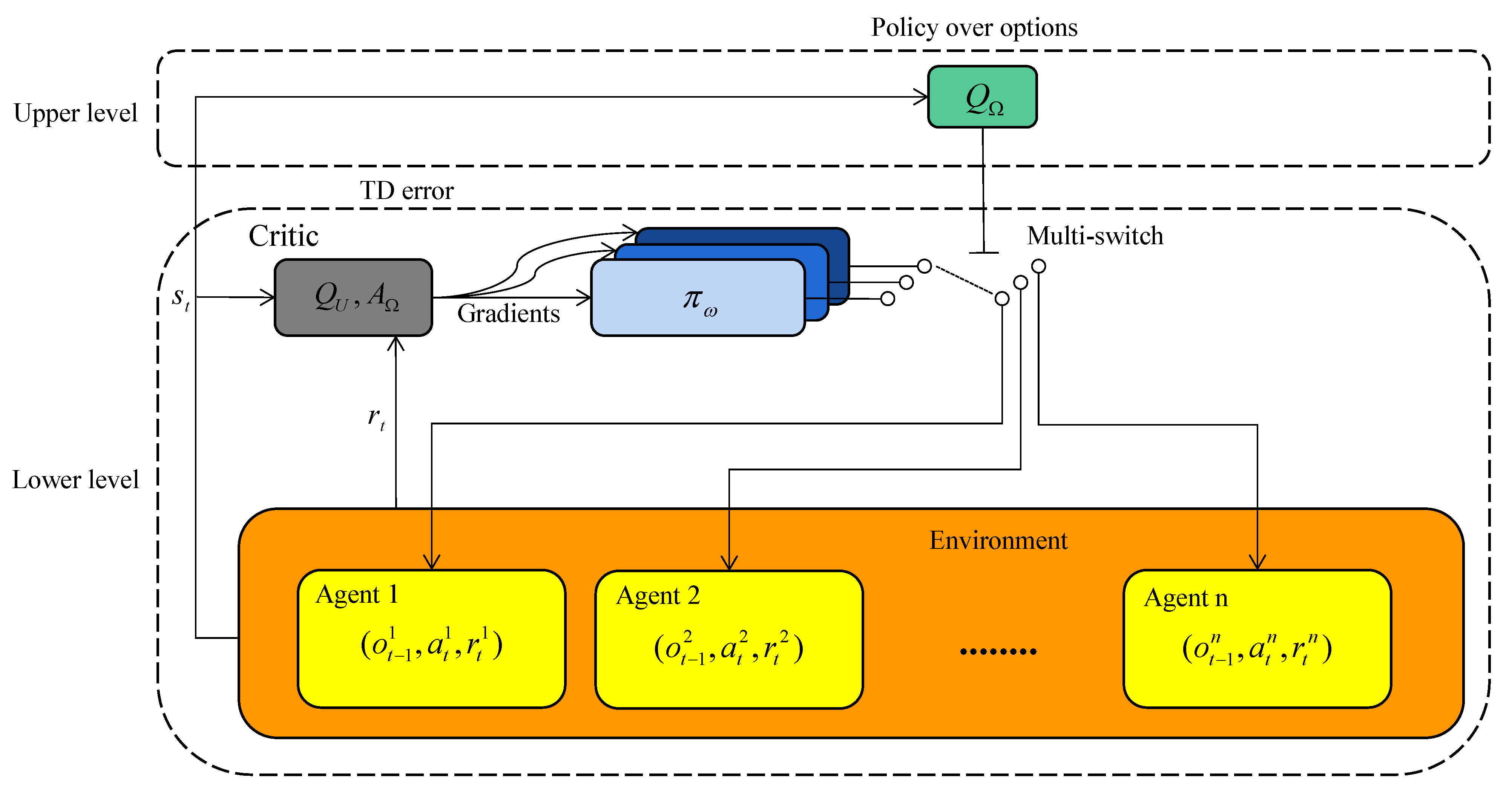
4.2. Option-Critic Architecture in MARL Scenario
4.3. Learning Algorithm and Training Setup
| Algorithm 1: Resource allocation based on multi-agent option-critic reinforcement learning |
| Start environment simulator, generating vehicles and links |
| Initialize option-critic network for all agents and overall Q network randomly |
| for each episode do |
| for each step t do |
| for each base station agent k do |
| Observe |
| Select option based on upper level policies |
| Choose action from and according to -greedy policy |
| end for |
| All agents take action and receive reward |
| Update channel small-scale fading |
| All agents calculate TD loss and update value function |
| Store in the buffer |
| if the buffer length is greater than the threshold value then |
| Update the upper-level and low-level networks using Monte-Carlo sampling |
| end if |
| end for |
| end for |
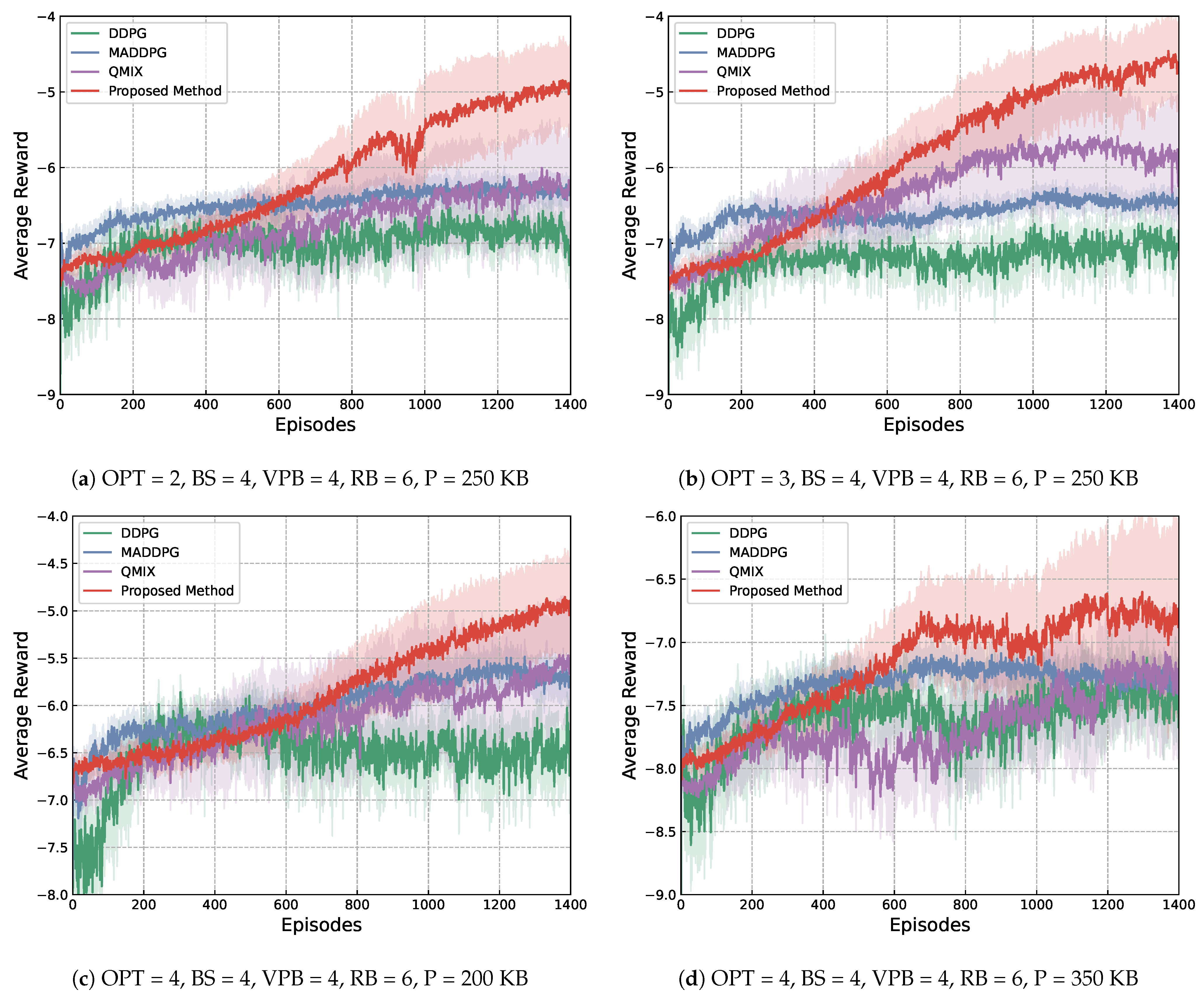
5. Simulation Results
5.1. Simulation Environment Setup
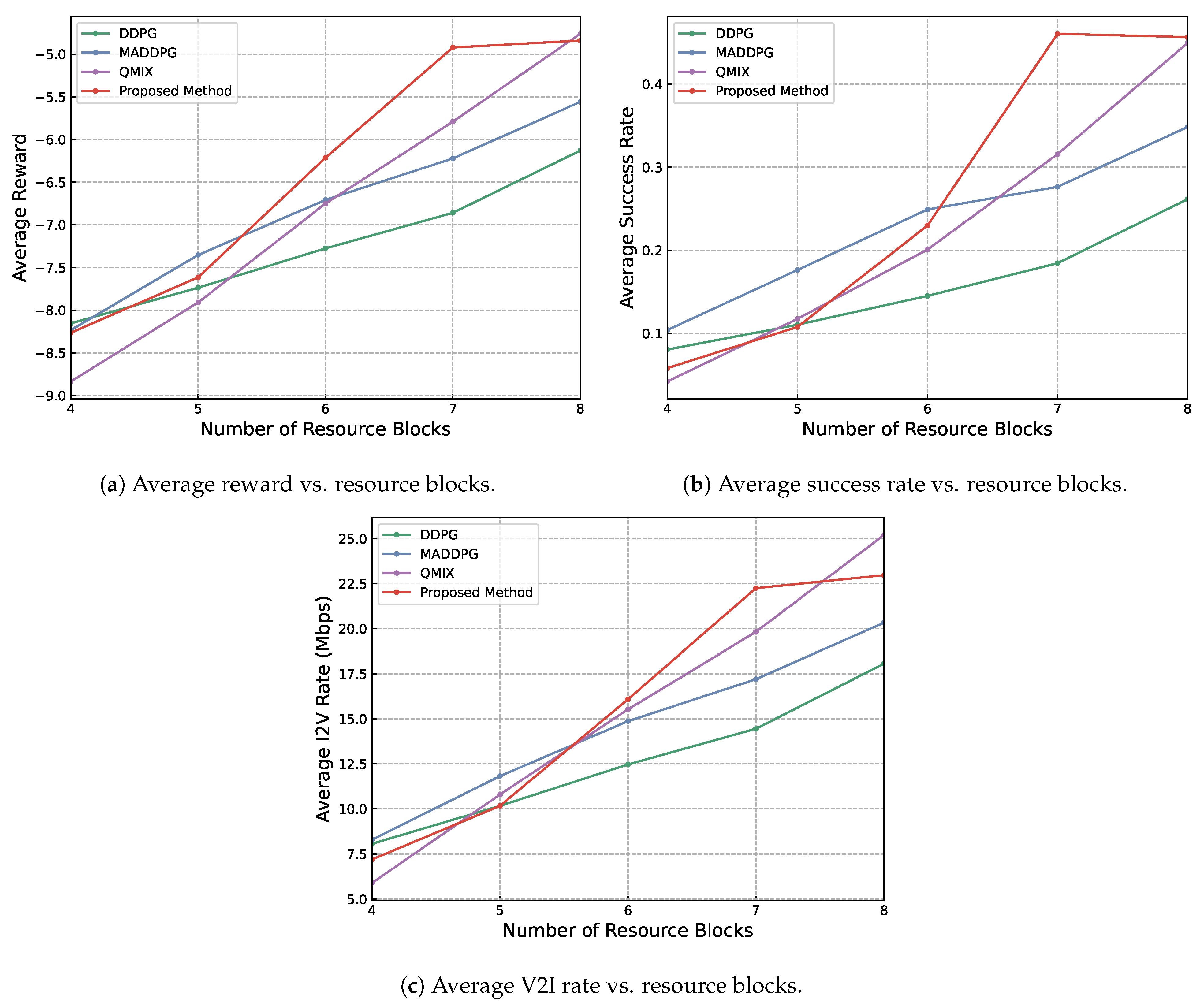
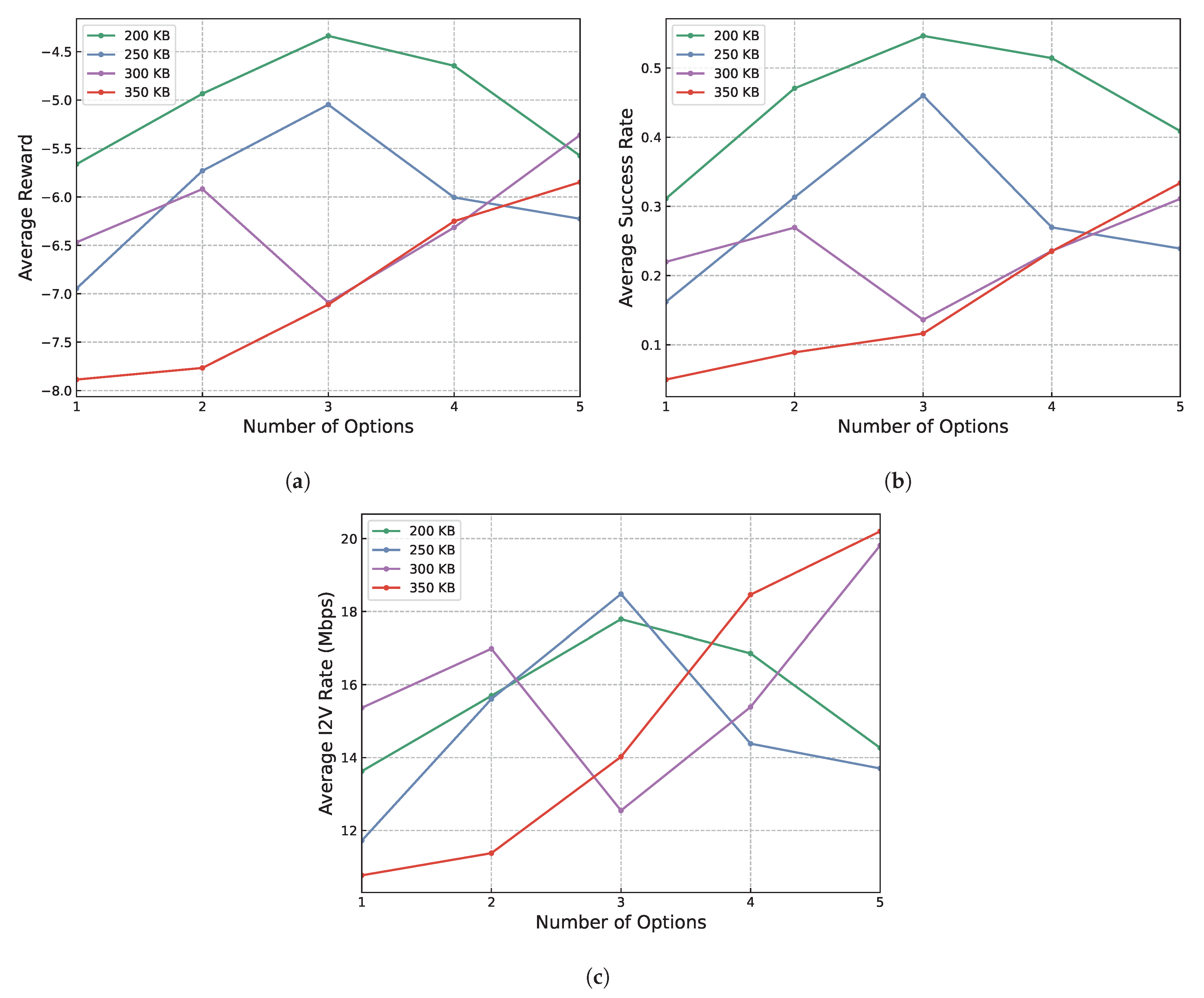
5.2. Results Analysis
- (1)
- Success rate: the average of the completed data transmission amount in total initiated transmissions. The calculation of the complete rate in one step of an episode follows Equation (16):where represents the complete rate reflecting the proportion of completed transmissions C in the total initiated transmissions. The total for the initiated transmissions is calculated by C plus the number of uncompleted transmissions U.
- (2)
- V2I rate: the average of the V2I transmission speed, which is measured by the unit Mbps.
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Fang, X.; Zhang, Q. Reinforcement Learning Driving Strategy Based on Auxiliary Task for Multi-Scenarios Autonomous Driving. In Proceedings of the 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 12–14 May 2023. [Google Scholar] [CrossRef]
- Mishra, A.; Purohit, J.; Nizam, M.; Gawre, S.K. Recent Advancement in Autonomous Vehicle and Driver Assistance Systems. In Proceedings of the 2023 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 18–19 February 2023. [Google Scholar] [CrossRef]
- Chib, P.S.; Singh, P. Recent Advancements in End-To-End Autonomous Driving Using Deep Learning: A Survey. IEEE Trans. Intell. Veh. 2023, 9, 103–118. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Y.; Yang, Z. An Overview about Emerging Technologies of Autonomous Driving. arXiv 2023. [Google Scholar] [CrossRef]
- Kosuru, V.S.R.; Venkitaraman, A.K. Advancements and Challenges in Achieving Fully Autonomous Self-Driving Vehicles. World J. Adv. Res. Rev. 2023, 18, 161–167. [Google Scholar] [CrossRef]
- Rawlley, O.; Gupta, S. Artificial Intelligence -Empowered Vision-Based Self Driver Assistance System for Internet of Autonomous Vehicles. Trans. Emerg. Telecommun. Technol. 2022, 34, e4683. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, M.A.; Malik, S.; Kulkarni, P.; Alkaabi, N.; Ullah, O.; El-Sayed, H.; Ahmed, A.; Turaev, S. Advancing C-V2X for Level 5 Autonomous Driving from the Perspective of 3GPP Standards. Sensors 2023, 23, 2261. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, S.; Yu, S.; Yu, J.J.Q.; Wen, M. Collision Avoidance Predictive Motion Planning Based on Integrated Perception and V2V Communication. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9640–9653. [Google Scholar] [CrossRef]
- Yang, K.; Yang, D.; Zhang, J.; Li, M.; Liu, Y.; Liu, J.; Wang, H.; Sun, P.; Song, L. Spatio-Temporal Domain Awareness for Multi-Agent Collaborative Perception. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023. [Google Scholar] [CrossRef]
- Hossain, E.; Rasti, M.; Tabassum, H.; Abdelnasser, A. Evolution toward 5G Multi-Tier Cellular Wireless Networks: An Interference Management Perspective. IEEE Wirel. Commun. 2014, 21, 118–127. [Google Scholar] [CrossRef]
- Kafafy, M.; Ibrahim, A.S.; Ismail, M.H. Optimal Placement of Reconfigurable Intelligent Surfaces for Spectrum Coexistence with Radars. IEEE Trans. Veh. Technol. 2022, 71, 6574–6585. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J.; Feng, Z.; Gao, Y. Multi-Agent Reinforcement Learning for Resource Allocation in IoT Networks with Edge Computing. China Commun. 2020, 17, 220–236. [Google Scholar] [CrossRef]
- Fu, J.; Qin, X.; Huang, Y.; Tang, L.; Liu, Y. Deep Reinforcement Learning-Based Resource Allocation for Cellular Vehicular Network Mode 3 with Underlay Approach. Sensors 2022, 22, 1874. [Google Scholar] [CrossRef]
- Alyas, T.; Ghazal, T.M.; Alfurhood, B.S.; Issa, G.F.; Thawabeh, O.A.; Abbas, Q. Optimizing Resource Allocation Framework for Multi-Cloud Environment. Comput. Mater. Contin. 2023, 75, 4119–4136. [Google Scholar] [CrossRef]
- Nurcahyani, I.; Lee, J.W. Role of Machine Learning in Resource Allocation Strategy over Vehicular Networks: A Survey. Sensors 2021, 21, 6542. [Google Scholar] [CrossRef]
- Hong, J.-P.; Park, S.; Choi, W. Base Station Dataset-Assisted Broadband Over-The-Air Aggregation for Communication-Efficient Federated Learning. IEEE Trans. Wirel. Commun. 2023, 22, 7259–7272. [Google Scholar] [CrossRef]
- Guo, W.; Wagan, S.A.; Shin, D.R.; Siddiqui, I.F.; Koo, J.; Qureshi, N.M.F. Periodic-Collaboration-Based Energy-Efficient Cell Dormancy in Heterogeneous Dense Networks. In Proceedings of the 2022 IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Belfast, UK, 14–17 June 2022. [Google Scholar] [CrossRef]
- Nasir, Y.S.; Guo, D. Deep Reinforcement Learning for Joint Spectrum and Power Allocation in Cellular Networks. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021. [Google Scholar] [CrossRef]
- Xiu, Z.; Wu, Z. Utility- and Fairness-Based Spectrum Allocation of Cellular Networks by an Adaptive Particle Swarm Optimization Algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 42–50. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y. Resource Allocation Strategy Based on Tripartite Graph in Vehicular Social Networks. IEEE Trans. Netw. Sci. Eng. 2022, 10, 3017–3031. [Google Scholar] [CrossRef]
- Qian, B.; Zhou, H.; Ma, T.; Xu, Y.; Yu, K.; Shen, X.; Hou, F. Leveraging Dynamic Stackelberg Pricing Game for Multi-Mode Spectrum Sharing in 5G-VANET. IEEE Trans. Veh. Technol. 2020, 69, 6374–6387. [Google Scholar] [CrossRef]
- Bacon, P.-L.; Harb, J.; Precup, D. The Option-Critic Architecture. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar] [CrossRef]
- Riemer, M.; Liu, M.; Tesauro, G. Learning Abstract Options; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2018; Volume 31. [Google Scholar]
- Schaul, T.; Horgan, D.; Gregor, K.; Silver, D. Universal Value Function Approximators; Bach, F., Blei, D., Eds.; PMLR: Birmingham, UK, 2015; Volume 37, pp. 1312–1320. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Li, G.Y.; Juang, B.-H.F. Deep Reinforcement Learning Based Resource Allocation for V2V Communications. IEEE Trans. Veh. Technol. 2019, 68, 3163–3173. [Google Scholar] [CrossRef]
- Tampuu, A.; Matiisen, T.; Kodelja, D.; Kuzovkin, I.; Korjus, K.; Aru, J.; Aru, J.; Vicente, R. Multiagent Cooperation and Competition with Deep Reinforcement Learning. PLoS ONE 2017, 12, e0172395. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, H.; Lee, S.-H.; Lee, I. Multi-Agent Deep Reinforcement Learning for Distributed Resource Management in Wirelessly Powered Communication Networks. IEEE Trans. Veh. Technol. 2020, 69, 14055–14060. [Google Scholar] [CrossRef]
- Wu, T.; Zhou, P.; Liu, K.; Yuan, Y.; Wang, X.; Huang, H.; Wu, D.O. Multi-Agent Deep Reinforcement Learning for Urban Traffic Light Control in Vehicular Networks. IEEE Trans. Veh. Technol. 2020, 69, 8243–8256. [Google Scholar] [CrossRef]
- Park, H.; Lim, Y. Deep Reinforcement Learning Based Resource Allocation with Radio Remote Head Grouping and Vehicle Clustering in 5G Vehicular Networks. Electronics 2021, 10, 3015. [Google Scholar] [CrossRef]
- Zhi, Y.; Tian, J.; Deng, X.; Qiao, J.; Lu, D. Deep Reinforcement Learning-Based Resource Allocation for D2D Communications in Heterogeneous Cellular Networks. Digit. Commun. Netw. 2021, 8, 834–842. [Google Scholar] [CrossRef]
- Sahin, T.; Khalili, R.; Boban, M.; Wolisz, A. VRLS: A Unified Reinforcement Learning Scheduler for Vehicle-To-Vehicle Communications. arXiv 2019, arXiv:1907.09319. [Google Scholar] [CrossRef]
- Liang, L.; Ye, H.; Li, G.Y. Spectrum Sharing in Vehicular Networks Based on Multi-Agent Reinforcement Learning. IEEE J. Sel. Areas Commun. 2019, 37, 2282–2292. [Google Scholar] [CrossRef]
- Vu, H.V.; Farzanullah, M.; Liu, Z.; Nguyen, D.H.; Morawski, R.; Le-Ngoc, T. Multi-Agent Reinforcement Learning for Joint Channel Assignment and Power Allocation in Platoon-Based C-V2X Systems. arXiv 2020. [Google Scholar] [CrossRef]
- Gündogan, A.; Gursu, H.M.; Pauli, V.; Kellerer, W. Distributed Resource Allocation with Multi-Agent Deep Reinforcement Learning for 5G-V2V Communication. arXiv 2020, arXiv:2010.05290. [Google Scholar] [CrossRef]
- He, H. Research on Key Technologies of Dynamic Spectrum Access in Cognitive Radio. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2014. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. J. Mach. Learn. Res. 2018, 21, 4292–4301. [Google Scholar]
- Zhou, Z.; Liu, G.; Tang, Y. Multi-Agent Reinforcement Learning: Methods, Applications, Visionary Prospects, and Challenges. arXiv 2023, arXiv:2305.10091. [Google Scholar] [CrossRef]
- Hou, W.; Wen, H.; Song, H.; Lei, W.; Zhang, W. Multiagent Deep Reinforcement Learning for Task Offloading and Resource Allocation in Cybertwin-Based Networks. IEEE Internet Things J. 2021, 8, 16256–16268. [Google Scholar] [CrossRef]
- Parvini, M.; Javan, M.R.; Mokari, N.; Abbasi, B.; Jorswieck, E.A. AoI-Aware Resource Allocation for Platoon-Based C-V2X Networks via Multi-Agent Multi-Task Reinforcement Learning. IEEE Trans. Veh. Technol. 2023, 72, 9880–9896. [Google Scholar] [CrossRef]
- Sheikh, H.U.; Bölöni, L. Multi-Agent Reinforcement Learning for Problems with Combined Individual and Team Reward. arXiv 2020, arXiv:2003.10598. [Google Scholar] [CrossRef]
- Jang, J.; Yang, H.J. Deep Reinforcement Learning-Based Resource Allocation and Power Control in Small Cells with Limited Information Exchange. IEEE Trans. Veh. Technol. 2020, 69, 13768–13783. [Google Scholar] [CrossRef]
- 3GPP TR 36.885. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2934 (accessed on 26 August 2023).


| Paper | Collaboration | Hierarchical Model | Global Observation | Use Options | Distributed Execution |
|---|---|---|---|---|---|
| [27] | ✓ | - | - | - | ✓ |
| [28] | ✓ | - | - | - | ✓ |
| [29] | ✓ | - | - | - | ✓ |
| [30] | ✓ | ✓ | ✓ | - | ✓ |
| [31] | ✓ | ✓ | - | - | ✓ |
| [32] | ✓ | - | - | - | ✓ |
| [33] | ✓ | - | ✓ | - | - |
| [34] | ✓ | - | - | - | ✓ |
| [35] | ✓ | - | ✓ | - | ✓ |
| [36] | ✓ | ✓ | - | - | ✓ |
| Proposed |
| Index | Value |
|---|---|
| V2I links M | 9 |
| Carrier freq. | 2 GHz |
| Bandwidth | 4 MHz |
| Base station antenna height | 25 m |
| Base station channel gain | 8 dBi |
| Base station receiver noise figure | 5 dB |
| Vehicle antenna height | m |
| Vehicle channel gain | 3 dBi |
| Vehicle receiver noise figure | 9 dB |
| Absolute moving speed v | 15 m/s |
| V2I transit power | 23 dBm |
| Noise power | dBm |
| Time constraint of payload transmission T | 100 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhu, X.; Li, Y.; Yuan, Q.; Li, L. Multi-Cell Cooperative Resource Allocation and Performance Evaluation for Roadside-Assisted Automated Driving. World Electr. Veh. J. 2024, 15, 253. https://doi.org/10.3390/wevj15060253
Yang S, Zhu X, Li Y, Yuan Q, Li L. Multi-Cell Cooperative Resource Allocation and Performance Evaluation for Roadside-Assisted Automated Driving. World Electric Vehicle Journal. 2024; 15(6):253. https://doi.org/10.3390/wevj15060253
Chicago/Turabian StyleYang, Shu, Xuanhan Zhu, Yang Li, Quan Yuan, and Lili Li. 2024. "Multi-Cell Cooperative Resource Allocation and Performance Evaluation for Roadside-Assisted Automated Driving" World Electric Vehicle Journal 15, no. 6: 253. https://doi.org/10.3390/wevj15060253
APA StyleYang, S., Zhu, X., Li, Y., Yuan, Q., & Li, L. (2024). Multi-Cell Cooperative Resource Allocation and Performance Evaluation for Roadside-Assisted Automated Driving. World Electric Vehicle Journal, 15(6), 253. https://doi.org/10.3390/wevj15060253






