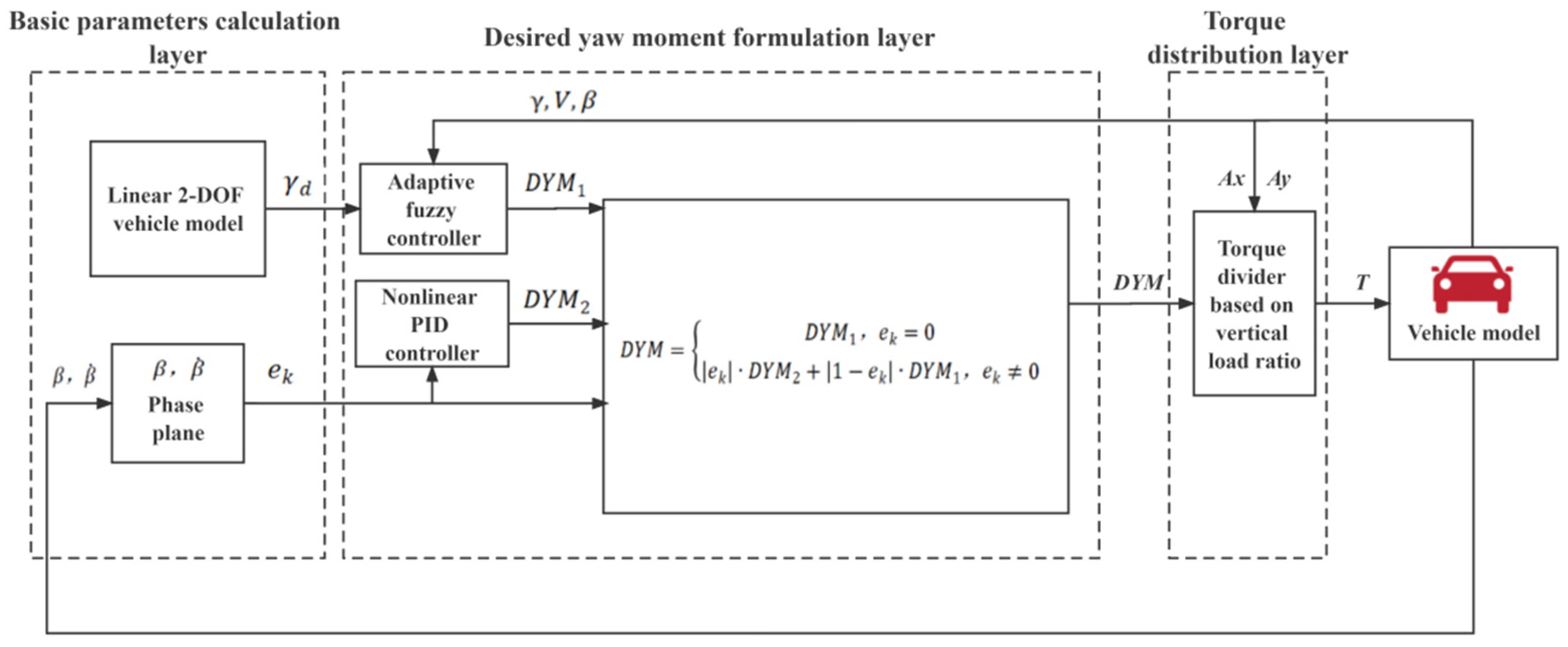
It is expected that the yaw moment formulation layer includes a stability domain calculation module, an instability compensation module, and a phase plane judgment calculation module. Yaw moment DYM1 is calculated by the fuzzy controller in the stability domain, and yaw moment DYM2 is calculated by the PID control in the instability compensation module. Finally, the phase plane judgment calculation module calculates the desired yaw moment, and the final output of DYM is based on the judgment condition of the stable parameter, .
4.2.1. Adaptive Fuzzy Controller
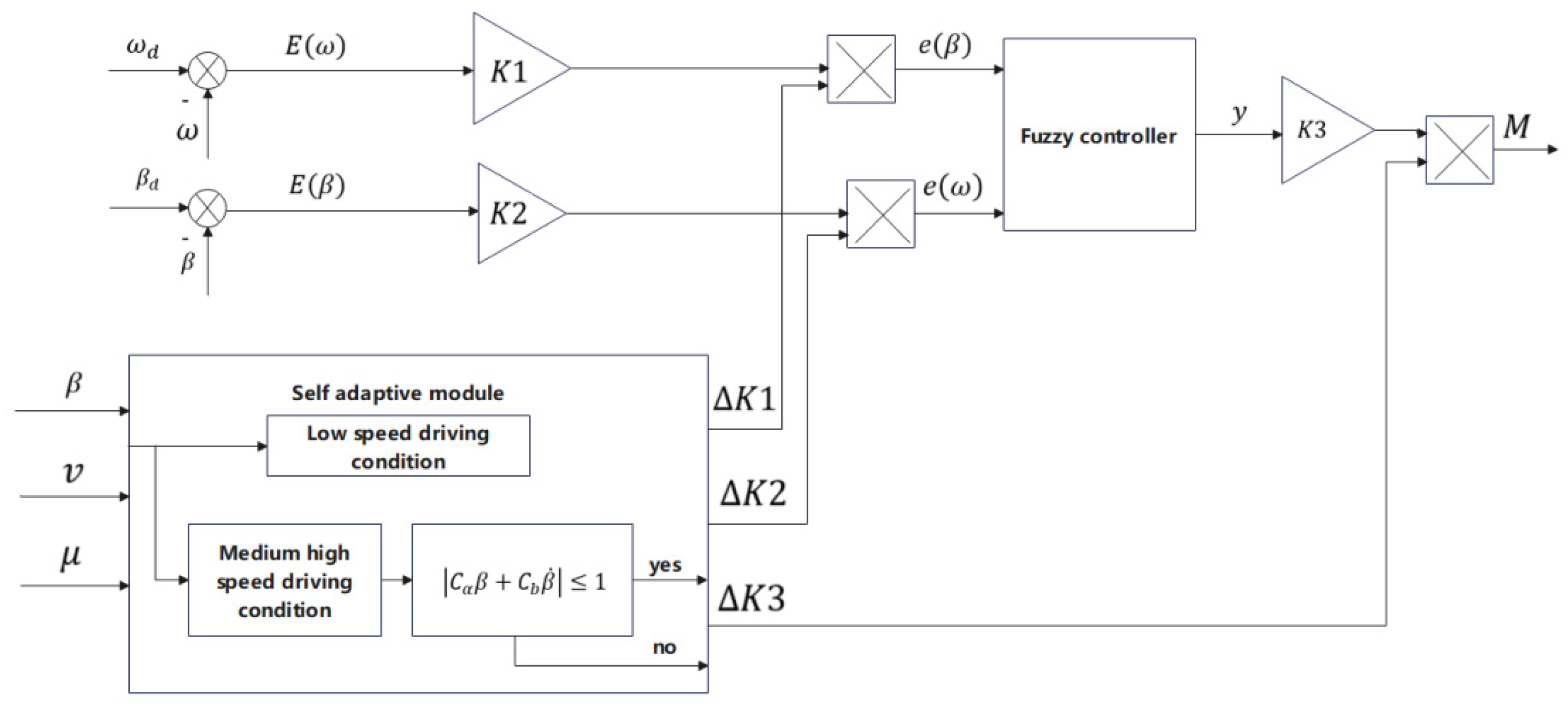
The adaptive fuzzy controller developed in this paper can dynamically adjust the quantization factor and scale factor to determine the desired yaw moment, thereby achieving the most suitable control scheme for the current operating conditions. When driving on a road with a high adhesion coefficient, the vehicle’s operating conditions are optimal. During vehicle turning, if there is a deviation between the actual and expected values of the yaw rate and sideslip angle, the quantization factor and scale factor can be simultaneously increased. This allows the actual yaw rate and sideslip angle to quickly converge to the expected values, thereby enhancing the response speed of the control system. Conversely, when driving on a road with a low adhesion coefficient, the vehicle’s operating conditions are suboptimal. In the event of a deviation between the actual and expected values of the yaw rate and sideslip angle during vehicle turning, the proportional factor output by the fuzzy controller can be reduced by increasing the quantified factor of the yaw rate and sideslip angle. This ensures an accelerated response of the control system and prevents excessive torque difference between the left and right sides of the bus, thereby enabling better performances on road surfaces with low adhesion. The design of the adaptive fuzzy controller is illustrated in
Figure 5.
The adaptive fuzzy control algorithm is as follows:
In Formula (13),
is the functional relationship between the input and output of the adaptive fuzzy control system, which is determined by the controller parameters and the de-fuzzification mode. It can be seen from Equations (12) and (13) that the input of the fuzzy controller not only depends on the input deviations
E(
ω) and
E(
β) and the quantization factors
K1 and
K2, but also on ∆
K1 and ∆
K2 as output by the adaptive module. Similarly, the magnitude of the expected swaying moment,
M, depends not only on scale factor
K3 but also on ∆
K3, as output by the adaptive module. The magnitude of the expected yaw moment,
M, is as follows:
In the process of its operation, the adaptive module can adjust the expected yaw moment, M, of the vehicle according to the corresponding values of ∆K1, ∆K2, and ∆K3, as output during actual working conditions; therefore, the vehicle can keep the best running state under any working conditions. Considering the calculation speed of the algorithm, the design of the adaptive module is as follows:
The inputs in the adaptive module are the speed, yaw rate, sideslip angle, and road adhesion coefficient, which can output the additional quantization factors ∆
K1 and ∆
K2, as well as scale factor ∆
K3, through additional fuzzy control according to the driving conditions of the vehicle and the actual yaw rate and sideslip angle of the vehicle to ensure the control effect and response speed. When the vehicle is running at a low speed and turning, it is believed that the vehicle can meet the requirements for stable operation only by controlling the yaw rate. The adaptive module will shield the deviation value of the sideslip angle. At the same time, in order to improve the response speed of the control, the module needs to increase the control effect of the pendulum velocity deviation and the total amplification ratio of the system, that is, the outputs
,
under this working condition. When the vehicle is driving at a high speed and turning, the change rate of the sideslip angle and the sideslip angle will be limited to
[
21]. When this range is not exceeded, the main control objective is to ensure the stability of the driving direction of the vehicle, as well as the steering speed of the vehicle. The yaw rate and sideslip angle are controlled simultaneously. At this time, the yaw rate and sideslip angle of the vehicle are equally important. The values of the two quantization factors output by the adaptive module are equal, that is,
. At the same time, when the vehicle is running at medium and high speeds, in order to ensure the stability while driving, the torque difference on both sides should be reduced, that is, the output
. When this range is exceeded, the only control objective is to ensure the stability of the driving direction of the vehicle. At this time, it is believed that control of the yaw rate will no longer play a role in vehicle stability, so only the control of the sideslip angle is used to ensure the vehicle operates stably. The adaptive module will shield the difference in the yaw rate. That is, the outputs are
,
. Through an analysis of the vehicle dynamics stability, and with reference to a large number of documents,
and
[
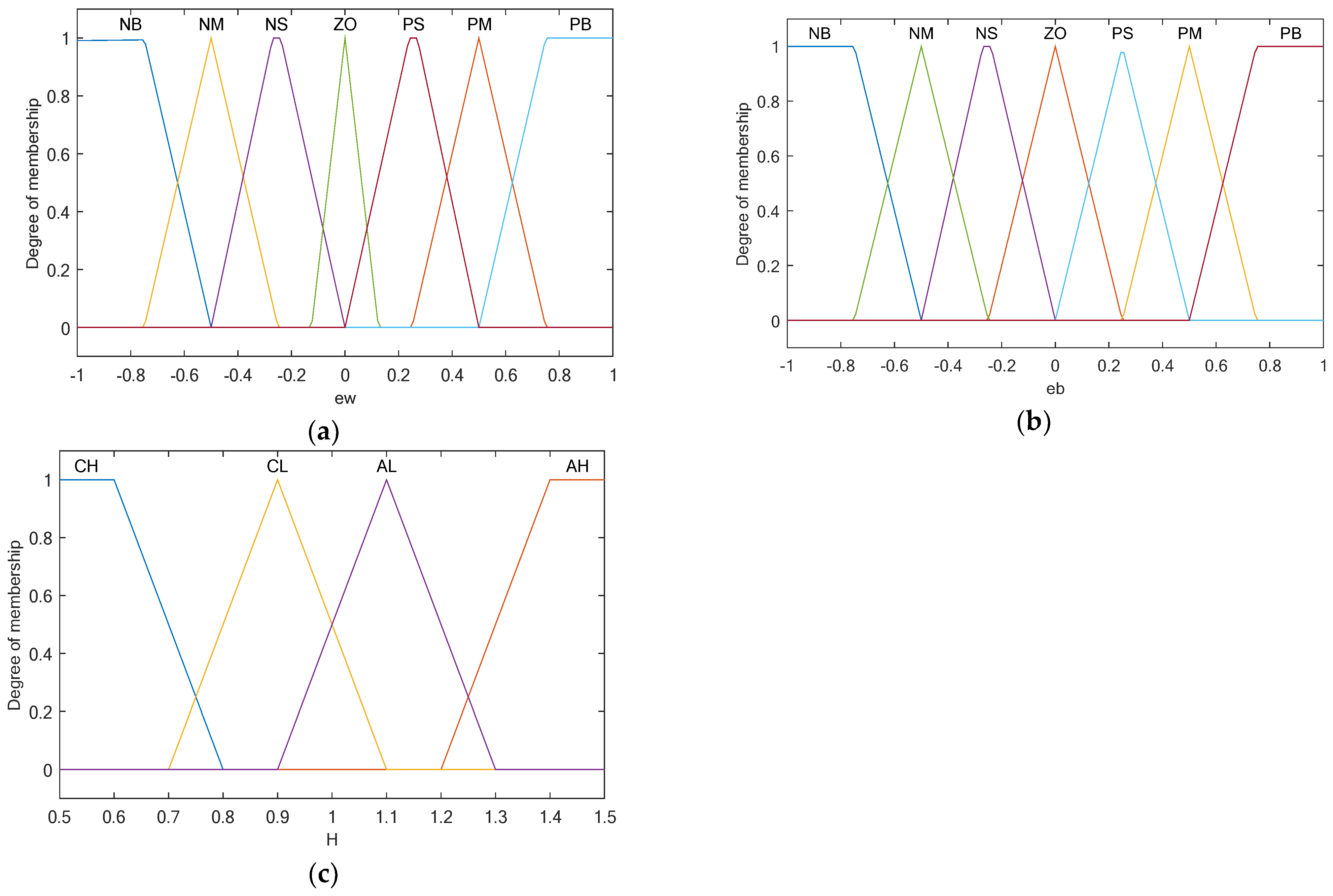
22]. The fuzzy control inputs of the adaptive module are the deviations from the ideal values of the yaw rate and the sideslip angle by the actual values, and the outputs are the additional quantization factors and scale factor of the outer fuzzy controller. There are seven fuzzy sets for the deviation between the input yaw rate and the sideslip angle of the center of mass, which are, respectively, negative large (NB), negative medium (NM), negative small (NS), zero (ZO), positive small (PS), positive medium (PM), and positive large (PB). There are four fuzzy sets for the additional quantization factor and scale factor outputs.
Figure 6a–c show the corresponding membership function.
The fuzzy rules for the adjustment of the quantization factors and scale factor are shown in
Table 5:
The outer fuzzy controller designed in this paper used fuzzy exact values of the deviation of the yaw rate and sideslip angle,
and
, into seven fuzzy sets, which were negative large (NB), negative medium (NM), negative small (NS), zero (ZO), positive small (PS), positive medium (PM), and positive large (PB). The output variable M is divided into nine fuzzy sets, which are negative very large (NVB), negative large (NB), negative medium (NM), negative small (NS), zero (ZO), positive small (PS), positive medium (PM), positive large (PB), and positive very large (PVB).
Figure 7a–c below show the corresponding membership function.
Fuzzy reasoning is the core of fuzzy control; that is, the combination of input variables and output variables of the fuzzy controller forms a one-to-one corresponding relationship rule, according to experts. The reasoning relationships, with 49 fuzzy rules, used in this paper are shown in
Table 6.
Also, the weighted average method was chosen to conduct the de-fuzzification. Finally, the calculation formula of the desired yaw moment, M, is shown in Equation (15).
4.2.2. Nonlinear PID Controller
A traditional PID control is a linear combination of errors, which can achieve a good control effect on linear and near-linear systems. Its general form is as follows:
where
is the proportional gain;
is the integral gain;
is the differential gain; and
is the deviation.
The vehicle dynamics model is a nonlinear model, and this linear combination is not the best combination mode in the nonlinear model. The more suitable and effective combination form is in the range of a nonlinear combination. Therefore, a nonlinear combination based on nonlinear PID control is proposed in this paper, as shown in the following equation:
where
;
is the difference between the output of the current controlled object and the set value of the controlled object;
is the difference between the output of the current controlled object and the change rate of the set value of the controlled object; and
is the interval length of the linear segment. The
function is a saturation function, as shown in Equation (18), as follows:
In this paper, the stability parameter, , was controlled, and the additional desired torque was output.