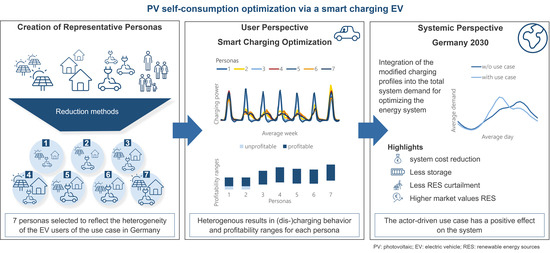
Systemic Evaluation of PV Self-Consumption Optimization Using Electric Vehicles
Abstract
1. Introduction
- Creating a methodology to integrate PV self-consumption optimization using EVs from a user perspective into an energy system model.
- Modeling the profitability of PV self-consumption optimization for different groups of people to analyze for which groups of people in Germany PV self-consumption optimization is profitable.
- Modeling the European energy system with a focus on Germany for the year 2030 while considering PV self-consumption optimization using EVs to answer the research question of whether PV self-consumption optimization using EVs is always beneficial to the energy system.
2. Methods
2.1. Methodology for the Definition of Relevant Personas
2.2. Methodology for the Evaluation of PV Self-Consumption Optimization Profitability to Obtain Profitable Personas
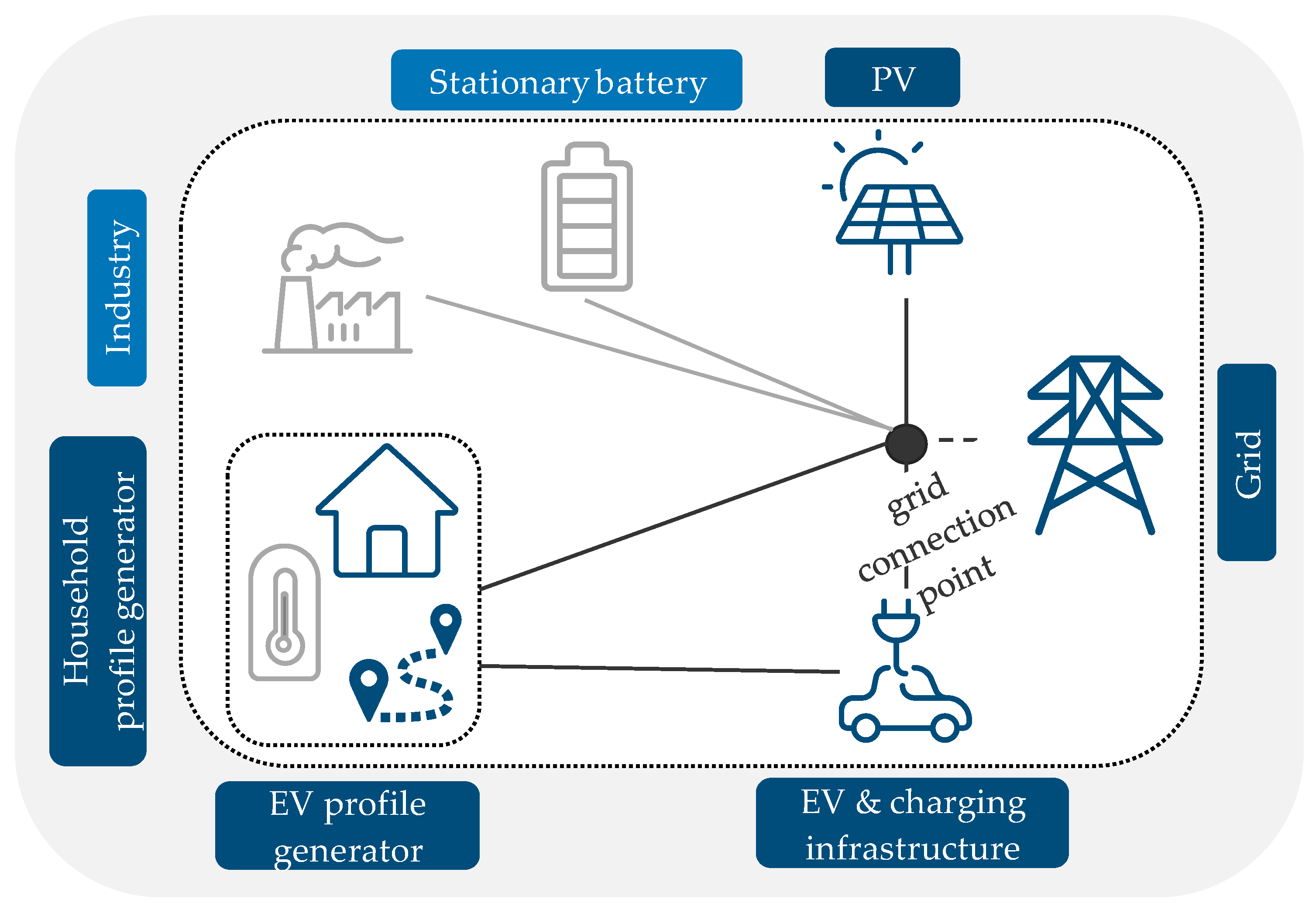
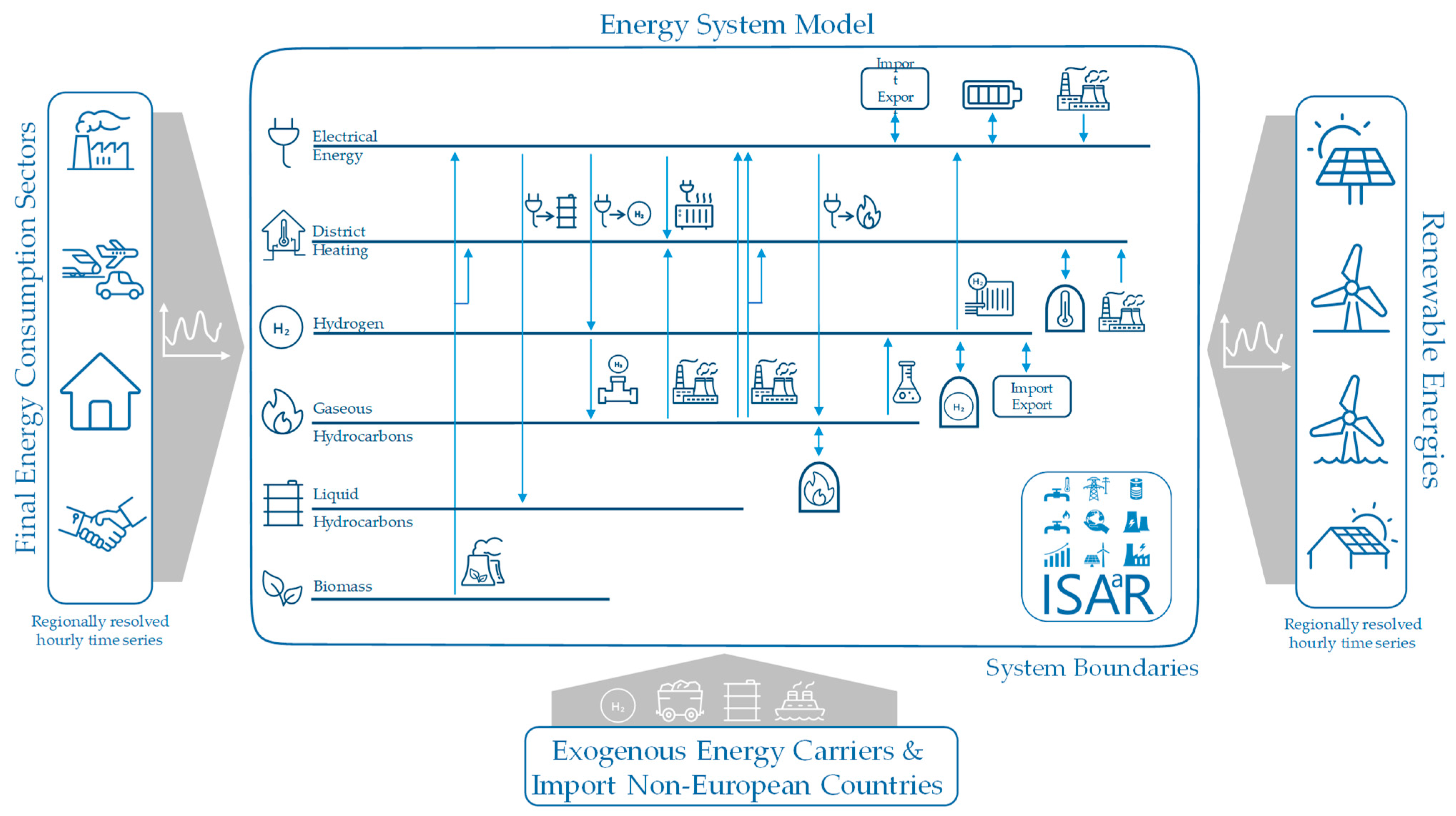
2.3. Methodology for the Evaluation of PV Self-Consumption Optimization from a Systemic Perspective
3. Results
3.1. Definition of Relevant Personas
- EV: consumption and battery capacity;
- Household: yearly electricity consumption (profile);
- PV: installed capacity;
- Type of actor/User group: number of children, amount of driving, work situation.
- Statement 1: No small PV system (PV1) with a large household load (HH3). It is assumed that households with higher demand install larger PV systems, as PV system installers or online guidelines recommend different PV sizes depending on the number of people and electricity consumption of the household. This impacts the typical household load-to-PV ratio, even if it also depends on other factors such as the suitable roof size. Additionally, larger demand often implies larger houses with a larger roof area.
- Statement 2: No large PV system (PV3) with a small household load (HH1). Same argumentation as in statement 1. PV system installers or online guidelines recommend different PV sizes depending on the number of people and electricity consumption of the household, and a small household load can imply a smaller roof area.
- Statement 3: No small PV system (PV1) with a large EV (EV3). It is assumed that wealthy people with expensive vehicles also more often invest in a medium or large PV system instead of a small PV system. Furthermore, larger EVs result in greater total demand.
- Statement 4: No large EV (EV3) with unemployed (UG6, UG7). It is assumed that unemployed people more often cannot afford a large, expensive EV.
- Statement 5: No childless (UG1, UG2, UG4, UG6, UG7) with a large household load (HH3). There is a correlation between household load and the number of persons in a household, which can be found in the data provided by destatis [31].
- Statement 6: No small EV (EV1) with a frequent driver (UG2, UG3, UG4, UG5, UG7). Frequent drivers are assumed to prefer comfort and generous space in the first row of seats as they spend much time driving. This often leads to larger vehicles, as the ADAC (German automobile club) also states. In addition, smaller EVs imply smaller battery capacities and shorter minimum driving distances.
- Statement 7: No small household load (HH1) with children (UG3, UG5). The same argumentation as in statement 5. There is a correlation between household load and the number of people in a household.
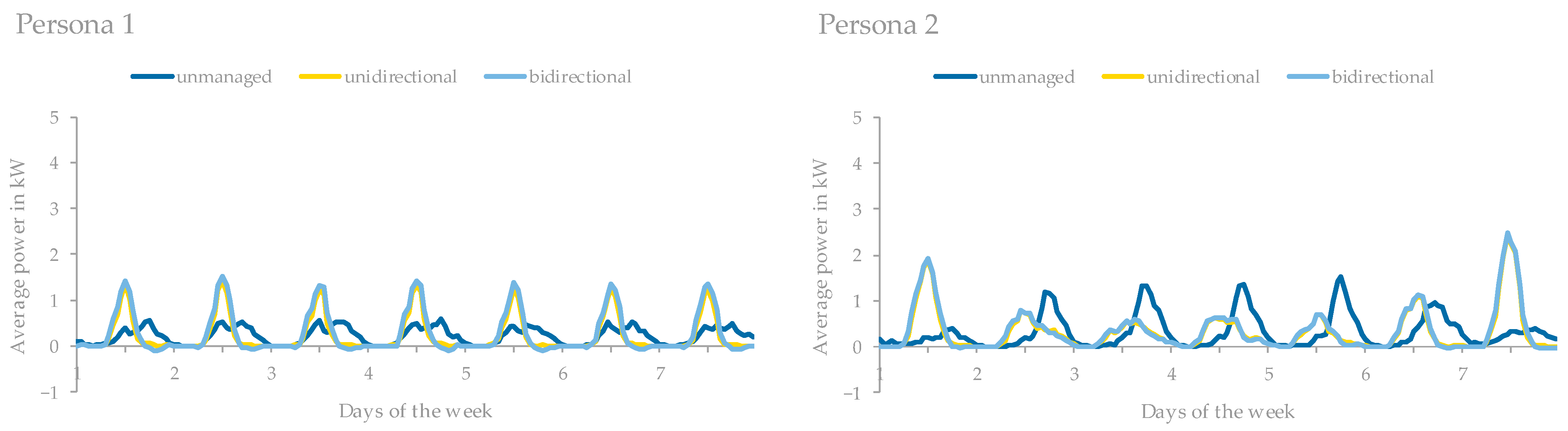
3.2. Evaluation of PV Self-Consumption Optimization Profitability to Obtain Profitable Personas
3.3. Evaluation of PV Self-Consumption Optimization from a Systemic Perspective
- Base: Base scenario without PV self-consumption optimization and fixed expansion of RES in Europe.
- PVSys: Scenario including PV self-consumption optimization and fixed expansion of RES in Europe.
4. Discussion and Conclusions
- (1)
- The total system costs decrease by about 53 million EUR/a.
- (2)
- The installed capacities change only marginally, but the usage does change, resulting in less RES curtailment and less electrical storage usage.
- (3)
- The market values of RES increase due to the demand shift, leading to a favorable framework for the expansion of RES.
Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ID | EV | Household | User Group | PV |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 6 | 1 |
| 3 | 1 | 2 | 1 | 2 |
| 4 | 1 | 2 | 6 | 2 |
| 5 | 2 | 1 | 1 | 1 |
| 6 | 2 | 1 | 2 | 1 |
| 7 | 2 | 1 | 4 | 1 |
| 8 | 2 | 1 | 6 | 1 |
| 9 | 2 | 1 | 7 | 1 |
| 10 | 2 | 2 | 1 | 2 |
| 11 | 2 | 2 | 2 | 2 |
| 12 | 2 | 2 | 3 | 2 |
| 13 | 2 | 2 | 4 | 2 |
| 14 | 2 | 2 | 5 | 2 |
| 15 | 2 | 2 | 6 | 2 |
| 16 | 2 | 2 | 7 | 2 |
| 17 | 2 | 3 | 3 | 3 |
| 18 | 2 | 3 | 5 | 3 |
| 19 | 3 | 2 | 1 | 2 |
| 20 | 3 | 2 | 2 | 2 |
| 21 | 3 | 2 | 3 | 2 |
| 22 | 3 | 2 | 4 | 2 |
| 23 | 3 | 2 | 5 | 2 |
| 24 | 3 | 3 | 3 | 3 |
| 25 | 3 | 3 | 5 | 3 |
Appendix B

References
- Klimaschutz in Zahlen—Aktuelle Emissionstrends und Klimaschutzmaßnahmen in Deutschland—Ausgabe 2022. Available online: https://www.bmwk.de/Redaktion/DE/Publikationen/Klimaschutz/klimaschutz-in-zahlen.pdf?__blob=publicationFile&v=8 (accessed on 19 October 2023).
- Germany’s Current Climate Action Status. Available online: https://www.bmwk.de/Redaktion/EN/Downloads/E/germany-s-current-climate-action-status.pdf?__blob=publicationFile&v=1 (accessed on 19 October 2023).
- Kern, T.; Dossow, P.; Morlock, E. Revenue opportunities by integrating combined vehicle-to-home and vehicle-to-grid applications in smart homes. Appl. Energy 2021, 307, 118187. [Google Scholar] [CrossRef]
- Chatzigeorgiou, N.G. Evaluating the Techno-Economic Effect of Pricing and Consumption Parameters on the Power-to-Energy Ratio for Sizing Photovoltaic-Battery Systems: An Assessment of Prosumers in the Mediterranean Area. Energies 2023, 16, 4073. [Google Scholar] [CrossRef]
- Ciocia, A. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies 2021, 14, 1591. [Google Scholar] [CrossRef]
- Keiner, D. Coupling heat and electricity storage technologies for cost and self-consumption optimised residential PV prosumer systems in Germany. Int. J. Sustain. Energy Plan. Manag. 2019, 21, 35–58. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Li, X.; Sun, B.; Liao, Q.; Tao, Y.; Wang, Z. Strategic integration of vehicle-to-home system with home distributed photovoltaic power generation in Shanghai. Appl. Energy 2020, 263, 114603. [Google Scholar] [CrossRef]
- Salpakari, J.; Rasku, T.; Lindgren, J.; Lund, P.D. Flexibility of electric vehicles and space heating in net zero energy houses: An optimal control model with thermal dynamics and battery degradation. Appl. Energy 2017, 190, 800–812. [Google Scholar] [CrossRef]
- Gudmunds, D.; Nyholm, E.; Taljegard, M.; Odenberger, M. Self-consumption and self-sufficiency for household solar producers when introducing an electric vehicle. Renew. Energy 2020, 148, 1200–1215. [Google Scholar] [CrossRef]
- Verteilnetzausbau für die Energiewende—Elektromobilität im Fokus. Available online: https://www.agora-verkehrswende.de/fileadmin/Projekte/2019/EV-Grid/Agora-Verkehrswende_Agora-Energiewende_EV-Grid_WEB.pdf (accessed on 15 June 2023).
- Yin, W.; Ming, Z.; Wen, T. Scheduling strategy of electric vehicle charging considering different requirements of grid and users. Energy 2021, 232, 121118. [Google Scholar] [CrossRef]
- Gemassmer, J.; Daam, C.; Reibsch, R. Challenges in Grid Integration of Electric Vehicles in Urban and Rural Areas. World Electr. Veh. J. 2021, 12, 206. [Google Scholar] [CrossRef]
- Müller, M.; Blume, Y.; Reinhard, J. Impact of behind-the-meter optimised bidirectional electric vehicles on the distribution grid load. Energy 2022, 255, 124537. [Google Scholar] [CrossRef]
- Müller, M. Netzintegration Dezentraler Flexibilitätsoptionen mit Fokus auf Ausgewählte Anwendungsfälle für Bidirektionale Elektrofahrzeuge. Ph.D. Thesis, TUM, Munich, Germany, 2023. [Google Scholar]
- Müller, M.; Schulze, Y. Future grid load with bidirectional electric vehicles at home. In Proceedings of the International ETG Congress, Berlin, Germany, 18–19 May 2021. [Google Scholar]
- Boström, T. The pure PV-EV energy system—A conceptual study of a nationwide energy system based solely on photovoltaics and electric vehicles. Smart Energy 2021, 01, 100001. [Google Scholar] [CrossRef]
- Kern, T.; Kigle, S. Modeling and Evaluating Bidirectionally Chargeable Electric Vehicles in the Future European Energy System. Energy Rep. 2022, 8, 2352–4847. [Google Scholar] [CrossRef]
- Kern, T. Assessment of the Added Value of Bidirectionally Chargeable Electric Vehicles for the User and the Energy System. Ph.D. Thesis, TUM, Munich, Germany, 2022. [Google Scholar]
- Hennig, C.; Meila, M.; Murtagh, F.; Rocci, R. Handbook of Cluster Analysis, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 8–12, 33 f., 114 f. [Google Scholar]
- Biedenbach, F.; Ziemsky, V. Opportunity or Risk? Model-based Optimization of Electric Vehicle Charging Costs for Different Types of Variable Tariffs from a Consumer Perspective. In Proceedings of the CIRED Porto Workshop 2022, Porto, Portugal, 2–3 June 2022. [Google Scholar]
- Biedenbach, F.; Blume, Y. Size matters: Multi-use Optimization of a Depot for Battery Electric Heavy-Duty Trucks. In Proceedings of the International Electric Vehicle Symposium and Exhibition (EVS36), Sacramento, CA, USA, 11–14 June 2023. [Google Scholar]
- Preis, V.; Biedenbach, F. Assessing the incorporation of battery degradation in vehicle-to-grid optimization models. Energy Inform. 2023, 23 (Suppl. 1), 33. [Google Scholar] [CrossRef]
- Müller, M.; Biedenbach, F.; Reinhard, J. Development of an Integrated Simulation Model for Load and Mobility Profiles of Private Households. Energies 2020, 13, 3843. [Google Scholar] [CrossRef]
- Morlock, E.S. Entwicklung eines techno-ökonomischen Bewertungsmodells für Vehicle-to-Home-Systeme—Analyse der Erlöspotenziale von Bidirektionalen Elektrofahrzeugen durch Eigenverbrauchserhöhung Sowie Durch Tarifoptimiertes Laden und Entladen anhand eines Optimierungsmodells in MATLAB. Master’s Thesis, TU Berlin, Berlin, Germany, 2020. [Google Scholar]
- Dossow, P.; Kern, T. Profitability of V2X Under Uncertainty: Relevant Influencing Factors and Implications for Future Business Models. Energy Rep. 2022, 8, 449–455. [Google Scholar] [CrossRef]
- Project Webpage: UnIT-e2 Reallabor für verNETZe E-Mobilität—Wir Mobilisieren die Digitale Energiewende. Available online: https://unit-e2.de/ (accessed on 19 October 2023).
- Böing, F.; Regett, A. Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems. Energies 2019, 12, 2260. [Google Scholar] [CrossRef]
- Kigle, S.; Ebner, M.; Guminski, A. Greenhouse Gas Abatement in EUROPE—A Scenario-Based, Bottom-Up Analysis Showing the Effect of Deep Emission Mitigation on the European Energy System. Energies 2022, 15, 1334. [Google Scholar] [CrossRef]
- Dossow, P.; Ganz, K.; Kern, T. Smart e-mobility: User potential in Germany today and in the future. In Proceedings of the NEIS Conference 2023, Hamburg, Germany, 4–5 September 2023. [Google Scholar]
- Bestand an Personenkraftwagen nach Segmenten und Modellreihen. Available online: https://www.kba.de/DE/Statistik/Fahrzeuge/Bestand/Segmente/segmente_node.html (accessed on 25 February 2023).
- Stromverbrauch der Privaten Haushalte nach Haushaltsgrößenklassen. Available online: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Umwelt/UGR/private-haushalte/Tabellen/stromverbrauch-haushalte.html (accessed on 25 February 2023).
- Statistisches Bundesamt: Privathaushalte und Haushaltsmitglieder—nach Haushaltsgröße und Gebietsstand. Available online: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Haushalte-Familien/Tabellen/1-1-privathaushalte-haushaltsmitglieder.html (accessed on 25 February 2023).
- Marktstammdatenregister. Available online: https://www.marktstammdatenregister.de/MaStR/Einheit/Einheiten/OeffentlicheEinheitenuebersicht (accessed on 25 February 2023).
- Fattler, S. Economic and Environmental Assessment of Electric Vehicle Charging Strategies. Ph.D. Thesis, TU Munich, Munich, Germany, 2021. [Google Scholar]
- Archivierte EEG-Vergütungssätze und Datenmeldungen. Available online: https://www.bundesnetzagentur.de/DE/Fachthemen/ElektrizitaetundGas/ErneuerbareEnergien/EEG_Foerderung/Archiv_VergSaetze/start.html (accessed on 1 March 2023).
- Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Kilius, N.; Lefevre, M.; Wald, L.; Wey, E.; Soboret, L. User’s Guide to the CAMS Radiation Service—Status December 2016; ECMWF: Reading, UK, 2016. [Google Scholar]
- Mehr Fortschritt Wagen—Bündnis für Freiheit, Gerechtigkeit und Nachhaltigkeit—Koalitionsvertrag 2021–2025. Available online: https://www.spd.de/fileadmin/Dokumente/Koalitionsvertrag/Koalitionsvertrag_2021-2025.pdf (accessed on 19 October 2023).

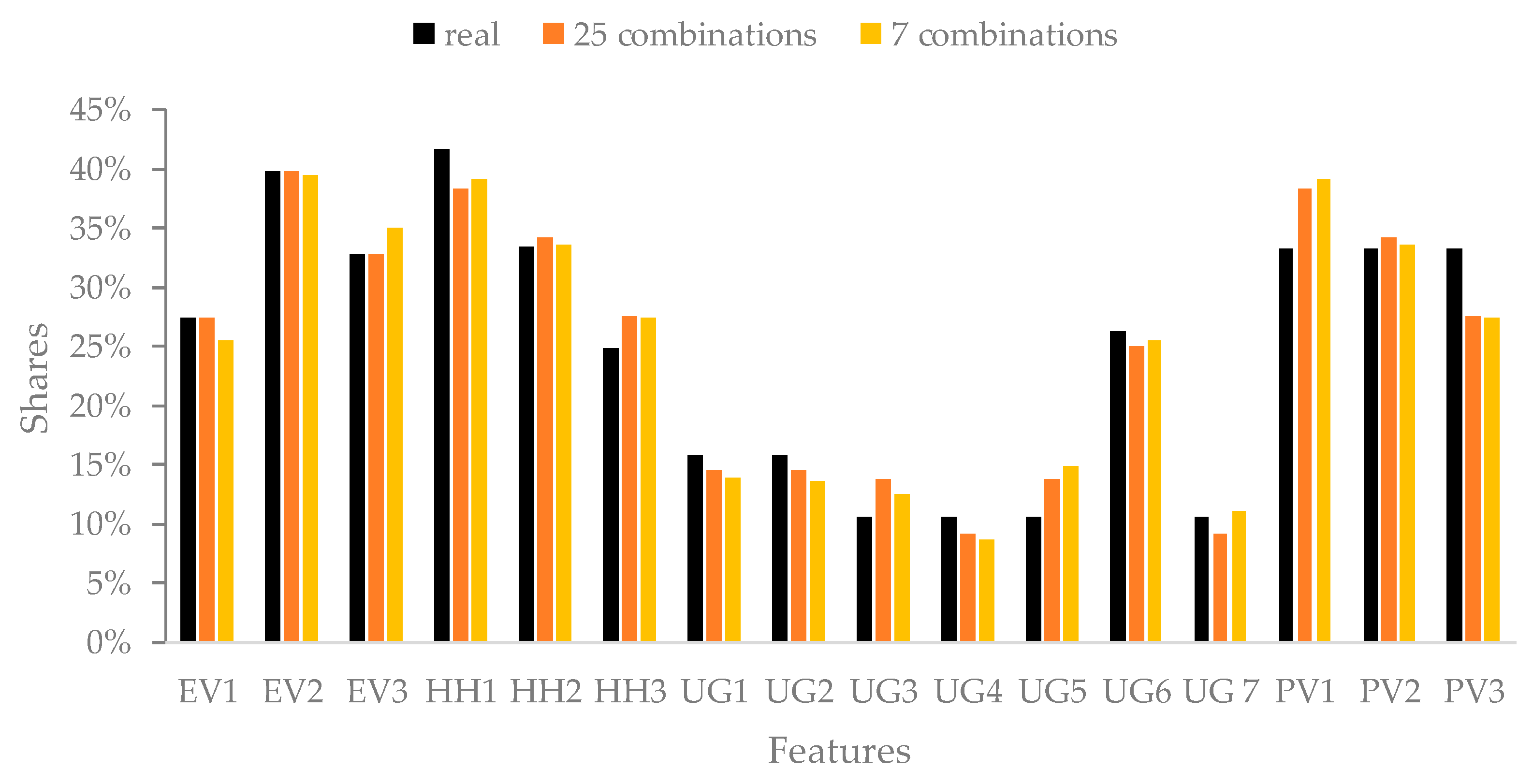
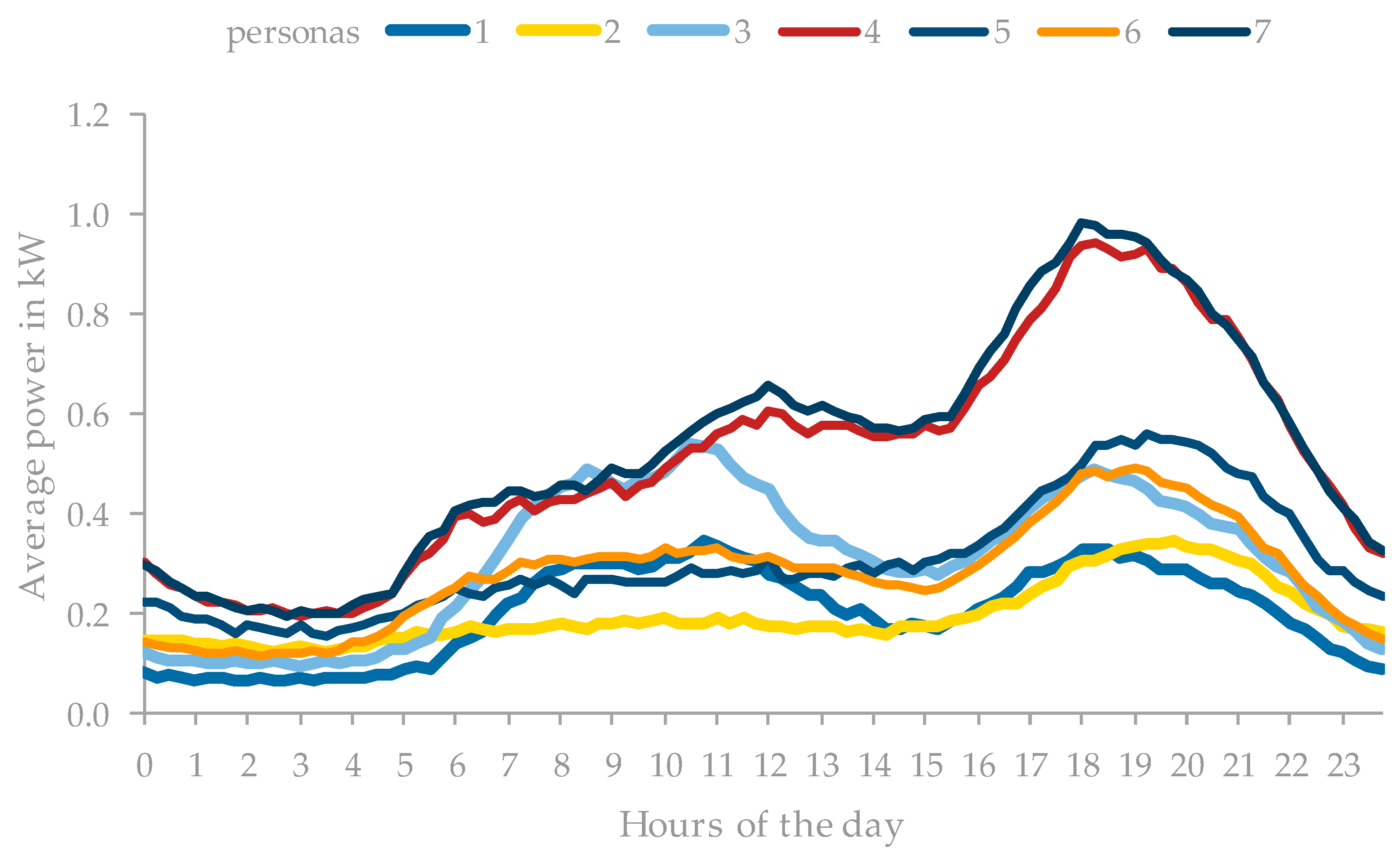
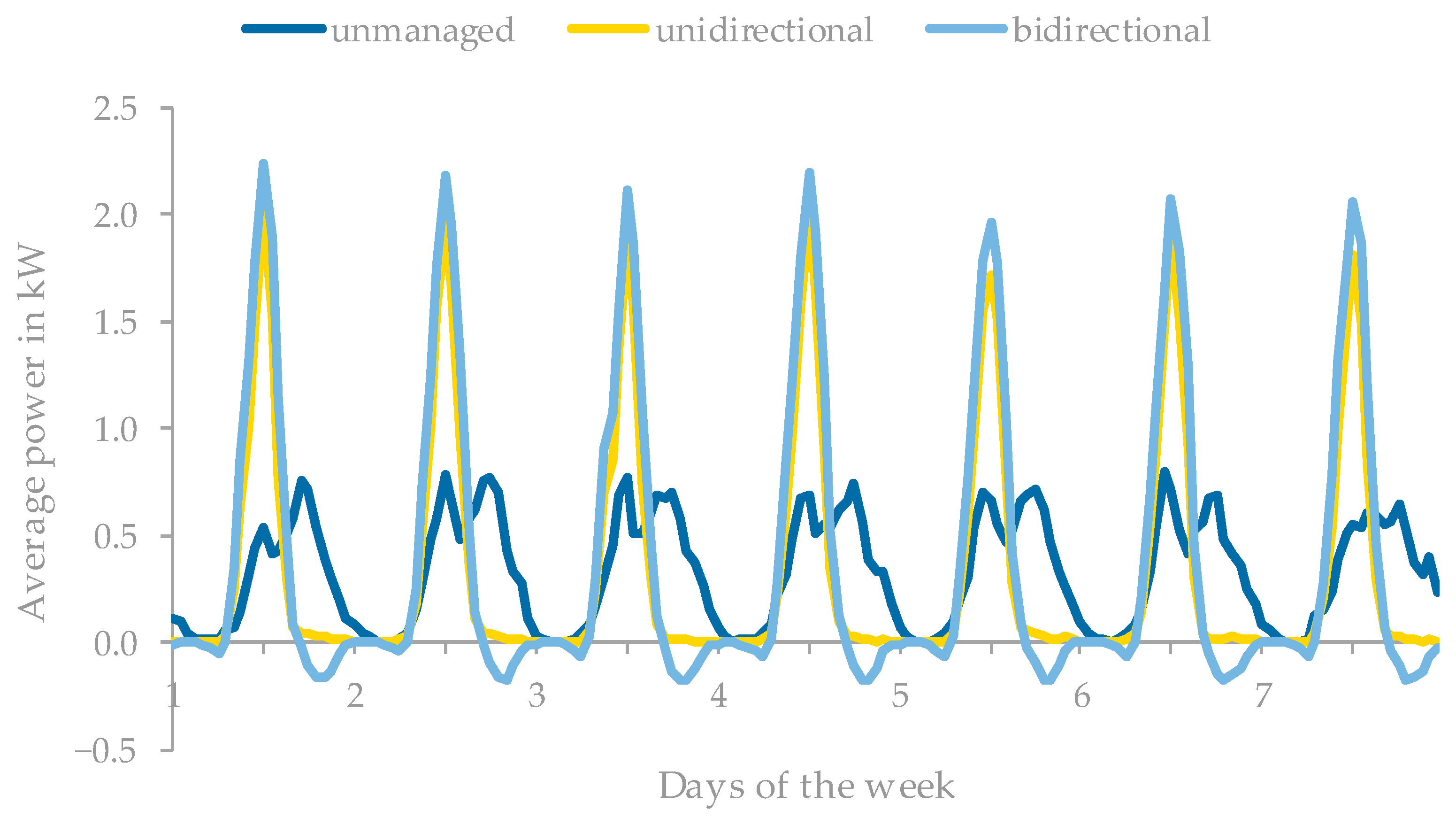
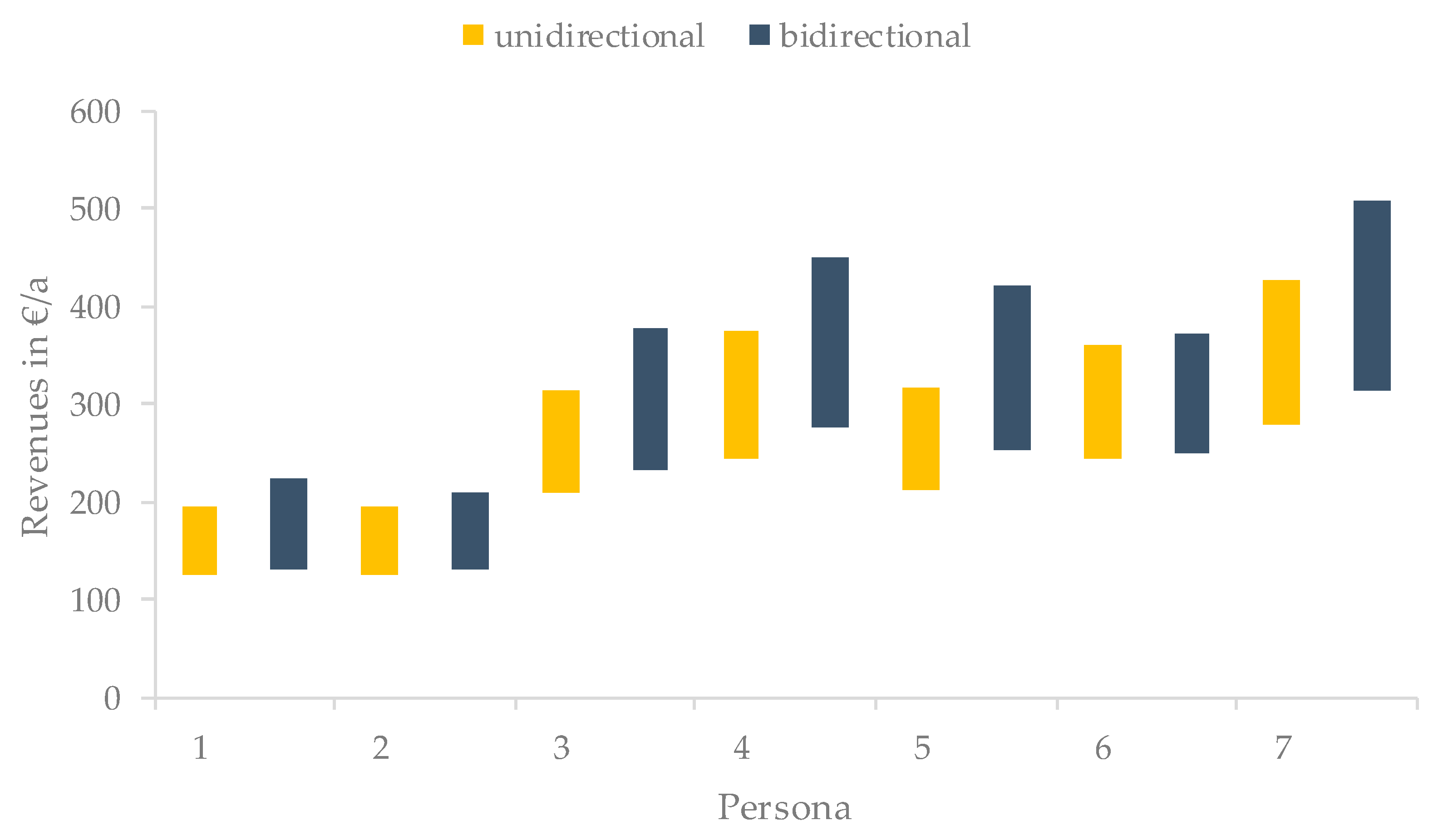
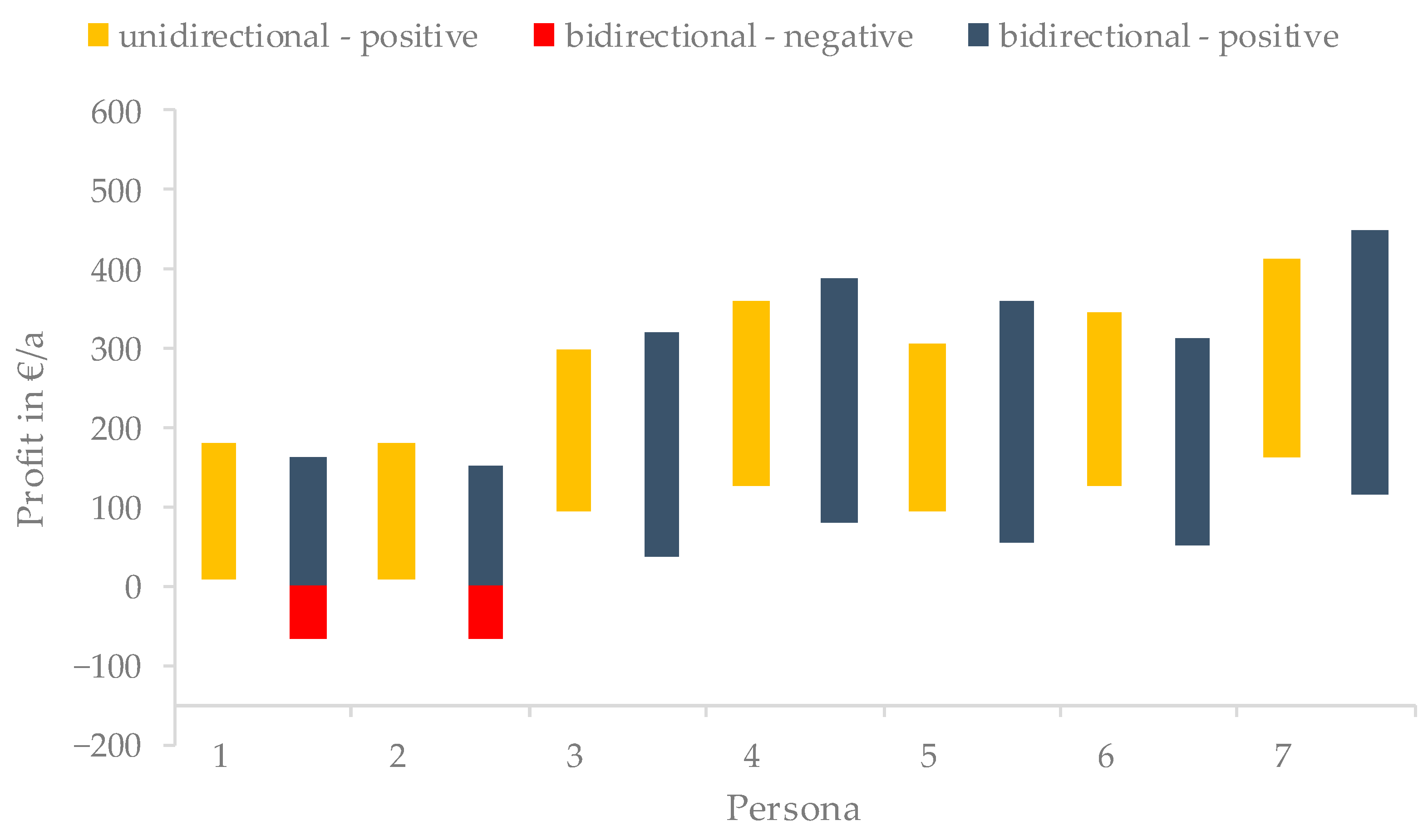
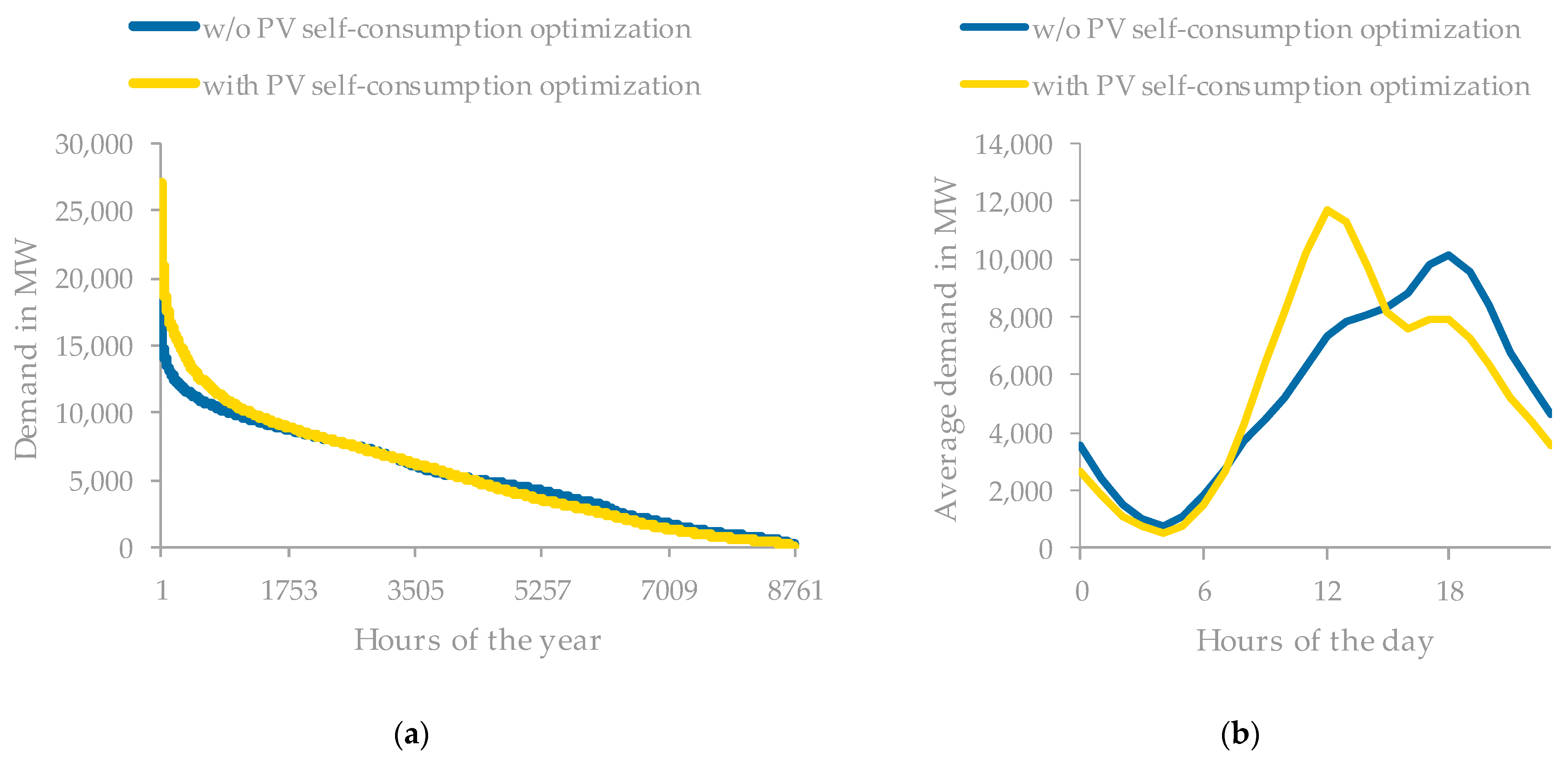
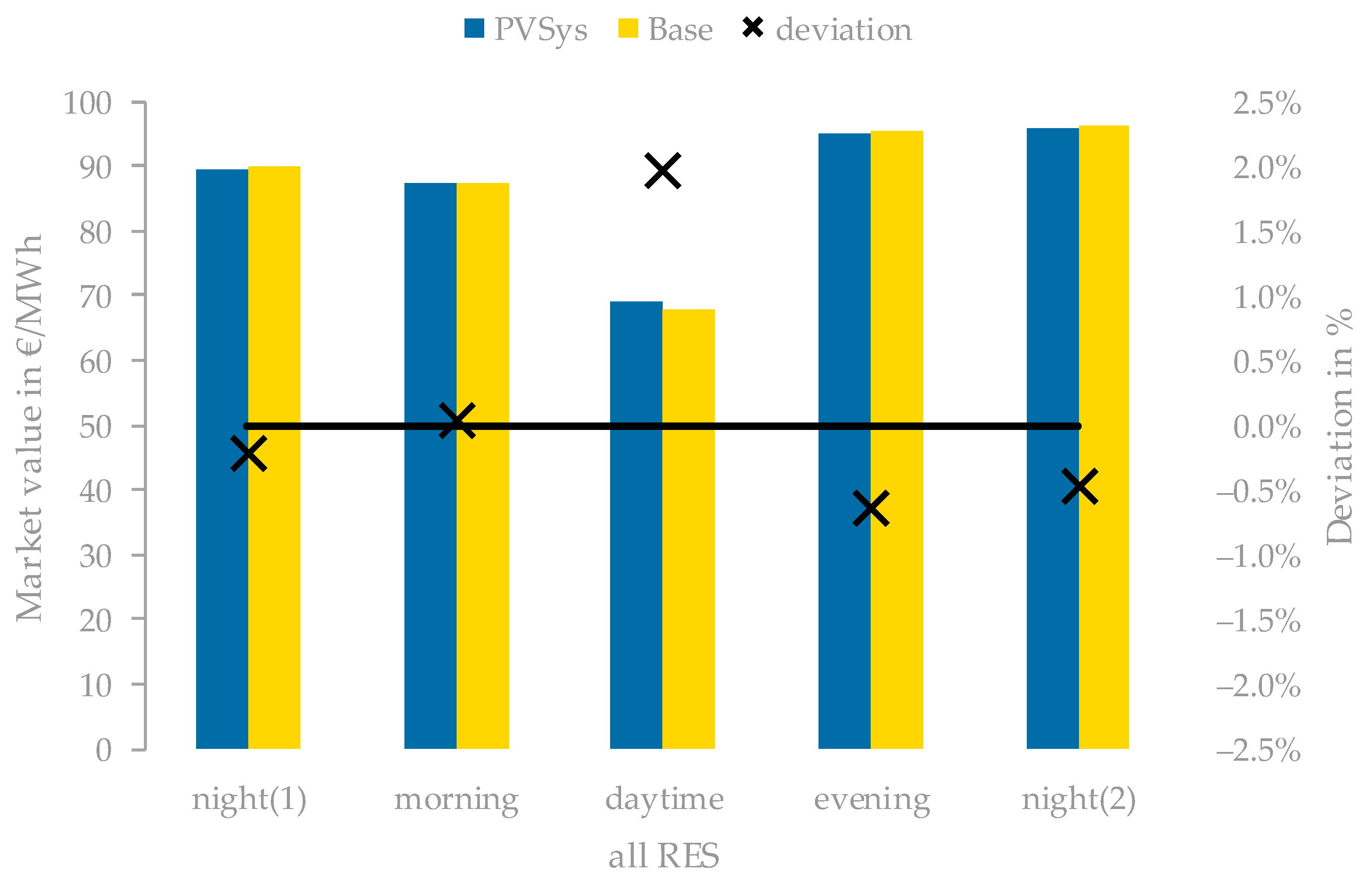
| Category | Feature | ID | Value | Share |
|---|---|---|---|---|
| EV | Small | EV1 | 47.5 kWh and 17.1 kWh/100 km | 27% |
| EV | Medium | EV2 | 80 kW and 20.5 kWh/100 km | 40% |
| EV | Large | EV3 | 120 kWh and 28.1 kWh/100 km | 33% |
| Household | Small | HH1 | 1623 kWh/a | 42% |
| Household | Medium | HH2 | 2731 kWh/a | 33% |
| Household | Large | HH3 | 4394 kWh/a | 25% |
| PV | Small | PV1 | 3.9 kWp | 33% |
| PV | Medium | PV2 | 7 kWp | 33% |
| PV | Large | PV3 | 11 kWp | 33% |
| User group | Group 1 | UG1 | Full-time, low driver, childless | 16% |
| User group | Group 2 | UG2 | Full-time, frequent driver, childless | 16% |
| User group | Group 3 | UG3 | Full-time, frequent driver, with children | 11% |
| User group | Group 4 | UG4 | Part-time, frequent driver, childless | 11% |
| User group | Group 5 | UG5 | Part-time, frequent driver, with children | 11% |
| User group | Group 6 | UG6 | Unemployed, low driver, childless | 26% |
| User group | Group 7 | UG7 | Unemployed, frequent driver, childless | 11% |
| ID | EV | Household | PV | User Group | Share |
|---|---|---|---|---|---|
| 1 | EV1 | HH1 | PV1 | UG6 | 26% |
| 2 | EV2 | HH1 | PV1 | UG2 | 14% |
| 3 | EV2 | HH2 | PV2 | UG7 | 11% |
| 4 | EV2 | HH3 | PV3 | UG5 | 15% |
| 5 | EV3 | HH2 | PV2 | UG1 | 14% |
| 6 | EV3 | HH2 | PV2 | UG4 | 9% |
| 7 | EV3 | HH3 | PV3 | UG3 | 12% |
| Component | Parameter | Value |
|---|---|---|
| EV+ EVSE | Type of vehicle | Depending on the persona (see Table 1) |
| EV+ EVSE | Battery capacity | Depending on the persona (see Table 1) |
| EV+ EVSE | Charging power | 11 kW |
| EV+ EVSE | SOC safety | 30% |
| EV+ EVSE | SOC departure | 60% |
| EV+ EVSE | Plug-in probability | 100% |
| EV+ EVSE | Efficiency | Variable plus const loss and standby loss |
| EV+ EVSE | Driving profiles | Generated by the EV profile generator (see Section 2.2, [23]) |
| PV | Power | Depending on the persona (see Table 1) |
| PV | Generation profile | Based on CAMS data [36] |
| Household | Yearly demand | Depending on the persona (see Table 1) |
| Household | Demand profile | Generated by the household demand generator (see Section 2.2, [23]) |
| Prices | Feed-in tariff | Depending on PV size and option |
| Prices | Household electricity price | 30 ct/kWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganz, K.; Kern, T.; Hinterstocker, M. Systemic Evaluation of PV Self-Consumption Optimization Using Electric Vehicles. World Electr. Veh. J. 2024, 15, 98. https://doi.org/10.3390/wevj15030098
Ganz K, Kern T, Hinterstocker M. Systemic Evaluation of PV Self-Consumption Optimization Using Electric Vehicles. World Electric Vehicle Journal. 2024; 15(3):98. https://doi.org/10.3390/wevj15030098
Chicago/Turabian StyleGanz, Kirstin, Timo Kern, and Michael Hinterstocker. 2024. "Systemic Evaluation of PV Self-Consumption Optimization Using Electric Vehicles" World Electric Vehicle Journal 15, no. 3: 98. https://doi.org/10.3390/wevj15030098
APA StyleGanz, K., Kern, T., & Hinterstocker, M. (2024). Systemic Evaluation of PV Self-Consumption Optimization Using Electric Vehicles. World Electric Vehicle Journal, 15(3), 98. https://doi.org/10.3390/wevj15030098