Abstract
In order to improve the shifting quality of pure electric commercial vehicles, a torque control strategy based on the driving intention during the shifting process is presented in this paper. Firstly, dynamic analysis is conducted on the lifting and twisting stage in the two-speed Automated Mechanical Transmission (AMT) shift process without a synchronizer. Secondly, fuzzy identification is performed on the driver’s expected acceleration, incorporating the driver’s acceleration intention into the lifting and twisting process, and, further, the output time correction factor k is deblurred. Finally, the control time of the lifting and reducing torque is corrected to achieve dynamic adjustment of the control parameters during the shift process. The actual vehicle test results indicate that the proposed control strategy can enhance the shifting quality and adapt the performance of a vehicle to the driver’s expectations and requirements.
1. Introduction
New energy vehicles are the trend in global development and vigorously developing new energy vehicles can effectively alleviate energy and environmental pressures [1]. Up until now, direct drive mode has been widely used in pure electric commercial vehicles, which has the problem of high energy consumption, while transmission can take advantage of the efficient working range of the driving motor to reduce the energy consumption of the vehicle. AMT can achieve automatic and manual shift mode switching, with relatively low technical difficulty and reliable operation, which solves the contradiction between the driving pleasure of manual shift and the safety and convenience of automatic shift. With the accelerated development of the “new four modernizations” trend in automobiles, competition among automobile enterprises is becoming increasingly fierce. Various manufacturers intensively release and launch their own AMT products for the purpose of improving the convenience and comfort of driving operations, reducing driver fatigue and improving fuel economy. Therefore, two-speed AMT with a high transmission efficiency and low development cost is an important development direction for the pure electric vehicle industry [2].
The core of AMT is the control strategy and the quality of this strategy directly determines the performance of the vehicle’s driving performance, which is a manifestation of intelligence. The higher the level of intelligence, the more capable it is of driving according to the driver’s inclination. Liu Wengguang et al. [3] made use of a fuzzy control algorithm to design a shift controller based on the driver’s power demands, but the shift process was not studied. Wang Dafang et al. [4] studied the shift control of AMT without a clutch synchronizer, but control optimization was only applied to the gearshift actuator. Xiao Lijun et al. [5] proposed a comprehensive coordinated control method for driving motors and the results of the bench tests prove that this method makes the shifting process faster. In [6,7], the objective of the research is focused on the motor speed control and the dynamic characteristics of the shift actuators, respectively, without taking the impact of the lifting and twisting stage on the transient state of the gear-shifting process into consideration. Based on the control strategy of the optimal controller, the quality of the shifting process is improved, and it is pointed out that the lifting and twisting stage of the driving motor has the most significant influence on the shifting quality [8,9].
With the rapid advancement of science and technology, intelligent control algorithms have been applied to AMT control systems, making AMT more adaptable to the needs of drivers. Aiming at the time-varying problem of shift actuator parameters, Lin Cheng et al. [10] developed a hierarchical state estimation and parameter identification method based on the nonlinear H∞ algorithm to improve the shift performance. Ref. [11] put forward a double-loop self-learning fuzzy control method, in which the outer loop adjusts the expected trajectory of the motor and the inner loop tracks the expected trajectory, effectively addressing the nonlinear problem during gear shifting. Refs. [12,13,14] presented a shift control strategy based on a variational method, which can actualize speedy shifting. By combining the Udwadia–Kalaba method with PID, trajectory tracking control for different shifting targets was materialized [15,16]. For the sake of solving the problem of frequent shifting, the multiobjective optimization particle swarm optimization method is adopted to eliminate unnecessary gear shifting [17]. Liu Tong et al. [18] exploited the segmented control concept based on model predictive control for the shifting process, which efficaciously improved the smoothness of shifting and reduced shift jerk. Also to reduce shift jerk, a study was carried out in which feedback compensation was applied to the speed command output of the PI speed controller, as well as the motor inertia and friction calculated for the feedforward compensation at actual speeds, and the real vehicle tests show that the proposed method had better speed response characteristics [19]. Furthermore, neural networks have a profound impact on gear-shifting strategies. For instance, Lin Xinyou et al. [20] utilized LVQNN and FNN to identify the driving style and driving intention in real time, respectively. Then, dynamic correction factors were introduced to optimize the shifting strategy. The hardware-in-the-loop experiments demonstrate that the proposed strategy can meet the requirements of various driving styles.
In the latest research, a concept of shift control based on dynamic programming was proffered, in which the shift loss caused by the shift actuator was considered and the efficiency was improved [21]. Taking the two-speed AMT of a battery electric vehicle as the research object, a combination shift control strategy including segmented speed regulation control and torque recovery control was developed in [22]. The switching points of proportional integral control and sliding mode control during the speed regulation process were adaptively optimized. The experiment verified that the proposed control strategy can not only ensure an impact within a predetermined range but also achieve the optimal shifting time. Md Ragib Ahssan et al. [23] came up with a three-parameter shift scheduling strategy, which used heuristic methods to develop two shifting schemes. The vehicle acceleration and road slope and the gradient descent and pattern search methods were used to optimize the transmission ratio and main shifting scheme, respectively. The experimental results showed that this method saved energy in large and small electric vehicles.
According to the aforementioned literature analysis, it is worth emphasizing that most studies fail to make real-time adjustments to the rate of torque unloading and the recovery stages of the drive motor for different driving conditions. This article takes the integrated system of the drive motor and AMT as the research object. Section 2 analyzes the shifting process of the two-speed AMT and identifies the driver’s intention using fuzzy identification to realise dynamic adjustment of the control parameters during the shifting process, which are given in Section 3. The actual vehicle test results show that this optimization method can meet the driver’s demands for the shifting time according to their expectations and achieve an improvement in the shift quality.
2. Analysis of Shift Process of AMT without Synchronizer
The shift control of the drive motor +AMT integrated system of pure electric vehicles mainly includes five processes: unloading, removing gear, driving motor speed regulation, gear hanging and torque recovery. The specific shift process is shown in Figure 1.
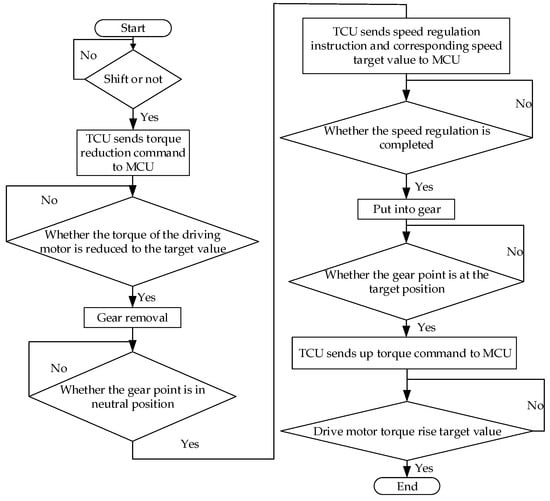
Figure 1.
Shift process diagram.
Preserving the main dynamic characteristics of motor, AMT input and output shafts, as well as the vehicle, and it is reasonable that ignoring secondary factors such as damping and internal friction, then a simplified dynamic model of the transmission system is established, as shown in Figure 2.
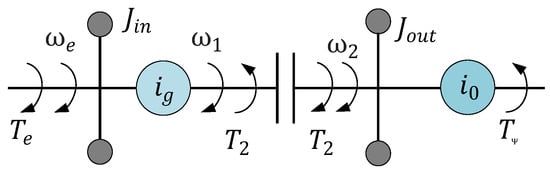
Figure 2.
Simplified Model of Electric Drive AMT Transmission System.
According to Newton’s Second Law, a dynamic relationship can be denoted as follows [24]:
where Jin and Jout are the moment of inertia converted to the AMT input shaft and output shaft, respectively. D represents the differential operator, is the rotor speed of the drive motor, is the target gear speed of the meshing sleeve, is the speed of the AMT output shaft; is the torque of the driving motor, is the torque of the AMT output shaft, Tᴪ is the ground resistance moment, is the AMT transmission ratio, is the main reduction ratio.
Analyze the various stages of the shifting process based on the established transmission system model:
2.1. Driving in Original Gear
Taking upshifting as an example, when the gearbox is in first gear without shifting, the gear end of the gear sleeve engages with the gear ring of the first gear. Power is transmitted from the gear ring of the first gear to the gear sleeve, and then to the output shaft through the gear sleeve. The following relationship can be obtained:
where Jin1 is the moment of inertia on the AMT input shaft in first gear, ig1 is the first gear ratio of the transmission.
Formula 1 = 2 can be formulated by ω1 = ω2, then eliminating T2(t), it can be written as:
where
Thus, jerk can be denoted by the following equation:
where rr is the rolling radius of the wheel.
According to (7), jerk mainly depends on the change rate of driving motor torque Te and the change rate of driving resistance moment . It is generally believed that the driving resistance acting on the vehicle that the change is very little during an extremely short shifting time, that is, ᴪ(t) = 0, so the jerk is positively correlated with the rate of change of the output torque of the motor. Therefore, the main factor that causes the impact change during the shift of transmission system is the change rate of output torque of driving motor.
2.2. Uninstall Phase
The first stage of the gear-shifting process is to unload the driving motor, which represents the process of setting the output torque of the drive motor to zero before the start of gear removal. Due to the unchanged position of each component during the unloading process, the dynamic analysis is the same as the original gear. According to Equation (7), the key factor leading to change in impacting during the unloading stage is the rate of change of the output torque of the driving motor.
2.3. Picking, Speed Regulation, and Hanging Gear Stages
The drive motor is in free mode without torque output during gear-shifting, and the vehicle jerk at this stage can be ignored. During the speed regulation stage, the power transmission between the power source and the transmission system is interrupted, so the torque change of the drive motor at this stage will not have an impact on jerk.
2.4. Torque Recovery Stage
The torque recovery process is the transition between gear-shifting and normal driving in the new gear, then the drive motor enters torque mode from free mode. It is the same as the position of AMT components when driving in a new gear, and the dynamic relationship is completely consistent, hence the relationship can be expressed as follows:
where Jin2 is the moment of inertia on the AMT input shaft in second gear, ig2 is the second gear ratio for the transmission.
Based on Equation (8)
where
Thus, jerk can be denoted by the following equation:
Like the unloading stage, the torque recovery stage also has a significant impact on vehicle impact. At the beginning of the torque recovery phase, the output torque of the drive motor is zero, and when TCU detects the output torque of the drive motor reaches the preset condition, the phase ends.
2.5. New Gear Driving
The end of the torque recovery phase signifies the completion of the gear-shifting. TCU continues to monitor information such as vehicle speed and pedals, and determines whether to enter the shift process based on the preset shifting pattern.
3. Control of Lifting and Twisting Process Based on Driver Intention Identification
Since the driver’s operation and the vehicle’s state are different during each shift, it is difficult to adapt to the driver’s demand for AMT shift quality under different conditions if the unified lifting and lifting torque rate is adopted. Therefore, the fuzzy control algorithm is used to recognize driving intention, which is apt to be realized in the controller and promote the current level of intelligent shifting [25].
There are two boundary conditions for the designed lifting torsional rate: one is the fastest lifting and twisting rate, which means that the lifting and twisting rate should not exceed the rate corresponding to the maximum impact standard adopted in this article; the other is the slowest lifting and twisting rate, which means that the lifting and twisting rate should not be less than the rate corresponding to the maximum lifting and twisting time allowed in this article. The corresponding lifting and twisting rate based on the driver’s expected lifting and twisting time should change between them, as shown in Figure 3.
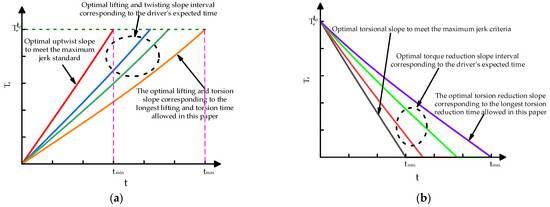
Figure 3.
(a) Range of torque slope variation during torque increase processes; (b) Range of torque slope variation during torque reduction processes.
As can be seen from these two figures, tmax is the maximum allowable time for torque reduction or increase set in this paper, tmin is the minimum torque reduction or increase time corresponding to the maximum jerk allowed in this article, and jmax is taken as 17.64 m/s2.
3.1. Establishing a Fuzzy Controller
In this paper, the accelerator pedal opening and its change rate are selected to reflect the driver’s expectation. According to the driver’s operation of the accelerator pedal, the driver’s intention is divided into sudden deceleration, general deceleration, cruise, general acceleration, and sudden acceleration, which correspond to slow gear shifting, medium-slow gear shifting, medium-speed gear shifting, medium-fast gear shifting, and fast gear shifting respectively. The membership function of the input and output variables of the fuzzy controller is shown in Figure 4.
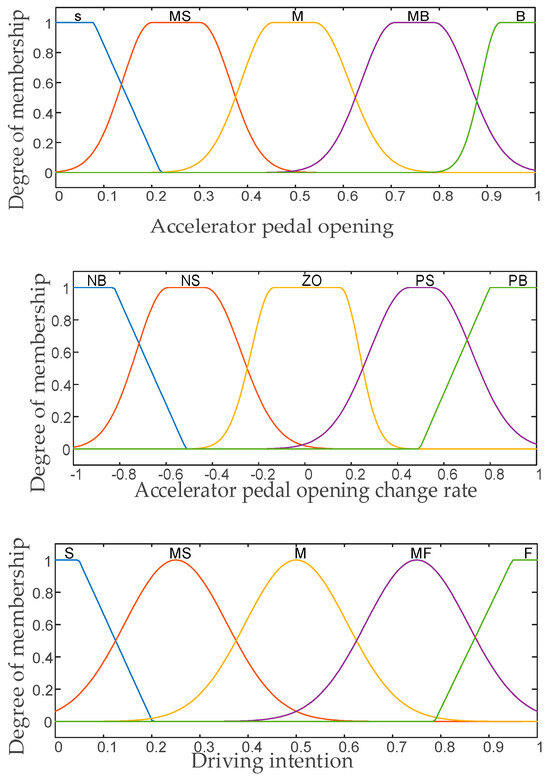
Figure 4.
Input−output membership function.
The fuzzy inference rules are shown in Table 1.

Table 1.
Fuzzy Rule Table for Driving Intention Identification.
The numerical model is shown in Figure 5.
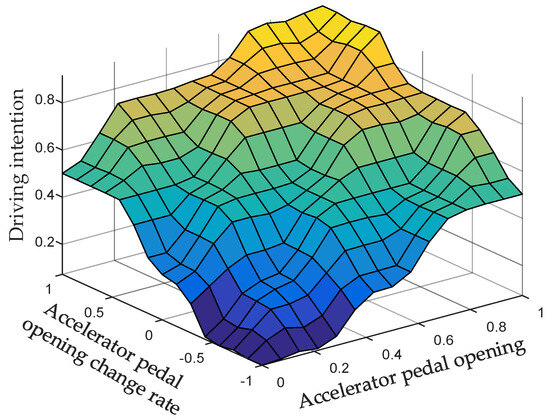
Figure 5.
Curved surface diagram for driving intention identification.
After using Mamdani fuzzy inference and barycenter method to identify the driver’s intention, the corresponding time correction factor k can be output and quantized to calculate the required time t for each stage of lifting and twisting [26], which is t = k × ( − ), as shown in Table 2. And the fuzzy control logic is shown in Figure 6.

Table 2.
Time correction factor k under different driving intentions.
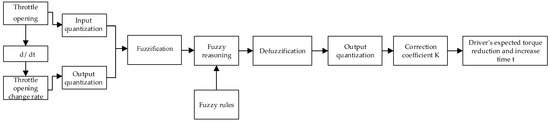
Figure 6.
Fuzzy control logic.
3.2. Simulation and Analysis of Driving Intention Recognition
The urban driving cycle (Figure 7) and suburban driving cycle (Figure 8) in WLTC driving cycle were used for simulation to validate the driver’s intention recognition model in this paper.
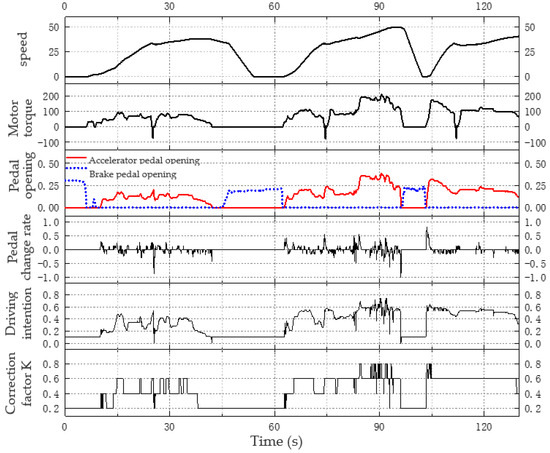
Figure 7.
Identification of driver expectation correction factors under urban conditions.
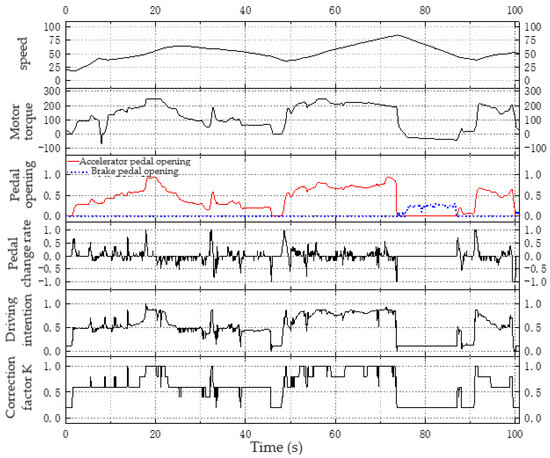
Figure 8.
Identification of driver expectation correction factors under suburban conditions.
In urban areas, vehicles mainly operate at low and medium speed, and the fluctuation of accelerator pedal opening and its rate of change fluctuate slightly and remain at a relatively low level. After identification by the off-line table of driving intention identification and the time correction factor table, it is recognized that the driving intention is mainly shifting at slow, medium slow and medium speed, with a time correction factor k of 0.2–0.6.
In suburban areas, vehicles mainly run at medium and high speed, with significant fluctuations in the opening and rate of change of the accelerator pedal, which is relatively maintained at a high level. Through the off-line table of driving intention identification and the time correction factor table, it is discerned that the driving intention is mainly medium speed, medium fast and fast shifting, with a time correction factor k of 0.6–1.
As a whole, it can be seen that the identified correction factor k is consistent with the driver’s expected shift quality requirements under different driving intentions in reality. Drivers shift gears gently when driving at a smooth deceleration to improve vehicle comfort; rapid gear-shifting during intense acceleration can ascending the vehicle’s dynamic performance, which indicates that the identification algorithm proposed in this paper is effective.
4. Real Vehicle Verification
4.1. Build a Real Vehicle Test Platform
After integrating the control strategy of the above test and other programs, it is burned into the pure electric test commercial vehicle TCU for real vehicle road test verification. The vehicle parameter configuration is shown in Table 3.

Table 3.
Vehicle parameter configuration table.
The test conditions are chose to be calm and straight to reduce the influence of traffic and road conditions on the test. Then the vehicle-following test is carried out to verify the availability of the torque control strategy based on driving intention on this commercial vehicle. The test sample vehicle and real vehicle test platform are shown in Figure 9.

Figure 9.
Test vehicle and real vehicle test platform.
By comparing the shifting time and shifting impact with traditional shifting strategies under the same accelerator pedal opening and accelerator pedal opening change rate, it is determined whether the shifting control is in line with the driver’s expectations under different driving intentions.
4.2. Analysis of Experimental Data
Under the same road conditions, several sets of shift curves with different accelerator pedal opening and its change rate were tested, and the required data of the whole vehicle were calibrated by CANape(12.0), as shown in Figure 10.
Figure 10.
Data collected by CANape.
Taking the example of shifting from first gear to second gear, slow shifting, medium slow shifting, medium fast shifting and fast shifting were tested according to the strategy. Due to space limitations, this article only provides examples of slow gear-shifting, medium fast gear-shifting and fast gear-shifting.
Figure 11, Figure 12 and Figure 13 show a comparison of the shifting quality of vehicle before and after optimization during slow, medium-speed and rapid shifting process, respectively. In Figure 11a, the accelerator pedal opening is reduced from 0.72 to 0.18 at a rate of 0.9/s. In Figure 11b, the driver’s intention is recognized, and at 0.73 s, the driver’s intention is 0.0981, which is a slow shifting with a corresponding time correction factor of 0.2. Figure 11c is a shift graph without optimized shift control strategy and it can be seen that the shift scheduling changes from 3 to 2 at 0.731 s, indicating that the TCU has switched from in-gear operation mode to gear change mode. At this time, the driving motor entered the torque reduction stage. With the gradual reduction of motor torque, the absolute value of vehicle jerk finally stabilizes at around 8.34 m/s3, and the final torque reduction time is 0.224 s. After the torque reduction of the driving motor is completed, it enters the process of picking, speed regulation and hanging gear, which takes 0.216 s. Then it enters the motor torque-up stage, and the vehicle jerk is stable at around 5.92 m/s3 with a torque-up time of 0.103 s. After the upshift is completed, the gear shift scheduling is switched from 2 to 3, and the TCU is switched from changing gear mode to in-gear operation mode, ending the gear shift process. Figure 11d shows the shift curve of the optimized shift control strategy. According to the identified driving intention and corresponding time correction factors, for shifting, the torque reduction time is 0.3 s, and the absolute value of vehicle jerk is maintained between 3.375 and 3.615 m/s3. The processes of gear shifting, speed regulation, and gear shifting on a total of 0.213 s and the time of upgrading the torque is 0.18 s. The absolute value of vehicle jerk is maintained between 2.683 and 2.724 m/s3. It can be concluded that the total shift time has been extended by about 30.18% and the shift impact has been reduced by about 56.6% after adopting the optimized control strategy. Although the shift time has been prolonged, the comfort has been obviously improved, which is in line with the driver’s intention.
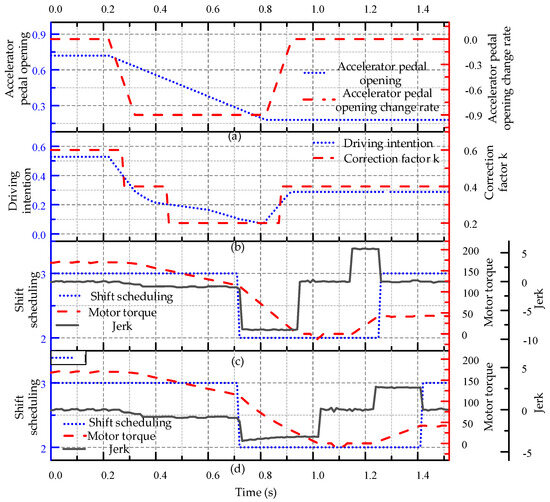
Figure 11.
Comparison diagram of vehicle shifting quality before and after optimization of slow shifting process.
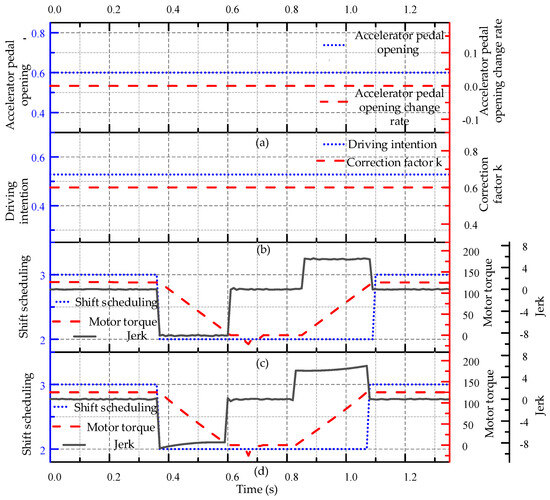
Figure 12.
Comparison diagram of vehicle shifting quality before and after optimization of medium-speed shifting process.
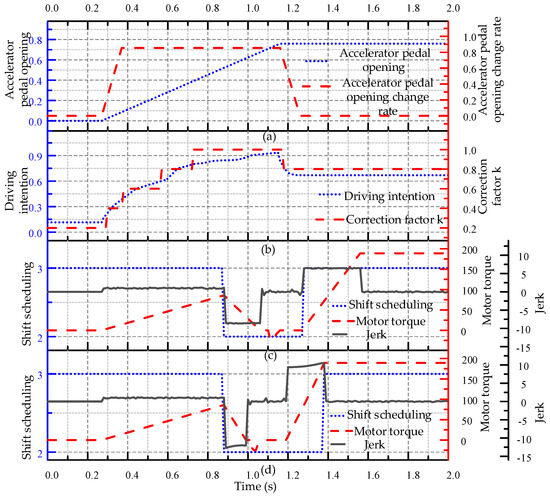
Figure 13.
Comparison diagram of vehicle shifting quality before and after optimization of rapid shifting process.
Figure 12a shows the accelerator pedal opening and Figure 12b shows the driving intention. From the shift curves without optimization in Figure 12c and optimized in Figure 12d, it can be seen that the torque reduction time is around 0.233, and the jerk is maintained between 7.987–8.3853 m/s3. The time of the off-gear, speed regulation and hanging gear is basically the same, the torque increase time is about 0.242 s, and the jerk is kept between 5.241–6.097 m/s3. From this, it can be seen that the driver’s intention is to shift at a medium speed, with basically the same shifting time and roughly the same jerk, and the shift quality is between power and comfort. However, when using the optimized shifting strategy for testing, the driver’s subjective feedback is better. The vehicle has neither a strong sense of power loss nor a noticeable sense of nodding and pushing back, which can strongly prove that the optimized control strategy can effectively improve the shift quality.
Figure 13a shows the accelerator pedal opening and Figure 13b shows the driving intention. As shown in Figure 13c. The torque reduction time is 0.179 s, the shifting impact is stable at around 8.514 m/s3, the torque rise time is 0.292 s and the vehicle jerk is stable at around 6.382 m/s3 when no optimization is adopted. From the optimized shift curve in Figure 13d, it can be seen that the torque reduction time is 0.112 s, the shifting impact is maintained between 12.053 and 12.712 m/s3, the torque increase time is 0.189 s, and the shifting impact is maintained between 9.398 and 10.387 m/s3. After adopting the optimization, the shifting time is reduced by 27.4% and the jerk is increased by 45.71%. It can be seen that according to the recognition of the driver’s intention, the shifting quality gradually shifts from comfort to shifting power with the acceleration of working conditions, which can prove the effectiveness of the control strategy proposed in this paper.
At the same time, it can be seen from the various figure that jerk is also generated during the stages of gear removal, speed regulation and gear hanging, but it is basically negligible compared with the impact in the motor lifting torque stage [23]. This is also the significance of this study, which is to determine the time of the lifting and twisting stage based on driving intentions to control the driving motor to achieve effective improvement of shifting quality at the corresponding lifting and twisting rate.
5. Discussion
This article is based on establishing a dynamic model of the shifting process, the mechanism of vehicle jerk at different stages of shifting process was analyzed. The fuzzy control algorithm was utilized to input the accelerator pedal opening and its change rate to identify the driver’s intention, then the driver’s expected time was judged by the corresponding time correction factor K under different driving intentions. The driving motor’s rise and fall torque rate was output through the control formula, and the driving motor was controlled by this rate, thus completing the shift control based on the driver’s intention recognition. A real vehicle test platform for experimental verification was built, and the experimental results verified that this optimization method can meet the driver’s demand for shifting quality based on their expectations and achieve the improvement of shifting quality.
In this paper, the research on two-speed AMT transmission has made some progress, but there are still some aspects that need to be perfected and improved. The fuzzy control algorithm is used to identify the driver’s expected shift type, which belongs to the empirical model, and there is a certain error between the identified result and the actual result. Subsequently, by collecting a large amount of actual driving data from drivers as a basis, or more intelligent algorithms can be used to identify the driver’s expected shifting type.
6. Conclusions
The shift process control strategy based on driving intention proposed in this study utilized a fuzzy controller to automatically identify the driver’s expected shifting type, and conducted real vehicle verification on slow, medium, and fast shift. After optimization, the jerk of the slow shifting process was reduced by 56.6%, and the shifting time was extended by 30.18%; the jerk and shifting time during medium speed shifting process were roughly the same; the fast shifting process shortened the shifting time by 27.4% and increased the jerk by 45.71%. In summary, this strategy can adjust the torque change rate of the driving motor during the unloading and recovery stages in real time, balance shifting time and jerk and improve shifting smoothness and shifting power, and can offer a theoretical reference for the real vehicle control engineering.
Author Contributions
Conceptualization, H.S., J.G. and J.X.; methodology, H.S., J.G. and J.X.; software H.S.; validation, J.G. and J.X.; data curation, J.X. and H.S.; writing—original draft preparation, H.S.; writing—review and editing, J.X. and H.S.; visualization, J.X.; supervision, J.X.; project administration, J.X.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Central Plains technological innovation leading talents, grant number [224200510014]. And The APC was funded by [224200510014].
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sarah, J.G.; André, P.C.F. Performance of batteries for electric vehicles on short and longer term. J. Power Sources 2012, 212, 111–129. [Google Scholar]
- Zheng, S. Analysis on the present situation and development trend of automobile automatic transmission. Auto Time 2021, 16, 149–150. [Google Scholar] [CrossRef]
- Liu, W.; Bi, S.; Xu, C. Shifting Strategy for Two-speed AMT of Electric Vehicle. J. Chongqing Inst. Technol. (Nat. Sci.) 2021, 35, 41–49. [Google Scholar]
- Wang, D.; Liu, G.; Jin, Y. Gear-shifting Control of Clutchless Automated Mechanical Transmission without Synchronizer in Short-distance Pure Electric Vehicle. China J. Highw. Transp. 2017, 30, 144–152. [Google Scholar]
- Xiao, L.; Wang, M.; Zhong, Z. Coordinated Shift Control and Experimental Study of Two-speed AMT for Pure Electric Vehicle. J. Hunan Univ. (Nat. Sci.) 2019, 46, 10–18. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, H.; Xi, J.; Wang, J.; Fang, Z. Robust speed synchronization control for clutchless automated manual transmission systems in electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 424–436. [Google Scholar] [CrossRef]
- Tseng, C.-Y.; Yu, C.-H. Advanced shifting control of synchronizer mechanisms for clutchless automatic manual transmission in an electric vehicle. Mech. Mach. Theory 2015, 84, 37–56. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, H.; Mo, W.; Zhou, S.; Zhang, N.; Walker, P.D. Optimal coordinating gearshift control of a two-speed transmission for battery electric vehicles. Mech. Syst. Signal Process. 2020, 136, 106521. [Google Scholar] [CrossRef]
- Dong, A. Study of Complete Torque Shifting Control for Clutchless AMT of Electric Vehicles. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Lin, C.; Yi, J.; Tian, Y. State estimation and parameter identification of AMT shift actuator for electric buses. Automot. Eng. 2022, 44, 1237–1250. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; He, K.; Liu, C. Dual-loop self-learning fuzzy control for AMT gear engagement: Design and experiment. IEEE Trans. Fuzzy Syst. 2018, 26, 1813–1822. [Google Scholar] [CrossRef]
- Roozegar, M.; Angeles, J. A two-phase control algorithm for gear-shifting in a novel multispeed transmission for electric vehicles. Mech. Syst. Signal Process. 2018, 104, 145–154. [Google Scholar] [CrossRef]
- Roozegar, M.; Setiawan, Y.D.; Angeles, J. Design, modelling and estimation of a novel modular multi-speed transmission system for electric vehicles. Mechatronics 2017, 45, 119–129. [Google Scholar] [CrossRef]
- Roozegar, M.; Angeles, J. The optimal gear-shifting for a multi-speed transmission system for electric vehicles. Mech. Mach. Theory 2017, 116, 7–15. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Qiu, M.; Qin, F. A new tracking control of shift displacement constraint for electric vehicle. J. Appl. Mech. 2020, 37, 1381–1389. [Google Scholar] [CrossRef]
- Zhang, D.; Zong, Z.; Feng, J. Multi-objective optimization of shifting rule of two-speed AMT based on NSGA-IIalgorithm. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2021, 40, 128–135. [Google Scholar]
- Wang, H.; Wu, H. Implementation of an Energy Management Strategy with Drivability Constraints for a Dual-Motor Electric Vehicle. World Electr. Veh. J. 2019, 10, 28. [Google Scholar] [CrossRef]
- Liu, T.; Zeng, X.; Song, D. MPC-Based Coordinated Control of Gear Shifting Process for a Power-split Hybrid Electric Bus with a Clutchless AMT. Chin. J. Mech. Eng. 2022, 35, 144. [Google Scholar] [CrossRef]
- Kim, Y.K.; Kim, H.W.; Lee, I.S.; Park, S.M.; Mok, H.S. A speed control for the reduction of the shift shocks in electric vehicles with a two-speed AMT. J. Power Electron. 2016, 1613, 55–1366. [Google Scholar] [CrossRef]
- Lin, X.; Li, Y.; Xia, B. An online driver behavior adaptive shift strategy for two-speed AMT electric vehicle based on dynamic corrected factor. Sustain. Energy Technol. Assess. 2021, 48, 101598. [Google Scholar] [CrossRef]
- Yang, L.; Park, D.; Lyu, S.; Zheng, C.; Kim, N. Optimal Control for Shifting Command of Two-Speed Electric Vehicles Considering Shifting Loss. Int. J. Automot. Technol. 2023, 24, 1051–1059. [Google Scholar] [CrossRef]
- Bing, W.; Mingyao, Y.; Jinglai, W.; Xianqian, H.; Nong, Z. Novel shift process control strategy for two-speed clutchless automatic mechanical transmission based on segmented speed regulation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 09544070221148233. [Google Scholar] [CrossRef]
- Ahssan, M.R.; Ektesabi, M.; Gorji, S. Evaluation of a Three-Parameter Gearshift Strategy for a Two-Speed Transmission System in Electric Vehicles. Energies 2023, 16, 2496. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, P.; Qin, D.; Li, G.; Chen, Z.; Zhang, Y. Driving intention identification based on long short-term memory and a case study in shifting strategy optimization. IEEE Access 2019, 7, 128593–128605. [Google Scholar] [CrossRef]
- Gao, J.; Zhao, J.; Yang, S.; Xi, J. Control Strategy of Plug-in Hybrid Electric Bus Based on Driver Intention. J. Mech. Eng. 2016, 52, 107–114. [Google Scholar] [CrossRef]
- Li, Y. Study on Transient Shift Control of Two-Speed AMT of Pure Electric Vehicle. Master’s Thesis, Hefei University of Technology, Hefei, China, 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).