Analysis and Design Considerations for Transmitter-Compensated Inductance Mistuning in a WPT System with LCC-S Topology
Abstract
1. Introduction
2. Detailed Analysis and Simulations for Instability of Commonly Used Compensation Inductor
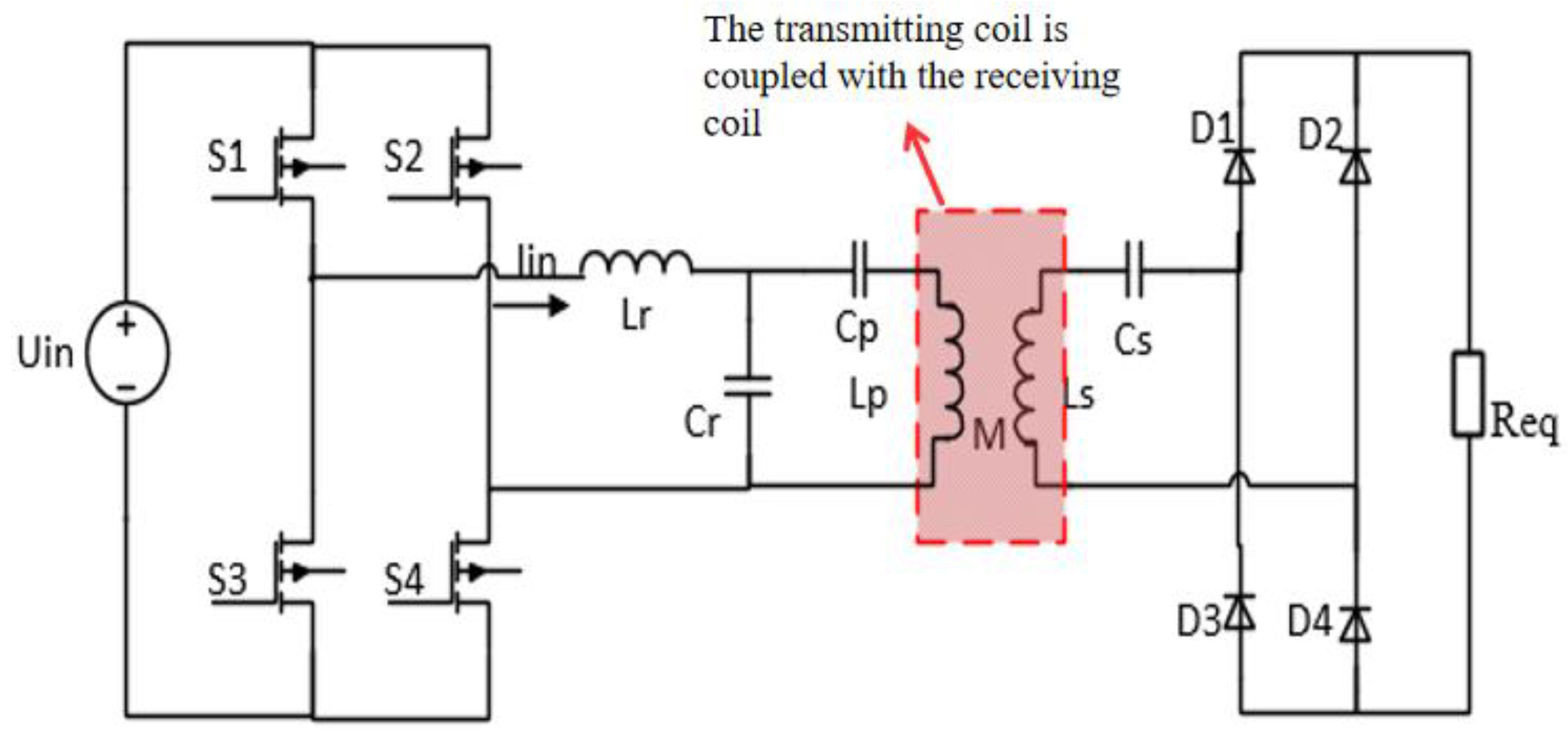
2.1. Fundamentals of WPT System with Commonly Used LCC-S Topology
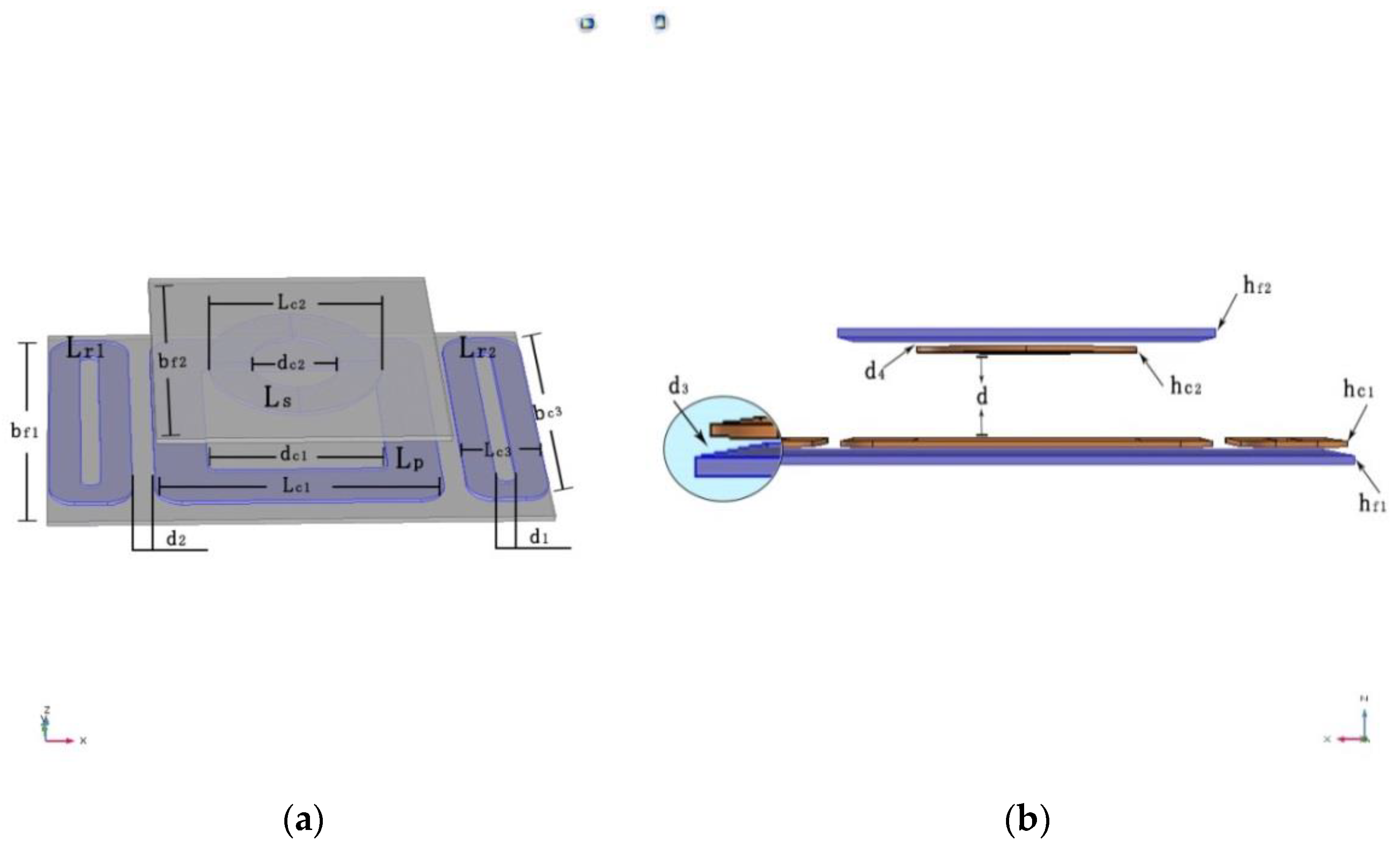
2.1.1. Coupler Structure and Elements
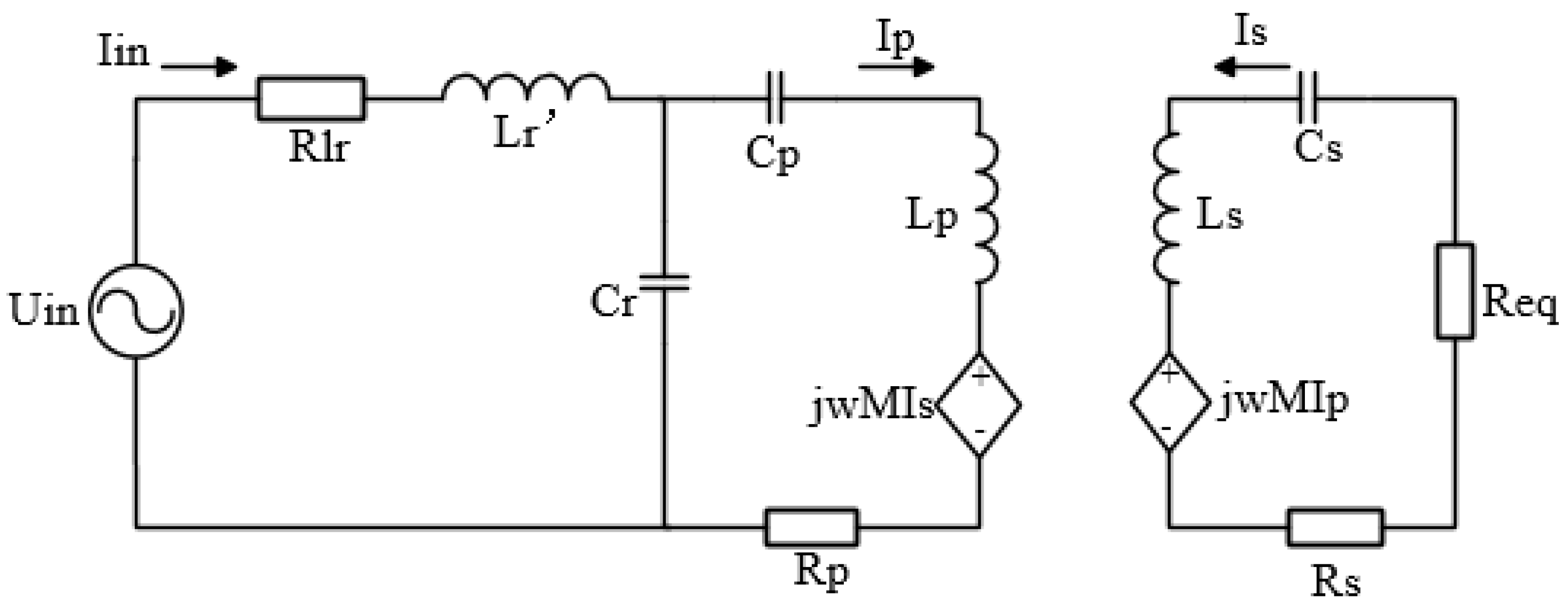
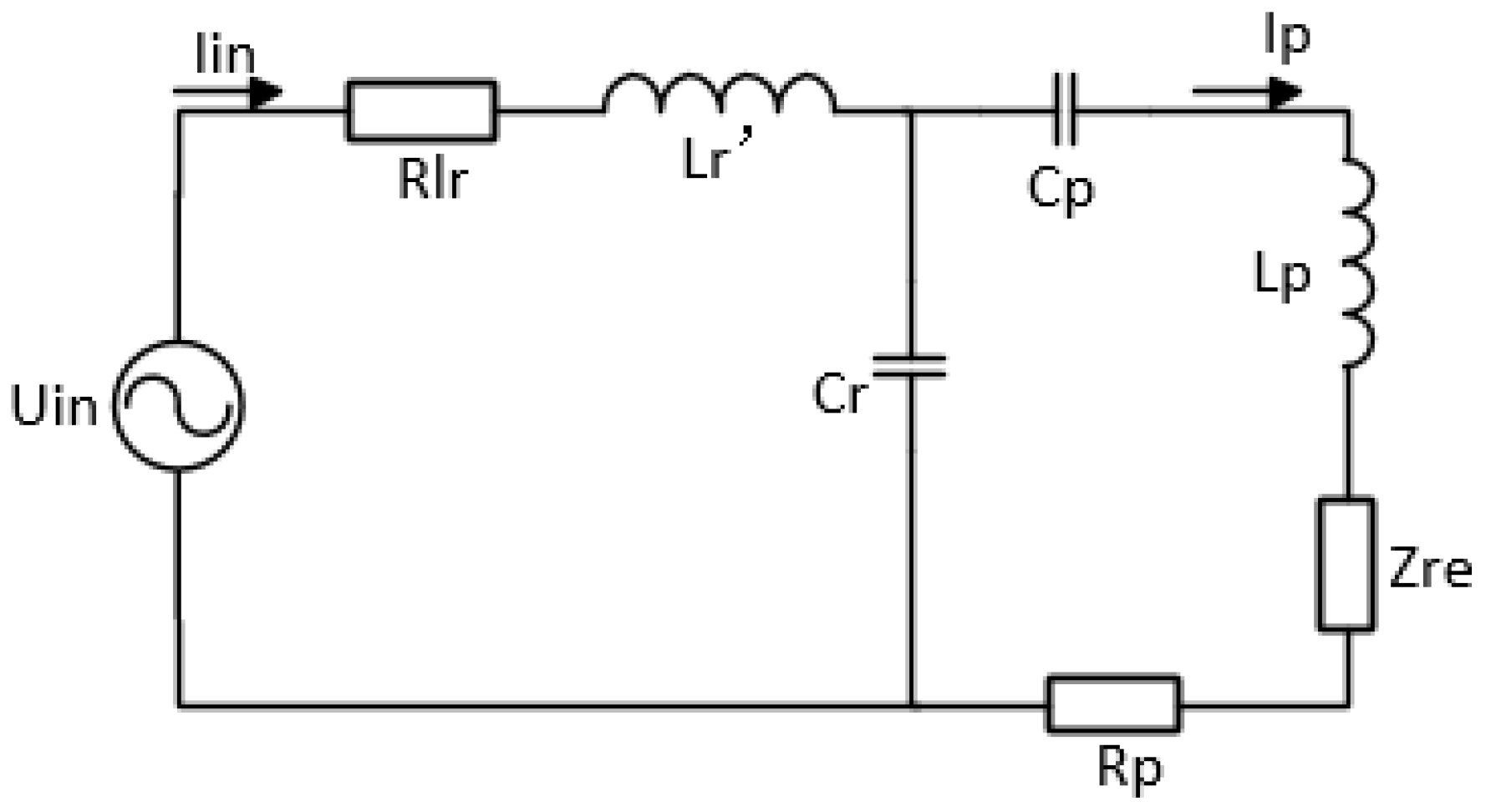
2.1.2. Analysis of the Relationship between Compensation Inductance and System Output Power and Transmission Efficiency
2.2. Simulations—Relationship between the Magnetic-Core Compensation Inductance and the Output Power and the Phase Shift Angle
3. Solution and Simulations
3.1. Analysis of the Proposed Integrated Compensation Inductor Structure
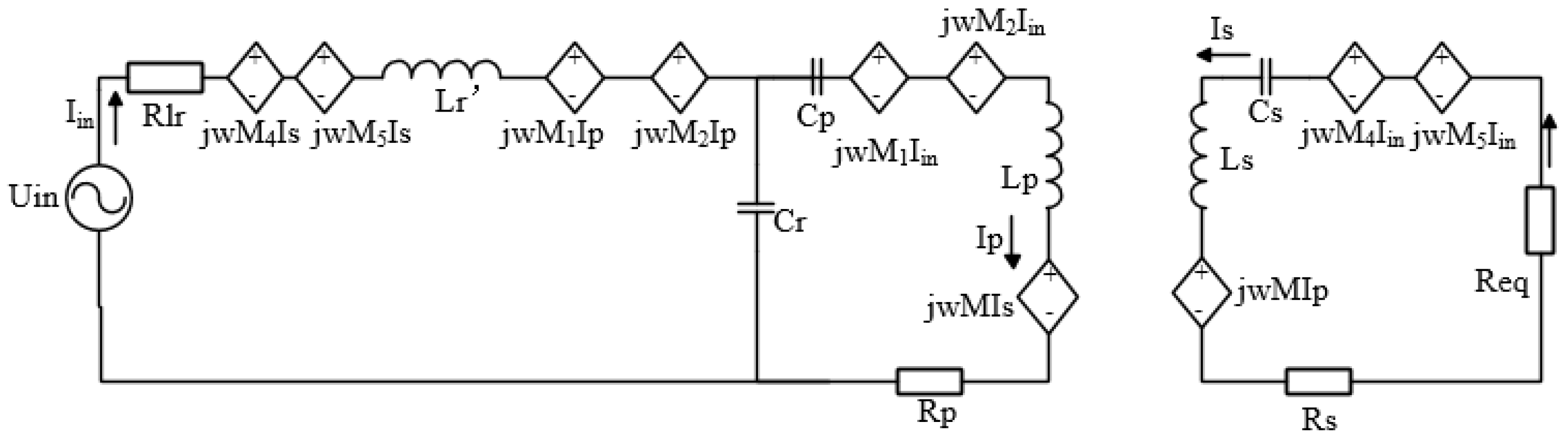
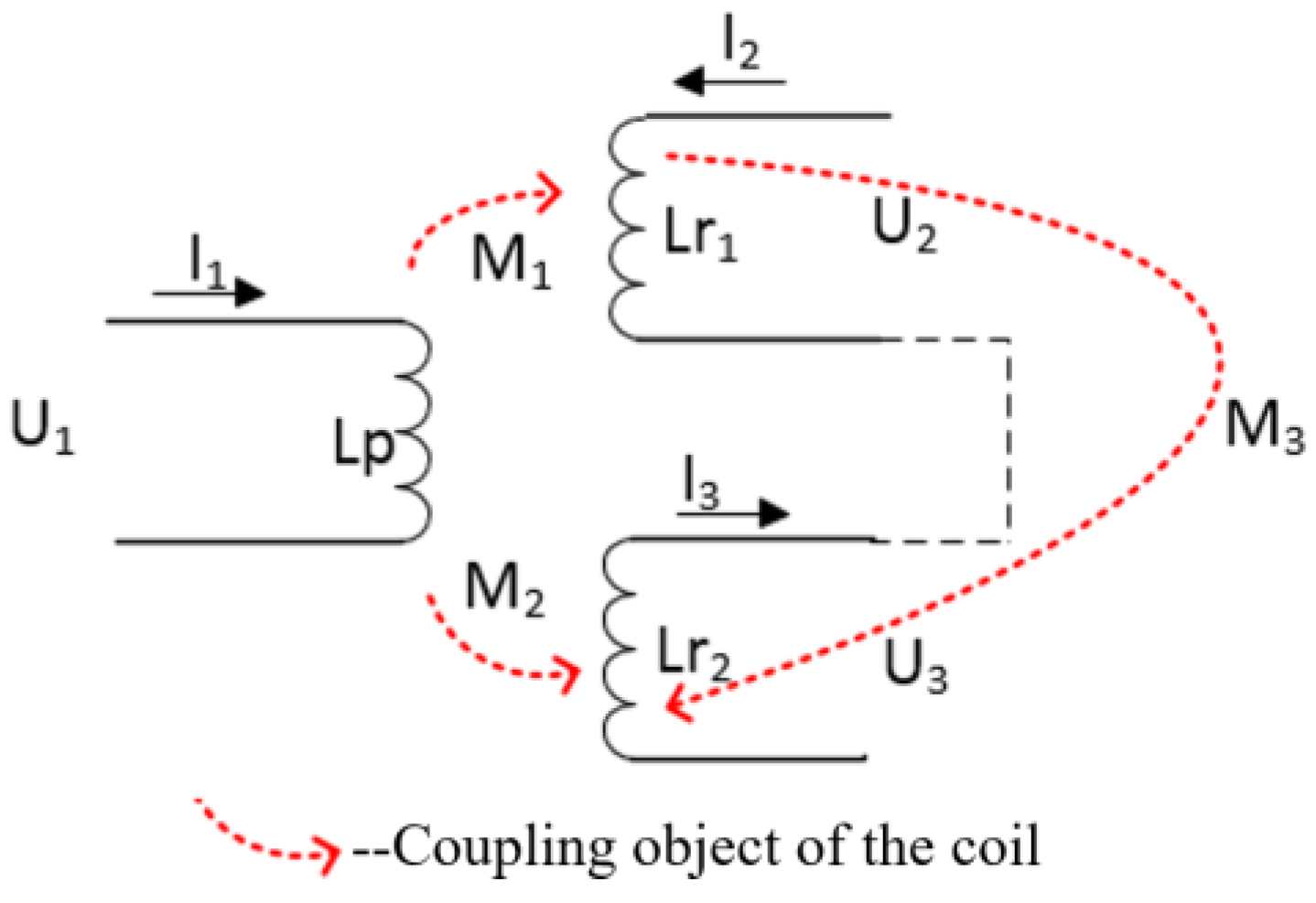
3.1.1. Analysis of Mutual Inductance between the Transmitting Coil and Integrated Compensation Inductor Coils
3.1.2. Analysis of Mutual Inductance between the Receiving Coil and Integrated Compensation Inductor Coils
- Analysis without misalignment.
- When the transmitting and the receiving coils are well aligned, and the integrated compensation coils are bipolar and distributed on both sides of the transmitting coil, then the total mutual inductance between the receiving coil and the compensation inductor coils is zero, which is also testified in the following part.
- Misalignment performance analysis.
3.2. Simulation of the WPT System with Integrated Inductor
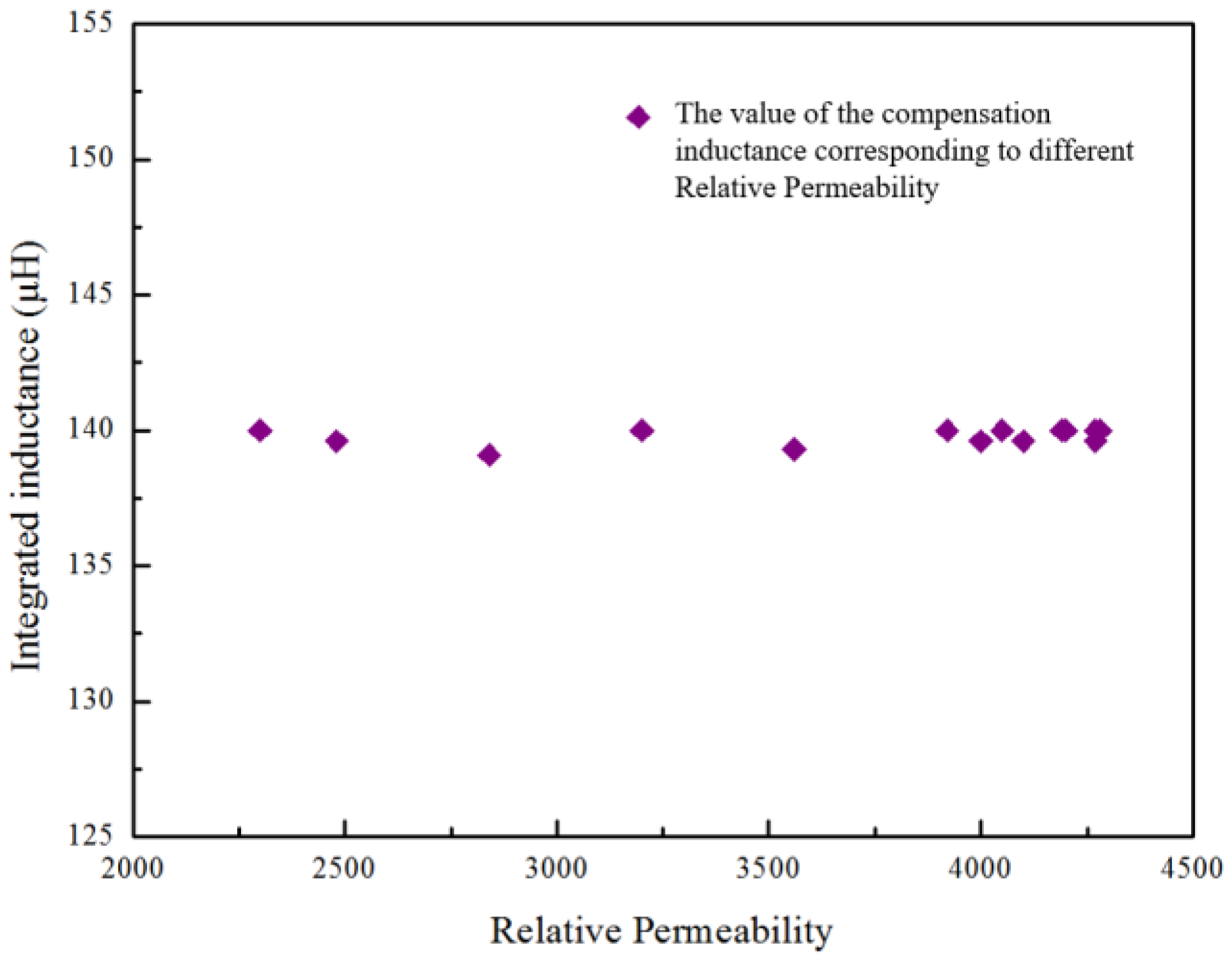
3.2.1. Simulation of the Stability of the Proposed Compensation Inductor
3.2.2. Simulation without Misalignment
3.2.3. Misalignment Performance Simulation
4. Experiment and Results
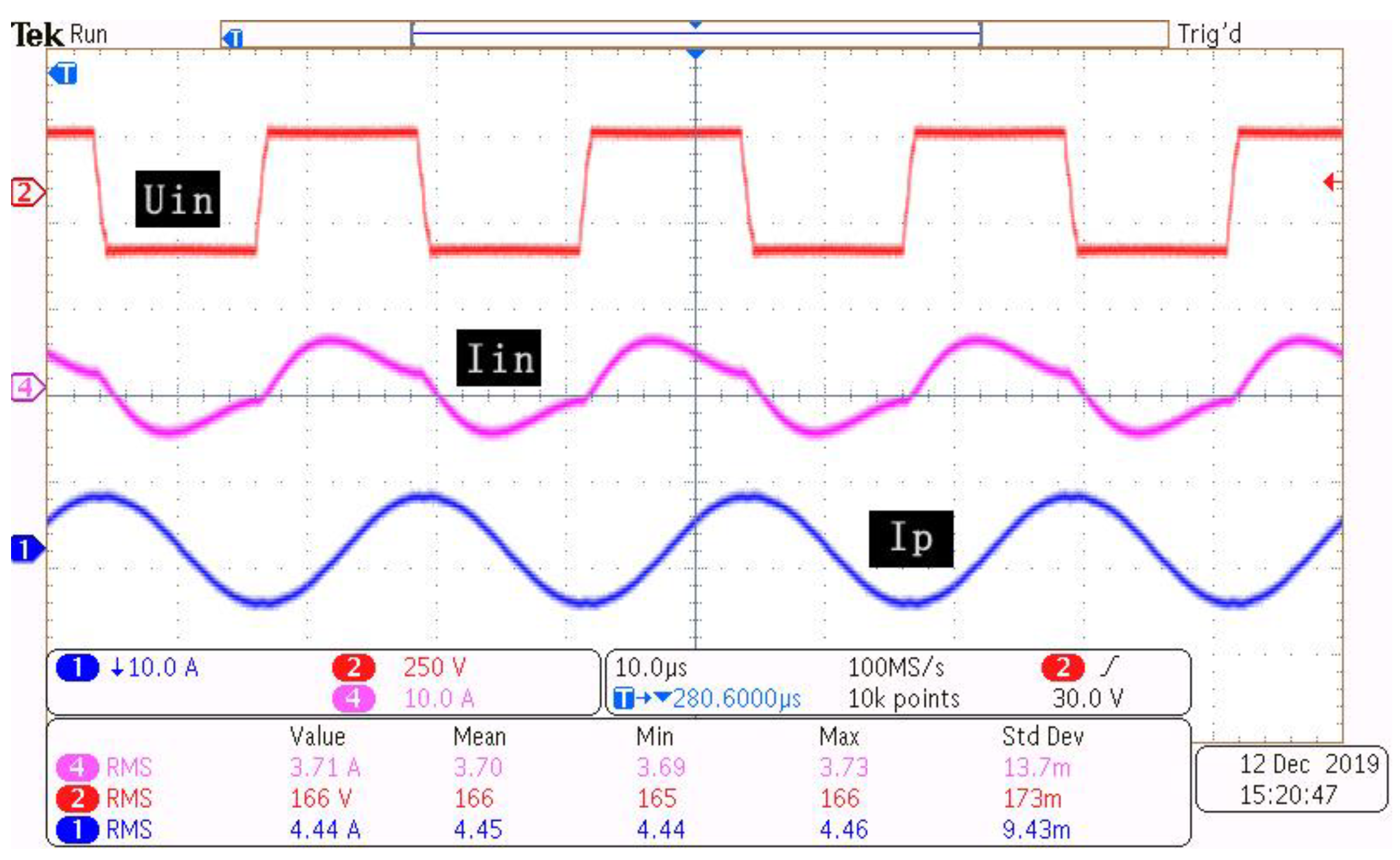
4.1. Experiment Setup
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Li, W.; Member, S. A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Moon, S.C.; Moon, G.-W. Wireless Power Transfer System with an Asymmetric 4-Coil Resonator for Electric Vehicle Battery Chargers. IEEE Trans. Power Electron. 2016, 31, 6844–6854. [Google Scholar] [CrossRef]
- Miller, J.M.; Daga, A. Elements of Wireless Power Transfer Essential to High Power Charging of Heavy Duty Vehicles. IEEE Transact. Transp. Elect. 2015, 1, 26–39. [Google Scholar] [CrossRef]
- Mi, C.C.; Buja, G.; Choi, S.Y.; Rim, C.T. Modern advances in wireless power transfer systems for roadway powered electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6533–6545. [Google Scholar] [CrossRef]
- Beh, H.Z.Z.; Neath, M.J.; Boys, J.T.; Covic, G.A. An Alternative IPT Pickup Controller for Materials Handling using a Current Doubler. IEEE Trans. Power Electron. 2018, 33, 10135. [Google Scholar] [CrossRef]
- Chen, L.J.; Boys, J.T.; Covic, G.A. Power Management for Multiple-Pickup IPT Systems in Materials Handling Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 163–176. [Google Scholar] [CrossRef]
- Boys, J.T.; Covic, G.A.; Green, A.W. Stability and control of inductively coupled power transfer systems. IEEE Proc.-Electr. Power Appl. 2000, 147, 37–43. [Google Scholar] [CrossRef]
- Kojima, T.; Tanabe, H.; Imakiire, A.; Fuji, K.; Kozako, M.; Hikita, M.; Imoto, Y.; Honda, K. Characterization of Contactless Power Transfer System and Investigation of Core Shape for AGV Application. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, Australia, 9–12 June 2015. [Google Scholar] [CrossRef]
- Nicholas, A.K.; Grant, A.C.; John, T.B. A Unity-Power-Factor IPT Pickup for High-Power Applications. IEEE Trans. Ind. Electron. 2010, 57, 744–751. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Modern trends in inductive power transfer for transportation applications. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Inductive power transfer. Proc. IEEE 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.J.; Cho, D.H. Design and implementation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles. IEEE Trans. Ind. Electron. 2014, 61, 1179–1192. [Google Scholar] [CrossRef]
- Yusop, Y.; Saat, S.; Nguang, S.K.; Husin, H.; Ghani, Z. Design of Capacitive Power Transfer Using a Class-E Resonant Inverter. J. Power Electron. 2016, 16, 1678–1688. [Google Scholar] [CrossRef]
- Geng, Y.; Li, B.; Yang, Z.; Lin, F.; Sun, H. A High Efficiency Charging Strategy for a Supercapacitor Using a Wireless Power Transfer System Based on Inductor/Capacitor/Capacitor (LCC) Compensation Topology. Energies 2017, 10, 135. [Google Scholar] [CrossRef]
- Ann, S.; Lee, W.-Y.; Choe, G.-Y.; Lee, B.K. Integrated Control Strategy for Inductive Power Transfer Systems with Primary-Side LCC Network for Load-Average Efficiency Improvement. Energies 2019, 12, 312. [Google Scholar] [CrossRef]
- Zahid, Z.U.; Dalala, Z.M.; Zheng, C.; Chen, R.; Faraci, W.E.; Lai, J.-S.J.; Lisi, G.; Anderson, D. Modeling and Control of Series–Series Compensated Inductive Power Transfer System. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 111–123. [Google Scholar] [CrossRef]
- Jia, H.; Chen, Q.; Wong, S.C.; Chi, K.T.; Ruan, X. Analysis and Control of Series/Series-Parallel Compensated Resonant Converter for Contactless Power Transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 124–136. [Google Scholar] [CrossRef]
- Sohn, Y.H.; Choi, B.H.; Lee, E.S.; Lim, G.C.; Cho, G.-H.; Rim, C.T. General Unified Analyses of Two-Capacitor Inductive Power Transfer Systems: Equivalence of Current-Source SS and SP Compensations. IEEE Trans. Power Electron. 2015, 30, 6030–6045. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.-C.; Tse, C.K.; Chen, Q. Analysis and Comparison of Secondary Series- and Parallel-Compensated Inductive Power Transfer Systems Operating for Optimal Efficiency and Load-Independent Voltage-Transfer Ratio. IEEE Trans. Power Electron. 2014, 29, 2979–2990. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Wang, W.; Liu, S.; Chen, Y. A Novel Wired/Wireless Hybrid Multiport Energy Router for Dynamic EV Energy Internet with Grid-Tied and Islanded Operations. IEEE Trans. Ind. Electron. 2024, 71, 3559–3571. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCC Compensated Resonant Converter Optimized for Robust Reaction to Large Coupling Variation in Dynamic Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Liu, C.; Ge, S.K.; Guo, Y.; Li, H.; Cai, G.W. Double-LCL resonant compensation network for electric vehicles wireless power transfer: Experimental study and analysis. IET Power Electron. 2016, 9, 2262–2270. [Google Scholar] [CrossRef]
- Fei, L.; Hua, Z.; Hofmann, H.; Mi, C. A High Efficiency 3.3 kW Loosely-Coupled Wireless Power Transfer System without Magnetic Material. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015. [Google Scholar] [CrossRef]
- Wei, Z.; Mi, C.C. Compensation Topologies of High-Power Wireless Power Transfer Systems. IEEE Trans. Veh. Technol. 2016, 65, 4768–4778. [Google Scholar] [CrossRef]
- Kalinikos, B.A.; Ustinov, A.B. Chapter Eight—Ferrites for RF Passive Devices. Solid State Phys. 2013, 64, 237–329. [Google Scholar]
- Mn-Zn Ferrite, Material Characteristics. Available online: https://product.tdk.com/info/en/catalog/datasheets/ferrite_mn-zn_material_characteristics_en.pdf (accessed on 1 May 2022).
- Lu, F.; Zhang, H.; Hofmann, H.; Su, W.; Mi, C.C. A Dual-Coupled LCC-Compensated IPT System with a Compact Magnetic Coupler. IEEE Trans. Power Electron. 2018, 33, 6391–6402. [Google Scholar] [CrossRef]
- Li, W.; Mi, C.C.; Li, S.; Deng, J.; Han, Z. Integrated LCC Compensation Topology for Wireless Charger in Electric and Plug-in Electric Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 4215–4224. [Google Scholar] [CrossRef]
- Budhia, M.; Boys, J.T.; Covic, G.A. Development of a Single-Sided Flux Magnetic Coupler for Electric Vehicle IPT Charging Systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Zhou, S.; Mi, C. Multi-Paralleled LCC Reactive Power Compensation Networks and Its Tuning Method for Electric Vehicle Dynamic Wireless Charging. IEEE Trans. Ind. Electron. 2016, 63, 6546–6556. [Google Scholar] [CrossRef]




| Symbol | Note | Value |
|---|---|---|
| f | Resonant frequency | 39 KHz |
| d | Distance between transmitting and receiving coils | 70 mm |
| Lp, Ls | Primary and secondary inductors | 403 µH, 30 µH |
| Lr | Compensation inductance | 0.1~320 µH |
| Cr | Compensation capacitor | 0.117 µF |
| Cp, Cs | Primary and secondary series capacitors | 0.065 µF, 0.52 µF |
| k | Coupling coefficient | 0.23 |
| Rp, Rs | Primary and secondary coil self-resistance | 0.2 Ω, 0.1 Ω |
| Rlr | compensation inductor self-resistance | 0.2 Ω |
| Req | Equivalent load | 1.4 Ω |
| Uin | Input voltage | 170 V |
| Symbol | Note | Value |
|---|---|---|
| lf1, bf1 | Length and width of magnetic plate (transmitting end) | 515 mm, 340 mm |
| bf2 | Length and width of magnetic plate (receiving end) | 298 mm |
| Lc1 | Side length of transmitting coil | 296 mm |
| dc1 | Hole pitch of transmitting coil | 186 mm |
| Lc2 | Diameter of receiving coil | 183 mm |
| dc2 | Hole pitch of receiving coil | 94 mm |
| Lc3, bc3 | Length and width of compensation coil | 295 mm, 85 mm |
| d | Distance between transmitting coil and receiving coil | 150 mm |
| d1 | Hole pitch of compensation coil | 20 mm |
| d2 | Distance between compensation coils and transmitting coil | 23 mm |
| d3, d4 | Distance between magnetic plate and coils | 3 mm |
| hc1, hc2 | Thickness of coils | 4 mm |
| hf1, hf2 | Thickness of magnetic plate | 6 mm |
| Np | Transmitting coil turns | 23 |
| Ns | Receiving coil turns | 10 |
| N1 | Number of turns of left compensation coil | 13 |
| N2 | Number of turns of right compensation coil | 13 |
| Symbol | Note | Value (μH) |
|---|---|---|
| Lp | Self-inductance of transmitting coil | 404.09 |
| M1 | Mutual inductance between Lp and Lr1 | 13.64 |
| M2 | Mutual inductance between Lp and Lr2 | −13.64 |
| Ls | Self-inductance of receiving coil | 31.60 |
| M4 | Mutual inductance between Ls and Lr1 | 1.20 |
| M5 | Mutual inductance between Ls and Lr2 | −1.20 |
| M | Mutual inductance between Lp and Ls | 32.37 |
| Symbol | Note | Value (μH) |
|---|---|---|
| Lp | Self-inductance of transmitting coil | 410.21 |
| M1 | Mutual inductance between Lp and Lr1 | 13.64 |
| M2 | Mutual inductance between Lp and Lr2 | −13.64 |
| Ls | Self-inductance of receiving coil | 31.60 |
| M4 | Mutual inductance between Ls and Lr1 (horizontal shift 50 mm) | −1.68 |
| M5 | Mutual inductance between Ls and Lr2 (horizontal shift 50 mm) | 0.77 |
| M | Mutual inductance between Lp and Ls | 28.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Cao, Y.; Hou, Y.; Hou, S.; Guo, Y.; Tian, J.; He, X. Analysis and Design Considerations for Transmitter-Compensated Inductance Mistuning in a WPT System with LCC-S Topology. World Electr. Veh. J. 2024, 15, 45. https://doi.org/10.3390/wevj15020045
Zhang B, Cao Y, Hou Y, Hou S, Guo Y, Tian J, He X. Analysis and Design Considerations for Transmitter-Compensated Inductance Mistuning in a WPT System with LCC-S Topology. World Electric Vehicle Journal. 2024; 15(2):45. https://doi.org/10.3390/wevj15020045
Chicago/Turabian StyleZhang, Benhui, Yan Cao, Yanjin Hou, Siyu Hou, Yanhua Guo, Jiawei Tian, and Xu He. 2024. "Analysis and Design Considerations for Transmitter-Compensated Inductance Mistuning in a WPT System with LCC-S Topology" World Electric Vehicle Journal 15, no. 2: 45. https://doi.org/10.3390/wevj15020045
APA StyleZhang, B., Cao, Y., Hou, Y., Hou, S., Guo, Y., Tian, J., & He, X. (2024). Analysis and Design Considerations for Transmitter-Compensated Inductance Mistuning in a WPT System with LCC-S Topology. World Electric Vehicle Journal, 15(2), 45. https://doi.org/10.3390/wevj15020045





