Thermal Performance Enhancement of Lithium-Ion Batteries Using Phase Change Material and Fin Geometry Modification
Abstract
1. Introduction
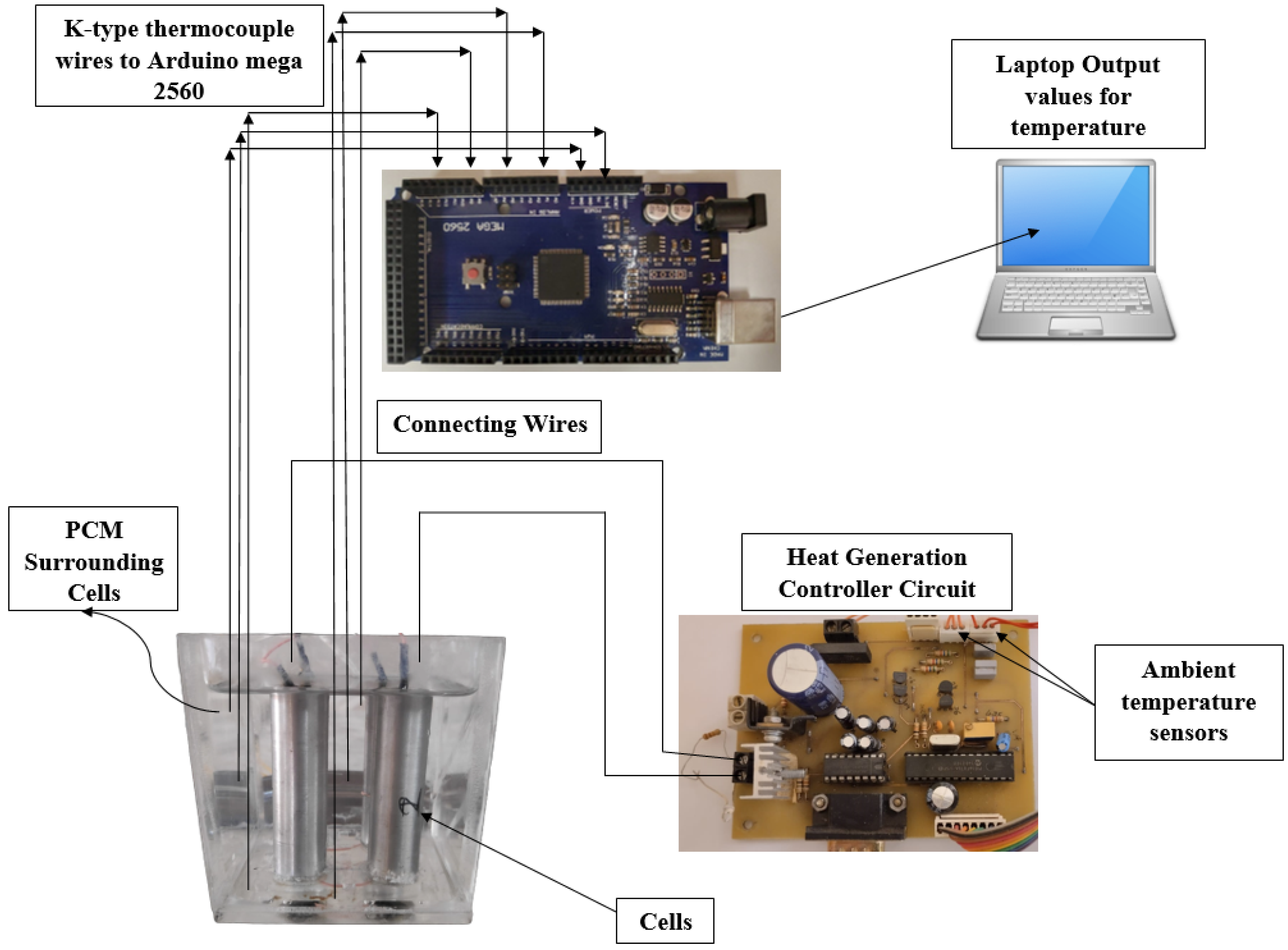
2. Experimental Setup
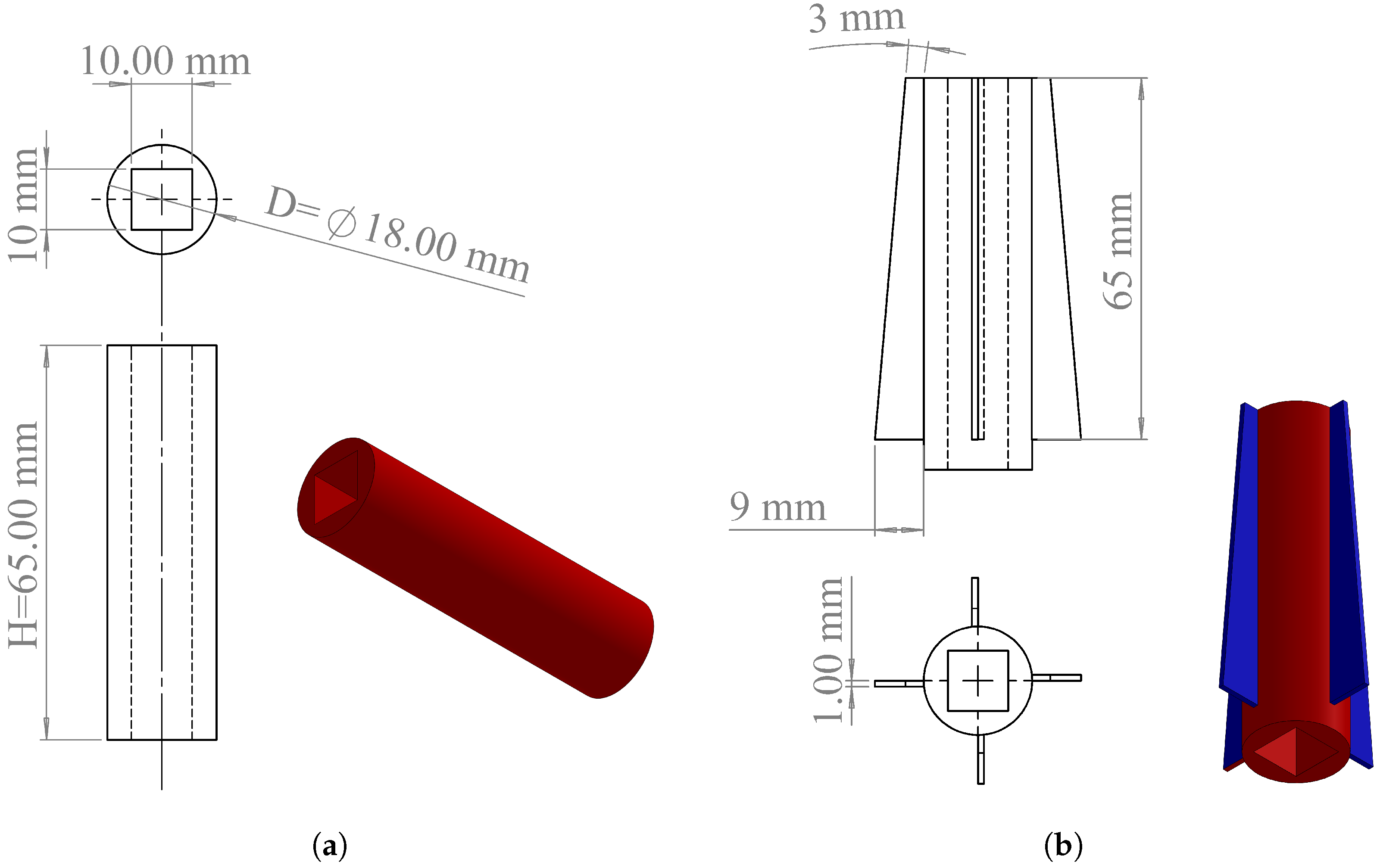
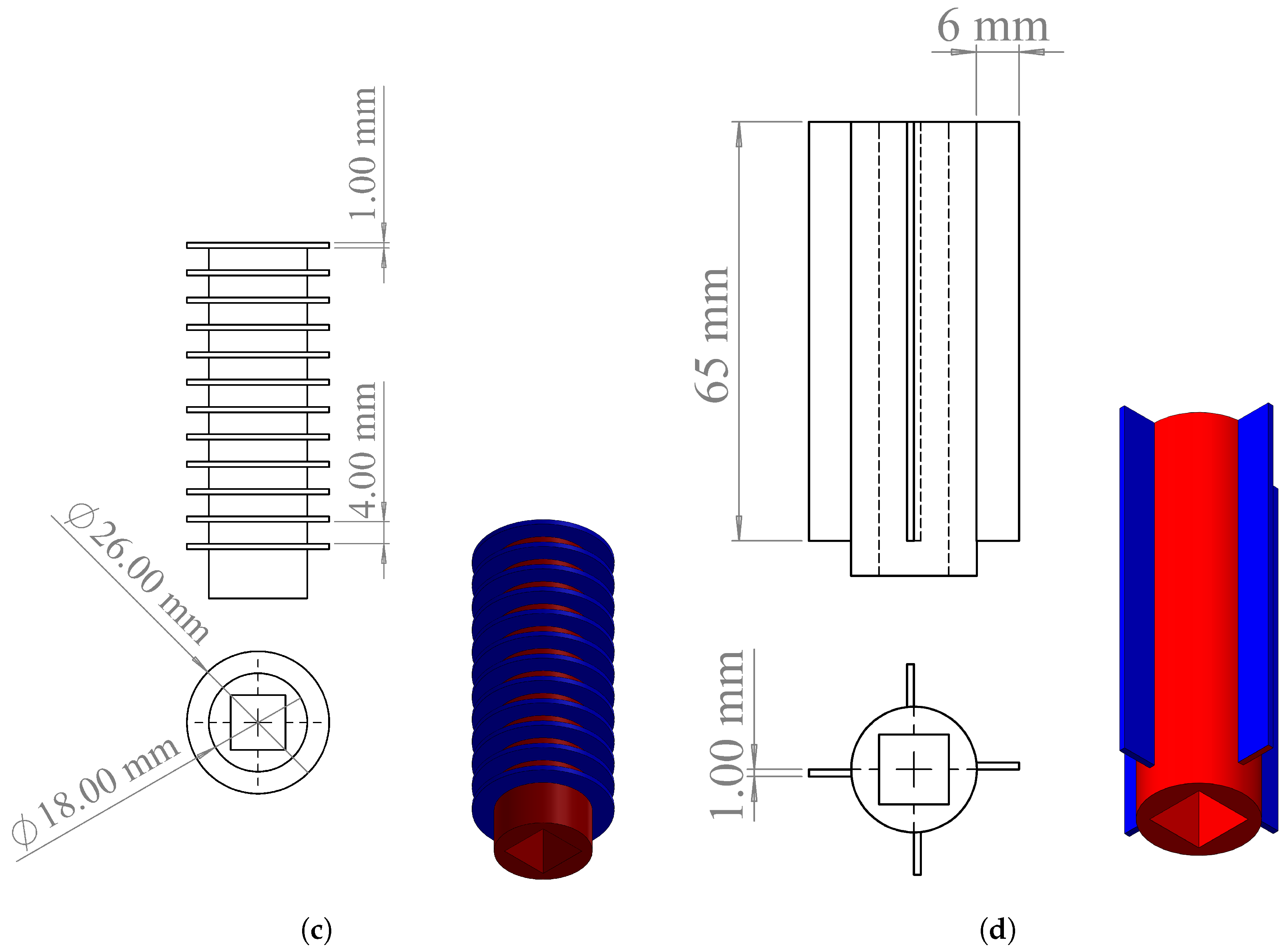
2.1. Battery Thermal Management System Design
2.2. Phase Change Material Selection Criteria
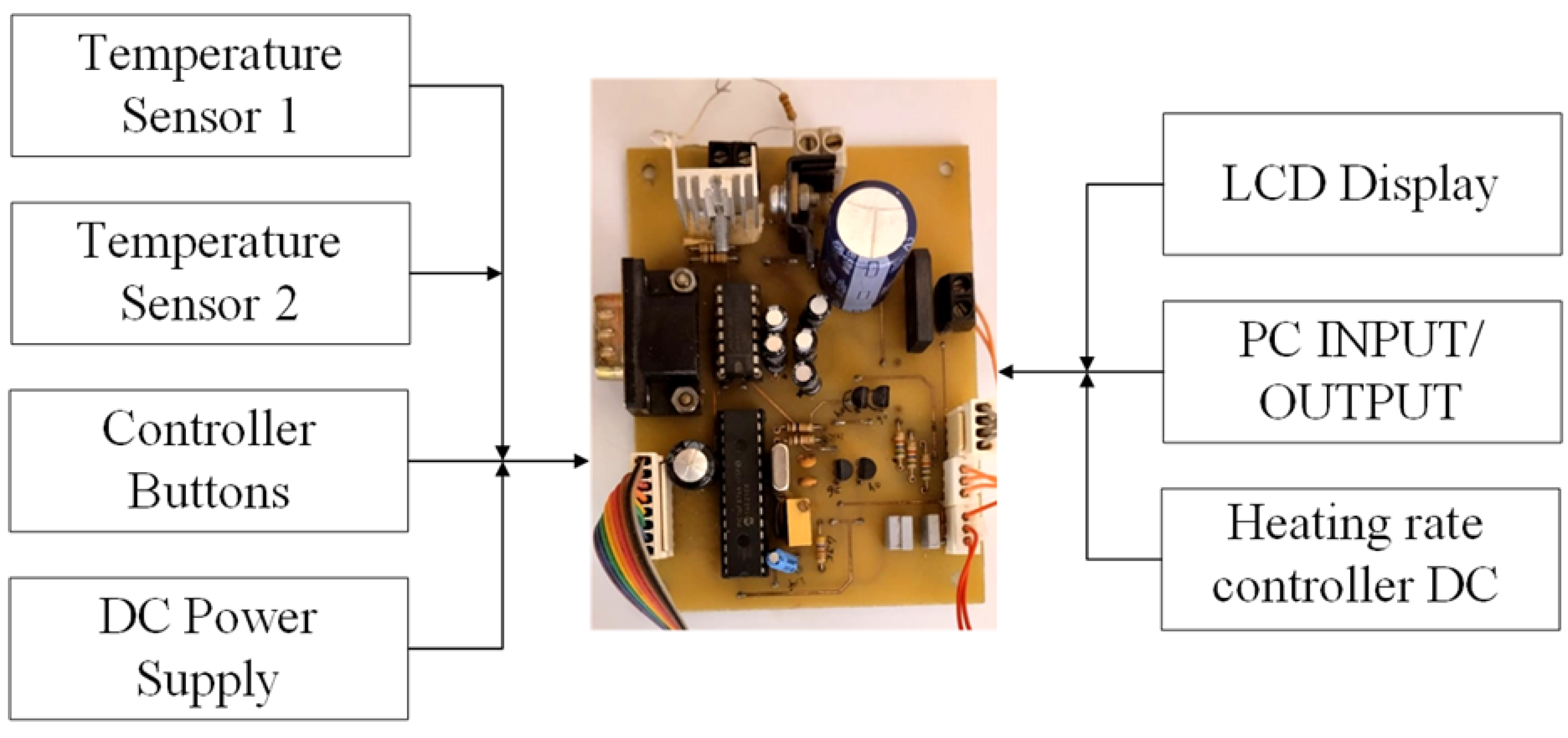
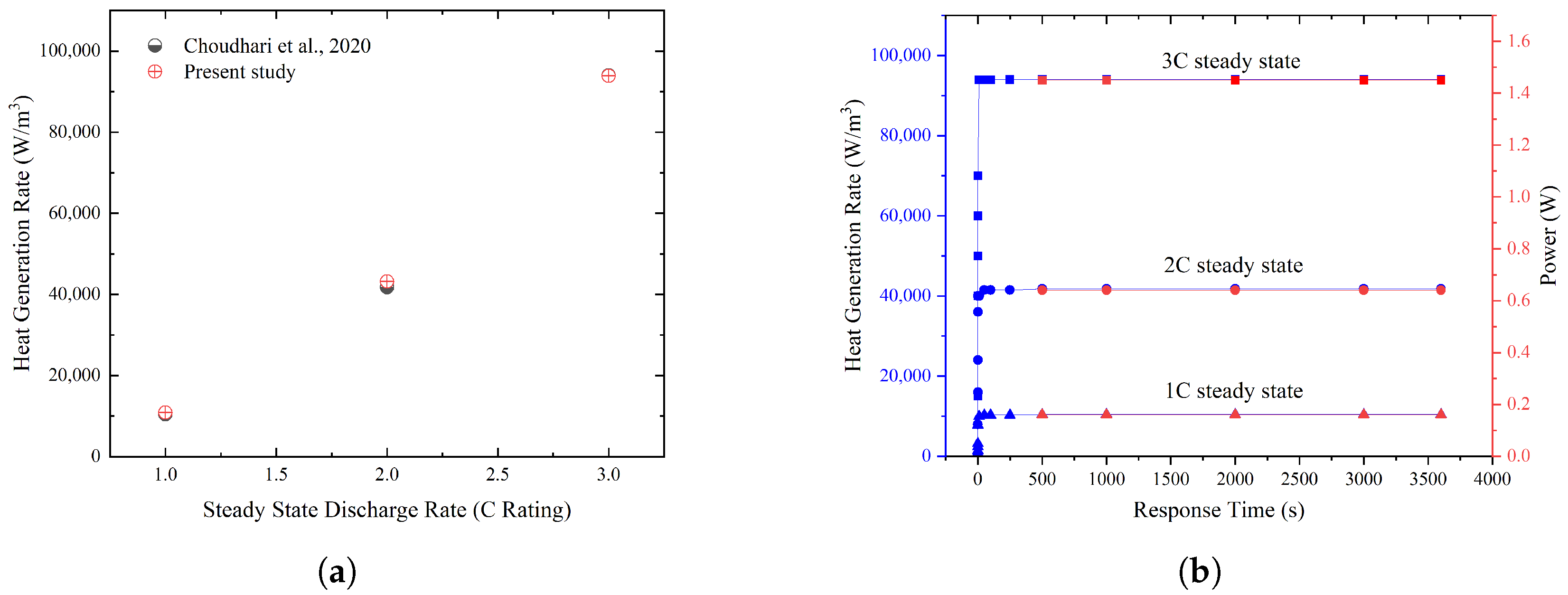
2.3. Controller Circuit and Heat Generation Rates
2.4. Boundary Conditions, Initial Conditions, and Thermophysical Properties
- The control volume for the heaters was given a volume condition as the heat generation rate (W/m3), according to Choudhari et al. [30], which was 94,023.8 (W/m3) for 3C, 41,788.37 (W/m3) for 2C, and 10447 (W/m3) for 1C;
- The walls were exposed to the environment as the system was not kept adiabatic and had a natural convection coefficient of 2.5 W/m2·K;
- The mushy zone constant was kept at the default level and solidification and melting were used to simulate the phase change process;
- All thermophysical properties for both the numerical and experimental setups are shown in Table 1;
- The solution was initialized and patched with 23.18 C for the cells and 26.29 C for the PCM, fins, and base plate temperatures, while the housing, which is exposed to the environment, was kept at 27 C. The reason for these selected temperatures was to maintain uniform reference temperatures for both the experimental and numerical analyses.
3. Numerical Problem Formulation
3.1. Governing Equations
3.2. Enthalpy Variations
3.3. Melting Fraction
3.4. Momentum Source Term
3.5. Discretization Schemes
3.6. Timestep and Mesh Independence Study
4. Results and Discussion
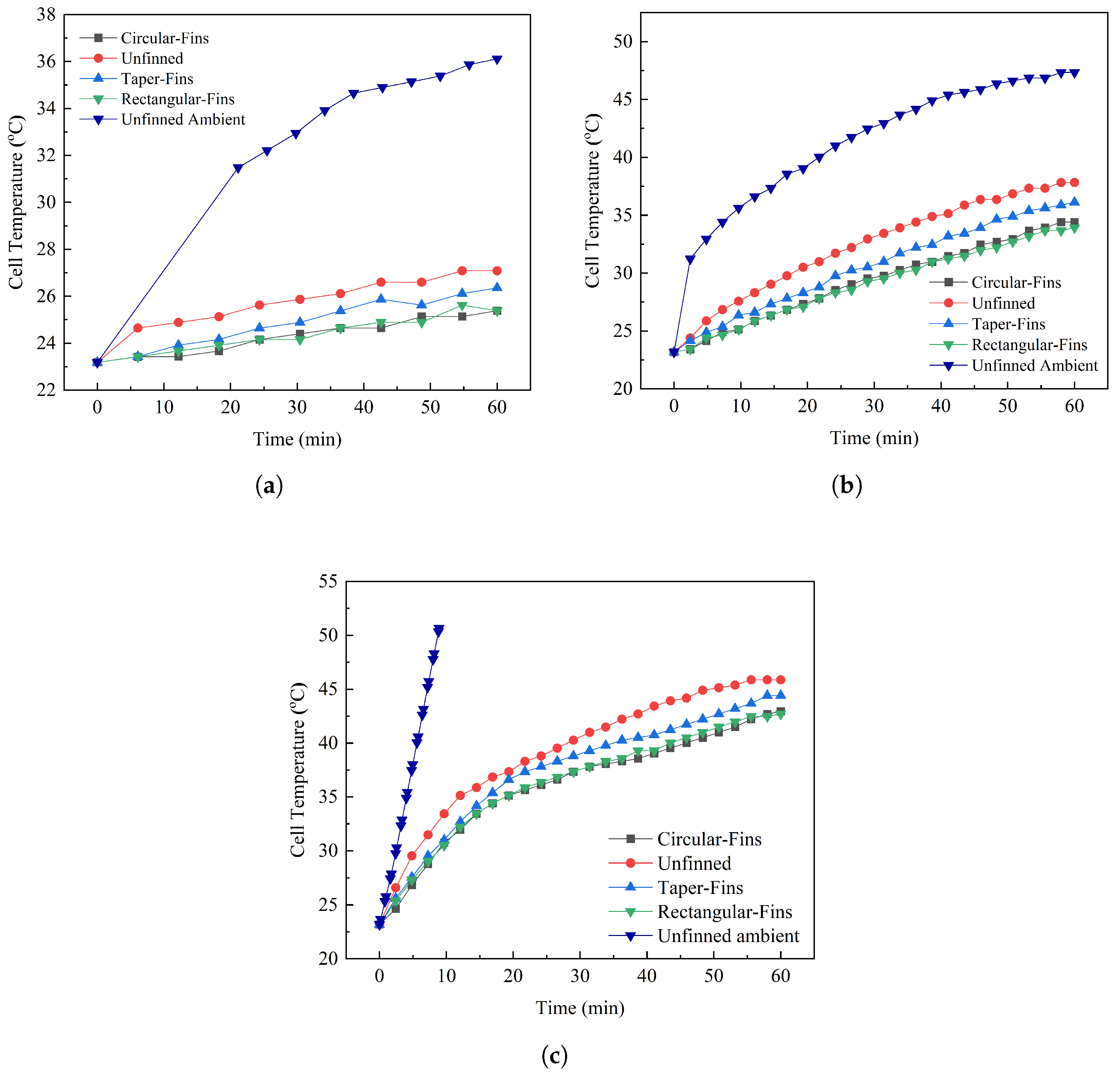
Experimental Results
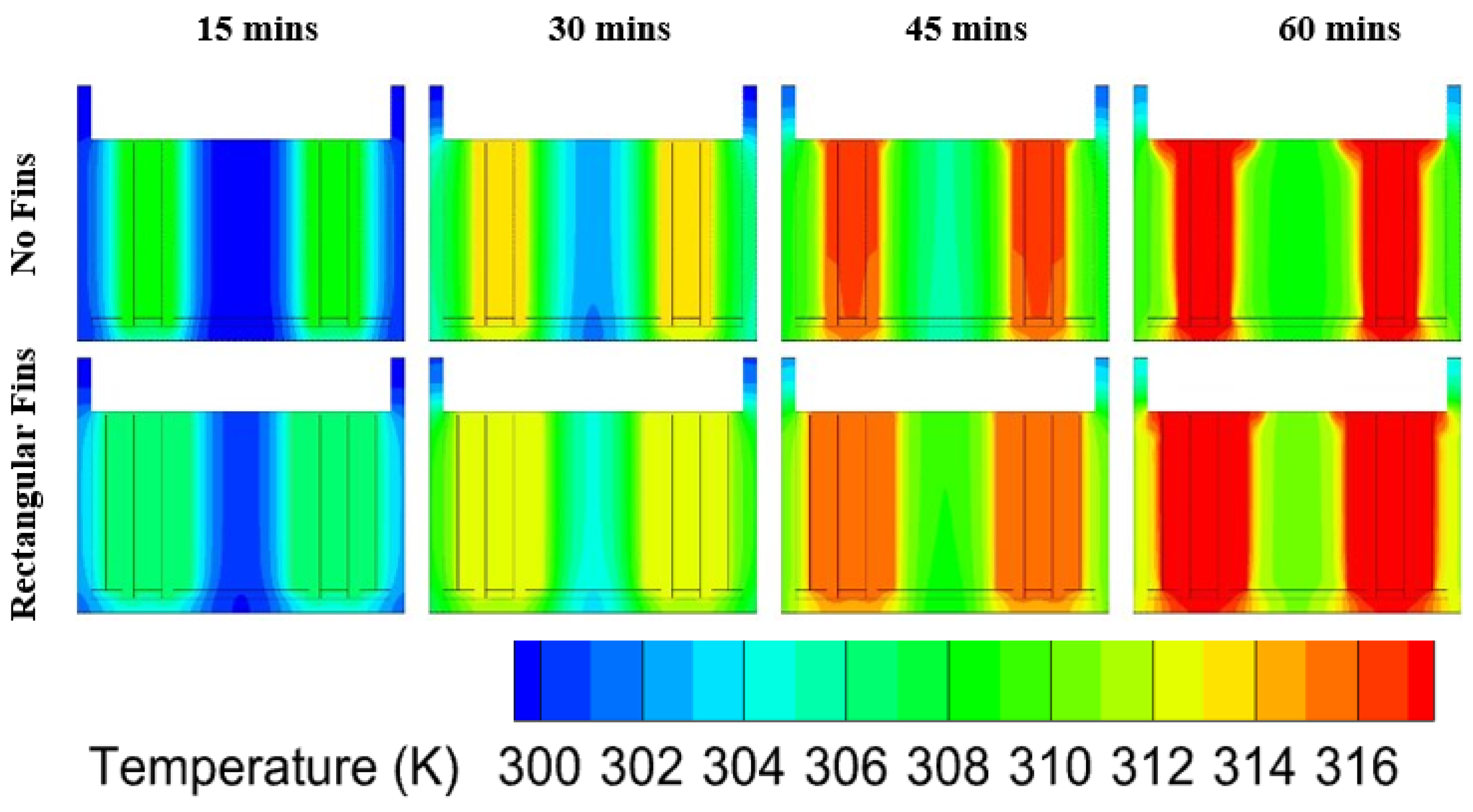
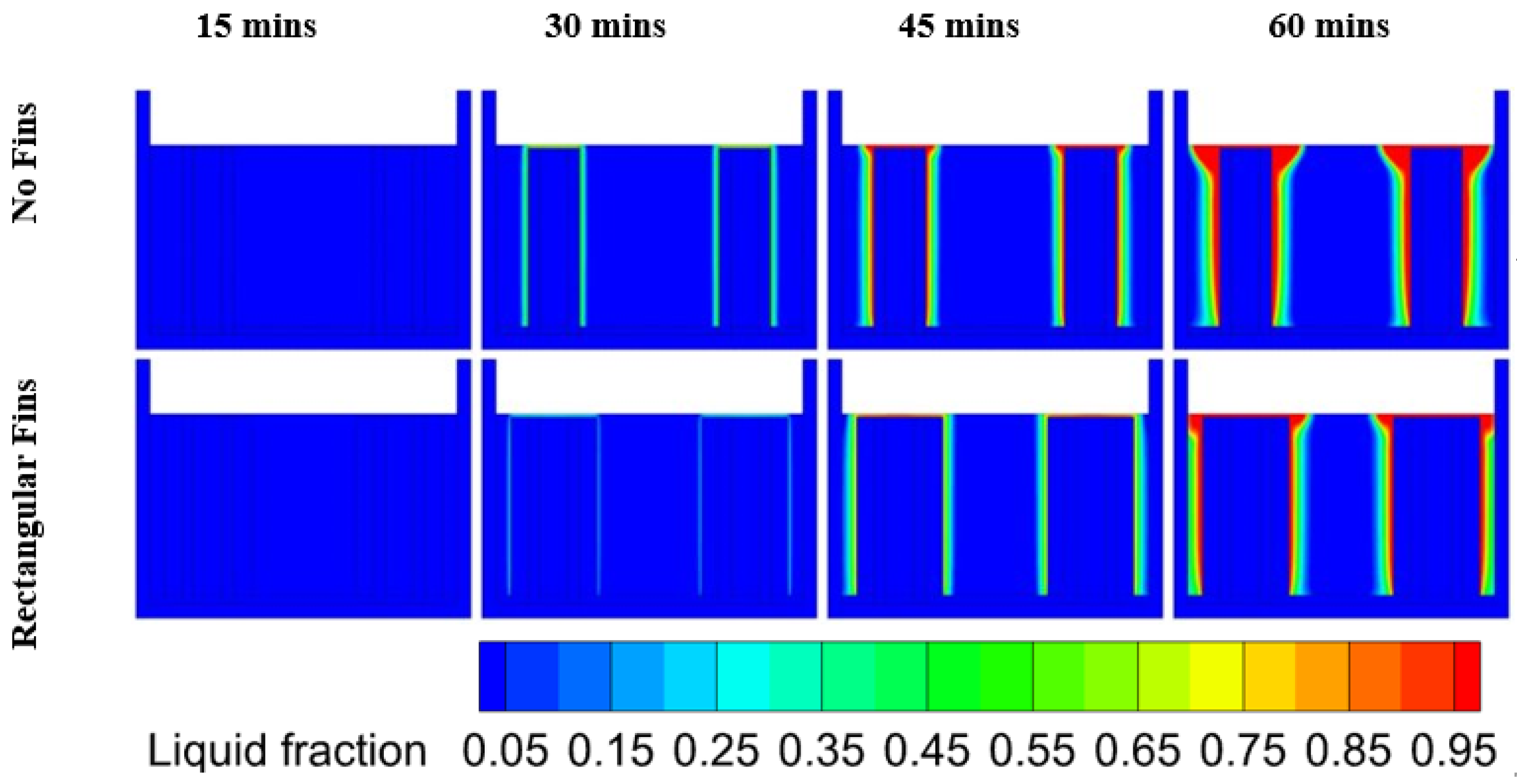
5. Thermal Performance of the BTMS
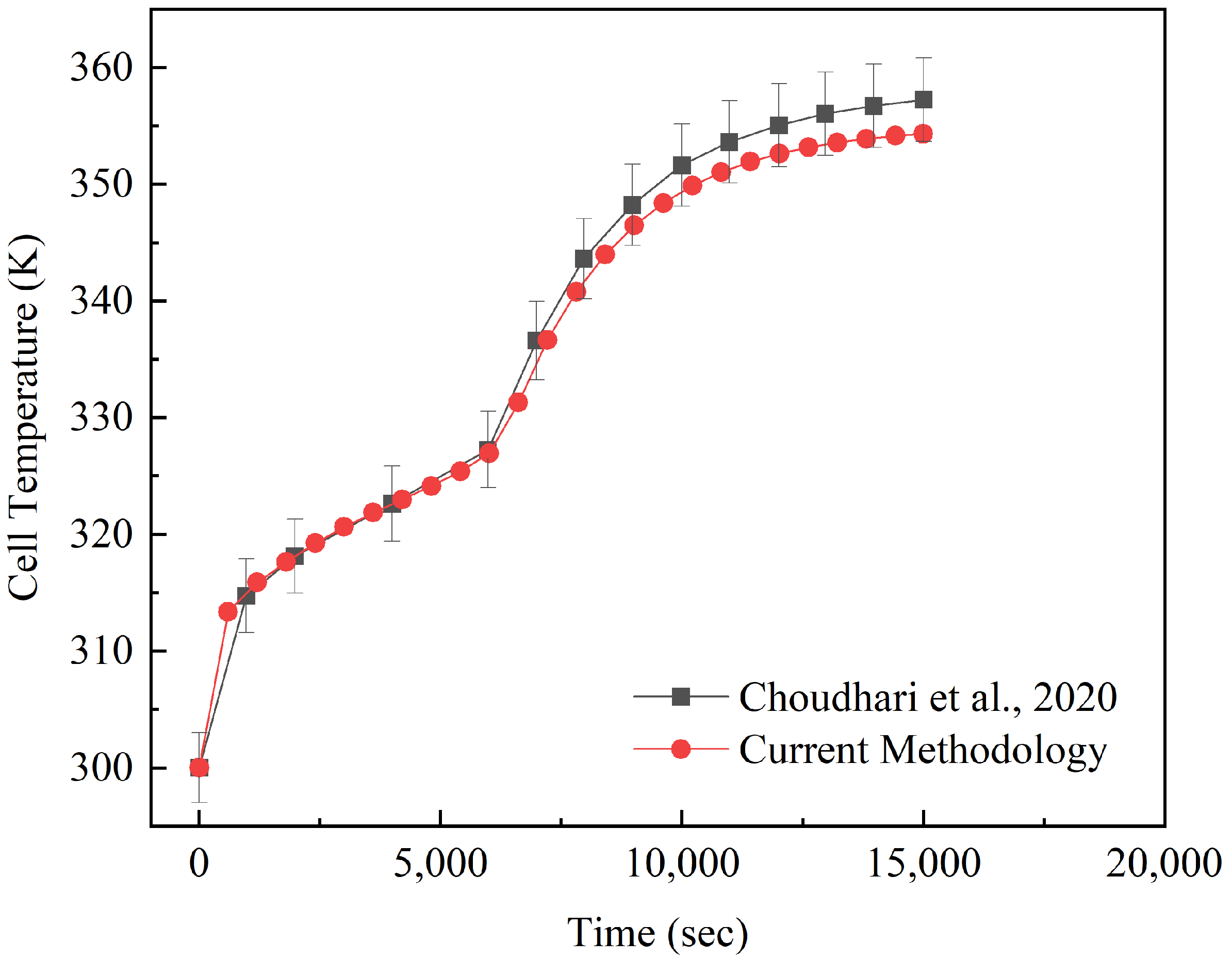
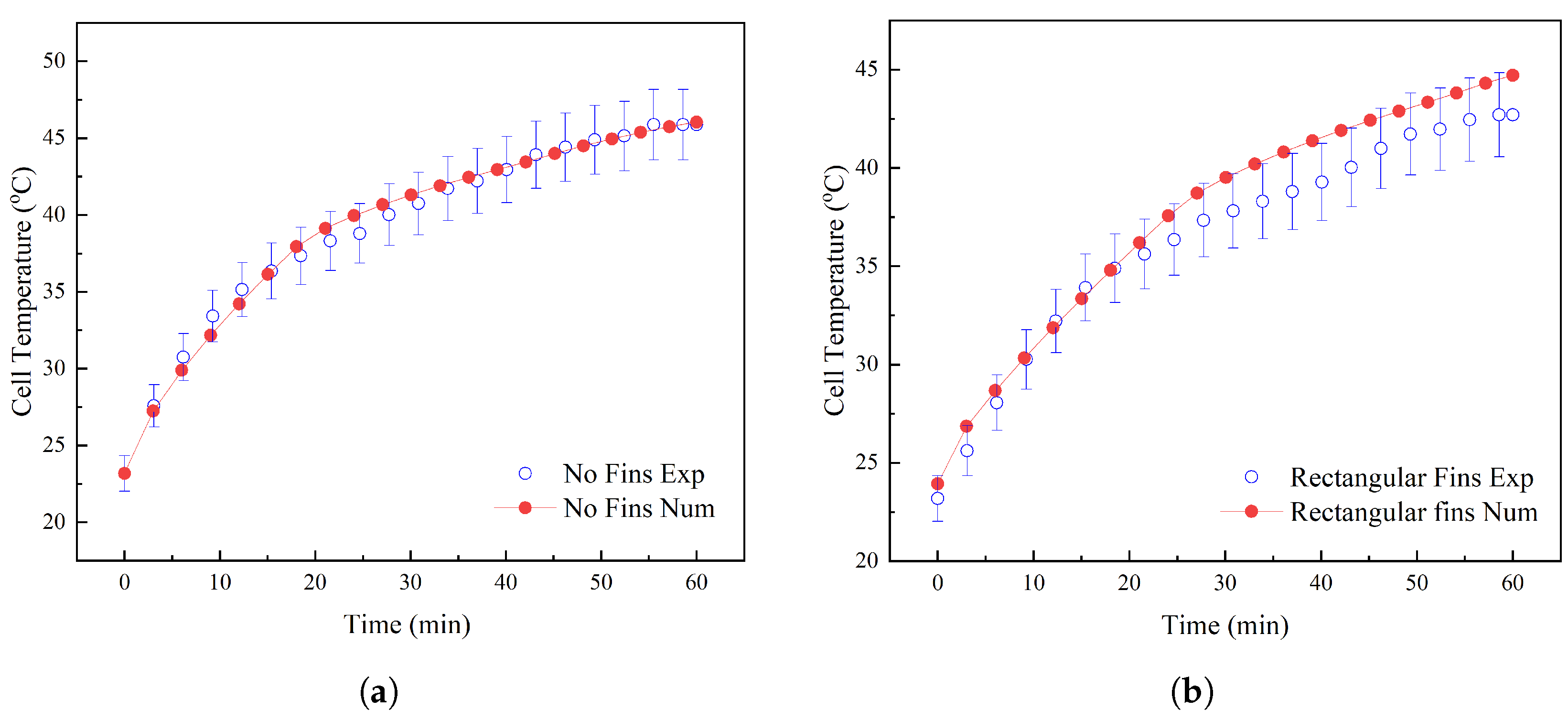
6. Comparison of Numerical and Experimental Results
6.1. Numerical Validation
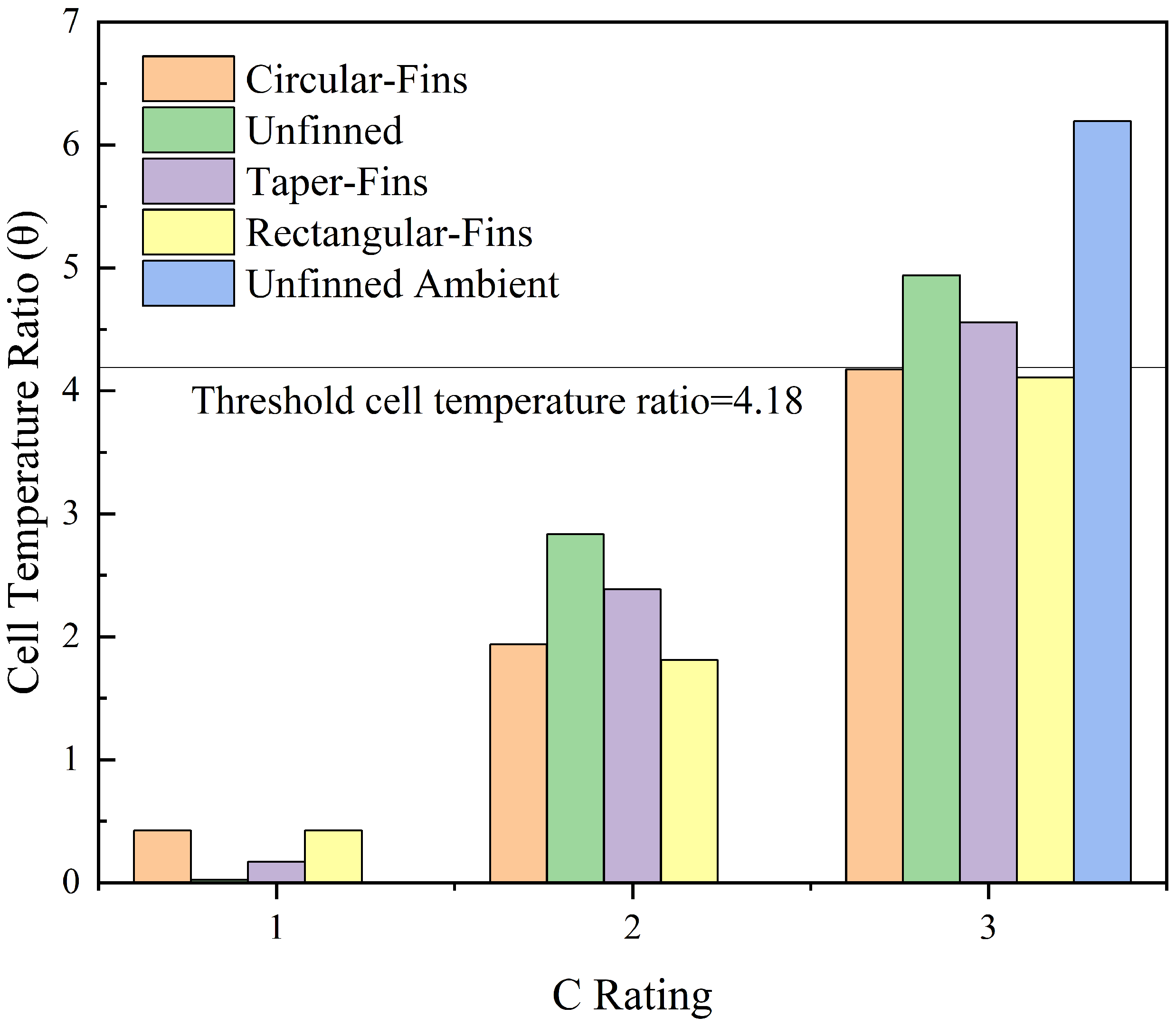
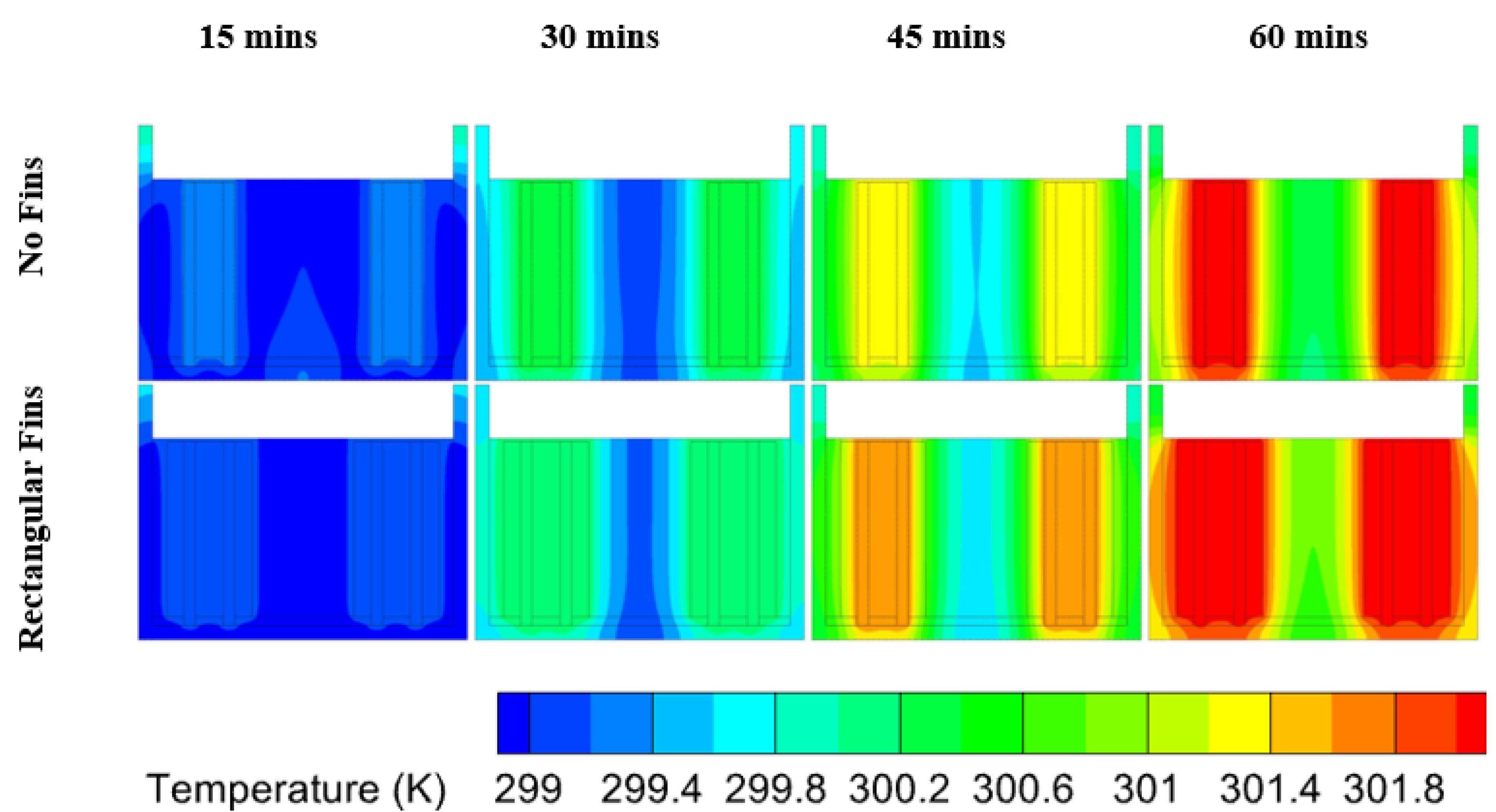
6.2. Heat Transfer in PCM at Different Discharge Rates
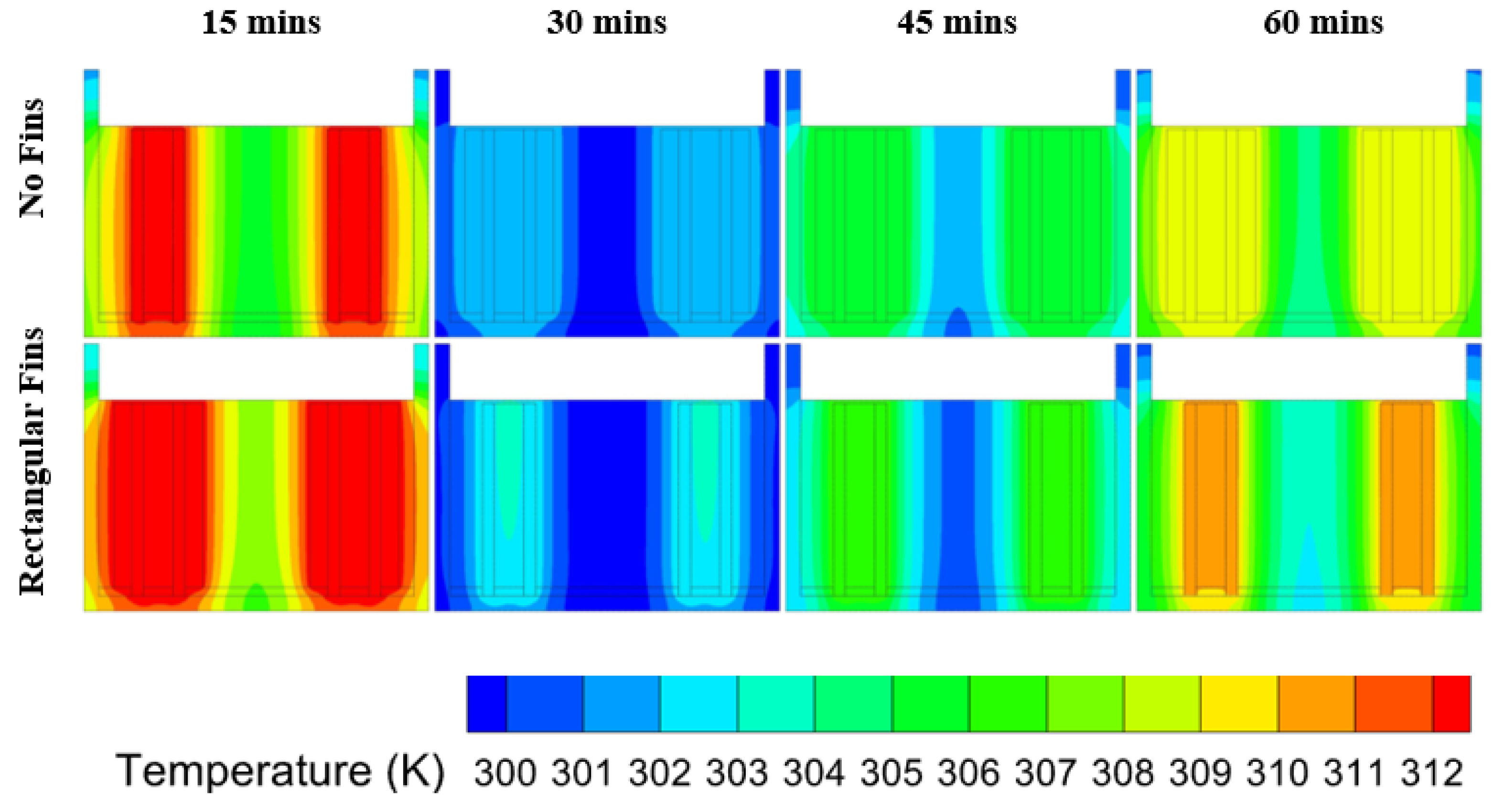
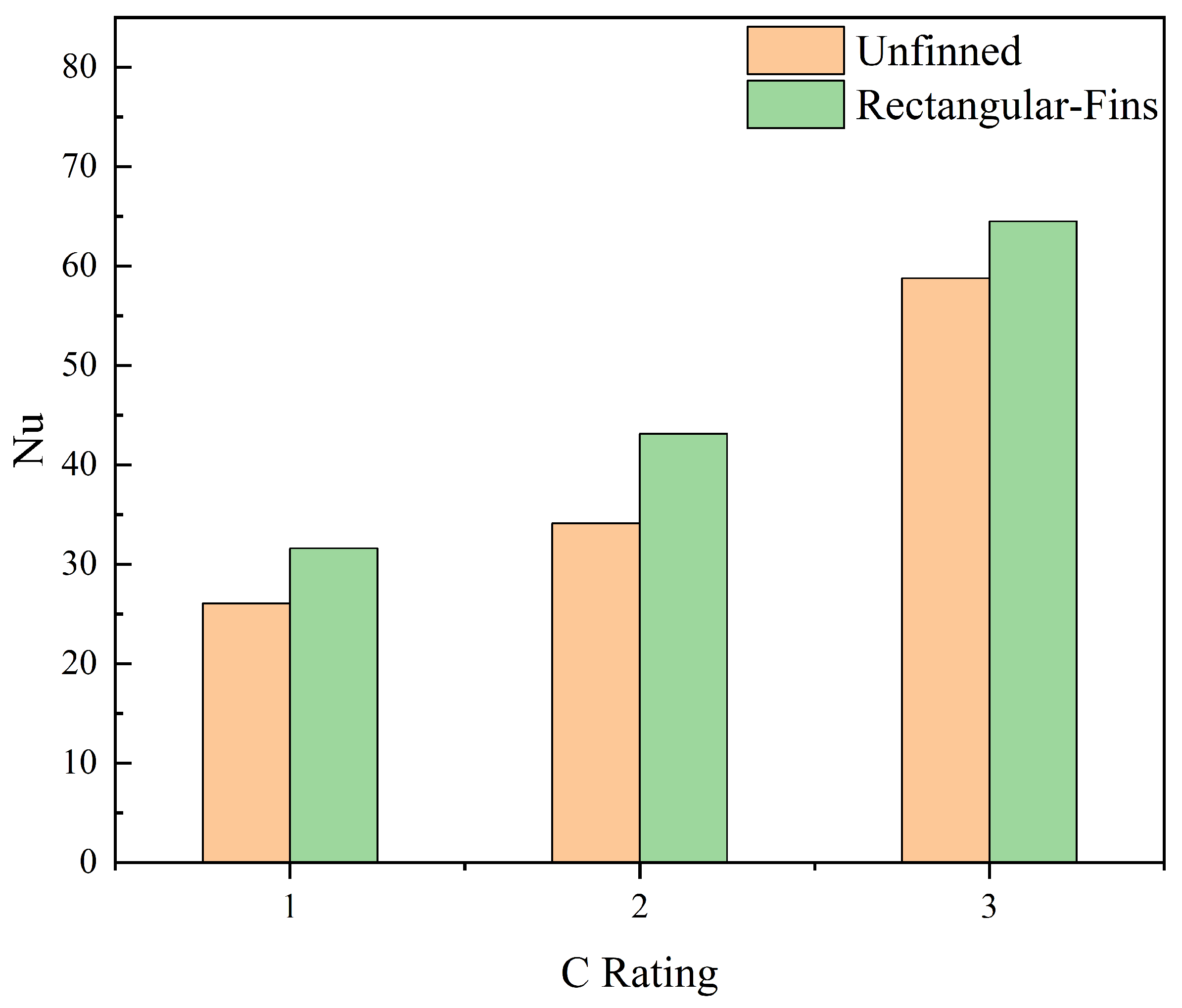
7. Average Nusselt Number and Heat Transfer Coefficient Variations
8. Conclusions
- The thermal performance at the 3C discharge rate for the unfinned case placed in natural convection compared to being placed in the PCM had a temperature enhancement of 9.44% at the time endpoint, while the naturally cooled system reached 40 C at 5.6 min and the system placed in the PCM reached 40 C at 28.42 min, which showed an enhancement in operating time of 185%;
- The optimal rectangular fin case produced the lowest temperatures at 60 min, which produced an operating time enhancement of 34.17% over the unfinned case, while the temperature enhancement for a 60-min cycle was 6.91%;
- During a complete cycle of 60 min, most of the cases exceeded the optimal cell temperature as heat accumulated due to the PCM having low thermal conductivity;
- Cases at the 1C and 2C discharge rates did not exceed the optimum cell temperature and the PCM remained in the conduction region for all the cases except the unfinned case;
- An improvement in Nusselt number of 9.72% was observed when the rectangular fin and unfinned cases were compared.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PCM | Phase change material |
| BTMS | Battery thermal management system |
| LIBs | Lithium-ion batteries |
References
- Chan, C.C. The state of the art of electric and hybrid vehicles. Proc. IEEE 2002, 90, 247–275. [Google Scholar] [CrossRef]
- Spiller, M.; Rancilio, G.; Bovera, F.; Gorni, G.; Mandelli, S.; Bresciani, F.; Merlo, M. A Model-Aware Comprehensive Tool for Battery Energy Storage System Sizing. Energies 2023, 16, 6546. [Google Scholar] [CrossRef]
- Hosen, M.S.; Youssef, R.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. Battery cycle life study through relaxation and forecasting the lifetime via machine learning. J. Energy Storage 2021, 40, 102726. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Source 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Youssef, R.; Hosen, M.S.; He, J.; Jaguemont, J.; Akbarzadeh, M.; De Sutter, L.; Van Mierlo, J.; Berecibar, M. Experimental and numerical study on the thermal behavior of a large lithium-ion prismatic cell with natural air convection. IEEE Trans. Ind. Appl. 2021, 57, 6475–6482. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Yang, T.; Yang, N.; Zhang, X.; Li, G. Investigation of the thermal performance of axial-flow air cooling for the lithium-ion battery pack. Int. J. Therm. Sci. 2016, 108, 132–144. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Xue, Q.; Sun, H.; Li, B.; Zou, H.; Yan, Y. Experimental investigation on EV battery cooling and heating by heat pipes. Appl. Therm. Eng. 2015, 88, 54–60. [Google Scholar] [CrossRef]
- Jaguemont, J.; Omar, N.; Van den Bossche, P.; Mierlo, J. Phase-change materials (PCM) for automotive applications: A review. Appl. Therm. Eng. 2018, 132, 308–320. [Google Scholar] [CrossRef]
- Ali, S.; Khan, M.M. Experimental Investigation of Battery Thermal Management System of Lithium-Ion Cells Using PCM. Eng. Proc. 2023, 45, 52. [Google Scholar]
- Lin, X.; Fu, H.; Perez, H.E.; Siege, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. Parameterization and observability analysis of scalable battery clusters for onboard thermal management. Oil Gas Sci. Technol. Rev. d’IFP Energ. Nouv. 2013, 68, 165–178. [Google Scholar] [CrossRef]
- Teng, H.; Ma, Y.; Yeow, K.; Thelliez, M. An analysis of a lithium-ion battery system with indirect air cooling and warm-up. SAE Int. J. Passeng. Cars Mech. Syst. 2011, 4, 1343–1357. [Google Scholar] [CrossRef]
- Motloch, C.G.; Christophersen, J.P.; Belt, J.R.; Wright, R.B.; Hunt, G.L.; Sutula, R.A.; Duong, T.; Tartamella, T.J.; Haskins, H.J.; Miller, T.J. High-power battery testing procedures and analytical methodologies for HEV’s. SAE Trans. 2002; 111, 797–802. [Google Scholar]
- Sabbah, R.; Kizilel, R.; Selman, J.; Al-Hallaj, S. Active (air-cooled) vs. passive (phase change material) thermal management of high power lithium-ion packs: Limitation of temperature rise and uniformity of temperature distribution. J. Power Source 2008, 182, 630–638. [Google Scholar] [CrossRef]
- Wei, Y.; Agelin-Chaab, M. Development and experimental analysis of a hybrid cooling concept for electric vehicle battery packs. J. Energy Storage 2019, 25, 100906. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Selman, J. A novel thermal management system for electric vehicle batteries using phase-change material. J. Electrochem. Soc. 2000, 147, 3231. [Google Scholar] [CrossRef]
- Chen, F.; Huang, R.; Wang, C.; Yu, X.; Liu, H.; Wu, Q.; Qian, K.; Bhagat, R. Air and PCM cooling for battery thermal management considering battery cycle life. Appl. Therm. Eng. 2020, 173, 115154. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Xia, X. Experimental investigation on the thermal behavior of cylindrical battery with composite paraffin and fin structure. Int. J. Heat Mass Transf. 2017, 109, 958–970. [Google Scholar] [CrossRef]
- Sun, Z.; Fan, R.; Yan, F.; Zhou, T.; Zheng, N. Thermal management of the lithium-ion battery by the composite PCM-Fin structures. Int. J. Heat Mass Transf. 2019, 145, 118739. [Google Scholar] [CrossRef]
- Zhao, Y.; Zou, B.; Li, C.; Ding, Y. Active cooling based battery thermal management using composite phase change materials. Energy Procedia 2019, 158, 4933–4940. [Google Scholar] [CrossRef]
- Weng, J.; Ouyang, D.; Yang, X.; Chen, M.; Zhang, G.; Wang, J. Experimental study on thermal behavior of PCM-module coupled with various cooling strategies under different temperatures and protocols. Appl. Therm. Eng. 2021, 197, 117376. [Google Scholar] [CrossRef]
- Safdari, M.; Ahmadi, R.; Sadeghzadeh, S. Numerical investigation on PCM encapsulation shape used in the passive-active battery thermal management. Energy 2020, 193, 116840. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Molaeimanesh, G.; Ranjbaran, Y.S. Improving the performance of a passive battery thermal management system based on PCM using lateral fins. Heat Mass Transf. 2019, 55, 1753–1767. [Google Scholar] [CrossRef]
- Youssef, R.; Hosen, M.S.; He, J.; Mohammed, A.S.; Van Mierlo, J.; Berecibar, M. Novel design optimization for passive cooling PCM assisted battery thermal management system in electric vehicles. Case Stud. Therm. Eng. 2022, 32, 101896. [Google Scholar] [CrossRef]
- Huang, R.; Li, Z.; Hong, W.; Wu, Q.; Yu, X. Experimental and numerical study of PCM thermophysical parameters on lithium-ion battery thermal management. Energy Rep. 2020, 6, 8–19. [Google Scholar] [CrossRef]
- El Idi, M.M.; Karkri, M.; Tankari, M.A. A passive thermal management system of Li-ion batteries using PCM composites: Experimental and numerical investigations. Int. J. Heat Mass Transf. 2021, 169, 120894. [Google Scholar] [CrossRef]
- Hémery, C.V.; Pra, F.; Robin, J.F.; Marty, P. Experimental performances of a battery thermal management system using a phase change material. J. Power Source 2014, 270, 349–358. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Farid, M.M.; Selman, J.R.; Al-Hallaj, S. Design and simulation of a lithium-ion battery with a phase change material thermal management system for an electric scooter. J. Power Source 2004, 128, 292–307. [Google Scholar] [CrossRef]
- Choudhari, V.; Dhoble, A.; Panchal, S. Numerical analysis of different fin structures in phase change material module for battery thermal management system and its optimization. Int. J. Heat Mass Transf. 2020, 163, 120434. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Olabi, A.; Maghrabie, H.M.; Adhari, O.H.K.; Sayed, E.T.; Yousef, B.A.; Salameh, T.; Kamil, M.; Abdelkareem, M.A. Battery thermal management systems: Recent progress and challenges. Int. J. Thermofluids 2022, 15, 100171. [Google Scholar] [CrossRef]




| Property | RT-42 | Aluminum | Acrylic | Ceramic Heaters |
|---|---|---|---|---|
| Solidus Temperature (C) | 38 | - | - | - |
| Liquidus Temperature (C) | 43 | - | - | - |
| Heat Storage Capacity (J/kg) | 165,000 | - | - | - |
| Specific Heat Capacity (kJ/kg·K) | 2 | 871 | 1300 | 850 |
| Solid Density (kg/m3) | 880 | 2719 | 1215 | 2630 |
| Liquid Density (kg/m3) | 760 | - | - | - |
| Thermal Conductivity (W/m·K) | 152 | 12 | ||
| Thermal Exp. Coefficient (K−1) | 0.0006 | - | - | - |
| Discharge Rate | Unfinned Case | Rectangular Fins | Taper Fins | Circular Fins |
|---|---|---|---|---|
| 1C | 0.023 | 0.42 | 0.17 | 0.42 |
| 2C | 2.83 | 1.81 | 2.38 | 1.94 |
| 3C | 4.94 | 4.11 | 4.56 | 4.18 |
| 3C Ambient | 6.19 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, S.; Khan, M.M.; Irfan, M. Thermal Performance Enhancement of Lithium-Ion Batteries Using Phase Change Material and Fin Geometry Modification. World Electr. Veh. J. 2024, 15, 42. https://doi.org/10.3390/wevj15020042
Ali S, Khan MM, Irfan M. Thermal Performance Enhancement of Lithium-Ion Batteries Using Phase Change Material and Fin Geometry Modification. World Electric Vehicle Journal. 2024; 15(2):42. https://doi.org/10.3390/wevj15020042
Chicago/Turabian StyleAli, Sarmad, Muhammad Mahabat Khan, and Muhammad Irfan. 2024. "Thermal Performance Enhancement of Lithium-Ion Batteries Using Phase Change Material and Fin Geometry Modification" World Electric Vehicle Journal 15, no. 2: 42. https://doi.org/10.3390/wevj15020042
APA StyleAli, S., Khan, M. M., & Irfan, M. (2024). Thermal Performance Enhancement of Lithium-Ion Batteries Using Phase Change Material and Fin Geometry Modification. World Electric Vehicle Journal, 15(2), 42. https://doi.org/10.3390/wevj15020042







